Belousov-Zhabotinsky type reactions: the non-linear behavior of chemical systems

Abstract

Chemical oscillators are open systems characterized by periodic variations of some reaction species concentration due to complex physico-chemical phenomena that may cause bistability, rise of limit cycle attractors, birth of spiral waves and Turing patterns and finally deterministic chaos. Specifically, the Belousov-Zhabotinsky reaction is a noteworthy example of non-linear behavior of chemical systems occurring in homogenous media. This reaction can take place in several variants and may offer an overview on chemical oscillators, owing to its simplicity of mathematical handling and several more complex deriving phenomena. This work provides an overview of Belousov-Zhabotinsky-type reactions, focusing on modeling under different operating conditions, from the most simple to the most widely applicable models presented during the years. In particular, the stability of simplified models as a function of bifurcation parameters is studied as causes of several complex behaviors. Rise of waves and fronts is mathematically explained as well as birth and evolution issues of the chaotic ODEs system describing the Györgyi-Field model of the Belousov-Zhabotinsky reaction. This review provides not only the general information about oscillatory reactions, but also provides the mathematical solutions in order to be used in future biochemical reactions and reactor designs.

1 Introduction

1.1 Historical background

The first evidence of chemical oscillations dates to the early nineteenth. These are the years of Lotka and Bray [1]. The former was the father of the well-known predator–prey mechanism. In 1910 he built up two kinetics mechanisms able to show self-sustained oscillations reactions [1]. The latter, during his work on the catalytic decomposition of hydrogen peroxide, he discovered the first real oscillating system: periodically variable concentrations of iodate ions and iodine were detected [2].

The discovery was, indeed, unlucky because of the difficulties in reproducing the system. The chemical scientific community retained oscillations impossible from a thermodynamic point of view and explained Bray’s data by the presence of solid impurities in the homogenous liquid media.

In the ‘50 s the soviet chemist B. P. Belousov was working on the Krebs cycle trying to reproduce it “in vitro”. He prepared a solution of bromate and cerium ions with citric acid and he noticed that after an induction period, the solution oscillated between colorless and yellow with a characteristic period. These were the colors of a solution containing respectively Ce (III) and Ce (IV) ions, a redox couple. Thus, the evidence brought the scientist to suppose periodic oscillations in the concentrations of the ions thanks to a series of redox reactions involving cerium oxidation states [3].

Belousov tried to publish his results. He enclosed his writings with photos and oscillographic measurements and sent them to two magazines in 1951 and 1957. They refused to publish, apparently without arguing a reason [4]. However, his writings were distributed in some Universities and research institutes of soviet Russia.

A few years later Zhabotinsky who graduated at the Moscow State University dealt with Belousov’s recipe which produced oscillations, advised by his biophysics professor. During his works, Zhabotinsky modified the recipe: he only preserved the bromate and substituted cerium with the complex Fe-phenantroline, also known as ferroin, and citric acid with malonic acid. The new system gave rise to oscillations between red and blue, typical colors of reduced ferroin and oxidized ferriin. Then, he proposed some steps of the reaction mechanism.

Zhabotinsky finally succeeded in publishing a report in the Russian magazine Biofizika, in 1964. He explained during an interview that his success was due to the “ignorance” of the biophysicists about the contrast between chemical homogenous oscillating systems and thermodynamics.

Belousov died in 1957 without reaching his aims. For years, the discovery was credited to Zhabotinsky without caring Belousov’s efforts. Nowadays the barriers imposed by ancient theories have been destroyed and the due to the scientist has been recognized.

1.2 Neghentropy concept, dissipative structures, chaos and Brusselator model

But, why did the scientific community refuse such a well reported work? At those times, most scientists faithfully followed the principles of thermodynamics and in this case, oscillations were apparently in contrast with the second principle. People were used to see a system evolving in a single direction, in order to increase its own entropy, for the same people, an oscillation was an inversion in this trend to return to the initial state. The solution was suggested by the Nobel Prize Ilya Prigogine. He used the concept of “Neghentropy”, introduced by Schrödinger in his assay “What is Life?” and underlined the validity conditions for the second principle of thermodynamics that is referred to isolated systems next to the equilibrium conditions [3]. Chemical oscillator reaction is a multicomponent and open system kept far from the thermodynamic equilibrium showingperiodic concentration changes in time and space [3]. An open reactive system is controlled by kinetic laws which at a certain non-linearity degree may show strange phenomena like bistability among two steady-states [3], deeply different from the presence of a single stable thermodynamic equilibrium. Entropy of these self-organizing systems seems to decrease but it is not true: even if parts of the system show this trend in time and/or space, in a general prospective they will increase their entropy [5].

Then, Prigogine focused his attention on what he called “dissipative structures”, patterns as spiral waves and propagating fronts formed in oscillatory systems [3]. This phenomenon occurs in spatially distributed media, with diffusion contributing to cause instability, and for highly non-linear systems. Considering these features, the scientist and his team developed a mathematical model called the “Brusselator” which allowed a simple study of oscillations.

In 1972 Field, Körös and Noyes after a deep study of the BZ reaction mechanism gathered the main steps of FKN mechanism. In order to study the behavior of the reaction and extend the main features of the Brusselator, the team developed a model called “Oregonator”. Then Field and Györgyi concentrated their attention on the generation of deterministic chaos from chemical oscillations and produced a more complex model with its four-variables simplification, as it is nowadays well known [6]. Chaos from chemical oscillations was also proved in the 80 s by analyzing data from experiments led into a CSTR reactor using a time delay reconstruction technique.

All these results have been particularly important in biology to extend the comprehension of organisms’ behavior. Oscillation in biochemical reactions is present in competitive inhibitions such as the glycolysis or in the regulation of the period of some metabolic processes. Self-organizing systems and birth of spatial patterns have been studied in biology to describe spots on animal furs or phenomena like slime-mold amoebae aggregation [7]. Eventually, chaos has been pointed out to be linked to ventricular fibrillation, occurring after a spiral wave is broken, into several others [8].

2 Belousov-Zhabotinsky reaction mechanism

2.1 Chemicals used in Belousov-Zhabotinsky reaction

Belousov-Zhabotinsky reaction includes several chemicals such as: oxidation agent, organic substrate, catalyst, ions and inorganic acid. Each of them is described as follow:

• 1. Oxidizing agent both scientists used bromates ions. It is an essential compound for the simple homogenous system.

• 2. Organic substrate Belousov used citric acid while Zhabotinsky the malonic acid. Some other derivatives have been exploited through the years.

• 3. Oxidation catalyst the catalyst will exchange one electron between the bromate and the substrate, consequently changing its oxidation number intermittently. Transition metals are particularly suitable for that, like manganese [9] and cerium, but do not present sharp visual changes. In order to better visualize oscillations, the solution must drastically change its color during the reaction, that is why Zhabotinsky used the complex ferroin. Some alternative systems have been studied such as “uncatalyzed” reactions containing certain aniline or phenol derivatives as organic substrates: the aromatic reactant substitutes the catalyst in exchanging electrons [10].

• 4. Ions Bromide ions are commonly used. Noszticzius carried on experiments on a simple BZ system by adding silver ions in order to keep bromide concentration low [10]. These results led to the evidence of “non-bromide control”. Another interesting variation to the recipe is the “minimal bromate oscillator” showing chemical oscillations in a system made of only bromate, bromide and catalyst [10].

• 5. Inorganic acid Acidity is an important parameter to control the kinetics of each reaction. In cerium-catalyzed systems it is commonly used sulphuric acid, but other systems have been coupled with nitric and perchloric acids [10]. Hydrogenion concentration has been taken into consideration for the Showalter-Noyes simplification of the Oregonator [11].

2.2 Reaction steps for Belousov-Zhabotinsky and FKN reactions

The overall reaction consists of broadly eight intermediate species and twenty reaction steps [1]. Belousov recognized and described some of them. First, the substrate was oxidized by the quadrivalent cerium present in the system with a change in the color of the solution. The following oxidation of the trivalent cerium constituted the rate limiting step. This happened owing to the production and accumulation in the media of bromide from the second reaction step. The bromide reacts with bromate in a fast chain reaction which produces bromine; the latter is captured by the first product of oxidation of the organic substrate, resulting in an acceleration of the oxidation rate of trivalent cerium. The process starts again and continues until citric acid and bromate are exhausted. This is what Belousov speculated [4]:

$${C}_{6}{O}_{7}{H}_{8}\left(citric\, acid\right)+{Ce}^{4+}\to {C}_{5}{O}_{5}{H}_{6}+{Ce}^{3+}+C{O}_{2}+{H}_{2}O$$

(1)

$$Br{O}_{3}^{-}+{Ce}^{3+}\to {Ce}^{4+}+{Br}^{-}$$

(2)

$${Br}^{-}+Br{O}_{3}^{-}+2{H}^{+}\to HBrO+HBr{O}_{2}$$

(3)

$${H}^{+}+{Br}^{-}+ HBrO\to 2{Br}_{2}+2{H}_{2}O$$

(4)

$${C}_{5}{O}_{5}{H}_{6}+5{Br}_{2}\to {C}_{3}OHBr\left(penta\, bromacetone\right)+5{Br}^{-}+2{CO}_{2}+5{H}^{+}$$

(5)

However, the most studied and suitable mechanism is the one described by Field, Körös and Noyes, called FKN mechanism. In 1972 the three scientists and their team had described the BZ reaction with the ten-steps mechanism [10, 12, 13] shown in Table 1.

Table 1 FKN Mechanism’s reaction scheme

Every reaction occurs simultaneously thus it was not easy to understand the mechanism step by step. Due to this simultaneity the proposals have been different through the years.

Let subdivide the FKN mechanism in three subprocesses. These are defined according to the factors that control the kinetics of the whole reaction, the concentrations of bromide and cerium ions. The subsequent reduction–oxidation and appearance-disappearance loops of those species determine the several rate-limiting steps that occur as time goes, by through the interaction of equilibrium and irreversible stages.

Process A occurs at high [${Br}^{-}$] values and causes its decreasing as show by Eq. (6), Stoichiometry (R1) - (R3):

$$\ Br{O}_{3}^{-}+5{Br}^{-}+6{H}^{+}\leftrightarrow 3{Br}_{2}+3{H}_{2}O$$

(6)

This reaction is the net stoichiometry of the first four steps of the FKN mechanism, but this was not the only proposal, in fact in Field and Burger (1985) [10] the steps (R1) − (R3) are coupled with (R8) obtaining:

(6) + (R8):

$$2{Br}^{-}+Br{O}_{3}^{-}+3{H}^{+}+3MA\to 3BrMA+3{H}_{2}O$$

(7)

This multiplicity of point of views shows the arbitrary nature of the subprocesses. The choice of (7) rather than (6) might be led by practical considerations: at the beginning of the experiment bromide salts and malonic acid are both injected into the reactor so that a not negligible effect is the one of bromination of the organic acid by bromide ions which causes an induction period. Hence, it may be quite interesting including (R8) in Process A mechanism.

Figure 1 represents the numerical solution of the Oregonator model, which consists in a simplification of the FKN mechanism, for bromide concentration, the kinetic leading factor. The kinetics of the process is sustainable for values of $\left[{Br}^{-}\right]>[{Br}^{-}{]}_{cr}$, differently the reaction rate of R2 becomes too small, and the prevailing process becomes Process B with R5. This one is an autocatalytic process in the sense that at a certain reaction step a reactant catalyzes its own production being reactant, product and catalyst. In this case it is bromous acid. An autocatalytic process shows a concentration sigmoid trend in time: at low concentrations of the key-compound the reaction rate is low, then the self-stimulated production of the same compound increases that value.

Fig. 1

Oscillations of [Br⁻] in time. Result from Simulink resolution of the Oregonator, corresponding to the set of parameters values: ε = 0.1, δ = 0.0004, q = 0.0008 and f = 1

The process broadly corresponds to (R5)–(R6) according to the overall reaction:

Net Stoichiometry (R5) − (R6):

$$ Br{O}_{3}^{-}+HBr{O}_{2}+2{Ce}^{3+}+3{H}^{+}\leftrightarrow 2HBr{O}_{2}+2{Ce}^{4+}+{H}_{2}O$$

(8)

Autocatalysis of bromous acid is evident from (8).

The mechanism involves radical species and redox mechanisms highlighted in (R5) − (R6). The $BrO_{2}^{ \cdot }$ is the plausible oxidant for Ce (III). The overall effect of the process is to activate a fast production of bromous acid when Process A is inhibited by the bromide concentration. Though, the accumulation of the acid is limited by its dismutation and by the cerium oxidation, which imposes a small equilibrium concentration to the acid, as depicted in Fig. 2:

Fig. 2

Oscillations of [HBrO₂] in time. Result from Simulink resolution of the Oregonator, corresponding to the set of parameters values: ε = 0.1, δ = 0.0004, q = 0.0008 and f = 1

Stoichiometry (R4)

$$2HBr{O}_{2}\leftrightarrow Br{O}_{3}^{-}+HBrO{ + H}^{+}$$

(9)

(8) + (9):

$$Br{O}_{3}^{-}+4{Ce}^{3+}+5{H}^{+}\leftrightarrow HBrO+4{Ce}^{4+}+{2H}_{2}O$$

(10)

At the beginning of the process, step (R5) is rate determining because of the low concentration of Ce (IV) and the steady-state concentration is $[HBrO_{2} ]_{{ss}} = k_{{{\text{R}}5}} /2k_{{{\text{R}}4}} \left[ {H^{ + } } \right]\left[ {BrO_{3}^{ - } } \right]$ [13]. The value is obtained in Field and Noyes (1974) [13] by considering the irreversible reaction equations of the Oregonator model corresponding to those of the FKN mechanism, that’s why the value doesn’t take into account some complex interactions which appear in the ten-reactions model.

$$\left|{r}_{4}\right|=2{k}_{O4}[HBr{O}_{2}{]}^{2}$$

(11)

$$\left|{r}_{O5}\right|={k}_{O5}\left[Br{O}_{3}^{-}\right]\left[{H}^{+}\right][HBr{O}_{2}]$$

(12)

At the stationary point $\left|{r}_{O4}\right|=\left|{r}_{O5}\right|$, where it comes the value of stationary bromous acid concentration.

The simplification of subprocesses is particularly useful in order to understand how bromide reaches its critical concentration and Process A switches to B. It is all due to the competition between bromate and bromide to react with bromous acid. During Process A, when bromide concentration is still high, the acid almost all reacts with the bromide according to step (R2). This reaction reduces bromide concentration which leaves the place to bromate reacting as shown in step (R5). The shift between the two processes occurs when the production rate of bromous acid in step (8) equals the depletion rate of step (R2), that is $[Br^{ - } ]_{{cr}} = k_{{R5}} /k_{{R2}} [BrO_{3}^{ - } ]$ [13]. During Process A the steady-state value of [HBrO₂] corresponds to $[HBrO_{2} ]_{{ss}} = k_{{R3}} /k_{{R2}} \left[ {H^{ + } } \right]\left[ {BrO_{3}^{ - } } \right]$ [13].

Process B theoretically ends when bromous acid and Ce (III) are exhausted, this gives rise to Process C. The high concentrations of ipobromous acid and Ce (IV) causes the oxidation of the organic compounds according to steps (R9)–(R10) with the influence of (R1) and (R8) [13]. On the whole, the process produces sufficient bromide to reinhibit Process B and it reinitializes the system by reducing the cerium ions. Figure 3 depicts a typical oscillating behavior of the cerium ions concentration.

Fig. 3

Oscillations of [Ce⁴⁺] in time. Result from Simulink resolution of the Oregonator, corresponding to the set of parameters values: ε = 0.1, δ = 0.0004, q = 0.0008 and f = 1

The most important simplification of the FKN model is the one of the Oregonator: Field’s team kept five steps of the mechanism in order to sum up the main features of the BZ reaction [13, 14] as described in Table 2. The expression of the reactions in Table 2 does not consider the hydrogenions as reactants in order to simplify the most the equations.

Table 2 Oregonator Model: reaction scheme.$X={HBrO}_{2},Y={Br}^{-},Z=Ce\left(IV\right)$, A and B are reactants and P, Q are products [12]

The model is a simplification of the whole reaction mechanism, but it has been deeply studied during the years because it is easy to handle and leads to different interesting results, that will be discussed in the following paragraphs.

In order to adapt the model to reality it has been introduced the parameter $f$ in the last step to sum up Process C. $f$ is a variable parameter depending on the bromination degree of malonic acid in cerium or ferroin-catalyzed system, according to a mechanism like:

$${Ce}^{4+}+MA+BrMA\to {Ce}^{3+}+f{Br}^{-}+\dots $$

(13)

The bromination degree is the number of moles of bromide ions produced by oxidation of malonic acid with a mole of quadrivalent cerium. It is directly linked to reactions like (R8) and is the first cause of the initial induction period during which $f$ increases, reaching the instability values of [${Br}^{-}$], which may give rise to oscillations [15].

$f$ has been used as a bifurcation parameter in mathematical modelling of the BZ reaction. It marks the transition between stationery and oscillations. One may note that the alternating steady states are yellow, at high $[Ce(IV)]$ and $[HBr{O}_{2}]$ and low $[{Br}^{-}]$, colorless otherwise, in case of absence of this transition, the system has reached the steady state. Hence, the parameter $f$ is deeply linked to oscillations rise. In some cases, the transition or bifurcation values have been computed to be around 0.5 and 2.4 [13, 15]. The computational method will be deeply discussed later.

A typical homogenous BZ system is made of quite common components like ions of transition metals, organic and inorganic acids. The real complexity of the system is linked to the interactions between these components in time and space. The aim of the analysis of the reaction mechanism is to highlight the difficulties in interpreting it and in representing it with a mathematical equation. To obtain a simple model, it is necessary to neglect some aspects with respect to others that in this case corresponds to isolating certain important reactions which sum up the main features of the evolving reactive media.

3 Oregonator model (The Oregonator (Orygunator) is the simplest realistic model of the chemical dynamics of the oscillatory Belousov-Zhabotinsky reaction)

3.1 General aspects of Oregonator model

In this section a stability study of the Oregonator model will be carried on in order to underline the mathematical conditions for an oscillating dynamic system [16]. Before considering the differential equations system, is convenient to described some important aspects. First, non-linearity in the kinetic equations which is often shown both in more than bimolecular reactions and in autocatalytic steps [3]. The process must be characterized by positive and negative feedback loops. The former increases the magnitude of small perturbations in terms of concentration in the system like autocatalysis does, the latter limits “explosions” caused by the positive feedback. The coupling may give rise to hysteresis. In this case the production of bromous acid is the positive feedback loop and its dismutation limits the exponential accumulation of the compound.

Non-linearity is necessary but not enough for showing oscillations: the system must be far from thermodynamic equilibrium. Such systems often show strange behavior like bistability. According to thermodynamics, the equilibrium is the only stable steady state which all isolated systems tend monotonically to converge. Bistability is described, instead, by the notion of quasi-stable state.

Considering the BZ reaction: it oscillates between red and blue if catalyzed by Fe-phenantroline. In this case, red and blue are properties of two different steady states characterized by certain concentrations of the key-species. The system can fix itself into one of the states, even if often there is a stronger one, and to absorb all the perturbations under a certain magnitude threshold. If the perturbation exceeds this value, the system will approach another quasi-stable state or will oscillate between them [17]. From that, it is evident the definition of bistable and excitable system.

3.2 Mathematical description of Oregonator model; stability, Hopf bifurcation, Poincaré-Bendixson theorem and Terman-Wang oscillator

Now, it will be shown how these features affects the Oregonator behavior. The model has been described in the previous paragraph, but the stability study requires an ODEs system, for that the kinetic equations are needed:

$$\frac{dX}{dt}={k}_{O1}AY-{k}_{O2}XY+{k}_{O3}AX-2{k}_{O4}{X}^{2}$$

(14)

$$\frac{dY}{dt}=-{k}_{O1}AY-{k}_{O2}XY+f{k}_{O5}BZ$$

(15)

$$\frac{dZ}{dt}={k}_{O3}AX-{k}_{O5}BZ$$

(16)

The reactions are treated as irreversible and the acidity effects are included in the rate constants. In this way it results $A={BrO}_{3}^{-},B=BrMA$. X, Y and Z are the variables of the model [13]. In this writing it will be followed the trace of Pulella (2009) [14] and the system is adimensionalized according to Tyson:

$$\left\{\begin{array}{c}\varepsilon \frac{d\xi }{d\tau }=a\xi +qa\eta -{\xi }^{2}-\xi \eta \\ \delta \frac{d\eta }{d\tau }=-qa\eta +fb\rho -\xi \eta \\ \frac{d\rho }{d\tau }=a\xi -b\rho \end{array}\right.$$

(17)

where the scaling factors are reported in Table 3 and: $\varepsilon = k_{{O5}} B_{0} /k_{{O3}} A_{0} \$ = 0.10,\;\delta = 2k_{{O5}} k_{{O4}} B_{0} /k_{{O2}} k_{{O3}} A_{0} = 0.0004,$

Table 3 Scaling factors of the simplified Oregonator (Tyson simplification). A₀ = B₀ = 1 M

$q = 2k_{{O1}} k_{{O4}} /k_{{O2}} k_{{O3}} = 0.0008\;{\text{and}}\;f = 1$. During all the analysis $a$ and $b$ will be kept constants and at unitary value, since they reflect concentrations imposed at the beginning of each experiments and supposed not to vary in a large range of values, if sufficiently high. In order to obtain the following simplification of the equations:

$$ \left\{ \begin{array}{l} \varepsilon \frac{{d\xi }}{{d\tau }} = \xi + q\eta - {\xi ^2} - \xi \eta \\ \delta \frac{{d\eta }}{{d\tau }} = - q\eta + f\rho - \xi \eta \\ \frac{{d\rho }}{{d\tau }} = \xi - \rho \end{array} \right. $$

(17bis)

Before starting the stability study, what is stability? The term refers to a steady state which a system returns to after applying a perturbation. A perturbed system reaches its stable steady state in different ways according to its properties and to the environment conditions: it can “directly” approach it or it can oscillate around this state with less and less extensive oscillations. Think of the harmonic oscillator made of a moving body anchored to a wall through a spring: depending on the magnitude of the extensive external impulse, the body moved away from its stable state will return to it by only a stage of compression of the spring or by a series of extension-compression stages. These dynamical systems are studied in their evolution in time and the spectrum of possible behaviors and complexities is due to their dimension, that is the number of variables necessary to describe them in a model. 2D systems evolution trajectories, built by a series of points that are the subsequent states reached, can be plotted and analyzed in the so called “phase plane”, where time does not appear [5]. To provide an example: the two ways of a system reaching the stable steady state, which have previously introduced, are represented into the phase plane as a bundle of parables sharing their summits, that is the equilibrium condition, or as spiral trajectories collapsing in a stable point [18]. These constructions are called “stable node” and “stable focus” [5, 18].

By increasing the dimension, it is enlarged the spectrum of evolutions. Particularly interesting is the limit cycle attractor birth, shown by n-dimensional systems with $n\ge 2$ [18]. A limit cycle, that is a closed curve, originates from an unstable focus which decreases with time the distance between different spiral trajectories [18]. It corresponds to constant amplitude oscillations. A limit cycle is defined attractor if both internal and external trajectories goes towards its border.

From a mathematical point of view the eigenvalues of the Jacobean matrix corresponding to the linearized system must be conjugate complexes, in order to obtain a focus. In this case the transition from stability to instability is called “Hopf bifurcation” [18, 19]. Thus, when an Hopf bifurcation occurs there is a change in the direction of the evolution from stable to unstable, but this doesn’t mean coming across an oscillating behavior. In order to find a limit cycle in the phase plane, the Poincaré-Bendixson theorem is particularly suitable for 2D systems because for higher dimensions the theorem does not ensure the proof of oscillations birth [5].

This proof can also be obtained by numerical integration of the ODEs system with certain parameters. This has been done with Simulink, whose block scheme is depicted in Fig. 4, and a phase portrait showing limit cycle behavior is represented in Fig. 5.

Fig. 4

Simulink flow scheme for the Oregonator resolution. Three-variables system obtained by Tyson adimensionalization with parameters values: ε = 0.1, δ = 0.0004, q = 0.0008 and f = 1

Fig. 5

Phase portrait of the Oregonator solved in unstable conditions

Now the bifurcation conditions are analyzed, and the limit cycle behavior sought. The system is simplified by applying a quasi-steady state approximation and considering that $\delta \ll \varepsilon$. The low value of δ imposes to the variable η to quickly reach the steady state, thus it is assumed to have already reached it. The system becomes [20]:

$$ \left\{ \begin{gathered} \varepsilon \frac{{d\xi }}{{d\tau }} = \xi + q\eta - \xi ^{2} - \xi \eta \hfill \\ \eta \sim\frac{{f\rho }}{{q + \xi }} \hfill \\ \frac{{d\rho }}{{d\tau }} = \xi - \rho \hfill \\ \end{gathered} \right.$$

(18)

Then, the Jacobean matrix from the linearization of the system is needed:

$$ J = \left| {\begin{array}{*{20}l} {1/\varepsilon \left( {1 - 2\xi - \frac{{qf\rho }}{{(q + \rho )^{2} }}} \right)} \hfill & {\frac{{f\left( {q - \xi } \right)}}{{\varepsilon \left( {q + \xi } \right)}}} \hfill \\ 1 \hfill & { - 1} \hfill \\ \end{array} } \right|$$

(19)

The matrix must be evaluated in the stationary solutions of the problem, normally two stables and one unstable. From this it comes bistability.

$$\left\{\begin{array}{c}\xi =(0, \frac{\left(1-f-\mathrm{q}\right)+\sqrt{{\left(1-f-\mathrm{q}\right)}^{2}+4\mathrm{q}\left(f+1\right)}}{2}, \frac{\left(1-f-\mathrm{q}\right)-\sqrt{{\left(1-f-\mathrm{q}\right)}^{2}+4\mathrm{q}\left(f+1\right)}}{2}\\ \rho =\xi \end{array}\right.$$

(20)

where the third term is physically non-sense because of its negative value. Consider that also according to the value of f, the terms f-dependent may have or not a physical meaning. Figures 6, 7 show the trend of the real and imaginary parts of the eigenvalues associated to the linearized system for the non-null stationary.

Fig. 6

Real parts of the eigenvalues of the Jacobian matrix of the simplified Oregonator as a function of the bifurcation parameter f. The instability region is highlighted and corresponds to positive real parts of the eigenvalues

Fig. 7

Imaginary parts of the eigenvalues of the Jacobian matrix of the simplified Oregonator as a function of the bifurcation parameter f. The figure helps to distinguish an unstable node from an unstable focus in presence or not of null imaginary parts

This representation helps to single out an instability region and to distinguish node, from focus, from saddle behavior. From the figures it emerges clearly a correlation between instability and $f$: it rises for values of $0.5<f<\mathrm{2,4}$ as it was said in Sect. 2. Then, unstable focus turns into unstable node and returns to a focus.

A direct consequence of the Poincaré-Bendixson theorem is employed to show the formation of a limit cycle in a phase plane. The simplified Oregonator will be used as a model and f will be set to $f=0.55$, for stability and graphical issues.

The necessity is to draw a close surface around a repellor stationary state which does not contain it, so that the flux of trajectories crossing its boundary is always directed towards the inland. If such a surface can be drawn around the stationary state $SS=\left( \frac{\left(1-f-\mathrm{q}\right)+\sqrt{{\left(1-f-\mathrm{q}\right)}^{2}+4\mathrm{q}\left(f+1\right)}}{2}, \frac{\left(1-f-\mathrm{q}\right)+\sqrt{{\left(1-f-\mathrm{q}\right)}^{2}+4\mathrm{q}\left(f+1\right)}}{2}\right)$ set as an unstable focus, according to f value, this implies the existence of a limit cycle and then of oscillations. The other two are not considered because $SS=(\mathrm{0,0})$ is not interesting from a practical point of view while the other has negative coordinates.

The construction of the trapping region is carried out by a trial and error method for determining the slope of the segment of the broken line. The iteratively applied condition is that the scalar product between the perpendicular to the segment and the directions of the trajectories in each point of the segment is negative:

$$ (c_{1} ,c_{2} ) \cdot (\dot{\xi },\dot{\rho }) < 0 $$

(21)

First, the nullcline must be drawn by setting the two derivative terms to zero [21]. Then a rough analysis of the directions of the trajectories in the four principal sections of the phase plane has been done, obtaining what is shown in Fig. 8.

Fig. 8

Flow map of the simplified Oregonator with reference to the nullclines. Rough representation of the trajectories around the steady state (SS)

It is possible by computing the signs of the derivative terms in each region between the nullclines and by imagining the trajectories built by an infinite number of local tangential direction-vectors.

Figure 9 shows the trapping region of the Poincaré-Bendixson theorem in the phase plane of the simplified Oregonator with respect to its nullclines. The slopes and positions of the segments of the broken external boundary of the region are pointed out:

Fig. 9

Construction of the trapping region around the steady state. Proof of the existence of an oscillating behavior for the simplified Oregonator, according to the Poincaré-Bendixson theorem

I segment: $\rho =0.5\xi$ ( $\left({c}_{1},{c}_{2}\right)=(0.5,-1))$.

The geometrical condition turns into:

$$0.5\left(\xi \left(1-\xi \right)+\frac{f\left(q-\xi \right)}{\left(q+\xi \right)}\rho \right)-\xi +\rho <0$$

(22)

Which is surely verified by the line from $(\mathrm{0,0})$ to the intersection with the ξ-nullcline. It was not valid for all the first section under both the nullclines, that is why it has not been drawn a segment linking the curves directly.

II segment: $\xi =0.726$ ($\left({c}_{1},{c}_{2}\right)=(\mathrm{1,0})$).

III segment: $\rho =0.8\xi +0.15$ ($\left({c}_{1},{c}_{2}\right)=(\mathrm{0.2,1})$).

In this case the condition turns into:

$$\rho >\frac{{0.2\xi }^{2}-1.2\xi }{0.2\frac{f\left(q-\xi \right)}{\left(q+\xi \right)}-1}$$

(23)

Considering the negativity of the denominator. It is valid for all the third section, thus, it has been chosen a segment tangential to the ξ-nullcline, for simplicity. The slope of the segment has been found graphically to be around 0.8.

IV segment: $\xi =0.283$ ($\left({c}_{1},{c}_{2}\right)=(-\mathrm{1,0})$).

V segment: $\rho =-x+0.566$ ($\left({c}_{1},{c}_{2}\right)=(-1,-1)$). The broken line is closed with a segment chosen to be always crossed by trajectories directed towards the inland.

The surface is concluded by excluding the stationary state in order to respect the hypothesis of the theorem, with an arbitrarily small circle.

In the simplified Oregonator one notice that the derivative term in ξ is multiplied by a parameter ε which can assume little values, like in our case. A similar evidence had justified the quasi-steady state simplification. Little values of the parameter accelerate the variation of [HBrO₂] causing relaxation oscillation. A relaxation oscillator consists in periodic evolution of two variables acting on two different time scales [22]: one fast, one slow. On the phase plane the trajectories are imposed by the value of ε: ξ and ρ vary in order to keep close to the fast manifold, that is the ξ-nullcline, and when this is not possible there are rapid jumps in ξ. This is a periodic repetition of aperiodic phenomena which exhibits discontinuous jumps.

In Fig. 10 the nullclines of the Terman-Wang oscillator are shown [22]. The oscillator has been chosen to simply represent a typical trajectory of a relaxation oscillator due to the shape of the equilibrium curves but also to introduce the concept of excitability. Varying the parameters of the model the system turns from exhibiting a single stationary state to three. The stable one, pointed as P, in Fig. 11, is an excitable state [23]. Excitability is characterized by small response to small perturbations while a large amplitude excursion for perturbations of magnitude above a threshold value, response that is directly linked to hysteresis [10]. This is a common mechanism to induce morphogenesis and oscillations in a BZ system set in stationary state.

Fig. 10

Typical trajectory of a relaxation oscillator with reference to the nullclines of the Terman-Wang oscillator. Qualitative representation. Adapted from [22]

Fig. 11

Excitable state (P) of the Terman-Wang oscillator. Motion of the nullclines according to the parameters of the model causes changes in the number of steady states. Qualitative representation. Adapted from [22]

4 Applications of the BZ reaction

4.1 Pattern formation

All the discussion carried on till now did not consider the experimental practice apart from mentions about open and close systems. Concentration and color oscillations are phenomena rising in common CSTR or Batch reactors and these configurations are normally coupled with a mixing mechanism in order to avoid inhomogeneities. Though, the complexity of the BZ reactive media is not limited to these evidences. The experiment can be achieved into an unstirred Petri dish with a thin layer of reactive phase: the consequences of this choice are noteworthy. The introduction of diffusional matter transport phenomena coupled with the reaction feedback loop and a perturbation give rise to morphogenesis in form of waves and spatial patterns [20].

The concept of wave is linked to the moving of a border between an excited and a recovered state [10]. A wave front in the BZ reactive media with Fe-phenantroline propagates from a leading center in form of concentric circles of oxidation, that are blue patterns rich in Fe³⁺ in a red media containing Fe²⁺ [10]. These concentration waves are also characterized by annihilation after collision [10]. We refer to them as “travelling waves” implying invariance in shape, wave speed and concentration features [24]. The birth of these geometrical figures into chemical and biological systems have been studied for years, but the studies of Alan Turing are particularly important and exemplified by his “The chemical basis of morphogenesis” [25].

The BZ reaction shows different undulatory behaviors. Firstly, propagating fronts, but an explanation of what they are is required: they are advancing transition zones which leave the system in different conditions with respect to the starting state [10]. Imagine having blocked the BZ media in a red stationary state. By applying a step perturbation to the system of normalized magnitude equal to the distance between the stationaries, after a certain period the media will be completely blue. The concept is schematically represented in Fig. 12.

Fig. 12

Qualitative scheme of a propagating step front in a BZ reactive medium. The perturbation leaves the systems in a new steady state characterized by blue

This is applicable only to models whose possible solution is a wave function as $f\left(x,t\right)=\phi (kx\pm ct)$, where k is the wave number, c is the frequency which gives information about the propagating speed and the signs depend on the propagating direction of the wave [26].

It has been used by Murray a different form of the Oregonator, to describe fronts, which in certain conditions can be approximated by a typical Fisher-Kolmogorov equation of the form.

$\frac{\partial \xi }{\partial t}=\frac{{\partial }^{2}\xi }{\partial {s}^{2}}+b\xi (1-\xi )$ [7]:

$$ \left\{ \begin{aligned} \frac{{\partial \xi }}{{\partial t}} &= \frac{{\partial ^{2} \xi }}{{\partial s^{2} }} + \xi (1 - \xi - r\eta ) \hfill \\ \frac{{\partial \eta }}{{\partial t}} &= \frac{{\partial ^{2} \eta }}{{\partial s^{2} }} - b\xi \eta \hfill \\ \end{aligned} \right. $$

(24)

By substituting a wave solution like $\phi \left(\gamma \right)$ with $\gamma =u+ct$ one obtains:

$$\left\{\begin{array}{l}{\mathrm{f}}^{{^{\prime}}{^{\prime}}}-c{\mathrm{f}}^{{^{\prime}}}+f\left(1-\mathrm{f}-r\mathrm{g}\right)=0\\ {\mathrm{g}}^{{^{\prime}}{^{\prime}}}-c{\mathrm{g}}^{{^{\prime}}}-bfg=0\end{array}\right.$$

(25)

With boundary conditions $\mathrm{f}\left(\infty \right)=\mathrm{g}\left(-\infty \right)=1\mathrm{ and f}\left(-\infty \right)=\mathrm{g}\left(\infty \right)=0$.

The wave function satisfies the equations of the system with a wave speed bounded in the following way [7]:

$$ \left( {\left( {r^{2} + {\raise0.7ex\hbox{${2b}$} \!\mathord{\left/ {\vphantom {{2b} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} - r} \right)\left( {2\left( {b + 2r} \right)} \right)^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \le c \le 2 $$

(26)

Another form of propagating wave is the one which leaves the system in the initial stationary. The reactive phase suffers from a pulse perturbation, then, if it is in its excitable state and the perturbation exceeds a certain threshold value, the system propagates it [10]. A brief explanation of the phenomenon is given below.

With the classical wave solution approach, it is obtained a system in the form [7]:

$$\left\{ \begin{array}{l} D{f^{\prime \prime }} - c{f^\prime } + f\left( {1 - f} \right) + \frac{{f\left( {q - \xi } \right)}}{{\left( {q + \xi } \right)}} = 0\\ D{g^{\prime \prime }} - c{g^\prime } + f - g = 0 \end{array} \right. $$

(27)

By setting certain parameters in order to stress the shape of the nullclines near the stationary state Fig. 13 has been obtained [27].

Fig. 13

a Qualitative representation of a propagating pulse in a BZ reactive medium referred to ξ and ρ variables. b Close trajectory directed to the stationary state and designed on the phase plane of the simplified Oregonator corresponding to a perturbation exceeding the threshold value

It depicts a pulse whose shape is linked to the characteristics of the phases of the dynamic evolution of the system along the nullclines. The shape of the pulse is directly linked to the position of the turning points from slow to fast motion of the closed trajectory. It corresponds to the solution of a linearized system of PDE with wave solution substitution such as in Field and Burger (1985) [10]. During the jumps D-A and B-C the variable ξ is the only one to vary, while ρ keeps almost constant; the opposite happens for the segment C-D.

The combination of front and pulse gives rise to the so-called “wave trains” [7].

Waves propagating in a BZ media may assume other shapes like spirals⁸ which are always associated to the Belousov-Zhabotinsky reaction, and in a 3D system “scroll waves” [10].

Though, propagation in space is not the only feature of pattern formation for reaction–diffusion systems. Turing highlighted a diffusion driven instability mechanism giving rise to stationary patterns, stripes, dots schematically represented in Fig. 14.

Fig. 14

Schematic appearance of a Turing pattern in form of dots alternating with the same period. Adapted from [10]

These are particular, since they oscillate between two stationaries in finite regions surrounded by others in opposite phase but oscillating with the same period.

Turing outlined four conditions for this diffusion-driven instability phenomenon. His analysis starts from the spatial homogeneous system and imposes a stability condition in order to find when diffusion turns it into unstable [7]. In our case, this is possible by computing the Jacobian matrix of the simplified Oregonator applying a linear analysis for the Turing bifurcation [28,29,30]:

$$J=\left|\begin{array}{cc}{\mathrm{f}}_{\xi }& {\mathrm{f}}_{\rho }\\ {\mathrm{g}}_{\xi }& {\mathrm{g}}_{\rho }\end{array}\right|$$

(28)

Schematized in this way for simplicity. The system will be stable for eigenvalues having $Re<0$, that corresponds to the two conditions: $Tr\left(J\right)<0,Det\left(J\right)>0$. It results:

$${\mathrm{f}}_{\xi }+{\mathrm{g}}_{\rho }<0$$

(29)

$${\mathrm{f}}_{\xi }{\mathrm{g}}_{\rho }-{\mathrm{f}}_{\rho }{\mathrm{g}}_{\xi }>0$$

(30)

Now it is necessary to consider the system with diffusion and to investigate the way it replies to a generic perturbation. Considering $U=\left(\delta \xi ,\delta \rho \right)={U}_{0}{e}^{\lambda t}\mathrm{cos}(kx)$. The perturbation will propagate according to the law:

$${U}_{t}=JU+{DU}_{xx}$$

(31)

$$\lambda U=[J-D{k}^{2}]U$$

(32)

With:

$$ D = \left| {\begin{array}{*{20}c} 1 & 0 \\ 0 & \sigma \\ \end{array} } \right|, \sigma = {\raise0.7ex\hbox{${D_{\rho } }$} \!\mathord{\left/ {\vphantom {{D_{\rho } } {D_{\xi } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{\xi } }$}} $$

(33)

This is an eigenvalue problem and it is known that to obtain instability one must satisfy.

$Tr(J^{\prime}) > {\text{0}}$ Or $Det(J\prime ) > {\text{0}}$where J^' is the new Jacobian matrix:

$$ Tr(J^{\prime}) = ({\text{f}}_{\xi } + {\text{g}}_{\rho } ) - k^{2} \left( {1 + \sigma } \right) $$

(34)

$$Det(J^{\prime}) = \left( {k^{2} - {\text{f}}_{\xi } } \right)\left( {\sigma k^{2} - {\text{g}}_{\rho } } \right) - {\text{f}}_{\rho } {\text{g}}_{\xi } = \sigma k^{4} - \left( {{\text{g}}_{\rho } + \sigma {\text{f}}_{\xi } } \right)k^{2} + Det(J) $$

(35)

It is easy to verify that the trace is always negative, while the determinant may be negative for

$$ g_{\rho } + \sigma f_{\xi } > 0 $$

(36)

Then, after substituting $z={k}^{2}$ in the expression for $Det(J^{\prime})$ one obtains the equation of a parabola of the form:

$$\mathrm{h}\left(z\right)=\sigma {z}^{2}-pz+q$$

(37)

The curve assumes negative values for a $\Delta >0$ of the equation $\sigma {z}^{2}-pz+q=0$, that is:

$${p}^{2}-4\sigma q>0$$

(38)

Or

$${\left({g}_{\rho }+{ \sigma f}_{\xi }\right)}^{2}-4\sigma \left({f}_{\xi }{g}_{\rho }-{f}_{\rho }{g}_{\xi }\right)>0$$

(39)

(27), (28), (34) and (37) are Turing’s conditions for diffusion-driven instability [31, 32].

In our case:

$$ J = \left| {\begin{array}{*{20}c} {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \varepsilon }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\varepsilon $}}\left( {1 - 2\xi - \frac{qf\rho }{{(q + \rho )^{2} }}} \right)} & {\frac{{f\left( {q - \xi } \right)}}{{\varepsilon \left( {q + \xi } \right)}}} \\ 1 & { - 1} \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} {0.8} & { - 13.2} \\ 1 & { - 1} \\ \end{array} } \right| $$

(40)

Within the matrix:

ξ ([HBrO2]) is the activator. The acid catalyzes its own production (${f}_{\xi }>0$) and stimulates Ce⁴⁺ production (${g}_{\xi }>0$).

ρ ([Ce⁴⁺]) is the inhibitor. Similarly, the inhibition is characterized by negative values of the remaining terms of the Jacobian matrix. Self-inhibition and inhibition of acid production are represented in the FKN mechanism by (R6) and (R4) respectively.

From this analysis it is evident that (3) becomes:

$$\sigma >const>1$$

(41)

And since $\sigma = D_{\rho } /D_{\xi }$, it automatically emerges that a condition for diffusion-driven instability is that the inhibitor must diffuse faster than the activator [1, 33].

It has been again underlined the different time scales on which the various components of the chemical media act, linked to the activation and inhibition in the production in certain key products.

4.2 Advanced applications of oscillators and deterministic chaos

Chemical oscillators offer a lot of variants in terms of composition and behavior but is it possible to design such a system according to certain necessities? In the ‘80 s some studies have been carried out about the subject. Design of oscillators exploiting the great variety of compounds with similar properties would have helped to achieve more specific goals [34].

An analysis phase opens the design: an autocatalytic reaction must be chosen and studied from a kinetic point of view in order to find a bistability region. The positive feedback species providing autocatalysis is then coupled with an additional species which causes inhibition, a negative feedback. The latter is added to the system in order to create a hysteresis behavior of the reactive phase and to narrow the bistability region to induce oscillations. In order to make the region disappear, the influence of the inhibitor must be increased. This helps to understand the theoretical strength of these phenomena in terms of applications and control.

To increase the complexity and explore each possible effect of oscillating systems it is often used a technique known as “coupling”. Two coupled oscillators show complex behaviors which are not possible otherwise. Coupling can be done in two ways: chemically or physically. A chemical coupling consists in mixing all the species in the same tank so that each subsystem is capable of independent oscillation, but connected to the other through a product, reactant or intermediate species in common which influences their typical relaxation times. In a physical coupling instead, the subsystems act in two different vessels and are linked by a bridge of matter transport [1].

Typical response of a coupled oscillator is entrainment which causes each subsystem to adapt its motion to the other in the way to have the same resulting frequency or two frequencies correlated by a fixed ratio.

An interesting twist linked to coupling is the rising of birhythmicity not existing before. The phenomenon consists in the periodic change in the way the system oscillates which is represented on the phase plane by two stable limit cycles connected by an unstable one. As for the concept it is like bistability even if the alternating states are not stationaries but oscillating motions. In addition to birhythmicity it may rise a compound oscillation behavior. To better understand it, imagine having a transition from a certain oscillation mode to another: compound oscillations are the result of a wider oscillation which presents features of both the modes.

Finally, the coupled oscillators may approach a stationary even if the separated subsystems would have oscillated in those conditions, we refer to the phenomenon as “oscillator death”. The opposite is possible and is known as “rhythmogenesis” [1]. This description is particularly useful to introduce the concept of deterministic chaos.

Into the term “deterministic chaos” lots of aperiodic phenomena are gathered, though there is not a precise definition. In this context the term is referred to the transition from periodic oscillations to aperiodic behavior according to the value of certain bifurcation parameters. Not all the models of chemical oscillators show chaotic transitions: necessary but not enough condition is to have dimension $n\ge 3$ [5].

The first quantitative description of deterministic chaos dates to the studies of Lorenz. The scientist built a very simple 3D model which showed chaotic oscillations by varying a parameter. The change in it caused subsequent doubling of the speed of oscillations. This variation of the period of oscillations is known as the “Feigenbaum scenario” [35, 36]. After a certain value of the parameter, chaotic oscillations were completely developed causing aperiodicity in wavelength and amplitude. A first period doubling may be represented on the phase plane by the connection between two limit cycles. Following the change in the bifurcation parameter the number of limit cycles increases until the phase plane or space is densely covered. Chaos occurs when the system does not follow the same trajectory more than one time⁵. It will result a so-called “strange attractor” in the phase space constituted by similar connected cycles changing in dimension⁵. The first attractor of this type has been the one resulting from Lorenz model associated to a butterfly because of the shape. The fact led people to get used to referring to chaos with the expression “butterfly effect”.

In order to better describe chaos, it has been introduced the concept of Poincaré map [37]. These maps are constituted by planes which cut the phase space at fixed values of a certain variable. These projections of the trajectories are represented by dots: for a periodic evolution the Poincaré map is a dot, if the limit cycle is only partially dissected, then the number of points increase until a curve appears, and the dots are so densely dispersed that it looks continuous. These graphs help to better understand the concept of bifurcation because like tree diagrams: the transition value causes a doubling in the number of dots.

The model which has been studied in order to show a typical chaotic behavior is the Györgyi-Field model of the BZ reaction, which is known in different forms according to the number of variables which constitute it.

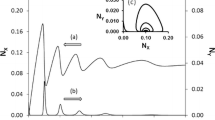
In [15] different sets of experimental parameters have been found to give rise to chaos. The shape of the chaotic dynamic response of the system appears intimately linked the CSTR flow-rate value adopted during the experience [38]. The phase plane graph turns from a densely covered plane with high amplitude chaotic oscillations at low flowrates, to a long induction period followed by the small diameter limit cycles of the strange attractor at high flowrates. Between the two scenarios, the one at high CSTR flowrate will be taken into consideration in this first brief explanation.

The model consists of seven reaction steps which sum up the BZ reaction mechanism as shown in Table 4.

Table 4 Györgyi-Field model. $Y = B{r^ - },X = HBr{O_2},\;Z = Ce(IV),\;V = BrCH{\left( {COOH} \right)_2},\;A = BrO_3^ - ,\;H = {H^ + },\;M = C{H_2}{(COOH)_2}$ and C is the total cerium ions concentration [6]

The simplification represents from R2 to R6, R9 and R10 of the FKN mechanism without considering some chemical species, that is why the last reaction step does not show any product.

By computing the kinetic equations relative to X, Y and V variables the Györgyi-Field model system can be obtained in its adimensional form:

$$ \frac{dx}{{d\tau }} = T_{0} \left[ { - k_{GF1} HY_{0} x\tilde{y} + \left( {{\raise0.7ex\hbox{${k_{GF2} AH^{2} Y_{0} }$} \!\mathord{\left/ {\vphantom {{k_{GF2} AH^{2} Y_{0} } {X_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${X_{0} }$}}} \right)\tilde{y} - 2k_{GF3} X_{0} x^{2} + 0.5k_{GF4} A^{0.5} H^{1.5} X_{0}^{ - 0.5} \left( {C - Z_{0} z} \right)x^{0.5} - k_{GF5} X_{0} xz - k_{f} x} \right] $$

(42)

$$ \frac{dz}{{d\tau }} = T_{0} \left[ {k_{GF4} A^{0.5} H^{1.5} X_{0}^{0.5} \left( {{\raise0.7ex\hbox{$C$} \!\mathord{\left/ {\vphantom {C {Z_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${Z_{0} }$}} - z} \right)x^{0.5} - k_{GF5} X_{0} xz - \alpha k_{GF6} V_{0} zv - \beta k_{GF7} Mz - k_{f} z} \right] $$

(43)

$$ \frac{dv}{{d\tau }} = T_{0} [\left( {{\raise0.7ex\hbox{${2k_{GF1} HX_{0} Y_{0} }$} \!\mathord{\left/ {\vphantom {{2k_{GF1} HX_{0} Y_{0} } {V_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${V_{0} }$}}} \right)x\tilde{y} + \left( {{\raise0.7ex\hbox{${k_{GF2} AH^{2} Y_{0} }$} \!\mathord{\left/ {\vphantom {{k_{GF2} AH^{2} Y_{0} } {V_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${V_{0} }$}}} \right)\tilde{y} - \left( {{\raise0.7ex\hbox{${k_{GF3} X_{0}^{2} }$} \!\mathord{\left/ {\vphantom {{k_{GF3} X_{0}^{2} } {V_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${V_{0} }$}}} \right)x^{2} - \alpha k_{GF6} Z_{0} zv - k_{f} v $$

(44)

where the scaling factors are reported in Table 5. ${k}_{f}=2.16x{10}^{-3}$ is the inverse of the residence time in the rector, or the flow-rate and, α = 666.7, β = 0.3478 adjustable factors added in order to correct the simplification from eleven-variables to four-variables model where a radical-transfer reaction of BrMA into bromide ions is not taken into account.

Table 5 Scaling factors of the Györgyi-Field model. A = 0.1 M, M = 0.25 M, H = 0.26 M, C = 0.000833 M [6]

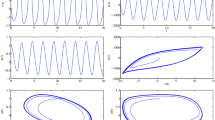
Then, the three-variables ODE system has been solved with Simulink, obtaining what is depicted in Figs. 15, 16.

Fig. 15

Phase portrait of the chaotic Györgyi-Field model

Fig. 16

Chaotic oscillations in time of variable v, corresponding to [BrMA]

The former represents the strange attractor in the phase space of the model while the latter depicts the oscillatory chaotic behavior obtained by period doubling and condensing of the oscillations in time.

In the figures it is well represented the typical evolution of a chaotic trajectory. The system rapidly moves from the initial conditions to an aperiodic series of limit cycles never repeated that are chaotic oscillations in time.

Though period doubling is only one of the complex ways to reach chaos thus, which are the common features of each chaotic system? Some features have been already cited: points evolving from a generic initial condition densely cover a region of the Poincaré map and this corresponds to an infinite number of limit cycles. But sensitivity to initial conditions is the most important. Two chaotic systems which differ infinitesimally in the initial conditions will probably evolve in totally different ways [5]. From this it comes the unpredictability of deterministic chaos. These phenomena are ruled by mathematical laws that are often well known but the complexity is inherent the non-linear interactions between the compounds at stake, so that a single system gathers infinite possible evolutions according to the initial conditions⁵. This is the core of the “butterfly effect” often known in the form: “Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?”, which stresses the dimension of the initial perturbation compared to the final effect.

Chaos has been studying for years but some issues are still opened. To provide some examples: techniques to distinguish noise from chaos, identical chaotic systems synchronization and chaos feedback controlling [39, 40]. The latter’s aim is to direct the evolution of the time-dependent variables, in order to increase the “performance” of a chaotic system, to rapidly reach the desired state or to prevent the system to enter an undesired region of the phase space. The second and the third targets are obtained with little local perturbations of the present state [41].

4.3 Sensitivity analysis of the Oregonator to temperature

The Oregonator model has been then studied in order to determine the answer of the system to a temperature change according to Pulella [14]. The aim of the experience is to understand the relation between temperature and oscillation birth. The link with temperature is imposed to the system of differential equations by the Arrhenius equation for the kinetic constants. Since it is associated a temperature-dependent kinetic constant to each reaction of the model, the system results to be sensitive to this parameter.

According to the Tyson simplification and adimensionalisation in (17bis), the three factors ε, δ and q are temperature-dependent according to the expression reported below, obtained by substituting the Arrhenius law to kinetic constants during the adimensionalisation of the system.

$$\varepsilon \left(T\right)=\frac{{k}_{O5}{B}_{0}}{{k}_{O3}H{A}_{0}}={\varepsilon }_{0}{e}^{\frac{{E}_{3}-{E}_{5}}{R}(\frac{1}{T}-\frac{1}{{T}_{0}})}$$

(45)

$$\delta \left(T\right)=\frac{{2{k}_{O4}k}_{O5}{B}_{0}}{{{k}_{O2}k}_{O3}{H}^{2}{A}_{0}}={\delta }_{0}{e}^{\frac{{E}_{3}+{E}_{2}-{E}_{4}-{E}_{5}}{R}(\frac{1}{T}-\frac{1}{{T}_{0}})}$$

(46)

$$q\left(T\right)=\frac{{2{k}_{O1}k}_{O4}}{{k}_{O2}{k}_{O3}}={q}_{0}{e}^{\frac{{{E}_{2}+E}_{3}-{E}_{1}-{E}_{4}}{R}(\frac{1}{T}-\frac{1}{{T}_{0}})}$$

(47)

The data exploited during the analysis have been obtained from Pulella (2009) [14], in particular the values of the activation energies and pre-exponential factors associated to the five kinetic constants of the Oregonator. The values are reported in the Table 6.

Table 6 Activation energies and pre-exponential factors of the Oregonator adimensionalized according to Tyson [14]

The values of the pre-exponential factors are the ones of the kinetic constants at the reference temperature which has been chosen to be 298 K, the same as Table 2. The experiment also considers the effect of the parameter of bromination $f$, which causes a different sensitivity to temperature. A set of four different values of $f$ has been used: $f$=0.6, 1, 1.5, 2.

The sensitivity analysis has been carried on starting from the resolution of the simplified version of the system according to Tyson. The results are depicted in Fig. 17 in the phase plane.

Fig. 17

Oregonator Temperature solution, where f = 0.6, f = 1, f = 1.5 and f = 2

What appears, instead from Fig. 18 is that the parameter $f$ has a direct impact on the sensibility of the system to the temperature. High temperatures have the effect to make oscillations disappear. At low values of $f,$ this effect is limited. This means that slightly higher temperatures are needed to put out oscillations in relation to high values of $f$. While at $f$=0.6 a temperature of 450 K is needed, at $f$=2 it is enough to reach 350 K.

Fig. 18

Oregonator Temperature solution, with f variable at fixed T = 350 K

It is useful to follow the position of the stationary point deducible from Fig. 19, in order to understand why oscillations, disappear. It results from the intersection of the nullclines associated to the system. In the simplified form of the Oregonator the temperature depending variables are ε, δ and q. Change in the values of these factors modifies the shape of the nullclines which explain the movement of the stationary at different concentrations and the disappearance of oscillations.

Fig. 19

Nullclines as a function of Temperature

First, it is necessary to underline that being the third equation of the system devoid of temperature depending factors, its nullcline will not be sensitive to the parameter. On the contrary the ξ-nullcline turns from a paraboloid shape at low temperatures to a hybrid form which shows to relative maxima whose relative distance increases with temperature. At sufficiently high temperatures this nullcline results in a monotonical decrease. The varying shape of the ξ-nullcline in relation to the linear nullcline of ρ shifts the stationary from its unstable middle branch to the stable left branch. It is this effect which causes disappearing of oscillations.

It is easy to carry on a qualitative assessment on the signs of the Jacobian derivative terms in order to study the stability of the stationary point. The derivative terms of the ρ-nullcline have fixed signs, positive as a function of ξ and negative as a function of ρ. The term in position (1,2) has fixed negative values since in our experimental conditions the value of ξ_ss is higher than the one of q. Since all the parameters have positive value in the first quadrant of the phase plane the only condition to impose is ${\xi }_{ss}<q$. The first term in (1,1) is more difficult to describe.

What has been obtained at $f=\mathrm{0,6}$ is:

$${J}_{298}=\left|\begin{array}{cc}\mathrm{7,84}& -\mathrm{5,91}\\ 1& -1\end{array}\right|, Det\left({J}_{298}\right)=-\mathrm{1,93}, Tr\left({J}_{298}\right)=\mathrm{6,84}$$

(48)

$${J}_{350}=\left|\begin{array}{cc}\mathrm{0,83}& -\mathrm{3,20}\\ 1& -1\end{array}\right|, Det\left({J}_{350}\right)=\mathrm{2,37}, Tr\left({J}_{350}\right)=-\mathrm{0,17}$$

(49)

$${J}_{450}=\left|\begin{array}{cc}-\mathrm{0,53}& -\mathrm{1,17}\\ 1& -1\end{array}\right|, Det\left({J}_{450}\right)=\mathrm{1,70}, Tr\left({J}_{450}\right)=-\mathrm{1,53}$$

(50)

where the last two results correspond to the change in the stability.

The temperature plays an important role also on the shape of the limit cycle in the oscillating domain of temperatures. As the parameter is increased the amplitude of the oscillations is reduced and coupled with an increasing frequency. Thus, the oscillations are accelerated and reduced in amplitude until they disappear. The stoichiometric factor $f$ increases the effect of amplitude reduction, as it grows. Figure 20 depicts the time-depending oscillations in the two variables at $f=2$.

Fig. 20

Oregonator Temperature solution, for f = 2. Time-dependent solution

It appears also clearer from Fig. 20 the differences in the oscillation period, directly linked to the exchange between the three subprocesses A, B and C.

Last remarkable effect of temperature on the mathematics of the Oregonator model is the nature of the eigenvalues of the associated Jacobean matrix. Temperature raise causes an increase in the complex domain of the eigenvalues losing the transitions from node to focus and vice-versa, as a function of $f$, as it is depicted in Fig. 21.

Fig. 21

Eigenvalues as a function of Temperature for 298, 350 and 450 K

From a thermodynamic point of view, the temperature has the property to accelerate all the reaction of the Oregonator model, which are considered irreversible.

The reaction will be differently accelerated according to their activation energies, so that the fastest will be the second with 25 kJ mol⁻¹, while the slowest the fifth with 70 kJ mol⁻¹. It is given that the first two reactions correspond to subprocess A and to consumption of Br⁻ ions, the seconds to autocatalytic Subprocess B and the fifth reaction to Subprocess C which reduces Ce⁴⁺ into in its Ce³⁺ form. From the analysis of activation energies this becomes evident that Br⁻ ions are consumed faster than HBrO₂ is produced, as temperature raises, so that the shift from Process A to B is accelerated, resulting in a shorter period of oscillation. This acceleration also causes an increasing in the equilibrium concentration of HBrO₂ given that it has been largely produced when its slower dismutation takes place and reduces its concentration.

Since Process A is much faster than B and C, the amplitude of oscillation is reduced. In the case of HBrO₂, its maximum and minimum concentrations approach because both its production and consumption are slower.

This effect leads at high temperatures to cause the complete disappearing of oscillations. The high initial concentration of bromide ions causes their fast consumption, favored by temperatures. The production of bromous acid and consumption Ce (IV) is not that fast so that the bromide ions produced the final step of the Oregonator are not as much as the beginning. In this state it is rapidly reached the stationary point where all concentration keep constant.

5 Materials and methods

The pathway through oscillations begins with the chemical simplifying models for the BZ reaction. All chemical reactions are considered reversible or irreversible according to the FKN mechanism. This is not true for the mathematical counterparts of these reactions in the Oregonator and Györgyi-Field model, which are all considered irreversible.

The analysis of the three subprocesses of the FKN mechanism is carried out and takes is focus on the alternating accelerated and slowed down states of the reactions which constitute them, rather than a chronological order.

The five reactions of the Oregonator are then analyzed from a dynamical point of view following the trace provided by Tyson simplification of the system in Pulella [14], and numerically by solving the entire system in Simulink. From Simulink results, oscillations in time and limit cycle in the phase plane have been depicted using Origin Pro.

In order to mathematically isolate a domain for oscillations in the phase plane the hypotheses of the Poincaré-Bendixon theorem.

As for the pattern formation section, the trace of Murray [7] has been followed while Györgyi [6] to compute the equations of the Györgyi-Field model. These equations are then solved with Simulink and the strange attractor of the chaotic state of the system has been depicted with Origin Pro.

The last assessment of the effect of temperature on the Oregonator Model has been all solved using MATLAB and following the trace of Pulella [14], computing the Arrhenius law to expand all the kinetic constants terms as a function of temperature.

6 Conclusions

The review dealt with the main features of Belousov-Zhabotinsky-type reactions. Several parameters, including temperature, flowrates and concentration of chemical compounds may affect chemical oscillators occurring under dynamic conditions. Studies of oscillations, patterns, and chaos in chemical systems constitute an exciting new frontier of chemistry, chemical engineering and biochemical processes. The field holds enormous promise and opportunity for unraveling the chemical complexities of nature. Studies of propagating waves and pattern formation have shown how chemical reactions are transformed when they are intimately coupled with diffusion, heat or other forms of transport. We also now know that it may be impossible to predict the future behavior of a chemical system if it contains elements of feedback appropriate for chaotic dynamics. In this review we propose a simple and accurate way able to model the most common oscillation reactions. This approach can be applied to any non-linear chemical process, as well as the complex behavior of natural systems.