1 Introduction

The PNLSE describes of soliton propagation in nonlinear optical fibers. It received a great attention of numerous research works in the literature. Mainly, the studies were focused on the different techniques used for solving PNLSE. In this area new exact solutions (ESs) to a PNLSE, among them, breather, multi-waves, periodic -cross kink, M-shaped, and Lump-two stripe solutions were derived in Ozisik (2022), and Gilson et al. (2003). The Riccati-Bernoulli Sub-ODE method, infinite series method and cosine-function method, were used to investigate ESs of the PNLSE in Shehata (2016), Zai-Yun et al. (2012), and Yusuf et al. (2019). The similarity solutions of the PNLSE was analyzed and the ESs were obtained via introducing similarity transformations and by using the extended unified method (Abdel-Gawad 2022). Solitons in optical fiber Bragg gratings for PNLSE having cubic-quartic dispersive reflectivity with parabolic-nonlocal combo law of refractive index were investigated (Benoudina et al. 2023). In Owyed et al. (2020), Mahak and Akram (2020), two algorithms for some expansion methods were suggested for constructing new optical solitons solutions for the fractional PNLSE. The generalized traveling wave (TW) method was developed for the NLSE with general perturbations in order to obtain the equations of motion for collective coordinates (Quintero et al. 2010; Ghanbari and Raza 2019).

An improved PNLSE with Kerr law non-linearity equation was studied in Jhangeer et al. (2021), and Mirzazadeh et al. (2017). In Khalil et al. (2021), and Bisws et al. (2012), the perturbation of the improved version of the NLSE was studied via the semi-inverse variational principle. The dynamical behavior of improved PNLSE was discussed by the extended rational sine-cosine/sinh-cosh techniques,\(\varphi ^{6}\) -model expansion method and generalized exponential rational function method (Younas et al. 2022). New exact TW solutions of the PNLSE were derived by using generalized (\(G\prime /G\)) -expansion method 17]. In Ray and Das (2022), the space-time fractional PNLSE) in nanofibers was studied using the improved\(tan(\phi (\xi )/2)\) expansion method to explore new exact solutions. The soliton solutions for the improved PNLSE with quadratic-cubic law nonlinearity by utilizing the log transformation and symbolic computation were studied (Rizvi et al. 2022).

In Alharbi et al. (2021), a new stochastic robust solver to solve several classes of nonlinear stochastic partial differential equations was introduced and applied to PNLSE. Bright, dark and singular soliton solutions to quadratic-cubic nonlinear media in the presence of perturbation were derived (Biswas et al. 2018; Rizvi et al. 2021). The dynamics of soliton propagation through optical fibers with non-Kerr law nonlinearities NLSE was integrated in the presence of perturbation terms (Biswas et al. 2012; Osman et al. 2022; Zhang and Z. -H. Liu X. -J. Miao, Y. -Z. Chen, 2010). Hyperbolic, periodic, singular, domain walls, dark-like dromions (solitons) for perturbed fractional NLSE were retrieved (Kodama 1985).The TW solutions to the PNLSE with Kerr law nonlinearity were constructed by using the modified (\(G^{\prime }/G)\)-expansion method and Jacobi elliptic ansatz method (Miao and Zhang 2011; Aslan and Inc 2019). The sub-equation method was implemented to construct exact solutions for the conformable PNLSE, where three different types of nonlinear perturbations were considered (Martínez et al. 2022). The exact two-soliton solution to the unperturbed NLSE and prediction of strongly inelastic collisions (Dmitriev et al. 2002). Further relevant works were presented in Kodama (1985), Wazwaz et al. (2023), Wazwaz (2021), Guan et al. (2023), Qiu and Zhang (2023), and Xu and Wazwaz (2023)

In the present work, we introduce a novel definition for MTPD and study the PNLSE with fourth order dispersion and cubic-quintic nonlinearity. The exact solutions are derived by implementing the unified method (UM) (Abdel-Gawad 2023; Abdel-Gawad et al. 2023; Abdel-Gawad 2023, 2023, 2012).

The organization of this paper is as follows. In Sect. 2, The MTPD is introduced, formulation of the problem is presented and description of the UM is outlined. Section 3 is devoted to distinguish different kinds of chaos solitons. Non chaotic solitons are presented in Sect. 4. In (5) and (6) analysis of modulation instability and investigation of global bifurcation are done. Section 5 is devoted to conclusions

2 Mathematical formulation

2.1 The novel TMPD

Proportional derivatives such as conformable derivative (Khalil et al. 2014; Abdelhakim and Machado 2019) and \(\beta\)-derivative (Hussain et al. 2020) were introduced in the literature. A truncated M derivative is, also, presented.

Definition 1

Let f: \(R^{+}\longrightarrow R, 0 < \rho ,\gamma \le 1\). The M-truncated derivative is defined (Hussain et al. 2020),

$$\begin{aligned} _{i}^{MT}D_{t}^{\rho ,\gamma }f(t)=Lim_{\epsilon \rightarrow 0}\frac{f(t_{i}E_{\rho }(\epsilon (t^{\gamma -1}))-f(t)}{\epsilon },0<\rho ,\gamma <1,{}_{i}E_{\rho }(t)=\sum _{j=1}^{j=i}\frac{t^{j}}{\Gamma (\rho j+1)}. \end{aligned}$$
(1)

where\(_{i}E_{\rho }(t)\) is the truncated Mittage–Leffler function.

Let \(f:R^{+}\rightarrow R\) be a continuous function, we define MTPD,

Definition 2

$$\begin{aligned} _{i}^{TMP}D_{t}^{\rho }f(t)=Lim_{\varepsilon \rightarrow 0}\frac{f(t+\varepsilon \frac{_{i}E_{\rho }(t)}{_{i}E_{\rho }^{\prime }(t)})-f(t)}{\varepsilon },0<\rho <1. \end{aligned}$$
(2)

If \(f\) \(\epsilon C^{1}(\mathbb {R}^{+})\), the (2) reduces to,

$$\begin{aligned} \begin{array}{c} _{i}^{TMP}D_{t}^{\rho }f(t)=\frac{_{i}E_{\nu }(t)}{_{i}E_{\rho }^{\prime }(t)}f^{\prime }(t)=\frac{df(t)}{dLog(_{i}E_{\rho }(t))}=\frac{d\bar{f}(\tau )}{d\tau },\\ f(t)=\bar{f}(\tau ),\tau =Log(_{i}E_{\rho }(t) \end{array}. \end{aligned}$$
(3)

Basic theorems

  1. (a)

    \(_{i}^{TMP}D_{t}^{\rho }(f(t)\) \(+g(t))=_{i}^{TMP}D_{t}^{\rho }f(t)+{}_{i}^{TMP}D_{t}^{\rho }g(t)\).

  2. (b)

    \(_{i}^{TMP}D_{t}^{\rho }(f(t)\) \(.g(t))=f(t)_{i}^{TMP}D_{t}^{\rho }g(t)+g(t)_{i}^{TMP}D_{t}^{\rho }f(t).\)

  3. (c)

    \(\overset{n=2}{\overbrace{_{i}^{TMP}D_{t}^{\rho }({}_{i}^{TMP}D_{t}^{\rho }}}(f(t))=H(Hf^{\prime \prime }+\) \(H^{\prime }f^{\prime }\)), \(H=\frac{_{i}E_{\rho }(t)}{_{i}E_{\rho }^{\prime }(t)}\).

  4. (d)

    \(\overset{n=3}{\overbrace{_{i}^{TMP}D_{t}^{\rho }({}_{i}^{TMP}D_{t}^{\rho }({}_{k}^{TMP}D_{t}^{\rho }}}(f(t)))=H(H^{2}f^{\prime \prime \prime }+3HH^{\prime }f^{\prime \prime }+f^{\prime }(H^{\prime 2}+HH^{\prime \prime })),H=\frac{iE_{\rho }(t)}{iE_{\rho }^{\prime }(t)}\).

  5. (e)

    If \(_{i}^{TMP}D_{t}^{\rho }f(t)=1\Rightarrow f(t)=Log({}_{i}E_{\rho }(t))\)

  6. (f)

    If \(_{i}^{TMP}D_{t}^{\rho }f(t)=f(t)\) \(\Rightarrow\) \(f(t)=_{i}E_{\rho }(t).\)

Generalizations of (2).

Definition 3

$$\begin{aligned} _{k}^{TMP}D_{t}^{\rho }f(t)=Lim_{\varepsilon \rightarrow 0}\frac{f\left( t+\varepsilon \frac{_{i}E_{\rho }(t^{\rho })}{\left( \frac{d_{i}E_{\rho }(t^{\rho })}{dt}\right) }\right) -f(t)}{\varepsilon },0<\rho <1. \end{aligned}$$
(4)

In (1), when \(i\rightarrow \infty ,\)

Definition 4

$$\begin{aligned} _{k}^{TMP}D_{t}^{\rho }f(t)=Lim_{\varepsilon \rightarrow 0}\frac{f\left( t+\varepsilon \frac{E_{\rho }(t^{\rho })}{\frac{d(E_{\rho }(t^{\rho }))}{dt}}\right) -f(t)}{\varepsilon },0<\rho <1. \end{aligned}$$
(5)

2.2 The PNLSE and TMPD-PNLSE

The PNLSE equation read (Yusuf et al. 2019),

$$\begin{aligned} \begin{array}{l} iw_{t}++\alpha w_{xx}+\beta \mid w\mid ^{2}w\\ \quad -i(\nu \,w_{x}+\mu (\mid w\mid ^{2}w)_{x}+\sigma (\mid w\mid ^{2})_{x}w=0, \end{array} \end{aligned}$$
(6)

where \(w\equiv w(x,t)\) is the complex field envelope, \(\alpha\) is the group dispersion velocity, \(\beta\) and is the Kerr nonlinearity coefficient, \(\mu\) and \(\sigma\) are the coefficients of self-steepening and self-phase modulation respectively.

The PNLSE with fourth order dispersion and quintic nonlinearity is,

$$\begin{aligned} \begin{array}{c} iw_{t}++\alpha w_{xx}+\delta w_{xxxx}+\beta \mid w\mid ^{2}w+\gamma \mid w\mid ^{4}w\\ -i(\nu \,w_{x}+\mu (\mid w\mid ^{2}w)_{x}+\sigma (\mid w\mid ^{2})_{x}w=0, \end{array} \end{aligned}$$
(7)

where \(\delta\) is the coefficients of forth order dispersion and \(\gamma\) is quintic nonlinearity coefficient. The MTPD-PNLSE takes the form,

$$\begin{aligned} \begin{array}{c} i(_{i}^{TMP}D_{t}^{\rho }w)+\alpha w_{xx}+\delta w_{xxxx}+\beta \mid w\mid ^{2}w+\gamma \mid w\mid ^{4}w\\ -i(\nu \,w_{x}+\mu (\mid w\mid ^{2}w)_{x}+\sigma (\mid w\mid ^{2})_{x}w=0. \end{array} \end{aligned}$$
(8)

In (8), by using (e) in the above, we introduce the transformation, \(w(x,t)=\bar{w}(x,\tau ),\) \(\tau =\) \(Log(_{i}E_{\rho }(t))\), and it reduces to,

$$\begin{aligned} \begin{array}{c} \bar{w_{\tau }}++\alpha \bar{w}_{xx}+\delta \bar{w}_{xxxx}+\beta \mid \bar{w}\mid ^{2}\bar{w}+\gamma \mid \bar{w}\mid ^{4}\bar{w}\\ -i(\nu \,\bar{w}_{x}+\mu (\mid \bar{w}\mid ^{2}\bar{w})_{x}+\sigma (\mid \bar{w}\mid ^{2})_{x}\bar{w}=0. \end{array} \end{aligned}$$
(9)

In (9), we use the transformation,

$$\begin{aligned} \bar{w}(x,\tau )=(u(x,\tau )+iv(x,\tau ))e^{i(kx-\omega \tau )}, \end{aligned}$$
(10)

and the equations for the real and imaginary parts, are given respectively by,

$$\begin{aligned}{} & {} \begin{array}{l} 4\delta k^{3}v_{x}(x,t)-6\delta k^{2}u_{xx}(x,t)-2\alpha kv_{x}-4\delta kv_{xxx}+\alpha u_{xx}+\nu v_{x}\\ -v_{\tau }+\delta k^{4}u(x,t)-\alpha k^{2}u+k\nu u++\delta u_{xxxx}+\mu u^{2}v_{x}+\beta u^{3}(+\omega u\\ +k\mu u^{3}+2\mu u_{x})uv+2\sigma u_{x}uv+\gamma u^{5}+3\mu v_{x}v^{2}+2\sigma v_{x}v^{2}\\ k\mu uv^{2}++\beta uv^{2}+\gamma uv^{4}+2\gamma u^{3}v^{2}=0, \end{array} \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \begin{array}{l} -4\delta k^{3}u_{x}-6\delta k^{2}v_{xx}+2\alpha ku_{x}-\nu u_{x}+u_{\tau }+\alpha v_{xx}+4\delta ku_{xxx}+\delta v_{xxxx}\\ \delta k^{4}v-\alpha k^{2}v+k\nu v)-3\mu u^{2}u_{x}-2\sigma u_{x}u{}^{2}+\omega v-2\mu uvv_{x}-2\sigma uvv_{x}\\ +k\mu u^{2}+k\mu v^{3}-\mu u_{x}v^{2}++\beta u^{2}v+2\gamma u^{2}v^{3}+\gamma u^{4}v+\beta v^{3}+\gamma v^{5}=0. \end{array} \end{aligned}$$
(12)

For traveling wave solution, we write \(u(x,\tau )=U(z),\;v(x,\tau )=V(z)\) and \(z=px+q\tau ,\)so (11) and (12) reduce to,

$$\begin{aligned}{} & \gamma U^{5}+U^{3}\left( \beta +k\mu +2\gamma V^{2}\right) +U\left( \delta k^{4}-\alpha k^{2}+k\nu +V^{2}(\beta +k\mu ) \right. \\ &\quad \left. +\omega 2p(\mu +\sigma )VU'++\gamma V^{4}\right) +\mu pU^{2}(V'+\left( p\left( 4\delta k^{3}-2\alpha k+\nu \right) -q\right. \\ &\quad \left. +p(3\mu +2\sigma )V^{2}\right) V'+p^{2}\left( \left( \alpha -6\delta k^{2}\right) U''+\delta p\left( pU^{(4)}-4kV^{(3)}\right) \right) =0, \end{aligned}$$
(13)
$$\begin{aligned}{} & V^{3}\left( \beta +k\mu +2\gamma U^{2}\right) +\gamma V^{5}+\left( q-p\left( 4\delta k^{3}-2\alpha k+\nu \right) \right. \\ &\quad \left. -p(3\mu +2\sigma )U^{2}\right) U'-\mu pV^{2}U'+V\left( \delta k^{4}-\alpha k^{2}+k\nu \right. \\ &\quad +U^{2}(\beta +k\mu )+\omega \left. +\gamma U^{4}-2p(\mu +\sigma )UV'\right) \\ &\quad +p^{2}\left( \left( \alpha -6\delta k^{2}\right) V''+\delta p\left( 4kU^{(3)}+pV^{(4)}\right) \right) =0. \end{aligned}$$
(14)

2.3 The unified method

The UM asserts that the solutions of a nonlinear evolution equation are expressed in polynomial form and rational form in an auxiliary function that satisfies an adequate auxiliary equation (Qiu and Zhang 2023).

2.3.1 Polynomial solutions

With relevance to (13) and (14), the solutions are written,

$$\begin{aligned} U(z)=\sum _{j=0}^{j=n_{1}}a_{j}\phi (z)^{j},\quad V(z)=\sum _{j=0}^{j=n_{2}}b_{j}\phi (z)^{j},\;(\phi ^{\prime }(z))^{r}=\sum _{j=0}^{j=rs}c_{j}\phi (z)^{j},r=1,2, \end{aligned}$$
(15)

where \(\phi (z)\)is the auxiliary function and the last equation in (15) is the auxiliary equation (AE).

The Painlevé analysis can be used to test the integrability of (13) and (14) but it is too lengthy.In view of (15), integrability is tested in the sense of existence of integers \(n_{1},n_{2},\)and s. To this issue, two conditions are examined, the balance condition and the consistency condition. We consider the case when \(r=1.\)

The balance condition is found by writing \(U\sim \phi ^{n_{1}}\), \(U^{\prime }\sim \phi ^{n_{1}-1}\phi ^{\prime }\) \(\Rightarrow \;U^{\prime }\sim \phi ^{n_{1}+(s-1)},\;U^{\prime \prime }\sim \phi ^{n_{1}+2(s-1)},...etc.\) We get \(n_{1}=n_{2}=s-1.\) To determine s, we use the consistency condition (CC). We need to calculate the following;

  1. (i)

    The number of equations that results when inserting (8) in (6) (or (7)) and by setting the coefficients of \(\phi ^{i}(z),i=0,1,2,...etc.\) equal to zero (which is \((5s-4)).\)

  2. (ii)

    The number of arbitrary parameters in (8), (which is (\(2s+1)).\)The CC reads \(5s-4-(2s+1)\le m,\) where m is the highest order derivative (\(m=3\)). Finally, we get \(0\le s\le 3.\)

2.3.2 Rational solutions

In this case, the solutions of (13) and (14) are written,

$$\begin{aligned} U(z)=\frac{\sum _{j=0}^{j=m}a_{j}\phi (z)^{j}}{\sum _{j=0}^{j=m}s_{j}\phi (z)^{j}},\;V(z)=\frac{\sum _{j=0}^{j=m}b_{j}\phi (z)^{j}}{\sum _{j=0}^{j=m}s_{j}\phi (z)^{j}},(\phi ^{\prime }(z))^{r}=\sum _{j=0}^{j=rs}c_{j}\phi (z)^{j},r=1,2 \end{aligned}$$
(16)

The balance condition is; \(m=s-1,s\ge 2\) and \(m=1\) when \(s=1.\)

It was found that a necessary condition for a complex field equation (cf.(9)) to be integrable is that the real and imaginary parts are linearly dependent. But this condition is not, in general, sufficient (Kodama 1985; Wazwaz et al. 2023).

2.4 Breathers, dromian shape and complex chirped soliton

2.4.1 Breathers

Here, we consider (15), when \(r=2\) and \(s=2,\)the solutions in (15) reduce to,

$$\begin{aligned} U(z) = a_{1}\phi (z)+a_{0},\;V(z) = b_{1}\phi (z)+b_{0},\;b_{0} = \frac{a_{0}b_{1}}{a_{1}}, \end{aligned}$$
(17)

and the AE is,

$$\begin{aligned} \phi '(z) = \sqrt{c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}}\left( m_{1}\phi (z)+m_{0}\right) . \end{aligned}$$
(18)

By plugging (17) and (18) into (13) and (14), and by setting the coefficients of \(\phi ^{i}(z),i=0,1,2,...etc,\) equal to zero gives rise to,

$$\begin{aligned} \begin{array}{l} k = \frac{\left( a_{1}^{2}+b_{1}^{2}\right) (3\mu +2\sigma )}{24c_{2}\delta m_{1}^{2}p^{2}},\;a_{0} = \frac{1}{4}a_{1}\left( \frac{c_{1}}{c_{2}}+\frac{2m_{0}}{m_{1}}\right) ,\;m_{1} {=} \frac{2c_{2}m_{0}}{c_{1}},\\ q = -\frac{1}{6\gamma ^{2}c_{1}^{2}c_{2}^{2}\left( a_{1}^{2}+b_{1}^{2}\right) }p\left( 6b_{1}^{2}c_{1}^{2}c_{2}^{2}\gamma (3\beta \mu +2\beta \sigma -\gamma \nu )\right. \\ \qquad +\gamma ^{2}(3\mu +2\sigma )b_{1}^{4}c_{1}^{2}\left( c_{1}^{2}-4c_{0}c_{2}\right) +2\gamma a_{1}^{2}c_{1}^{2}c_{2}^{2}(3(3\beta \mu +2\beta \sigma -\gamma \nu )\\ \qquad +\gamma (3\mu +2\sigma )\left. \left. b_{1}^{2}\left( c_{1}^{2}-4c_{0}c_{2}\right) \right) +16c_{2}^{5}m_{0}^{2}p^{2}\sigma (3\mu +2\sigma )^{2}\right) ,\\ \alpha = -\frac{1}{192\gamma c_{2}^{5}m_{0}^{2}p^{2}}\left( 5a_{1}^{4}\gamma ^{2}c_{1}^{2}\left( c_{1}^{2}-4c_{0}c_{2}\right) +24\beta b_{1}^{2}\gamma c_{1}^{2}c_{2}^{2}\right. \\ \qquad +5b_{1}^{4}\gamma ^{2}c_{1}^{2}\left( c_{1}^{2}-4c_{0}c_{2}\right) \left. +48c_{2}^{5}m_{0}^{2}p^{2}\left( 3\mu ^{2}+8\mu \sigma +4\sigma ^{2}\right) \right) \\ \qquad +2a_{1}^{2}\gamma c_{1}^{2}\left( 5b_{1}^{2}\gamma \left( c_{1}^{2}-4c_{0}c_{2}\right) +12\beta c_{2}^{2}\right) ,\\ \omega = -\frac{1}{1152\gamma ^{2}c_{1}^{4}c_{2}^{4}\delta }\left( 27a_{1}^{4}\gamma ^{3}\left( c_{1}^{2}-4c_{0}c_{2}\right) {}^{2}c_{1}^{4}\delta +27b_{1}^{4}\gamma ^{3}c_{1}^{4}\delta \right. \\ \qquad \left( c_{1}^{2}-4c_{0}c_{2}\right) {}^{2}-323\mu +2\sigma c_{2}^{5}m_{0}^{2}\left( 6\sqrt{6}\sqrt{-\gamma }c_{1}^{2}\sqrt{\delta }(-3\beta \mu -\right. \\ \qquad 2\beta \sigma +2\gamma \nu )\left. c_{2}m_{0}^{2}+(3\mu +2\sigma )^{2}(3\mu +10\sigma )\right) +8b_{1}^{2}\gamma c_{1}^{2}c_{2}^{2}\\ \qquad \left( c_{1}^{2}-4c_{0}c_{2}\right) \sqrt{\delta }\left( 18\beta \gamma c_{1}^{2}\sqrt{\delta }+\sqrt{6}\sqrt{-\gamma }\left( 27\mu ^{2}+48\mu \sigma +20\sigma ^{2}\right) \right. \\ \qquad \left. c_{2}m_{0}^{2}\right) +2\gamma \sqrt{\delta }a_{1}^{2}c_{1}^{2}c_{1}^{2}-4c_{0}c_{2}\left( 27b_{1}^{2}\gamma ^{2}c_{1}^{2}\left( c_{1}^{2}-4c_{0}c_{2}\right) \sqrt{\delta }\right. \\ \qquad \left. \left. +4c_{2}^{2}\left( 18\beta \gamma c_{1}^{2}\sqrt{\delta }+\sqrt{6}\sqrt{-\gamma }c_{2}m_{0}^{2}\left( 27\mu ^{2}+48\mu \sigma +20\sigma ^{2}\right) \right) \right) \right) ,\\ p = \frac{\root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{1}^{2}+b_{1}^{2}}}{2^{3/4}c_{2}\root 4 \of {\delta }},\gamma <0. \end{array} \end{aligned}$$
(19)

The solutions of (1) and (12) are,

$$\begin{aligned} \begin{array}{l} u(x,\tau )=\frac{a_{1}\sqrt{4c_{0}c_{2}-c_{1}^{2}}\text {sech}\left( \frac{\sqrt{c_{2}}\sqrt{4c_{0}c_{2}-c_{1}^{2}}\left( m_{0}z+c_{1}c_{1}\right) }{c_{1}}\right) }{2c_{2}},\\ v(x,\tau )=\frac{b_{1}u(x,t)}{a_{1}},z=\frac{x\left( \root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{1}^{2}+b_{1}^{2}}\right) }{2^{3/4}c_{2}\root 4 \of {\delta }}-\frac{p\,\tau }{6\gamma ^{2}c_{1}^{2}c_{2}^{2}\left( a_{1}^{2}+b_{1}^{2}\right) }\\ \left( a_{1}^{4}\gamma ^{2}c_{1}^{2}\left( c_{1}^{2}-4c_{0}c_{2}\right) (3\mu +2\sigma )+6b_{1}^{2}\gamma c_{1}^{2}c_{2}^{2}(3\beta \mu +2\beta \sigma -\gamma \nu )\right. \\ b_{1}^{4}+\gamma ^{2}c_{1}^{2}\left( c_{1}^{2}-4c_{0}c_{2}\right) (3\mu +2\sigma )+2\gamma a_{1}^{2}c_{1}^{2}\left( 3c_{2}^{2}(3\beta \mu +2\beta \sigma -\gamma \nu )\right. \\ \left. \left. b_{1}^{2}+\gamma \left( c_{1}^{2}-4c_{0}c_{2}\right) (3\mu +2\sigma )\right) +16c_{2}^{5}m_{0}^{2}p^{2}\sigma (3\mu +2\sigma )^{2}\right) ,\\ \tau =Log\left( _{i}E_{\rho }(t)\right) ,\;i=10. \end{array}, \end{aligned}$$
(20)

By using (20), \(Rew(x,t)\,\)

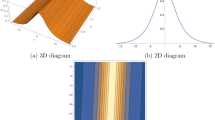
$$\begin{aligned} Rew(x,t)=u(x,t)(cos(kx-\omega Log({}_{10}E_{\rho }(t)))-\frac{b_{1}}{a_{1}}sin(kx-\omega Log({}_{10}E_{\rho }(t)))), \end{aligned}$$
(21)

is displayed in Fig. 1(i)–(iv). We mention that in all the figures shown the following parameters are fixed, \(\mu = 0.8,\sigma = 0.4,\gamma = -0.3,\delta = 0.8,\nu = 0.3,A = 2,\alpha =0.4,\beta =1.2.\)

Fig. 1
figure 1

(i)–(iv), the 3D plot and contour plot for Rew(x, t) respectively when \(a_{1} = 0.5,b_{1} = 0.7,m_{0} = 0.2,c_{1} = 0.9,c_{0} = 0.5,c_{2} = 0.8.\)

Full size image

Figure 1(i) shows complex rhombus shaped soliton, Fig. 1(ii)–(iv) exhibit hyper chaos.

Figure 1(iii) show fractals that occurs intermediately, when \(t=0.3.\)

2.4.2 Complex chirped soliton

Here, we consider (16), when \(r=2,s=2\) and \(m=1.\)

Here, (16) is reduced to,

$$\begin{aligned} \begin{array}{c} U(z) = \frac{a_{1}\phi (z)+a_{0}}{s_{1}\phi (z)+s_{0}},\;V(z) = \frac{b_{1}\phi (z)+b_{0}}{s_{1}\phi (z)+s_{0}},\;b_{0} = \frac{a_{0}b_{1}}{a_{1}},\end{array} \end{aligned}$$
(22)

and the auxiliary equation (AE) is,

$$\begin{aligned} \phi '(z) = \sqrt{c_{4}\phi (z)^{4}+c_{3}\phi (z)^{3}+c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}} \end{aligned}$$
(23)

By inserting (22) and (23) into (13) and (14) leads to,

$$\begin{aligned} \begin{array}{l} q=\frac{1}{Q}\root 4 \of {2}\root 4 \of {-\gamma }\left( 32\sqrt{2}\sqrt{-\gamma }c_{2}\delta ks_{1}^{2}\sqrt{\delta }+\frac{63\sqrt{3}s_{1}^{3}\left( c_{3}s_{0}+c_{2}s_{1}\right) \left( 4\delta k^{3}-2\alpha k+\nu \right) }{a_{1}^{2}+b_{1}^{2}}\right. \\ \qquad \left. +6\sqrt{2}\sqrt{-\gamma }\delta k\sqrt{16c_{2}^{2}s_{1}^{4}-7m^{2}}\right) ,\\ Q=189\ 3^{3/4}\delta ^{3/4}s_{1}^{7/2}\left( \frac{c_{3}s_{0}+c_{2}s_{1}}{a_{1}^{2}+b_{1}^{2}}\right) {}^{3/2},\;a_{0} = -\frac{a_{1}s_{0}}{3s_{1}},\;c_{4} = \frac{s_{1}^{2}\left( c_{2}s_{0}-2c_{0}c_{1}s_{1}\right) }{s_{0}^{3}},\\ \qquad \omega \text { =}\frac{1}{P}\left( -486b_{1}^{2}\sqrt{\delta }ks_{1}^{4}\left( c_{3}s_{0}+c_{2}s_{1}\right) {}^{2}\left( \delta k^{3}-\alpha k+\nu \right) -4a_{1}^{6}\gamma \sqrt{\delta }\right. \\ \qquad -4b_{1}^{6}\gamma \sqrt{\delta }\left( 3c_{3}^{2}s_{0}^{2}+6c_{2}c_{3}s_{1}s_{0}-c_{2}^{2}s_{1}^{2}\right) +\left( 3c_{3}^{2}s_{0}^{2}+6c_{2}c_{3}s_{1}s_{0}-c_{2}^{2}s_{1}^{2}\right) \\ \qquad +9\sqrt{6}\sqrt{-\gamma }b_{1}^{4}s_{1}^{2}\left( 3c_{3}^{2}s_{0}^{2}+10c_{2}c_{3}s_{1}s_{0}+7c_{2}^{2}s_{1}^{2}\right) \left( \alpha -6\delta k^{2}\right) \\ \qquad -6a_{1}^{2}\left( c_{3}s_{0}+c_{2}s_{1}\right) \left( -3\sqrt{6}b_{1}^{2}\sqrt{-\gamma }c_{2}s_{1}^{2}\left( \alpha -6\delta k^{2}\right) \right. \\ 2b_{1}^{4}\gamma \sqrt{\delta }\left( 3c_{3}s_{0}-c_{2}s_{1}\right) +\left( 24\gamma c_{3}\delta s_{0}+7s_{1}\right) +81\sqrt{\delta }k\left( \delta k^{3}-\alpha k+\nu \right) \\ \qquad \left. s_{1}^{4}\left( c_{3}s_{0}+c_{2}s_{1}\right) \right) -3a_{1}^{4}c_{3}s_{0}+c_{2}s_{1}\left( 4b_{1}^{2}\gamma \sqrt{\delta }\left( 3c_{3}s_{0}-c_{2}s_{1}\right) \right. \\ \qquad \left. \left. -3\sqrt{6}\sqrt{-\gamma }s_{1}^{2}\left( 3c_{3}s_{0}+7c_{2}s_{1}\right) \left( \alpha -6\delta k^{2}\right) \right) \right) ,\\ P=486\sqrt{\delta }s_{1}^{4}\left( a_{1}^{2}+b_{1}^{2}\right) \left( c_{3}s_{0}+c_{2}s_{1}\right) {}^{2},\\ \beta = \frac{\alpha \sqrt{-\gamma }}{\sqrt{6}\sqrt{\delta }}-k\left( \sqrt{6}\sqrt{-\gamma }\sqrt{\delta }k+\mu \right) +\frac{5a_{1}^{2}\gamma \left( 3c_{3}s_{0}+7c_{2}s_{1}\right) }{27s_{1}^{2}\left( c_{3}s_{0}+c_{2}s_{1}\right) }\\ \qquad +\frac{5b_{1}^{2}\gamma \left( 3c_{3}s_{0}+7c_{2}s_{1}\right) }{27s_{1}^{2}\left( c_{3}s_{0}+c_{2}s_{1}\right) },\;c_{0} = \frac{c_{3}s_{0}^{2}+2c_{2}s_{1}s_{0}}{c_{1}s_{1}^{2}}.p = \frac{\root 4 \of {-\frac{1}{3}(2\gamma )}\sqrt{a_{1}^{2}+b_{1}^{2}}}{3\root 4 \of {\delta }\sqrt{\left( c_{3}s_{0}+c_{2}s_{1}\right) s_{1}^{\square }}},\\ k = -\frac{3\sqrt{\delta }\mu +2\sigma }{2\sqrt{6}\sqrt{-\gamma }\sqrt{\delta }},s_{0} = \frac{\sqrt{16c_{2}^{2}s_{1}^{4}-7m^{2}}-11c_{2}s_{1}^{2}}{7c_{3}s_{1}},\gamma <0 \end{array} \end{aligned}$$
(24)

The solutions of (11) and (12) are,

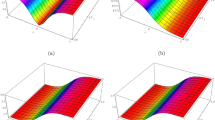
$$\begin{aligned} \begin{array}{l} u(x,\tau )=\frac{P_{1}}{Q_{1}},\;\\ P_{1}=-7a_{1}\left[-2m\text {sn}\left(\frac{(A+z)\sqrt{\left( 30c_{2}^{2}s_{1}^{4}-m^{2}\right) \left( 16c_{2}s_{1}^{2}+7m+3\sqrt{16c_{2}^{2}s_{1}^{4}-7m^{2}}\right) }}{2\sqrt{14}s_{1}},\right. \right. \\ \qquad \times \left. \left. \frac{14m}{16c_{2}s_{1}^{2}+m+3\sqrt{16c_{2}^{2}s_{1}^{4}-7m^{2}}}\right)^{2}\right],\;v(x,\tau )=\frac{b_{1}}{a_{1}}u(x,\tau ),\\ z=\frac{x\left( \root 4 \of {-\frac{1}{3}(2\gamma )}\sqrt{a_{1}^{2}+b_{1}^{2}}\right) }{3\root 4 \of {\delta }\sqrt{s_{1}\left( c_{3}s_{0}+c_{2}s_{1}\right) }}+\frac{1}{H}\tau \left( \root 4 \of {2}\root 4 \of {-\gamma }\left( 32\sqrt{2}\sqrt{-\gamma }c_{2}\delta ks_{1}^{2}\right. \right. \\ \qquad \left. \left. +\sqrt{\delta }\left( \frac{63\sqrt{3}s_{1}^{3}\left( c_{3}s_{0}+c_{2}s_{1}\right) \left( 4\delta k^{3}-2\alpha k+\nu \right) }{a_{1}^{2}+b_{1}^{2}}\right) +6\sqrt{2}\sqrt{-\gamma }\delta k\sqrt{16c_{2}^{2}s_{1}^{4}-7m^{2}}\right) \right) ,\\ \tau =Log\left( _{i}E_{\rho }(t)\right) ,i=10 \end{array} \end{aligned}$$
(25)

The results in (25) are used to display Rew(x, t) in Fig. 2(i)–(iv).

Fig. 2
figure 2

(i)–(iv) When \(a_{1} = 2.5, b_{1}=1.3,c_{2}=-1.5,m=6,s_{1}=3,\alpha =0.7.\)

Full size image

Figure 2 (i) shows complex chirped solitons.

Figure 2(ii) and (iii) show hyper chaos. Figure 2(iii) and (iv) exhibit the behavior in space for different values of t and of the fractional order respectively.

2.4.3 Dromian soliton

We consider (22) when the AE is,

$$\begin{aligned} \phi '(z) = \sqrt{c_{2}\phi (z)^{2}+c_{0}}\left( m_{1}\phi (z)+m_{0}\right) . \end{aligned}$$
(26)

From (22) and (26) into (13) and (14) gives rise to,

$$\begin{aligned} \begin{array}{l} m_{1} = \frac{m_{0}s_{1}\left( 3c_{2}s_{0}^{2}+2c_{0}s_{1}^{2}\right) }{4c_{2}s_{0}^{3}+3c_{0}s_{1}^{2}s_{0}},\;a_{0} = \frac{2a_{1}s_{0}}{s_{1}},\;c_{2} = -\frac{c_{0}s_{1}^{2}}{2s_{0}^{2}},\;\delta = -\frac{8\gamma s_{0}^{4}\left( a_{1}^{2}+b_{1}^{2}\right) {}^{2}}{3c_{0}^{2}m_{0}^{4}p^{4}s_{1}^{8}}\\ q = p\left( \frac{a_{1}^{2}(3\mu +2\sigma )}{s_{1}^{2}}-4c_{0}\delta km_{1}^{2}p^{2}+4\delta k^{3}-2\alpha k+\nu \right. \\ \qquad \left. +\frac{3b_{1}^{2}\mu }{s_{1}^{2}}+\frac{2b_{1}^{2}\sigma }{s_{1}^{2}}-\frac{4c_{2}\delta kp^{2}\left( 6m_{1}^{2}s_{0}^{2}-6m_{0}m_{1}s_{1}s_{0}+m_{0}^{2}s_{1}^{2}\right) }{s_{1}^{2}}\right) ,\\ \sigma = -\frac{8a_{1}^{2}\gamma ks_{0}^{2}+8b_{1}^{2}\gamma ks_{0}^{2}+3c_{0}\mu m_{0}^{2}p^{2}s_{1}^{4}}{2c_{0}m_{0}^{2}p^{2}s_{1}^{4}},\;c_{2} = -\frac{c_{0}s_{1}^{2}}{2s_{0}^{2}},\\ \beta = -\frac{1}{12c_{0}m_{0}^{2}p^{2}s_{0}^{2}s_{1}^{4}\left( a_{1}^{2}+b_{1}^{2}\right) }\left( 12b_{1}^{2}c_{0}k\mu m_{0}^{2}p^{2}s_{0}^{2}s_{1}^{4}+3\alpha c_{0}^{2}m_{0}^{4}p^{4}s_{1}^{8}\right. \\ \qquad +4a_{1}^{4}\gamma s_{0}^{2}\left( 5c_{0}m_{0}^{2}p^{2}s_{1}^{2}+12k^{2}s_{0}^{2}\right) +4b_{1}^{4}\gamma s_{0}^{2}\left( 5c_{0}m_{0}^{2}p^{2}s_{1}^{2}+12k^{2}s_{0}^{2}\right) \\ \qquad \left. +4a_{1}^{2}s_{0}^{2}\left( 2b_{1}^{2}\gamma \left( 5c_{0}m_{0}^{2}p^{2}s_{1}^{2}+12k^{2}s_{0}^{2}\right) +3c_{0}k\mu m_{0}^{2}p^{2}s_{1}^{4}\right) \right) ,\\ \omega = \frac{1}{12c_{0}^{2}m_{0}^{4}p^{4}s_{0}^{2}s_{1}^{8}}\left( 3c_{0}^{2}m_{0}^{4}p^{4}s_{1}^{8}\left( \alpha c_{0}m_{0}^{2}p^{2}s_{1}^{2}+4ks_{0}^{2}(\alpha k-\nu )\right) \right. \\ \qquad +2a_{1}^{4}\gamma s_{0}^{2}\left( 24c_{0}k^{2}m_{0}^{2}p^{2}s_{1}^{2}s_{0}^{2}+c_{0}^{2}m_{0}^{4}p^{4}s_{1}^{4}+16k^{4}s_{0}^{4}\right) \\ \qquad +4a_{1}^{2}b_{1}^{2}\gamma s_{0}^{2}\left( 24c_{0}k^{2}m_{0}^{2}p^{2}s_{1}^{2}s_{0}^{2}+c_{0}^{2}m_{0}^{4}p^{4}s_{1}^{4}+16k^{4}s_{0}^{4}\right) \\ \qquad \left. +2b_{1}^{4}\gamma s_{0}^{2}\left( 24c_{0}k^{2}m_{0}^{2}p^{2}s_{1}^{2}s_{0}^{2}+c_{0}^{2}m_{0}^{4}p^{4}s_{1}^{4}+16k^{4}s_{0}^{4}\right) \right) . \end{array} \end{aligned}$$
(27)

The solutions of (11) and (12) are,

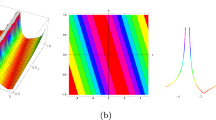
$$\begin{aligned} \begin{array}{l} u(x,\tau )=\frac{P}{Q},\;P=\left( a_{1}\left( -2s_{0}s_{1}\text {sech}^{2}(\frac{A}{2}-\frac{\sqrt{-c_{0}}zms_{1}}{2s_{0}})\right. \right. \\ \qquad \left. +\sqrt{2}\sqrt{s_{0}^{2}s_{1}^{2}\tanh ^{2}(\frac{A}{2}-\frac{\sqrt{-c_{0}}zms_{1}}{2s_{0}})\left( 1-\tanh ^{2}(\frac{A}{2}-\frac{\sqrt{-c_{0}}zms_{1}}{2s_{0}})\right) }\right) ,\\ Q=s_{1}\left( s_{0}s_{1}\tanh ^{2}(\frac{A}{2}-\frac{\sqrt{-c_{0}}zms_{1}}{2s_{0}})+\sqrt{2}\sqrt{s_{0}^{2}s_{1}^{2}\tanh ^{2}(\frac{A}{2}-\frac{\sqrt{-c_{0}}zms_{1}}{2s_{0}})}\right) \\ \qquad \sqrt{1-\tanh ^{2}(\frac{A}{2}-\frac{\sqrt{-c_{0}}zms_{1}}{2s_{0}}},\;v(x,\tau )=\frac{b_{1}}{a_{1}}u(x,\tau ),\;z=px-\frac{\tau }{3c_{0}^{2}m_{0}^{4}p^{3}s_{1}^{8}}\\ \qquad \left( -3c_{0}^{2}\right. m_{0}^{4}p^{4}s_{1}^{8}(\nu -2\alpha k)16a_{1}^{2}b_{1}^{2}\gamma ks_{0}^{2}++8a_{1}^{4}\gamma ks_{0}^{2}\left( c_{0}m_{0}^{2}p^{2}s_{1}^{2}+4k^{2}s_{0}^{2}\right) \\ \qquad \left. 8b_{1}^{4}\gamma ks_{0}^{2}\left( c_{0}m_{0}^{2}p^{2}s_{1}^{2}+4k^{2}s_{0}^{2}\right) +\left( c_{0}m_{0}^{2}p^{2}s_{1}^{2}+4k^{2}s_{0}^{2}\right) \right) . \end{array} \end{aligned}$$
(28)

Rew(x, t) is displayed in Fig. 3(i)–(iv), by using (28).

Fig. 3
figure 3

(i)–(iv), when \(a_{1} = 0.05,b_{1} = 0.03,c_{0} = -1.5,m_{1} = 0.6,m_{0} = 1.5,s_{1} = 1.3,s_{0} = 1.8,k = 15,p = 0.007.\)

Full size image

Figure 3(i) shows complex dromian pattern soliton, while Fig. 3(ii)–(iv) show oscillatory behavior.

2.5 Geometric chaos

2.5.1 Complex chirped soliton

Here, we employ (22), together with the AE,.

$$\begin{aligned} \phi '(z) = \sqrt{c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}}\sqrt{m_{2}\phi (z)^{2}+m_{1}\phi (z)+m_{0}}. \end{aligned}$$
(29)

From (22) and (29) into (13) and (14) gives rise to,

$$\begin{aligned} \begin{array}{l} k = \frac{\left( a_{1}^{2}+b_{1}^{2}\right) (3\mu +2\sigma )}{24c_{2}\delta m_{2}p^{2}},\;a_{0} = \frac{1}{4}a_{1}\left( \frac{c_{1}}{c_{2}}+\frac{m_{1}}{m_{2}}\right) ,\;c_{1} = -\frac{c_{2}m_{1}}{m_{2}},\;m_{0} = \frac{c_{0}m_{2}}{c_{2}},\\ q = \frac{1}{Q}\sqrt{a_{1}^{2}+b_{1}^{2}}\left( -\left( \left( 6\sqrt{3}\sqrt{-\gamma }\gamma \sqrt{\delta }\nu -6\sqrt{3}\beta \sqrt{-\gamma }\sqrt{\delta }(3\mu +2\sigma )\right. \right. \right. \\ \qquad \left. \left. +\sqrt{2}\sigma (3\mu +2\sigma )^{2}\right) m_{2}^{2}\right) +4\sqrt{3}a_{1}^{2}\sqrt{-\gamma }\gamma \sqrt{\delta }(3\mu +2\sigma )\left( 2m_{2}^{2}n^{2}+m_{1}^{2}\right) \\ \qquad \left. +4\sqrt{3}b_{1}^{2}\sqrt{-\gamma }\gamma \sqrt{\delta }(3\mu +2\sigma )\left( 2m_{2}^{2}n^{2}+m_{1}^{2}\right) \right) ,\\ Q=6\ 6^{3/4}(-\gamma )^{5/4}\sqrt{c_{2}}\delta ^{3/4}m_{2}^{5/2},\;\alpha =\frac{1}{4\sqrt{6}(-\gamma )^{3/2}m_{2}^{2}}(\\ \qquad m_{2}^{2}\left( 24\beta \gamma \sqrt{\delta }+\sqrt{6}\sqrt{-\gamma }\left( 3\mu ^{2}+8\mu \sigma +4\sigma ^{2}\right) \right) \\ \qquad +20a_{1}^{2}\gamma ^{2}\sqrt{\delta }\left( 2m_{2}^{2}n^{2}+m_{1}^{2}\right) +20b_{1}^{2}\gamma ^{2}\sqrt{\delta }\left( 2m_{2}^{2}n^{2}+m_{1}^{2}\right) ,\\ \omega = -\frac{1}{576\gamma ^{2}\delta m_{2}^{4}}\left( -\left( 3\mu +2\sigma \left( 48\sqrt{6}\gamma \sqrt{-\gamma }\sqrt{\delta }\nu +27\mu ^{3}+126\mu ^{2}\sigma \right. \right. \right. \\ \qquad \left. \left. +40\sigma ^{3}-24\sqrt{6}\beta \sqrt{-\gamma }\sqrt{\delta }(3\mu +2\sigma )\right) m_{2}^{4}\right) \\ \qquad +4\gamma \sqrt{\delta }\left( 72\beta \gamma \sqrt{\delta }+\sqrt{6}\sqrt{-\gamma }\left( 27\mu ^{2}+48\mu \sigma +20\sigma ^{2}\right) \right) +72a_{1}^{4}\gamma ^{3}\delta \\ \qquad \left( 8m_{2}^{4}n^{4}+12m_{2}^{2}m_{1}^{2}n^{2}+3m_{1}^{4}\right) +72b_{1}^{4}\gamma ^{3}\delta +b_{1}^{2}m_{2}^{2}\left( 2m_{2}^{2}n^{2}+m_{1}^{2}\right) \\ \qquad 8m_{2}^{4}n^{4}+12m_{2}^{2}m_{1}^{2}n^{2}+3m_{1}^{4}+4a_{1}^{2}\left( \gamma \sqrt{\delta }\left( 72\beta \gamma \sqrt{\delta }+\sqrt{6}\sqrt{-\gamma }\left( 27\mu ^{2}\right. \right. \right. \\ \qquad \left. \left. \left. \left. +48\mu \sigma +20\sigma ^{2}\right) \right) m_{2}^{2}2m_{2}^{2}n^{2}+m_{1}^{2}+36b_{1}^{2}\gamma ^{3}\delta \left( 8m_{2}^{4}n^{4}+12m_{2}^{2}m_{1}^{2}n^{2}+3m_{1}^{4}\right) \right) \right) ,\\ c_{0} = -n^{2}c_{2},\;p = \frac{\root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{1}^{2}+b_{1}^{2}}}{2^{3/4}\sqrt{c_{2}}\root 4 \of {\delta }\sqrt{m_{2}}},\gamma <0. \end{array} \end{aligned}$$
(30)

The solutions of (11) and (12) are,

$$\begin{aligned} \begin{array}{l} u(x,\tau ) = \frac{1}{Q}\left( \text {sn}\left( \sqrt{2}n^{2}(A+z)\sqrt{c_{2}m_{2}^{3}K},\frac{2m_{2}^{2}n^{2}-\sqrt{4m_{2}^{2}m_{1}^{2}n^{2}+m_{1}^{4}}+m_{1}^{2}}{2m_{2}^{2}n^{2}+\sqrt{4m_{2}^{2}m_{1}^{2}n^{2}+m_{1}^{4}}+m_{1}^{2}}\right) \right. \\ \qquad a_{1}(2m_{2}^{4}n^{4}+m_{1}^{2}\left( -\sqrt{4m_{2}^{2}m_{1}^{2}n^{2}+m_{1}^{4}}\right) -2m_{2}^{2}n^{2}\sqrt{4m_{2}^{2}m_{1}^{2}n^{2}+m_{1}^{4}}\\ \qquad +4m_{2}^{2}n^{2}+m_{1}^{4}),\;Q=K\left( 2m_{2}^{2}n^{2}-\sqrt{4m_{2}^{2}m_{1}^{2}n^{2}+m_{1}^{4}}+m_{1}^{2}\right) {}^{2}\\ K=\sqrt{\frac{m_{2}^{2}}{2m_{2}^{2}n^{2}-\sqrt{4m_{2}^{2}m_{1}^{2}n^{2}+m_{1}^{4}}+m_{1}^{2}}},\;v(x,\tau )=\frac{b_{1}}{a_{1}}u(x,\tau ),\\ z=\frac{x\left( \root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{1}^{2}+b_{1}^{2}}\right) }{2^{3/4}\sqrt{c_{2}}\root 4 \of {\delta }\sqrt{m_{2}}}+\frac{\tau }{Q}\left( \sqrt{a_{1}^{2}+b_{1}^{2}}\left( -\left( \left( 6\sqrt{3}\sqrt{-\gamma }\gamma \sqrt{\delta }\nu -6\sqrt{3}\beta \sqrt{-\gamma })\right. \right. \right. \right. \\ \sqrt{\delta }(3\mu +2\sigma )\left. \left. +\sqrt{2}\sigma (3\mu +2\sigma )^{2}\right) m_{2}^{2}\right) +4\sqrt{3}a_{1}^{2}\sqrt{-\gamma }\gamma \sqrt{\delta }(3\mu +2\sigma )\\ \left( 2m_{2}^{2}n^{2}+m_{1}^{2}\right) \left. \left. +4\sqrt{3}b_{1}^{2}\sqrt{-\gamma }\gamma \sqrt{\delta }(3\mu +2\sigma )\left( 2m_{2}^{2}n^{2}+m_{1}^{2}\right) \right) \right) ,\\ Q=6\ 6^{3/4}(-\gamma )^{5/4}\sqrt{c_{2}}\delta ^{3/4}m_{2}^{5/2},\tau =Log\left( _{i}E_{\rho }(t)\right) . \end{array} \end{aligned}$$
(31)

We use (31) to display Rew(x, t) in Fig. 4(i) and (ii).

Fig. 4
figure 4

(i) and (ii), when \(a_{1} = 0.5,b_{1} = 0.7,m_{1} = 0.7,m_{2} = 0.5,n = 0.3,c_{2} = 0.8\)

Full size image

Figure 4(i) shows complex chirped solitons, while Fig. 4(ii) shows geometric chaos.

Case (b). Complex M-shaped soliton

In this case, we write,

$$\begin{aligned} \begin{array}{l} U(z) = a_{2}\phi (z)^{2}+a_{1}\phi (z)+a_{0},\;V(z) = b_{2}\phi (z)^{2}+b_{1}\phi (z)+b_{0},\\ b_{0} = \frac{a_{0}b_{2}}{a_{2}},\;b_{1} = \frac{a_{1}b_{2}}{a_{2}},\;\phi '(z) = c_{3}\phi (z)^{3}+c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}. \end{array} \end{aligned}$$
(32)

By using (32) into (13) and (14), we get,

$$\begin{aligned} \begin{array}{l} a_{1} = \frac{2a_{2}c_{2}}{3c_{3}},\;k = \frac{3\mu +2\sigma }{2\sqrt{6}\sqrt{-\gamma }c_{2}\sqrt{\delta }},\;c_{0} = \frac{9c_{1}c_{2}c_{3}-2c_{2}^{3}}{27c_{3}^{2}},\;a_{0} = -\frac{a_{2}\left( c_{2}^{2}-9c_{1}c_{3}\right) }{18c_{3}^{2}},\\ \alpha = -\frac{1}{36\sqrt{6}(-\gamma )^{3/2}c_{3}^{4}}\left( -9\left( \sqrt{6}\sqrt{-\gamma }\left( 3\mu ^{2}+8\mu \sigma +4\sigma ^{2}\right) \left. +24\beta \gamma c_{2}\sqrt{\delta }\right) c_{3}^{4}\right. \right. \\ \qquad \left. -10a_{2}^{2}\gamma ^{2}c_{2}\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}\sqrt{\delta }-10b_{2}^{2}\gamma ^{2}c_{2}\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}\sqrt{\delta }\right) ,\\ q = -\frac{1}{108\ 2^{3/4}\root 4 \of {3}(-\gamma )^{7/4}c_{2}^{3/2}c_{3}^{5}\delta ^{3/4}}\left( \sqrt{a_{2}^{2}+b_{2}^{2}}\left( 3\left( \sqrt{6}\sqrt{-\gamma }\sigma (3\mu +2\sigma )^{2}\right. \right. \right. \\ \qquad \left. +18\gamma c_{2}\sqrt{\delta }(3\beta \mu +2\beta \sigma -\gamma \nu )\right) c_{3}^{4}+2a_{2}^{2}\gamma ^{2}c_{2}\sqrt{\delta }(3\mu +2\sigma )\\ \qquad \left. \left. +\left( 2a_{2}^{2}\gamma ^{2}c_{2}\sqrt{\delta }(3\mu +2\sigma )+2b_{2}^{2}\gamma ^{2}c_{2}\sqrt{\delta }(3\mu +2\sigma )\right) \right) \right) ,\\ \omega = -\frac{1}{5184\gamma ^{2}c_{2}^{2}c_{3}^{8}\delta }\left( -93\mu +2\sigma \left( (3\mu +2\sigma )^{2}(3\mu +10\sigma )\right. \right. \\ \qquad \left. +24\sqrt{6}\sqrt{-\gamma }c_{2}\sqrt{\delta }(-3\beta \mu -2\beta \sigma +2\gamma \nu )\right) c_{3}^{8}+2\gamma \sqrt{\delta }b_{2}^{2}c_{2}\\ \qquad \left( \sqrt{6}\sqrt{-\gamma }(27\mu ^{2}\right. +48\mu \sigma +20\sigma ^{2})\left. +72\beta \gamma c_{2}\sqrt{\delta }\right) c_{3}^{4}\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}\\ \qquad +4a_{2}^{4}\gamma ^{3}c_{2}^{2}\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{4}\delta +4b_{2}^{4}\gamma ^{3}c_{2}^{2}\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{4}\delta \\ \qquad +2a_{2}^{2}\left( \gamma \sqrt{\delta }c_{2}\left( \sqrt{6}\sqrt{-\gamma }\right. \right. \left. 72\beta \gamma c_{2}\sqrt{\delta }+\left( 27\mu ^{2}+48\mu \sigma +20\sigma ^{2}\right) \right) \\ \qquad c_{3}^{4}\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}\left. \left. +4b_{2}^{2}\gamma ^{3}c_{2}^{2}\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{4}\delta \right) \right) ,\\ p = \frac{\root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{2}^{2}+b_{2}^{2}}}{2\ 2^{3/4}\sqrt{c_{2}}c_{3}\root 4 \of {\delta }},\gamma <0. \end{array} \end{aligned}$$
(33)

The solutions of (11) and (12) are,

$$\begin{aligned} \begin{array}{l} u(x,\tau ) = \frac{a_{2}\left( c_{2}^{2}-3c_{1}c_{3}\right) \left( e^{2c_{1}(A+z)}-e^{\frac{2c_{2}^{2}(A+z)}{3c_{3}}}\right) }{6c_{3}^{2}\left( e^{2c_{1}(A+z)}+e^{\frac{2c_{2}^{2}(A+z)}{3c_{3}}}\right) },v(x,\tau )=\frac{b_{1}}{a_{1}}u(x,\tau ),\\ z=\frac{x\left( \root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{2}^{2}+b_{2}^{2}}\right) }{2\ 2^{3/4}\sqrt{c_{2}}\root 4 \of {\delta }m_{2}}-\frac{\root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{2}^{2}+b_{2}^{2}}\tau }{\left( 2\ 2^{3/4}\sqrt{c_{2}}\root 4 \of {\delta }m_{2}\right) \left( 27\gamma ^{2}c_{3}^{4}\left( a_{2}^{2}+b_{2}^{2}\right) \right) }\\ \qquad \left( 27b_{2}^{2}\gamma c_{3}^{4}(3\beta \mu +2\beta \sigma -\gamma \nu )+72c_{3}^{6}p^{2}\sigma (3\mu +2\sigma )^{2}+a_{2}^{4}\gamma ^{2}\right. \\ \qquad \left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}(3\mu +2\sigma )+b_{2}^{4}\gamma ^{2}\left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}(3\mu +2\sigma )\\ \qquad \left. a_{2}^{2}+\gamma \left( 2b_{2}^{2}\gamma \left( c_{2}^{2}-3c_{1}c_{3}\right) {}^{2}(3\mu +2\sigma )+27c_{3}^{4}(3\beta \mu +2\beta \sigma -\gamma \nu )\right) \right) ,\\ \tau =Log\left( _{i}E_{\rho }(t)\right) . \end{array} \end{aligned}$$
(34)

In Fig. 5(i) and (ii), Rew(x, t) is displayed, by using (34).

Fig. 5
figure 5

(i) and (ii), when \(a_{2} = 2.5,b_{2} = 1.7,c_{1} = 0.7,c_{2} = 1.5,c_{3} = 0.3,m_{2} = c_{3}.\)

Full size image

Figure 5(i) shows complex undulated M-shaped solitons, while Fig. 4(ii) exhibits geometric chaos.

2.5.2 Breathers-line

Here, we use consider (22) and the AE is taken,

$$\begin{aligned} \phi '(z) = \sqrt{c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}}\sqrt{m_{2}\phi (z)^{2}+m_{1}\phi (z)+m_{0}.} \end{aligned}$$
(35)

From (22) and (35) into (13) and (14) results,

$$\begin{aligned} \begin{array}{l} a_{0} = \frac{a_{1}s_{0}\left( c_{1}s_{0}-2c_{0}s_{1}\right) }{4c_{2}s_{0}^{2}+s_{1}\left( 2c_{0}s_{1}-3c_{1}s_{0}\right) },\;m_{0} = \frac{m_{1}s_{0}}{2s_{1}},\;c_{1} = \frac{c_{2}rs_{0}}{s_{1}},\;m_{1} = \frac{m_{2}rs_{0}}{s_{1}}\\ q = \frac{\root 4 \of {\frac{2}{3}}\root 4 \of {-\gamma }\sqrt{r}\sqrt{a_{1}^{2}+b_{1}^{2}}}{3\root 4 \of {\delta }(r-2)^{2}s_{0}s_{1}^{2}\sqrt{c_{2}m_{2}}}\left( -2\sqrt{6}a_{1}^{2}\sqrt{-\gamma }\sqrt{\delta }k\left( 2r^{2}-4r+1\right) \right. \\ \qquad \left. 3(r-2)s_{1}^{2}\left( 4\delta k^{3}-2\alpha k+\nu \right) -2\sqrt{6}b_{1}^{2}\sqrt{-\gamma }\sqrt{\delta }k\left( 2r^{2}-4r+1\right) \right) ,\\ \omega = \frac{1}{576(-\gamma )^{5/2}\delta (r-2)^{2}s_{1}^{4}}\left( 192a_{1}^{4}(-\gamma )^{5/2}\gamma \delta \left( 2r^{4}-8r^{3}+13r^{2}-16r+11\right) \right. \\ \qquad +192b_{1}^{4}\gamma (-\gamma )^{5/2}\delta \left( 2r^{4}-8r^{3}+13r^{2}-16r+11\right) +24\sqrt{6}\gamma ^{2}\sqrt{\delta }\\ \qquad \left( 2r^{3}-8r^{2}+9r-2\right) b_{1}^{2}s_{1}^{2}\left( 4\alpha \gamma +(r-2)^{2}(3\mu +2\sigma )^{2}\right) -\\ \qquad (r-2)^{3}(3\mu +2\sigma )\left( 27\sqrt{-\gamma }\mu ^{3}(r-2)^{3}+54\sqrt{-\gamma }\mu ^{2}(r-2)^{3}\sigma \right. \\ \qquad +36\sqrt{-\gamma }\mu (r-2)^{3}\sigma ^{2}+24\alpha \sqrt{-\gamma }\gamma (r-2)(3\mu +2\sigma )-\\ \qquad 8\left( 6\sqrt{6}\gamma ^{2}\sqrt{\delta }\nu \right. \left. \left. \sqrt{-\gamma }\left( -(r-2)^{3}\right) \sigma ^{3}\right) \right) s_{1}^{4}+24a_{1}^{2}\left( -16b_{1}^{2}(-\gamma )^{7/2}\delta (2r^{4}\right. \\ \qquad -8r^{3}+13r^{2}-16r+11)+\sqrt{6}2r^{3}-8r^{2}+9r-2\gamma ^{2}\sqrt{\delta }\left( 4\alpha \gamma +(r-2)^{2}\right. \\ \qquad \left. \left. \left. (3\mu +2\sigma )^{2}\right) s_{1}^{2}\right) \right) ,\;\beta = \frac{\gamma }{24(-\gamma )^{3/2}\sqrt{\delta }(r-2)^{2}}\left( \sqrt{6}r-2\left( 4\alpha \gamma +(r-2)^{2}\right. \right. \\ \qquad \left. 3\mu ^{2}+8\mu \sigma +4\sigma ^{2}\right) -\frac{8a_{1}^{2}(-\gamma )^{3/2}\sqrt{\delta }\left( 16r^{2}-44r+23\right) }{s_{1}^{2}}\left. -\frac{8b_{1}^{2}(-\gamma )^{3/2}\sqrt{\delta }\left( 16r^{2}-44r+23\right) }{s_{1}^{2}}\right) ,\\ c_{0} = \frac{c_{2}\left( 3r^{2}-6r+4\right) s_{0}^{2}}{2rs_{1}^{2}},\;k = -\frac{(r-2)(3\mu +2\sigma )}{2\sqrt{6}\sqrt{-\gamma }\sqrt{\delta }},\;p = \frac{\root 4 \of {-\frac{1}{3}(2\gamma )}\sqrt{r}\sqrt{a_{1}^{2}+b_{1}^{2}}}{\root 4 \of {\delta }(r-2)s_{0}\sqrt{c_{2}m_{2}}}.\\ \\ \end{array} \end{aligned}$$
(36)

The solution of (11) and (12) are,

$$\begin{aligned} \begin{array}{l} u(x,\tau ) = \frac{a_{1}\left( -\sqrt{c_{2}}(r-2)s_{0}+\sqrt{\frac{c_{2}(r-2)^{3}s_{0}^{2}}{r}}\text {sn}\left( \frac{\sqrt{(r-2)r}(A+z)\sqrt{c_{2}}\sqrt{m_{2}}s_{0}}{2s_{1}},\frac{(r-2)^{2}}{r^{2}}\right) \right) }{s_{1}\left( \sqrt{\frac{c_{2}(r-2)^{3}s_{0}^{2}}{r}}\text {sn}\left( \frac{\sqrt{(r-2)r}(A+z)\sqrt{c_{2}}\sqrt{m_{2}}s_{0}}{2s_{1}},\frac{(r-2)^{2}}{r^{2}}\right) +\sqrt{c_{2}}(r-2)s_{0}\right) },\\ v(x,\tau )=\frac{b_{1}}{a_{1}}u(x,\tau ),z=\frac{x\left( \root 4 \of {-\frac{1}{3}(2\gamma )}\sqrt{r}\sqrt{a_{1}^{2}+b_{1}^{2}}\right) }{\root 4 \of {\delta }(r-2)s_{0}\sqrt{c_{2}m_{2}}}+\frac{\tau }{3\root 4 \of {\delta }(r-2)^{2}s_{0}s_{1}^{2}\sqrt{c_{2}m_{2}}}\\ \qquad \root 4 \of {\frac{2}{3}}\sqrt{r}\root 4 \of {-\gamma }\sqrt{a_{1}^{2}+b_{1}^{2}}\left( -2\sqrt{6}a_{1}^{2}\sqrt{-\gamma }\sqrt{\delta }k\left( 2r^{2}-4r+1\right) \right. \\ \qquad \left. 3(r-2)s_{1}^{2}\left( 4\delta k^{3}-2\alpha k+\nu \right) -2\sqrt{6}b_{1}^{2}\sqrt{-\gamma }\sqrt{\delta }k\left( 2r^{2}-4r+1\right) \right) ,\tau =\log \left( _{i}E_{\rho }(t)\right) . \end{array} \end{aligned}$$
(37)

The results in (34) is used to display Rew(x, t) is displayed in Fig. 6(i) and (ii).

Fig. 6
figure 6

(i) and (ii), when \((\rho = 0.6,r = 2.5,a_{1} = 1.5,b_{1} = 1.3,c_{2} = 0.05,m_{2} = 0.08,s_{1} = 3,s_{0} = 0.3.\)

Full size image

Figure 6(i) shows rogue waves vector- lumps vector interaction with breathers, while Fig. 6(ii) shows geometric chaos. Figure 6(iii) consolidate the chaotic behavior for high time values.

3 M shaped solitons

Here, consider polynomial solutions.

3.1 Case (a)

Here, we consider (17) and the AE is,

$$\begin{aligned} \phi '(z) = c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}. \end{aligned}$$
(38)

From (17) and (38) into (13) and (14) gives rise to,

$$\begin{aligned} \begin{array}{l} a_{0} = \frac{a_{1}c_{1}}{2c_{2}},\;k = \frac{3\mu +2\sigma }{2\sqrt{6}\sqrt{-\gamma }\sqrt{\delta }},\;p = \frac{\root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{1}^{2}+b_{1}^{2}}}{2^{3/4}c_{2}\root 4 \of {\delta }}\\ c_{0} = \frac{1}{40\gamma ^{2}c_{2}\sqrt{\delta }\left( a_{1}^{2}+b_{1}^{2}\right) }\left( 10a_{1}^{2}\gamma ^{2}c_{1}^{2}\sqrt{\delta }+10b_{1}^{2}\gamma ^{2}c_{1}^{2}\sqrt{\delta }+\left( 4\sqrt{6}\alpha \gamma \sqrt{-\gamma }\right. \right. \\ +24\beta \gamma \sqrt{\delta }\left. \left. +\sqrt{6}\sqrt{-\gamma }\left( 3\mu ^{2}+8\mu \sigma +4\sigma ^{2}\right) \right) c_{2}^{2}\right) ,\\ q\text {:=}\frac{1}{15\gamma ^{2}\left( a_{1}^{2}+b_{1}^{2}\right) }p\left( 3a_{1}^{2}\gamma (-3\beta \mu -2\beta \sigma +5\gamma \nu )+3\gamma (-3\beta \mu \right. \\ \left. +5\gamma \nu -2\beta \sigma )b_{1}^{2}+2c_{2}^{2}p^{2}(3\mu +2\sigma )\left( 12\alpha \gamma +9\mu ^{2}+9\mu \sigma +2\sigma ^{2}\right) \right) ,\\ \omega = \frac{1}{14400\gamma ^{2}\delta }(864\alpha ^{2}\gamma ^{2}+3456\beta ^{2}\gamma \delta -72\sqrt{6}\beta \sqrt{-\gamma }\\ \sqrt{\delta }\left( 33\mu ^{2}+28\mu \sigma +4\sigma ^{2}\right) -24\alpha \gamma (12\sqrt{6}\beta \sqrt{-\gamma }\sqrt{\delta }+81\mu ^{2}\\ +96\mu \sigma +28\sigma ^{2})+(3\mu +2\sigma )+(1200\sqrt{6}\gamma \sqrt{-\gamma }\sqrt{\delta }\nu +27\mu ^{3}+\\ \\ 846\mu ^{2}\sigma +900\mu \sigma ^{2}+232\sigma ^{3})). \end{array} \end{aligned}$$
(39)

The solution of (11) and (12) are,

$$\begin{aligned} \begin{array}{l} u(x,\tau ) = -\frac{a_{1}}{2c_{2}\sqrt{10\gamma ^{2}\sqrt{\delta }\left( a_{1}^{2}+b_{1}^{2}\right) }}\sqrt{K}\\ \qquad tanh\left( \frac{(A+z)\sqrt{-\frac{c_{2}^{2}\left( 4\sqrt{6}\alpha \gamma \sqrt{-\gamma }+24\beta \gamma \sqrt{\delta }+\sqrt{6}\sqrt{-\gamma }\left( 3\mu ^{2}+8\mu \sigma +4\sigma ^{2}\right) \right) }{\gamma ^{2}\sqrt{\delta }\left( a_{1}^{2}+b_{1}^{2}\right) }}}{2\sqrt{10}}\right) ,\\ K=-c_{2}^{2}(4\sqrt{6}\alpha \gamma \sqrt{-\gamma }+24\beta \gamma \sqrt{\delta }+\sqrt{6}\sqrt{-\gamma }(3\mu ^{2}\\ \qquad +8\mu \sigma +4\sigma ^{2})),v(x,\tau ) = \frac{b_{1}u(x,\tau )}{a_{1}},\;z = \frac{x\left( \root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{1}^{2}+b_{1}^{2}}\right) }{2^{3/4}c_{2}\root 4 \of {\delta }}\\ \qquad +\frac{\tau }{15\gamma ^{2}\left( a_{1}^{2}+b_{1}^{2}\right) }p\left( 3a_{1}^{2}\gamma (-3\beta \mu -2\beta \sigma +5\gamma \nu )+3\gamma (-3\beta \mu +5\gamma \nu \right. \\ \qquad \left. -2\beta \sigma )b_{1}^{2}+2c_{2}^{2}p^{2}(3\mu +2\sigma )\left( 12\alpha \gamma +9\mu ^{2}+9\mu \sigma +2\sigma ^{2}\right) \right) ,\tau =Log\left( _{i}E_{\rho }(t)\right) . \end{array} \end{aligned}$$
(40)

By using (40), Rew(x, t) is displayed in Fig. 7(i) and (ii).

Fig. 7
figure 7

(i) and (ii), when \(a_{1} = 2.5,b_{1} = 1.5,\nu = 0.3,c_{2} = -0.6,A = 2.\)

Full size image

Figure 7(i) shows undulated M-shaped solitons.

3.2 Case (b)

In this case, we write,

$$\begin{aligned} \begin{array}{l} U(z) = a_{2}\phi (z)^{2}+a_{1}\phi (z)+a_{0},\;V(z) = b_{2}\phi (z)^{2}+b_{1}\phi (z)+b_{0},\\ \;b_{0} = \frac{a_{0}b_{2}}{a_{2}},\;b_{1} = \frac{a_{1}b_{2}}{a_{2}},\\ \phi '(z) = \sqrt{c_{2}\phi (z)^{2}+c_{1}\phi (z)+c_{0}}\left( m_{2}\phi (z)^{2}+m_{1}\phi (z)+m_{0}\right) . \end{array} \end{aligned}$$
(41)

From (41) into (13) and (14) leads to,

$$\begin{aligned} \begin{array}{l} k = \frac{\left( a_{2}^{2}+b_{2}^{2}\right) (3\mu +2\sigma )}{96c_{2}\delta m_{2}^{2}p^{2}},\;a_{1} = \frac{1}{3}a_{2}\left( \frac{c_{1}}{c_{2}}+\frac{2m_{1}}{m_{2}}\right) ,\;c_{1} = -\frac{c_{2}m_{1}}{m_{2}},\\ m_{0} = \frac{1}{18}\left( -\frac{5c_{1}^{2}m_{2}}{c_{2}^{2}}+\frac{c_{1}m_{1}}{c_{2}}+\frac{18c_{0}m_{2}}{c_{2}}+\frac{4m_{1}^{2}}{m_{2}}\right) \\ a_{0} = \frac{a_{2}\left( -8c_{2}^{2}\left( m_{1}^{2}-9m_{0}m_{2}\right) +4c_{2}m_{2}\left( 7c_{1}m_{1}+9c_{0}m_{2}\right) -11c_{1}^{2}m_{2}^{2}\right) }{144c_{2}^{2}m_{2}^{2}},\\ \\ q = -\frac{m_{1}}{H}\left( \sqrt{a_{2}^{2}+b_{2}^{2}}\left( 4\sqrt{6}a_{2}^{2}\gamma \sqrt{-\gamma }\sqrt{\delta }m_{1}^{4}(3\mu +2\sigma )\right. \right. \\ \qquad +4\sqrt{6}\gamma \sqrt{-\gamma }b_{2}^{2}\sqrt{\delta }m_{1}^{4}(3\mu +2\sigma )+81\left( 3\sqrt{6}\sqrt{-\gamma }\gamma \sqrt{\delta }\nu -\right. \\ \qquad 3\sqrt{6}\beta \sqrt{-\gamma }\sqrt{\delta }(3\mu +2\sigma )\left. \left. +\sigma (3\mu +2\sigma )^{2}\right) m_{2}^{4}\right) ,\\ H=1944\root 4 \of {2}3^{3/4}(-\gamma )^{5/4}\sqrt{c_{0}}\delta ^{3/4}m_{2}^{6},\;c_{2} = \frac{4c_{0}m_{2}^{2}}{m_{1}^{2}},\\ \alpha = -\frac{-4\sqrt{6}\beta \sqrt{-\gamma }\sqrt{\delta }+3\mu ^{2}+8\mu \sigma +4\sigma ^{2}}{4\gamma },p = \frac{\root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{2}^{2}\qquad +b_{2}^{2}}}{2\ 2^{3/4}\sqrt{c_{2}}\root 4 \of {\delta }m_{2}},\\ \omega = \frac{3\mu +2\sigma }{576\gamma ^{2}\delta }\left( 27\mu ^{3}+48\sqrt{6}\sqrt{-\gamma }\gamma \sqrt{\delta }\nu +126\mu ^{2}\sigma \right. \\ \qquad \left. -24\sqrt{6}\beta \sqrt{-\gamma }\sqrt{\delta }(3\mu +2\sigma )+132\mu \sigma ^{2}+40\sigma ^{3}\right) . \end{array} \end{aligned}$$
(42)

The solutions of (11) and (12) are,

$$\begin{aligned} \begin{array}{c} u(x,\tau ) = -\frac{8a_{2}\left( -1+3e^{\frac{16}{9}\sqrt{2}\sqrt{c_{1}}m_{2}\left( z+36c_{1}m_{2}\right) }\right) }{9+27e^{\frac{16}{9}\sqrt{2}\sqrt{c_{1}}m_{2}\left( z+36c_{1}m_{2}\right) }},\;v(x,\tau ) = \frac{b_{2}u(x,\tau )}{a_{2}},\\ z\text {:=}\frac{x\left( \root 4 \of {-\frac{\gamma }{3}}\sqrt{a_{2}^{2}+b_{2}^{2}}\right) }{2\ 2^{3/4}\sqrt{c_{2}}\root 4 \of {\delta }m_{2}}+q\tau ,\;\tau =Log\left( _{i}E_{\rho }(t)\right) ,\\ \\ \end{array} \end{aligned}$$
(43)

and q is given in (42). The results in (43) are used to display Rew(x, t) in Fig. 8(i) and (ii).

Fig. 8
figure 8

(i) and (ii) when \(a_{2} = 0.5,b_{2} = 0.7,\nu = 0.3,A = 2,m_{1} = 0.7,m_{2} = -0.5,c_{0} = 0.8.\)

Full size image

Figure 8(i) and (ii) show M-shaped solitons.

4 Modulation instability

The study of modulation instability ( MI) holds for systems governed by complex field equations, which possess normal mode (plane wave) solutions. Indeed Eq. (9) has the solution,

$$\begin{aligned} \bar{w}(x,\tau ) = Ae^{i(Kx-\tau \Omega )},A>0, \end{aligned}$$
(44)

where,

$$\begin{aligned} \Omega = -A^{4}\gamma -A^{2}\beta -A^{2}K\mu -\delta K^{4}+\alpha K^{2}-K\nu . \end{aligned}$$
(45)

The study of MI is based on determining the dominant parameter in the system, which is taken, here, \(\delta .\) We inspect the critical value of \(\delta\), above it MI triggers.

Now we use the perturbation expansion,

$$\begin{aligned} \begin{array}{c} \bar{w}(x,\tau ) = e^{i(Kx-\tau \Omega )}\left( A+e^{\lambda \tau }\left( \varepsilon _{1}\bar{U}(x)+i\varepsilon _{2}\bar{V}(x)\right) +O(\varepsilon _{i}^{2})\right) ,\\ \bar{w}^{*}(x,\tau ) = e^{-i(Kx-\tau \Omega )}\left( A+e^{\lambda \tau }\left( \varepsilon _{1}\bar{U}(x)-i\varepsilon _{2}\bar{V}(x)\right) +O(\varepsilon _{i}^{2})\right) ,\;i=1,2. \end{array} \end{aligned}$$
(46)

From(46) into (9), calculations give rise to,

$$\begin{aligned} \begin{array}{c} A\left( \begin{array}{l} \varepsilon _{1}\\ \varepsilon _{2} \end{array}\right) =0,\quad A=\left( \begin{array}{cc} a_{11} &{} a_{12}\\ a_{21} &{} a_{22} \end{array}\right) ,\\ a_{11}-6\delta K^{2}\bar{U}''+\delta \bar{U}^{(4)}+\alpha \bar{U}''+4A^{4}\gamma \bar{U}\\ +2A^{2}K\mu \bar{U}+2A^{2}\beta \bar{U},\\ a_{12} = A^{2}\mu \bar{V}'+4\delta K^{3}\bar{V}'-4\delta K\bar{V}^{(3)}-2\alpha K\bar{V}'\\ +\nu \bar{V}'-\lambda +\nu \bar{V}'-\lambda \bar{V},\\ a_{21}-3A^{2}\mu \bar{U}'-2A^{2}\sigma \bar{U}'-4\delta K^{3}\bar{U}'+2\alpha K-\nu \bar{U}'+\lambda \bar{U}'\\ -\nu \bar{U}'+\lambda \bar{U},\\ a_{22}=-6\delta K^{2}\bar{V}''+\delta \bar{V}^{(4)}+\alpha \bar{V}''. \end{array} \end{aligned}$$
(47)

Equation (47) solves to.\(detA=0\), which results to the eigenvalue equation,

$$\begin{aligned} \begin{array}{l} -\lambda \bar{V}\bar{U}'\left( A^{2}(3\mu +2\sigma )+4\delta K^{3}-2\alpha K+\nu \right) +\bar{U}'(x)\bar{V}'(x)\left( 4\alpha ^{2}K^{2}\right. \\ -16\alpha \delta K^{4}+8\delta K^{3}\left( A^{2}(2\mu +\sigma )+\nu \right) -4\alpha A^{2}K(2\mu +\sigma )+16\delta ^{2}K^{6}\\ +\left( A^{2}\mu +\nu \right) \left. \left( A^{2}(3\mu +2\sigma )+\nu \right) -4\alpha K\nu \bar{U}'\bar{V}'\right) +\bar{U}''\bar{V}''\left( \alpha -6\delta K^{2}\right) ^{2}\\ \delta \left( \alpha -6\delta K^{2}\right) -4\delta K\bar{V}^{(3)}\bar{U}'\left( A^{2}(3\mu +2\sigma )+4\delta K^{3}-2\alpha K+\nu \right) \\ \bar{U}^{(4)}\bar{V}''+\delta \bar{V}^{(4)}\bar{U}''\left( \alpha -6\delta K^{2}\right) +\delta ^{2}\bar{U}^{(4)}\bar{V}^{(4)}+\bar{U}(x)\left( \lambda ^{2}V(x)\right. \\ -\lambda \left( 4\delta K^{3}-2\alpha K\right. \left. +A^{2}\mu +\nu \right) V'(x)+2A^{2}V''\left( \alpha -6\delta K^{2}\right) \\ \left( 2A^{2}\gamma +\beta +K\mu \right) \left. 2A^{2}\delta \bar{V}^{(4)}\left( 2A^{2}\gamma +\beta +K\mu \right) ++4\delta \lambda K\bar{V}^{(3)}(x)\right) =0. \end{array} \end{aligned}$$
(48)

We solve the eigenvalue problem in (48) subjected to the boundary conditions (BCs) \(\bar{U}(\pm \infty )=0\) and \(\bar{V}(\pm \infty )=0\). Thus, we can take,

$$\begin{aligned} \begin{array}{c} \bar{U}(x)=B_{1}{\left\{ \begin{array}{ll} e^{-hx} &{},x>0,h>0\\ e^{hx} &{} x<0 \end{array}\right. }\\ \bar{V}(x)=B_{2}{\left\{ \begin{array}{ll} e^{-hx} &{},x>0,h>0\\ e^{hx} &{} x<0 \end{array}\right. } \end{array} \end{aligned}$$
(49)

From (49) into (48), we find that,

$$\begin{aligned} \begin{array}{c} \lambda =2\alpha hK+2\delta h^{3}K-4\delta hK^{3}-2A^{2}h\mu -h\nu -A^{2}h\sigma \pm \surd \Delta ,\\ \Delta =-h^{2}(2\alpha A^{2}\beta +4\alpha A^{4}\gamma -12A^{2}\beta \delta K^{2}-24A^{4}\gamma \delta K^{2}+\delta ^{2}h^{6}-\\ A^{4}\mu ^{2}-2A^{4}\mu \sigma -A^{4}\sigma ^{2}-12A^{2}\delta K^{3}\mu +2\alpha A^{2}K\mu +2\delta h^{4}\left( \alpha -8\delta K^{2}\right) \\ +h^{2}+4\alpha K\nu (\alpha ^{2}+2\delta (2A^{4}\gamma +A^{2}(\beta -K(\mu +2\sigma ))+18\delta K^{4})\\ -12\alpha \delta K^{2})-4\alpha h^{2}K\nu ). \end{array} \end{aligned}$$
(50)

From (50) the MI triggers when \(2\alpha hK+2\delta h^{3}K-4\delta hK^{3}-2A^{2}h\mu -h\nu -A^{2}h\sigma >0,\)whatever the sign of \(\Delta .\)Thus, we get,

$$\begin{aligned} 0<h<\sqrt{2}\sqrt{K^{2}},K<0,\delta >\frac{-2A^{2}\mu -A^{2}\sigma +2\alpha K-\nu }{4K^{3}-2h^{2}K}. \end{aligned}$$
(51)

Now, we estimate the gain in the modulated wave is given by \(\sim \lambda (K).\) It is displayed in Fig. 9(i)–(iv).

Fig. 9
figure 9

(i)–(iv), when \(h = 0.1,\alpha = 0.7,A = 0.5,\nu = 0.3,\gamma \text {:=}0.6,\delta = 1.2,\mu = 0.6,\sigma = 0.4,\beta = 1.2.\)

Full size image

5 Conclusions

The study carried here is quite complex and fascinating. It involves the proposal of a novel Mittage–leffeler- (M) truncated proportional derivative. It is applied to the perturbed nonlinear Schrödinger equation with fourth order dispersion and quintic nonlinearity. The exact solutions of this equation are derived by implementing the unified method and they are represented graphically. These solutions exhibit various phenomena such as: geometric chaos, complex patterns like chirped solitons, breathers, and dromian patterns. In geometric chaos, undulated M-shaped solitons, complex M-shaped solitons, lump vector, and breathers interaction are visulalized. Also, the modulation instability is studied, and it is established that it triggers when the coefficient of the fourth order dispersion exceeds a critical value. The gain in the modulated wave is estimated and represented graphically. The present work contributes significantly to the understanding the behavior of complex systems.