1 Introduction

Modern photonic devices have complex structures that require efficient numerical techniques capable of modelling such designs. In this regard, the finite element method (FEM) attracts the interest of many researchers (Hoole et al. 1988). The conventional FEM (Obayya et al. 2000a, b, 2002) is a robust technique for analyzing various optical devices. However, getting accurate results requires fine meshing. This in turn demands high computational resources due to the produced large number of degrees of freedom (DOF) (Fernandez et al. 1993). A possible way to reduce the DOF is to use higher order elements. Although higher order solution reduces the DOF, it produces less sparse matrices, reduces the flexibility of placing nodes, and complicates the problem (Koshiba et al. 2000). Another way to reduce the DOF is to use first order elements with improved accuracy as in smoothed FEM method (Atia et al. 2015). This method relies on smoothing the derivatives across the boundaries between elements to fix numerical discontinuities inherited in the conventional FEM shape functions derivatives. Alternatively, one can reduce the DOF by selectively meshing areas where most of the field exists with small element sizes. However, large element sizes are used for areas where the field vanishes. This technique requires a proper knowledge of the solution where the field is confined. Therefore, adaptive meshing techniques have been proposed (Hoole et al. 1988; Fernandez et al. 1993; Tsuji and Koshiba 2000). The main challenge of any adaptive algorithm is the selection criteria of regions that need more meshing. The node points are distributed based on the errors in these regions. Hence, various error estimators have been developed in order to distribute the node points. An adaptive technique for solving Poisson equation that uses the node perturbation technique as an error estimator was developed (Hoole et al. 1988). Later, a predefined user function to calculate the error over the elements was proposed (Fernandez et al. 1993). Another error estimator was introduced based on power distribution inside the waveguide (Tsuji and Koshiba 2000). However, the field variation in the computational domain reported in Hoole et al. (1988), Fernandez et al. (1993), Morimoto et al. (2021) was not considered. Therefore, the previous adaptive algorithms fail to follow rapid field variations. This is very important for instance to photonic cavities because accurate representation of field decay significantly affects the cavity quality factor. In Schmidt (1993), a beam propagation technique based on new error estimator that compares the linear FEM solution with the local improved quadratic solution was developed. This technique needs an extra effort at each propagation step due to the required iterative calculations to obtain the local improved quadratic solution.

Here, in order to select the refinement elements, the local errors are estimated for each element. The local error is the difference between the linear FEM solution and the recovered solution calculated using the least-squares technique. Such technique is called “recovery-type” estimator (Kikuchi and Saito 2007). Further, the recovery technique is considered as a post processing method to reconstruct and improve the FEM solution (Yan and Zhou 2001). The new adaptive FEM technique is proposed to enhance the numerical accuracy of the solution of the light propagation in integrated photonic devices. The adaptive technique can refine the elements based on the initial field distribution. Our approach can be used in time and frequency domain simulations. However, here we only apply it on frequency domain method (Tsuji and Koshiba 2002). Three different photonic structures are tested and analyzed using the suggested approach. First, the transmission through reflectionless slab waveguide is calculated. Then, 2D-photonic crystal (PhC) cavity is studied which ensures the high accuracy of the quality factor and resonance frequency calculated by the reported algorithm. Further, 2D-PhC multiplexer-demultiplexer is analyzed for wavelengths of 1.3 µm and 1.55 µm where each wavelength is propagated through different PhC channels. It is shown that the reported technique has a node distribution allocated at the field location with fast convergence rate compared to conventional random refinement techniques.

2 Basic Equations

2.1 Finite Element Formulation

For a 2D computational domain (\(\Omega \)) where the variation is in xy/ plane, the weak form of the Helmholtz wave equation in the frequency domain can be expressed as

$${\int }_{\Omega } -\left[{\mathrm{p}}_{\mathrm{y}}\frac{\partial\upphi }{\partial \mathrm{x}}\frac{\partial\uppsi }{\partial \mathrm{x}}+{\mathrm{p}}_{\mathrm{x}}\frac{\partial\upphi }{\partial \mathrm{y}}\frac{\partial\uppsi }{\partial \mathrm{y}}\right]+{\mathrm{k}}_{\mathrm{o}}^{2}\mathrm{q\phi \psi d\Omega }=0$$
(1)

with,

 

\(\upphi \)

\({\mathrm{p}}_{\mathrm{x}}\)

\({\mathrm{p}}_{\mathrm{y}}\)

\(\mathrm{Q}\)

TE

\({\mathrm{E}}_{\mathrm{z}}\)

\({\mathrm{s}}_{\mathrm{x}}/{\mathrm{s}}_{\mathrm{y}}\)

\({\mathrm{s}}_{\mathrm{y}}/{\mathrm{s}}_{\mathrm{x}}\)

\({\mathrm{s}}_{\mathrm{y}}{\mathrm{s}}_{\mathrm{x}}{\mathrm{n}}^{2}\)

TM

\({\mathrm{H}}_{\mathrm{z}}\)

\({\mathrm{s}}_{\mathrm{x}}/\left({\mathrm{s}}_{\mathrm{y}}{\mathrm{n}}^{2}\right)\)

\({\mathrm{s}}_{\mathrm{y}}/\left({\mathrm{s}}_{\mathrm{x}}{\mathrm{n}}^{2}\right)\)

\({\mathrm{s}}_{\mathrm{y}}{\mathrm{s}}_{\mathrm{x}}\)

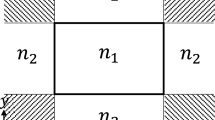
where \({\mathrm{k}}_{\mathrm{o}}\) is the wave number, n is the refractive index, and \(\uppsi \) is the weight function which is expanded using the same basis as \(\upphi \) according to Galerkin formulation. The Ez and Hz are respectively the electric and magnetic field components in z-direction. The \({\mathrm{s}}_{\mathrm{x}}\) and \({\mathrm{s}}_{\mathrm{y}}\) are the PML parameters in x- and y-directions as shown in Fig. 1 that can be found in Tsuji and Koshiba (2002).

Fig. 1
figure 1

Schematic diagram of FEM discretization of 2D optical waveguide problem

Full size image

After dividing into first order triangular elements, Eq. 1 is rewritten as

$$[\mathrm{G}]\{\upphi \}=\{0\}$$
(2)

where

$$\begin{array}{c}[G]={k}_{o}^{2}\sum_{e} {\int }_{{\Omega }_{e}} q\{N\}\{N{\}}^{T}d{\Omega }_{e}-\sum_{\mathrm{e}} {\int }_{{\Omega }_{\mathrm{e}}} \left[{\mathrm{p}}_{\mathrm{y}}\frac{\partial \{\mathrm{N}\}}{\partial \mathrm{x}}\frac{\partial \{\mathrm{N}{\}}^{\mathrm{T}}}{\partial \mathrm{x}}+{\mathrm{p}}_{\mathrm{x}}\frac{\partial \{\mathrm{N}\}}{\partial \mathrm{y}}\frac{\partial \{\mathrm{N}{\}}^{\mathrm{T}}}{\partial \mathrm{y}}\right]d{\Omega }_{\mathrm{s}}\\ \end{array}$$

Here, \(\{\mathrm{N}\}\) is the FEM shape function vector, and \(\sum_{\mathrm{e}}\) extends over all elements. To excite the structure, we define the source plane \(\Gamma \) which divides the analysis region into \({\Omega }_{1}\) and \({\Omega }_{2}\) subregions. Thus, due to the continuity condition across \(\Gamma \), Eq. 2 can be rewritten as Tsuji and Koshiba (2002)

$$[\mathrm{G}]\{\upphi \}=\sum_{\Gamma } {\int }_{\mathrm{l}} {\mathrm{p}}_{\mathrm{y}}\{\mathrm{N}{\}}_{\Gamma }\left(\frac{\partial {\upphi }_{1}}{\partial \mathrm{z}}-\frac{\partial {\upphi }_{2}}{\partial \mathrm{z}}\right)\mathrm{dl}$$
(3)

where \(\sum_{\Gamma }\) extends over the elements attached to\(\Gamma \), \(\{\mathrm{N}{\}}_{\Gamma }\) is the 1D shape functions vector, \({\int }_{\mathrm{l}}\) refers to a line integral over \(\Gamma ,\;\mathrm{ and }\;{\upphi }_{1}\) and \({\upphi }_{2}\) are the incident fields in the sub-regions \(, {\Omega }_{1}\) and\({\Omega }_{2}\), respectively. The fields \({\upphi }_{1}\) and \({\upphi }_{2}\) are expressed using the eigenmodes. The linear system of equation presented in Eq. 3 is then solved for the field distribution over the computational domain.

2.2 Field-Based Recovery Technique

The proposed adaptive technique is considered as a posteriori error estimate method where the exact solution is replaced, in the expression of the true error, with an approximation recovered from the numerical solution. Figure 2 shows a flow chart of the presented technique. At each iteration, the problem is solved and an error calculation for each element is obtained. Then, the mesh is refined in zones where high errors exist. The error estimation \(({\upvarepsilon }_{\mathrm{i}})\) at each element is calculated by the formula

$${\upvarepsilon }_{\mathrm{i}}={\Vert \mathrm{R}\left\{\widetilde{\mathrm{u}}\right\}-\widetilde{\mathrm{u}}\Vert }_{\mathrm{i}} \quad \mathrm{ i}=\mathrm{1,2}, \dots ,\mathrm{ k}$$
(4)

where \(\mathrm{k}\) is the number of elements in the computational domain, \(\Vert \cdots \Vert \) is the \({\mathrm{L}}_{2}\) norm, \(\widetilde{\mathrm{u}}\) is the linear FEM approximation to the exact solution \(\mathrm{u}\) and \(\mathrm{R}\left\{\widetilde{\mathrm{u}}\right\}\) is the recovered solution of \(\widetilde{\mathrm{u}}\). Once the estimation of the local is calculated at each element, the refinements take place in the elements that satisfy \({\upvarepsilon }_{\mathrm{i}}>\mathrm{\alpha }{\upvarepsilon }_{\mathrm{max}}\), where \({\upvarepsilon }_{\mathrm{max}}\) is the maximum local error in the domain and \(\mathrm{\alpha }\left(0<\mathrm{\alpha }<1\right)\) is a parameter that controls the number of refined elements. When \(\mathrm{\alpha }\) is close to 1, the refinement takes place only in the elements with an error close to the maximum. On the other hand, when \(\mathrm{\alpha }\) is close to 0, a large number of elements is refined, even those with a small error. The global error \(\left({\upvarepsilon }_{\mathrm{g}}\right)\) is given by

$${\upvarepsilon }_{\mathrm{g}}=\sqrt{\sum\nolimits_{\mathrm{i}=1}^{\mathrm{k}}{\left({\upvarepsilon }_{\mathrm{i}}\right)}^{2}}$$
(5)

where the adaptation process iterates until \({\upvarepsilon }_{\mathrm{g}}\) is less than a certain tolerance \((\upepsilon )\) (Kikuchi and Saito 2007). In order to obtain the recovered solution \(\mathrm{R}\left\{\widetilde{\mathrm{u}}\right\}\) at a certain mesh node \(\mathrm{z}\), a patch \({\Omega }_{\mathrm{z}}\) of mesh elements directly attached to \(\mathrm{z}\) is selected as shown in Fig. 3a. Then, the linear FEM solution is extended to the mid-edges by interpolation (Zhang and Naga 2005; Naga and Zhang 2004).

Fig. 2
figure 2

Flowchart of the suggested adaptive FEM

Full size image
Fig. 3
figure 3

a Node patch \({{\varvec{\Omega}}}_{\mathbf{z}}\) and b Nodes in \({{\varvec{\Omega}}}_{\mathbf{z}}\) for least squares polynomial (LSP)

Full size image

Next, a quadratic polynomial \({\mathcal{P}}_{\mathrm{z}}\) that best fits the FEM solution \(\widetilde{\mathrm{u}}\) is constructed, using the least-squares method, at the nodes shown in Fig. 3b. The recovered solution \(\mathrm{R}\left\{\widetilde{\mathrm{u}}\right\}\) at a certain interior node \(\mathrm{z}\) is defined as the fitting polynomial, i.e.

$$\mathrm{R}\left\{\widetilde{\mathrm{u}}\left(\mathrm{z}\right)\right\}={\mathcal{P}}_{\mathrm{z}}\left(\mathrm{z}\right)$$
(6)

At any boundary node \(\widehat{\mathrm{z}}\), the recovered solution is equal to the FEM solution.

$$\mathrm{R}\left\{\widetilde{\mathrm{u}}\left(\widehat{\mathrm{z}}\right)\right\}=\widetilde{\mathrm{u}}\left(\widehat{\mathrm{z}}\right).$$
(7)

3 Numerical Results

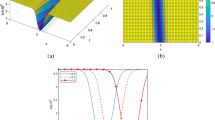
Figure 4a shows a silica slab with refractive index n = 1.44 surrounded by air. The length of the silica slab \(\mathrm{d}=\frac{\mathrm{m\lambda }}{2\mathrm{n}}\) (where \(\mathrm{m}=\mathrm{1,2},3,\dots \) and \(\uplambda \) is the operating wavelength in air) is chosen to obtain complete transmission with no reflection. During this study, the slab thickness is taken as 1615 nm which corresponds to m = 3. The purpose of this example is to show the convergence of the proposed technique to the exact solution with transmission of unity. An initial mesh is first used then the proposed adaptive technique is applied. Figure 4b, d show the distributed field \({\mathrm{E}}_{\mathrm{y}}\) of the travelling wave through the slab waveguide at wavelengths of \(\uplambda =1.55\;{\upmu}\text{m}\) and \(\uplambda =0.775\;{\upmu}\text{m}\). Figure 4c, e illustrate the mesh distribution after applying the proposed technique at the studied wavelengths after applying the mesh refinement technique. It may be noticed that the mesh density follows the electric field pattern produced in the computational domain. This coincides with the idea of the technique where the mesh follows the field unlike the previous work done in this area where the refinement is based on the gradient of the field (Babuvška and Rheinboldt 1978). Figure 4f shows the mesh distribution after applying the proposed refinement technique with DOF = 82,300 at λ = 1.55 µm. The solid green triangles represent the largest element with size \(1.25\times {10}^{-7}\mathrm{\mu m}\), while the dark red triangles represent the smallest elements with size \(3.88\times {10}^{-9}\;{\upmu}\text{m}\). It is clear from the figure that the mesh density increases at the peak regions of the electric field shown in Fig. 4b regardless it is a maximum or minimum value. This is due to at the peak regions the gradient of the field component increases that required the mesh to be denser at these regions in order to mimic the rapid changes in the field values.

Fig. 4
figure 4

a Silica slab embedded in Air b, d the distributed field \({\mathrm{E}}_{\mathrm{y}}\) of the travelling wave through the studied photonic structure at wavelengths of 1.55 µm and 0.755 µm c, e mesh distribution after applying the proposed technique at the studied wavelengths. f shows the mesh distribution after applying the proposed refinement technique with DOF = 82,300 at λ = 1.55 µm

Full size image

Figure 5 shows the variation of the absolute error versus the number of degrees of freedom (DOF). The absolute error is computed using \(\left|{\mathrm{T}}_{\mathrm{exact}}-{\mathrm{T}}_{\mathrm{r}}\right|\). The problem is designed to have Texact = 1.0 while \({\mathrm{T}}_{\mathrm{r}}\) is the transmission obtained by the suggested technique after mesh refinement process i.e. \({\mathrm{T}}_{\mathrm{r}}=\left|{\mathrm{S}}_{21}\right|\). It may be noticed that the absolute error drops down rapidly when the DOF is between 8 × 104 and 1 × 105. Then the error stabilizes afterward.

Fig. 5
figure 5

The change of the absolute error as a function of the number of degrees of freedom

Full size image

In order to test the advantages of the proposed method in modeling complex photonic structures, a \(5\times 5\) PhC cavity shown in Fig. 6 is analyzed. The PhC devices demand numerous numbers of elements for accurate analysis. The selected square lattice PhC cavity (Esquerre et al. 2005) consists of dielectric wires with radius \(\mathrm{r}=0.2\times \mathrm{a}\) with a lattice constant of \(\mathrm{a}=0.58652\;\upmu {\text{m}}\). The dielectric wires are embedded in air and have a refractive index \({\mathrm{n}}_{\mathrm{wire}}=3.4\). The central wire is removed in order to form the required cavity. Further, perfectly matched layer boundary condition is applied around the studied PhC to truncate the computational domain. Here, not only the field inside the cavity that dictates the cavity quality factor and normalized frequency but also the field decay and since our approach cares about the error in field no matter how weak it is, the computations of the quality factor is more precise.

Fig. 6
figure 6

a Schematic diagram of \(5\times 5\) PhC cavity and b the electric field distribution of the resonant mode inside the cavity at normalized frequency of 0.3788

Full size image

In the proposed adaptive FEM, an initial conventional FEM solution is obtained where the computational domain is discretized into \(35744\) elements. After applying the recovery technique, the recovered solution is obtained at each iteration. Based on the initial and the recovered solutions, the local error given by Eq. (1) can be estimated. It is required to refine the elements based on a certain ratio \(\mathrm{\alpha }\). In this example, the tolerance \(\upepsilon \) is equal to \({10}^{-6}\). Figure 7a, b show the initial discretized computational domain and after five iterations, respectively. The field distribution inside the cavity is shown in Fig. 6b. It may be seen that the mesh is refined in the subdomains where the field exists without sacrificing the mesh where the field decays. Therefore, this method is called the field-based mesh refinement technique.

Fig. 7
figure 7

The initial mesh and b final mesh of the studied 2D-PhC cavity

Full size image

Figure 8 shows the normalized frequency and the quality factor variations with the DOF using the adaptive proposed refinement. It is revealed from these figures that the normalized frequency and the quality factor converge to \(0.3788\) and \(177.88\), respectively at DOF of \(696{,}29\). On the other side, Fig. 9 illustrates the studied parameters with the DOF using random refinement. It is evident from these figures that neither the normalized frequency nor the quality factor could converge even for DOF higher than \(7\times {10}^{4}\). Table 1 shows the calculated values of the quality factor \(\mathrm{Q}\), and resonance frequency \({\mathrm{f}}_{0}\) and DOF by the suggested algorithm and that obtained in Esquerre et al. (2005). It may be seen from this table that an excellent agreement is achieved. Further, the DOF is reduced by 35% using the proposed adaptive technique.

Fig. 8
figure 8

Variation of a the normalized frequency and b the quality factor with the DOF for the studied 2D-PhC cavity using the adaptive proposed refinement

Full size image
Fig. 9
figure 9

Variation of a the normalized frequency and b the quality factor with the DOF for the studied 2D-PhC cavity using the random refinement

Full size image
Table 1 The calculated values of the quality factor \(\mathbf{Q}\), resonance frequency \({\mathbf{f}}_{0}\) and DOF by the suggested algorithm and that obtained in Esquerre et al. (2005)
Full size table

Next, photonic crystal multiplexer-demultiplexer (MUX/DEMUX) is studied for wavelengths of 1310/1550 nm (Bhatia and Gupta 2014). Figure 10 shows the schematic diagram of the studied PhC demultiplexer that consists of rectangular lattice of silicon pillars embedded in air. The lattice constant is \(\mathrm{a}=570\mathrm{ nm}\) and the rod diameter is \(\mathrm{d}=0.36\mathrm{a}\) while the refractive index of the rods is \(\mathrm{n }=3.4\) (Yan and Zhou 2001). Two filters are formed through the T-junction by adjusting the pillars diameter. Filter 1 has diameter defect of d1 = 0.5a which allows wavelength 1310 nm goes upward towards port 3 and filter 2 has diameter defect of d2 = 0.72a which allows wavelength 1550 nm goes downward towards port 2. Figure 11 shows mesh refinement generated from the proposed technique at (a) \(\uplambda =1.31\;{\upmu}\text{m}\) and (b) \(\uplambda =1.55\;{\upmu}\text{m}\) while DOF is fixed to \(8.5\times {10}^{4}\). It can be easily noticed that mesh refinement occurs in accordance with propagation of the field inside the device.

Fig. 10
figure 10

Schematic diagram of the optical MUX /DEMUX based on a PhC waveguide

Full size image
Fig. 11
figure 11

The corresponding mesh refinement generated from the proposed algorithm at a \(\uplambda =1.31\;{\upmu}\text{m}\) and b \(\uplambda =1.55\;{\upmu}\text{m}\)

Full size image

The computed electromagnetic field distribution \({\mathrm{E}}_{\mathrm{z}}\) for the studied demultiplexer is shown in Fig. 12 for two transmitted signals with wavelength 1.31 \(\mathrm{\mu m}\) (Fig. 12a) and 1.55 \(\mathrm{\mu m}\) (Fig. 12b). It can be seen that wavelength of 1.31 \(\mathrm{\mu m}\) is guided in the upper channel while the lower channel guides the wavelength of 1.55 \(\mathrm{\mu m}\) as received by monitor 2 which ensures the high accuracy of the proposed model.

Fig. 12
figure 12

Ez field distribution through the proposed multiplexer-demultiplexer at a \(\uplambda =1.31\;{\upmu}\text{m}\) and b \(\uplambda =1.55\;{\upmu}\text{m}\)

Full size image

It should be noted that the polynomial-preserving recovery (PPR) technique has been extended to recover solution or continuous gradient from a finite element solution of an arbitrary order in 2D and 3D problems (Naga and Zhang 2005). Therefore, it is believed that the proposed field based recovery technique is applicable to three-dimensional (3D) problems and will be considered for our future work. Typically, the 3D FEM is based on tetrahedron element with four faces which is analogous to the triangle shape in the 2D implementation. Therefore, each FEM node will have three translational degrees of freedom. Consequently, the 3D models are more complex with more variables than 2D models where more computational resources will be needed with long execution time.

4 Conclusion

A novel adaptive mesh generation is proposed and tested. The technique consists of posterior error estimation calculated based on a previous approximate solution, to guide the generation of a new mesh. This new mesh is built starting from a minimal number of triangular elements, which are then, in several sweeps, repeatedly refined according to the field locations. This method allows optimum use of the available degree of freedom in order to obtain accurate solution. The high accuracy of the reported technique is tested using the transmission through photonic structure, a 2D photonic crystal cavity and 2D photonic crystal multiplexer-demultiplexer.