Analytical solutions for the guided modes of rectangular silicon optical waveguides: a plane-wave approach

Abstract

Marcatili’s analytical solution for the guided modes of rectangular optical waveguides (ROWGs) depends on (1) using the separation of variables (SOV) and (2) applying the paraxial approximation. It results in two classes of modes: the TE-like and the TM-like modes which are supported by these waveguides. These modes are uncoupled under low-index-contrast conditions. In the case of silicon-on-insulator (SOI) waveguides, the coupling between them can no longer be neglected. This paper extends using the SOV to find analytical modal solutions of SOI-ROWGs. It expands these solutions in quadruples of plane waves and develops a novel non-paraxial scattering model to account for the polarization coupling between these waves under high-index-contrast conditions. This model yields approximate analytical expressions of the field components of the guided modes which are the sum of major and minor Marcatili’s TE-like and TM-like modal fields. Numerical examples show excellent agreement with the field components of full-vectorial mode solvers.

1 Introduction

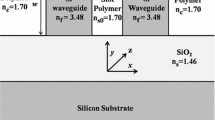
Marcatili’s famous analytical solution for the guided modes of rectangular optical waveguides (ROWGs) has been used since the early days of integrated optics (Marcatili 1969). It sets up, in addition to other approximate analytical approaches, the foundations of the theory of integrated optical waveguides. It neglects the fields in the shaded regions of the cladding (see Fig. 1), which applies under strong confinement conditions. Then, it employs two basic assumptions. The first assumption uses the separation of variables (SOV) to get a simplified modal field solutions in the core and cladding regions. The second assumption selects modes made of paraxial plane waves. It results in two uncoupled TE-like and TM-like modes which are essentially TEM waves of orthogonal polarizations. These modes belong to low-index-contrast waveguides which are not used in high-density photonic integrated circuits made by the silicon-on-insulator (SOI) technology. This technology has attracted the attention of the photonics community for more than two decades and is expected to have a potential impact on the photonics industry in the future. One of the main deficiencies in the toolbox of designers of the photonic components in this high-index-contrast technology is the lack of full-vectorial analytical solutions of the guided modes of optical waveguides. These solutions enable using fast full-vectorial mode propagation analysis of silicon integrated optical devices, including couplers, ring resonators, arrayed waveguide gratings, and polarization splitters, e.g., in (Sui et al. (2015); Xie et al. 2023; Li et al. 2023; Pan and Rahman 2016). Despite the inherent assumptions and approximations used in analytical solutions, they help designers in choosing their initial design parameters before being subsequently refined and optimized using sophisticated 3D numerical computational and simulation tools. As a result, they save tremendous amount of time and effort in the design and optimization process. In this sense, the continuous improvement of existing approximate analytical solutions is significantly important.

Fig. 1

Schematic of the cross section of a ROWG showing the refractive indexes of the core and the cladding. The hatched regions of the cladding have no contact surface with the core

While an improved method has been reported in Westerveld et al. (2012) that adopts SOV solutions and extends the use of Marcatili’s approach to SOI-ROWGs, this method does not apply boundary conditions to all modal field components. Due to a gap between the number of boundary conditions and the number of unknown field parameters, they are only applied to selected field components in favor of others (Westerveld et al. 2012). This selective application of boundary conditions gives rise to an error which is minimized by minimizing a contour-integration metric that may intuitively be interpreted as energy density but does not have a rigorous physical meaning (Westerveld et al. 2012). While the derived analytical expressions show excellent agreement with the numerical computations for the first three modes of a typical SOI waveguide, they fail to yield accurate results under the so-called “avoid-crossing” conditions, where two guided modes have similar effective index (Westerveld et al. 2012). To overcome these limitations and ambiguities, there is a need for a rigorous model that adopts simple SOV solutions yet applies boundary conditions to all modal field components and gives a physical insight to the propagation of modes in SOI-ROWGs.

This paper invokes a plane-wave ray scattering approach to develop this model. As a ray approach, it gives a “visual” picture that provides better understanding of modal propagation. To the best of our knowledge, it has not been previously applied to describe modal propagation in SOI-ROWGs. To retain the basic physical picture while minimizing the mathematical complexity, this paper only considers symmetric ROWGs with uniform cladding refractive index, as shown in Fig. 1. Nevertheless, the developed model may directly be extended to the general case of asymmetric ROWGs considered in Westerveld et al. (2012). It follows Marcatili’s approach in assuming SOV solutions. Yet it expands these solutions in quadruples of plane waves to apply exact analytical scattering rules which are not limited by the paraxiality of the waves or by the index-contrast conditions. These rules ensure that boundary conditions are applied to all field components. Total internal reflection (TIR) matrices are derived to enable full-vectorial analysis of the scattered plane waves. This scattering analysis reveals coupling between the modes of the slabs made by the boundaries of the core in the vertical and horizontal directions. It results in two quasi-guided (QG) modes that propagate as pairs of TE or TM modes of these slabs. These modes are referred to as the TE–TE and TM–TM modes. They are the modified version of Marcatili’s TE-like and TM-like modes which incorporate polarization coupling. Their field components are the sum of coupled major and minor field components of these modes. Under strong polarization coupling, they do not exactly satisfy the Marcatili’s resonance conditions, which results in phase and polarization errors. These errors are minimized to identify the effective indexes of these modes and the amplitudes of their minor field components. The paper is organized as follows. Section 2 expresses the SOV modal solutions as a superposition of plane waves. It presents a full-vectorial model of the scattering of these waves inside the core of the ROWGs. Section 3 introduces the errors in satisfying the Marcatili’s resonance conditions which are induced by polarization coupling. It uses optimization to find the modal effective indexes. Section 4 uses optimization to find the modal polarization. It gives analytical expressions of the field components of the TE–TE and TM–TM modes. Section 5 compares the plane-wave scattering approach with the improved Marcatili’s method reported in Westerveld et al. (2012). Finally, Sect. 6 presents the conclusion.

2 Plane-wave scattering model

2.1 Plane-wave recycling

Consider a ROWG of width $a$ and thickness$b$. The core has refractive index ${n}_{1}$ surrounded by a cladding of lower refractive index,${n}_{2}$, as shown in Fig. 1. The SOV solution of Helmholtz equation for the fields of the guided modes in the core of the waveguide is the product of sinusoidal functions in the $x$ and $y$ directions. It is straightforward to show that this product may be replaced by a quadruple of plane waves whose propagation constant vectors, $\underline{k}=\left(\begin{array}{ccc}{\pm k}_{x}& {\pm k}_{y}& \beta \end{array}\right)$. The signs$\left(+,+\right)$,$\left(+ ,-\right)$, $\left(-,+\right)$, and $\left(-,-\right)$ correspond to waves 1, 2, 3, and 4, respectively. Starting from wave$i$, the TIR at the horizontal or vertical boundaries of the core recycles it into another wave $f$ of the same quadruples of waves and then back into itself after consecutive reflections, see Fig. 2.

Fig. 2

Schematic of the propagation of plane-wave rays inside the core of a ROWG showing consecutive reflections which recycle one wave into another

2.2 Total internal reflection matrices

To incorporate their field polarization, the TIR of these waves is described by the following matrices,

$$\underset{\_}{\underline{H}}=\left(\begin{array}{ccc}{\overline{\beta }}_{x}^{2}{\rho }_{0y}-{\rho }_{\parallel y}& 0& \mp {\overline{k}}_{x}{\overline{\beta }}_{x}{\rho }_{0y}\\ 0& {\rho }_{\parallel y}& 0\\ \mp {\overline{k}}_{x}{\overline{\beta }}_{x}{\rho }_{0y}& 0& {\overline{k}}_{x}^{2}{\rho }_{0y}-{\rho }_{\parallel y}\end{array}\right)$$

(1)

and

$$\underset{\_}{\underline{V}}=\left(\begin{array}{ccc}{\rho }_{\parallel x}& 0& 0\\ 0& {\overline{\beta }}_{y}^{2}{\rho }_{0x}-{\rho }_{\parallel x}& \mp {\overline{k}}_{y}{\overline{\beta }}_{y}{\rho }_{0x}\\ 0& \mp {\overline{k}}_{y}{\overline{\beta }}_{y}{\rho }_{0x}& {\overline{k}}_{y}^{2}{\rho }_{0x}-{\rho }_{\parallel x}\end{array}\right)$$

(2)

at the horizontal and vertical boundaries of the core, respectively. See Appendix A for details. The parameters, ${\overline{k}}_{x}={k}_{x}/\sqrt{{k}_{x}^{2}+{\beta }^{2}}$, ${\overline{k}}_{y}={k}_{y}/\sqrt{{k}_{y}^{2}+{\beta }^{2}}$, ${\overline{\beta }}_{x}=\beta /\sqrt{{{k}_{x}^{2}+\beta }^{2}}$, ${\overline{\beta }}_{y}=\beta /\sqrt{{{k}_{y}^{2}+\beta }^{2}}$, and ${\rho }_{0x/y}={\rho }_{\perp x/y}+{\rho }_{\parallel x/y}$, where ${\rho }_{\parallel x/y}$ and ${\rho }_{\perp x/y}$ are the TIR coefficients of the parallel and normal polarizations at the horizontal and vertical directions, respectively. The upper and lower signs of the off-diagonal elements of $\underset{\_}{\underline{H}}$ and $\underset{\_}{\underline{V}}$ correspond to incident waves with positive and negative signs of ${k}_{x}$ and ${k}_{y}$, respectively.

2.3 Coupling between slab waveguide modes

The normalized electric field vectors of the i^th plane waves which constitute the modes of the slabs made by the horizontal and vertical boundaries of the core are denoted by ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$, respectively (see Appendix B). They are the eigen vectors of the double reflection matrices ${\underset{\_}{\underline{H}}}^{2}$ and ${\underset{\_}{\underline{V}}}^{2}$ corresponding to the TE or TM polarization. They transform to field vectors of the same mode when reflected by the boundaries of the same slab. This transformation is described by,

$$\underset{\_}{\underline{H}} {\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}={\rho }_{\perp y/ \parallel y} {\underset{\_}{\mathrm{\rm E}}}_{{\text{f}}}$$

(3)

and

$$\underset{\_}{\underline{V}} {\underset{\_}{\delta }}_{i}= {(-1)}^{\varepsilon }{\rho }_{\perp x/\parallel x }{\underset{\_}{\delta }}_{f},$$

(4)

where ${\underset{\_}{\mathrm{\rm E}}}_{{\text{f}}}$ and ${\underset{\_}{\delta }}_{f}$ are the final field vectors in the recyclying process. The recycled pairs ($i$,$f$) are (1, 2) and (3, 4) at the horizontal surfaces and (1, 3) and (2, 4) at the vertical surfaces. The left and right suffix of the reflection coefficients correspond to the TE and TM modes, respectively. The parameter $\varepsilon$ is zero for TE modes and unity for TM modes. The field vectors, ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$ couple at the boundaries of the slab waveguide where they are no longer eigen vectors. This coupling is described by,

$$\underset{\_}{\underline{V}}{ \underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}= {\left(-1\right)}^{1+\varepsilon } {\rho }_{\parallel x/\perp x }{\underset{\_}{\mathrm{\rm E}}}_{{\text{f}}}+\sigma {\rho }_{ox} {\underset{\_}{\delta }}_{f}$$

(5)

and

$$\underset{\_}{\underline{H}} {\underset{\_}{\delta }}_{i}= -{\rho }_{\parallel y/\perp y } {\underset{\_}{\delta }}_{f}+{\left(-1\right)}^{\varepsilon } \sigma {\rho }_{oy} {\underset{\_}{\mathrm{\rm E}}}_{{\text{f}}}$$

(6)

where the parameter, $\sigma ={\overline{k}}_{x}{\overline{k}}_{y}$ is a measure of paraxiality of the waves for both TE and TM polarizations. These equations describe back and forth coupling between ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$ as the plane waves propagate along the ROWG. They couple the TE/TM polarized modes of the horizontal slab represented by ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ to the mode of the same polarization of the vertical slab which is represented by ${\underset{\_}{\delta }}_{f}$. This coupling means that the TE (TM) polarized wave continues to propagate as a TE (TM) wave either with respect to the horizontal or vertical boundaries of the waveguide core. Apart from a propagation phase, Eqs. (3) through (6) represent the equations of “motion” of the plane waves inside the core of the ROWG.

2.4 TE–TE and TM–TM modes

Since the field vectors ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$ of the modes of the horizontal and vertical slabs are coupled at the boundaries of the core as described by (5 and 6), the field vector ${\underset{\_}{\mathcal{E}}}_{{\text{i}}}$ of the plane waves constituting the guided modes of the ROWG must be a linear combination of these two vectors,

$${\underset{\_}{\mathcal{E}}}_{{\text{i}}}={u}_{i} {\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}+{{\text{w}}}_{i} {\underset{\_}{\delta }}_{i}$$

(7)

These guided modes are either TE–TE or TM–TM modes depending on the polarization of ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$. The amplitudes ${u}_{i}$ and ${{\text{w}}}_{i}$ are, by definition, invariant along the direction of propagation. Unless otherwise stated, we assume that the waves are initially reflected by the horizontal boundaries, i.e., ${k}_{y}/{k}_{x}>b/a$. This assumption implies that ${u}_{i}$ is the independent mode amplitude while ${{\text{w}}}_{i}$ is a dependent amplitude that results from polarization coupling at the vertical sidewalls. It puts no restriction on the analysis as the horizontal and vertical parameters may always be interchanged. Because of symmetry, ${u}_{i}$ is the same for all waves except for a possible change in sign that accounts for the even and odd symmetry of the modal fields in the horizontal and vertical directions. Also because of symmetry, the polarization coupling parameter, ${c}_{p}\equiv {{\text{w}}}_{i}/{u}_{i}$ is independent of the wave number $i$. According to (5), this parameter vanishes in the paraxial limit, $\sigma \to 0$, and the modes become entirely determined by ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$. In this limit the TE–TE and TM–TM modes are identical to the Marcatili’s TE-like (${E}_{pq}^{x}$) and TM-like (${E}_{pq}^{y}$) modes, respectively (Marcatili 1969). Away from this limit, they add to both of the major components of these modes other minor field components which result from the polarization coupling, as shown below.

2.5 Transport matrices

Since ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$ are known eigen vectors (see Appendix B), it is sufficient to monitor the evolution of the amplitude vector, ${\underline{A}}_{i}={\left(\begin{array}{cc}{u}_{i}& {{\text{w}}}_{i}\end{array}\right)}^{t}$, of the scattered waves, where the superscript $t$ stands for transpose. This is done by reducing the above equations of motion of ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$ in (3–6) to the following transport equations of ${\underline{A}}_{i}$,

$${\underline{A}}_{f}={\underset{\_}{\underline{T}}}_{ H/V} {\underline{A}}_{i}$$

(8)

where

$${\underset{\_}{\underline{T}}}_{ H}=\left(\begin{array}{cc}{\rho }_{\perp y/ \parallel y}& {\left(-1\right)}^{\varepsilon }\sigma {\rho }_{oy}\\ 0& -{\rho }_{\parallel y/\perp y}\end{array}\right)$$

(9)

and

$${\underset{\_}{\underline{T}}}_{ V}={\left(-1\right)}^{\varepsilon }\left(\begin{array}{cc}-{\rho }_{\parallel x/\perp x }& 0\\ {\left(-1\right)}^{\varepsilon }\sigma {\rho }_{ox}& {\rho }_{\perp x/\parallel x}\end{array}\right)$$

(10)

are the transport matrices of the horizontal and vertical surfaces of the core, respectively. These matrices are, indeed, unitary matrices, which conserve the Euclidean norm of ${\underline{A}}_{i}$. Inspection of (9 and 10) shows that they do not commute.

3 Guided-mode resonance conditions

3.1 Polarization-coupling induced errors

A plane wave executing even number of reflections in either vertical or horizontal directions must replicate itself to sustain modal propagation. Suppose that the wave executes $2{m}_{1}$ reflections at the top and bottom horizontal surfaces of the core followed by one reflection at the vertical sidewall. Then it executes $2{m}_{2}$ reflections at the horizontal surfaces followed by another reflection at the other vertical sidewall before it replicates its path, as shown in Fig. 2. The transport matrix of the wave along this path, $\underset{\_}{\underline{M}}{= \underset{\_}{\underline{T}}}_{V}{\underset{\_}{\underline{T}}}_{H}^{2{m}_{2}}{\underset{\_}{\underline{T}}}_{V}{\underset{\_}{\underline{T}}}_{H}^{2{m}_{1}}$. To constitute a guided mode, the vector ${\underline{A}}_{i}$ must be an eigen vector of $\underset{\_}{\underline{M}}$. In addition, to ensure consistent propagation of this modes, its eigen value $\lambda$ must satisfy the transverse resonance condition (TRC),

$${\lambda e}^{-2j{k}_{x}a}{e}^{-2j\left({m}_{1}+{m}_{2}\right){k}_{y}b}=1$$

(11)

In the paraxial limit ($\sigma \to 0$) $\lambda ={{(\rho }_{\parallel x/\perp x})}^{2}{({\rho }_{\perp y/ \parallel y})}^{2\left({m}_{1}+{m}_{2}\right)}$ and (11) reduces to the Marcatili’s resonance conditions, ${{(\rho }_{\parallel x/\perp x})}^{2}{e}^{-2j{k}_{x}a}=1$ and ${({\rho }_{\perp y/ \parallel y})}^{2}{e}^{-2j{k}_{y}b}=1$ of the TE-like and TM-like modes which are independent of ${m}_{1}$ and ${m}_{2}$. Away from this limit, there is no solution of (11) which is independent of ${m}_{1}$ and ${m}_{2}$. This result shows that there is a tradeoff between the accuracy of satisfying the TRCs and the strength of polarization coupling. As the coupling increases the accuracy of Maractili’s resonance conditions decreases and vice versa. It implies invoking optimization techniques to compute the modal effective indexes of the modes of high-index-contrast waveguides.

3.2 Multipath interference

To investigate the effect of varying the number of double reflections in the vertical and horizontal directions on satisfying the TRC, we carry out numerical computations of the matrix $\underset{\_}{\underline{M}}$ for an ensemble of rays executing different number of reflections. In these computations we assume that the ${i}^{th}$ waves of the quadruples of plane waves constituting the QG mode executes $N$ double reflections at the vertical sidewalls of the core. Its trajectory traverses $2N$ half zigzag paths (HZPs) in the horizontal direction (x–z plane). Each HZP is labeled by an integer $s$ that increases from unity to $2N$ along the direction of propagation, as shown by the schematic in Fig. 3 Copies of the initial field vector are transmitted by different rays which all execute the same $2N$ horizontal reflections. Consider now the reflections of the wave in the y–z^’ plane at the top and bottom surfaces of the core. Since the number of horizontal reflections is fixed, the ray path is determined by the number of vertical reflections it executes between the start and end point. Suppose that $q$ is an integer that counts the number of vertical reflections along a single HZP. Then the minimum and maximum number of these reflections are ${q}_{min}=1$ and ${q}_{max}=Q\left(s\right)-Q\left(s-1\right)$, where $Q\left( s \right) = \left[ {s\left( {k_{y} /k_{x} } \right)\left( {a/b} \right)} \right]$ and $\lfloor x \rfloor$ denotes the floor of $x$. The expression of ${q}_{max}$ is derived by applying simple geometrical rules. It assumes initial reflection of the wave in the vertical direction, i.e., $\left({k}_{y}/{k}_{x}\right)\left(a/b\right)>1$. Otherwise, the vertical and horizontal parameters must exchange. Each selection of $q$ and $s$ identifies a different path of the ray. Again, all these paths start at the same initial point and end up at the same final point after the wave executes $2N$ horizontal reflections and different number of vertical reflections that depend on $q$ and $s$. The transport matrix of the ray that executes $2N$ horizontal reflections and $q$ vertical reflections in the ${s}^{th}$ HZP is,

$${\underset{\_}{\underline{M}}}{\prime}={e}^{-j\left(2N-s+1\right){k}_{x}a}{e}^{-jq{k}_{y}b}{{\underset{\_}{\underline{T}}}_{V}}^{\left(2N-s+1\right)}{{\underset{\_}{\underline{T}}}_{H}}^{q}{\underset{\_}{\underline{M}}}_{o}{\prime}$$

(12)

with

Fig. 3

Schematic of the propagation of plane-wave rays along the x–z and y–z^’ planes of the core of a ROWG. The rays are formed as the plane waves fold in both vertical and horizontal directions. The folded waves interfere at the end of the wave trajectory

$${\underset{\_}{\underline{M}}}_{o}{\prime}={e}^{-j{\left(s-1\right)k}_{x}a}{e}^{-j{Q\left(s-1\right)k}_{y}b}{{\underset{\_}{\underline{T}}}_{V}}^{\left(s-1\right)}{{\underset{\_}{\underline{T}}}_{H}}^{Q\left(s-1\right)}$$

(13)

Note that unlike $\underset{\_}{\underline{M}}$ the transport matrix ${\underset{\_}{\underline{M}}}{\prime}$ incorporates the propagation phase. Also note that $Q\left(s-1\right)$ represents the number of vertical reflections executed by the ray in the initial $s-1$ HZPs. Only when these reflections have been executed when the ray execute other $q$ vertical reflections at the subsequent HZP. The number of reflected rays, ${Z}_{N}=\sum_{s=1}^{2N}{q}_{max}$. It is the same as the overall number of vertical reflections executed along the wave trajectory. Only rays with an index ${q}^{*}$ which yields an even number of the sum, ${q}^{*}+Q\left(s-1\right)$ execute double vertical reflections. Each of these rays satisfy a TRC.

3.3 Modal effective indexes

Once ${\underset{\_}{\underline{M}}}{\prime}$ is computed for a given ray path $\left({q}^{*},s,N\right)$, its trace and determinant are computed to get its eigen value ${\lambda }{\prime}$. Unlike $\lambda$ of Sect. 3.1, ${\lambda }{\prime}$ incorporates the propagation phase delay. Thus, the TRC in (11) reduces to ${\lambda }{\prime}=1$. Because of the unitarity of ${\underset{\_}{\underline{M}}}{\prime}$, this condition is automatically satisfied in magnitude. The error ${{\text{r}}}_{\theta }\left(s,{q}^{*},N\right)$ in satisfying the phase condition equals the wrapped phase $\theta \left(s,{q}^{*},N\right)$ of ${\lambda }{\prime}$, which is limited between $-\pi$ and $\pi$. The effective indexes of the QG modes are calculated by minimizing the absolute phase error $\left|{{\text{r}}}_{\theta }\left(s,{q}^{*},N\right)\right|$ for all the rays executing double reflections at all $N$. This is done by searching for the minima of the error function,

$$f\left({k}_{x},{k}_{y}\right)\equiv \frac{1}{{Z}_{T}}\sum_{N=1}^{{N}_{max}}\sum_{s=1}^{2N}\sum_{q}\left|{{\text{r}}}_{\theta }\left(s,{q}^{*},N\right)\right|$$

(14)

where ${Z}_{T}=$ ${\sum }_{N=1}^{{N}_{max}}{Z}_{N}$ is the total number of rays in the statistical ensemble while ${N}_{max}$ is an arbitrary large number that ideally tends to infinity. The entire parameter space over which the search is done is bounded by ${k}_{x}^{2}+{k}_{y}^{2}<\left({n}_{1}^{2}-{n}_{2}^{2}\right){k}_{o}^{2}$. This bound ensures that $\beta >{n}_{2}{k}_{o}$. In addition, the vertical (${k}_{x}=0$) and horizontal (${k}_{y}=0$) axes corresponding to the modes of the horizontal and vertical slab waveguides are excluded from the search space. It is subdivided into two subspaces. The subspace where ${k}_{y}/{k}_{x}>b/a$, as assumed by default in this work, and the subspace where ${k}_{y}/{k}_{x}<b/a$. In this latter subspace ${\underset{\_}{\underline{T}}}_{V}$ and ${\underset{\_}{\underline{T}}}_{H}$ as well as ${k}_{x}a$ and ${k}_{y}b$ interchange in the computation of ${\underset{\_}{\underline{M}}}{\prime}$.

3.4 Numerical examples

Consider computing the effective indexes of the TE–TE and TM–TM modes of a ROWG with ${n}_{1}$= 3.5, ${n}_{2}$=1.5, $a$=0.5 µm, and $b$=0.2 µm. The error function in (14) is computed at ${N}_{max}$=20 (200 rays) and a uniform discretization step of 0.01 µm⁻¹ in ${k}_{x}$ and ${k}_{y}$. All computations are done at a free-space wavelength of 1.55 µm. The results show that the average error fluctuates around 1.5 rad in the entire computational space except at two points where it has local minima of different depths. These points appear in the contour plot of Fig. 4a. The first point corresponds to a TE–TE mode. It reaches a minimum of 0.28 rad (depth of 1.22 rad) at ${k}_{x}$ =5.90 µm⁻¹ and ${k}_{y}$=8.48 µm⁻¹. The corresponding modal effective index is 2.40. The second point corresponds to a TM–TM mode. It reaches a minimum of 0.69 rad (depth of 0.81 rad) at ${k}_{x}$=4.76 µm⁻¹ and ${k}_{y}$=11.74 µm⁻¹. The corresponding modal effective index is 1.58. The values of ${k}_{x}$ and ${k}_{y}$ for the TE–TE and TM–TM modes coincide with the solution of Marcatili’s resonance conditions of the fundamental TE-like (circle) and TM-like (square) modes. This result shows that the Marcatili’s resonance conditions compute the effective indexes of the QG modes beyond the paraxial limit from a statistical average perspective. Numerical computations with a commercial mode solver that employs finite difference approach (Zhu and Brown 2002) with PML boundary conditions yield effective indexes which are within 10% of the computed values. See the rows of Table 1 corresponding to $a/b=2.5$ for details.

Fig. 4

Contour plot of the error function in (14) in the ${{\text{k}}}_{x}$-${{\text{k}}}_{y}$ space for a ROWG with ${{\text{n}}}_{1}=3.5$, ${{\text{n}}}_{2}=1.5$, and $a=0.5$ µm. The thickness $b$ equals 0.2 µm in (a) and 0.5 µm in (b). The circles and squares surround points corresponding to the Marcatili’s TE-like and TM-like modes, respectively. Blue and red colors denote the TE–TE and TM–TM modes, respectively. All solutions lie in the yellow region where $\beta >{{\text{n}}}_{2}{{\text{k}}}_{o}$

Table 1 Parameters of the modes of the ROWGs in the numerical examples of Sect. 3.4

Consider now a square waveguide with $a$=$b$=0.5 µm with all other parameters unchanged. A contour plot of the error function in (14) of both TE–TE and TM–TM modes is shown in Fig. 4b. There are two TM–TM modes and one TE–TE mode supported by the waveguide. Because of the geometrical symmetry of the core, these modes have two-fold degeneracy. The points of the space corresponding to each mode exist in pairs with ${k}_{x}$ and ${k}_{y}$ interchanged. One solution in each pair corresponds to a TE-like mode while the other solution corresponds to a TM-like mode. The TE–TE mode has one solution pair at ${k}_{y}/{k}_{x}$=5.90 µm⁻¹ and ${k}_{x}/{k}_{y}$=9.31 µm⁻¹. The solution at (${k}_{x}$,${k}_{y}$) = (5.90, 9.31) corresponds to the Marcatili’s TE-like (${E}_{01}^{x}$) mode while the other solution at (9.31,5.90) corresponds to the Maractili’s TM-like (${E}_{10}^{y}$) mode. The TM–TM mode have two pairs of solutions at ${k}_{y}/{k}_{x}=5.90$ µm⁻¹ and ${k}_{x}/{k}_{y}=4.76$ µm⁻¹ and at ${k}_{y}/{k}_{x}=11.26$ µm⁻¹ and ${k}_{x}/{k}_{y}=4.76$ µm⁻¹. The first pair at (5.90,4.76) and (4.76,5.90) correspond to the TE-like (${E}_{00}^{x}$) and TM-like (${E}_{00}^{y}$) modes, respectively. The second pair at (11.26, 4.76) and (4.76,11.26) correspond to the TE-like (${E}_{10}^{x}$) and TM-like (${E}_{01}^{y}$) modes, respectively. As expected, this result shows that because of the symmetry of the core in the case of unity aspect ratio the TE–TE /TM–TM modes are no longer affiliated with the Marcatili’s TE-like/ TM-like modes. They may be regarded as the supermodes which result from coupling between the TE-like and TM-like modes. In this case, the aspect ratio plays a role similar to asynchronicity in conventional couplers (Nishihara et al. 1989). It controls the weights of the coupled modes so that under unity aspect ratio they are equally weighted. Table 1 shows the computed effective indexes of the TE–TE and TM–TM modes of the ROWG in this example ($a/b=1$) and compares them with those computed by the numerical mode solver used in the previous example. It shows that the error in effective indexes remains within 11%. It also shows a discrepancy in the effective indexes computed by the numerical solver for modes that have identical effective indexes due to symmetry.

4 Field components of quasi-guided TE-TE and TM-TM modes

4.1 Analytical expressions

The field vectors of the plane-waves constituting the TE–TE and TM–TM modes are expressed by the linear combination in (7) which has one independent constant, ${u}_{i}$. The other constant,${w}_{i}={u}_{i}{c}_{p}$, is completely determined in terms of the polarization coupling parameter, ${c}_{p}$, as explained above. Due to symmetry, the constants,${u}_{i}=\pm u$, for all$i=\mathrm{1,2},\mathrm{3,4}$. The ray path dependence of eigen values of ${\underset{\_}{\underline{M}}}{\prime}$ outlined in Sect. 3.2 gives rise to statistical variations in ${c}_{p}$. To arrive at an optimized solution of the minor field components of the modes made by the scattered waves a least-square approximation is invoked, which replaces ${c}_{p}$ with its statistical average ${\overline{c}}_{p}$. Then their plane wave field vectors are added after assigning their retardation phase. This addition constructs modes with four different even/odd symmetries with respect to the vertical and horizontal axes passing through the center of the core. For convenience these forms have been unified in one form. In this unified form, the electric field components of the TE–TE modes are the sum of (a) major field components (Marcatili’s TE-like Mode),

$${\overline{E} }_{Jx}=A {\overline{\beta }}_{x}{\text{sin}}{\varphi }_{x}{\text{sin}}{\varphi }_{y}$$

(15)

$${\overline{E} }_{Jz}=-jA {\overline{k} }_{x}{\text{cos}}{\varphi }_{x}{\text{sin}}{\varphi }_{y},$$

(16)

with ${\overline{E} }_{Jy}=0$, (b) major field components due to polarization coupling,

$${\widetilde{E}}_{Jx/y/z}=\kappa {\overline{E} }_{Jx/y/z},$$

(17)

where, $\kappa =\sigma {\overline{c}}_{p}$, and (c) minor Maractili’s TM-like field components,

$${\widetilde{E}}_{Nx}=-\kappa F {\overline{k}}_{x}{{\text{K}}}_{y} A{\text{sin}}{\varphi }_{x}{\text{sin}}{\varphi }_{y},$$

(18)

$${\widetilde{E}}_{Ny}=-\kappa F\sqrt{{{\text{K}}}_{x}^{2}+{\upbeta }^{2}} A{\text{cos}}{\varphi }_{x}{\text{cos}}{\varphi }_{y},$$

(19)

$${\widetilde{E}}_{Nz}=-j\kappa F {{\text{K}}}_{y}{\overline{\beta }}_{x}A{\text{cos}}{\varphi }_{x}{\text{sin}}{\varphi }_{y}$$

(20)

where $A$ is an arbitrary amplitude while ${\varphi }_{x}={k}_{x}\left(x-a/2\right)+\left({m}_{x}+1\right)\pi /2$, and ${\varphi }_{y}={k}_{y}\left(y-b/2\right)+\left({m}_{y}+1\right)\pi /2$. The parameters ${m}_{x}$ and ${m}_{y}$ are the mode orders in the $x$ and $y$ directions. The origin of the $x$ and $y$ coordinate axes in this unified form coincides with the lower left corner of the waveguide core. The bar denotes the components of the Marcatili’s modes in the absence of polarization coupling while the tilde denotes the extra components due to this coupling. The suffixes $J$ and $N$ stands for major and minor, respectively. The parameter, $F=\beta /{k}_{x}{k}_{y}$ while $\upbeta$, ${{\text{K}}}_{x}$, and ${{\text{K}}}_{y}$ are normalized propagation constants as defined in Appendix B. Similarly, the magnetic field components of the TM–TM modes are the sum of (a) major field components (Marcatili’s TM-like Mode), ${\overline{H} }_{Jx}$, ${\overline{H} }_{Jy}=0$, and ${\overline{H} }_{Jz}$, (b) major field components due to polarization coupling, ${\widetilde{H}}_{Jx}$, ${\widetilde{H}}_{Jy}=0$, and ${\widetilde{H}}_{Jz}$, and (c) minor Marcatili’s TE-like field components, ${\widetilde{H}}_{Nx}$, ${\widetilde{H}}_{Ny}$, and ${\widetilde{H}}_{Nz}$. All these components are obtained after replacing the electric field $E$ with the magnetic field $H$ and $\kappa$ with $-\kappa$ in (15-20). It should be noted that the field expressions in (15-20) are only valid for modes satisfying the condition ${k}_{y}/{k}_{x}>b/a$, as assumed by default in this work. If this condition is not satisfied, then the $x$ and $y$ components of the fields as well as all other $x$ and $y$ parameters must interchange.

4.2 Numerical examples

To verify the utility of the derived analytical expressions in (15-20), they are compared to the modal fields computed by a full-vectorial mode solver that employs finite element method with PML boundary conditions. Since Maxwell’s equations relate electric and magnetic fields, it is sufficient to compare the analytical with the numerical solutions for only one of these fields. The error metric that describes the difference between the two solutions of the ${\nu }^{th}$ field component of the TE–TE modes is,

$${\Delta }_{\nu }=\sum_{j}\sum_{i}{\left|{E}_{A\nu }^{(n)}\left({x}_{i},{y}_{j}\right)-{E}_{N\nu }^{(n)}\left({x}_{i},{y}_{j}\right)\right|}^{2}$$

(21)

The electric field $E$ is replaced with the magnetic field $H$ for the error of the TM–TM modes. The double sum in (21) is over the points $\left({x}_{i},{y}_{j}\right)$ of the 2D grid in the $x$-$y$ plane where computations are done. The suffix $A$ and $N$ stands for the analytically and numerically computed fields respectively. Both analytical and numerical fields are normalized such that the sum of the square of their Euclidean norms inside the core of the waveguide is unity. This normalization ensures equal energies of both fields inside the core. Computations of ${\Delta }_{x}$, ${\Delta }_{y}$, ${\Delta }_{z}$, and their sum (total error) were carried out for the $x$, $y$, and $z$ field components of the TE–TE and TM–TM modes of SOI-ROWGs with different core dimensions. The results of computations in Table 2 show that the error remains below ~ 4% for the individual field components while the total error remains below ~ 6% for all SOI-ROWGs, even for those waveguides with unity aspect ratio.

Table 2 Error in the analytical expressions of the field components of the TE–TE and TM–TM modes compared to numerical computations

The improved Marcatili’s method reported in Westerveld et al. (2012) fails under the so-called “avoid crossing” condition where two of the waveguide modes have similar effective indexes. To inspect the utility of the derived analytical expressions in (15-20) under this condition, the effective indexes of the modes of an SOI-ROWG of thickness $b=0.3$ µm were computed using the numerical mode solver as a function of waveguide width $a$. Figure 5 shows that that the effective index branches of the TM–TM (TM-like ${E}_{00}^{y}$) and the TE–TE (TE-like ${E}_{20}^{x}$) modes avoid crossing at a point where the width $a=1.4$ µm. The contour plots of the analytically and numerically computed fields of both modes are shown in Fig. 6. The corresponding error metrics in Table 2 are all within ~ 5%. This result shows that the analytical expressions presented in (15-20) are in good agreement with the numerical computations under this “avoid crossing” condition.

Fig. 5

Effective index of the TM–TM (TM-like ${E}_{00}^{y}$) mode (blue) and the TE–TE (TE-like ${E}_{20}^{x}$) mode (red) against waveguide width a in µm for a SOI-ROWG with ${{\text{n}}}_{1}=3.5$, ${{\text{n}}}_{2}=1.5$, and $b=0.3$ µm. The inset zooms in on the point where the two modes have similar effective index

Fig. 6

Contour plot of the field components of the TM–TM (TM-like ${E}_{00}^{y}$) mode (top) and the TE–TE (TE-like ${E}_{20}^{x}$) mode (bottom). The analytical solutions are shown to the left in (a) and (c) while the numerical solutions are shown to the right in (b) and (d). The SOI-ROWG parameters are ${{\text{n}}}_{1}=3.5$, ${{\text{n}}}_{2}=1.5$, $a=1.4$ µm, and $b=0.3$ µm

5 Comparison with the improved Marcatili’s method

This section compares the plan-wave scattering approach with the improved Marcatili’s method in Westerveld et al. (2012) for the purpose of outlining the similarities and differences between the two. This comparison refers to the field components and waveguide axes according to the coordinate system of the current paper which is different from that in Westerveld et al. (2012). The analytical expressions of the modal fields in section II-A in Westerveld et al. (2012) result in modal solutions with ${E}_{{\text{y}}}=0$ (or ${H}_{{\text{y}}}=0$) when boundary conditions are applied at the interfaces parallel (or normal) to the dominant field component. These solutions may directly be obtained by adding the field vectors ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ of the plane waves 1, 2, 3, and 4 in Appendix B after assigning their retardation phase. Since ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ has two polarizations corresponding to the TE and TM modes of the horizontal slab (of thickness $b$), two types of modes result from this addition. They are the Maractili-type modes reported in Westerveld et al. (2012) where ${E}_{{\text{y}}}=0$ and ${H}_{{\text{y}}}=0$ for the TE and TM polarizations, respectively. The addition of the four plane waves to get these solutions is equivalent to the superposition of two modes of the horizontal slab made by the plane wave pairs (1, 2) and (3, 4) of field vector ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ which propagate at an angle with the z-axis (see Fig. 2). The interference between these slab modes results in a standing-wave along the wider dimension of the waveguide core (the $x$-axis). It gives a field solution which is the superposition of two slab modes that, indeed, satisfies the boundary conditions of the horizontal slab (along the $y$-axis) and yet varies along the $x$-axis ($\partial /\partial x\ne 0$). This variation led to the conclusion in Westerveld et al. (2012) that the dispersion relations of the horizontal slab of the TE and TM polarization are “in fact more general”. It motivated extending the Marcatili-type modes to the SOI waveguides. Unlike the traditional Marcatili’s modes which exactly satisfy the boundary conditions of both horizontal and vertical slabs under the paraxial approximation ($\sigma \to 0$) (Marcatili 1969), the analytical solutions of modes in Westerveld et al. (2012) admit non-paraxial solutions ($\sigma \ne 0$) at the cost of satisfying exact boundary conditions only of the horizontal slab. Note that the waveguide core may always be rotated to make this slab vertical, e.g., in Fig. 1d in Westerveld et al. (2012).

Despite the non-paraxiality of the analytical expressions in Westerveld et al. (2012) which is required to describe the modes of SOI waveguides, they do not account for polarization coupling between ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$ at the boundaries of the vertical slab (of width $a$($>b$)). This coupling is clearly seen by referring to (5) in Sect. 2.3 where the coupling between ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{f}$ is described by the product of $\sigma$ and ${\rho }_{ox}$. The parameter ${\rho }_{ox}$ is the sum of the reflection coefficients of the normal and parallel polarizations, ${\rho }_{\perp x}$ and ${\rho }_{\parallel x}$, at the boundaries of the vertical slab (See Sect. 2.2). It never vanishes, and as a result polarization coupling cannot, in principle, be ignored under non-paraxiality conditions ($\sigma \ne 0$), which is obviously the case of the modes of SOI waveguides. Neglecting the coupling between ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$ in Westerveld et al. (2012) resulted in four unknown field parameters in the waveguide core, namely, ${A}_{1}$, ${A}_{2}$, $\eta$, and $\xi$. These four parameters are equivalent to the four amplitudes needed to describe the four interfering waves of Sect. 2.1, yet of only the field vector ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ (i.e. excluding ${\underset{\_}{\delta }}_{i}$). Since the amplitudes of ${\underset{\_}{\delta }}_{i}$ (${{\text{w}}}_{i}$’s) are independent of the amplitudes of ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ (${u}_{i}$’s) until boundary conditions are applied, the work in Westerveld et al. (2012) missed four unknown field parameters corresponding to the amplitudes ${{\text{w}}}_{i}$’s of the vector ${\underset{\_}{\delta }}_{i}$ that result from the polarization coupling at the vertical sidewalls. This vector must be incorporated for general description of modal polarization as is done in (7) of Sect. 2.4. Note that while ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}$ and ${\underset{\_}{\delta }}_{i}$ are not orthogonal they are linearly independent vectors which span all possible polarizations of a given plane wave. These four missing unknowns fill in the gap between the 16 boundary-condition equations and the 12 unknown field parameters (${A}_{1}-{A}_{10}$, $\eta$, and $\xi$) reported in Westerveld et al. (2012). Their absence led to an overdetermined system of equations that necessitates applying boundary conditions on selected field components in favor of the others, i.e., exact boundary conditions are not applied in Westerveld et al. (2012). This is a fundamental difference between the analytical expressions of the modal fields obtained by the improved Marcatili’s method and those given in (15-20) which satisfy all boundary conditions. The selective application of boundary conditions limits the application of the improved method to cases where the unselected components may be ignored. Namely, when the width of the core is much larger than its thickness. It adds extra limitations to those already set by the SOV solutions which increase the error in the analytical expressions; particularly for higher-order modes or for SOI-ROWGs with aspect ratios close to unity.

Applying boundary conditions to all field components using exact scattering rules ensures that only the errors due to the SOV solutions are encountered in computations which is the best that can be done under the SOV assumption. These errors are described by the function $f\left({k}_{x},{k}_{y}\right)$ defined by (14) of Sect. 3.3 whose minima are close to zero but never exactly zero. They result from the mismatch between the exact modal solutions of the SOI-ROWGs (which may be obtained by numerical solvers) and the approximate analytical solutions which are based on the SOV assumption. The fact that the minima of $f\left({k}_{x},{k}_{y}\right)$ of the SOI-ROWGs take place at the Marcatili’s resonance conditions, as is shown in Sect. 3.4, is one of the main outcomes of this work. In (Marcatili 1969) these conditions were only applied to weakly-guided waveguides with no clue about their extension to high-index contrast waveguides. In (Westerveld et al. 2012), their use was extended to SOI-ROWGs, with no verification that they yield the optimum choice of ${k}_{x}$ and ${k}_{y}$ that minimizes the errors of the SOV solutions of the modes of these waveguides. Finally, the minimization of the contour integration metric ${U}_{mm}$ in Westerveld et al. (2012) is entirely different from the minimization of the error function $f\left({k}_{x},{k}_{y}\right)$ for two reasons. First, ${U}_{mm}$ not only minimizes the error in the SOV solutions but also due to the selective application of boundary conditions. Second, while ${U}_{mm}$ may intuitively be interpreted as energy density that cannot be attached to a rigorous physical meaning, $f\left({k}_{x},{k}_{y}\right)$ has a well-defined physical meaning. It represents the sum of the absolute values of the phase errors in satisfying the guided-mode resonance conditions by the interfering plane-wave rays.

6 Conclusion

A novel plane-wave scattering model has been developed to describe modal propagation in SOI-ROWGs.The model assumes SOV solutions of the modal fields. It satisfies the boundary conditions of all field components and incorporates polarization coupling at the boundaries of the waveguide core. It yields approximate full-vectorial analytical expressions of the fields of the guided modes of these waveguides. These expressions reduce to the field expressions of the Marcatili’s TE-like and TM-like modes when polarization coupling is neglected. The Marcatili’s resonance conditions compute the modal propagation constants which minimize the error in the SOV solutions for all the modes. The derived expressions enable using mode propagation analysis to get fast full-vectorial analysis of silicon photonic integrated circuits. Although the modal solutions are only given in the core, their extension in the cladding (excluding the hatched regions of Fig. 1) may directly be obtained by applying the boundary conditions along the core surface. The analytical model developed for the derivation of the guided modes applies exact scattering rules of the plane waves which may directly be extended to other asymmetric ROWGs under different metallic or dielectric boundary conditions. It enables incorporating different wave propagation effects such as nonlinearity or anisotropy in future work.

Appendices

Appendix A: Total internal reflection matrices

Consider the TIR of a plane wave of propagation constant ${\overrightarrow{k}}_{i}$ at the planar interface between two semi-infinite dielectric media. The unit vector normal to the plane of incidence, $\widehat{n}={\overrightarrow{k}}_{i}\times \widehat{g}/\Vert {\overrightarrow{k}}_{i}\times \widehat{g}\Vert$, where $\underset{\_}{\widehat{g}}$ is the unit vector normal to the interface. The electric field of the incident wave ${\underline{E}}_{i}$ is the sum of the field normal to the plane of incidence, ${\underline{E}}_{\perp i}=\underset{\_}{\underline{N}} {\underline{E}}_{i}$, and the field parallel to the plane of incidence, ${\underline{E}}_{\parallel i}=\left(\underset{\_}{\underline{I}}-\underset{\_}{\underline{N}}\right){\underline{E}}_{i}$. Here, $\underset{\_}{\underline{I}}$ is the identity matrix while $\underset{\_}{\underline{N}}$ is the matrix whose element ${N}_{ij}={\widehat{n}}_{i}{\widehat{n}}_{j}$, where ${\widehat{n}}_{i}$ is the ${i}^{th}$ components of $\widehat{n}$. The electric fields of the reflected wave which are normal and parallel to the plane of incidence are, ${\underline{E}}_{\perp r}={\rho }_{\perp }\underset{\_}{\underline{N}} {\underline{E}}_{i}$ and ${\underline{E}}_{\parallel r}={\rho }_{\parallel }\left(2\underset{\_}{\underline{G}}-\underset{\_}{\underline{I}}\right)\left(\underset{\_}{\underline{I}}-\underset{\_}{\underline{N}}\right){\underline{E}}_{i}$. Here $\underset{\_}{\underline{G}}$ is the matrix whose element ${G}_{ij}={\widehat{g}}_{i}{\widehat{g}}_{j}$ where ${\widehat{g}}_{i}$ is the ${i}^{th}$ components of $\widehat{g}$. Thus, the overall reflected field vector, ${\underline{E}}_{r}=\underset{\_}{\underline{R}} {\underline{E}}_{i}$, where $\underset{\_}{\underline{R}}={\rho }_{\perp }\underset{\_}{\underline{N}}+{\rho }_{\parallel }\left(2\underset{\_}{\underline{G}}+\underline{N}-\underset{\_}{\underline{I}}\right)$. The reflection matrix $\underset{\_}{\underline{R}}$ is a symmetric matrix that is invariant under the transformations, $\underset{\_}{\widehat{n}}\leftrightarrow -\underset{\_}{\widehat{n}}$ or $\hat{\underline {g} } \to - \hat{\underline {g} }$. It is also invariant to translation of the planar dielectric interface. Under time reversibility condition, $t \to - t$, the TIR coefficients, $\rho_{ \bot } \to \rho_{ \bot }^{*}$ and $\rho_{\parallel } \to \rho_{\parallel }^{*}$ while, $\underset{\_}{\underline{G}}$, $\underset{\_}{\underline{N}}$, and $\underset{\_}{\underline{I}}$ remain the same. Hence the matrix, $\underline{\underline{R}} \to \underline{\underline{R}}^{*}$, which means that, ${\underline{E}}_{i}= {\underset{\_}{\underline{R}}}^{*}{\underline{E}}_{r}$ and since ${\underline{E}}_{i}= {\underset{\_}{\underline{R}}}^{-1}{\underline{E}}_{r}$, then the ${\underset{\_}{\underline{R}}}^{-1}={\underset{\_}{\underline{R}}}^{*}$. Combining this equality with the symmetry property shows that the reflection matrix is a unitary matrix, ${\underset{\_}{\underline{R}}}^{-1}={\underset{\_}{\underline{R}}}^{*t}$. The $\underset{\_}{\underline{H}}$ and $\underset{\_}{\underline{V}}$ matrices in (1 and 2) are the reflection matrices of the horizontal and vertical surfaces of the core of ROWGs corresponding to $\widehat{g}=\pm {\widehat{a}}_{y}$ and $\widehat{g}=\pm {\widehat{a}}_{x}$, respectively.

Appendix B: normalized plane-wave field vectors

The normalized field vector of the i^th plane waves constituting the TE modes of the horizontal slab waveguide, ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}={\left(\pm \begin{array}{ccc}{\overline{\beta }}_{x}& 0& -{\overline{k}}_{x}\end{array}\right)}^{t}$ where the upper sign is for $i=\mathrm{1,2}$ and the lower sign for $i=\mathrm{3,4}$. The corresponding field vector of the vertical slab waveguide, ${\underset{\_}{\delta }}_{i}={\left(\begin{array}{ccc}0& \pm {\overline{\beta }}_{y}& -{\overline{k}}_{y}\end{array}\right)}^{t}$ where the upper sign is for $i=\mathrm{1,3}$ and the lower sign for $i=\mathrm{2,4}$. The normalized field vector of the i^th plane waves constituting the TM modes of the horizontal slab waveguide, ${\underset{\_}{\mathrm{\rm E}}}_{{\text{i}}}={\left(\pm \begin{array}{ccc}{{\text{K}}}_{y}{\overline{k}}_{x}& -\sqrt{{{\text{K}}}_{x}^{2}+{\upbeta }^{2}}& \pm {{\text{K}}}_{y}{\overline{\beta }}_{x}\end{array}\right)}^{t}$ where the pairs $\left(+,+\right)$, $\left(-,-\right)$, $\left(-,+\right)$, and $\left(+,-\right)$, correspond to $i=\mathrm{1,2},\mathrm{3,4}$, respectively. The corresponding field of the vertical slab waveguide, ${\underset{\_}{\delta }}_{i}={\left(\begin{array}{ccc}\pm \sqrt{{{\text{K}}}_{y}^{2}+{\upbeta }^{2}}& {{{\text{K}}}_{x}\overline{k}}_{y}& \pm {{\text{K}}}_{x}{\overline{\beta }}_{y}\end{array}\right)}^{t}$, where the pairs $\left(-,+\right)$, $\left(+,-\right)$, $\left(+,+\right)$, and $\left(-,-\right)$, correspond to $i=\mathrm{1,2},\mathrm{3,4}$, respectively. The normalized propagation constants, $\upbeta =\beta /{n}_{1}{k}_{o}$ and ${{\text{K}}}_{x/y}\equiv {k}_{x/y}/{n}_{1}{k}_{o}$.