1 Introduction

Optical fiber communication systems transmit information from one place to another by sending optical pulses through an optical fiber. These systems suffer from many propagation problems. One of these problems is the pulse dispersion that degrades the overall system performance. In a common dispersive medium, the optical pulse is broadened with its propagation through the optical fiber channel Mustafa et al. (2021). Dispersion occurs as a result of the group velocity delay (GVD). GVD means that the velocity of the propagated signal through the optical fiber is wavelength dependent. Due to dispersion, the broadened optical pulses may be overlapped and intersymbol interference (ISI) phenomenon occurs. In the worst cases, ISI may cause the received signal undistinguished. Also, dispersion has a great impact on the transmission bit rate and transmission distance (Ibarra-Villalon et al. 2021). Therefore, in high speed long haul optical fiber communication systems, we have to compensate for chromatic dispersion. Many compensation techniques have been proposed in the research literature (Meena and Meena 2020; Sayed et al. 2021). FBG is one of the most effective dispersion compensation techniques (Meena and Meena 2020).

There are two types of FBG based on the gratings distribution spaces. Uniform FBG (UFBG) has an equidistant grating, while chirped FBG (CFBG) has unequal distant gratings. FBG works as a dispersion compensator by narrowing the full width at half maximum (FWHM) with acceptable level of reflectivity. The connection scheme of the FBG in the optical fiber communication system affects the system performance. There three FBG connection schemes. In pre-compensation scheme, FBG is connected before the fiber link. In contrast, FBG is connected after the fiber link in post-compensation scheme. FBG is connected before and after the fiber link in a symmetrical compensation scheme (Mohapatra et al. 2014). In this work, we investigate the post-compensation scheme. To enhance dispersion compensation with FBG, n-stages of cascaded FBG are used. The number of stages is determined based on the FBG reflectivity and the output FWHM. The best number is that achieves maximum reflectivity and minimum FWHM (Sayed et al. 2020a).

The optical modulation technique has a great impact on dispersion compensation. Therefore, we have to use the suitable and efficient modulation scheme. Digital modulation techniques maximize spectral efficiency and improve tolerance to chromatic dispersion (Mohapatra et al. 2013). In this paper, we focus on OQPSK and DPSK modulation techniques.

The aim of this study is to enhance the performance of chromatic dispersion compensation in a standard single mode optical fiber (SSMF). We propose a model that consists of four stages identical linear chirped cascaded FBGs under DPSK modulation technique. A comparative study between using DPSK and OQPSK modulation technique is conducted. Optisystem 7.0 is used to simulate and evaluate the performance of the proposed model in a 10 Gbps WDM link in terms of Q-factor and BER.

The remainder of this paper is organized as follows. Section 2 explains the digital modulation techniques. Chirped FBG is illustrated in Sect. 3. The proposed model is discussed in Sect. 4. Section 5 displays and discusses the simulation results. Section 6 is devoted to the main conclusions.

2 Digital modulation formats

Modulation plays an important role in transmitting the signal from the transmitter to the receiver in all communication systems (Mohapatra et al. 2013). The spectral efficiency of the modulation system is one of the key factors that affect the overall performance of the communication system. In this section, we discuss the two digital modulation techniques used in our study.

2.1 OQPSK modulation format

Advantageously, the use of OQPSK reduces the intensity variations (Huang et al. 2010). Figure 1 illustrates the OQPSK modulator (El-Nahal 2018).

Fig. 1
figure 1

OQPSK modulator (El-Nahal 2018)

Full size image

In the beginning, the OQPSK modulator splits the binary input into two channels (i.e. I-channel and Q-channel). Odd bits are assigned to the I-channel, while the even bits are assigned to the Q-channel. Then, the Q-channel is delayed by a half of the symbol period. The local oscillator generates the carrier signal. The original carrier signal is multiplied by the I-channel to provide the I component. A 90° phase shifted version of the carrier is multiplied by the delayed Q-channel to provide the Q component. Finally, the OQPSK signal is generated by summing the two components (El-Nahal 2018).

In OQPSK, the phase of a signal is varied based on the source symbols. The phase values are calculated by Benedetto et al. (1987)

$$ \varphi_{i} = \left( {\frac{2\pi }{4} \left( {i - 1} \right) + \phi } \right),\quad i = 1, 2, 3, 4 $$
(1)

where ϕ is the phase offset.

The amplitudes of the in-phase (I) and quadrature (Q) channels are given by Benedetto et al. (1987)

$$ I_{i} = \cos \left( {\varphi_{i} } \right),\quad i = 1, 2, 3, 4 $$
(2)
$$ Q_{i} = \sin \left( {\varphi_{i} } \right),\quad i = 1, 2, 3, 4 $$
(3)

The output from the OQPSK modulator is a composite signal s(t). This signal can be written as (Pawula 1984)

$$ s\left( t \right) = \mathop \sum \limits_{n} \left[ {g\left( {t - nT_{s} } \right)s_{i,n} \cos \left( {2\pi f_{c} t} \right) - g\left( {t - nT_{s} - \frac{{T_{s} }}{2}} \right) s_{Q,n} \sin \left( {2\pi f_{c} t} \right)} \right] $$
(4)

where g(t) is the pulse shape, n is the symbol order, \(s_{I,n}\) and \(s_{Q,n}\) are the input symbol of the I and Q channels, and Ts is the symbol period.

2.2 DPSK modulation format

The principle of DPSK modulation is transmitting bit stream by varying the phase of the carrier signal (Haridim et al. 2021). Thus, the phase of the modulated signal is changed to the element of an earlier bit. The earlier element low or high state are traced by the phase of the signal (Mahmood and Ahmed 2018). The input binary stream can be changed so that the next bit depends upon the earlier bit, see Fig. 2. Therefore, the receiver uses the earlier received bit to detect the current bit.

Fig. 2
figure 2

Principle of DPSK modulation (Mahmood and Ahmed 2018)

Full size image

Figure 3 displays the DPSK modulator (Gill et al. 2019). Each one of the modulating signals (i.e. output of the logic gate) and the carrier (i.e. c(t)) has a phase shift of 180°. The DPSK modulation conveys data by changing the phase of the carrier wave. The phase of the modulated signal is shifted relative to the state of the previous signal element. If the data bit is low, i.e., 0, then the phase of the signal is not reversed, but continues as it is. If the data is a high, i.e., 1, then the phase of the signal is reversed, i.e., the phase shift is 180°.

Fig. 3
figure 3

DPSK modulator (Gill et al. 2019)

Full size image

The output signal (i.e. m(t)) from the DPSK modulator is given by Gill et al. (2019)

$$ m\left( t \right) = A\left( t \right)\cos \left( {2\pi f_{c} t + \varphi \left( t \right) + \phi } \right) $$
(5)

where A(t) is the signal amplitude, \(\varphi \left( t \right)\) is the signal phase, and \(\phi\) is the phase shift due to channel.

The phase values are calculated by Mehnaz and Islam (2017)

$$ \varphi_{i} = \varphi_{i - 1} + \left( {\frac{2\pi }{4} \left( {i - 1} \right) + \phi } \right),\quad i = 1, 2, 3, 4 $$
(6)

where \(\varphi_{i}\) is the current symbol phase, and \(\varphi_{i - 1}\) is the previous symbol phase.

The DPSK modulator is very simple and is not expensive. Also, there is no need for synchronization at the receiver side (Gill et al. 2019).

3 Linear chirped FBG

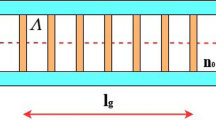
CFBG is an FBG with unequal distant gratings which are distributed based on a chirp function. Therefore, the refractive index modulation varies along the grating length (Toba and Mustafa 2019). Figure 4 shows the basic structure of CFBG.

Fig. 4
figure 4

Basic structure and principle of CFBG

Full size image

The grating period Ʌ(z) in linear CFBG varies linearly over the grating length and is given by Erdogan (1997)

$$ \Lambda \left( {\text{z}} \right) = \Lambda_{0} - \frac{{{\text{z}} - ({\text{l}}_{g} /2)}}{{{\text{l}}_{{\text{g}}} }}{\text{x}} $$
(7)

where Ʌ0 is the period at the grating center, lg is the grating length, and x is the linear chirp parameter.

The CFBG reflection power is inversely proportional to the linear chirp parameter. While, the group delay response slope is directly proportional to this parameter. For optimal CFBG performance in chromatic dispersion compensation the linear chirp parameter, x, is 1 × 10−4 µm (Dar and Jha 2017).

In CFBG, each segment reflects only the wavelength that meets the Bragg condition. Bragg condition is the wavelength at which the total internal reflection occurs and called the Bragg wavelength λB(z) and given by Dar and Jha (2017)

$$ \lambda_{B} = 2n\left( z \right)\Lambda \left( z \right) $$
(8)

where n(z) is the modulated refractive index along the core axis. The modulated refractive index n(z) is given by Dar and Jha (2017)

$$ n\left( z \right) = n_{eff} + \Delta nA\left( z \right)\cos \left( {\frac{{2\pi {\text{z}}}}{{\Lambda_{0} }}\left( {1 + {\text{xz}}} \right)} \right) $$
(9)

where neff is the effective refractive index of the fiber core, and A(z) is the apodization function.

Here, we focus on the uniform CFBG, i.e. A(z) = 1. The effective refractive index is the modal index of FBG and given by Erdogan (1997)

$$ n_{eff} = \beta \frac{{\lambda_{0} }}{2\pi } $$
(10)

where β is the propagation constant of FBG, and λ0 is the free space wavelength.

The chromatic dispersion of CFBG is calculated by Dar and Jha (2017)

$$ D_{grating} = \frac{{2n_{eff} }}{\Delta \lambda c}{\text{l}}_{{\text{g}}} $$
(11)

where c is the speed of light, and Δλ is the wavelength difference between two ends of the grating and given by Dar and Jha (2017)

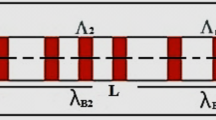
$$ \Delta \lambda = 2n_{eff} \left( {\Lambda_{long} - \Lambda_{short} } \right) $$
(12)

3.1 Cascaded CFBG

It consists of n-stages cascaded CFBG as shown in Fig. 5. The input optical signal is applied on the input port I1 of the first stage (i.e., CFBG-1). Then, the reflected signal R1 is the input I2 of the second stage CFBG-2 and so on. The output signal of the cascaded CFBG is the reflected signal Rn of the last stage CFBG-n (Toba and Mustafa 2019).

Fig. 5
figure 5

Cascaded FBG

Full size image

The cascaded CFBG is based on the standard FBG (i.e., Type I FBG), in which the reflection and transmission spectrums are complementary at the Bragg wavelength λB (Poulin and Kashyap 2009). Figure 6 shows the reflection/transmission spectrum of the standard FBG.

Fig. 6
figure 6

Reflection/transmission spectrum of the standard FBG (Poulin and Kashyap 2009)

Full size image

The reflectivity of n-stages cascaded FBGs is calculated by coupling theory (El-Nahal 2018). Where there is a small loss of the reflected power as a result of the reflection into the cladding. The main objective of the n-stages cascaded CFBGs is to reduce FWHM at an acceptable level of reflectivity which achieves better dispersion compensation performance (i.e., maximum Q-factor at minimum BER). Therefore, the number of stages is selected to achieve minimum FWHM at maximum reflectivity (Sayed et al. 2021).

4 Proposed model

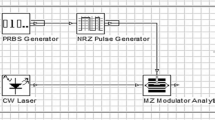
To enhance the chromatic dispersion compensation in SSMF, we propose the model shown in Fig. 7. It consists of a DPSK transmitter, 4-stages cascaded identical CFBG and a direct modulator.

Fig. 7
figure 7

Proposed model

Full size image

A directly modulated laser measured generates a carrier with a frequency of 193.1 THz (1553.6 nm) and a power of 20 dBm. The carrier signal is fed to LiNbO3 electro-optic modulator. Other inputs of LiNbO3 are the DPSK modulated signal and two RZ pulses. These RZ pulses are generated based on the user defined bit sequences. The output of LiNbO3 modulator is lunched into a SSMF. The optical signal from SSMF is amplified by an optical fiber amplifier with a gain of 20 dB. Then, the amplified signal is injected into a 4-stages cascaded identical CFBGs. Finally, the signal is detected by the direct modulator.

At the receiver side, the modulated optical signal is filtered from ripples by a low pass Bessel optical filter. The APD photodiode converts the optical signal into an electrical signal. The modulated electrical signal is filtered from the noise by the low pass Bessel filter. Finally, the electrical signal is modified by the regenerator, and is analyzed by the BER analyzer.

To evaluate the proposed model, we use the simulation parameters shown in Table 1. These simulation parameters are the most used parameters in the optical fiber communication field (Sayed et al. 2021).

Table 1 Simulation parameters (Sayed et al. 2021)
Full size table

The evaluation is performed through a comparative study in terms of Q-factor and BER using Optisystem 7. It includes two cases based on which digital modulation format we use: OQPSK or DPSK. Each case has two sub-cases. The procedure of this comparative study is illustrated in Fig. 8.

Fig. 8
figure 8

Comparison study procedure

Full size image

5 Results and discussion

In this section, we present and discuss the results of the comparative study. The acceptable model is that meets the minimum operational requirements in terms of Q-factor > 6 and BER < 10−9 (Palacharla et al. 1995).

5.1 Case one: OQPSK

5.1.1 OQPSK with CFBG

Figure 9 illustrates the structure of the OQPSK based model with a 4-stages cascaded identical CFBGs.

Fig. 9
figure 9

OQPSK based model of sub-case one

Full size image

This sub-case achieves a maximum Q-factor of 6.94, and a minimum BER of 1.89 × 10−12, see Fig. 8.

In this sub-case, the obtained Q-factor and BER exceed the minimum operational requirements. This means that the received signal is distinguishable and the model is accepted (Fig. 10).

Fig. 10
figure 10

a BER of OQPSK with CFBG. b Q-factor of OQPSK with CFBG

Full size image

5.1.2 OQPSK without CFBG

Without CFBG, a significant decrease in the performance is noticed. As shown in Fig. 11, this model achieves a maximum Q-factor of 2.7 and a minimum BER of 3.47 × 10−3.

Fig. 11
figure 11

a BER of OQPSK without CFBG. b Q-factor of OQPSK without CFBG

Full size image

The obtained results do not meet the minimum operational requirements. Therefore, the received signal is indistinguishable, and the model is not accepted.

5.2 Case two: DPSK

5.2.1 DPSK with CFBG

The basic structure of this model shown in Fig. 7. The results are very good, where the Q-factor is 7.22 and BER is 2.59 × 10−13, see Fig. 12.

Fig. 12
figure 12

a BER of DPSK with CFBG. b Q-factor of DPSK with CFBG

Full size image

Here, the model is accepted where it satisfies the minimum operational parameters condition.

5.2.2 DPSK without CFBG

In this sub-case, the results do not meet the minimum operational requirements. As shown in Fig. 13, the obtained values are: Q-factor of 2.71 and BER of 3.37 × 10−3.

Fig. 13
figure 13

a BER of DPSK without CFBG. b Q-factor of DPSK without CFBG

Full size image

From the above figure, the number of error bits is large and the received signal is distorted. Therefore, this sub-case is not accepted.

5.3 Summarized results

This section provides summarized results of the proposed models and the previous studies results. Table 2 summarizes the obtained results of our models. One can note that the DPSK with CFBG gives the best results: a maximum Q-factor of 7.22 at a minimum BER of 2.59 × 10−13.

Table 2 Summarized results
Full size table

The improvement in the proposed system performance is evaluated by comparing our model with those of the related studies, Table 3.

Table 3 A Comparison between the proposed model (all cases) with the related work
Full size table

6 Conclusion

In this work, we proposed a model that consists of a 4-stages CFBGs. An efficient DPSK modulation format is applied on the proposed model. Through a comparative study with OQPSK modulation format, the model performance is evaluated. The best performance sub-case is DPSK with CFBG. Its results are: Q-factor of 7.22 and BER of 2.59 × 10−13. The percentages of improvement in performance over the previous studies shown in the Table 3 are 97% over the work in Gill et al. (2019), 100% over the work in Huang et al. (2018), Zhang et al. (2019), and 53% over the work in Sayed et al. 2020b. As a future work, different digital modulation formats [e.g., continuous-phase frequency shift keying (CPFSK), Binary frequency shift keying (BFSK) and Binary phase shift keying (BPSK)] could be studied.