1 Introduction

Optical fiber cables are widely used in telecommunication systems, allowing digital data transmission at longer distances with higher data rates (Kareem et al. 2021). The main transmission challenge in optical fibers is the chromatic dispersion (Mustafa et al. 2022; Zaky et al. 2022). Chromatic dispersion is the spread of the propagated signal in a single mode optical fiber. It occurs due to group velocity delay (GVD) phenomenon, where the signal wavelength depends on the fiber core refractive index (Ibarra-Villalon et al. 2021). In the worst case, chromatic dispersion leads to intersymbol interferences (ISI), which creates undistinguishable signal at the receiving side. Different techniques are developed to alleviate the effects of chromatic dispersion (Khalaf et al. 2022; Aly et al. 2022). One of the most efficient technique is fiber Bragg grating (FBG) (Toba and Mustafa 2019).

FBG is a very small segment of optical fiber. A small amount of the optical signal propagating through FBG is totally reflected at a certain wavelength which is called Bragg wavelength, λB. The other wavelengths are transparent to FBG except some side lobes which distort the output reflected signal (Mustafa et al. 2021a, b). These side lobes can be suppressed using apodization. These side lobes can be suppressed using apodization. There are two types of FBG based on the gratings distribution inside the core. These FBGs can be fabricated by a femtosecond laser line-by-line (LbL) scanning technique (He et al. 2021) and by using a femtosecond laser point-by-point (PbP) technique (Xu et al. 2021). Uniform FBG (UFBG) is a type of FBG with equal distant gratings. The other one is chirped FBG (CFBG), where the gratings are distributed through the core with unequal distant. This CFBG can be fabricated using a high photosensitive benzy dimethy ketal (BDK) doped core fiber that allows to obtain chirped Bragg gratings by means of a single krypton fluoride laser pulse (Min et al. 2018). The working principle of FBG as a chromatic dispersion compensator is reducing the full width at half maximum (FWHM), which leads to minimizing the time delay of the propagated signal (Sayed et al. 2020a, b).

The transmission technique used in the optical fiber communication systems greatly affects the system performance. Maximum Time Division Multiplexing (MTDM) is one of the transmission techniques used in optical fiber communication systems (). It is based on splitting the transmission time into a number of time slots. Each time slot represents one channel of the n-channels of the communication system (Prince et al. 2022).

The aim of this paper is to minimize the chromatic dispersion in a standard single mode fiber (SSMF). This is achieved by a proposed model that consists of a single stage tanh-apodized AUFBG in a post-compensation connection scheme under MTDM transmission. Reducing dispersion for the MTDM/WDM system leads to: (1) increase the system capacity which serving a lot of users, (2) enhance the MTDM/WDM performance, (3) reduce the transmitted power to achieve a suitable BER, which improves the power budget, (4) increase the bit rate, which enables introducing advanced technologies like Internet of Things (IoT), Big data, 5G and 6G of mobile services.

Optisystem 7.0 is used to simulate and evaluate the performance of the proposed model in a 10 Gbps WDM link in terms of Q-factor and BER. We start investigating the most common apodization functions to determine the best function. Then, we examine different AUFBG connection schemes (pre, post and symmetrical schemes). Many comparative studies are conducted to evaluate the system performance and to compare the obtained results with the previously published ones.

The remainder of this paper is organized as follows. Section 2 illustrates the mathematical model. The proposed model is explained in Sect. 3. Section 4 displays and discusses the simulation results. Section 5 is devoted to the main conclusions.

2 Mathematical model

2.1 Uniform and apodized FBG

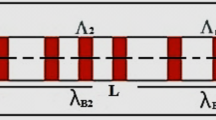
Uniform FBGs are the simplest and most common gratings. The basic structure of such gratings is shown in Fig. 1 (Sayed et al. 2021).

Fig. 1
figure 1

Uniform FBG basic structure (Sayed et al. 2021)

Full size image

The light (corresponding to Bragg wavelength) is partially reflected at each grating period, forming a beam reflected in the opposite direction to the introduced light (Sayed et al. 2021). The reflectance of this FBG is determined by superposition of the reflected waves from each grating in the fiber. Thus, in this condition, the grating period, Ʌ, between each adjacent pair of gratings must be equal to half an optical wavelength divided by effective core effective refractive index. This condition is called the Bragg condition and is be expressed as (Sayed et al. 2020a, b)

$$ \lambda_{{\text{B}}} = 2n_{{{\text{eff}}}} \Lambda $$
(1)

where neff is the core effective refractive index.

The reflectivity of FBG has side lobes, which can be minimized by applying different index profiles, called as apodization profiles. The refractive index modulation of UFBG can be calculated by (Dahir and Yu 2020)

$$ n\left( z \right) = n_{{{\text{eff}}}} + \Delta n_{o} \cdot n_{d} \left( z \right) \cdot A\left( z \right) $$
(2)

where Δn0 is the maximum index variation, nd(z) is the index variation function and A(z) is the apodization function.

In Fig. 2, it can be observed that apodization reduces the reflectivity by a small extent, and minimized side lobes, which is a main advantage (Li et al. 2020).

Fig. 2
figure 2

Power reflection spectrum of UFBG: a without apodization and b with apodization (Li 2020)

Full size image

There are many apodization functions which depend on the grating length, lg. In this work, we focus on the most useful functions as illustrated in Table 1 ().

Table 1 Most common apodization functions (Mustafa et al. 2021a, b)
Full size table

2.2 Dispersion compensation with UFBG

FBGs are suitable candidates for compensating the chromatic dispersion that occurs along the optical fiber link. Dispersion compensation utilizing FBGs is based on the introduction of wavelength-specific time delays through the use of a precisely fabricated FBG (Meena and Meena, 2020). The time delay, τ(λ), for each wavelength along the apodized FBG (AFBG) can be obtained by ()

$$ \tau \left( \lambda \right) = \left( {\lambda_{{\text{B}}} - \lambda } \right)\frac{{2n_{{{\text{eff}}}} }}{\Delta \lambda c} L $$
(3)

where Δλ is the wavelength difference between two ends of the grating. The value of Δλ is depended on the type of the FBG. In case of uniform FBG Δλ is given by (Mustafa et al. 2021a, b)

$$ \Delta \lambda = 2\Lambda \left( {n_{\max } - n_{\min } } \right) $$
(4)

where nmax and nmin are, respectively, the maximum and minimum values of induced refractive index.

The chromatic dispersion parameter of the FBG, Dgrating, can be obtained by (Mustafa et al. 2021a, b)

$$ D_{{{\text{grating}}}} = \frac{{2n_{{{\text{eff}}}} }}{\Delta \lambda c} l_{{\text{g}}} $$
(5)

By combining such FBG with a standard optical circulator, a highly effective dispersion compensation module (DCM) can be realized. This is illustrated in Fig. 3 (Mustafa et al. 2021a, b).

Fig. 3
figure 3

FBG dispersion compensation model (Mustafa et al. 2021a, b)

Full size image

2.3 MTDM transmission technique

MTDM is a technique where several optical signals are combined, transmitted together, and separated again based on different arrival times. Figure 4 displays the MTDM transmission link block diagram (Lohani and Prasad 2015).

Fig. 4
figure 4

MTDM block diagram (Lohani and Prasad 2015)

Full size image

In the MTDM transmitter, the baseband signal pulse streams having a baseband bit rate enters into the multiplexer (MUX). The MTDM multiplexer allows n baseband channels to be multiplexed together. A high bit rate optical time division multiplexed signal ultimately becomes the output of the MTDM multiplexer. It is then fed to the optical fiber to transmit over a considerable distance where the signal gets affected by the fiber dispersion. After traversing a distance, high bit rate multiplexed signal is then fed to the receiver (Mohammed and Rashed 2010).

The first order dispersion is considered the main issue that limits the bit rate in MTDM communication system. In terms of total dispersion parameter, Dt, and though a distance, L, the transmission bit rate, Br, for MTDM/WDM is calculated by (Mustafa et al. 2021a, b)

$$ B_{{\text{r}}} = \frac{0.25}{{D_{t} \cdot \Delta \lambda \cdot L }} $$
(6)

3 The proposed model

Here, we propose a model to achieve the aim of this study which is chromatic dispersion compensation in SSMF. It consists of a single stage apodized uniform FBG under MTDM transmission technique in different connection schemes. Figure 5 displays the block diagram of the proposed model in pre-compensation scheme.

Fig. 5
figure 5

Proposed model block diagram (pre-compensation)

Full size image

From the above figure, the modulated signal is reshaped through the single stage apodized UFBG before it passes through the SSMF. At the receiver side, the optical signal from SSMF is amplified by an optical fiber amplifier. The signal is detected by a photodetector PIN and is converted into an electrical signal. Then, it is filtered by a low pass Bessel filter.

The proposed model is connected in a 10 Gbps WDM link. Through a comparative study, we evaluate the performance of the proposed model in terms of Q-factor and BER. Figure 6 shows the procedure of this comparison.

Fig. 6
figure 6

Comparative study procedure

Full size image

The comparative study includes four cases: without the proposed model, with the proposed model in pre-scheme, with the proposed model in post-scheme and with the proposed model in symmetrical-scheme. Under each scheme, we apply, in one-by-one manner, all the most common apodization functions shown in Table 1. Optisystem 7.0 is used in simulation for the 10 Gbps WDM link. The best configuration is the one having the highest Q-factor and the lowest BER.

3.1 Case one: simulation without the proposed model

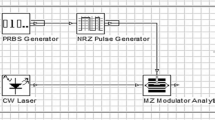
Figure 7 shows the configuration of the WDM link without the proposed model. The optical fiber link consists of three parts: transmitter, optical fiber, and receiver.

Fig. 7
figure 7

Case one: without the proposed model

Full size image

3.1.1 Transmitter

It consists of pseudo random generator which generates a data sequence with a bit rate of 10 Gbps connected to a Non Return to Zero pulse generator (NRZ). It creates a sequence of non-return to zero pulses coded by an input digital signal with a 0.1 ns duration. A continuous wave (CW) laser diode with a transmitted power 0 dBm and a wavelength 1553.6 nm is connected to a Mach–Zehnder modulator (MZM) as an optical signal. On the other hand, MZM is connected to NRZ pulse generator output as an electrical signal. MZM modulates the optical signal from CW according to NRZ pulse generator electrical signal. The modulated optical signal is fed to the optical fiber cable as transmitted signal.

3.1.2 Optical fiber

This part consists of an optical fiber SSMF has 70 km distance with a reference wavelength 1553.6 nm, an attenuation coefficient 0.2 dB/km, and a dispersion coefficient of 17 ps/nm km.

3.1.3 Receiver

It consists of a 30 dB gain Erbium Doped Fiber Amplifier (EDFA) with noise figure of 4 dB. A photodiode detector with responsivity 1 A/W and dark current 30 nA detects the optical signal to the electrical. A low pass Bessel filter with a cutoff frequency of 750 MHz (i.e., the cutoff frequency = 0.75 × Br) is filtered the signal to 3R generator, where the signal is (re-amplified, re-shaped, and retimed) to restore the transmission impairments stemming from fiber chromatic dispersion and other nonlinearities. A BER analyzer is used to display the Q-factor and BER of the received signal. Table 2 summarizes the simulation parameters of this study for the FBG, SSMF and the link. For the proposed configuration to be acceptable, it must meet the minimum operational requirements in terms of Q-factor (> 6) and BER (< 10–9) (Hussein et al. 2019).

Table 2 Comparative study simulation parameters (Dahir and Yu 2020)
Full size table

3.2 Case two: simulation of pre-compensation scheme

The structure of the proposed model in pre-compensation scheme is shown in Fig. 8. The transmitted optical signal is fed to the proposed AUFBG before transmitting into the optical fiber. The AUFBG is connected between the MZM and the SSMF at the transmitter.

Fig. 8
figure 8

Case two: Pre-compensation scheme

Full size image

3.3 Case three: simulation of post-compensation scheme

The basic structure of the post-compensation scheme is shown in Fig. 9. After the received optical signal is amplified by EDFA, the proposed AUFBG is connected between EDFA and PIN photodetector at the receiver.

Fig. 9
figure 9

Case three: Post-compensation scheme

Full size image

3.4 Case four: symmetrical-compensation scheme

The symmetrical compensation scheme structure is shown in Fig. 10. The AUFBG is connected between the MZM and the SSMF at the transmitter and another one is connected between EDFA and PIN photodetector at the receiver.

Fig. 10
figure 10

Case four: Symmetrical compensation scheme

Full size image

4 Results and discussion

Both the evaluation parameters (Q-factor and BER) results are investigated in the four cases. All the obtained results in the cases are displayed and compared to determine the overall best results in all cases.

4.1 Case one: simulation results without the proposed model

Figure 11A, b show the results of Q-factor and BER versus bit period, respectively. For the Q-factor, as the time (bit period) increases, Q-factor also increases until reaching a maximum value of 8.53. After that, as time still increases, the Q-factor decreases sharply. Concerning the BER, as the time (bit period) increases, the BER decreases sharply to its minimum peak at 7.15 × 10–18, after that BER increases with time.

Fig. 11
figure 11

Case one: a Q-factor, and b BER

Full size image

4.2 Case two: Simulation results of pre-compensation scheme

Similar graphs are obtained, like Fig. 11, and Table 3 illustrates the obtained results of all apodization functions. It is noticed the tanh profile achieves the maximum Q-factor of 9.13 and a minimum BER of 3.4 × 10–20.

Table 3 Results of case two: pre-compensation
Full size table

Figure 12 shows (a) the Q-factor and (b) the BER versus time (bit period) for pre-compensation scheme. It is noted that, the Q-factor increases with time for all apodization functions. Different peaks are achieved by different apodization functions ranging from 8.15 for the raised cosine profile to 9.13 for tanh profile. For BER, it is clear that BER decreases with time, for all apodization functions, to a minimum value ranging from 1.8 × 10–16 for the raised cosine profile to 3.4 × 10–20 for the tanh profile. As a result, all functions exceed the minimum operational requirements, and the tanh function gives the maximum Q-factor (9.13) and the minimum BER (3.4 × 10–20).

Fig. 12
figure 12

Pre-compensation scheme a Q-factor and b BER

Full size image

4.3 Case three: results of simulation of post-compensation scheme

In this case, the AUFBG is connected between EDFA and the PIN photodetector at the receiver. The obtained results of the all apodization functions are summarized in Table 4. It is found that, the tanh apodization gives the best results with a Q-factor of 9.2 and a BER of 3.4 × 10–20.

Table 4 Results of case three: post-compensation
Full size table

Figure 13a, b show the obtained Q-factor and BER, respectively, with time (bit period) using the mentioned apodization profiles. Similar to the discussion of Figs. 11 and 12, Fig. 13 displays the obtained Q-factor and BER for all apodization functions. The obtained results in Fig. 13 reveal that the maximum Q-factor ranges from 8.15 for the raised cosine to 9.2 for the tanh profile. Also, the minimum BER obtained ranges from 3.25 × 10–20 for the tanh profile to 1.8 × 10–16 for the raised cosine profile. After that, all functions decrease to its minimum values. Again, the tanh apodization profile achieves the highest Q-factor (9.2) and the minimum BER (3.25 × 10–20).

Fig. 13
figure 13

Post-compensation scheme a Q-factor and b BER

Full size image

4.4 Case four: simulation results of symmetrical-compensation scheme

An AUFBG is connected between the MZM and the SSMF at the transmitter and another one between EDFA and PIN photodetector at the receiver. Table 5 illustrates the obtained results of this case for all apodization functions. Again, the tanh profile shows the maximum Q-factor (8.8) and the minimum BER (8.22 × 10–19).

Table 5 Results of symmetrical compensation scheme
Full size table

Figure 14 displays the obtained results of Q-factor and BER, respectively, for all apodization functions. The same conclusions, like previously discussed results, are obtained in this case also. The tanh profile achieves the best Q-factor and BER with values 8.8 and 8.22 × 10–19, respectively.

Fig. 14
figure 14

Symmetrical scheme a Q-factor and b BER

Full size image

4.5 Summary of Q-factor and BER for all cases

4.5.1 Q-factor

Table 6 summarizes the obtained Q-factor for all previous cases. A comparison is also shown in Fig. 15. It is noticed tanh profile in case three (post-compensation scheme) achieves the best Q-factor (9.2).

Table 6 Summary of Q-factor results
Full size table
Fig. 15
figure 15

Comparison of Q-factor for all cases

Full size image

4.5.2 BER

Table 7 summarizes the obtained values of BER for all cases. A comparison also is shown in Fig. 16. Clearly, the tanh profile in case three (post-compensation scheme) achieves the minimum BER (3.25 × 10–20).

Table 7 Summary of BER results
Full size table
Fig. 16
figure 16

Comparison of BER for all cases

Full size image

4.5.3 Comparison with related work

Now, we compare the best results obtained in our proposed model (case three: post-compensation scheme) with the previously published results, see Table 8.

Table 8 Comparison between the presents results and previous work
Full size table

Sayed et al. (2020a, b), the Hamming function was used to enhance the performance at a bit rate of 10 Gbps. The obtained values of Q-factor and BER were, respectively, 8.27 and 6.46 × 10–17. Also, in Sayed et al. (2021), Cauchy profile achieved 6.135 for the Q-factor and 4.24 × 10–10 for the BER at 10 Gbps bit rate. Finally, in Hussein (2019), the tanh perform achieved a Q-factor of 7.106 and and a BER of 5.47 × 10–13 at the same at bit rate (10 Gbps). Comparing with these results, our proposed system enhanced the system performance by 68–99%, assuring its superiority.

5 Conclusion

We proposed a model that consists of a single stage apodized UFBG in three connection schemes under MTDM transmission technique. Through a comparative study with different apodization functions and connection schemes, the model performance is evaluated, in terms of Q-factor and BER. The tanh apodization function achieves the best results in all connection schemes. The best results are obtained in the pre-compensation scheme, achieving a maximum Q-factor of 9.2 and a minimum BER of 3.25 × 10–20. The proposed model realizes an improvement over the related work at least by ~ 68%.