1 Introduction

The propagated signal through an optical fiber suffers many propagation problems; attenuation and dispersion. Attenuation is the reduction of propagated signal power with distance (Mustafa 2021). The attenuation problem has been solved by the development of optical fiber amplifiers, such as erbium doped fiber amplifier (EDFA). The chromatic dispersion is considered as the main obstacle to enhance the performance of the optical fiber communication system (Ibarra-Villalon 2021). Chromatic dispersion is the pulse broadening due to the dependency of core refractive index on the propagated signal wavelength (Meena 2020). This makes different wavelengths propagate with different velocities, which leads to group velocity delay (GVD). These pulses overlap together and cause in the worst case intersymbol interference (ISI) at the receiver side. Also, dispersion decreases transmission bit rate and the overall system performance (Dahir 2020). To solve this, researches developed many dispersion compensation (DC) techniques; FBG is one of the most efficient one of them (Smith 1997).

There are two types of FBG according to the spatial gratings distribution. These are uniform FGB and chirped FBG (CFBG) (Dar 2017). In uniform FGB, the gratings are equal distant while in CFBG they are unequal distant. The gratings refractive index depends on the propagated signal wavelength in the case of uniform FBG (Toba 2019). A small amount of the optical signal propagating through FBG is totally reflected at a certain wavelength which is called Bragg wavelength, λB (Sayed 2020). The other wavelengths are transparent to FBG except some sidelobes which distort the output reflected signal. These sidelobes can be suppressed using apodization. The key operation principle of FBG in compensation mode is minimizing the full width at half maximum (FWHM). To do that, one can use a chain of n-stages cascaded FBG (Hussein 2019). This number is selected to provide the required FWHM at an acceptable power reflectivity.

There are many other factors that affect the signal propagation through the optical fiber communication systems. Such as, transmission techniques, modulation and multiplexing schemes (Khalaf 2021).

In this work, we use MTDM with FBG to enhance the overall system performance. The aim of this work is to enhance the overall optical fiber communication system performance by enhancing the chromatic dispersion compensation in SSMF. MTDM is designed to accomplish the high-capacity and high-speed transmission. Being able to adopt nonlinear soliton transmission and other useful technologies, MTDM can eliminate the effect of chromatic dispersion in the high-speed transmission. At the same time, MTDM is able to eliminate the rate effect of electronic devices to accomplish the high-speed transmission on a single wavelength. As an effectively optical multiplexing way, MTDM can make full use of spectral resources and greatly improves the utilization of spectral bandwidth. Unlike WDM, MTDM is free of the limitations resulted from the nonlinear effect of fibers, thus effectively utilizing optical wavelength and operating in various network of different distances and capacities. Though still immature, MTDM is a more long-term technology than WDM.

We propose a compensation model consisting of four identical stages cascaded apodized linear CFBG in the post-compensation connection scheme. It is based on the MTDM transmission technique. The model is simulated by using Optisystem 7, and is evaluated through a comparative study in terms of Q-factor and BER. In this study, the most common apodization functions and connection schemes (i.e., pre, post and symmetrical schemes) are investigated. The simulated system is connected in a 10 Gbps WDM link under a set of practical operational parameters. Using this proposal, the simulation is performed through Optisystem ver. 7.

The rest of this paper is organized as follows. The basic model and analysis are illustrated in Sect. 2. Section 3 explains the proposed model. The simulation results are displayed and discussed in Sect. 4. Section 5 is devoted to the main conclusions.

2 Basic model and analysis

2.1 Principles of FBG

The key idea of FBG is based on Fresnel reflection principle, where a propagated optical signal through a medium with different refractive indices can be reflected or refracted at the interface (Aly 2021). Uniform FGB is the basic type of FBG, where the gratings are equidistant along the core axis.

The relation between the Bragg wavelength, \({\lambda }_{\text{B}}\), and the grating periodicity, \({\Lambda}\), is given by (Sharma 2018)

$${\lambda}_{\text{B}}=2{\text{n}}_{\text{e}\text{f}\text{f}}{\Lambda}$$
(1)

where neff is the core effective refractive index.

In uniform FBG, the refractive index modulation through the core axis is given by (Sharma 2018)

$$\text{n}\left(\text{z}\right)={\text{n}}_{\text{e}\text{f}\text{f}}+{\Delta }{n}_{o}.{n}_{d}\left(z\right)$$
(2)

where Δn0 is the maximum index variation and nd(z) is the index variation function.

The index modulation depth variation has a great impact on sidelobes peaks. The reflected spectrum of FBG with a uniform modulation has a significant undesirable sidelobes. To solve this issue, apodized index modulation is used (Mustafa 2021).

2.1.1 Chirped FBG and apodization

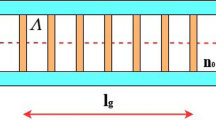
Chirped FBG is an FBG with unequal gratings period, where it varies along the core axis z. Therefore, the refractive index modulation varies along the grating length and the chirp pattern is defined by l(z). Figure 1 illustrates CFBG structure (Sonne 2021).

Fig. 1
figure 1

CFBG structure

Full size image

From Fig. 1, one can notice that each grating reflects a different Bragg wavelength or it works as a filter bank.

In CFBG, the Bragg wavelength varies along the propagation axis (i.e., λB(z)) according to (El-Gammal 2015)

$${\lambda }_{B}\left(z\right)=2n\left(z\right){\Lambda}\left(z\right)$$
(3)

where Ʌ(z) is the grating period along the propagation axis.

The modulated refractive index n(z) is given by (El-Gammal 2015)

$$n\left(z\right)= {n}_{eff}+\varDelta nd\left(z\right)\text{cos}\left(\frac{2\pi z}{{\Lambda}_{0}}\left(1+xz\right)\right)$$
(4)

where d(z) is the selected apodization function, Ʌ0 is the first grating period, and x is the chirp parameter.

  • As the case of uniform FBG, sidelobes cause a great problem in CFBG. Therefore, apodized CFBG is used to suppress these sidelobes.

(Ghosh 2018).

In the apodized CFBG, the refractive index modulation is reshaped (i.e., apodized). There are many apodization functions, d(z), with different characteristics. Here, we study the most common apodization functions, see Table 1.

Table 1 The most common apodization functions (Mustafa 2021)
Full size table

where \(0\ll z\ll {l}_{g}\).

Figure 2 illustrates the used apodization functions at different grating lengths.

Fig. 2
figure 2

Apodization functions

Full size image

Using apodized CFBG as a chromatic dispersion compensator relies on introducing a time delay that is a function of wavelength. The CFBG chromatic dispersion coefficient is given by (Sharshar 2013)

$${D}_{grating}=\frac{{2n}_{eff}}{\varDelta {\lambda} \text{v}}{l}_{g}$$
(5)

where v is the speed of light, and Δλ is the wavelengths difference between the grating two ends calculated by (Sharshar 2013)

$$\varDelta \lambda =2{n}_{eff} \left({\Lambda}_{long}- {\Lambda}_{short}\right)$$
(6)

2.1.2 Cascaded CFBG

Figure 3 illustrates the basic idea of the cascaded FBGs. It is based on a successive reduction of FWHM through its stages (Abd-Alla 2010).

Fig. 3
figure 3

Cascaded CFBGs

Full size image

In operation, the input of the first CFBG stage is the output from the optical transmitter. Then, the reflected part of the first stage is lunched into the input port of the second CFBG stage. This process proceeds to the last stage (Abd-Alla 2010). The output of the 4-stages cascaded CFBG is the reflected signal of the fourth one. A standard optical circulator is used with each CFBG stage. To compensate the chromatic dispersion, a four cascaded CFBG is used where this number achieves the optimal values of FWHM and reflectivity.

2.2 MTDM transmission technique

The objective of WDM technology is achieving a high transmission bit rate. The maximum bit rates are determined by numerous factors, including the signal modulation rate, the transmission bandwidth, and the response time of the optoelectronic devices. Therefore, the total pulse broadening, Δτ, due to the first order dispersion that limits the bit rates in MTDM-based communication system can be expressed as (Khalaf 2021)

$$\varDelta {\tau }={\text{D}}_{\text{t}}.\varDelta {\lambda }.\text{L}$$
(7)

where ∆λ is the FWHM, L is the transmission distance, and Dt is the total chromatic dispersion parameter.

The MTDM transmission bit rate for a WDM link is given by (Khalaf 2021)

$${\text{B}}_{\text{r}}= \frac{0.25}{\varDelta {\tau } }$$
(8)

3 Proposed model

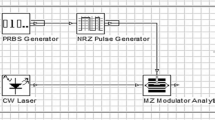
The proposed model aims to enhance the overall optical fiber communication system performance by compensating the chromatic dispersion in SSMF. We propose a compensation model that includes identical four stages cascaded linear apodized CFBG in post-compensation connection scheme, see Fig. 4. It is based on the MTDM transmission technique.

Fig. 4
figure 4

Proposed model block diagram

Full size image

The reflected signal of the last stage which is the final output of the cascaded CFBG detected by the PIN photodiode. The output of photodiode is an electrical signal which passes through a low pass Bessel filter to recover the required signal. Optisystem 7.0 is used in simulation for the 10 Gbps WDM link. Through a comparative study, the proposed model performance is evaluated in terms of two metrics (Q-factor and BER). Figure 5 shows the study procedure.

Fig. 5
figure 5

Comparative study procedure

Full size image

The comparative study includes three cases based on the used connection scheme (i.e. pre, post or symmetrical compensation). Under each connection scheme, we apply, in one-by-one manner, all the most common apodization functions shown in Table 1.

4 Results and discussion

This study focuses on enhancing the optical communication system performance using MTDM transmission technique and four identical stages cascaded apodized linear CFBGs. Each case has six sub-cases based on the used apodization function. Table 2 displays the simulation parameters. These parameters are the normal and most used parameters in the optical fiber communication field.

Table 2 Simulation parameters of the comparative study (Hussein 2019)
Full size table

4.1 Case one: pre-compensation model

Figure 6 illustrates the structure of the proposed model in pre-compensation scheme.

Fig. 6
figure 6

Case one: Pre-compensation scheme

Full size image

It is found that, in Gaussian and tanh cases, the signal is totally lost (i.e. Q-factor of 0 and BER of 1). Table 3 illustrates the other sub-cases results.

Table 3 Case one results
Full size table

The raised cosine apodization gives the best results: Q-factor = 7.66 and BER = 8.99 × 10− 15. Figure 7 shows the Q-factor and BER of the raised cosine apodization.

Fig. 7
figure 7

(a) Q-factor of the raised cosine apodization (b) BER of the raised cosine apodization

Full size image

4.2 Case two: post-compensation model

The basic structure of the post-compensation scheme of case two is shown in Fig. 8.

Fig. 8
figure 8

Case two: Post-compensation scheme

Full size image

The signal is totally lost in Gaussian sub-case. The results of the other apodization functions are summarized in Table 4.

Fig. 9
figure 9

(a) Q-factor of the raised sine apodization (b) BER of the raised sine apodization

Full size image
Table 4 Case two results
Full size table

4.3 Case three: symmetrical-compensation model

The symmetrical compensation scheme structure is shown in Fig. 10.

Fig. 10
figure 10

Case three: Symmetrical compensation

Full size image

Again, in Gaussian and tanh cases the signal is totally lost. Table 5 illustrates the results of case three for the remaining apodization functions.

Table 5 Case three results
Full size table

The raised sine apodization gives the best results: Q-factor = 7.49 and BER = 3.5 × 10− 14. Figure 11 shows the Q-factor and BER of the raised sine apodization.

Fig. 11
figure 11

(a) Q-factor of the raised sine apodization. (b) BER of the raised sine apodization

Full size image

4.4 Comparison with related (published) work

In this section, we compare our proposed model results with related works, see Table 6.

Table 6 Summarized results of the proposed model and previous work
Full size table

One can note the superiority of our results as compared with the previous published works.

5 Conclusion

We proposed a model that consists of a 4-identical stages of cascaded apodized linear CFBGs in three connection schemes. MTDM transmission technique is applied on the proposed model. Through a comparative study with different apodization functions and connection schemes the model performance is evaluated, in terms of two metrics (i.e., Q-factor and BER). The proposed model achieves the highest results in the pre-compensation scheme: Q-factor = 7.664 and BER = 8.99 × 10− 15, using the raised cosine apodization function. Using the raised sine apodization in the post-compensation connection realizes the best performance: Q-factor = 8.58 and BER = 4.77 × 10− 18. In the symmetrical-compensation scheme and using the raised sine apodization, the proposed model attains the highest results: Q-factor = 7.49 and BER = 3.53 × 10− 14. The proposed model achieves at least 93% improvement over the related studies.