1 Introduction

Soliton theory is one of the most studied areas in applied sciences, in particular, nonlinear dynamical media. In this sense, Divo-Matos et. al. have firstly investigated the new model for gas adsorption isotherm at high pressures (Divo-Matos et al. 2021). This observation comes from the hydrogen which has been considered as an ideal energy source in the future. They have observed the new isotherm model for supercritical gas adsorption by using the Redlich-Kwong’s equation of state at high pressures. Another a new model to estimate permeability has been formed to explain the carbonate and shale samples (Liu et al. 2020). They have calculated the curvatures from the mercury saturation data by using the Fermic-Dirac function. Gunasekeran and his team introduced the digital health during COVID-19 (Gunasekeran et al. 2021). As it is well known by almost everybody, COVID-19 has affected many peoples from all over the world. In these works, they presented the mathematical perspective to the Covid-19 disease by giving deeper properties such as dynamical structures (Gao et al. 2020), modeling the dynamics of novel coronavirus (2019-nCov) (Khan and Atangana 2020), stochastic COVID-19 Lvy jump model with isolation strategy (Danane et al. 2021), unreported cases of 2019-nCOV epidemic outbreaks (Gao et al. 2020), threshold condition and non pharmaceutical interventions control strategies (Zamir et al. 2021), the spread of COVID-19 with new fractal-fractional operators (Atangana 2020), the total digitalization in education during the Covid pandemi (Yuce 2022). Moreover, many real world problems have been also studied by using mathematical methods and tools such as sine-Gordon expansion method (Eskitascioglu et al. 2019), tanh and extended tanh methods (Bibi and Mohyud-Din 2014; Zayed and Tala-Tebue 2018; Fan 2000). Some important properties of reduced higher-order and perturbed nonlinear Schrödinger equation (Kudryashov 2021, 2020) and so on were presented (Wazwaz 2018; Kaplan et al. 2017; Cattani 2018; Zhang et al. 2015; Bridges and Ratliff 2017a, b). Therefore, such nonlinear evaluation equations (NLEs) have always been one of the most inspiring tools for researchers to study real phenomena and models arising in mathematics, physics, engineering and various fields of science (Chen and Ren 2022; Nabti and Ghanbari 2021; Wang et al. 2020; Ghanbari and Kumar 2021; Hu et al. 2022; Akbulut and Kaplan 2018; Durur and Yokus 2021; Sulaiman et al. 2021; Gao et al. 2020; Ghanbari and Djilali 2020; Rajesh Kanna et al. 2020; Ghanbari 2020; Kaplan and Akbulut 2021; Ghanbari and Atangana 2020; McCue et al. 2021; Djilali and Ghanbari 2021; Gao et al. 2020; Ghanbari 2020a, b; Srivastava et al. 2019; Erturk and Kumar 2020; Ghanbari 2021; Saouli 2020; Ghanbari 2021; Munusamy et al. 2020; Ghanbari et al. 2020; Kaplan 2017; Ghanbari et al. 2019; Kudryashov 2020; Djilali and Ghanbari 2021), (Ali Akbar et al. 2021; Eslami et al. 2021; Rezazadeh et al. 2019; Akinyemi et al. 2021; Hosseini et al. 2020; Nisar et al. 2022; Pinar et al. 2020; Khodadad et al. 2021; Ozkan et al. 2021; Halidou et al. 2022; Can et al. 2020).

The remaining parts of research manuscript are organized as follows. In Sect. 2, overview of the conformable derivative and its general properties are presented. Section 3 provides the general properties of the projected scheme, namely, generalized exponential rational function method GERFM. Main results showing that the system can exhibit some interesting properties of the governing models such as Zakharov–Kuznetsov–Benjamin–Bona–Mahony (ZKBBM) equation and complex Kundu–Eckhaus equation with conformable derivative are given in Sect. 4. The meaning of the parameters of the new findings is given there in terms of different simulations. We discuss and conclude our results in the last section of the paper.

Firstly, ZKBMM equation (lzaidy 2013; Khodadad et al. 2017; Aksoy et al. 2016) given as

$$\begin{aligned} u_t\left( x,t\right) + u_{xx}\left( x,t\right) -2au\left( x,t\right) u_x\left( x,t\right) -bu_{txx}\left( x,t\right) =0, \end{aligned}$$
(1)

where a, b are real-valued constants is studied.

Secondly, nonlinear complex Kundu–Eckhaus equation defined by Khater et al. (2018), Khodadad et al. (2017), Mirzazadeh et al. (2018):

$$\begin{aligned}&i q_t\left( x,t\right) + q_{xx}\left( x,t\right) -2\rho |q|^2\left( x,t\right) q\left( x,t\right) +\delta ^2|q|^4\left( x,t\right) q\left( x,t\right) \nonumber \\&\quad +2i\delta \left( |q\left( x,t\right) |^2\right) _xq\left( x,t\right) =0, \end{aligned}$$
(2)

where \(\rho , \delta\) are real-valued constants is investigated by using projected method to extract some important properties.

2 Overview of the conformable derivative

Recently, an operator called conformable was formulated by Khalil in Khalil et al. (2014). The conformable calculus satisfies all the properties of the standard calculus. This operator may be considered to be a natural extension of the classical properties (Usta 2018; Abdeljawad 2015; Benkhettou et al. 2016; Ünal and Gökdogan 2017).

Definition 2.1

Let \(f:[0,\infty )\rightarrow {\mathbb {R}}\), the conformable derivative of a function f(t) of order \(\alpha\), is defined as (Khalil et al. 2014)

$$\begin{aligned} D_t^{\alpha }f(t)=\lim \limits _{\epsilon \rightarrow 0}\frac{f(t+\epsilon t^{1-\alpha })-f(t)}{\epsilon } ,\quad \alpha \in (0,1],\quad t>0. \end{aligned}$$
(3)

This new definition satisfies the properties in the following theorem:

Theorem 1

(Khalil et al. 2014) Let \(\alpha \in (0,1]\), f, g be \(\alpha\)-differentiable at a point t, then

  • \(D_t^{\alpha }(af+bg)=a D_t^{\alpha }(f)+b D_t^{\alpha }(g)\), for \(a,b \in {\mathbb {R}}\).

  • \(D_t^{\alpha }(t^\mu )=\mu t^{\mu -\alpha }\), for \(\mu \in {\mathbb {R}}\).

  • \(D_t^{\alpha }(fg)=fD_t^{\alpha }(g)+gD_t^{\alpha }(f)\).

  • \(D_t^{\alpha }(\frac{g}{g})=\frac{gD_t^{\alpha }(f)-fD_t^{\alpha }(g)}{g^2}\).

If, in addition, f is differentiable, then \(D_t^{\alpha }(f)(t)=t^{1-\alpha } \frac{df}{dt}\). (Abdeljawad 2015) established the chain rule for conformable derivatives as following theorem:

Theorem 2

Let \(f:(0,1]\rightarrow {\mathbb {R}}\), be a function such that f is differentiable and also \(\alpha\)-conformable differentiable. Let g be a differentiable function defined in the range of f. Then

$$\begin{aligned} D_t^{\alpha }(fog)(t) = t^{1-\alpha } g'(t)f' (g(t)), \end{aligned}$$

where prime denotes the classical derivatives with respect to t.

3 Overview of the generalized exponential rational function method

In this section, we state the main steps of GERFM as follows (Biazar and Ghanbari 2012; Ghanbari and Kuo 2021; Kumar et al. 2021; Ghanbari and Akgül 2020; Ismael et al. 2020; Ghanbari et al. 2020)

  1. 1.

    Let us take into account the following nonlinear partial differential equation

    $$\begin{aligned} {\mathscr {L}}(\Upsilon ,\Upsilon _x,\Upsilon _{t},\Upsilon _{xx},\cdots )=0. \end{aligned}$$
    (4)

    Via the transformations \(\Upsilon ={\Upsilon }(\xi )\) and \(\xi =\sigma x-\varphi t\), in nonlinear partial differential equation (4), we attain

    $$\begin{aligned} \mathscr {L}({\Upsilon },{\Upsilon }',{\Upsilon }'',\cdots )=0, \end{aligned}$$
    (5)

    which is indeed an ordinary differential equation; where the values of \(\sigma\) and \(\varphi\) will be found later.

  2. 2.

    Consider equation (5) has the solution of the form

    $$\begin{aligned} {\Upsilon }(\xi )=A_0+\sum _{k=1}^{M}A_k \Psi (\xi ) ^{k}+ \sum _{k=1}^{M}B_k \Psi (\xi ) ^{-k}, \end{aligned}$$
    (6)

    where

    $$\begin{aligned} \Psi (\xi )=\frac{r _1 e^{s_1 \xi }+r _2 e^{s_2 \xi }}{r _3 e^{s_3 \xi }+r _4 e^{s_4 \xi }}. \end{aligned}$$
    (7)

    The values of constants \(r _i, s_i(1 \le i \le 4)\), \(A_0, A_k\) and \(B_k (1 \le k \le M)\) are determined, in such a way that solution (6) always persuade equation (5). By considering the homogenous balance principle the value of M is determined.

  3. 3.

    Putting equation (6) into Eq. (5) we give the following algebraic equation \(\Xi (\Lambda _1, \Lambda _2, \Lambda _3, \Lambda _4)=0\), in terms of \(\Lambda _i=e^{s_i \xi }\) for \(i=1,\ldots , 4\). After setting each of the coefficients of variables in \(\Xi\) to zero, a system of nonlinear equations in terms of these parameters is constructed.

  4. 4.

    By solving the above system of equations using any symbolic computation software, the values of \(r _i, s_i(1 \le i \le 4)\), \(A_0, A_k\), and \(B_k(1 \le k \le M)\) are determined, replacing these values in Eq. (6) provides us the soliton solutions of Equation (4).

4 Main results

In this section, we apply GERFM into the governing models to find some important properties.

4.1 The ZKBMM equation with conformable derivative

In this subsection, we investigate exact wave solutions in studying the conformable version of the ZKBMM Eq. (1), giving by

$$\begin{aligned} {\mathscr {D}}_t^\alpha u\left( x,t\right) +{\mathscr {D}}_x^{2\alpha } u\left( x,t\right) -2au{\mathscr {D}}_x^\alpha u\left( x,t\right) -b{\mathscr {D}}_{txx}^{3\alpha } u\left( x,t\right) =0. \end{aligned}$$
(8)

By considering the wave transformation

$$\begin{aligned} u\left( x,t\right) ={\mathscr {U}}(\xi ),\quad \xi =\left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha }, \end{aligned}$$
(9)

where c, k are non zero constants. Utilizing the wave transformation (33), we get

$$\begin{aligned} \left( k-c\right) {\mathscr {U}}' -2ak{\mathscr {U}}{\mathscr {U}}'+bck^2 {\mathscr {U}}'''=0. \end{aligned}$$
(10)

When we integrate once and setting the integration constant to zero in (10), we obtain

$$\begin{aligned} \left( k-c\right) {\mathscr {U}} -ak{\mathscr {U}}^2+bck^2 {\mathscr {U}}''=0. \end{aligned}$$
(11)

Applying the balance principle on the terms \({\mathscr {U}}^2\) and \({\mathscr {U}}''\) in Eq. (11), we have \(2M=M+2\). Consequently, we find \(M=2\). Using Eq. (7) together with \(M=2\), we have

$$\begin{aligned} {{\mathscr {U}}}(\xi )=A_0+ A_1 \Psi (\xi ) +A_2 \Psi ^2(\xi ) + \frac{B_1 }{\Psi (\xi )}+ \frac{B_2 }{\Psi ^2(\xi )}. \end{aligned}$$
(12)

The following results are provided by processing the general steps required in the method.

Set 1:

One obtains \(r=[2,0, 1, 1]\) and \(s=[-1,0,1,-1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{\cosh \left( \xi \right) -\sinh \left( \xi \right) }{\cosh \left( \xi \right) }} . \end{aligned}$$
(13)

Case 1.1: We also obtain

$$\begin{aligned} c={\frac{k}{4\,b{k}^{2}+1}},k=k,A_{{0}}=\,{\frac{4b{k}^{2} }{4\,ab{k}^{2}+a}},A_{{1}}=-\,{\frac{12b{k}^{2}}{4\,ab{k}^{2}+a}},A_{ {2}}=\,{\frac{6b{k}^{2}}{4\,ab{k}^{2}+a}},B_{{1}}=0,B_{{2}}=0 .\end{aligned}$$

Putting values in Equations (12) and (13), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) ={\frac{2 \left( 2\, \cosh ^{2} \left( \xi \right) -3 \right) b{k}^{2}}{a \left( 4\,b{k}^{2}+1 \right) \cosh ^{2} \left( \xi \right) }} . \end{aligned}$$

Consequently, we get the solution of Equation (8) as

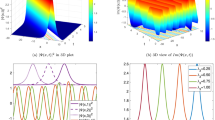
$$\begin{aligned} u_{1} \left( x,t \right) = {\frac{2 \left( 2\, \cosh ^{2} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) -3 \right) b{k}^{2}}{a \left( 4\,b{k}^{2}+1 \right) \cosh ^{2} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) }}. \end{aligned}$$
(14)

Figure 1 shows the dynamic properties of \(u_{1} \left( x,t \right)\) for \(a = 0.5, b = 0.1, k = 0.3\), and for two different values of \(\alpha\)’s.

Fig. 1
figure 1

Dynamic behaviours modulus of solution \(u_{1} \left( x,t \right)\) for \(a = 0.5, b = 0.1, k = 0.3\)

Full size image

Case 1.2: We also obtain

$$\begin{aligned} c=-{\frac{k}{4\,b{k}^{2}-1}},k=k,A_{{0}}=0,A_{{1}}=\,{ \frac{12b{k}^{2}}{4\,ab{k}^{2}-a}},A_{{2}}=-\,{\frac{6b{k}^{2}}{4\,ab{ k}^{2}-a}},B_{{1}}=0,B_{{2}}=0 . \end{aligned}$$

Putting values in Equations (12) and (13), yields the following solution

$$\begin{aligned} {{\mathscr {U}}} \left( \xi \right) ={\frac{6b{k}^{2}}{a \left( 4\,b{k}^{2}-1 \right) \cosh ^{2} \left( \xi \right) }} . \end{aligned}$$

Consequently, we get the solution of Equation (8) as

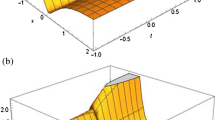
$$\begin{aligned} u_{2} \left( x,t \right) ={\frac{6b{k}^{2}}{a \left( 4\,b{k}^{2}-1 \right) \cosh ^{2} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) }}. \end{aligned}$$
(15)

Figure 2 shows the dynamic properties of \(u_{2} \left( x,t \right)\) for \(a =1.6, b = 0.5, k = 0.5\), and for two different values of \(\alpha\)’s.

Fig. 2
figure 2

Dynamic behaviours modulus of solution \(u_{2} \left( x,t \right)\) for \(a = 1.6, b = 0.5, k = 0.5\)

Full size image

Set 2:

One obtains \(r=[1-i,-1-i, -1, 1]\) and \(s=[i,-i,i,-i]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{\cosh \left( \xi \right) -\sinh \left( \xi \right) }{\cosh \left( \xi \right) }} . \end{aligned}$$
(16)

Case 2.1: We also obtain

$$\begin{aligned} c={\frac{k}{4\,b{k}^{2}+1}},k=k,A_{{0}}=\,{\frac{12b{k}^{2} }{4\,ab{k}^{2}+a}},A_{{1}}=0,A_{{2}}=0,B_{{1}}=\,{\frac{24b{k}^{2}}{4 \,ab{k}^{2}+a}},B_{{2}}=\,{\frac{24b{k}^{2}}{4\,ab{k}^{2}+a}} .\end{aligned}$$

Putting values in Equations (12) and (16), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) =-\,{\frac{12b{k}^{2}}{a \left( 4\,b{k}^{2}+1 \right) \left( 2\,\cos \left( \xi \right) \sin \left( \xi \right) -1 \right) }} .\end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{3} \left( x,t \right) = -\,{\frac{12b{k}^{2}}{a \left( 4\,b{k}^{2}+1 \right) \left( 2\,\cos \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) \sin \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) -1 \right) }}. \end{aligned}$$
(17)

Figure 3 shows the dynamic properties of \(u_{3} \left( x,t \right)\) for \(a = 0.3, b = 0.15, k = 0.7\), and for two different values of \(\alpha\)’s.

Fig. 3
figure 3

Dynamic behaviours modulus of solution \(u_{3} \left( x,t \right)\) for \(a = 0.3, b = 0.15, k = 0.7\)

Full size image

Case 2.2: We also obtain

$$\begin{aligned}&c=-{\frac{k}{4\,b{k}^{2}-1}},k=k,A_{{0}}=-\,{\frac{8b{k}^{2 }}{4\,ab{k}^{2}-a}},A_{{1}}=0,A_{{2}}=0,B_{{1}}=-\,{\frac{24b{k}^{2} }{4\,ab{k}^{2}-a}},\\&\quad B_{{2}}=-\,{\frac{24b{k}^{2}}{4\,ab{k}^{2}-a}} . \end{aligned}$$

Putting values in Equations (12) and (16), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) ={\frac{8b{k}^{2} \left( \cos \left( \xi \right) \sin \left( \xi \right) +1 \right) }{a \left( 4\,b{k}^{2}-1 \right) \left( 2\,\cos \left( \xi \right) \sin \left( \xi \right) -1 \right) }} . \end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{4} \left( x,t \right) ={\frac{8b{k}^{2} \left( \cos \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) \sin \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) +1 \right) }{a \left( 4\,b{k}^{2}-1 \right) \left( 2\,\cos \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) \sin \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) -1 \right) }}. \end{aligned}$$
(18)

Figure 4 shows the dynamic properties of \(u_{4} \left( x,t \right)\) for \(a = 0.15, b = 0.35, k = 0.5\), and for two different values of \(\alpha\)’s.

Fig. 4
figure 4

Dynamic behaviours modulus of solution \(u_{4} \left( x,t \right)\) for \(a = 0.15, b = 0.35, k = 0.5\)

Full size image

Set 3:

One obtains \(r=[2,0, 1,-1]\) and \(s=[1,0,1,-1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{\cosh \left( \xi \right) -\sinh \left( \xi \right) }{\cosh \left( \xi \right) }} . \end{aligned}$$
(19)

Case 3.1: We also obtain

$$\begin{aligned} c={\frac{k}{4\,b{k}^{2}+1}},k=k,A_{{0}}=\,{\frac{4b{k}^{2} }{4\,ab{k}^{2}+a}},A_{{1}}=-\,{\frac{12b{k}^{2}}{4\,ab{k}^{2}+a}},A_{ {2}}=\,{\frac{6b{k}^{2}}{4\,ab{k}^{2}+a}},B_{{1}}=0,B_{{2}}=0 . \end{aligned}$$

Putting values in Equations (12) and (19), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) ={\frac{2 \left( 2\, \cosh ^{2}\left( \xi \right) +1 \right) b{k}^{2}}{a \left( 4\,b{k}^{2}+1 \right) \sinh ^{2} \left( \xi \right) }} . \end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{5} \left( x,t \right) ={\frac{2 \left( 2\, \cosh ^{2}\left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) +1 \right) b{k}^{2}}{a \left( 4\,b{k}^{2}+1 \right) \sinh ^{2} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) }}. \end{aligned}$$
(20)

Case 3.2: We also obtain

$$\begin{aligned} c=-{\frac{k}{4\,b{k}^{2}-1}},k=k,A_{{0}}=0,A_{{1}}=\,{ \frac{12b{k}^{2}}{4\,ab{k}^{2}-a}},A_{{2}}=-\,{\frac{6b{k}^{2}}{4\,ab{ k}^{2}-a}},B_{{1}}=0,B_{{2}}=0 . \end{aligned}$$

Putting values in Equations (12) and (19), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) =-{\frac{6b{k}^{2}}{a \left( 4\,b{k}^{2}-1 \right) \left( \sinh \left( \xi \right) \right) ^{2}}} . \end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{6} \left( x,t \right) =-{\frac{6b{k}^{2}}{a \left( 4\,b{k}^{2}-1 \right) \left( \sinh \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) \right) ^{2}}}. \end{aligned}$$
(21)

Figure 5 shows the dynamic properties of \(u_{6} \left( x,t \right)\) for \(a = 0.8, b = 0.9, k = 0.9\), and for two different values of \(\alpha\)’s.

Fig. 5
figure 5

Dynamic behaviours modulus of solution \(u_{6} \left( x,t \right)\) for \(a = 0.15, b = 0.35, k = 0.5\)

Full size image

Set 4:

One obtains \(r=[-1,0, 1,1]\) and \(s=[0,0,1,0]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) =- \left( 1+{\mathrm{e}^{\xi }} \right) ^{-1} . \end{aligned}$$
(22)

We also obtain

$$\begin{aligned} c={\frac{k}{b{k}^{2}+1}},k=k,A_{{0}}={\frac{b{k}^{2}}{a \left( b{k}^{2}+1 \right) }},A_{{1}}=\,{\frac{6b{k}^{2}}{a \left( b{ k}^{2}+1 \right) }},A_{{2}}=\,{\frac{6b{k}^{2}}{a \left( b{k}^{2}+1 \right) }},B_{{1}}=0,B_{{2}}=0 . \end{aligned}$$

Putting values in Equations (12) and (22), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) =-{\frac{b{k}^{2} \left( -{\mathrm{e}^{2\,\xi }}+4\, {\mathrm{e}^{\xi }}-1 \right) }{a \left( b{k}^{2}+1 \right) \left( 1+{ \mathrm{e}^{\xi }} \right) ^{2}}} . \end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{7} \left( x,t \right) =-{\frac{b{k}^{2} \left( -{\mathrm{e}^{\,\left( \frac{2k}{\alpha }\right) x^\alpha -\left( \frac{2c}{\alpha }\right) t^{\alpha } }}+4\, {\mathrm{e}^{\left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } }}-1 \right) }{a \left( b{k}^{2}+1 \right) \left( 1+{ \mathrm{e}^{\left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } }} \right) ^{2}}} . \end{aligned}$$
(23)

Figure 6 shows the dynamic properties of \(u_{7} \left( x,t \right)\) for \(a = 0.65, b = 0.35, k = 0.85\), and for two different values of \(\alpha\)’s.

Fig. 6
figure 6

Dynamic behaviours modulus of solution \(u_{7} \left( x,t \right)\) for \(a = 0.65, b = 0.35, k = 0.\)

Full size image

Set 5:

One obtains \(r=[3,2, 1,1]\) and \(s=[1,0,1,0]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{3\,{\mathrm{e}^{\xi }}+2}{1+{\mathrm{e}^{\xi }}}} . \end{aligned}$$
(24)

We also obtain

$$\begin{aligned} c= {\frac{\sqrt{aA_{{2}}+6}\sqrt{a}\sqrt{A_{{2}}}}{6 \sqrt{b}}},k={\frac{\sqrt{a}\sqrt{A_{{2}}}}{\sqrt{b}\sqrt{aA_{{2 }}+6}}},A_{{0}}=6\,A_{{2}},A_{{1}}=-5\,A_{{2}},A_{{2}}=A_{{2}},B_{{1}} =0,B_{{2}}=0 . \end{aligned}$$

Putting values in Equations (12) and (24), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) =-{\frac{A_{{2}}{\mathrm{e}^{\xi }}}{ \left( 1+{ \mathrm{e}^{\xi }} \right) ^{2}}} .\end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{8} \left( x,t \right) =-{\frac{A_{{2}}{\mathrm{e}^{\left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } }}}{ \left( 1+{ \mathrm{e}^{\left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } }} \right) ^{2}}} . \end{aligned}$$
(25)

Figure 7 shows the dynamic properties of \(u_{8} \left( x,t \right)\) for \(a = 0.5, b = 0.35, A_2 =3\), and for two different values of \(\alpha\)’s.

Fig. 7
figure 7

Dynamic behaviours modulus of solution \(u_{8} \left( x,t \right)\) for \(a = 0.5, b = 0.35, A_2 =3\)

Full size image

Set 6:

One obtains \(r=[-3,-2, 1,1]\) and \(s=[1,0,1,0]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{-3-2\,{\mathrm{e}^{\xi }}}{1+{\mathrm{e}^{ \xi }}}} . \end{aligned}$$
(26)

We also obtain

$$\begin{aligned} c={\frac{2}{3\sqrt{-b}}},k=-{\frac{2}{\sqrt{-b}}},A_ {{0}}={\frac{148}{3\,a}},A_{{1}}=0,A_{{2}}=0,B_{{1}}=240\,{a}^{-1},B_ {{2}}=288\,{a}^{-1} . \end{aligned}$$

Putting values in Equations (12) and (26), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) =-{\frac{4\left( -4\,{\mathrm{e}^{2\,\xi }}+24\,{ \mathrm{e}^{\xi }}-9\right) }{3a \left( 3+2\,{\mathrm{e}^{\xi }} \right) ^{2}}} .\end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{9} \left( x,t \right) =-{\frac{4\left( -4\,{\mathrm{e}^{\left( \frac{2k}{\alpha }\right) x^\alpha -\left( \frac{2c}{\alpha }\right) t^{\alpha } }}+24\,{ \mathrm{e}^{\left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } }}-9\right) }{3a \left( 3+2\,{\mathrm{e}^{\left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } }} \right) ^{2}}} . \end{aligned}$$
(27)

Set 7:

One obtains \(r=[i,-i, 1,1]\) and \(s=[i,-i,i,-i]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) =-{\frac{\sin \left( \xi \right) }{\cos \left( \xi \right) }} . \end{aligned}$$
(28)

We also obtain

$$\begin{aligned} c={\frac{k}{16\,b{k}^{2}+1}},k=k,A_{{0}}= {\frac{12b{k}^{2 }}{16\,ab{k}^{2}+a}},A_{{1}}=0,A_{{2}}={\frac{6b{k}^{2}}{16\,ab{k}^ {2}+a}},B_{{1}}=0,B_{{2}}={\frac{6b{k}^{2}}{16\,ab{k}^{2}+a}} . \end{aligned}$$

Putting values in equations (12) and (28), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) = {\frac{6b{k}^{2}}{a \left( 16\,b{k}^{2}+1 \right) \sin ^{2} \left( \xi \right) \cos ^{2} \left( \xi \right) }} . \end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{10} \left( x,t \right) ={\frac{6b{k}^{2}}{a \left( 16\,b{k}^{2}+1 \right) \sin ^{2} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) \cos ^{2} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) }} . \end{aligned}$$
(29)

Figure 8 shows the dynamic properties of \(u_{10} \left( x,t \right)\) for \(a = 0.5, b = 1.5, k=0.8\), and for two different values of \(\alpha\).

Fig. 8
figure 8

Dynamic behaviours modulus of solution \(u_{10} \left( x,t \right)\) for \(a = 0.5, b = 1.5, k=0.8\)

Full size image

Set 8:

One obtains \(r=[1,1,- 1,1]\) and \(s=[1,-1,1,-1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) =-{\frac{\cosh \left( \xi \right) }{\sinh \left( \xi \right) }} . \end{aligned}$$
(30)

We also obtain

$$\begin{aligned} c={\frac{k}{16\,b{k}^{2}+1}},k=k,A_{{0}}= {\frac{4b{k}^{2} }{16\,ab{k}^{2}+a}},A_{{1}}=0,A_{{2}}= {\frac{6b{k}^{2}}{16\,ab{k}^{ 2}+a}},B_{{1}}=0,B_{{2}}={\frac{6b{k}^{2}}{16\,ab{k}^{2}+a}} .\end{aligned}$$

Putting values in Equations (12) and (30), yields the following solution

$$\begin{aligned} {\mathscr {U}} \left( \xi \right) ={\frac{b{k}^{2} \left( 6 \mathrm{coth} ^{4} \left( \xi \right) +4 \mathrm{coth} ^{2} \left( \xi \right) +6 \right) }{ \left( 16\,ab{k}^{2}+a \right) \mathrm{coth}^{2} \left( \xi \right) }} .\end{aligned}$$

Consequently, we get the solution of Equation (8) as

$$\begin{aligned} u_{11} \left( x,t \right) ={\frac{b{k}^{2} \left( 6 \mathrm{coth} ^{4} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) +4 \mathrm{coth} ^{2} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) +6 \right) }{ \left( 16\,ab{k}^{2}+a \right) \mathrm{coth}^{2} \left( \left( \frac{k}{\alpha }\right) x^\alpha -\left( \frac{c}{\alpha }\right) t^{\alpha } \right) }} . \end{aligned}$$
(31)

4.2 The conformable Kundu–Eckhaus equation

In this part, we aim to construct exact wave solutions in studying the conformable version of the Kundu–Eckhaus equation (32), giving by

$$\begin{aligned}&i\mathscr {D}_t^{\alpha }q\left( x,t\right) +\mathscr {D}_{xx}^{2\alpha } q_{xx}\left( x,t\right) -2\rho |q|^2\left( x,t\right) q\left( x,t\right) \nonumber \\&\quad +\delta ^2|q|^4\left( x,t\right) q\left( x,t\right) +2i\delta \mathscr {D}_{x}^{\alpha }\left( |q\left( x,t\right) |^2\right) q\left( x,t\right) =0, \end{aligned}$$
(32)

In order to find solutions of Equation (32), following new variables are introduced

$$\begin{aligned}&\quad q\left( x,t\right) =\mathscr {Q}(\xi )e^{i {\Phi }(x,t)},\qquad \qquad \xi =k\left( \left( \frac{1}{\alpha }\right) x^\alpha -\left( \frac{2\omega }{\alpha }\right) t^\alpha \right) , \qquad \qquad \nonumber \\&\quad {\Phi }(x,t)=\left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha }, \end{aligned}$$
(33)

where \(\omega , k\) and \(\epsilon\) are constants to be determined.

Taking Eq. (33) into account in Eq. (32) yields

$$\begin{aligned} -\left( \epsilon +\omega ^2\right) \Theta -k^2 \Theta '' -2\rho \Theta ^3+\delta ^2\Theta ^5-4\delta k\Theta ^2\Theta '=0, \end{aligned}$$
(34)

If we balance the highest derivative term of \(\Theta ''\) and nonlinear term of \(\Theta ^5\) in Eq. (34) as \(M+2=5M\), we obtain \(M=\frac{1}{2}\).

So, we need to use a new transformation \(\Theta \left( \xi \right) ={\mathscr {U}}^{1\over 2}\left( \xi \right)\) in Eq. (34) to get

$$\begin{aligned} -4\left( \epsilon +\omega ^2\right) {\mathscr {U}}^2+k^2 {\mathscr {U}}'^2 -2k^2 {\mathscr {U}}{\mathscr {U}}''-8\rho {\mathscr {U}}^3+4\delta ^2 {\mathscr {U}}^4-8k\delta {\mathscr {U}}^2{\mathscr {U}}'=0, \end{aligned}$$
(35)

Now if we apply the balance principle on the terms \({\mathscr {U}}^4\) and \({\mathscr {U}}{\mathscr {U}}''\) in Eq. (35), we have \(4M=M+M+2\), so \(M=1\). Using Eq. (7) together with \(M=1\), we have

$$\begin{aligned} \Theta (\xi )=A_0+ A_1 \Psi (\xi ) + \frac{B_1 }{\Psi (\xi )}. \end{aligned}$$
(36)

The following results are provided by processing the general steps required in the method.

Set 1:

One obtains \(r=[-1,0, 1, 1]\) and \(s=[0,0,1,1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) =-{\frac{1 }{1+e^ \xi }} . \end{aligned}$$
(37)

Case 1.1: In this case we also obtain

$$\begin{aligned} \epsilon = {\frac{-8\,{\omega }^{2}{\sigma }^{2}-{\rho }^{2} \sqrt{7}-4\,{\rho }^{2}}{8{\sigma }^{2}}},k=- {\frac{ \left( 1+ \sqrt{7} \right) \rho }{2\sigma }},\omega =\omega ,A_{{0}}=0,A_{{1}}=- \,{\frac{\rho \, \left( 4+\sqrt{7} \right) }{2 \left( 3+\sqrt{7} \right) {\sigma }^{2}}},B_{{1}}=0 . \end{aligned}$$

Putting values in Equations (36) and (37), yields the following solution

$$\begin{aligned} \mathscr {Q}\left( \xi \right) = {\frac{\rho \, \left( 4+\sqrt{7} \right) }{2 \left( 3+\sqrt{7} \right) {\sigma }^{2} \left( 1+{\mathrm{e}^{\xi }} \right) }} , \end{aligned}$$

and

$$\begin{aligned} q_{1} \left( x,t \right) = \left( {\frac{\rho \, \left( 4+\sqrt{7} \right) }{ 2\left( 3+\sqrt{7} \right) {\sigma }^{2}\left( 1+{\mathrm{e}^{-{\frac{ \left( 1+ \sqrt{7} \right) \rho }{2\sigma } \left( x-\,{\frac{2\omega \,{t}^{ \alpha }}{\alpha }} \right) }}} \right) } } \right) ^{1/2} \times e^{ i \left( \left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha } \right) }. \end{aligned}$$
(38)

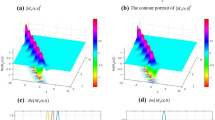
Figure 9 shows the dynamic behavior of solution \(q_{1} \left( x,t \right)\) for \(\sigma =0.75, \rho = 0.95, \omega = 0.6\), and \(\alpha =0.9\).

Fig. 9
figure 9

Dynamic behaviours modulus of solution \(q_{1} \left( x,t \right)\), real part (left) and imaginary part (right) for \(\sigma =0.75, \rho = 0.95, \omega = 0.6\), and \(\alpha =0.9\)

Full size image

Case 1.2: In this case we also obtain

$$\begin{aligned}&\epsilon = {\frac{-24\,{\omega }^{2}{\sigma }^{2}\sqrt{7}- 64\,{\omega }^{2}{\sigma }^{2}-20\,{\rho }^{2}\sqrt{7}-53\,{\rho }^{2}}{8{ \sigma }^{2} \left( 8+3\,\sqrt{7} \right) }},k= {\frac{ \left( 1+ \sqrt{7} \right) \rho }{2\sigma }},\omega =\omega ,\\&\quad A_{{0}}= {\frac{ \rho \, \left( 4+\sqrt{7} \right) }{ 2\left( 3+\sqrt{7} \right) { \sigma }^{2}}}, A_{{1}}= {\frac{\rho \, \left( 4+\sqrt{7} \right) }{2 \left( 3+\sqrt{7} \right) {\sigma }^{2}}},B_{{1}}=0 . \end{aligned}$$

Putting values in Equations (36) and (37), yields the following solution

$$\begin{aligned} \mathscr {Q}\left( \xi \right) ={\frac{\rho \, \left( 4+\sqrt{7} \right) { \mathrm{e}^{\xi }}}{2 \left( 3+\sqrt{7} \right) {\sigma }^{2} \left( 1+{ \mathrm{e}^{\xi }} \right) }} ,\end{aligned}$$

and

$$\begin{aligned} q_{2} \left( x,t \right) = \left( {\frac{\rho \, \left( 4+\sqrt{7} \right) { \mathrm{e}^{{ { {\frac{ \left( 1+\sqrt{7} \right) \rho }{2\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha -\,{\frac{2\omega \,{t}^{\alpha }}{ \alpha }} \right) }}}}}}{2 \left( 3+\sqrt{7} \right) {\sigma }^{2} \left( 1+{ \mathrm{e}^{{ { {\frac{ \left( 1+\sqrt{7} \right) \rho }{2\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha -\,{\frac{2\omega \,{t}^{\alpha }}{ \alpha }} \right) }}}}} \right) }} \right) ^{1/2} \times e^{ i \left( \left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha } \right) }. \end{aligned}$$
(39)

Figure 10 shows the dynamic behavior of solution \(q_{2} \left( x,t \right)\) for \(\sigma =0.75, \rho = 0.8, \omega = 0.69\), and \(\alpha =0.9\).

Fig. 10
figure 10

Dynamic behaviours modulus of solution \(q_{2} \left( x,t \right)\), real part (left) and imaginary part (right) for \(\sigma =0.75, \rho = 0.8, \omega = 0.69\), and \(\alpha =0.9\)

Full size image

Set 2:

One obtains \(r=[2,0, 1, -1]\) and \(s=[1,0,1,-1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{\cosh \left( \xi \right) +\sinh \left( \xi \right) }{\sinh \left( \xi \right) }} . \end{aligned}$$
(40)

Case 2.1: In this case we also obtain

$$\begin{aligned}&\epsilon ={\frac{-1796320\,{\omega }^{2}{\sigma }^{2} \sqrt{7}+4752616\,{\omega }^{2}{\sigma }^{2}-1492237\,{\rho }^{2}\sqrt{ 7}+3948088\,{\rho }^{2}}{8{\sigma }^{2} \left( -594077+224540\,\sqrt{7} \right) }},k={\frac{ \left( -1+\sqrt{7} \right) \rho }{4\sigma }} ,\\&\quad \omega =\omega ,\\&A_{{0}}={\frac{\rho \, \left( 47\,\sqrt{7}-125 \right) }{4\left( -53+20\,\sqrt{7} \right) {\sigma }^{2}}},A_{{1}}=-{\frac{\rho \, \left( -4+\sqrt{7} \right) }{4{\sigma }^{2} \left( - 3+\sqrt{7} \right) }},B_{{1}}=0 . \end{aligned}$$

Putting values in equations(36) and (40), yields the following solution

$$\begin{aligned} \mathscr {Q}\left( \xi \right) ={\frac{ \left( 133\,\sqrt{7}-352 \right) \rho \, \left( \cosh \left( \xi \right) -\sinh \left( \xi \right) \right) }{ 4\left( -53+20\,\sqrt{7} \right) {\sigma }^{2} \left( -3+ \sqrt{7} \right) \sinh \left( \xi \right) }} ,\end{aligned}$$

and

$$\begin{aligned}&q_{3} \left( x,t \right) = \left( {\frac{ \left( 133\,\sqrt{7}-352 \right) \rho \, \left( \cosh \left( {\frac{ \left( -1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha -{ \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) -\sinh \left( {\frac{ \left( -1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha -{ \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) \right) }{ 4\left( -53+20\,\sqrt{7} \right) {\sigma }^{2} \left( -3+ \sqrt{7} \right) \sinh \left( {\frac{ \left( -1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha -{ \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) }\right) }} \right) ^{1/2} \nonumber \\&\quad \times e^{ i \left( \left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha } \right) }. \end{aligned}$$
(41)

Case 2.2: In this case we also obtain

$$\begin{aligned}&\epsilon = {\frac{-2105120\,{\omega }^{2}{\sigma }^{2} \sqrt{7}+5569624\,{\omega }^{2}{\sigma }^{2}-1748763\,{\rho }^{2}\sqrt{ 7}+4626792\,{\rho }^{2}}{8{\sigma }^{2} \left( -696203+263140\,\sqrt{7} \right) }},\\&\quad k= {\frac{ \left( 1-\sqrt{7} \right) \rho }{4\sigma } },\omega =\omega ,\\&\quad A_{{0}}=0,A_{{1}}= {\frac{ 3\left( -1225+463\, \sqrt{7} \right) \rho }{ 8\left( -1561+590\,\sqrt{7} \right) {\sigma }^ {2}}},B_{{1}}=0 . \end{aligned}$$

Putting values in equations (36) and (40), yields the following solution

$$\begin{aligned} \mathscr {Q}\left( \xi \right) = {\frac{3 \left( -1225+463\,\sqrt{7} \right) \rho \, \left( \cosh \left( \xi \right) +\sinh \left( \xi \right) \right) }{8 \left( -1561+590\,\sqrt{7} \right) {\sigma }^{2} \sinh \left( \xi \right) }} ,\end{aligned}$$

and

$$\begin{aligned}&q_{4} \left( x,t \right) = \left( {\frac{3 \left( -1225+463\,\sqrt{7} \right) \rho \, \left( \cosh \left( {\frac{ \left( 1-\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha -{ \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) +\sinh \left( {\frac{ \left( 1-\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha -{ \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) \right) }{8 \left( -1561+590\,\sqrt{7} \right) {\sigma }^{2} \sinh \left( {\frac{ \left( 1-\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha -{ \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) }} \right) ^{1/2} \nonumber \\&\quad \times e^{ i \left( \left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha } \right) }. \end{aligned}$$
(42)

Set 3:

One obtains \(r=[1,2,1,1]\) and \(s=[0,1,0,1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{1+2\,{\mathrm{e}^{\xi }}}{1+{\mathrm{e}^{\xi }}}} . \end{aligned}$$
(43)

We also obtain

$$\begin{aligned}&\epsilon = {\frac{-8\,{\omega }^{2}{\sigma }^{2}-{\rho }^{2} \sqrt{7}-4\,{\rho }^{2}}{{8\sigma }^{2}}},k={\frac{ \left( 1+ \sqrt{7} \right) \rho }{2\sigma }},\omega =\omega ,\\&\quad A_{{0}}=- {\frac{ \left( -5+\sqrt{7} \right) \rho }{{2\sigma }^{2}}},A_{{1}}=0,B_{{1}}={\frac{ \left( -5+\sqrt{7} \right) \rho }{{2\sigma }^{2}}} . \end{aligned}$$

Putting values in equations(36) and (43), yields the following solution

$$\begin{aligned} \mathscr {Q}\left( \xi \right) =-{\frac{ \left( -5+\sqrt{7} \right) \rho \,{\mathrm{e}^{\xi }}}{{2\sigma }^{2} \left( 2\,{\mathrm{e}^{\xi }}+1 \right) }} ,\end{aligned}$$

and

$$\begin{aligned} q_{5} \left( x,t \right) = \left( -{\frac{ \left( -5+\sqrt{7} \right) \rho \,{\mathrm{e}^{{\frac{ \left( 1+\sqrt{7} \right) \rho }{2\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) }}}}{{2\sigma }^{2} \left( 2\,{\mathrm{e}^{{\frac{ \left( 1+\sqrt{7} \right) \rho }{2\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) }}}+1 \right) }} \right) ^{1/2} \times e^{ i \left( \left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha } \right) }. \end{aligned}$$
(44)

Figure 11 shows the dynamic behavior of solution \(q_{5} \left( x,t \right)\) for \(\sigma =0.8, \rho = 0.2, \omega = 0.8\), and \(\alpha =0.7\).

Fig. 11
figure 11

Dynamic behaviours modulus of solution \(q_{5} \left( x,t \right)\), real part (left) and imaginary part (right) for \(\sigma =0.8, \rho = 0.2, \omega = 0.8\), and \(\alpha =0.7\)

Full size image

Set 4:

One obtains \(r=[-3,-2,1,1]\) and \(s=[0,1,0,1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{-3-2\,{\mathrm{e}^{\xi }}}{1+{\mathrm{e}^{ \xi }}}} . \end{aligned}$$
(45)

We also obtain

$$\begin{aligned}&\epsilon ={\frac{-8\,{\omega }^{2}{\sigma }^{2}-{\rho }^{2} \sqrt{7}-4\,{\rho }^{2}}{{8\sigma }^{2}}},k=-{\frac{ \left( 1+ \sqrt{7} \right) \rho }{2\sigma }},\omega =\omega ,A_{{0}}=-{\frac{3 \left( -5+\sqrt{7} \right) \rho }{{4\sigma }^{2}}},\\&\quad A_{{1}}=0,B_{{1}}=-{\frac{3 \left( -5+\sqrt{7} \right) \rho }{{2\sigma }^{2}}} . \end{aligned}$$

Putting values in equations (36) and (45), yields the following solution

$$\begin{aligned} \mathscr {Q}\left( \xi \right) =-{\frac{ 3\left( -5+\sqrt{7} \right) \rho }{{4\sigma }^{2} \left( 2\,{\mathrm{e}^{\xi }}+3 \right) }} ,\end{aligned}$$

and

$$\begin{aligned} q_{6} \left( x,t \right) = \left( -{\frac{ 3\left( -5+\sqrt{7} \right) \rho }{{4\sigma }^{2} \left( 2\,{\mathrm{e}^{{\frac{ \left( 1+\sqrt{7} \right) \rho }{2\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) }}}+3 \right) }} \right) ^{1/2} \times e^{ i \left( \left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha } \right) }. \end{aligned}$$
(46)

Set 5:

One obtains \(r=[ 2,0,1,1]\) and \(s=[-1,0,-1,1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{\cosh \left( \xi \right) -\sinh \left( \xi \right) }{\cosh \left( \xi \right) }} . \end{aligned}$$
(47)

We also obtain

$$\begin{aligned} \epsilon = {\frac{-8\,{\omega }^{2}{\sigma }^{2}-{\rho }^{2} \sqrt{7}-4\,{\rho }^{2}}{{8\sigma }^{2}}},k=- {\frac{ \left( 1+ \sqrt{7} \right) \rho }{4\sigma }},\omega =\omega ,A_{{0}}=0,A_{{1}}=- \,{\frac{ \left( -5+\sqrt{7} \right) \rho }{{8\sigma }^{2}}},B_{{1}}=0 . \end{aligned}$$

Putting values in equation (36) and (47), yields the following solution

$$\begin{aligned} \mathscr {Q}\left( \xi \right) =- {\frac{ \left( -5+\sqrt{7} \right) \rho \, \left( \cosh \left( \xi \right) -\sinh \left( \xi \right) \right) }{{8\sigma }^{2}\cosh \left( \xi \right) }} ,\end{aligned}$$

and

$$\begin{aligned}&q_{7} \left( x,t \right) = \left( - {\frac{ \left( -5+\sqrt{7} \right) \rho \, \left( \cosh \left( -{\frac{ \left( 1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) -\sinh \left( -{\frac{ \left( 1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) \right) }{{8\sigma }^{2}\cosh \left( -{\frac{ \left( 1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) }} \right) ^{1/2} \nonumber \\&\quad \times e^{ i \left( \left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha } \right) }. \end{aligned}$$
(48)

Figure 12 shows the dynamic behavior of solution \(q_{7} \left( x,t \right)\) for \(\sigma =0.45, \rho = 0.85, \omega = 0.35\), and \(\alpha =0.95\).

Fig. 12
figure 12

Dynamic behaviours modulus of solution \(q_{7} \left( x,t \right)\), real part (left) and imaginary part (right) for \(\sigma =0.45, \rho = 0.85, \omega = 0.35\), and \(\alpha =0.95\)

Full size image

Set 6:

One obtains \(r=[ -3,-1,1,1]\) and \(s=[1,-1,1,-1]\), so Eq. (7) turns to

$$\begin{aligned} \Psi \left( \xi \right) ={\frac{-2\,\cosh \left( \xi \right) -\sinh \left( \xi \right) }{\cosh \left( \xi \right) }} . \end{aligned}$$
(49)

We also obtain

$$\begin{aligned} \epsilon= & {} {\frac{-24\,{\omega }^{2}{\sigma }^{2}\sqrt{7}+ 64\,{\omega }^{2}{\sigma }^{2}-20\,{\rho }^{2}\sqrt{7}+53\,{\rho }^{2}}{{ 8\sigma }^{2} \left( -8+3\,\sqrt{7} \right) }},k= {\frac{ \left( - 1+\sqrt{7} \right) \rho }{4\sigma }},\omega =\omega ,\\ A_{{0}}= & {} -{\frac{\rho \, \left( -4+\sqrt{7} \right) }{{4\sigma }^{2} \left( -3+\sqrt{7} \right) }},A_{{1}}=0,B_{{1}}=- {\frac{3\rho \, \left( -4+\sqrt{7} \right) }{{4\sigma }^{2} \left( -3+\sqrt{7} \right) }} . \end{aligned}$$

Putting values in equations (36) and (49), yields the following solution

$$\begin{aligned} \mathscr {Q}\left( \xi \right) ={\frac{\rho \, \left( -4+\sqrt{7} \right) \left( \cosh \left( \xi \right) -\sinh \left( \xi \right) \right) }{ 4{\sigma }^{2} \left( -3+\sqrt{7} \right) \left( 2\,\cosh \left( \xi \right) +\sinh \left( \xi \right) \right) }} ,\end{aligned}$$

and

$$\begin{aligned}&q_{8} \left( x,t \right) = \left( {\frac{\rho \, \left( -4+\sqrt{7} \right) \left( \cosh \left( {\frac{ \left( -1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) -\sinh \left( {\frac{ \left( -1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) \right) }{ 4{\sigma }^{2} \left( -3+\sqrt{7} \right) \left( 2\,\cosh \left( {\frac{ \left( -1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) +\sinh \left( {\frac{ \left( -1+\sqrt{7} \right) \rho }{4\sigma } \left( \left( \frac{1}{\alpha }\right) x^\alpha - { \frac{2\omega \,{t}^{\alpha }}{\alpha }} \right) } \right) \right) }} \right) ^{1/2} \nonumber \\&\quad \times e^{ i \left( \left( \frac{\omega }{\alpha }\right) x^\alpha -\left( \frac{\epsilon }{\alpha }\right) t^{\alpha } \right) }. \end{aligned}$$
(50)

Figure 13 shows the dynamic behavior of solution \(q_{8} \left( x,t \right)\) for \(\sigma =0.5, \rho = 0.5, \omega = 0.5\), and \(\alpha =1\).

Fig. 13
figure 13

Dynamic behaviours modulus of solution \(q_{8} \left( x,t \right)\), real part (left) and imaginary part (right) for \(\sigma =0.5, \rho = 0.5, \omega = 0.5\), and \(\alpha =1\)

Full size image

5 Conclusions

In this research, the projected method has been effectively applied to the nonlinear complex Kundu–Eckhaus and Zakharov–Kuznetsov–Benjamin–Bona–Mahony equations in conformable domain used to explain the most fascinating problems of modern optics. Some important optical soliton solutions such as single (dark, bright and singular), complex solitons, as well as a hyperbolic, travelling wave and trigonometric function solutions have been successfully extracted. The graphical simulations of the reported solutions have been also presented in Figs. (1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12, 13). While some of these figures symbolize singular wave properties, others gives travelling wave distributions. The results are entirely new, interesting and play an important roles in the field of the nonlinear Schrödinger equation because the studied model, namely nonlinear complex Kundu–Eckhaus equation is one of the part of NLSE. When we consider the obtained results, it is clear that the method has less limitations than other methods in determining the exact solutions of the equations. Despite the simplicity and ease of use of this method, it has a very powerful performance and is able to introduce a wide range of various types of solutions to such mathematical models. The idea used in this paper is readily applicable to solving other partial differential equations in mathematical physics. Finally, we observed that the propagation dynamics of these solutions obtained in this paper via GERFM may be used to explain the general properties of the nonlinear optical wave distributions (Weisstein 2002).