Self-steepening, Raman scattering and self-phase modulation-interactions via the perturbed Chen–Lee–Liu equation with an extra dispersion. Modulation insability and spectral analysis

Abstract

It is worth mentioning that the perturbed Chen–Lee–Liu equation (PCLLE) exhibits the effects of self-steepening (SS), Raman scattering (RS) and self-phase modulation (SPM). Our attention is focused, here, to inspect the challenge between these phenomena may lead to a dominant one among them. On the other hand, we investigate the dominant phenomena produced due to these interactions. Furthermore, the structure of the configuration of pulses propagation in optical fibers are depicted. These phenomena are illustrated, here, via studying the PCLLE with an extra dispersion. This equation is formulated and the exact solutions of this new equation are found by using the unified method (UM). The importance of the UM stems from the fact that, in the applications, we have found that the UM is of low time cost in symbolic computation. So, we think that it prevails the known methods in the literature. On the other hand, the solutions for the complex envelope field equations, found in the literature, are always considered with real wave amplitude. Here, a transformation based on using complex wave amplitude is introduced. Indeed, in this case, solutions describe the waves that result from soliton- periodic wave collision, which may reveal novel phenomena. The solutions obtained are evaluated numerically and represented in graphs. It is shown that pulses compression occurs which may be due to self-phase modulation. Also, dispersive shock wave can be produced which may be argued to the presence of the extra dispersion and self-sdteepening. It is worthy to mention that, self-steepening arises for a small value of the related coefficient. The results obtained, here, are novel. The modulation instability is analyzed and it is found that it triggers at a critical values of SS and RS coefficients. At this stage, shock wave may occur. It is observed that the spectrum shows soliton with periodic waves background.

1 Introduction

The perturbed nonlinear Schrodinger equations, among them the PCLLE describes the propagation of optical pulses in optical fibers, retaining the interactions of self-steepening, Raman scattering and self phase modulation phenomena (Chen et al. 1979). In Chen et al. (1979) the inverse scattering method was used to study the integrability of nonlinear Hamiltonian systems. The PCLLE was currently studied in the literature. A generalized PCLLE with high nonlinearity perturbation terms were also considered. In this case, a PCLLE was taken full nonlinearity via integration algorithms, where solutions exhibit bright, dark, singular solitons were shown (Yıldırıma et al. 2020). In Kudryashov (2019), the traveling wave reduction was used where two first integrals for the system of equations of the real and imaginary parts of the solution of PCLLE were found. A higher-order extension of the PCLLE with third-order dispersion and quintic nonlinearity terms was studied in Zhang et al. (2015) by constructing the n-fold Darboux transformation. By using modified 1/G $^\prime$ -expansion and modified Kudryashov methods, traveling wave solutions of PCLLE, where different aspects of the solutions produced by both analytical methods were discussed (Yokuş et al. 2021). Analytical bright soliton solutions, dark soliton solutions, periodic solutions of the fractional PCLLE were obtained by the modified exp$(- \Omega (\xi ))$-expansion function method (Martínez et al. 2021). In Houwe et al. (2021), the chirped and the corresponding chirp with their stability to the PCLLE with self-phase modulation and nonlinear dispersions were presented. The Jacobi elliptic function technique was used to find solutions of PCLLE (Sarla et al. 2022). A novel modification for the generalized exponential rational function method was used to determine novel analytical solutions of PCLLE (Mohamed et al. 2022).The conservation laws of PCLLE in optical fibers together with he conserved densities were retrieved by Lie symmetry analysis (Karaa et al. 2018).The collective variable method to study two types of the CLLE, the classical and perturbed ones was employed (Alrashed et al. 2021). The classical Lie symmetry analysis was used to exhibit optical solitons to PCLLE (Bansal et al. 2020). Construction of different optical soliton solutions to the CLLE of monomode fibers, by executing the extended sinh-Gordon equation expansion method, logarithmic transformation, and the ansatz functions method, was executed (Bilal et al. 2021). The CLLE in birefringent fibers is examined to uncover dark, bright and also singular solitons (Yıldırım 2019). In Gaxiola and Biswas (2018), the CLLE in optical fibers was dealt with by the aid of Laplace Adomian decomposition method. The CLLE was investigated by the aid of fully shifted Jacobi’s collocation method with two independent approaches, via discretization of the spatial variable and the temporal variable (Abdelkawy et al. 2021). Periodic wave trains of the CLLE evolved from fully developed modulation instability was found in Liu et al. (2021). Therein it was shown that a highly nontrivial spectral evolution of such waves leads to strong asymmetry of its components.The effect of fractional temporal evolution on chirped soliton solutions of the CLLE was studied by adopting the new modified sub-equation method to derive bright and dark solitons, periodic and singular function solutions (Dépélair et al. 2021). The classification of possible wave structures evolving from initially discontinuous profiles for the photon fluid propagating in a normal dispersion fiber was carried based on the generalized CLLE (Ivanov 2021). We mention that the PCLLE can be considered as kind of perturbed nonlinear Schrodinger equation (PNLSE), so that they may share many physical insights concerning the propagation of optical pulses in fiber optics. The PNLSE has received the attention of a variety of works. In Mihalache et al. (1993), the inverse scattering transform was used to find one-parameter and the breather-like four-parameter soliton solutions of a PNLSE.The Riccati-Bernoulli Sub-ODE method was used to investigate exact wave solution of the PNLSE (Shehata 2016). In Mahak and Akram (2019), the extension of the rational sine-cosine method and rational sinh-cosh method to construct new exact solutions of PNLSE. The two (G$^\prime$ /G,1/G)-expansion methods were suggested to obtain abundant closed form wave solutions to thePNLSE and the cubic-quintic Ginzburg-Landau equation Miah et al. (2016). In Neirameh (2016), a new class of conformable fractional derivative for constructing new exact solitary wave solutions to the fractional PNLSE was proposed. New complex solitons to the PNLSE model with the help of an analytical method were obtained (Gao et al. 2020). In Zhang et al. (2010), the modified mapping method and the extended mapping method we were used to derive some new exact solutions of the PNLSE. In the presence of parabolic law nonlinear fibers, Raman effect and self-steepening, the PNLSE was investigated using the sub-equation expansion method (Zhou 2014). The PNLSE was studied by utilizing two analytical methods, namely the extended modified auxiliary equation mapping and the generalized Riccati equation mapping methods (Osman et al. 2021). For the PNLSE, the exact traveling wave solutions solutions, trigonometric, hyperbolic, rational, soliton and complex function solutions,, via the extended (G$^\prime$ G2)-expansion method and the first integral method were obtained (Akram and Mahak 2018). An aternative method used to inspect the local and nonlocal integrability is the inverse scattering method was used emplopyed in Ma (2022, 2021) and Ma and Yong (2021)

It is worthy to mention that, always in the literature, solutions of theNLSE. extended NLSE and Perturbed NlSE, for the complex envelope, were found by introducing real amplitude transformation. Very recently numerous works were carried by introducing complex amplitude transformation which inspect the waves that result from solion-periodic wave collision. It reveals many new phenomena which were hidden in the traditional transformation (Abdel-Gawad 2012, 2021a, b, c, d, 2022; Abdel-Gawad et al. 2022; Tantawy and Abdel-Gawad 2020), and It is estabished that NLSE-type equtions, they are integrabe when the the real and imaginary parts are linearly dependent. In the present work, we study the PCLLE in the presence of third order dispersion, where the interaction of self-steepening (SS), Raman scattering (RS) and self-phase modulation (SPM) is investigated, which is completely new. This is established by investigating the exact solutions of the PCLLE which are found by using the UM.

The outlines of this work are as follows.

In Sect. 2 the model equation and the method are presented. Section 3 is devoted to solutions in hyperbolic function forms. While, elliptic solutions are presented in Sect. 4. Modulation instability and the spectral analysis are studied in Sect. 5. Section 6 is devoted to conclusions.

2 The Model Eq. and outlines of the UM

2.1 The model Eq.

The propagation of optical pulses inside in a monomode fibers modeled by the CLL equation,which reads

$$\begin{aligned} iw_{t}+\alpha \,w_{xx}+\gamma \,\mid w\mid ^{2}w_{x}=0, \end{aligned}$$

(1)

where $w\equiv w(x.,t)$ is the complex envelope field, $\alpha$ is the group dispersion velocity and $\gamma$ is the coefficient of Raman scattering.

The perturbed Chen–Lee–Liu equation describe the propagation of optical pulses in plasma and optical fibers reads,

$$\begin{aligned} iw_{t}+\alpha \,w_{xx}+\gamma \,\mid w\mid ^{2}w_{x}=i[cw_{x}+\mu (\mid w\mid ^{2}w)_{x}+\sigma (\mid w\mid ^{2})_{x}w], \end{aligned}$$

(2)

where c is the phase velocity, $\mu$ is the coefficient of self-steepening for short pulses and $\sigma$ is the coefficient of self-phase modulation (nonlinear dispersion).

The PCLLE with high nonlinearity is,

$$\begin{aligned} iw_{t}+\alpha \,w_{xx}+\gamma \,\mid w\mid ^{2}w_{x}=i[cw_{x}+\mu (\mid w\mid ^{2n}w)_{x}+\sigma (\mid w\mid ^{2n})_{x}w],n>1,n\,\epsilon \mathbb {N}, \end{aligned}$$

(3)

Here, we consider the Eq (2) with an extra dispersion,

$$\begin{aligned} iw_{t}+\alpha \,w_{xx}+i\beta w_{xxx}+\gamma \,\mid w\mid ^{2}w_{x}=i[cw_{x}+\mu (\mid w\mid ^{2}w)_{x}+\sigma (\mid w\mid ^{2})_{x}w], \end{aligned}$$

(4)

where $\beta$ is the coefficient of the highest order dispersion. We proceed by introducing a transformation with complex amplitude solution for w(x, t) in the form,

$$\begin{aligned} w(x,t)=(u(x,t)+iv(x,t))e^{i(kx-\omega t)},\quad w^{*}(x,t)=(u(x,t)-iv(x,t))e^{-i(kx-\omega t)}, \end{aligned}$$

(5)

into (4), and the equations for the real and imaginary parts are given respectively by,

$$\begin{aligned}&ku^{3}(\mu -\gamma )-v_{t}+u\left( ck-\alpha k^{2}+\beta k^{3}+kv^{2}(\mu -\gamma )+2u_{x}v(\mu +\sigma )+\omega \right) \nonumber \\&\quad +v_{x}\left( c+3\beta k^{2}-2\alpha k\right) +\left[ u^{2}(\mu -\gamma )+v^{2}(-\gamma +3\mu +2\sigma )\right] v_{x}\nonumber \\&\quad +u_{xx}(\alpha -3\beta k)-\beta v_{xxx}=0, \end{aligned}$$

(6)

$$\begin{aligned}&kv^{3}(\mu -\gamma )+u_{t}+\left[ -c-3\beta k^{2}+2\alpha k+u^{2}(\gamma -3\mu -2\sigma ) \right. \nonumber \\&\quad \left. +v^{2}(\gamma -\mu )\right] u_{x}\nonumber \\&\quad +v\left( ck-\alpha k^{2}+\beta k^{3}+ku^{2}(\mu -\gamma )-2u(\mu +\sigma )v_{x}+\omega \right) \nonumber \\&\quad +v_{\text {xx}}(\alpha -3\beta k)+\beta u_{\text {xxx}}=0. \end{aligned}$$

(7)

Here we use the transformations for the traveling wave solutions of (6) and (7), $u(x,t)=U(z),\quad v(x,t)=V(z),\;z=hx+dt$, thus (6) and (7) reduce respectively to,

$$\begin{aligned}&V'\left( -d+h\left( c+3\beta k^{2}-2\alpha k\right) +hV^{2}(-\gamma +3\mu +2\sigma )\right) \nonumber \\&\quad +h^{2}\left( U''(\alpha -3\beta k)-\beta hV^{(3)}\right) \nonumber \\&\quad +U\left( ck+2hV(\mu +\sigma )U'-\alpha k^{2}+\beta k^{3}+kV^{2}(\mu -\gamma )+\omega \right) \nonumber \\&\quad +hU^{2}(\mu -\gamma )V'+kU^{3}(\mu -\gamma )=0, \end{aligned}$$

(8)

$$\begin{aligned}&U'\left( d-h\left( c+3\beta k^{2}-2\alpha k\right) +hU^{2}(\gamma -3\mu -2\sigma )\right) \nonumber \\&\quad +h^{2}\left( \beta hU^{(3)}+V''(\alpha -3\beta k)\right) \nonumber \\&\quad +V\left( ck-2hU(\mu +\sigma )V'-\alpha k^{2}+\beta k^{3}+kU^{2}(\mu -\gamma )+\omega \right) \nonumber \\&\quad +hV^{2}(\gamma -\mu )U'+kV^{3}(\mu -\gamma )=0. \end{aligned}$$

(9)

The exact solutions of (8) and (9) (or (6) and (7)) are obtained via the UM [ ]. It asserts that the solutions of nonlinear partial differential equations are expressed in polynomial an rational forms, in an auxiliary function that satisfied an auxiliary equation.

2.2 Outlines of the UM

2.2.1 Polynomial forms

The solutions of (8) and (9) are written,

$$\begin{aligned} \begin{array}{c} U(z)=\sum _{j=0}^{j=n_{1}}a_{j}g(z)^{j},\quad V(z)=\sum _{j=0}^{j=n_{2}}b_{j}g(z)^{j},\\ (g^{\prime }(z))^{r}=\sum _{j=0}^{j=rk}c_{j}g(z)^{j},r=1,2, \end{array} \end{aligned}$$

(10)

where g(z)is the auxiliary function together with the auxiliary equation (AE).

The polynomial solution (10) of (8) and (9) exists, in the sense of polynomial form, if there exist integers$n_{1},n_{2}$ and k. To this issue, we analyze two conditions, the balance and consistency We consider the case $r=1.$ With relevance to (8) and (9), the balance condition leads to $n_{1}=n_{2}=k-1$. For the consistency condition we determine the number of equations that result from inserting (10) into these equation and by setting the coefficients of $g(z)^{i},i=0,1,2,...$equal to zero (say $p(k)=4k-3)$. Also, we determine the numbers of arbitrary parameters $\{a_{j},b_{j},c_{j}\}$ (say $q(k)=2k-1).$The condition for the existence of (10) reads $p(k)-q(k)\le m$ , m is the highest order derivative in (8) and (9). (here $m=3).$We find that $1\le k\le 7/2,$thus $k=1,2,3.$ The case when $r=2$ is discussed by the same way. It is worth noticing that when $r=1$the solutions of (10) are hyperbolic functions, while when $r=2$, they are periodic or elliptic functions.

2.2.2 Rational forms

In this case, for simplicity, we write directly,

$$\begin{aligned} \begin{array}{c} U(z)=\frac{a_{1}g(z)+a_{0}}{s_{1}g(z)+s_{0}},\quad V(z)=\frac{b_{1}g(z)+b_{0}}{s_{1}g(z)+s_{0}},\\ (g^{\prime }(z))^{r}=\sum _{j=0}^{j=rk}c_{j}g(z)^{j},r=1,2. \end{array} \end{aligned}$$

(11)

Indeed , rational solutions may be considered to describe “indirect” interactions, while (10) describes “direct” interactions. The discussion of existence of the rational forms is done by the same way as in the case of polynomial forms. Indeed the determination of the values k in (11) depends the high nonlinearity and the highest order derivative in (8) and (9).

The importance of the unified method results from the fact that it is of low time cost in symbolic computations. Furthermore, it provide a wide class of solutions ranges from hyperbolic solutions, periodic solutions to elliptic solutions in Jacobi elliptic functions. So, think that it prevails the known methods in the literature.

3 Hyperbolic functions solutions of (8) and (9)

We consider the solution in (10) and find the polynomial and rational solutions.

3.1 Polynomial solutions

3.1.1 When $r=1,$ $k=2$

Here, we write,

$$\begin{aligned} U(z)=a_{1}g(z)+a_{0},\quad V(z)=b_{1}g(z)+b_{0},b_{0}=\frac{b_{1}}{a_{1}}a_{0}, \end{aligned}$$

(12)

together with,the A E,

$$\begin{aligned} \begin{array}{c} g^{\prime }(z)=c_{2}g(z)^{2}+c_{1}g(z)+c_{0}\\ \\ \end{array} \end{aligned}$$

(13)

In (12) the real part and imaginary part are taken linearly dependent. By inserting (12) and (13) into (8) and (9) and by setting the coefficients of $g(z)^{i},i=0,1,2,..$equal to zero, we get,

$$\begin{aligned} \begin{array}{c} \beta =\frac{a_{1}^{2}(-\gamma )+3a_{1}^{2}\mu +2a_{1}^{2}\sigma -b_{1}^{2}\gamma +3b_{1}^{2}\mu +2b_{1}^{2}\sigma }{6c_{2}^{2}h^{2}},\\ \\ d=\frac{\sqrt{a_{1}^{2}+b_{1}^{2}}\left( -6ck(\gamma +\sigma )(\mu +\sigma )+3\omega (\mu +\sigma )(\gamma -3\mu -2\sigma )+4\alpha k^{2}(\gamma +\sigma )^{2}\right) }{9\sqrt{\alpha }c_{2}\sqrt{k}(\mu -\gamma )\sqrt{\mu +\sigma }},\\ \\ c_{0}=\frac{1}{12c_{2}k\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -\mu )(\mu +\sigma )}(3a_{1}^{2}c_{1}^{2}k(\gamma -\mu )(\mu +\sigma )+3b_{1}^{2}c_{1}^{2}k(\gamma -\mu )\\ \\ (\mu +\sigma )+2c_{2}^{2}\left( -6ck(\mu +\sigma )+\alpha k^{2}(\gamma +3\mu +4\sigma )-6\omega (\mu +\sigma )\right) ,\\ h=\frac{\sqrt{k}\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{\mu +\sigma }}{\sqrt{\alpha }c_{2}},\quad a_{0}=\frac{a_{1}c_{1}}{2c_{2}}. \end{array} \end{aligned}$$

(14)

The solution of (13) is,

$$\begin{aligned} \begin{array}{c} g(z)=\frac{1}{6c_{2}\sqrt{k}\sqrt{a_{1}^{2}+b_{1}^{2}}(\mu -\gamma )\sqrt{\mu +\sigma }}(3c_{1}\sqrt{k}\sqrt{a_{1}^{2}+b_{1}^{2}}(\gamma -\mu )\sqrt{\mu +\sigma }+\\ \\ \sqrt{6}c_{2}\sqrt{\gamma -\mu }\sqrt{6ck(\mu +\sigma )-\alpha k^{2}(\gamma +3\mu +4\sigma )+6\omega (\mu +\sigma )}\\ \tanh \left( \frac{c_{2}\left( A_{0}+z\right) \sqrt{6ck(\mu +\sigma )-\alpha k^{2}(\gamma +3\mu +4\sigma )+6\omega (\mu +\sigma )}}{\sqrt{6}\sqrt{k}\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{\gamma -\mu }\sqrt{\mu +\sigma }}\right) ,\gamma >\mu . \end{array} \end{aligned}$$

(15)

Finally, the solutions of (6) and (7) are,

$$\begin{aligned} \begin{array}{c} u(x,t)=-\frac{1}{\sqrt{6}\sqrt{k}\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{\gamma -\mu }\sqrt{\mu +\sigma }}(a_{1}\sqrt{6ck(\mu +\sigma )-\alpha k^{2}(\gamma +3\mu +4\sigma )+6\omega (\mu +\sigma )}\\ \tanh \left( \frac{c_{2}\left( A_{0}+z\right) \sqrt{6ck(\mu +\sigma )-\alpha k^{2}(\gamma +3\mu +4\sigma )+6\omega (\mu +\sigma )}}{\sqrt{6}\sqrt{k}\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{\gamma -\mu }\sqrt{\mu +\sigma }}\right) ,\;v(x,t)=\frac{b_{1}}{a_{1}}u(x,t)\\ \\ z=\frac{1}{9\sqrt{\alpha }c_{2}\sqrt{k}(\mu -\gamma )\sqrt{\mu +\sigma }}\left( 4\alpha k^{2}t(\gamma +\sigma )^{2}-3k(\mu +\sigma )(2ct(\gamma +\sigma )+3x(\gamma -\mu ))\right. \\ \\ +3t\omega (\mu +\sigma )(\gamma -3\mu -2\sigma ))\sqrt{a_{1}^{2}+b_{1}^{2}}. \end{array} \end{aligned}$$

(16)

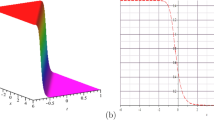
The solutions in (15) are used to calculate $Re$ $w(x,t)$ which is evaluated numerically and the results are shown in Fig. 1(i)–(iv).

Fig. 1

(i)–(iv) When $c=0.7,\omega =7,k=4,\alpha =0.7,a_{1}=1.7,b_{1}=1.3,c_{2}=1,A_{0}=-10.$

In Fig 1 (i), Rew(x, t) is displayed against x for different values of t when $\mu =1.1,\gamma =2.5,{{\sigma =}0.8.}$ Rew(x, t) is displayed against t by varying $\mu$ when $\gamma =2.5,{{\sigma =}0.8.}$in Fig. 1(ii).

In Fig. 1(iii), by varying when $\mu =1.1,{{\sigma =}0.8.}$ and in Fig. 1(iv) by varying $\sigma$ when $\mu =1.1,\gamma =2.5.$Together, when $x=-3$.

Figure 1(i) shows pulses compression with quasi SPM Fig. 1(ii), shows the behavior when varying the coefficient of SS towards high values $\mu .$

This figure consolidates the occurrence of self-steepening and we think that pulses progress to shock wave at a value of $\mu =\mu _{cr}$.

Figure 1(iii) shows Raman scattering effect, while Fig. (iv) shows again self-steepening with raising the coefficient of self-phase modulation.

3.1.2 When $r=2$and $k=2$

We consider (12) with AE,

$$\begin{aligned} g^{\prime }(z)=g(z)\sqrt{c_{2}g(z)^{2}+c_{1}g(z)+c_{0}}. \end{aligned}$$

(17)

From (12) and (17) into (8) and (9) gives rise to,

$$\begin{aligned} \begin{array}{c} \beta =-\frac{\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )}{6c_{2}h^{2}},\;a_{0}=\frac{a_{1}c_{1}}{4c_{2}},\quad c_{0}=\frac{c_{1}^{2}}{4c_{2}}\\ \\ d\,=\,\frac{1}{48\text {hc}_{2}^{2}}\left( a_{1}^{2}\left( 8c_{2}\left( c_{0}h^{2}-3k^{2}\right) -3c_{1}^{2}h^{2}\right) (\gamma -3\mu -2\sigma )+48c_{2}^{2}h^{2}(c-2\alpha k)\right. \\ \left. +\left( b_{1}^{2}\left( 8c_{2}\left( c_{0}h^{2}-3k^{2}\right) -3c_{1}^{2}h^{2}\right) (\gamma -3\mu -2\sigma )\right) \right) ,\\ \\ h\,=\frac{\sqrt{k}\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{\mu +\sigma }}{\sqrt{\alpha }\sqrt{c_{2}}},\quad \omega =\frac{1}{48c_{2}^{2}(\mu +\sigma )}\left( k\left( 3a_{1}^{2}c_{1}^{2}(\gamma -\mu )(\mu +\sigma )\right. \right. \\ \\ \left. \left. +3b_{1}^{2}c_{1}^{2}(\gamma -\mu )(\mu +\sigma )+8c_{2}^{2}(\alpha k(\gamma +3\mu +4\sigma )-6c(\mu +\sigma ))\right) \right) . \end{array} \end{aligned}$$

(18)

Finally the solutions of (6) and 7 are,

$$ \begin{array}{*{20}c} {u\{ x,t) = - \frac{{a_{1} c_{1} \left( {2A_{0} c_{2} e^{{\frac{{c_{1} z}}{{2\sqrt {c_{2} } }}}} + 1} \right)}}{{4c_{2} \left( {2A_{0} c_{2} e^{{\frac{{c_{1} z}}{{2\sqrt {c_{2} } }}}} - 1} \right)}},\quad v(x,t) = \frac{{b_{1} }}{{a_{1} }}u(x,t),} \\ {} \\ {z = - \frac{1}{{48\alpha c_{2} {\text{c}}_{2}^{2} }}\left( {a_{1}^{4} c_{1}^{2} kt(\mu + \sigma )(\gamma - 3\mu - 2\sigma ) + b_{1}^{4} c_{1}^{2} kt(\mu + \sigma )(\gamma - 3\mu - 2\sigma )} \right.} \\ {\quad \quad \quad \quad \quad + \,24b_{1}^{2} c_{2}^{2} kt(\alpha k(\gamma + \mu + 2\sigma ) - 2c(\mu + \sigma )) + 2kta_{1}^{2} \left( {b_{1}^{2} c_{1}^{2} (\mu + \sigma )(\gamma - 3\mu - 2\sigma ) + 12} \right.} \\ {\left. {\left. {\quad \quad \quad + \,12c_{2}^{2} (\alpha k(\gamma + \mu + 2\sigma ) - 2c(\mu + \sigma ))} \right) - 48\sqrt \alpha \sqrt {c_{2} } {\text{c}}_{2}^{2} \sqrt k x\sqrt {a_{1}^{2} + b_{1}^{2} } \sqrt {\mu + \sigma } } \right).} \\ \end{array} $$

(19)

The solutions in (19) are used to display Rew(x, t) in Fig. 2 (i)–(iv).

Fig. 2

(i)–(iv).When $c=0.7,\omega =7,k=5,\alpha =0.7,a_{1}=1.7,b_{1}=1.3,A_{0}=-10,c_{2}=2,c_{1}=0.7.$

In Fig 2 (i), Rew(x, t) is displayed against x for different values of t when $\mu =1.1,\gamma =2.5,\sigma =0.8,$

Rew(x, t) is displayed against t by varying $\mu$when $\gamma =2.5,\sigma =0.8$ in Fig. 2 (ii).

In Fig. 2(iii) by varying $\gamma$ when $\mu =1.1,\sigma =0.8,$and by varying $\sigma$ in Fig. 2 (iv) when $\mu =1.1,\gamma =2.5$, and when $x=-3$.

Figure 2 (i) shows pulses compression with quasi-self-phase modulation on $x>0$. Fig. 2 (ii) shows also wave compression of shock waves.

Fig. 2 (iii) exhibits the extra dispersion effect while Fig. 2 (iv) shows SPM.

3.2 Rational solutions

We write the solutions, when $r=2$ and $k=2$, in the form,

$$\begin{aligned} \begin{array}{c} U(z)=\frac{a_{1}g(z)+a_{0}}{s_{1}g(z)+s_{0}},\quad V(z)=\frac{b_{1}g(z)+b_{0}}{s_{1}g(z)+s_{0}},\quad b_{0}=\frac{a_{0}b_{1}}{a_{1}}, \end{array} \end{aligned}$$

(20)

together with AE,

$$\begin{aligned} g^{\prime }(z)=g(z)\sqrt{-b^{2}g(z)^{2}+a^{2}.} \end{aligned}$$

(21)

From (20) and (21) into (8) and (9) yields,

$$\begin{aligned} \begin{array}{c} \beta =\frac{(m-1)(\gamma -3\mu -2\sigma )\left( a_{0}^{2}m^{2}s_{1}^{2}+b_{1}^{2}s_{0}^{2}\right) }{3a^{2}h^{2}m^{2}s_{0}^{2}s_{1}^{2}},\;a_{1}=\frac{m\left( a_{0}s_{1}\right) }{s_{0}}\quad s_{1}\text {:=}\frac{\sqrt{2}bs_{0}}{\sqrt{a^{2}(m+1)}},\\ \\ \omega =\frac{a^{2}h^{2}m^{2}\alpha s_{0}^{2}}{3(m-1)^{2}(\mu +\sigma )^{2}\left( a^{2}b_{1}^{2}(m+1)+2a_{0}^{2}b^{2}m^{2}\right) {}^{2}}\left( 6a_{0}^{2}b^{2}\text {c3}(m-1)m^{2}(\mu +\sigma )\right. \\ \\ \left. +a^{2}\left( 2\alpha ^{2}b^{2}h^{2}m^{2}s_{0}^{2}+3b_{1}^{2}\text {c3}\left( m^{2}-1\right) (\mu +\sigma )\right) \right) ,\\ \\ d=h\left( \frac{a^{2}b_{1}^{2}\left( m^{2}+3m+2\right) (\mu +\sigma )}{3b^{2}m^{2}s_{0}^{2}}+\frac{2a_{0}^{2}(m+2)(\mu +\sigma )}{3s_{0}^{2}}+\text {c}\right. \\ \\ \left. +\frac{a^{2}\alpha ^{2}b^{2}h^{2}m^{2}s_{0}^{2}}{(m-1)(\mu +\sigma )\left( a^{2}b_{1}^{2}(m+1)+2a_{0}^{2}b^{2}m^{2}\right) }\right) ,\\ \\ k=-\frac{a^{2}\alpha b^{2}h^{2}m^{2}s_{0}^{2}}{(m-1)(\mu +\sigma )\left( a^{2}b_{1}^{2}(m+1)+2a_{0}^{2}b^{2}m^{2}\right) },\quad \gamma \text {:=}\mu . \end{array} \end{aligned}$$

(22)

The solution of (21) is,

$$\begin{aligned} g(z)=\frac{a\text {sech}\left( a\left( A_{0}+z\right) \right) }{b}. \end{aligned}$$

(23)

The solutions of (6) and (7) are,

$$\begin{aligned} \begin{array}{c} u(x,t)=\frac{a_{0}\left( \sqrt{a^{2}(m+1)}+\sqrt{2}am\text {sech}\left( a\left( A_{0}+z\right) \right) \right) }{s_{0}\left( \sqrt{a^{2}(m+1)}+\sqrt{2}a\text {sech}\left( a\left( A_{0}+z\right) \right) \right) },\quad v(x,t)=\frac{b_{1}}{a_{1}}u(x,t),\\ z=h\left( x+t\left( \frac{a^{2}b_{1}^{2}\left( m^{2}+3m+2\right) (\mu +\sigma )}{3b^{2}m^{2}s_{0}^{2}}+\frac{2a_{0}^{2}(m+2)(\mu +\sigma )}{3s_{0}^{2}}+\text {c3}\right. \right. \\ \left. \left. +\frac{a^{2}\alpha ^{2}b^{2}h^{2}m^{2}s_{0}^{2}}{(m-1)(\mu +\sigma )\left( a^{2}b_{1}^{2}(m+1)+2a_{0}^{2}b^{2}m^{2}\right) }\right) \right) .\\ \end{array} \end{aligned}$$

(24)

The solutions in (24) are used to display Rew(x, t) in Fig. 3 (i)–(vi).

Fig. 3

(i)–(iv). When $c=0.7,\alpha =0.7,\beta =0.6,a_{0}=2.7,b_{1}=2.3,h\text {:=}1.5,m=1.2,A_{0}=5,s_{0}=5,\text {a}=1.5,\text {b}=1.3$

In Fig 3 (i), Rew(x, t) is displayed against x for different values oft when $\mu =1.1,{{\sigma }=1.8}$.

In Fig 3(ii) and Fig 3(iii) Rew(x, t) is displayed against t by varying $\mu$ when ${{\sigma }=1.8}$and by varying $\sigma$ when

$\mu\, =\,1.1.$and when $x=-10.$ In Fig. 3 (iv) the 3D plot is displayed for the same values as in Fig. 3(i).

Figure 3(i) show pulses compression, while Fig. 3(ii) and 3(iii) show quasi SPM.These figures show , almost, shock waves. .

4 Elliptic solutions

In this case in (10) and (11), we take $r=2.$Here, also, polynomial and rational solutions are found.

4.1 Polynomial solutions

4.1.1 When $p=2$ and $k=2$

We consider two cases.

Case (I)

We consider (12) with the AE,

$$\begin{aligned} g^{\prime }(z)=\sqrt{c_{4}g(z)^{4}+c_{2}g(z)^{2}+c_{0}}. \end{aligned}$$

(25)

By inserting (12) and (20) into (8) and (9), we have,

$$\begin{aligned}&\beta =-\frac{\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )}{6c_{4}h^{2}},\;d=\frac{c_{2}h\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )}{6c_{4}}-\frac{k^{2}\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )}{2c_{4}h}+\text {c}h-2\alpha hk, \nonumber \\&k=\frac{\alpha c_{4}h^{2}}{\left( a_{1}^{2}+b_{1}^{2}\right) (\mu +\sigma )},\quad \omega =\frac{h^{2}\alpha }{6\left( a_{1}^{2}+b_{1}^{2}\right) {}^{2}(\mu +\sigma )^{3}}\left( -3a_{1}^{4}c_{2}(\gamma -\mu )(\mu +\sigma )^{2}-3b_{1}^{4}c_{2}(\gamma -\mu )(\mu +\sigma )^{2}\right. \nonumber \\&\left. -6a_{1}^{2}(\mu +\sigma )^{2}\left( b_{1}^{2}c_{2}(\gamma -\mu )+c_{4}\text {c}\right) -6b_{1}^{2}c_{4}\text {c}(\mu +\sigma )^{2}+\alpha ^{2}c_{4}^{2}h^{2}(\gamma +3\mu +4\sigma )\right) , a_{0}=0. \end{aligned}$$

(26)

In (18), we remark that $c_{i},i=0,2,4$ are arbitrary. We consider the case when $c_{4}=-m^{2},c_{2}=2m^{2}-1,c_{0}=m^{2}-1$

In this case $g(z)=\text {cn}\left( \left. z+A_{0}\right| m\right)$ and the solutions of (6) and (7) are,

$$\begin{aligned} \begin{array}{c} u(x,t)=a_{1}\text {cn}\left( \left. z+A_{0}\right| m\right) ,v(x,t)=b_{1}\text {cn}\left( \left. z+A_{0}\right| m\right) ,\\ z=t\left( -\frac{\alpha ^{2}c_{4}h^{3}(\gamma -3\mu -2\sigma )}{2\left( a_{1}^{2}+b_{1}^{2}\right) (\mu +\sigma )^{2}}-\frac{2\alpha ^{2}c_{4}h^{3}}{\left( a_{1}^{2}+b_{1}^{2}\right) (\mu +\sigma )}+\frac{c_{2}h\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )}{6c_{4}}+\text {c}h\right) +hx. \end{array} \end{aligned}$$

(27)

By using (27), Rew(x, t) is displayed in figures 4 (i)–(iv).

Fig. 4

(i)–(iv). When $k=4,\alpha =0.7,a_{1}=3.7,b_{1}=5.3,m=0.999,h=3,A_{0}=-5,\text {c}=0.7.$

In Fig 4 (i), Rew(x, t) is displayed againstx for different values of t when $\gamma =2.5,\mu =1.1,\sigma =0.8$.

In Fig. 4(ii), (iii) and (iv) , Rew(x, t) is displayed against t for different values of $\mu$when $\gamma =2.5,\sigma =0.8,$

against $\gamma$ when $\mu =1.1,\sigma =0.8,$and against $\sigma$ when $\gamma =2.5,\mu =1.1,$ respectively and when $x=3$.

Figure 4(i) shows chirped waves. Fig. 4(ii) shows highly dispersive waves induced by the the extra dispersion.

While Fig. 4 (ii) and (iv) show highly oscillatory pulses with SPM.

Case (II)

Here consider (12) with the AE,

$$\begin{aligned} g'(z)=\sqrt{c_{2}g(z)^{2}+c_{1}g(z)+c_{0}}\sqrt{r_{2}g(z)^{2}+r_{1}g(z)+r_{0}}. \end{aligned}$$

(28)

By inserting (12) and (28) gives rise to,

$$\begin{aligned}&h=\frac{\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{-\gamma +3\mu +2\sigma }}{\sqrt{6}\sqrt{\beta }\sqrt{c_{2}}\sqrt{r_{2}}},\quad a_{0}=\frac{1}{4}a_{1}\left( \frac{c_{1}}{c_{2}}+\frac{r_{1}}{r_{2}}\right) , \nonumber \\&d=\frac{\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{-\gamma +3\mu +2\sigma }}{48\sqrt{6}\sqrt{\beta }c_{2}^{5/2}r_{2}^{5/2}}\left( 8c_{2}^{2}r_{0}r_{2}\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )\right. \nonumber \\&\quad +8c_{0}c_{2}r_{2}^{2}\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )+8c_{1}c_{2}r_{1}r_{2}\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )\nonumber \\&\quad \left. +48c_{2}^{2}\text {c3}r_{2}^{2}-3\left( a_{1}^{2}+b_{1}^{2}\right) \left( c_{2}r_{1}+c_{1}r_{2}\right) {}^{2}(\gamma -3\mu -2\sigma )+144\beta c_{2}^{2}k^{2}r_{2}^{2}-96\alpha c_{2}^{2}kr_{2}^{2}\right) ,\nonumber \\&k=\frac{\alpha (-\gamma +3\mu +2\sigma )}{6\beta (\mu +\sigma )},\quad \omega =\frac{\alpha (\gamma -3\mu -2\sigma )}{216\beta ^{2}c_{1}r_{2}^{2}(\mu +\sigma )^{3}}\left( -9a_{1}^{2}\beta c_{1}r_{1}^{2}(\gamma -\mu )(\mu +\sigma )^{2}\right. \nonumber \\&\quad - 18a_{1}^{2}\beta c_{1}r_{0}r_{2}(\gamma -\mu )(\mu +\sigma )^{2}+9\beta b_{1}^{2}c_{1}r_{1}^{2}(\gamma -\mu )(\mu +\sigma )^{2}+18\beta b_{1}^{2}c_{1}r_{0}r_{2}\nonumber \\&(\gamma -\mu )(\mu +\sigma )^{2}+18a_{1}^{2}\beta c_{0}r_{1}r_{2}(\gamma -\mu )(\mu +\sigma )^{2}+18\beta b_{1}^{2}c_{0}r_{1}r_{2}(\gamma -\mu )(\mu +\sigma )^{2}\nonumber \\&\quad \left. +\alpha ^{2}c_{1}r_{2}^{2}(\gamma -3\mu -2\sigma )^{2}+36\beta c_{1}\text {c3}r_{2}^{2}(\mu +\sigma )^{2}+6\alpha ^{2}c_{1}r_{2}^{2}(\mu +\sigma )(\gamma -3\mu -2\sigma )\right) ,\nonumber \\&c_{2}=\frac{c_{1}r_{2}}{r_{1}}. \end{aligned}$$

(29)

The solution of (28) is,

$$\begin{aligned} g(z)=-\frac{\sqrt{r_{1}^{2}-4r_{0}r_{2}}\text {sn}\left( \frac{1}{2}\left( z+A_{0}\right) \sqrt{c_{1}r_{1}-4c_{0}r_{2}}|\frac{c_{1}\left( r_{1}^{2}-4r_{0}r_{2}\right) }{r_{1}\left( c_{1}r_{1}-4c_{0}r_{2}\right) }\right) +r_{1}}{2r_{2}}. \end{aligned}$$

(30)

Finally the solutions of (6) and (7) are,

$$\begin{aligned}&u(x,t)=-\frac{a_{1}\sqrt{r_{1}^{2}-4r_{0}r_{2}}\text {sn}\left( \frac{1}{2}\left( z+A_{0}\right) \sqrt{c_{1}r_{1}-4c_{0}r_{2}}|\frac{c_{1}\left( r_{1}^{2}-4r_{0}r_{2}\right) }{r_{1}\left( c_{1}r_{1}-4c_{0}r_{2}\right) }\right) }{2r_{2}},\nonumber \\&\quad v(x,t)=\frac{b_{1}}{a_{1}}u(x,t), \nonumber \\&z=\frac{c_{1}\sqrt{a_{1}^{2}+b_{1}^{2}}\sqrt{-\gamma +3\mu +2\sigma }}{12\sqrt{6}\sqrt{\beta }\sqrt{r_{2}}\left( \frac{c_{1}r_{2}}{r_{1}}\right) {}^{5/2}}\left( \frac{12c_{1}r_{2}^{2}x}{r_{1}^{2}}+t\left( c_{1}\left( a_{1}^{2}+b_{1}^{2}\right) (-(\gamma -3\mu -2\sigma ))\right. \right. \nonumber \\&\quad +\frac{2c_{1}r_{0}r_{2}\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )}{r_{1}^{2}}+\frac{2c_{0}r_{2}\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -3\mu -2\sigma )}{r_{1}}\nonumber \\&\quad \left. \left. +\frac{12c_{1}\text {c3}r_{2}^{2}}{r_{1}^{2}}+\frac{4\alpha ^{2}c_{1}r_{2}^{2}(\gamma -3\mu -2\sigma )}{\beta r_{1}^{2}(\mu +\sigma )}+\frac{\alpha ^{2}c_{1}r_{2}^{2}(\gamma -3\mu -2\sigma )^{2}}{\beta r_{1}^{2}(\mu +\sigma )^{2}}\right) \right) . \end{aligned}$$

(31)

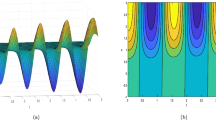
The results in (31) are evaluated numerically and Rew(x, t) is shown in Fig. 5 (i)–(vi).

Fig. 5

(i)–(iv).When $\omega =7,k=4,\alpha =0.7,a_{1}=1.7,b_{1}=1.3,c_{0}=1.2,r_{1}=2.3,r_{0}=0.5,r_{2}=0.3,$

$c_{1}=3.3,\beta =1.2,A_{0}=4,\text {c}=0.7.$

In Fig. 5(i), Rew(x, t) is displayed against x for different values oft when $\gamma =2.5,\mu =1.1,\sigma =0.8,$ .

In Fig. 5(ii), (iii) and (iv) , Rew(x, t) is displayed againstt for different values of $\mu$

when $\gamma =2.5,\sigma =1.8$. $,\gamma$ when $\mu =1.1,\sigma =1.8,$and $\sigma$ when $\gamma =2.5,\mu =1.1.$ respectively when $x=3$.

In Fig. 5 (v) and (vi) the 3D and contour plots are displayed for the same values in Fig. 5(i).

Figure 5(i) shows quasi-self-phase modulation. Fig. 5 (ii) shows more narrower waves than in

Figure 5(i), for a small value of $\mu$ which corresponds to self-steepening effect.

Fig. 5 (iii) shows scattered dense pulses compression, while Fig. 5(iv) show

highly dispersive waves which may be argued to the presence of the extra dispersion.

Fig. 5 (v) shows quasi-self-phase modulation, while Fig. 5 (vi) shows lattice wave.

4.2 Rational solutions

Now, we consider (20) together with the AE,

$$\begin{aligned} g^{\prime }(z)=\sqrt{c_{4}g(z)^{4}+c_{2}g(z)^{2}+c_{0}}. \end{aligned}$$

(32)

From (20) and (32) into (8) and (9) yields,

$$\begin{aligned}&\omega =\frac{a_{0}^{2}k\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -\mu )}{a_{1}^{2}s_{0}^{2}}+\frac{2a_{1}c_{0}h^{2}s_{0}s_{1}(\alpha -3\beta k)}{a_{0}s_{0}^{2}}\nonumber \\&\quad -\frac{2c_{0}h^{2}s_{1}^{2}(\alpha -3\beta k)}{s_{0}^{2}}-k\left( \text {c3}+\beta k^{2}-\alpha k\right) , \nonumber \\&\beta \text {:=}\frac{-2a_{0}^{3}k\left( a_{1}^{2}+b_{1}^{2}\right) (\gamma -\mu )+\alpha a_{1}^{2}a_{0}h^{2}\left( c_{2}s_{0}^{2}+4c_{0}s_{1}^{2}\right) +2\alpha a_{1}^{3}c_{0}h^{2}s_{0}s_{1}}{3a_{1}^{2}h^{2}k\left( 2a_{1}c_{0}s_{0}s_{1}+a_{0}\left( c_{2}s_{0}^{2}+4c_{0}s_{1}^{2}\right) \right) },\;a_{0}=-\frac{a_{1}s_{0}}{s_{1}},\nonumber \\&c_{0}=\frac{c_{4}s_{0}^{4}}{s_{1}^{4}},\;d=\frac{1}{3hks_{1}^{2}\left( 2c_{4}s_{0}^{2}+c_{2}s_{1}^{2}\right) }\left( -h^{2}2c_{4}s_{0}^{2}+c_{2}s_{1}^{2}\left( 6\alpha c_{4}h^{2}s_{0}^{2}\right. \right. \nonumber \\&\left. \quad +\left( \alpha c_{2}h^{2}+3k(\alpha k-\text {c3})s_{1}^{2}\right) \right) +ka_{1}^{2}\left( 6c_{4}h^{2}s_{0}^{2}(\gamma +\mu +2\sigma ) \right. \nonumber \\&\quad +\left( 6k^{2}(\mu -\gamma )+h^{2}(-\gamma +7\mu \right. \nonumber \\&\left. \left. \quad +6\sigma )c_{2}\right) s_{1}^{2}\right) +b_{1}^{2}k\left( s_{1}^{2}\left( c_{2}h^{2}(-\gamma +7\mu +6\sigma )+6k^{2}(\mu -\gamma )\right) \right. \nonumber \\&\left. \left. \quad +6c_{4}h^{2}s_{0}^{2}(\gamma +\mu +2\sigma )\right) \right) ,\nonumber \\&k=\frac{\alpha h^{2}\left( 2c_{4}s_{0}^{2}+c_{2}s_{1}^{2}\right) }{4\left( a_{1}^{2}+b_{1}^{2}\right) (\mu +\sigma )},\quad c_{2}=-m^{2}. \end{aligned}$$

(33)

The solution of (32) is,

$$\begin{aligned} \begin{array}{c} g(z)=\frac{\sqrt{2}\left( s_{1}^{2}\left( m^{2}\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}-m^{4}s_{1}^{2}\right) +2c_{4}^{2}s_{0}^{4}\right) }{\sqrt{c_{4}}s_{1}^{4}\left( m^{2}s_{1}^{2}-\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}\right) {}^{3/2}}\\ \text {sn}\left( \frac{\left( A_{0}+z\right) \left( \sqrt{2}c_{4}s_{0}^{2}\right) }{\sqrt{m^{2}s_{1}^{2}-\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}}}|\frac{m^{2}s_{1}^{2}-\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}}{\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}+m^{2}s_{1}^{2}}\right) . \end{array} \end{aligned}$$

(34)

The solutions of (6) and (7) are,

$$\begin{aligned}&u(x,t)=\frac{\frac{a_{1}}{s_{1}^{2}}(-\sqrt{c_{4}}s_{0}s_{1}^{4}\left( m^{2}s_{1}^{2}-\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}\right) {}^{3/2}+s_{1}H)}{\sqrt{c_{4}}s_{1}^{3}s_{0}\left( m^{2}s_{1}^{2}-\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}\right) {}^{3/2}+H},\;v(x,t)=\frac{b_{1}}{a_{1}}u(x,t),\nonumber \\&H=\sqrt{2}\left( m^{2}s_{1}^{2}\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}+2c_{4}^{2}s_{0}^{4}-m^{4}s_{1}^{4}\right) \text {sn}\left( \frac{\sqrt{2}\left( z+A_{0}\right) c_{4}s_{0}^{2}}{\sqrt{m^{2}s_{1}^{2}-\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}}}|\frac{m^{2}s_{1}^{2}-\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}}{m^{2}s_{1}^{2}+\sqrt{m^{4}s_{1}^{4}-4c_{4}^{2}s_{0}^{4}}}\right) . \end{aligned}$$

(35)

The solutions in (35) are used to display Rew(x, t0 in Fig. 6 (i)–(vi).

Fig. 6

(i)–(iv) When $m=0.5,n=0.75,c_{2}=-m^{2},A_{0}=-5,s_{1}=5,\text {c}=0.7,\alpha =0.7,\beta =0.6,a_{1}=1.7,b_{1}=1.3,h=0.8.$

In Fig 6 (i), Rew(x, t) is displayed against x for different values of t when $\gamma =2.5,\mu =1.1,\sigma =1.8.$

Rew(x, t) is displayed againstt for different values of $\mu ,$when $\gamma =2.5,\sigma =1.8$ in Fig. 6(ii), against $\gamma$ when $\mu =1.1,\sigma =1.8$in

Figure 6(iii) and against $\sigma$, when $\gamma =2.5,\mu =1.1$in Fig. 6(iv), and when $x=-10$.

\In Fig. 6 (v) and (vi) the 3D and contour plots are displayed for the same values in Fig. 5(i).

Figure 6(i) shows SPM interaction. Fig. 5 (ii) shows that self-steepening holds for small values of $\mu .$

Fig. 6 (iii) shows SPM-RS interaction, while Fig. 5(iv) show dispersive waves due to the extra dispersion.

Fig 6 (v) shows complex chirped waves, while Fig. 6 (vi) shows lattice wave.

5 Modulation instability and spectral analysis

5.1 Modulation instability

The study of modulation instability (MI) holds in a system which posses normal mode solution. This occurs for systems with complex envelope field. In Eq. (4), it has a solution of the form,

$$\begin{aligned} w(x,t)=Ae^{i(Kx-t\,\Omega )},\quad w^{*}(x,t)=Ae^{-i(Kx-t\,\Omega )},A\epsilon \mathbb {R}. \end{aligned}$$

(36)

The solution in (36) holds when,

$$\begin{aligned} \Omega =-cK+\alpha K^{2}-\beta K^{3}+\gamma K-K\mu . \end{aligned}$$

(37)

Noe, we use the perturbation expansion,

$$\begin{aligned} \begin{array}{c} w(x,t)=e^{i(Kx-t\,\Omega )}\left( A+e^{\lambda t}\left( \epsilon _{1}U_{1}(x)+i{{\epsilon _{2}}}V_{1}(x)\right) \right) ,\\ w^{*}(x,t)=e^{-i(Kx-t\,\Omega )}\left( A+e^{\lambda t}\left( \epsilon _{1}U_{1}(x)-i {{\epsilon _{2}}}V_{1}(x)\right) \right) . \end{array} \end{aligned}$$

(38)

From (38) into (4) gives rise to,

$$\begin{aligned}&H\left( \begin{array}{c} \epsilon _{1}\\ \epsilon _{2} \end{array}\right) =0,\quad H=\left( \begin{array}{cc} h_{11} &{} h_{12}\\ h_{21} &{} h_{22} \end{array}\right) , \nonumber \\&h_{11}=U_{1}(x)\left( 3A^{2}K(\mu -\gamma )+cK-\alpha K^{2}+\beta K^{3}+\Omega \right) +(\alpha -3\beta K)U_{1}''(x),\nonumber \\&h_{21}\text {:=}V_{1}'(x)\left( A^{2}(\mu -\gamma )+c+3\beta K^{2}-2\alpha K\right) -\beta V_{1}{}^{({3})}(x)+\lambda \left( -V_{1}(x)\right) ,\nonumber \\&h_{12}=-U_{1}'(x)\left( A^{2}(-(\gamma -3\mu ))+c+3\beta K^{2}-2\alpha K\right) +\lambda U_{1}(x)-+U_{1}{}^{(3)}(x), \nonumber \\&h_{22}\text {:=}V_{1}(x)\left( A^{2}K(\mu -\gamma )+cK-\alpha K^{2}+\beta K^{3}+\Omega \right) +(\alpha -3\beta K)V_{1}''(x). \end{aligned}$$

(39)

The solution of (39) is $det(H)=0$, which yields a lengthy equation which will not produced her. It describes the eigenvalue problem. This equation is solved when subjected to boundary conditions (BCs) . Here, we assume that U($\pm \infty )=-0$ and $V(\pm \infty )=-0$. The BCs suggest to write the solutions,

$$\begin{aligned} \left( \begin{array}{c} \begin{array}{c} U(x)\\ V(x) \end{array}\end{array}\right) =\left( \begin{array}{c} A_{1}\\ A_{2} \end{array}\right) {\left\{ \begin{array}{ll} e^{-rx}, &{} r>0,x>0,\\ e^{rx}, &{} x<0. \end{array}\right. } \end{aligned}$$

(40)

By inserting (40) into the eigenvalue equation, we get,

$$\begin{aligned}&A_{2}\left( \left( 3A^{4}-4A^{2}+1\right) K^{2}(\gamma -\mu )^{2}+2\left( 2A^{2}-1\right) Kr^{2}(\gamma -\mu )(3\beta K-\alpha )+r^{4}(\alpha -3\beta K)^{2}\right) \nonumber \\&\quad -A_{1}\left( r\left( -A^{2}(\gamma -3\mu )+3\beta K^{2}-2\alpha K\right) +cr+\lambda +r^{3}\right) ^{2}=0, \end{aligned}$$

(41)

Which solves to,

$$\begin{aligned}&\lambda =\frac{1}{A_{1}}\left( -A_{1}cr-A_{1}r^{3}+2\alpha A_{1}Kr-3A_{1}\beta K^{2}r+A^{2}A_{1}\gamma r-3A^{2}A_{1}\mu r+\right. \sqrt{\Delta },\nonumber \\&\Delta =A_{1}B_{1}(\left( 3A^{4}-4A^{2}+1\right) K^{2}(\gamma -\mu )^{2}+2\left( 2A^{2}-1\right) Kr^{2}(\gamma -\mu )(3\beta K-\alpha ) \nonumber \\&\quad \quad +r^{4}(\alpha -3\beta K)^{2}). \end{aligned}$$

(42)

The MI does not depend on the sign of $\Delta$and it holds when,

$$\begin{aligned} \mu>\frac{\gamma \left( A^{2}\gamma -c-3\beta K^{2}+2\alpha K-r^{2}\right) }{3A^{2}},\quad \gamma >\frac{c+3\beta K^{2}-2\alpha K+r^{2}}{A^{2}}. \end{aligned}$$

(43)

That is when $\mu >\mu _{cr}$ and $\gamma >\gamma _{cr}$.When MI occurs, it triggers, SS , shock waves and RS effect is produced.

5.2 Spectral analysis

Here we define the average wave number and the frequency and the spectrum content,

$$ \bar{k} = \frac{{\iint_{{\mathbb{R} \times \mathbb{R}^{ + } }} {\left| {w(x,t)_{x} } \right|}dxdt}}{{\iint_{{\mathbb{R} \times \mathbb{R}^{ + } }} {\left| {w(x,t)} \right|}dxdt}},\quad \bar{\omega } = \frac{{\iint_{{\mathbb{R} \times \mathbb{R}^{ + } }} {\left| {w(x,t)_{t} } \right|}dxdt}}{{\iint_{{\mathbb{R} \times \mathbb{R}^{ + } }} {\left| {w(x,t)} \right|}dxdt}}.{\text{ }} $$

(44)

The spectral content is defined by,

$$\begin{aligned} W(\kappa ,t)=\frac{1}{2\pi }\mid \int _{\mathbb {R}}e^{-i\kappa x}w(x,t)dx\mid . \end{aligned}$$

(45)

Here, by using (44) and (45), we illustrate the spectral analysis of the solutions in (16). This is demonstrated in Fig. 7(i)–(iv).

$$\begin{aligned} \text {c}:=0.7,\omega \text {:}7,k=4;\alpha \text {:=}0.7,a_{1}=1.7,b_{1}=1.3,c_{2}=1,A_{0}=-10. \end{aligned}$$

Fig. 7

(i)–(vii). When $\text {c}=0.7,\omega \text {}7,k=4;\alpha \text {:=}0.7,a_{1}=1.7,b_{1}=1.3,c_{2}=1,A_{0}=-10.$

In Fig. 7 (i) $\gamma =2.5,\sigma =1.8$ In Fig. 7(ii) $\mu =0.5,\sigma =0.8$

In Fig. 7(iii) $\mu =0.5,\gamma =0.9$. The same hold in Fig. 7(iv)–(vi). In Fig. 7(vii) $\gamma =2.5,\mu =0.5,\sigma = 0.8$

In Fig. 7(i)–(iii) the wave number is displayed. In Fig. 7 (iv)–(vi) the frequency is displayed. The spectrum is shown in Fig. 7(vii).

After Fig. 7 (i)–(vi), we the values of $\bar{k}$and $\bar{\omega }$ do not vary significantly when varying the parameters $\mu ,\gamma$ and $\sigma .$

Figure 7(vii) shows that the spectrum exhibits soliton with periodic waves background.

6 Conclusions

The perturbed Chen–Lee–Liu equation with third order dispersion is studied for the objective of investigating the effects of the self-steepening, Raman scattering, self -phase modulation, and the extra dispersion on the configuration of pulses propagation in optical fibers. This is inspected via the exact solutions, which are found by using the unified method. The results obtained are evaluated numerically and the are represented in figures which demonstrate the behavior of the solutions with relevance with the aforementioned phenomena. Also, it is found that self phase modulation occurs currently. While self-steepening is triggered by modulation instability. Also, highly dispersive oscillatory waves are observed which may be argued to the presence of an extra dispersion. These results are new. Further, pulses compression are, also, currently remarked. The modulation instability is studied and it is established that when it holds, it triggers self-steepening which progresses to shock waves. It is remarked that the wave spectrum exhibits soliton with background periodic waves. In a future work, the perturbed Chen–Lee–Liu equation with time dependent coefficients will be studied.