To extract stationary solutions to (1), initial assumption (Adem et al. 2020, 2020, 2021; Biswas and Khalique 2011, 2013; Biswas et al. 2018, Ekici et al. 2018, 2021; Sonmezoglu et al. 2021; Sucu et al. 2021)
$$\begin{aligned} q(x,t)=\phi (x) e^{i \lambda t} \end{aligned}$$
(2)
is considered. Here the constant \(\lambda\) is the wave number. Substituting (2) into (1), it is reached that
$$\begin{aligned}&- \left( \gamma +\lambda \right) \phi ^2 + b \phi ^2 G\left( \phi ^2\right) -2 (\alpha -2 \beta ) \left( \phi ^{\prime }\right) ^2 +a n (n+1) \phi ^n \left( \phi ^{\prime }\right) ^2\nonumber \\&\quad -2 \alpha \phi \phi ^{\prime \prime } +a (n+1) \phi ^{n+1} \phi ^{\prime \prime } =0. \end{aligned}$$
(3)
Equation (3) will now be analyzed according to the type of nonlinear media in next subsections.
2.1 Kerr law
For this nonlinearity,
$$\begin{aligned} F(s)=s. \end{aligned}$$
(4)
Thus, (1) becomes
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + b \left| q \right| ^{2} q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q. \end{aligned}$$
(5)
For \(n=1\), Eq. (5) can be integrated. Thus, Eq. (5) simplifies to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| q\right) _{xx} + b \left| q \right| ^{2} q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(6)
and Eq. (3) changes to
$$\begin{aligned} - \left( \gamma +\lambda \right) \phi ^2 +b \phi ^4 -2 (\alpha -2 \beta ) \left( \phi ^{\prime }\right) ^2 +2 a \phi \left( \phi ^{\prime }\right) ^2 - 2 \alpha \phi \phi ^{\prime \prime } +2 a \phi ^2 \phi ^{\prime \prime } =0. \end{aligned}$$
(7)
Generalized \((G^{\prime }/G)\)-expansion approach will now be applied to deal with (7). To kick off, suppose Eq. (7) possess the solution as (Zayed 2009; Malik et al. 2012)
$$\begin{aligned} \phi (x)=\sum _{i=0}^{N}\alpha _i\left( \frac{G^{\prime }}{G}\right) ^i \end{aligned}$$
(8)
where \(G=G(x)\) holds
$$\begin{aligned}{}[G^{\prime }(x)]^2=e_2G^4(x)+e_1G^2(x)+e_0 \end{aligned}$$
(9)
that is called Jacobi elliptic (JE) equation. Here \(\alpha _i\), \(e_0\), \(e_1\) and \(e_2\) are the arbitrary constants that need to be fixed such that \(\alpha _n \ne 0\). The solutions of Eq. (9) are presented as follows (Zayed 2009; Malik et al. 2012):
$$\begin{aligned} \begin{array}{llllll} \hline \text{ Case } &{} e_0 &{} e_1 &{} e_2 &{} G (x) &{} G^{\prime } (x) \\ \hline 1 &{} 1 &{} -(1+k^2) &{} k^2 &{} {{\,\mathrm{sn}\,}}x &{} {{\,\mathrm{cn}\,}}x {{\,\mathrm{dn}\,}}x \\ 2 &{} 1 &{}-(1+k^2) &{} k^2 &{} {{\,\mathrm{cd}\,}}x &{} -(1-k^2) {{\,\mathrm{sd}\,}}x {{\,\mathrm{nd}\,}}x \\ 3 &{} 1-k^2 &{}2k^2-1 &{} -k^2 &{} {{\,\mathrm{cn}\,}}x &{} -{{\,\mathrm{sn}\,}}x {{\,\mathrm{dn}\,}}x \\ 4 &{} k^2-1 &{}2-k^2 &{} -1 &{} {{\,\mathrm{dn}\,}}x &{} -k^2{{\,\mathrm{sn}\,}}x {{\,\mathrm{cn}\,}}x \\ 5 &{} k^2 &{}-(k^2+1) &{} 1 &{} {{\,\mathrm{ns}\,}}x &{} -{{\,\mathrm{ds}\,}}x {{\,\mathrm{cs}\,}}x \\ 6 &{} k^2 &{}-(k^2+1) &{} 1 &{} {{\,\mathrm{dc}\,}}x &{} (1-k^2) {{\,\mathrm{nc}\,}}x \, \text{ sc }\, x \\ 7 &{} -k^2 &{}2k^2-1 &{} 1-k^2 &{} {{\,\mathrm{nc}\,}}x &{} \text{ sc }\, x {{\,\mathrm{dc}\,}}x \\ 8 &{} -1 &{}2-k^2 &{} k^2-1 &{} {{\,\mathrm{nd}\,}}x &{} k^2{{\,\mathrm{sd}\,}}x {{\,\mathrm{cd}\,}}x \\ 9 &{} 1-k^2 &{} 2-k^2 &{} 1 &{} {{\,\mathrm{cs}\,}}x &{} -{{\,\mathrm{ns}\,}}x {{\,\mathrm{ds}\,}}x \\ 10 &{} 1 &{}2-k^2 &{} 1-k^2 &{} \text{ sc }\, x &{} {{\,\mathrm{nc}\,}}x {{\,\mathrm{dc}\,}}x \\ 11 &{} 1 &{}2k^2-1 &{} k^2(k^2-1) &{} {{\,\mathrm{sd}\,}}x &{} {{\,\mathrm{nd}\,}}x {{\,\mathrm{cd}\,}}x \\ 12 &{} k^2(k^2-1) &{} 2k^2-1 &{} 1 &{} {{\,\mathrm{ds}\,}}x &{} -{{\,\mathrm{cs}\,}}x {{\,\mathrm{ns}\,}}x \\ 13 &{} \frac{1}{4} &{} \frac{1}{2}(1-2k^2) &{} \frac{1}{4} &{} {{\,\mathrm{ns}\,}}x \pm {{\,\mathrm{cs}\,}}x &{}-{{\,\mathrm{ds}\,}}x {{\,\mathrm{cs}\,}}x \mp {{\,\mathrm{ns}\,}}x {{\,\mathrm{ds}\,}}x \\ 14 &{} \frac{1}{4}(1-k^2) &{} \frac{1}{2}(1+k^2) &{} \frac{1}{4}(1-k^2) &{} {{\,\mathrm{nc}\,}}x \pm \text{ sc }\, x &{} \text{ sc }\, x {{\,\mathrm{dc}\,}}x \pm {{\,\mathrm{nc}\,}}x {{\,\mathrm{dc}\,}}x \\ 15 &{} \frac{k^2}{4} &{} \frac{1}{2}(k^2-2) &{} \frac{1}{4} &{} {{\,\mathrm{ns}\,}}x \pm {{\,\mathrm{ds}\,}}x &{} -{{\,\mathrm{ds}\,}}x {{\,\mathrm{cs}\,}}x \mp {{\,\mathrm{cs}\,}}x {{\,\mathrm{ns}\,}}x \\ 16 &{} \frac{k^2}{4} &{} \frac{1}{2}(k^2-2) &{} \frac{k^2}{4} &{} {{\,\mathrm{sn}\,}}x \pm i {{\,\mathrm{cn}\,}}x &{} {{\,\mathrm{dn}\,}}x {{\,\mathrm{cn}\,}}x \mp i{{\,\mathrm{sn}\,}}x {{\,\mathrm{dn}\,}}x \\ 17 &{} 0 &{} 1 &{} -1 &{} {{\,\mathrm{sech}\,}}x &{} -{{\,\mathrm{sech}\,}}x \tanh x \\ 18 &{} 0 &{} 1 &{} 1 &{} {{\,\mathrm{csch}\,}}x &{} -{{\,\mathrm{csch}\,}}x \coth x \\ 19 &{} 0 &{} -1 &{} 1 &{} \sec x &{} \sec x \tan x \\ 20 &{} 0 &{} 0 &{} 1 &{} \frac{1}{\xi }&{} -\frac{1}{\xi ^2} \\ 21 &{} 0 &{} -(1+k^2) &{} k^2 &{} {{\,\mathrm{sn}\,}}x &{} {{\,\mathrm{cn}\,}}x {{\,\mathrm{dn}\,}}x \\ \hline \end{array} \end{aligned}$$
Here, the modulus of JE functions is stood for by k \((0<k<1)\) and \(i=\sqrt{-1}\).
Balancing \(\phi ^4\) with \(\phi \left( \phi ^{\prime }\right) ^2\) or \(\phi ^2 \phi ^{\prime \prime }\) leads to \(N=2\). Then Eq. (8) becomes
$$\begin{aligned} \phi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) +\alpha _2\left( \frac{G'}{G}\right) ^2. \end{aligned}$$
(10)
Inserting (10) along with (9) into (7), one recovers a polynomial in \(G^j\), \(G^{\prime }G^j\) \((j=\pm 1, \pm 2,\ldots )\). Equating each coefficient of the polynomial obtained to zero and then overcoming the resulting systems yields
$$\begin{aligned} b&= \frac{80 a^2 e_1}{\alpha }, \quad \alpha _0= 0, \quad \alpha _1= 0, \quad \alpha _2= -\frac{\alpha }{4 a e_1}, \quad \beta = \frac{3 \alpha }{4}, \quad \lambda = -\gamma +5 \alpha e_1+\frac{12 \alpha e_0 e_2}{e_1}, \end{aligned}$$
(11)
$$\begin{aligned} b&= -\frac{20 a^2 e_1}{\alpha }, \quad e_0= 0, \quad \alpha _0= -\frac{\alpha }{a}, \quad \alpha _1= 0, \quad \alpha _2= \frac{\alpha }{a e_1}, \quad \beta = \frac{\alpha }{4}, \quad \lambda = -\gamma -12 \alpha e_1 . \end{aligned}$$
(12)
Substituting (11) into (10) and employing (2) gives
$$\begin{aligned} q(x,t)= -\frac{\alpha }{4 a e_1} \left( \frac{G'}{G}\right) ^2 \exp \left[ i \left( -\gamma +5 \alpha e_1+\frac{12 \alpha e_0 e_2}{e_1} \right) t \right] . \end{aligned}$$
(13)
Next, solutions for the model under consideration (6) are attained as below:
If \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \frac{\alpha }{4 a \left( k^2+1\right) } {{\,\mathrm{cs}\,}}^2x {{\,\mathrm{dn}\,}}^2x \exp \left[ -i \left( \gamma +5 \alpha \left( k^2+1\right) +\frac{12 \alpha k^2}{k^2+1} \right) t \right] \end{aligned}$$
(14)
or
$$\begin{aligned} q(x,t)= \frac{\alpha \left( 1-k^2\right) ^2}{4 a \left( k^2+1\right) } \text{ sc}^2x {{\,\mathrm{nd}\,}}^2x \exp \left[ -i \left( \gamma +5 \alpha \left( k^2+1\right) +\frac{12 \alpha k^2}{k^2+1} \right) t \right] . \end{aligned}$$
(15)
For \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= -\frac{\alpha }{4 a \left( 2k^2-1 \right) } \text{ sc}^2x {{\,\mathrm{dn}\,}}^2 x \exp \left[ i \left( -\gamma +5 \alpha \left( 2k^2-1 \right) +\frac{12 \alpha k^2\left( k^2-1 \right) }{ 2k^2-1 } \right) t \right] . \end{aligned}$$
(16)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= -\frac{\alpha k^4}{4 a \left( 2-k^2 \right) } {{\,\mathrm{sd}\,}}^2x {{\,\mathrm{cn}\,}}^2x \exp \left[ i \left( -\gamma +5 \alpha \left( 2-k^2 \right) +\frac{12 \alpha \left( 1-k^2 \right) }{2-k^2} \right) t \right] . \end{aligned}$$
(17)
Whenever \(e_0=k^2\), \(e_1=-\left( k^2+1\right)\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \frac{\alpha }{4 a \left( k^2+1\right) } {{\,\mathrm{ds}\,}}^2x {{\,\mathrm{cn}\,}}^2x \exp \left[ -i \left( \gamma +5 \alpha \left( k^2+1\right) +\frac{12 \alpha k^2}{k^2+1} \right) t \right] \end{aligned}$$
(18)
or
$$\begin{aligned} q(x,t)= \frac{\alpha \left( 1-k^2\right) ^2 }{4 a \left( k^2+1\right) } \text{ sc}^2x {{\,\mathrm{nd}\,}}^2x \exp \left[ -i \left( \gamma +5 \alpha \left( k^2+1\right) +\frac{12 \alpha k^2}{k^2+1} \right) t \right] . \end{aligned}$$
(19)
In the case of \(e_0=1\), \(e_1=2k^2-1\), \(e_2=k^2\left( k^2 -1 \right)\),
$$\begin{aligned} q(x,t)= -\frac{\alpha }{4 a \left( 2k^2-1 \right) } {{\,\mathrm{cd}\,}}^4x {{\,\mathrm{ns}\,}}^2x \exp \left[ i \left( -\gamma +5 \alpha \left( 2k^2-1 \right) +\frac{12 \alpha k^2\left( k^2 -1 \right) }{2k^2-1} \right) t \right] . \end{aligned}$$
(20)
For the case \(e_0=\frac{k^2 }{4}\), \(e_1=\frac{1}{2}\left( k^2 -2\right)\), \(e_2=\frac{1}{4}\),
$$\begin{aligned} q(x,t)= -\frac{\alpha }{2 a \left( k^2 -2\right) } {{\,\mathrm{cs}\,}}^2x \exp \left[ i \left( -\gamma + \frac{5 \alpha \left( k^2 -2\right) }{2} +\frac{3 \alpha k^2}{2 \left( k^2 -2\right) } \right) t \right] . \end{aligned}$$
(21)
If \(e_0=\frac{k^2 }{4}\), \(e_1=\frac{1}{2}\left( k^2 -2\right)\), \(e_2=\frac{k^2}{4}\),
$$\begin{aligned} q(x,t)= \frac{\alpha }{2 a \left( k^2 -2\right) } {{\,\mathrm{dn}\,}}^2x \exp \left[ i \left( -\gamma + \frac{5 \alpha \left( k^2 -2\right) }{2} +\frac{3 \alpha k^4}{2 \left( k^2 -2\right) } \right) t \right] . \end{aligned}$$
(22)
Here, the solutions from (14) to (22) represent JE function solutions to the model.
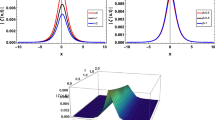
Next, for \(e_0=0\), \(e_1=1\), \(e_2=-1\), dark soliton (Fig. 1) is
$$\begin{aligned} q(x,t)= -\frac{\alpha }{4 a } \tanh ^2x \exp \left[ i \left( -\gamma +5 \alpha \right) t \right] . \end{aligned}$$
(23)
When \(e_0=0\), \(e_1=1\), \(e_2=1\), singular soliton is
$$\begin{aligned} q(x,t)= -\frac{\alpha }{4 a } \coth ^2x \exp \left[ i \left( -\gamma +5 \alpha \right) t \right] . \end{aligned}$$
(24)
Finally, if \(e_0=0\), \(e_1=-1\), \(e_2=1\), periodic solution is
$$\begin{aligned} q(x,t)= \frac{\alpha }{4 a } \tan ^2x \exp \left[ -i \left( \gamma + 5 \alpha \right) t \right] . \end{aligned}$$
(25)
Similarly, plugging (12) into (10) and utilizing (2) gives
$$\begin{aligned} q(x,t)=\left\{ -\frac{\alpha }{a} + \frac{\alpha }{a e_1} \left( \frac{G'}{G}\right) ^2 \right\} \exp \left[ -i \left( \gamma +12 \alpha e_1 \right) t \right] \end{aligned}$$
(26)
and then one gets the following solutions:
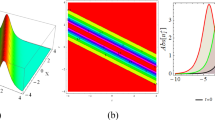
For \(e_0=0\), \(e_1=1\), \(e_2=-1\), bright soliton (Fig. 2) is
$$\begin{aligned} q(x,t)= -\frac{\alpha }{a} {{\,\mathrm{sech}\,}}^2 x \exp \left[ -i \left( \gamma +12 \alpha \right) t \right] . \end{aligned}$$
(27)
If \(e_0=0\), \(e_1=1\), \(e_2=1\), other type of singular soliton emerges as
$$\begin{aligned} q(x,t)= \frac{\alpha }{a} {{\,\mathrm{csch}\,}}^2 x \exp \left[ -i \left( \gamma +12 \alpha \right) t \right] . \end{aligned}$$
(28)
When \(e_0=0\), \(e_1=-1\), \(e_2=1\), periodic wave is
$$\begin{aligned} q(x,t)= -\frac{\alpha }{a} \sec ^2 x \exp \left[ -i \left( \gamma -12 \alpha \right) t \right] . \end{aligned}$$
(29)
2.2 Power law
Power law is formulated as
$$\begin{aligned} F(s)=s^m . \end{aligned}$$
(30)
Then Eq. (1) changes to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + b \left| q \right| ^{2m} q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(31)
When \(n=m\), (31) can be integrated. Thus, (31) simplifies to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{m} q\right) _{xx} + b \left| q \right| ^{2m} q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(32)
and Eq. (3) changes to
$$\begin{aligned}&- (\gamma +\lambda )\phi ^2 +b \phi ^{2 m+2} -2 (\alpha -2 \beta ) \left( \phi ^{\prime }\right) ^2 +a m (m+1) \phi ^m \left( \phi ^{\prime }\right) ^2 \nonumber \\&\quad -2 \alpha \phi \phi ^{\prime \prime } +a (m+1) \phi ^{m+1} \phi ^{\prime \prime } =0 . \end{aligned}$$
(33)
Set
$$\begin{aligned} \phi = \varphi ^{\frac{2}{m}} \end{aligned}$$
(34)
so that Eq. (33) transforms to
$$\begin{aligned}&-m^2 (\gamma +\lambda ) \varphi ^2 +b m^2 \varphi ^6 +4 (4 \beta +\alpha (m-4)) \left( \varphi ^{\prime }\right) ^2 +2 a \left( m^2+3 m+2\right) \varphi ^2 \left( \varphi ^{\prime }\right) ^2 \nonumber \\&\quad -4 \alpha m \varphi \varphi ^{\prime \prime } +2 am (m+1) \varphi ^3 \varphi ^{\prime \prime } =0 . \end{aligned}$$
(35)
Balance principle causes \(N=1\). Then Eq. (8) becomes
$$\begin{aligned} \varphi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) . \end{aligned}$$
(36)
Proceeding as in the case of Kerr law, one has the solution set as:
$$\begin{aligned} \begin{array}{c} \displaystyle b= \frac{2 a^2 e_1 (m+1)^3 (3 m+2)}{\alpha m^3}, \quad \alpha _0= 0, \quad \alpha _1= \frac{1}{m+1} \sqrt{-\frac{\alpha m}{a e_1}}, \\ \\ \displaystyle \beta = \alpha -\frac{\alpha m}{4}, \quad \gamma = \frac{2 \alpha e_1^2 (3 m+2)+8 \alpha e_0 e_2 (m+2)-e_1 \lambda m (m+1)}{e_1 m (m+1)} . \end{array} \end{aligned}$$
(37)
Substituting (37) into (36) and employing (2) gives
$$\begin{aligned} q(x,t)= \left\{ \frac{1}{m+1} \sqrt{-\frac{\alpha m}{a e_1}} \left( \frac{G^{\prime }}{G}\right) \right\} ^\frac{2}{m} e^{ i \lambda t } \end{aligned}$$
(38)
and thus, the solutions to (32) are derived as:
For \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \left\{ \frac{1}{m+1} \sqrt{\frac{\alpha m}{a \left( k^2+1\right) }} {{\,\mathrm{cs}\,}}x {{\,\mathrm{dn}\,}}x \right\} ^\frac{2}{m} e^{ i \lambda t } \end{aligned}$$
(39)
or
$$\begin{aligned} q(x,t)= \left\{ \frac{k^2-1}{m+1} \sqrt{\frac{\alpha m}{a \left( k^2+1\right) }} \text{ sc }\; x {{\,\mathrm{nd}\,}}x \right\} ^\frac{2}{m} e^{ i \lambda t } . \end{aligned}$$
(40)
If \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{1}{m+1} \sqrt{\frac{\alpha m}{a \left( 1-2k^2 \right) }} \text{ sc }\; x {{\,\mathrm{dn}\,}}x \right\} ^\frac{2}{m} e^{ i \lambda t } . \end{aligned}$$
(41)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{k^2}{m+1} \sqrt{\frac{\alpha m}{a \left( k^2 -2 \right) }} {{\,\mathrm{sd}\,}}x {{\,\mathrm{cn}\,}}x \right\} ^\frac{2}{m} e^{ i \lambda t } . \end{aligned}$$
(42)
Whenever \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{1}{m+1} \sqrt{-\frac{\alpha m}{a }} \tanh x \right\} ^\frac{2}{m} e^{ i \lambda t } . \end{aligned}$$
(43)
Finally, for \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{1}{m+1} \sqrt{-\frac{\alpha m}{a }} \coth x \right\} ^\frac{2}{m} e^{ i \lambda t } . \end{aligned}$$
(44)
Here, the solutions (40)–(42) stands for JE function solutions, while the solutions (43) and (44) are respectively dark and singular solitons.
2.3 Parabolic law
For this law,
$$\begin{aligned} F(s)=b_1 s + b_2 s^{2} \end{aligned}$$
(45)
with the constants \(b_1\) and \(b_2\). Then (1) changes to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx}+ \left( b_1\left| q \right| ^{2}+b_2\left| q \right| ^{4}\right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(46)
When \(n=2\), (46) can be integrated. Thus, (46) simplifies to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{2} q\right) _{xx}+ \left( b_1\left| q \right| ^{2}+b_2\left| q \right| ^{4}\right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(47)
and Eq. (3) becomes
$$\begin{aligned} -(\gamma + \lambda ) \phi ^2 + b_ 1\phi ^4 + b_ 2\phi ^6 -2 (\alpha -2 \beta ) \left( \phi ^{\prime }\right) ^2 +6a \phi ^2 \left( \phi ^{\prime }\right) ^2 -2 \alpha \phi \phi ^{\prime \prime } +3a \phi ^{3} \phi ^{\prime \prime } =0. \end{aligned}$$
(48)
Balance principle causes \(N=1\). Then Eq. (8) becomes
$$\begin{aligned} \phi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) . \end{aligned}$$
(49)
Proceeding as in previous sections, the results procured are:
$$\begin{aligned} \begin{array}{c} \displaystyle b_2= \frac{3 a \left( 18 a e_1-b_1\right) }{\alpha }, \quad \alpha _0= 0, \quad \alpha _1= \frac{2 \sqrt{\alpha }}{\sqrt{b_1-18 a e_1}}, \\ \\ \displaystyle \beta = \frac{\alpha }{2}, \quad \gamma = \frac{6 a \left( 8 \alpha e_1^2+16 \alpha e_0 e_2-3 e_1 \lambda \right) +b_1 \left( \lambda -4 \alpha e_1\right) }{18 a e_1-b_1} . \end{array} \end{aligned}$$
(50)
Substituting (50) into (49) and employing (2) gives
$$\begin{aligned} q(x,t)=\ \frac{2 \sqrt{\alpha }}{\sqrt{ b_1-18 \alpha e_1} } \left( \frac{G^{\prime }}{G}\right) e^{ i \lambda t } \end{aligned}$$
(51)
and thus, the solutions to (47) are found as:
For \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \frac{2 \sqrt{\alpha }}{\sqrt{ b_1 + 18 \alpha \left( k^2+1\right) } } \text{ cs }\; x {{\,\mathrm{dn}\,}}x \, e^{ i \lambda t } \end{aligned}$$
(52)
or
$$\begin{aligned} q(x,t)= -\frac{2 \left( 1-k^2\right) \sqrt{\alpha }}{\sqrt{ b_1 + 18 \alpha \left( k^2+1\right) } } \text{ sc }\; x {{\,\mathrm{nd}\,}}x \, e^{ i \lambda t }. \end{aligned}$$
(53)
If \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= -\frac{2 \sqrt{\alpha }}{\sqrt{ b_1-18 \alpha \left( 2k^2-1\right) } } \text{ sc }\; x {{\,\mathrm{dn}\,}}x \, e^{ i \lambda t }. \end{aligned}$$
(54)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= -\frac{2 k^2\sqrt{\alpha }}{\sqrt{ b_1-18 \alpha \left( 2-k^2\right) } } \text{ sd }\; x {{\,\mathrm{cn}\,}}x \, e^{ i \lambda t } . \end{aligned}$$
(55)
Whenever \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= -\frac{2 \sqrt{\alpha }}{\sqrt{ b_1-18 \alpha } } \tanh x \, e^{ i \lambda t } . \end{aligned}$$
(56)
Finally, when \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= -\frac{2 \sqrt{\alpha }}{\sqrt{ b_1-18 \alpha } } \coth x \, e^{ i \lambda t } . \end{aligned}$$
(57)
Here, JE function solutions are represented by Eqs. (52)–(55), while dark and singular solitons are respectively indicated in Eqs. (56) and (57).
2.4 Dual-power law
This law occurs when
$$\begin{aligned} F(s)= b_1 s^m + b_2 s^{2m} \end{aligned}$$
(58)
with the constants \(b_1\) and \(b_2\). Thus, (1) changes to
$$\begin{aligned}&iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( b_1 \left| q \right| ^{2m}+ \ b_2 \left| q \right| ^{4m}\right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} \right. \nonumber \\&\quad \left. - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(59)
For the integration of Eq. (59), \(n=2m\) is selected. Thus, (59) simplifies to
$$\begin{aligned}&iq_{t} + a \left( \left| q \right| ^{2m} q\right) _{xx} + \left( b_1 \left| q \right| ^{2m}+ \ b_2 \left| q \right| ^{4m}\right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} \right. \nonumber \\&\quad \left. - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(60)
and (3) reduces to
$$\begin{aligned} \begin{array}{c} \displaystyle -(\gamma +\lambda ) \phi ^2 +b_1 \phi ^{2m+2} +b_2 \phi ^{4m+2} -2 (\alpha -2 \beta ) \left( \phi ^{\prime }\right) ^2 +2 a m (2 m+1) \phi ^{2 m} \left( \phi ^{\prime }\right) ^2 \\ \quad -2 \alpha \phi \phi ^{\prime \prime } +a (2 m+1) \phi ^{2 m+1} \phi ^{\prime \prime } =0 . \end{array} \end{aligned}$$
(61)
Set
$$\begin{aligned} \phi = \varphi ^{\frac{1}{m}}. \end{aligned}$$
(62)
Then Eq. (61) becomes
$$\begin{aligned}&-m^2 \left( \gamma + \lambda \right) \varphi ^2 + b_1 m^2 \varphi ^4+ b_2 m^2 \varphi ^6+ 2 \left( \alpha \left( m-2\right) + 2 \beta \right) \left( \varphi ^{\prime } \right) ^{2} \nonumber \\&+a \left( 2m ^2 + 3m + 1 \right) \varphi ^2 \left( \varphi ^{\prime } \right) ^{2} -2 m \alpha \varphi \varphi ^{\prime \prime } + am \left( 2m+1 \right) \varphi ^3 \varphi ^{\prime \prime } =0 . \end{aligned}$$
(63)
Balance principle causes \(N=1\). In this case, Eq. (8) reads as
$$\begin{aligned} \varphi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) . \end{aligned}$$
(64)
Following the path in the previous sections yields
$$\begin{aligned} \begin{array}{c} \displaystyle b_1=-\frac{4 b_2 \alpha m}{a \left( 6 m^2+5m+1 \right) }+ \frac{2 a (2 m+1)^2 e_1}{m^2}, \quad \alpha _0=0, \quad \alpha _1= \frac{\sqrt{-a (m (6 m+5)+1)}}{ m \sqrt{b_2}}, \\ \beta = \alpha -\frac{\alpha m }{2}, \quad \\ \\ \displaystyle \gamma =\frac{m^3 b_2 \left( 4 \alpha e_1 -m \lambda \right) -\left( m+1 \right) \left( 3m+1 \right) \left( 2 a m+a \right) ^2 \left( e_1^2-4 e_0 e_2\right) }{m^4 b_2 } . \end{array} \end{aligned}$$
(65)
Putting (65) into (64) and utilizing (2) leads to
$$\begin{aligned} q(x,t)= \left\{ \frac{\sqrt{-a (m (6 m+5) + 1)}}{m \sqrt{b_2} } \left( \frac{G'}{G}\right) \right\} ^\frac{1}{m} e^{ i \lambda t } \end{aligned}$$
(66)
and as a consequence, Eq. (60) possess the following solutions:
If \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \left\{ \frac{\sqrt{-a (m (6 m+5)+1)}}{m \sqrt{b_2} } {{\,\mathrm{cs}\,}}x {{\,\mathrm{dn}\,}}x \right\} ^\frac{1}{m} e^{ i \lambda t } \end{aligned}$$
(67)
or
$$\begin{aligned} q(x,t)= \left\{ -\frac{\left( 1-k^2 \right) \sqrt{-a (m (6 m+5)+1)}}{m \sqrt{b_2} } \text{ sc } \, x {{\,\mathrm{nd}\,}}x \right\} ^\frac{1}{m} e^{ i \lambda t }. \end{aligned}$$
(68)
For \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= \left\{ - \frac{\sqrt{-a (m (6 m+5)+1)}}{m \sqrt{b_2} } \text{ sc } x {{\,\mathrm{dn}\,}}x \right\} ^\frac{1}{m} e^{ i \lambda t }. \end{aligned}$$
(69)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{k^2 \sqrt{-a (m (6 m+5)+1)}}{m \sqrt{b_2} } {{\,\mathrm{sd}\,}}x {{\,\mathrm{cn}\,}}x \right\} ^\frac{1}{m} e^{ i \lambda t } . \end{aligned}$$
(70)
Whenever \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{\sqrt{-a (m (6 m+5)+1)}}{m \sqrt{b_2} } \tanh x \right\} ^\frac{1}{m} e^{ i \lambda t }. \end{aligned}$$
(71)
In the case of \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{\sqrt{-a (m (6 m+5) + 1)}}{m \sqrt{b_2} } \coth x \right\} ^\frac{1}{m} e^{ i \lambda t }. \end{aligned}$$
(72)
Here, JE function solutions are stood for by Eqs. (67)–(70), while dark and singular solitons are respectively given in Eqs. (71) and (72).
2.5 Quadratic-cubic law
This nonlinear form arises when
$$\begin{aligned} F(s)=b_{1}\sqrt{s}+b_{2}s \end{aligned}$$
(73)
with the constants \(b_1\) and \(b_2\). Thus, the model (1) becomes
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( b_1 \left| q \right| + b_2 \left| q \right| ^2 \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(74)
Picking \(n=1\), Eq. (74) can be integrated. Thus, (74) modifies to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| q\right) _{xx} + \left( b_1 \left| q \right| + b_2 \left| q \right| ^2 \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(75)
and Eq. (3) reduces to
$$\begin{aligned} - \left( \gamma +\lambda \right) \phi ^2+b_1 \phi ^3+ b_2 \phi ^4- 2 (\alpha -2 \beta ) \left( \phi ^{\prime }\right) ^2+2a \phi \left( \phi ^{\prime }\right) ^2-2\alpha \phi \phi ^{\prime \prime } +2 a \phi ^2 \phi ^{\prime \prime } =0 . \end{aligned}$$
(76)
Balance principle causes \(N=2\). Then Eq. (8) becomes
$$\begin{aligned} \phi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) + \alpha _2\left( \frac{G^{\prime }}{G}\right) ^2 . \end{aligned}$$
(77)
Proceeding as in previous sections, one secures two solution set as
$$\begin{aligned}&\begin{array}{c} \displaystyle b_1= -\frac{2 \alpha b_2}{5 a}+32 a e_1, \quad \alpha _0= 0, \quad \alpha _1= 0, \quad \alpha _2= -\frac{20 a}{b_2}, \\ \\ \displaystyle \beta = \frac{3 \alpha }{4}, \quad \lambda =\frac{b_2 \left( 8 \alpha e_1 - \gamma \right) +240 a^2 \left( 4 e_0 e_2-e_1^2\right) }{b_2} . \end{array} \end{aligned}$$
(78)
$$\begin{aligned}&\begin{array}{c} \displaystyle e_0= 0, \quad \alpha _0= \frac{20 a e_1}{b_2}, \quad \alpha _1= 0, \quad \alpha _2= -\frac{20 a}{b_2}, \\ \\ \displaystyle \beta = \frac{5 \left( a \left( 16 a e_1+b_1\right) +\alpha b_2\right) }{4 b_2}, \quad \lambda =\frac{20 a e_1 \left( 16 a e_1+b_1\right) -b_2 \left( \gamma -4 \alpha e_1\right) }{b_2} . \end{array} \end{aligned}$$
(79)
Substituting (78) into (77) and employing (2) gives
$$\begin{aligned} q(x,t)= -\frac{20a}{b_2} \left( \frac{G'}{G}\right) ^2 \exp \left[ i \left( \frac{b_2 \left( 8 \alpha e_1 - \gamma \right) +240 a^2 \left( 4 e_0 e_2-e_1^2\right) }{b_2} \right) t \right] \end{aligned}$$
(80)
and consequently, the solutions for the governing model (75) are:
For \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= -\frac{20a}{b_2} {{\,\mathrm{cs}\,}}^2x {{\,\mathrm{dn}\,}}^2x\ \exp \left[ -i \left( \frac{b_2 \left( 8 \alpha k^2+8 \alpha +\gamma \right) +240 a^2 \left( k^4-2k^2+1\right) }{b_2} \right) t \right] \end{aligned}$$
(81)
or
$$\begin{aligned} q(x,t)= -\frac{20 a\left( 1-k^2\right) ^2}{b_2} \text{ sc}^2x {{\,\mathrm{nd}\,}}^2x \exp \left[ - i \left( \frac{b_2 \left( 8 \alpha k^2+8 \alpha +\gamma \right) +240 a^2 \left( k^4-2k^2+1\right) }{b_2} \right) t \right] . \end{aligned}$$
(82)
If \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= - \frac{20a}{b_2} \text{ sc}^2x {{\,\mathrm{dn}\,}}^2 x \exp \left[ i \left( \frac{b_2 \left( 16 \alpha k^2- 8 \alpha -\gamma \right) -240 a^2 }{b_2} \right) t \right] . \end{aligned}$$
(83)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= -\frac{20ak^4}{b_2} \ {{\,\mathrm{sd}\,}}^2x {{\,\mathrm{cn}\,}}^2x \exp \left[ - i \left( \frac{b_2 \left( 8 \alpha k^2 - 16 \alpha + \gamma \right) +240 a^2 k^4 }{b_2} \right) t \right] . \end{aligned}$$
(84)
For the case \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= -\frac{20a}{b_2} \tanh ^2 x \exp \left[ i \left( \frac{b_2 \left( 8 \alpha - \gamma \right) -240 a^2 }{b_2} \right) t \right] . \end{aligned}$$
(85)
In the case of \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= -\frac{20a}{b_2} \coth ^2 x \exp \left[ i \left( \frac{b_2 \left( 8 \alpha - \gamma \right) -240 a^2 }{b_2} \right) t \right] . \end{aligned}$$
(86)
Here, the solutions given by Eqs. (81)–(84) are JE function solutions, while the solutions mentioned in Eqs. (85) and (86) are dark and singular solitons, respectively.
Similarly, inserting (79) into (77) and using (2) gives rise to
$$\begin{aligned} q(x,t)= \left\{ \frac{20 a e_1}{b_2}-\frac{20 a}{b_2} \left( \frac{G^{\prime }}{G}\right) ^2 \right\} \exp \left[ i \left( \frac{20 a e_1 \left( 16 a e_1+b_1\right) -b_2 \left( \gamma -4 \alpha e_1\right) }{b_2} \right) t \right] \end{aligned}$$
(87)
and hence, the solutions are listed as follows:
For \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \frac{20 a }{b_2} {{\,\mathrm{sech}\,}}^2 x \exp \left[ i \left( \frac{20 a \left( 16 a +b_1\right) -b_2 \left( \gamma -4 \alpha \right) }{b_2} \right) t \right] . \end{aligned}$$
(88)
If \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= - \frac{20 a }{b_2}{{\,\mathrm{csch}\,}}^2 x \exp \left[ i \left( \frac{20 a \left( 16 a +b_1\right) -b_2 \left( \gamma -4 \alpha \right) }{b_2} \right) t \right] . \end{aligned}$$
(89)
When \(e_0=0\), \(e_1=-1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= - \frac{20 a }{b_2}\sec ^2 x \exp \left[ i \left( \frac{20 a \left( 16 a -b_1\right) -b_2 \left( \gamma +4 \alpha \right) }{b_2} \right) t \right] . \end{aligned}$$
(90)
Here, bright and singular solitons are respectively given by Eqs. (88) and (89), while periodic wave is given Eq. (90).
2.6 Log law
In the case of this law,
$$\begin{aligned} F(s)=\ln s . \end{aligned}$$
(91)
Then Eq. (1) changes to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + 2 b q \ln \left| q \right| = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(92)
and Eq. (3) modifies to
$$\begin{aligned}&- \left( \gamma +\lambda \right) \phi ^2 +2b \phi ^2 \ln \left| \phi \right| -2 (\alpha -2 \beta ) \left( \phi ^{\prime } \right) ^2 +a n (n+1) \phi ^n \left( \phi ^{\prime } \right) ^2\nonumber \\&\quad -2 \alpha \phi \phi ^{\prime \prime } + a (n+1) \phi ^{n+1} \phi ^{\prime \prime } =0. \end{aligned}$$
(93)
Employing
$$\begin{aligned} \phi = \exp \frac{1}{\varphi } \end{aligned}$$
(94)
one transforms Eq. (93) into
$$\begin{aligned}&2 b \varphi ^3 - (\gamma +\lambda ) \varphi ^4 + \left( a (n+1)^2 e^{\frac{n}{\varphi }}-4 \alpha +4 \beta \right) \left( \varphi ^{\prime } \right) ^2 - \left( a (n+1) e^{\frac{n}{\varphi }}-2 \alpha \right) \varphi ^2\varphi ^{\prime \prime } \nonumber \\&\quad +2 \left( a (n+1) e^{\frac{n}{\varphi }}-2 \alpha \right) \varphi \left( \varphi ^{\prime } \right) ^2 =0 . \end{aligned}$$
(95)
To carry out the integration, \(n=0\) must be selected. Therefore, Eq. (92) falls in
$$\begin{aligned} iq_{t} + a q_{xx} + 2 b q \ln \left| q \right| = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(96)
and Eq. (95) modifies to
$$\begin{aligned} 2 b \varphi ^3-(\gamma +\lambda ) \varphi ^4+(a-4 \alpha +4 \beta ) \left( \varphi ^{\prime }\right) ^2 + 2 (a-2 \alpha ) \varphi \left( \varphi ^{\prime }\right) ^2-(a-2 \alpha ) \varphi ^2 \varphi ^{\prime \prime } =0 . \end{aligned}$$
(97)
Balance principle causes \(N=2\). Then Eq. (8) becomes
$$\begin{aligned} \varphi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) + \alpha _2 \left( \frac{G^{\prime }}{G}\right) ^2 \end{aligned}$$
(98)
and then, proceeding as in previous sections, one has
$$\begin{aligned} \begin{array}{c} \displaystyle b= 2 e_1 (2 \alpha -a), \quad e_0=0, \quad \alpha _0= -\alpha _2 e_1, \quad \alpha _1= 0, \quad \displaystyle \beta = \alpha -\frac{a}{4}, \quad \lambda = \frac{2 (a-2 \alpha )}{\alpha _2}-\gamma . \end{array} \end{aligned}$$
(99)
Substituting (99) into (98) and employing (2) gives
$$\begin{aligned} q(x,t)= \exp \left[ - \alpha _2 e_1+ \alpha _2 \left( \frac{G^{\prime }}{G}\right) ^2 \right] ^{-1} \exp \left[ i \left( \frac{2 (a-2 \alpha )}{\alpha _2}-\gamma \right) t \right] \end{aligned}$$
(100)
and consequently, Gaussian solitary waves to the model adopted (96) are listed as below:
If \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \exp \left[ -\alpha _2 {{\,\mathrm{sech}\,}}^2 x \right] ^{-1} \exp \left[ i \left( \frac{2 (a-2 \alpha )}{\alpha _2}-\gamma \right) t \right] . \end{aligned}$$
(101)
For \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \exp \left[ \alpha _2 {{\,\mathrm{csch}\,}}^2 x \right] ^{-1} \exp \left[ i \left( \frac{2 (a-2 \alpha )}{\alpha _2}-\gamma \right) t \right] . \end{aligned}$$
(102)
When \(e_0=0\), \(e_1=-1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \exp \left[ \alpha _2 \sec ^2 x \right] ^{-1} \exp \left[ i \left( \frac{2 (a-2 \alpha )}{\alpha _2}-\gamma \right) t \right] . \end{aligned}$$
(103)
2.7 Anti-cubic law
In the case of the type of this nonlinearity,
$$\begin{aligned} F(s)=\frac{b_{1}}{s^{2}}+b_{2}s+b_{3}s^{2} \end{aligned}$$
(104)
where \(b_j\) for \(j=1, 2, 3\) are constants. Then Eq. (1) changes to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( \frac{b_1}{ \left| q \right| ^{4}} + b_2 \left| q \right| ^{2}+ b_3 \left| q \right| ^{4}\right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(105)
When \(n=2\), Eq. (105) can be integrated. Thus, Eq. (105) simplifies to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{2} q\right) _{xx} + \left( \frac{b_1}{ \left| q \right| ^{4}} + b_2 \left| q \right| ^{2}+ b_3 \left| q \right| ^{4}\right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(106)
and Eq. (3) modifies to
$$\begin{aligned} b_1 \phi ^{-2}- \left( \gamma +\lambda \right) \phi ^2 +b_2 \phi ^{4}+b_3 \phi ^{6} -2 (\alpha -2 \beta ) \left( \phi ^{\prime } \right) ^2 +6a \phi ^2 \left( \phi ^{\prime } \right) ^2 -2 \alpha \phi \phi ^{\prime \prime } +3a \phi ^{3} \phi ^{\prime \prime } =0. \end{aligned}$$
(107)
Balance principle causes \(N=1\). Then Eq. (8) becomes
$$\begin{aligned} \phi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) \end{aligned}$$
(108)
and then, following the same path as in previous sections leads to
$$\begin{aligned} \begin{array}{c} \displaystyle b_1= 0, \quad b_3= \frac{3 a \left( 18 a e_1-b_2\right) }{\alpha }, \quad \alpha _0= 0, \quad \alpha _1= \frac{2 \sqrt{\alpha }}{\sqrt{b_2-18 a e_1}}, \\ \\ \displaystyle \beta = \frac{\alpha }{2}, \quad \gamma = \frac{6 a \left( 8 \alpha e_1^2+16 \alpha e_0 e_2-3 e_1 \lambda \right) +b_2 \left( \lambda -4 \alpha e_1\right) }{18 a e_1-b_2}. \end{array} \end{aligned}$$
(109)
Plugging (109) into (108) and utilizing (2) yields
$$\begin{aligned} q(x,t)= \frac{2 \sqrt{\alpha }}{\sqrt{b_2-18 a e_1}} \left( \frac{G^{\prime }}{G}\right) e^{ i \lambda t } . \end{aligned}$$
(110)
Since \(b_1 = 0\) from the solution set (109), this form of the nonlinearity collapses to parabolic law nonlinear media. Also, because the solution (110) is the same as that of in case of parabolic law. Hence, the solutions that will be recovered are omitted.
2.8 Polynomial law
For nonlinear form
$$\begin{aligned} F(s)=b_{1}s+b_{2}s^2+b_{3}s^{3} \end{aligned}$$
(111)
where \(b_j\) for \(j=1, 2, 3\) are constants. Therefore, (1) changes to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( b_1 \left| q \right| ^{2}+ b_2 \left| q \right| ^{4}+ b_3 \left| q \right| ^{6} \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(112)
In the case of \(n=4\), the integration of Eq. (112) can be performed. Then Eq. (112) condenses to:
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{4} q\right) _{xx} + \left( b_1 \left| q \right| ^{2}+ b_2 \left| q \right| ^{4}+ b_3 \left| q \right| ^{6} \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(113)
and Eq. (3) simplifies to
$$\begin{aligned} - \left( \gamma +\lambda \right) \phi ^2 + b_1 \phi ^4+ b_2 \phi ^6+ b_3 \phi ^8 -2 (\alpha -2 \beta ) \left( \phi ^{\prime } \right) ^2 +20a\phi ^4 \left( \phi ^{\prime } \right) ^2 -2 \alpha \phi \phi ^{\prime \prime } +5a \phi ^{5} \phi ^{\prime \prime } =0. \end{aligned}$$
(114)
Balance principle causes \(N=1\). Then Eq. (8) becomes
$$\begin{aligned} \phi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) \end{aligned}$$
(115)
and following the same path in the previous sections leads to
$$\begin{aligned} \begin{array}{c} \displaystyle b_1= \frac{4 \left( \alpha -5 a \alpha _1^4 \left( e_1^2-4 e_0 e_2\right) \right) }{\alpha _1^2},\quad b_2= 50 a e_1, \quad b_3= -\frac{30 a}{\alpha _1^2}, \quad \alpha _0= 0,\\ \displaystyle \beta = \frac{\alpha }{2}, \quad \lambda = 4 \alpha e_1-\gamma . \end{array} \end{aligned}$$
(116)
Substituting (116) into (115) and employing (2) gives
$$\begin{aligned} q(x,t)= \alpha _1 \left( \frac{G^{\prime }}{G}\right) \exp \left[ i \left( 4 \alpha e_1-\gamma \right) t \right] \end{aligned}$$
(117)
and consequently, one possess the solutions for Eq. (113) as follows:
For \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \alpha _1 {{\,\mathrm{cs}\,}}x {{\,\mathrm{dn}\,}}x \exp \left[ - i \left( 4 \alpha \left( k^2+1 \right) +\gamma \right) t \right] \end{aligned}$$
(118)
or
$$\begin{aligned} q(x,t)= \alpha _1 \left( k^2-1 \right) \text{ sc }\, x {{\,\mathrm{nd}\,}}x \exp \left[ - i \left( 4 \alpha \left( k^2+1 \right) +\gamma \right) t \right] . \end{aligned}$$
(119)
If \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= - \alpha _1 \text{ sc }\; x {{\,\mathrm{dn}\,}}x \exp \left[ i \left( 4 \alpha \left( 2k^2-1 \right) -\gamma \right) t \right] . \end{aligned}$$
(120)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= - \alpha _1 k^2 {{\,\mathrm{sd}\,}}x {{\,\mathrm{cn}\,}}x \exp \left[ i \left( 4 \alpha \left( 2-k^2 \right) -\gamma \right) t \right] . \end{aligned}$$
(121)
Whenever \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= - \alpha _1 \tanh x \exp \left[ i \left( 4 \alpha -\gamma \right) t \right] . \end{aligned}$$
(122)
Finally, when \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= - \alpha _1 \coth x \exp \left[ i \left( 4 \alpha -\gamma \right) t \right] . \end{aligned}$$
(123)
Here, JE function solutions are represented by from (118) to (121), while dark and singular solitons are introduced in Eqs. (122) and (123), respectively.
2.9 Triple power law
For this media,
$$\begin{aligned} F(s)=b_{1}s^m+b_{2}s^{2m}+b_{3}s^{3m} \end{aligned}$$
(124)
where \(b_j\) for \(j=1, 2, 3\) are constants. Thus, (1) changes to
$$\begin{aligned}&iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( b_1 \left| q \right| ^{2m}+ b_2 \left| q \right| ^{4m}+ b_3 \left| q \right| ^{6m} \right) q \nonumber \\&\quad = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(125)
By taking \(n=4m\), one can integrate Eq. (125). Then, Eq. (125) reads as
$$\begin{aligned}&iq_{t} + a \left( \left| q \right| ^{4m} q\right) _{xx} + \left( b_1 \left| q \right| ^{2m}+ b_2 \left| q \right| ^{4m}+ b_3 \left| q \right| ^{6m} \right) q \nonumber \\&\quad = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(126)
and (3) reduces to
$$\begin{aligned}&- (\gamma +\lambda )\phi ^2 +b_1 \phi ^{2 m+2} +b_2 \phi ^{4 m+2} +b_3 \phi ^{6 m+2} -2 \left( \alpha - 2 \beta \right) \left( \phi ^{\prime } \right) ^2 \nonumber \\&+ 4am \left( 4m+1 \right) \phi ^ {4m} \left( \phi ^{\prime } \right) ^2 -2 \alpha \phi \phi ^{\prime \prime } + a \left( 4m+1 \right) \phi ^ {4m+1} \phi ^{\prime \prime } =0 . \end{aligned}$$
(127)
Setting
$$\begin{aligned} \phi = \varphi ^{\frac{1}{m}} \end{aligned}$$
(128)
Eq. (127) can be turned into
$$\begin{aligned}&-m^2 (\gamma +\lambda ) \varphi ^2 \displaystyle +b_1 m^2 \varphi ^4 +b_2 m^2 \varphi ^6 +b_3 m^2 \varphi ^8 +2 (\alpha (m-2) + 2 \beta ) \left( \varphi ^{\prime } \right) ^2 \nonumber \\&+ a \left( 12 m^2+7 m+1\right) \varphi ^4 \left( \varphi ^{\prime } \right) ^2 -2 m \alpha \varphi \varphi ^{\prime \prime } +a m (4 m+1) \varphi ^5 \varphi ^{\prime \prime } =0 . \end{aligned}$$
(129)
Balance principle causes \(N=1\). Then Eq. (8) becomes
$$\begin{aligned} \varphi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) \end{aligned}$$
(130)
and proceeding as in previous sections brings about
$$\begin{aligned} \begin{array}{c} \displaystyle b_1= \frac{4 \alpha m-a \alpha _1^4 \left( e_1^2-4 e_0 e_2\right) (3 m+1) (4 m+1)}{\alpha _1^2 m^2}, \quad b_2= \frac{2 a e_1 (4 m+1)^2}{m^2}, \\ b_3= -\frac{a (4 m+1) (5 m+1)}{\alpha _1^2 m^2}, \quad \\ \\ \displaystyle \alpha _0= 0, \quad \beta = \alpha -\frac{\alpha m}{2}, \quad \lambda = \frac{4 \alpha e_1}{m}-\gamma . \end{array} \end{aligned}$$
(131)
Putting (131) into (130) and utilizing (2) yields
$$\begin{aligned} q(x,t)= \left\{ \alpha _1 \left( \frac{G^{\prime }}{G}\right) \right\} ^ \frac{1}{m} \exp \left[ i \left( \frac{4 \alpha e_1}{m}-\gamma \right) t \right] \end{aligned}$$
(132)
and so, the solutions for the model under consideration (126) are extracted as the following:
For \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\), JE function solutions are
$$\begin{aligned} q(x,t)= \left\{ \alpha _1 {{\,\mathrm{cs}\,}}x {{\,\mathrm{dn}\,}}x \right\} ^ \frac{1}{m} \exp \left[ -i \left( \frac{4 \alpha \left( k^2+1\right) }{m}+\gamma \right) t \right] \end{aligned}$$
(133)
or
$$\begin{aligned} q(x,t)= \left\{ \alpha _1\left( k^2-1\right) \text{ sc }\; x {{\,\mathrm{nd}\,}}x \right\} ^ \frac{1}{m} \exp \left[ -i \left( \frac{4 \alpha \left( k^2+1\right) }{m}+\gamma \right) t \right] . \end{aligned}$$
(134)
If \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\), JE function solution is
$$\begin{aligned} q(x,t)= \left\{ -\alpha _1\text{ sc }\; x {{\,\mathrm{dn}\,}}x \right\} ^ \frac{1}{m} \exp \left[ i \left( \frac{4 \alpha \left( 2k^2-1\right) }{m}-\gamma \right) t \right] . \end{aligned}$$
(135)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\), JE function solution is
$$\begin{aligned} q(x,t)= \left\{ - \alpha _1 k^2 {{\,\mathrm{sd}\,}}x {{\,\mathrm{cn}\,}}x \right\} ^ \frac{1}{m} \exp \left[ i \left( \frac{4 \alpha \left( 2-k^2\right) }{m}-\gamma \right) t \right] . \end{aligned}$$
(136)
In the case of \(e_0=0\), \(e_1=1\), \(e_2=-1\), dark soliton is
$$\begin{aligned} q(x,t)= \left\{ - \alpha _1 \tanh x \right\} ^ \frac{1}{m} \exp \left[ i \left( \frac{4 \alpha }{m}-\gamma \right) t \right] . \end{aligned}$$
(137)
Finally, if \(e_0=0\), \(e_1=1\), \(e_2=1\), singular soliton is
$$\begin{aligned} q(x,t)= \left\{ - \alpha _1 \coth x \right\} ^ \frac{1}{m} \exp \left[ i \left( \frac{4 \alpha }{m}-\gamma \right) t \right] . \end{aligned}$$
(138)
2.10 Parabolic law medium with weak non-local nonlinearity
This nonlinear media arises when
$$\begin{aligned} F(s)=b_1s + b_2 s^{2} + b_3 s_{xx} \end{aligned}$$
(139)
where \(b_j\) for \(j=1, 2, 3\) are constants. Therefore Eq. (1) changes to
$$\begin{aligned}&iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( b_1 \left| q \right| ^{2}+ b_2 \left| q \right| ^{4}+ b_3 \left( \left| q \right| ^{2} \right) _{xx} \right) q \nonumber \\&\quad = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(140)
For the integration of Eq. (140), \(n=2\) is picked. Then Eq. (140) simplifies to
$$\begin{aligned}&iq_{t} + a \left( \left| q \right| ^{2} q\right) _{xx} + \left( b_1 \left| q \right| ^{2}+ b_2 \left| q \right| ^{4}+ b_3 \left( \left| q \right| ^{2} \right) _{xx} \right) q \nonumber \\&\quad = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(141)
and Eq. (3) changes to
$$\begin{aligned} - \left( \lambda + \gamma \right) \phi ^2 +b_1 \phi ^4 +b_2 \phi ^6 -2 (\alpha -2 \beta ) \left( \phi ^{\prime } \right) ^ {2} + 6a \phi ^2 \left( \phi ^{\prime } \right) ^ {2} -2 \alpha \phi \phi ^{\prime \prime } +3a \phi ^3 \phi ^{\prime \prime } =0 . \end{aligned}$$
(142)
Balance principle causes \(N=1\). Then Eq. (8) becomes
$$\begin{aligned} \phi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) \end{aligned}$$
(143)
and then one recovers the following results:
$$\begin{aligned}&\begin{array}{c} \displaystyle b_1= e_1 \left( 2 a-\frac{4 \alpha _1^2 b_2}{3} \right) +\frac{4 \alpha }{\alpha _1^2}, \quad b_3= -2 a-\frac{\alpha _1^2 b_2}{6} , \quad \alpha _0= 0, \quad \\ \\ \displaystyle \beta = \frac{\alpha }{2}, \quad \lambda = 2 a \alpha _1^2 \left( e_1^2-4 e_0 e_2\right) -\frac{\alpha _1^4 b_2 \left( e_1^2-4 e_0 e_2\right) }{3}-\gamma +4 \alpha e_1. \end{array} \end{aligned}$$
(144)
$$\begin{aligned}&\begin{array}{c} \displaystyle b_1= \frac{\alpha }{\alpha _1^2}-\frac{12 a e_1}{5}, \quad b_2= \frac{3 a}{5 \alpha _1^2}, \quad b_3= -\frac{21 a}{10}, \quad e_0=0, \quad \alpha _0= \alpha _1 \sqrt{e_1}, \\ \beta = \frac{5 \alpha }{4}, \quad \lambda = 4 \alpha e_1-\gamma . \end{array} \end{aligned}$$
(145)
Substituting (144) into (143) and using (2) yields
$$\begin{aligned} q(x,t)= \alpha _1 \left( \frac{G^{\prime }}{G}\right) \exp \left[ i \left( 2 a \alpha _1^2 \left( e_1^2-4 e_0 e_2\right) -\frac{\alpha _1^4 b_2 \left( e_1^2-4 e_0 e_2\right) }{3}-\gamma +4\alpha e_1 \right) t \right] \end{aligned}$$
(146)
and hence, the solutions to the governing equation (141) are:
If \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \alpha _1 {{\,\mathrm{cs}\,}}x {{\,\mathrm{dn}\,}}x \exp \left[ i \left( 2 a \alpha _1^2 \left( k^2-1\right) ^2 -\frac{\alpha _1^4 b_2 \left( k^2-1\right) ^2}{3} -\gamma -4 \alpha \left( k^2+1\right) \right) t \right] \end{aligned}$$
(147)
or
$$\begin{aligned} q(x,t)= \alpha _1 \left( k^2-1 \right) \text{ sc }\; x {{\,\mathrm{nd}\,}}x \exp \left[ i \left( 2 a \alpha _1^2 \left( k^2-1\right) ^2-\frac{\alpha _1^4 b_2 \left( k^2-1\right) ^2}{3} -\gamma -4 \alpha \left( k^2+1\right) \right) t \right] . \end{aligned}$$
(148)
For \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= - \alpha _1 \text{ sc }\; x {{\,\mathrm{dn}\,}}x \exp \left[ i \left( 2 a \alpha _1^2 -\frac{\alpha _1^4 b_2}{3} -\gamma +4 \alpha \left( 2k^2-1\right) \right) t \right] . \end{aligned}$$
(149)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= - \alpha _1 k^2 {{\,\mathrm{sd}\,}}x {{\,\mathrm{cn}\,}}x \exp \left[ i \left( 2 a \alpha _1^2 k^4 -\frac{\alpha _1^4 b_2 k^4}{3} -\gamma -4 \alpha \left( k^2-2\right) \right) t \right] . \end{aligned}$$
(150)
Here, the solutions (147)–(150) are JE function solutions.
Next, whenever \(e_0=0\), \(e_1=1\), \(e_2=-1\), dark soliton is
$$\begin{aligned} q(x,t)= - \alpha _1 \tanh x \exp \left[ i \left( 2 a \alpha _1^2 -\frac{\alpha _1^4 b_2}{3} -\gamma +4 \alpha \right) t \right] . \end{aligned}$$
(151)
Finally, for \(e_0=0\), \(e_1=1\), \(e_2=1\), singular soliton is
$$\begin{aligned} q(x,t)= - \alpha _1 \coth x \exp \left[ i \left( 2 a \alpha _1^2 -\frac{\alpha _1^4 b_2}{3} -\gamma +4 \alpha \right) t \right] . \end{aligned}$$
(152)
Similarly, plugging (145) into (143) and utilizing (2) gives rise to
$$\begin{aligned} q(x,t)= \alpha _1 \left\{ \sqrt{e_1} + \left( \frac{G'}{G}\right) \right\} \exp \left[ i \left( 4 \alpha e_1-\gamma \right) t \right] \end{aligned}$$
(153)
and then one has the solution as:
For \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \alpha _1 \left( 1 - \tanh x \right) \exp \left[ i \left( 4 \alpha -\gamma \right) t \right] . \end{aligned}$$
(154)
When \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \alpha _1 \left( 1 - \coth x \right) \exp \left[ i \left( 4 \alpha -\gamma \right) t \right] . \end{aligned}$$
(155)
If \(e_0=0\), \(e_1=-1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \alpha _1 \left( i + \tan x \right) \exp \left[ -i \left( 4 \alpha +\gamma \right) t \right] . \end{aligned}$$
(156)
2.11 Generalized anti-cubic law
For this nonlinear media,
$$\begin{aligned} F(s)= \frac{b_1}{s^{m+1}}+b_{2}s^{m}+b_{3}s^{m+1} \end{aligned}$$
(157)
where \(b_j\) for \(j=1, 2, 3\) are constants. Then Eq. (1) becomes to
$$\begin{aligned}&iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( \frac{b_1}{\left| q \right| ^{2m+2}} + b_2 \left| q \right| ^{2m} + b_3 \left| q \right| ^{2m+2} \right) q \nonumber \\&\quad = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(158)
To integrate Eq. (158), \(n=m+1\) is chosen. Thus, Eq. (158) simplifies to
$$\begin{aligned}&iq_{t} + a \left( \left| q \right| ^{m+1} q\right) _{xx} + \left( \frac{b_1}{\left| q \right| ^{2m+2}} + b_2 \left| q \right| ^{2m} + b_3 \left| q \right| ^{2m+2} \right) q \nonumber \\&\quad = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(159)
and Eq. (3) changes to
$$\begin{aligned}&- \left( \gamma +\lambda \right) \phi ^2 + b_1 \phi ^{-2m} + b_2 \phi ^{2m+2}+b_3 \phi ^{2m+4} -2 (\alpha -2 \beta ) \left( \phi ^{\prime }\right) ^2 \nonumber \\&+a (m+1) (m+2) \phi ^{m+1} \left( \phi ^{\prime } \right) ^2 -2 \alpha \phi \phi ^{\prime \prime } +a (m+2) \phi ^{m+2} \phi ^{\prime \prime } =0. \end{aligned}$$
(160)
Considering
$$\begin{aligned} \phi = \varphi ^\frac{1}{m+1} \end{aligned}$$
(161)
one turns Eq. (160) into
$$\begin{aligned}&b_1 (m+1)^2 \displaystyle - (m+1)^2 (\gamma +\lambda )\varphi ^2 + b_3 (m+1)^2 \varphi ^4 + 2 ( \alpha (m-1)+2\beta ) \left( \varphi ^{\prime } \right) ^2 \nonumber \\&+ a (m+2) \varphi \left( \varphi ^{\prime } \right) ^2-2 \alpha (m+1) \varphi \varphi ^{\prime \prime } +a (m+1) (m+2) \varphi ^2 \varphi ^{\prime \prime } + b_2 (m+1)^2 \varphi (x)^{\frac{2 m}{m+1}+2} =0 . \end{aligned}$$
(162)
To proceed further, it is assume that \(b_2=0\). Then, Eq. (159) changes to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{m+1} q\right) _{xx} + \left( \frac{b_1}{\left| q \right| ^{2m+2}} + b_3 \left| q \right| ^{2m+2} \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(163)
and Eq. (162) reads as
$$\begin{aligned}&b_1 (m+1)^2 \displaystyle - (m+1)^2 (\gamma +\lambda )\varphi ^2 + b_3 (m+1)^2 \varphi ^4 + 2 ( \alpha (m-1)+2\beta ) \left( \varphi ^{\prime } \right) ^2 \nonumber \\&+ a (m+2) \varphi \left( \varphi ^{\prime } \right) ^2-2 \alpha (m+1) \varphi \varphi ^{\prime \prime } +a (m+1) (m+2) \varphi ^2 \varphi ^{\prime \prime } =0 . \end{aligned}$$
(164)
Balance principle leads to \(N=2\). This means that Eq. (8) becomes
$$\begin{aligned} \varphi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) +\alpha _2\left( \frac{G^{\prime }}{G}\right) ^2 \end{aligned}$$
(165)
and then two solution set are constructed as below:
$$\begin{aligned}&\begin{array}{c} \displaystyle b_1= -\frac{8 a \alpha _2^3 \left( e_1^3-36 e_0 e_1 e_2\right) ^2 (m+2)}{81 \left( e_1^2+12 e_0 e_2\right) (m+1)^2}, \quad b_3= -\frac{2 a (m+2) (3 m+5)}{\alpha _2 (m+1)^2}, \quad \alpha _0= -\frac{2\alpha _2 e_1}{3} , \quad \alpha _1= 0, \\ \\ \displaystyle \alpha = \frac{a \alpha _2 e_1 \left( e_1^2-36 e_0 e_2\right) (m+2)}{9 \left( e_1^2+12 e_0 e_2\right) (m+1)}, \quad \beta = \frac{a \alpha _2 e_1 \left( e_1^2-36 e_0 e_2\right) (m+2) (m+5)}{36 \left( e_1^2+12 e_0 e_2\right) (m+1)}, \quad \\ \\ \displaystyle \gamma =-\lambda -\frac{2 a \alpha _2 \left( e_1^2+12 e_0 e_2\right) (m+2) (m+3)}{3 (m+1)^2} . \end{array} \end{aligned}$$
(166)
$$\begin{aligned}&\begin{array}{c} \displaystyle b_1= 0, \quad b_3= -\frac{2 a (m+2) (3 m+5)}{\alpha _2 (m+1)^2}, \quad e_0= 0, \quad \alpha _0= - \alpha _2 e_1, \quad \alpha _1= 0, \\ \\ \displaystyle \alpha = \frac{a \alpha _2 e_1 (m+2)^2}{m+1}+\frac{(m+1) (\gamma +\lambda )}{4 e_1}, \quad \beta = \frac{a \alpha _2 e_1 (m+2)^2}{m+1}+\frac{(m+1) (m+5) (\gamma +\lambda )}{16 e_1} . \end{array} \end{aligned}$$
(167)
Substituting (166) into (165) and employing (2) gives
$$\begin{aligned} q(x,t)= \left\{ -\frac{2\alpha _2 e_1}{3} + \alpha _2\left( \frac{G^{\prime }}{G}\right) ^2 \right\} ^\frac{1}{m+1} e^{ i \lambda t } \end{aligned}$$
(168)
and thus, the solutions to (163) are listed as:
If \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \left\{ \frac{2\alpha _2 \left( k^2+1\right) }{3} + \alpha _2 {{\,\mathrm{cs}\,}}^2 x {{\,\mathrm{dn}\,}}^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } \end{aligned}$$
(169)
or
$$\begin{aligned} q(x,t)= \left\{ \frac{2\alpha _2 \left( k^2+1\right) }{3} + \alpha _2 \left( 1-k^2\right) ^2 \text{ sc }\;^2 x {{\,\mathrm{nd}\,}}^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } . \end{aligned}$$
(170)
For \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{2\alpha _2 \left( 2k^2-1\right) }{3} + \alpha _2 \text{ sc }\;^2 x {{\,\mathrm{dn}\,}}^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } . \end{aligned}$$
(171)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{2\alpha _2 \left( 2-k^2 \right) }{3} + \alpha _2 k^4 {{\,\mathrm{sd}\,}}^2 x {{\,\mathrm{cn}\,}}^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } . \end{aligned}$$
(172)
Whenever \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{2\alpha _2}{3} + \alpha _2 \tanh ^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } . \end{aligned}$$
(173)
Finally, if \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \left\{ -\frac{2\alpha _2}{3} + \alpha _2 \coth ^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } . \end{aligned}$$
(174)
Here, JE function solutions are represented by Eqs. (169)–(172), while dark and singular solitons are respectively indicated in Eqs. (173) and (174).
Similarly, putting (167) into (165) and using (2) leads to
$$\begin{aligned} q(x,t)= \left\{ -\alpha _2 e_1 + \alpha _2 \left( \frac{G^{\prime }}{G}\right) ^2 \right\} ^\frac{1}{m+1} e^{ i \lambda t } \end{aligned}$$
(175)
and thus, one acquires bright and singular solitons and also periodic wave solution, respectively as:
If \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ -\alpha _2 {{\,\mathrm{sech}\,}}^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } . \end{aligned}$$
(176)
For \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \left\{ \alpha _2 {{\,\mathrm{csch}\,}}^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } . \end{aligned}$$
(177)
When \(e_0=0\), \(e_1=-1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \left\{ \alpha _2 \sec ^2 x \right\} ^\frac{1}{m+1} e^{ i \lambda t } . \end{aligned}$$
(178)
2.12 Cubic–quartic law
For CQ nonlinearity,
$$\begin{aligned} F(s)=b_1 s + b_2 s^{ \frac{3}{ 2} } \end{aligned}$$
(179)
with the constants \(b_1\) and \(b_2\). Thus Eq. (1) becomes
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( b_1 \left| q \right| ^{2}+ b_2 \left| q \right| ^{3} \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(180)
By selecting \(n=2\), one can perform the integration of Eq. (180). Therefore Eq. (180) condenses to:
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{2} q\right) _{xx} + \left( b_1 \left| q \right| ^{2}+ b_2 \left| q \right| ^{3} \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(181)
and Eq. (3) simplifies to
$$\begin{aligned} - \left( \gamma +\lambda \right) \phi ^2 + b_1 \phi ^4+ b_2 \phi ^5 -2 (\alpha -2 \beta ) \left( \phi ^{\prime }\right) ^2 +6a \phi ^2 \left( \phi ^{\prime }\right) ^2 -2 \alpha \phi \phi ^{\prime \prime } +3a \phi ^{3} \phi ^{\prime \prime } =0. \end{aligned}$$
(182)
Balance principle causes \(N=2\). Then Eq. (8) becomes
$$\begin{aligned} \phi (x)=\alpha _0+\alpha _1\left( \frac{G^{\prime }}{G}\right) + \alpha _2\left( \frac{G^{\prime }}{G}\right) ^2 \end{aligned}$$
(183)
and then the results given below are derived:
$$\begin{aligned}&\begin{array}{c} \displaystyle b_1= 72 a e_1, \quad b_2= -\frac{42 a}{\alpha _2}, \quad \alpha _0= 0, \quad \alpha _1= 0, \quad \alpha = \frac{15 \alpha _2^2 a \left( e_1^2-4 e_0 e_2\right) }{4} , \\ \\ \displaystyle \beta = \frac{45 \alpha _2^2 a \left( e_1^2-4 e_0 e_2\right) }{16} , \quad \lambda = 30 a \alpha _2^2 e_1 \left( e_1^2-4 e_0 e_2\right) -\gamma . \end{array} \end{aligned}$$
(184)
$$\begin{aligned}&\begin{array}{c} \displaystyle b_1= -36 a e_1, \quad b_2= -\frac{42 a}{\alpha _2}, \quad e_0=0, \quad \alpha _0= - \alpha _2 e_1, \quad \alpha _1= 0, \quad \displaystyle \beta = \frac{5 \alpha }{4}, \quad \lambda = 4 \alpha e_1-\gamma . \end{array} \end{aligned}$$
(185)
Substituting (184) into (183) and employing (2) gives
$$\begin{aligned} q(x,t)= \alpha _2 \left( \frac{G'}{G}\right) ^2 \exp \left[ i \left( 30 a \alpha _2^2 e_1 \left( e_1^2-4 e_0 e_2\right) -\gamma \right) t \right] . \end{aligned}$$
(186)
As a results, JE function solutions, dark and singular solitons to the model (181) are written down as:
If \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \alpha _2 {{\,\mathrm{cs}\,}}^2 x {{\,\mathrm{dn}\,}}^2 x \exp \left[ -i \left( 30 a \alpha _2^2 \left( k^2+1\right) \left( k^2-1\right) ^2+\gamma \right) t \right] \end{aligned}$$
(187)
or
$$\begin{aligned} q(x,t)= \alpha _2 \left( 1-k^2\right) ^2 \text{ sc }\; ^2 x {{\,\mathrm{nd}\,}}^2 x \exp \left[ -i \left( 30 a \alpha _2^2 \left( k^2+1\right) \left( k^2-1\right) ^2+\gamma \right) t \right] . \end{aligned}$$
(188)
For \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= \alpha _2 \text{ sc }\; ^2 x {{\,\mathrm{dn}\,}}^2 x \exp \left[ i \left( 30 a \alpha _2^2 \left( 2k^2-1\right) -\gamma \right) t \right] . \end{aligned}$$
(189)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \alpha _2 k^4 {{\,\mathrm{sd}\,}}^2 x {{\,\mathrm{cn}\,}}^2 x \exp \left[ i \left( 30 a \alpha _2^2 k^4 \left( 2-k^2\right) -\gamma \right) t \right] . \end{aligned}$$
(190)
While \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \alpha _2 \tanh ^2 x \exp \left[ i \left( 30 a \alpha _2^2 -\gamma \right) t \right] . \end{aligned}$$
(191)
Finally if \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \alpha _2 \coth ^2 x \exp \left[ i \left( 30 a \alpha _2^2 -\gamma \right) t \right] . \end{aligned}$$
(192)
Similarly, inserting (185) into (183) and employing (2) brings about
$$\begin{aligned} q(x,t)= \left\{ - \alpha _2 e_1 + \alpha _2 \left( \frac{G^{\prime }}{G}\right) ^2 \right\} \exp \left[ i \left( 4 \alpha e_1-\gamma \right) t \right] \end{aligned}$$
(193)
and then one obtains bright and singular solitons and also periodic wave, respectively as:
For \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= - \alpha _2 {{\,\mathrm{sech}\,}}^2 x \exp \left[ i \left( 4 \alpha -\gamma \right) t \right] . \end{aligned}$$
(194)
If \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \alpha _2 {{\,\mathrm{csch}\,}}^2 x \exp \left[ i \left( 4 \alpha -\gamma \right) t \right] . \end{aligned}$$
(195)
When \(e_0=0\), \(e_1=-1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \alpha _2 \sec ^2 x \exp \left[ -i \left( 4 \alpha +\gamma \right) t \right] . \end{aligned}$$
(196)
2.13 Generalized CQ law
For generalized CQ nonlinearity,
$$\begin{aligned} F(s)=b_1 s^m+ b_2 s^{\frac{3m}{2}} \end{aligned}$$
(197)
with the constants \(b_1\) and \(b_2\). Thus, Eq. (1) becomes to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{n} q\right) _{xx} + \left( b_1 \left| q \right| ^{2m}+ b_2 \left| q \right| ^{3m} \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q . \end{aligned}$$
(198)
To integrate Eq. (198), it should be \(n=2m\). Then, Eq. (198) modifies to
$$\begin{aligned} iq_{t} + a \left( \left| q \right| ^{2m} q\right) _{xx} + \left( b_1 \left| q \right| ^{2m}+ b_2 \left| q \right| ^{3m} \right) q = \frac{1}{ \left| q \right| ^{2}q^{*}}\left[ \alpha \left| q \right| ^{2}\left( \left| q \right| ^{2}\right) _{xx} - \beta \left\{ \left( \left| q \right| ^{2}\right) _{x}\right\} ^{2}\right] + \gamma q \end{aligned}$$
(199)
and Eq. (3) changes to
$$\begin{aligned}&- \left( \gamma +\lambda \right) \phi ^2 + b_1 \phi ^ {2m+2}+ b_2 \phi ^ {3m+2} -2 (\alpha -2 \beta ) \left( \phi ^{\prime } \right) ^2 +2a m (2m+1) \phi ^{2m} \left( \phi ^{\prime } \right) ^2 \nonumber \\&\quad -2 \alpha \phi \phi ^{\prime \prime } +a (2m+1) \phi ^{2m+1} \phi ^{\prime \prime } =0. \end{aligned}$$
(200)
Applying the transformation given by
$$\begin{aligned} \phi = \varphi ^{\frac{2}{m}} \end{aligned}$$
(201)
one transforms Eq. (200) to
$$\begin{aligned}&-m^2 (\gamma +\lambda ) \varphi ^2 +b_1 m^2 \varphi ^6 +b_2 m^2 \varphi ^8 +4 ( \alpha (m-4) + 4 \beta ) \left( \varphi ^{\prime }\right) ^2 \nonumber \\&+2 a \left( 6 m^2+7 m+2\right) \varphi ^4 \left( \varphi ^{\prime } \right) ^2 -4 m \alpha \varphi \varphi ^{\prime \prime } +2 a m (2 m+1) \varphi ^5 \varphi ^{\prime \prime } =0 . \end{aligned}$$
(202)
Balance principle yields \(N=1\). Then Eq. (8) becomes
$$\begin{aligned} \varphi (x)=\alpha _0+\alpha _1\left( \frac{G'}{G}\right) \end{aligned}$$
(203)
and then the following results fall out:
$$\begin{aligned} \begin{array}{c} \displaystyle b_1= \frac{8 a e_1 (2 m+1)^2}{m^2}, \quad b_2= -\frac{2 a (2 m+1) (5 m+2)}{\alpha _1^2 m^2}, \\ \alpha _0= 0, \quad \alpha = \frac{a \alpha _1^4 \left( e_1^2-4 e_0 e_2\right) (m (6 m+7)+2)}{4 m}, \\ \\ \displaystyle \beta = -\frac{a \alpha _1^4 \left( e_1^2-4 e_0 e_2\right) (m-4) (2 m+1) (3 m+2)}{16 m}, \\ \lambda = \frac{2 a \alpha _1^4 e_1 \left( e_1^2-4 e_0 e_2\right) ( 6m ^2+7m+2)}{m^2}-\gamma . \end{array} \end{aligned}$$
(204)
Utilizing (204) into (203) and using (2) leads to
$$\begin{aligned} q(x,t)= \left\{ \alpha _1 \left( \frac{G^{\prime }}{G}\right) \right\} ^ {\frac{2}{m}} \exp \left[ i \left( \frac{2 a \alpha _1^4 e_1 \left( e_1^2-4 e_0 e_2\right) ( 6m ^2+7m+2)}{m^2}-\gamma \right) t \right] \end{aligned}$$
(205)
and thus, JE function solutions, dark and singular solitons to the model equation (199) are reported as:
If \(e_0=1\), \(e_1=-\left( k^2+1\right)\), \(e_2=k^2\),
$$\begin{aligned} q(x,t)= \left\{ \alpha _1 {{\,\mathrm{cs}\,}}x {{\,\mathrm{dn}\,}}x \right\} ^ {\frac{2}{m}} \exp \left[ -i \left( \frac{2 a \alpha _1^4 \left( k^2+1\right) \left( k^2-1\right) ^2 (6m ^2+7m+2)}{m^2}+\gamma \right) t \right] \end{aligned}$$
(206)
or
$$\begin{aligned} q(x,t)= \left\{ \alpha _1 \left( k^2-1\right) \text{ sc }\; x {{\,\mathrm{nd}\,}}x \right\} ^ {\frac{2}{m}} \exp \left[ -i \left( \frac{2 a \alpha _1^4 \left( k^2+1\right) \left( k^2-1\right) ^2 ( 6m ^2+7m+2)}{m^2}+\gamma \right) t \right] . \end{aligned}$$
(207)
For \(e_0=1-k^2\), \(e_1=2k^2-1\), \(e_2=-k^2\),
$$\begin{aligned} q(x,t)= \left\{ -\alpha _1 \text{ sc }\; x {{\,\mathrm{dn}\,}}x \right\} ^ {\frac{2}{m}} \exp \left[ i \left( \frac{2 a \alpha _1^4 \left( 2k^2-1\right) (6m ^2+7m+2)}{m^2}-\gamma \right) t \right] . \end{aligned}$$
(208)
When \(e_0=k^2-1\), \(e_1=2-k^2\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ - \alpha _1 k^2 {{\,\mathrm{sd}\,}}x {{\,\mathrm{cn}\,}}x \right\} ^ {\frac{2}{m}} \exp \left[ i \left( \frac{2 a \alpha _1^4 k^4 \left( 2-k^2\right) ( 6m ^2+7m+2)}{m^2}-\gamma \right) t \right] . \end{aligned}$$
(209)
Whenever \(e_0=0\), \(e_1=1\), \(e_2=-1\),
$$\begin{aligned} q(x,t)= \left\{ -\alpha _1 \tanh x \right\} ^ {\frac{2}{m}} \exp \left[ i \left( \frac{2 a \alpha _1^4 ( 6m ^2+7m+2)}{m^2}-\gamma \right) t \right] . \end{aligned}$$
(210)
Finally, for \(e_0=0\), \(e_1=1\), \(e_2=1\),
$$\begin{aligned} q(x,t)= \left\{ -\alpha _1 \coth x \right\} ^ {\frac{2}{m}} \exp \left[ i \left( \frac{2 a \alpha _1^4 ( 6m ^2+7m+2)}{m^2}-\gamma \right) t \right] . \end{aligned}$$
(211)