Optical solitons with complex Ginzburg–Landau equation

Abstract

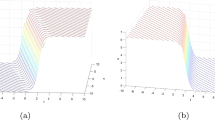
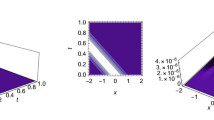
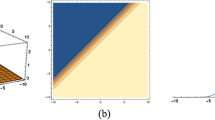
The paper revisits in a systematic way the complex Ginzburg–Landau equation with Kerr and power law nonlinearities. Several integration techniques are applied to retrieve various soliton solutions to the model for both forms of nonlinearity. Bright, dark as well as singular soliton solutions are obtained. Several other solutions such as periodic singular solutions and plane waves emerge as a by-product of integration algorithms. Constraint conditions hold all of these solutions in place. The numerical simulations for bright soliton solutions are given for Kerr and power law.

Appendices

Appendix 1

Relations between values of (P, Q, R) and the corresponding F(s) in Eq. (185), where A, B and C are arbitrary constants and $m_1=\sqrt{1-m^2}$.

Case	P	Q	R	F(s)
1	$m^2$	$-(1+m^2)$	1	${{\mathrm{sn}}}s$
2	$m^2$	$-(1+m^2)$	1	${{\mathrm{cd}}}s={{\mathrm{cn}}}s/ {{\mathrm{dn}}}s$
3	$-m^2$	$2m^2-1$	$1-m^2$	${{\mathrm{cn}}}s$
4	$-1$	$2-m^2$	$m^2-1$	${{\mathrm{dn}}}s$
5	1	$-(1+m^2)$	$m^2$	${{\mathrm{ns}}}s=({{\mathrm{sn}}}s)^{-1}$
6	1	$-(1+m^2)$	$m^2$	${{\mathrm{dc}}}s={{\mathrm{dn}}}s / {{\mathrm{cn}}}s$
7	$1-m^2$	$2m^2-1$	$-m^2$	${{\mathrm{nc}}}s=({{\mathrm{cn}}}s)^{-1}$
8	$m^2-1$	$2-m^2$	$-1$	${{\mathrm{nd}}}s=({{\mathrm{dn}}}s)^{-1}$
9	$1-m^2$	$2-m^2$	1	$\text {sc} \ s={{\mathrm{sn}}}s/ {{\mathrm{cn}}}s$
10	$-m^2(1-m^2)$	$2m^2-1$	1	${{\mathrm{sd}}}s={{\mathrm{sn}}}s/ {{\mathrm{dn}}}s$
11	1	$2-m^2$	$1-m^2$	${{\mathrm{cs}}}s={{\mathrm{cn}}}s/ {{\mathrm{sn}}}s$
12	1	$2m^2-1$	$-m^2(1-m^2)$	${{\mathrm{ds}}}s={{\mathrm{dn}}}s/{{\mathrm{sn}}}s$
13	1 / 4	$(1-2m^2)/2$	1 / 4	${{\mathrm{ns}}}s\pm {{\mathrm{cs}}}s$
14	$(1-m^2)/4$	$(1+m^2)/2$	$(1-m^2)/4$	${{\mathrm{nc}}}s\pm s$
15	1 / 4	$(m^2-2)/2$	$m^2/4$	${{\mathrm{ns}}}s\pm {{\mathrm{ds}}}s$
16	$m^2/4$	$(m^2-2)/2$	$m^2/4$	${{\mathrm{sn}}}s\pm i{{\mathrm{cn}}}s$
17	$m^2/4$	$(m^2-2)/2$	$m^2/4$	$\sqrt{1-m^2}{{\mathrm{sd}}}s\pm {{\mathrm{cd}}}s$
18	1 / 4	$(1-m^2)/2$	1 / 4	$m{{\mathrm{cd}}}s\pm i\sqrt{1-m^2}{{\mathrm{nd}}}s$

Case	P	Q	R	F(s)
19	1 / 4	$(1-2m^2)/2$	1 / 4	$m{{\mathrm{sn}}}s\pm i{{\mathrm{dn}}}s$
20	1 / 4	$(1-m^2)/2$	1 / 4	$\sqrt{1-m^2} \text {sc} \ s\pm {{\mathrm{dc}}}s$
21	$(m^2-1)/4$	$(m^2+1)/2$	$(m^2-1)/4$	$m{{\mathrm{sd}}}s\pm {{\mathrm{nd}}}s$
22	$m^2/4$	$(m^2-2)/2$	1 / 4	$\frac{{{\mathrm{sn}}}s}{1\pm {{\mathrm{dn}}}s}$
23	$-1/4$	$(m^2+1)/2$	$(1-m^2)^2/4$	$m{{\mathrm{cn}}}s\pm {{\mathrm{dn}}}s$
24	$(1-m^2)^2/4$	$(m^2+1)/2$	1 / 4	${{\mathrm{ds}}}s\pm {{\mathrm{cs}}}s$
25	$\frac{m^4(1-m^2)}{2(2-m^2)}$	$\frac{2(1-m^2)}{m^2-2}$	$\frac{1-m^2}{2(2-m^2)}$	${{\mathrm{dc}}}s\pm \sqrt{1-m^2} {{\mathrm{nc}}}s$
26	$P>0$	$Q<0$	$\frac{m^2Q^2}{(1+m^2)^2 P}$	$\sqrt{\frac{-m^2Q}{(1+m^2) P}} {{\mathrm{sn}}}\left( \sqrt{\frac{-Q}{1+m^2}}s\right)$
27	$P<0$	$Q>0$	$\frac{(1-m^2)Q^2}{(m^2-2)^2 P}$	$\sqrt{\frac{-Q}{(2-m^2) P}} {{\mathrm{dn}}}\left( \sqrt{\frac{Q}{2-m^2}}s\right)$
28	$P<0$	$Q>0$	$\frac{m^2(m^2-1)Q^2}{(2m^2-1)^2 P}$	$\sqrt{-\frac{m^2Q}{(2m^2-1) P}} {{\mathrm{cn}}}\left( \sqrt{\frac{Q}{2m^2-1}}s\right)$
29	1	$2-4m^2$	1	$\frac{{{\mathrm{sn}}}s {{\mathrm{dn}}}s}{{{\mathrm{cn}}}s}$
30	$m^4$	2	1	$\frac{{{\mathrm{sn}}}s {{\mathrm{cn}}}s}{{{\mathrm{dn}}}s}$
31	1	$m^2+2$	$1-2m^2+m^4$	$\frac{{{\mathrm{dn}}}s {{\mathrm{cn}}}s}{{{\mathrm{sn}}}s}$
32	$\frac{A^2(m-1)^2}{4}$	$\frac{m^2+1}{2}+3m$	$\frac{(m-1)^2}{4A^2}$	$\frac{{{\mathrm{dn}}}s {{\mathrm{cn}}}s}{A(1+{{\mathrm{sn}}}s)(1+m{{\mathrm{sn}}}s)}$
33	$\frac{A^2(m+1)^2}{4}$	$\frac{m^2+1}{2}-3m$	$\frac{(m+1)^2}{4A^2}$	$\frac{{{\mathrm{dn}}}s {{\mathrm{cn}}}s}{A(1+{{\mathrm{sn}}}s)(1-m{{\mathrm{sn}}}s)}$
34	$-\frac{4}{m}$	$6m-m^2-1$	$-2m^3+m^4+m^2$	$\frac{m{{\mathrm{cn}}}s {{\mathrm{dn}}}s}{m{{\mathrm{sn}}}^2 s+1}$
35	$\frac{4}{m}$	$-6m-m^2-1$	$2m^3+m^4+m^2$	$\frac{m{{\mathrm{cn}}}s {{\mathrm{dn}}}s}{m{{\mathrm{sn}}}^2 s-1}$
36	1 / 4	$\frac{1-2m^2}{2}$	1 / 4	$\frac{{{\mathrm{sn}}}s}{1\pm {{\mathrm{cn}}}s}$
37	$\frac{1-m^2}{4}$	$\frac{1+m^2}{2}$	$\frac{1-m^2}{4}$	$\frac{{{\mathrm{cn}}}s}{1\pm {{\mathrm{sn}}}s}$
38	$4m_1$	$2+6m_1-m^2$	$2+2m_1-m^2$	$\frac{m^2{{\mathrm{sn}}}s{{\mathrm{cn}}}s}{m_1 - {{\mathrm{dn}}}^2 s}$
39	$-4m_1$	$2-6m_1-m^2$	$2-2m_1-m^2$	$-\frac{m^2{{\mathrm{sn}}}s {{\mathrm{cn}}}s}{m_1 + {{\mathrm{dn}}}^2 s}$
40	$\frac{2-m^2-2m_1}{4}$	$\frac{m^2}{2}-1-3m_1$	$\frac{2-m^2-2m_1}{4}$	$\frac{m^2{{\mathrm{sn}}}s {{\mathrm{cn}}}s}{ {{\mathrm{sn}}}^2 s+(1+m_1) {{\mathrm{dn}}}s-1-m_1}$
41	$\frac{2-m^2+2m_1}{4}$	$\frac{m^2}{2}-1+3m_1$	$\frac{2-m^2+2m_1}{4}$	$\frac{m^2{{\mathrm{sn}}}s {{\mathrm{cn}}}s}{ {{\mathrm{sn}}}^2 s+(-1+m_1) {{\mathrm{dn}}}s-1+m_1}$
42	$\frac{C^2m^4-(B^2+C^2)m^2+B^2}{4}$	$\frac{m^2+1}{2}$	$\frac{m^2-1}{4(C^2m^2-B^2)}$	$\frac{\sqrt{\frac{(B^2-C^2)}{(B^2-C^2m^2)}}+{{\mathrm{sn}}}s}{B{{\mathrm{cn}}}s+ C{{\mathrm{dn}}}s}$
43	$\frac{B^2+C^2m^2}{4}$	$\frac{1}{2}-m^2$	$\frac{1}{4(C^2m^2+B^2)}$	$\frac{\sqrt{\frac{(C^2m^2+B^2-C^2)}{(B^2+C^2m^2)}}+{{\mathrm{cn}}}s}{B{{\mathrm{sn}}}s+ C{{\mathrm{dn}}}s}$
44	$\frac{B^2+C^2}{4}$	$\frac{m^2}{2}-1$	$\frac{m^4}{4(C^2+B^2)}$	$\frac{\sqrt{\frac{(B^2+C^2-C^2m^2)}{(B^2+C^2)}}+{{\mathrm{dn}}}s}{B{{\mathrm{sn}}}s+ C{{\mathrm{cn}}}s}$
45	$-(m^2+2m+1)B^2$	$2m^2+2$	$\frac{2m-m^2-1}{B^2}$	$\frac{m{{\mathrm{sn}}}^2 s-1}{B(m{{\mathrm{sn}}}^2 s+1)}$
46	$-(m^2-2m+1)B^2$	$2m^2+2$	$-\frac{2m+m^2+1}{B^2}$	$\frac{m{{\mathrm{sn}}}^2 s+1}{B(m{{\mathrm{sn}}}^2 s-1)}$

Appendix 2

Weierstrass elliptic function solutions for Eq. (185), where $D=\frac{1}{2}\left( -5Q\pm \sqrt{9Q^2-36{\textit{PR}}}\right)$ and $\wp '(s;g_2,g_3)=\frac{d\wp (s;g_2,g_3)}{ds}.$

Case	$g_2$	$g_3$	F(s)
47	$\frac{4}{3}(Q^2-3{\textit{PR}})$	$\frac{4Q}{27}(-2Q^2+9{\textit{PR}})$	$\sqrt{\frac{1}{P}(\wp (s;g_2,g_3) -\frac{1}{3}Q)}$
48	$\frac{4}{3}(Q^2-3{\textit{PR}})$	$\frac{4Q}{27}(-2Q^2+9{\textit{PR}})$	$\sqrt{\frac{3R}{3 \wp (s;g_2,g_3) -Q}}$
49	$-\frac{5QD+4Q^2+33{\textit{PQR}}}{12}$	$\frac{21Q^2D-63{\textit{PR}}D+20Q^3-27{\textit{PQR}}}{216}$	$\frac{\sqrt{12R \wp (s;g_2,g_3) +2R(2Q+D)}}{12 \wp (s;g_2,g_3)+D}$
50	$\frac{1}{12}Q^2+{\textit{PR}}$	$\frac{1}{216}Q(36{\textit{PR}}-Q^2)$	$\frac{\sqrt{R}[6 \wp (s;g_2,g_3)+Q]}{3 \wp '(s;g_2,g_3)}$
51	$\frac{1}{12}Q^2+{\textit{PR}}$	$\frac{1}{216}Q(36{\textit{PR}}-Q^2)$	$\frac{3 \wp '(s;g_2,g_3)}{\sqrt{P}[6 \wp (s;g_2,g_3)+Q]}$
52	$\frac{2Q^2}{9}$	$\frac{Q^3}{54}$	$\frac{Q\sqrt{-15Q/2P}\wp (s;g_2,g_3)}{3\wp (s;g_2,g_3)+Q},$	$R=\frac{5Q^2}{36P}$

Appendix 3

The Jacobian elliptic functions degenerate into hyperbolic functions when $m\rightarrow 1^-$ as follows:

$$\begin{aligned} \begin{array}{lll} {{\mathrm{sn}}}s\rightarrow \tanh s,&{}{{\mathrm{cn}}}s\rightarrow \mathrm{sech}s,&{} {{\mathrm{dn}}}s \rightarrow \mathrm{sech}s, \\ \text {sc} \ s \rightarrow \sinh s,&{} {{\mathrm{sd}}}s\rightarrow \sinh s,&{}{{\mathrm{cd}}}s\rightarrow 1,\\ {{\mathrm{ns}}}s\rightarrow \coth s,&{}{{\mathrm{nc}}}s\rightarrow \cosh s,&{} {{\mathrm{nd}}}s\rightarrow \cosh s, \\ {{\mathrm{cs}}}s\rightarrow \mathrm{csch}s,&{}{{\mathrm{ds}}}s\rightarrow \mathrm{csch}s,&{}{{\mathrm{dc}}}s \rightarrow 1. \end{array} \end{aligned}$$

The Jacobian-elliptic functions degenerate into trigonometric functions when $m\rightarrow 0^+$ as follows:

$$\begin{aligned} \begin{array}{lll} {{\mathrm{sn}}}s\rightarrow \sin s,&{}{{\mathrm{cn}}}s\rightarrow \cos s,&{}{{\mathrm{dn}}}s\rightarrow 1, \\ \text {sc} \ s\rightarrow \tan s,&{}{{\mathrm{sd}}}s \rightarrow \sin s,&{}{{\mathrm{cd}}}s \rightarrow \cos s,\\ {{\mathrm{ns}}}s\rightarrow \csc s,&{}{{\mathrm{nc}}}s\rightarrow \sec s,&{}{{\mathrm{nd}}}s \rightarrow 1, \\ {{\mathrm{cs}}}s\rightarrow \cot s,&{}{{\mathrm{ds}}}s\rightarrow \csc s,&{} {{\mathrm{dc}}}s \rightarrow \sec s. \end{array} \end{aligned}$$