Abstract
In this work, AlGaAs/GaAs superlattices with layer composition imitating the active region of quantum cascade lasers emitting in the mid infrared spectral range were investigated. Using optical spectroscopy techniques (photoreflectance and photoluminescence) together with numerical calculations performed within the effective mass approximation, we studied the band structure of the formed conduction minibands including the modification of the wave functions with the external electric field. In addition, the applied growth rates of the GaAs/AlGaAs superlattices have been verified by investigating the Stokes shift between the emission and absorption spectra. Finally, it has been shown that testing the structure imitating the operational laser device might be performed (without the electric field applied) by photoluminescence measurements realized within the Fourier Transformed Infrared Spectroscopy based concept.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum Cascade Lasers (QCL) are one of the ideas to construct laser devices emitting in the mid infrared spectral range (Faist et al. 1994; Sirtori et al. 1998). Based on intersubband transitions, the QCL can emit radiation at wavelengths longer than common semiconductor-based laser structure, normally limited by the band gap energy (as in case of type I quantum well based lasers (Vizbaras and Amann 2012)) or proper wave functions overlapping of the adjacent layers (as in case of type II quantum well based Interband Cascade Laser (ICL) (Vurgaftman et al. 2012)). Compact laser device operation in the mid infrared spectral range is an important component in many disciplines, like spectroscopy, environmental protection, security, or medicine, where it can be used to detect dangerous gases or substances [(e.g. breath analysis (Wang and Sahay 2009) in medical diagnostics].
The Quantum Cascade Lasers based on low dimensional semiconductor structures (in this example, GaAs/AlGaAs multiple quantum wells form superlattice systems) operate on optical between the levels and mini bands within the conduction band (Sirtori et al. 1998). Two main elements of the QCL are the emitting part (active region) and the injector, which are responsible for final laser emission and the carriers transport between the following cascades of the active region, providing multiplication of the radiative emission by the same carrier. Such a concept allows for the coverage of a broad spectral range (by the proper layer widths application), which makes them an important source of the laser light in the mid infrared spectral range. Superlattices investigated in this work are designed based on those proposed by Page et al. (2001). Nevertheless, in our case, layers were not doped (as originally) and deposited on semi-insulating substrate.
The fabrication process of QCL’s requires very high precision with respect to the multilayer structure of the entire device consisting of a lot of very thin layers. In particular, one has to provide procedures which allow the control of parameters such as a width, content and doping level in the growth process of all the barriers and quantum wells layers (Kosiel et al. 2009). As a result, the fabrication of SL’s-based testing samples imitating the final structure might help with calibration and achievement of the growth accuracy before final QCL growth starts (Kosiel et al. 2012). Proper calibration might have also very important meaning from the point of view thermal processes connected to heat distribution and further to optical QCl’s performances (Pierściński et al. 2012).
Optical spectroscopy, for instance, photoluminescence (PL, emission like measurement) and photoreflectance (PR, high sensitivity absorption like modulation technique) realized by the application of a grating based (Pollak and Shen 1993; Janiak et al. 2012) or Fourier spectrometer (Motyka et al. 2009) (depending on the spectral range), can provide the information about the electronic structure of the low-dimensional semiconductor system, because of the possibility of detecting the interband and intersubband optical transitions . The combination of the obtained from the measured spectra (after fitting procedure) energies of the confined levels with theoretical calculations provides the growth accuracy verification before the final structure fabrication (e.g. before the growth of the full operational quantum cascade multilayer laser structure).
In this work, we present results of experimental and theoretical studies of GaAs/AlGaAs superlattices designed as the active and injector region of QCL emitting at 9 \(\upmu \)m at 300 K (after Page et al. 2001). The set of the samples with different interface repeatability (by modifying the growth parameters) have been investigated. In our studies, we have used different experiments realized within interband transition range involving electron and holes states (like e.g. photoluminescence and photoreflectance) and also intersubband transition range (using Fourier transformed photoluminescence experiment) involving electron states only.
2 Materials and methods
The investigated undoped heterostructures are composed of a superlattice (SL) region placed on 0.5 \(\upmu \)m thick GaAs buffer layer, and capped by a 5 nm thick GaAs layer. The SL’s of three different samples (A, B and C) consist of 20 periods of Al\(_{0.45}\)Ga\(_{0.55}\)As barrier layers and GaAs wells. The layer sequence starting from the injection barrier is 4.6, 1.9, 1.1, 5.4, 1.1, 4.8, 2.8, 3.4, 1.7, 3.0,1.8, 2.8, 2.0, 3.0, 2.6, 3.0 nm. All of the samples were grown by molecular beam epitaxy (MBE) on the (100) oriented GaAs substrates in a Riber Compact 21T machine. The molecular beams of group III elements were generated from the standard ABN 80 DF effusion cells (filled with Al 6N5 and Ga 7N). Arsenic was emitted as As\(_{{4}}\) molecules, from the valved cracking cell. The temperature of the crystalline surface during the growth process was controlled by a pyrometer, and had a constant value of 580 \(^\circ \)C. In this work, three samples were investigated. The samples were deposited with different growth rates, i.e. the growth rate of GaAs binary was 0.5 ML/s for sample A, and 1ML/s for samples B and C. Samples B and C were grown in the same growth parameter for verifications of the growth process repeatability. For each sample, AlAs binary growth rates were adjusted in order to achieve the planned 45 % of Al in barriers of all these superlattices. For verification and confirmed assume growth parameters, high-resolution x-ray diffraction (HRXRD) measurements were done. So the main difference between samples A and B is the growth rate of GaAs (0.5 and 1 ML/s, respectively). Samples B and C are nominally the same, but they were grown with a different process.
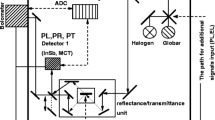
In order to measure the PR spectra, what we will refer to as the bright configuration has been used (Kudrawiec 2009). Light from a halogen lamp was reflected off of the sample and then came through a single-grating 0.55 m focal-length monochromator and was detected by an InGaAs thermoelectrically cooled PIN photodiode. The pump beam was provided by an Ar ion laser (514.5 nm line) and mechanically chopped at a frequency of 275 Hz. Phase sensitive detection of the normalized reflectivity changes was performed using a lock-in amplifier. In this configuration, the PL spectra related to interband transitions were measured.
For the low temperature intersubband photoluminescence (FTPL) measurements, a Bruker FTIR vacuum spectrometer Vertex 80 v was used in the stepscan mode together with an external chamber for experiments with an additional modulated laser beam (Motyka et al. 2009, 2011a). For detection, a liquid nitrogen cooled mercury cadmium telluride photodetector was used.
3 Results and discussion
Figure 1 shows PR and PL spectra measured at low temperature (10 K) for sample A in the range of interband transitions. The PL spectrum (bottom line–in red) exhibits only one peak related to the fundamental transition between the first electron and first heavy hole levels (h1e1) with the transition energy equal to 1.575 eV. The PR spectrum (top line–in black) exhibits a large number of the features (resonances) connected to both the energy gap of the GaAs substrate (\(\sim \)1.5 eV) and to the superlattice part of the structure (energies higher than 1.575). In this second part, a number of the resonances connected to optical transitions between ground and excited states in a minibands formed within the superlattice can be seen. Dashed lines represent the transition energies obtained from numerical calculations (where h(n)e(n) or l(n)e(n) notations means heavy (light) hole n-th level and electron n-th level). In this layout of superlattices layers designed as a QCL active region and injector, the energy width of the minibands is negligible, as distinct from the typical superlattices where \(\Gamma \) and \(\Pi \) points related optical transitions might be observed (Motyka et al. 2011b). There is a difference between ground state transition energies obtained from these two experiments (PR and PL), which can be better seen in Fig. 2. These results show that the comparisons of these two (emission like and absorption like) experiments can give the information about the real sample structure obtained after the growth process. Based on energy of optical transitions and results of theoretical calculations, we can get the information about positions of the electron and hole levels in the investigated structure. In this way we can verify the assumed growth parameters (width and the contents of the layers), by analysis of the estimated quantum fine structure.
Figure 2 shows the comparison of the low temperature (10 K) ground state (h1e1) interband PL (top panel) and PR (bottom panel) spectra measured for all three investigated samples. Gray lines represent the fit of PR spectra defined by the formula:
where \(C\) is the signal amplitude, \(\theta \) the phase, \(E\) the photon energy, and \(E_{0}\) the transition energy, \(\Gamma \) a broadening parameter and \(n\) the exponent which depends on the type of critical point (Aspnes 1980; Janiak et al. 2012). In order to visualize the energy of optical transitions more directly, a modulus of the PR line shape has been derived according to the following expression (red lines on bottom parts):
The dashed lines show energies of PR transitions taken from the fitting procedure. The energy of PL is taken from the maximum of the peak. The difference between the emission (PL) and absorption (PR) energies is usually referred as Stokes shift. This effect, described as a degradation of the optical energy at low temperatures can be taken as an index of heterointerface quality (Lourenço et al. 2007; Kothiyal and Bhattacharya 1988). The magnitude of the Stokes shift might be analyzed in a function of growth parameters changes or post growth treatment (e.g. annealing (Kothiyal and Bhattacharya 1988)). In our case, as it was mentioned above (in Sect. 2), the important difference between the structures was their deposition rate, as it was twice as fast for Samples B and C than it was for Sample A. The Stokes shift magnitude has been found for Sample A and is equal to 10 meV. Samples B and C have the same energy of emission and absorption spectra (no Stokes shift). This result has been connected with growth parameters changes, which influence the AlGaAs/GaAs interfaces repeatability (comparing e.g. Samples A and B). In this case application of the higher deposition rate allow to posses better uniformity of the following interfaces. Presented results and conclusions have also been supported by high-resolution x-ray diffraction (HRXRD) measurements (Kosiel et al. 2009). On the other hand, by the lack of the Stokes shift determined for Samples B and C, which were deposited in the same conditions in different growth process, high uniformity obtained for the growth processes has been shown. Such analysis based on comparison of the spectra taken from the two different experiments shows that optical spectroscopy could be an effective tool to characterize of QCL samples.
Intersubband (left side) and interband (right side) low temperature photoluminescence spectra of samples A,B and C. Intersubband photoluminescence has been measured on FTIR spectrometer (FTPL), interband photoluminescence has been measured on grating-based monochromator setup. Gray line represents Gauss fit of FTPL spectrum
Comparison between interband and intersubband PL spectra is shown in Fig. 3. The left side represents intersubband emission for all investigated samples, measured on FTIR spectrometer (FTPL). The right part shows interband PL spectra measured on monochromator-based setup. Both experiments were made at 77K temperature. On the right side, we can observe the same situation as in Fig. 2—a shift between PL energy peaks of Samples A and the two others. Samples B and C also have the same transition energy. A similar situation is on the left side—intersubband PL spectra measured on Fourier transformed spectrometer (FTPL). This is transition between e3 and e1 levels in conduction bands, which will be explained later in this article. Experimental results have been fitted by Gaussian-line line shape (gray line). All of these measurements were made for unpolarized samples (without applying electric field). The energy of the maximum peak is still the same for Samples B and C, similar like in interband transitions. The PL energy difference between Sample A and two others results from the changing of the interface quality in investigated structures. For Samples B and C interband transition energy is higher than for Sample A, which may be caused by changes of the effective width of the layers (decreasing of barrier and increasing of well layers thickness) correlated to an increase in interface roughness in Samples B and C).
The energy peak of the FTPL spectrum for sample A is equal to 0.166 eV (7.46 \({\upmu }\)m). To better understand the following situation, we have made the calculation of the wave function within the conduction band. Figure 4 shows the calculation of the wave function concerning three first quantum wells responsible for the light emission (active region). In such a design of the layer thicknesses, application of an electric field of about 48 kV/cm (panel a) allows to obtain 9 \({\upmu }\) m emission at room temperature (Page et al. 2001; Kosiel et al. 2009), which is a consequence of the electron transition between E3 (blue curve) and E2 (red curve) levels. In a polarized (biased) structure the overlap integral of such transition is higher than for the transition between E3 and E1 (green curve) levels, nevertheless in case of an unpolarized structure (no electric field), which is actually the case of this paper (panel b), the overlap integral for E3-E1 transition becomes larger. Therefore, we observe the fundamental PL transition (Fig. 3) at 0.166 eV (7.46 \({\upmu }\) m). This Magnitude of the external field (in working devices) causing on the one side, the proper wave function overlapping of the E2 and E3 levels and, on the other side proper energy distance between E1 and E2 levels. In the mentioned situation, E2–E1 distance should be around \(\sim \)30 meV (GaAs optical phonon energy), which provides tunneling the electron from E2 to E1 and further through injector part to the next cascade.
4 Conclusions
GaAs/AlGaAs superlattices designed as an active and injector region of QCL were experimentally and theoretically investigated. Results obtained in interband protoreflectance, photoluminescence and intersubband photoluminescence experiments confirms established in the growth process differences in an AlGaAs/GaAs interfaces. In addition, assumed repeatability of the samples’ growth processes has been also shown. Finally, we presented the Fourier Transformed photoluminescence as a perspective tool to investigate intersubband emission from the structures imitating active region of the QCLs.
References
Aspnes, D.E.: In: Balkanski, M. (ed.) Handbook on Semiconductors, vol. 2. North-Holland Publishing Company, New York (1980)
Faist, J., Capasso, F., Sivco, D.L., Sirtori, C., Hutchinson, A.L., Cho, A.Y.: Quantum cascade laser. Science 22, 553–556 (1994)
Janiak, F., Sek, G., Motyka, M., Ryczko, K., Misiewicz, J., Bauer, A., Höfling, S., Kamp, M., Forchel, A.: Increasing the optical transition oscillator strength in GaSb-based type II quantum wells. Appl. Phys. Lett. 100, 231908 (2012)
Kosiel, K., Kubacka-Traczyk, J., Karbownik, P., Szerling, A., Muszalski, J., Bugajski, M., Romanowski, P., Gaca, J., Wojcik, M.: Molecular-beam epitaxy growth and characterization of mid-infrared quantum cascade laser structures. Microelectron. J. 40, 565–569 (2009)
Kosiel, K., Kubacka-Traczyk, J., Sankowska, I., Szerling, A., Gutowski, P., Bugajski, M.: Multi-step interrupted-growth MBE technology for GaAs/AlGaAs (similar to 9.4 \(\mu \)m) room temperature operating quantum-cascade lasers. Opto-Electron. Rev. 20, 239–246 (2012)
Kothiyal, G.P., Bhattacharya, P.: Optical properties and Stokes shifts in lamp-annealed InGaAs/GaAs strained layer superlattice. J. Appl. Phys. 63, 2760 (1988)
Kudrawiec, R., Misiewicz, J.: Photoreflectance and contactless electroreflectance measurements of semiconductor structures by using bright and dark configurations. Rev. Sci. Instrum. 80, 096103 (2009)
Lourenço, S.A., da Silva, M.A.T., Dias, I.F.L., Duarte, J.L., Laureto, E., Quivy, A.A., Lamas, T.E.: Correlation between luminescence properties of AlxGa1\(-\)xAs/GaAs single quantum wells and barrier composition fluctuation. J. Appl. Phys. 101, 113536 (2007)
Motyka, M., Sęk, G., Misiewicz, J., Bauer, A., Dallner, M., Höfling, S., Forchel, A.: Fourier transformed photoreflectance and photoluminescence of mid infrared GaSb-based type II quantum wells. Appl. Phys. Exp. 2, 126505 (2009)
Motyka, M., Sęk, G., Janiak, F., Misiewicz, J., Kłos, K., Piotrowski, J.: Fourier-transformed photoreflectance and fast differential reflectance of HgCdTe layers. The issues of spectral resolution and Fabry-Perot oscillations. Meas. Sci. Technol. 22, 125601 (2011a)
Motyka, M., Janiak, F., Misiewicz, J., Wasiak, M., Kosiel, K., Bugajski, M.: Determination of energy difference and width of minibands in GaAs/AlGaAs superlattices by using Fourier transform photoreflectance and photoluminescence. Opto-Electron. Rev. 19, 151 (2011b)
Page, H., Becker, C., Robertson, A., Glastre, G., Ortiz, V., Sirtori, C.: 300-K operation of a GaAs-based quantum cascade laser at = 9 \(\mu \)m. Appl. Phys. Lett. 78, 3529–3531 (2001)
Pierściński, K., Pierścińska, D., Iwińska, M., Kosiel, K., Szerling, A., Karbownik, P., Bugajski, M.: Investigation of thermal properties of mid-infrared AlGaAs/GaAs quantum cascade lasers. J. Appl. Phys. 112, 043112 (2012)
Pollak, F.H., Shen, H.: Modulation spectroscopy of semiconductors: bulk/thin film, microstructures, surfaces/interfaces and devices. Mater. Sci. Eng. R. 10, 275 (1993)
Sirtori, C., Kruck, P., Barbieri, S., Collot, P., Nagle, J., Beck, M., Faist, J., Oesterle, U.: GaAs/Al\(_{{\rm x}}\)Ga\(_{{1-{\rm x}}}\)As quantum cascade lasers. Appl. Phys. Lett. 73, 3486–3488 (1998)
Vizbaras, K., Amann, M.C.: Room-temperature 3.73 \(\mu \) m GaSb-based type-I quantum-well lasers with quinternary barriers. Semicond. Sci. Technol. 27, 032001 (2012)
Vurgaftman, I., Bewley, W.W., Canedy, C.L., Kim, C.S., Kim, M., Merritt, C.D., Abell, J., Lindle, J.R., Meyer, J.R.: Rebalancing of internally generated carriers for mid-infrared interband cascade lasers with very low power consumption. Nat. Commun. 2, 585 (2012)
Wang, C., Sahay, P.: Breath analysis using laser spectroscopic techniques: breath biomarkers, spectral fingerprints, and detection limits. Sensors 9, 8230–8262 (2009)
Acknowledgments
We would like to acknowledge the financial support from the National Science Center by the grant no. DEC 2011/03/D/ST3/0264 and no. 5028/B/T02/2011/40. In addition, the work was realized within MPNS COST ACTION MP1204 - “TERA-MIR Radiation: Materials, Generation, Detection and Applications”.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Janiak, F., Dyksik, M., Motyka, M. et al. Advanced optical characterization of AlGaAs/GaAs superlattices for active regions in quantum cascade lasers. Opt Quant Electron 47, 945–952 (2015). https://doi.org/10.1007/s11082-014-9991-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11082-014-9991-2