1 Introduction

The development of very precise and controllable techniques of material deposition, such as molecular beam epitaxy (MBE) and metal organic chemical vapor deposition (MOCVD), allowed the realization of a concept of a quantum cascade laser (QCL) operating in the range of terahertz (THz). It is highly demanded to cover that particular spectral range with compact, low power consumption, solid-state sources. Many bio-chemical molecules have strong spectral fingerprints at terahertz frequencies that enables a variety of applications in the field of spectroscopy and sensing [1]. The astronomical research community is also interested in THz-QCLs, as a number of atomic and molecular emission lines in the THz range are key diagnostic probes of the interstellar medium [2].

More than a decade after the first demonstration of a working THz-QCL device [3], the room temperature operation has still not been reached. The highest reported operating temperature of 199.5 K was realized by the well-optimized Al0.15Ga0.85As/GaAs structure within the longitudinal optical phonon depopulation scheme by Fathololoumi et al. in 2012 [4].

Over the years a number of modeling techniques has been developed in order to study the phenomena occurring in QCLs, including such sophisticated methods as the density matrix approach or the non-equilibrium Green’s function formalism [5]. These, combined with the advances in the technology, led to a higher gain and lower waveguide losses through the application of novel lasing schemes. Several of them provide a possible route towards obtaining high operation temperature of the THz-QCLs, i.e., a four level design [6], an optimization of the overlap integral of wavefunctions related to lasing transitions [4], application of a strong magnetic field [7] or using wide-bandgap nitride-based semiconductors [8]. Recently, a room temperature operating terahertz source has been presented, however radiation is generated indirectly, based on intracavity difference frequency generation within a mid-infrared QCL [9].

Optical techniques are versatile for examining semiconductor multiple quantum wells and superlattice properties. They may provide important information in a fast in-situ and non-destructive manner. Among several methods, we may distinguish Raman scattering, photoluminescence and absorption-like methods, such as photoreflectance (PR), transmission and differential transmittance measurements.

A well-established technique to study the intersubband (intraband) transitions is to perform absorption measurement in nonstandard geometries in order to enhance the coupling of light with intersubband electric field components [10]. The standard approach is to wedge a sample at a certain angle, shine the light on it, and perform waveguide-based measurements. In such a case, the incident radiation undergoes several total internal reflections in the sample and the effective coupling factor can be enhanced by orders of magnitude. However, this approach requires sample processing, special experiment configuration as well as a certain doping level. Therefore, in this work a novel approach for the determination of intersubband transitions in the THz range, based on the differential transmittance, will be presented. It is more straightforward than typically used techniques, since it requires no additional sample preparation. Moreover, the data analysis is simple due to the differential character of the spectra, allowing for direct indication of the respective singularities as the optical transitions between the confined states.

Previously, we reported that photoluminescence (emission) and photoreflectance (high sensitivity absorption-like modulation technique), realized within a Fourier-transform (FT) spectrometer-based experimental configuration [11], can provide the information about the electronic structure of the AlGaAs/GaAs superlattices due to the possibility of detecting the interband and intersubband optical transitions [12]. Furthermore, these techniques were successfully employed to examine the growth rates accuracy by the analysis of the Stokes shift between the emission and absorption spectra of the active region of a mid-infrared QCL (at approx. 9 μm) based on an AlGaAs/GaAs material system [13].

In this work, we present the results of experimental and theoretical studies of GaAs/AlGaAs superlattice designed to imitate the active and injector regions of a QCL aimed at much longer wavelengths, corresponding to the terahertz range of radiation. We employed optical spectroscopy techniques, photoreflectance, and differential transmittance to probe the inter- and intra-band transitions, respectively. The differential transmittance has been performed in a broad range, including the terahertz region, to probe the intersubband transitions in the conduction band. The transition energies obtained from the spectroscopic data are compared with theoretical calculations in order to interpret the optical transitions and to provide quantitative information about the growth accuracy. The aim of this work is to show that the described procedure allows for verification of a design of a THz-QCL, before the final structure fabrication (e.g., before processing to a fully operational quantum cascade laser structure) [13].

2 2. Materials and Methods

The investigated sample was grown by molecular beam epitaxy on an (100) oriented semi-insulating GaAs substrate in a Riber Compact 21 T machine. Molecular beams of group III elements were generated from the standard ABN 80 DF effusion cells (filled with Al 6 N5 and Ga 7 N). Arsenic was evaporated from the source as As4 molecules and the As2/As4 ratio were controlled by the temperature of a cracking zone. The temperature of the crystalline surface during the growth process was controlled by a pyrometer and had a constant value of 580 °C.

The layer sequence of the investigated heterostructure starting from the substrate is as follows: 1 μm GaAs buffer layer, 30 nm AlAs layer, 100 nm Si doped GaAs layer, and the active region described in the next paragraph. The entire structure was capped by a 100-nm thick Si doped GaAs layer, which was chemically etched for the purpose of optical characterization. The standard wet etching procedure in a mixture of H3PO4:H2O2:H2O was used in order to ensure smooth surface and prevent the light scattering during the optical investigation.

The active region of the investigated structure consists of 228 periods of alternating Al0.15Ga0.85As and GaAs layers of barrier and well, respectively. The layers’ width sequence of an individual period, with 5 % correction estimated from the X-ray diffraction ω-2θ scan, is as follows: 4.33; 17.88; 4.54; 9.4; 2.6; 8.6; 4.33 nm, where barriers are in bold and the Si doped layer is underlined (doping level of 6 × 1016 cm−3). Figure 5 illustrates the layers’ sequence and band edge alignment (not in scale for clarity).

The aforesaid structure designed for emission in the terahertz range has been compared with a reference sample also being an AlGaAs/GaAs superlattice, however designed to be an active region of a mid-infrared QCL. For more information about the reference sample (its structure and optical properties) the reader is referred to Refs. [13–15].

In order to study the optoelectronic properties of the investigated sample, three independent optical absorption-like techniques were utilized: transmission, photoreflectance, and differential transmittance. Photoreflectance was employed to detect the interband transitions between the confined levels in the wells. In this case, a standard setup was used in the so-called bright configuration, where the tungsten halogen lamp light is reflected off the sample and then dispersed by a single-grating 0.55-m focal length monochromator. The same spot on the sample was illuminated by the pump beam—60 mW of 660 nm continuous-wave semiconductor diode laser, which was mechanically modulated at a reference frequency of 280 Hz (duty cycle of 50 %). A phase-sensitive detection was enabled by a lock-in amplifier coupled to an Si photodiode as a detector. The sample was mounted in a liquid-helium closed-cycle refrigerator system for the measurements from 10 to 250 K, at 50 K intervals. A more detailed description of the PR experimental setup and its schematic diagram can be found in Ref. [16]. Transmission and differential transmittance measurements were performed with a Bruker FTIR vacuum spectrometer Vertex 80v. The differential transmittance, an analogy to differential reflectance [17], is a spectroscopy technique highly sensitive to optical transitions, performed by using rapid-scan mode provided by an FT spectrometer. The schematic setup configuration is presented in Fig. 1. The glowbar and mercury light sources were employed as probe beams. In order to maximize the detector signal in the respective spectral ranges, the former one was used for measurements up to 100 cm−1, while the latter beyond that. A commercial Mylar multilayer beamsplitter was utilized. The Si bolometer was used as a detector to spectrally cover the range of far infrared with a 700 cm−1 cut-off low-pass filter. Both experiments were performed at 10 K, with spectral resolution of 2 cm−1. The sample was mounted inside a liquid-helium cryostat, with polyethylene windows providing suitable transmission in the far infrared. A custom-designed cryostat sample holder was used, providing a 60° angle of incidence in order to increase the coupling of incident light with electric field components in the growth direction.

Fig. 1
figure 1

The scheme of Fourier-transform spectrometer. Although this study focuses on rapid-scan mode measurements, a step-scan measurement with phase-sensitive detection (provided by chopper and lock-in amplifier) is also possible involving such experiments as photoluminescence (PL) or phototransmittance (PT)

Full size image

In the case of differential transmittance, the same 60 mW 660 nm semiconductor laser diode was used as a probe beam. The laser beam was focused onto the sample to the spot of ~1 mm2. Taking into account the electron–hole pair lifetime in the range of 1–10 ns [18] the density of photoexcited electrons’ is about 5 × 1015 cm−3.

3 Results and Discussion

Figure 2 shows transmission spectrum for the investigated sample in a broad spectral range. The spectrum is dominated by phonon-related minima, with no evidence of the intersubband transitions. The 150–650 cm−1 spectral range contains the GaAs-related and AlAs-related minima, segregated into two groups. In the region of 250–300 cm−1 the transmission drops to zero as a result of the strong absorption on longitudinal optical modes (LO), transverse optical modes (TO) and their combinations. The measured energies are in a good agreement with the previously reported data [19, 20]. The region of weak minima from 160 to 235 cm−1 is related to two-phonon absorption. The far infrared radiation field can simultaneously interact with two phonons either via the second-order terms of the dipole momentum or via the third-order terms in the lattice potential [21]. The assignment of the spectral features to the critical points of two-phonon absorption is as follows: the minimum at 195 cm−1 corresponds to the TO-TA two-phonon combination at the L point in the Brillouin zone [22]. The weak absorption dip at the edge of the transmission spectra near 161 cm−1 is understood as the 2TA2 (TA—transverse acoustic) at the Σ point in the Brillouin zone [20]. The AlAs-related Reststrahlen region includes the TO and LO modes marked by blue arrows in Fig. 2 [23].

Fig. 2
figure 2

A broad range transmission spectra measured for resolutions of 2 cm−1. Multiple phonon-absorption lines related to GaAs and AlAs vibration modes are indicated by arrows

Full size image

At this point, it is worth pointing out that in the analyzed transmission spectrum it is impossible to distinguish spectral features corresponding to optical transitions between the confined states in the investigated superlattice. The relevant singularities are invisible mostly due to their overlap with features of structural origin and the probe beam only passing through the sample’s active region once, resulting in a weak absorption. In contrast, the differential transmittance approach is able to overcome the abovementioned drawbacks at almost identical measurement conditions. The spectrum of differential transmittance will be presented below (see. Fig. 4) and the advantages will be emphasized.

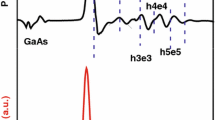
Figure 3a presents the PR results of the investigated superlattice structure in the above-GaAs spectral range, i.e., in the range of QW interband transitions. The spectrum exhibits six well-resolved features corresponding to the transitions between the confined states in the valence and conduction bands. The notation h (l) iej in the figure denotes the transition between the ith heavy-hole (light-hole) state and the jth conduction subband. In order to fit the PR data, there has been used a well-known formula originating from the derivative of the unperturbed dielectric function [24, 25]:

$$ \frac{\varDelta R}{R}(E)=Re\left[{\displaystyle \sum_{j=1}^n{C}_j\cdot {e}^{i{\theta}_j}}{\left(E-{E}_j+i\cdot {\varGamma}_j\right)}^{-{m}_j}\right] $$
Fig. 3
figure 3

The photoreflectance spectra a measured in the above-GaAs spectral range. Each singularity represent optical transition between hole and electron state. Solid lines stand for fitting curves. b Transition energies evolution in a broad range of temperatures

Full size image

where n is the number of optical transitions and the number of independent spectral functions used in the fit, C j and θ j are the amplitude and phase parameters, E j and Γ j are the energy and broadening parameters of the transition, respectively. The parameter m refers to the type of an optical transition and the critical point in the Brillouin zone. It has been proven that m = 3 approximates well the lineshape of spectral features related to optical transitions between the confined states in a quantum well or superlattice [26]. Solid lines in Fig. 3a stand for the fitting curves. The vertical bars represent the calculated transition energies between the respective states and well agree with the E j energies obtained from the fitting procedure.

Figure 3b presents the energy versus temperature dependence of each individual transition. All the transitions follow the same trend, preserving the constant difference between each other in a broad range of temperatures from 10 to 200 K. Such a behavior proves that the analyzed singularities are related to the consecutive confined state transitions in the investigated superlattice.

At this point, it is worth mentioning that the e2 and e3 states located in the active double-well are the lower and upper lasing states, respectively, in an operational terahertz emitting device. The gain of an operational device is built upon all allowed optical transitions in the system. The e2e3 optical transition was shown to have a dominant contribution to the overall gain when the external electric field reaches the target value of 12.2 kV/cm [4]. The energy spacing between these two particular states may be estimated by subtracting the h3e3 and h2e2 energies taken from PR data (Fig. 4) and equals to 10 meV. The above approximation differs from the actual value by the h3h2 energy, calculated to be of the order of 1 meV. A more profound discussion can be found in the next paragraphs.

Fig. 4
figure 4

The differential transmittance spectra of quantum well (solid) and reference (dotted) samples. Two intraband transitions within conduction band are labeled by arrows, while the dashed ellipse indicates the intra-valence band absorption. For both samples, a broad region related to GaAs Reststrahlen band is visible and shaded

Full size image

Figure 4 presents the differential transmittance spectra of the quantum well and the reference samples in solid and dotted lines, respectively. According to the calculations, the wavefunctions of the second and third confined states have the largest overlap integral in the active double-well, which makes this optical transition a parity-allowed one and intensive in the optical spectra. The energy difference between the states e2 and e3 were calculated to be 8.8 meV. It corresponds well with the singularity at around 75 cm−1 (9.3 meV) observed for non-biased structure and attributed to the intersubband transition between the two mentioned states confined in the conduction band well. Absence of that spectral feature for the reference sample proves that it is not a material property related to GaAs or AlAs binary compounds. It is the first time when the intersubband transition in the conduction band is reported for AlGaAs/GaAs material system, in the differential transmittance measurement. The transition between the states e1 and e4 (Fig. 4) is designed to be equal to GaAs LO-phonon energy and thus lies inside the Reststrahlen region (gray shaded). At around 362 cm−1 another feature is present and understood as a transition between the e4 and e5 confined states. A broad region marked with dashed ellipse is attributed to the intra-valence band absorption (IVBA)—multiple transitions between hole states. Such intersubband transitions in the valence band have already been seen in similar material systems [22].

The advantage of the differential-like approach is clearly visible. The spectrum lies on a zero-baseline, thus the determination of the transition energy is straightforward. Although the experiment was performed in a single-pass mode, the modulation introduced by the external cw illumination allows for observation of the relevant singularities.

A summary of all the transition energies extracted from the PR data (gray and light gray arrows) is presented in Fig. 5, together with the band diagram of one stage of the sample’s active region (for clarity, the confined states are shifted vertically). Both intersubband transitions, e2e3 and e4e5, measured by means of differential transmittance, are also indicated.

Fig. 5
figure 5

The one period of an investigated superlattice. The measured optical transitions are indicated by arrows and respective label. The calculated confined states are vertically shifted for clarity

Full size image

In order to better understand the optical properties of the investigated active region (AlGaAs/GaAs superlattice) designed for terahertz applications we supported our measured data with numerical calculations of the energy level structure. All results were computed by solving the Schrödinger equation within the effective mass approximation for one period of the investigated superlattice. Figure 5 shows the conduction band profile of the investigated quantum well structure, with five confined states in the conduction band and six hole states in the valence band. As mentioned in the previous section, the energy separation between the states e2 and e3 may be estimated indirectly by subtracting the h3e3 and h2e2 energies taken from the PR spectra. The calculated values of these transitions are 1.5424 and 1.5328 eV, respectively, with the difference of 9.6 meV. The measured energy spacing extracted from the fitting procedure of the PR data equals to 10 meV. Taking into account the calculated energy difference between the h2 and h3 heavy hole states of ~1 meV, one can estimate the e2-e3 energy to be ~9 meV. It is worth noticing that both the experimental and numerically calculated data were required to make such estimation. The differential transmittance measurement probes transitions between the individual confined states in the conduction band, thus the information about the energy of intersubband transition is more accurate. The wavefunction overlap of the e2 and e3 states has its maximum in the active double-well and is reflected by the singularity at 75 cm−1 (9.3 meV) in Fig. 4. The measured value is in excellent agreement with the calculated energy spacing between mentioned states e2 and e3—(8.8) meV. The optical transition between e1 and e4 states should also be visible in the differential transmittance spectra, however in that spectral range the transmission drops down to almost zero due to very strong absorption related to GaAs vibrational modes and related singularity could not be seen there. The e4e5 (see Fig. 4) transition has also been detected with the energy of 44.9 meV, while the calculated value equals to 46.1 meV, showing a good agreement.

4 Conclusions

Transmission and differential transmittance measurements with the Fourier-transform spectrometer-based concept were performed on AlGaAs/GaAs superlattices imitating the active and injector region of a quantum cascade laser. A singularity at around 75 cm−1 was found and understood as intersubband transition involving second and third confined states in the conduction band, which are expected to predominantly contribute to the lasing in the full device structure under operational conditions. The Schrödinger equation was solved within the effective mass approximation in order to verify that energy spacing. In addition, the analysis of above-GaAs photoreflectance data provided compatible information about the energy distance between the upper and lower lasing states. Eventually, we confirmed that the optical spectroscopy supported by band structure calculations can be used as an efficient tool for the verification of the design of terahertz quantum cascade laser structures and the methods of optical spectroscopy allow for preliminary characterization of the active region without the need of processing the sample to a fully operating device.