Abstract
A semi-intrusive approach for robust design optimization is presented. The stochastic moments of the objective function and constraints are estimated using a Taylor series-based approach, which requires derivatives with respect to design variables, random variables as well as mixed derivatives. The required derivatives with respect to design variables are determined using the intrusive adjoint method available in commercial software. The partial derivatives with respect to random parameters as well as the mixed second derivatives are approximated non-intrusively using finite differences. The presented approach provides a semi-intrusive procedure for robust design optimization at reasonable computational cost while allowing an arbitrary choice of random parameters. The approach is implemented as an add-on for commercial software. The method and its limitations are demonstrated by academic test cases and industrial applications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Deterministic optimization approaches tend to provide designs that are sensitive to variations of parameters such as the applied load, the part geometry or material properties. This motivated a large and broad community of researchers to incorporate considerations of uncertainty in design optimization. One possibility to distinguish these activities is by the approach to quantify uncertainties. The current paper focuses on the widespread concept of probabilistic approaches. Those approaches considering a certain probability (e.g. probability of failure) as objective or constraint for optimization are referred to as reliability-based design optimization (RBDO) approaches, see for instance the overview article by Schuëller and Valdebenito (2010). However, this is not the scope of the current paper. We focus on robust design optimization (RDO) approaches, which aim at reducing the sensitivity of the design. An overview of different approaches to tackle RDO problems is given by, for instance, Park et al. (2006) and more recently by Kanno (2020). Other approaches to robust optimization include the consideration of worst-case designs or load-cases (Ben-Tal et al. 2009; Elishakof and Ohsaki 2010). What all previously mentioned approaches have in common is that the computational cost of optimization under uncertainty is significantly larger (often order of magnitude larger) compared to deterministic optimization.
Maute and Frangopol (2003) were amongst the firsts who incorporated probabilistic analysis into topology optimization, considering a random load component. Various following studies considered loads as random parameters (e.g. Jung and Cho 2004; Kharmanda et al. 2004; Mogami et al. 2006), as this typically involves a small number of random parameters. The first study incorporating random fields, describing the spatial variation of Young’s modulus or geometry, into topology optimization is the paper of Schevenels (2011). They dealt with the large number of random parameters by using Monte Carlo simulations to predict mean and standard deviation of the objective function, which in their study increased the computational cost by factor of 100 compared to a strictly deterministic optimization. Using surrogate models to speed up the Monte Carlo simulations, as for instance in (Balokas et al. 2021), seems challenging due to the high dimension of the parameter space. Hence, Lazarov et al. (2012a) picked up the approach proposed by Doltsinis and Kang (2004) and used the perturbation technique to perform the probabilistic analysis more efficiently, which they embedded into topology optimization. The perturbation technique is based on a Taylor expansion of the residuum and the number of linear equation systems to be solved scales with the number of random parameters. Kriegesmann and Lüdeker (2019) proposed to use the first-order second-moment method for robust design optimization, which is based on a Taylor series of the objective function. This approach requires the solution of only one additional adjoint system and hence, it is the RDO approach with the lowest computational cost. However, due to the linear approximation of the objective function, the approach fails to provide a robust design for certain parameters, such as random loads (Kriegesmann 2021).
The aforementioned approaches, which are based on Taylor series, are highly intrusive. Each combination of objective function or constraints, random variables and design parameters requires a new implementation of adjoint systems to be solved. Commercial software already offers a variety of combinations of objective functions, constraints and parameters for deterministic design optimization, which can easily be used for RDO with Monte Carlo simulations. In contrast, this paper presents a semi-intrusive approach for robust design optimization using a Taylor expansion for the design responses considered as objective function or constraints. The gradients used for deterministic design optimization, which are available in commercial software, are used and the partial and mixed partial derivatives with respect to random parameters are approximated using finite differences. This semi-intrusive approach is implemented as an add-on and does not require modifications of the core source code of the solver. Simultaneously, the implementation offers an arbitrary choice of design variables, objective functions and constraints for the RDO at a much lower computational cost when compared to RDO using Monte Carlo simulations. The application to an academic test case and industrial use cases demonstrates the potentials and limitations of the present semi-intrusive approach.
Often numerical approaches for probabilistic analyses or optimization are referred to as “non-intrusive” if the objective function is called as a “black box”. The method presented in this paper assumes that the gradients with respect to (deterministic) design variables are determined by the adjoint method. This part of course requires a dedicated implementation. Therefore, the approach is referred to as “semi-intrusive”. However, given the fact that these gradients are available in many commercial software, the approach could also be referred to as “non-intrusive”.
2 Semi-intrusive robust design optimization
The current section describes the present optimization setup, the probabilistic approach and the corresponding gradients for mathematical programming optimization.
2.1 Robust design optimization approach
A function g(x,y) is considered as a function of realizations x of the random vector X and the design vector y. Typical examples of such a function are the structural compliance, the maximal stress or the reaction forces at certain locations of the structure. Due to the variability of X, g is also randomly distributed, having the mean value μg and the standard deviation σg.
Typically, robust design optimization aims at minimizing both the mean value μg and the standard deviation σg, compiled in the optimization objective \(\tilde{g}\) defined as
where κ is the weight factor for the standard deviation. The present formulation in Eq. (1) can be interpreted as a multi objective optimization problem, where varying κ provides the Pareto front. However, \(\tilde{g}\) can also be regarded as a quantile of g. For instance, assuming g to be Gaussian and choosing κ = 3 means that \(\tilde{g}\) is a value of g which is exceeded with a probability of 0.135%, whereas the probability of exceedance equals 1.19% when assuming Gumbel distribution (Haldar and Mahadevan 1999). However, during the optimization the distribution type of g is unknown and may change. Therefore, this consideration only helps to find a reasonable magnitude for κ. Note Eq. (1) does not represent a risk averse approach, as demonstrated by Shapiro (2008).
The function \(\tilde{g}\) may serve as an optimization constraint by restricting it to be lower than a given value \(\overline{g}\). Finally, multiple functions \(\tilde{g}_{i}\) may be considered at the same time as objective and constraints (for instance compliance and stress), each having its own weight factor κi. Hence, the optimization problem yields
where I is the number of probabilistic constraints, R is the residual of the state equations, \({\mathbf{\underline {y} }}\) and \({\overline{\mathbf{y}}}\) are the lower and upper bounds of the design variables defined by the vector y. The derivative of the probabilistic objective or a probabilistic constraint \(\tilde{g}_{i}\) is determined by
where the probabilistic methods used in the following determine the variances \(\sigma_{g,i}^{2}\) and their gradients.
Generally, the mean value and the variance of a function g are defined by
where the function fX(x) defines the probability density function of the random vector X.
The simplest but numerically most expensive approach to determine μg and σg is the Monte Carlo method. For that, realizations x(i) of X are generated based on its distribution, and g is numerically evaluated for each realization. The mean and variance using the Monte Carlo method are then estimated using
Typically, the number of realizations m must be very large. Thus, the Monte Carlo approach is numerically very costly when each realization is a full finite element solution for the state equation \({\mathbf{R}}\left( {\mathbf{y}} \right) = {\mathbf{0}}\) in Eq. (2). For the present work, the Monte Carlo method is used only as verification and validation method of the optimization results. Several methods exist for improving the efficiency of the Monte Carlo simulations by reducing the number of realizations for the state equation in Eq. (2) as importance sampling (Haldar and Mahadevan 1999), use of surrogate models (Papadrakakis et al. 1996; Sudret et al. 2017) and multilevel approaches (Krumscheid et al. 2020). However, all the present Monte Carlo simulation approaches are considered computationally too expensive for the present non-parametric optimization including uncertainties.
Consequently, a different type of approach is applied for estimating the stochastic moments, which is based on a Taylor series expansion of the function g at the mean vector μ of the random input vector X. The approach is sometimes referred to as a first-order second-moment (FOSM) method (Kriegesmann and Lüdeker 2019) or a method of moments (Papoutsis‐Kiachagias et al. 2012), and similar to the perturbation approach used in (Doltsinis and Kang 2004; Lazarov et al. 2012a). Thereby, the Taylor expansion of g at μ reads
where n is the number of entries xi of x (i.e. the number of random parameters) and μi are the entries of μ. Inserting Eq. (6) into Eq. (4) yields
and
where cov(Xi, Xj) is the covariance of the i-th and j-th entries of X.
Considering only linear terms of the Taylor expansion in Eq. (6) for the derivation of Eqs. (7) and (8) is referred to as first-order second-moment method. Considering also quadratic terms is referred to as second-order fourth-moment (SOFM) approach, see Appendix A.
2.2 Semi-intrusive determination of gradients
The derivatives with respect to the design variables \({{\partial g} \mathord{\left/ {\vphantom {{\partial g} {\partial y_{k} }}} \right. \kern-\nulldelimiterspace} {\partial y_{k} }}\) are assumed to be known using the adjoint sensitivity approach given by Michaleris et al. (1994) and implemented in, e.g., Abaqus (2021). Then, it is straightforward to implement the gradients of the mean value when using the Monte Carlo method as
where the realization of the value \(g\left( {{\mathbf{x}}^{\left( i \right)} ,{\mathbf{y}}} \right)\) and of the gradient \({{\partial g\left( {{\mathbf{x}}^{\left( i \right)} ,{\mathbf{y}}} \right)} \mathord{\left/ {\vphantom {{\partial g\left( {{\mathbf{x}}^{\left( i \right)} ,{\mathbf{y}}} \right)} {\partial y_{k} }}} \right. \kern-\nulldelimiterspace} {\partial y_{k} }}\) are obtained from the same function call for solving the state equation. Hence, the computational cost for carrying out a Monte Carlo simulation scales with the number of realizations m.
When using the FOSM approach, the derivative of the mean value is simply given by
and the derivative of the variance is given by
The computation of the variance Eq. (8) and its derivative Eq. (11) requires the derivatives of g with respect to the random parameters xi and the mixed derivatives \({{\partial^{2} g} \mathord{\left/ {\vphantom {{\partial^{2} g} {\partial x_{i} \partial y_{k} }}} \right. \kern-\nulldelimiterspace} {\partial x_{i} \partial y_{k} }}\). These mixed derivatives can be determined analytically using, for example, the adjoint method as shown by Kriegesmann and Lüdeker (2019) for a topology optimization minimizing the mean and variance of the compliance subject to a random Young’s modulus or random geometrical properties. For the approach in (Kriegesmann and Lüdeker 2019), only one adjoint system has to be solved in addition to the residual R for the equilibrium. However, the approach in (Kriegesmann and Lüdeker 2019) is highly intrusive for the numerical implementation and requires the analytical implementation of the gradient computation for each combination of objective function g0 and constraints gi (e.g. compliance, stress, displacement, reaction force, …), design variable types yj (relative densities, nodal coordinates, thicknesses, …) and random parameter types xi (e.g. Young’s modulus, load direction, geometry, …).
Therefore, we propose using finite differences with the step size \(\Delta {x}_{i}\) for determining the derivatives with respect to random parameters as follows:
Note that Eqs. (12) and (13) are determined from the same simulation, i.e. n + 1 simulations have to be carried out, where n equals the number of random parameters (i.e. the length of X). If central differences are applied for Eqs. (12) and (13), then 2n + 1 simulations have to be carried out. For the second-order approach the necessary number of simulations is 2n + 1 + ½ (n2–n).
When the number of random parameters xi is small (n ≤ 50), robust design optimization using FOSM and the present finite difference approach in Eqs. (12) and (13) is computationally favorable compared to numerically costly sampling-based probabilistic methods as, for example, the Monte Carlo method. If a spatially varying variable, i.e. a random field is considered, the number of random parameters can easily become much larger. However, the method may still be applied when using a discrete Karhunen-Loève transform to reduce the number of random parameters and perform the finite difference steps with the reduced parameters. This procedure is described in Appendix B. How much the random parameters can be reduced depends on the convergence of the Karhunen-Loève expansion, i.e. on the correlation length of the random field. For instance, Lazarov (2012a) reduced a random field discretized with 40000 elements to only 8 independent parameters. Additionally, the finite difference analyses for the mixed derivatives can be submitted in parallel on an HPC cluster, yielding no or just an insignificant increase in computational runtime when the number of random variables is increased.
Note that the derivatives \({\partial g}/{{\partial y}}\) with respect to the design variables are determined using the adjoint sensitivity approach. The linearization of Eqs. (12) and (13) with respect to design variables yj and the random parameters xi are only quantitatively valid in a given interval of yj and xi. However, numerical experiments show that even if the mathematically linearization of Eqs. (12) and (13) is only valid for a certain interval, equations Eqs. (12) and (13) can still qualitatively capture the overall behavior of the functions g optimized in Eq. (2) when used for a larger interval (Kriegesmann et al. 2011). The approximations of the stochastic moments Eqs. (10) and (11) depend significantly on the step size for the finite differences in Eqs. (12) and (13). A step size of magnitude \(\Delta {x}_{i}=1\dots 1.5\times {\sigma }_{{x}_{i}}\) was found to provide good results for the approximation of stochastic moments (Kriegesmann et al. 2011). Therefore, the larger step size is chosen for its improved approximation of the stochastic moments over a small step size possibly yielding improved local gradient approximations.
3 Numerical implementation
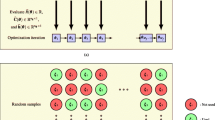
The approach presented in Sect. 2 is implemented as an add-on to commercial software using, for example, Abaqus (2021), Tosca (2021) and Isight (2021). For the present work, Abaqus is used for both the finite element modeling and simulations as well as adjoint derivatives with respect to the design variables. Tosca defines the design variables and reads the derivatives with respect to the design variables from Abaqus. Isight is applied for the finite difference calculations determining the mixed derivatives with respect to the random parameters and the design variables. Figure 1 shows the overall workflow implemented by connecting the different modules using python scripts. The design variables are updated per optimization iteration using mathematical programming based upon the Method of Moving Asymptotes (MMA) approach implemented in Tosca. The individual commercial software components may be replaced by similar software providing the same functionality with respect to the adjoint derivatives and gradient based optimization algorithm.
4 Numerical results
The present approach will be tested on three different optimization targets. Initially, the numerical optimization results address topology strength optimization for an academic test case where the objective is to minimize the mass subject to stress constraints. Secondly, numerical optimization results show the classic topology stiffness optimization for compliance minimization subject to a relative material volume constraint applied to an industrial use case of a bracket design. Finally, the strength optimization problem is also applied to the industrial use case of the bracket design, considering different ranges of input scatter. A worst-case approach to robust strength optimization is compared to the Taylor-based approach presented in this work.
All the present numerical topology optimization results use the so-called SIMP-model [Solid Isotropic Material with Penalization (Bendsøe and Sigmund 2004)] for modeling the constitutive material model as being proportional to a power-law of the relative elemental density for the design variables of all structural design elements in the design domain. Additionally, a density filter is applied for regularization introducing a length-scale and for suppressing checkerboards, see (Sigmund and Maute 2013). The radius of the density filter for all present optimization results is 1.3 compared to the average element size for all elements specified in the design domain. The optimization iteration convergence is considered achieved when the change in elemental densities is equal to or lower than 0.001.
4.1 Strength optimization of an L-bracket
The present section addresses strength topology optimization of an L-bracket model shown in Fig. 2 by minimizing the mass g0 subject to a stress constraint \(\overline{g}_{1}\) of 100 MPa. An elastic material is applied with a Young’s modulus of 70 GPa and a Poisson’s ratio of 0.3, respectively. Figure 2 also shows the discretization of the L-bracket being fully clamped at the top. The deterministic force P = 100 kN is applied at the mid-top of the right leg where also the two random loads x1 = PRV1 and x2 = PRV2 are applied perpendicular to the deterministic force P for the robust design optimization. The L-bracket model mesh consists of 382′684 hexahedral elements (C3D8) yielding 1′213′560 DOFs. Except for the elements attached and close to the clamping and loading, all elements are defined as design space and thereby being the design variables y for Eq. (1). All stresses of elemental integration points of the elements attached to the clamping and to the loading are excluded in the stress calculations for equation Eq. (2) to avoid stress singularities for the optimization setup.
The design response g1 is the von Mises stress of the elemental integration points being applied as a single aggregated response. The stress response is constrained by the stress constraint value \(\overline{g}_{1}\). The stress response for the topology optimization is applied using a relaxation similar to (Bruggi 2008; Holmberg et al. 2013). Additionally, the applied aggregation function is in the form of a p-norm approach for the elemental integration stress points similar to (Bruggi 2008; Duysinx and Bendsøe, 1998; Holmberg et al. 2013; Verbart et al. 2016), avoiding having a stress design response per elemental stress integration point. However, the p-norm approach does not accurately approximate the maximum stress value when using, e.g, \(p=6\). This approximation issue also persists for higher p-values. Therefore, we apply an adaptive scaling method as suggested in (Le et al. 2009; Oest and Lund 2017; Zhang et al. 2019) which ensures that the true maximum stress of the optimized design fulfills the applied stress constraint.
Figure 3a shows the optimized results for the deterministic optimized design where x1 = PRV1 = 0 and x2 = PRV2 = 0. The robust optimized design is shown in Fig. 3b. The random parameters PRV1 and PRV2 are assigned the following values for the robust design optimization: μRV1 = 0, σRV1 = 0.01 P = 1 kN, μRV2 = 0, σRV2 = 0.01 P = 1 kN. The finite difference step size for Eqs. (12) and (13) is \(\Delta x={\sigma }_{\mathrm{RV}}=1\) kN. The robust design optimization is carried out using the FOSM approach and a weight factor κ = 1.
Both optimization approaches yield well converged optimized results as shown by the histograms for the optimized element density distributions in Fig. 4 and the optimization iteration histories shown in Fig. 5. The histograms show a clear solid/void material distribution for both the deterministically optimized design as well as the robust optimized design. Additionally, the present optimized designs have a low volume fraction compared to the design domain. The present robust design optimization approach also yields clear solid/void material distributions for this challenging case. Nonetheless, the differences of the topologies of the optimized designs are only small. The numerical results of the optimizations are listed in Table 1. The performance of each optimized design in terms of robustness shown in Table 2 is determined using the Taylor-based FOSM and SOFM approaches and validated by Monte Carlo simulations considering 100 realizations of random loads. By using the descriptive sampling method in Isight (2021) for generating the samples of random variables, the number of realizations can be reduced from 1000 to 100 without losing the required accuracy. The descriptive sampling technique is used for all subsequent Monte Carlo analyses. The FOSM approach yields a lower mean compliance for the robust optimized design at the cost of slightly higher weight. The standard deviations of the deterministically and robust optimized designs are almost identical. However, the validation of the FOSM approximation of stochastic moments fails. This shows a limitation of the approach considering random loads. For symmetric load cases FOSM yields a standard deviation of 0. Due to small deviations from perfect symmetry of both designs as well as the non-symmetric random parameter PRV1, the estimated standard deviation is not exactly 0 but close to 0, nonetheless. In contrast, the Monte Carlo simulations show that the standard deviation of the maximum stress is in fact larger than estimated by the FOSM approximation. Consequently, the FOSM method should not be used as probabilistic approach for robust design optimization for the present use case.
The limitation of the FOSM approach can be overcome by using a quadratic approximation as the SOFM method for approximating the stochastic moments. In contrast to the invalid FOSM approximation, the numerical performance of the robust optimized design using FOSM estimated by SOFM is valid when compared to the Monte Carlo (MC) simulation as shown in Table 2. Therefore, a second robust design optimization is carried out using the SOFM approach. The optimized design is shown in Fig. 6. The histogram for the relative elemental density distribution in Fig. 7 shows acceptable solid/void material distribution in the design variables. The optimized topology differs significantly from the deterministically optimized design. The numerical results shown in Table 2 show that the robustness, i.e. the standard deviation of the compliance, is significantly reduced at the cost of higher weight. The comparison of the SOFM approximation with Monte Carlo shows the validity of the approach. The increase in computational cost in comparison to the FOSM approach is small (one additional FE analysis per iteration) due to the small number of random parameters.
In summary, robust design optimization of the three-dimensional L-bracket subject to random loads is not valid when using the FOSM method. However, robust design optimization using the SOFM approach yields a structure having an overall improved performance at small computational cost. Additionally, both approaches yield clear results for the solid/void material distribution of the robust designs.
4.2 Compliance optimization of an aircraft bracket
The present section addresses the objective of generating a robust stiffness design for an aircraft bracket. An elastic material is applied having a Young’s modulus of 68 GPa and a Poisson’s ratio of 0.33. Figure 8 shows a bracket being meshed using 448′914 first order linear tetrahedron elements (C3D4) as well as the design and non-design partitions. The loading is introduced using a distribution coupling at the top hole of the bracket and four load cases are considered. The forces F = ± 11.27 kN of load cases 1 and 2 are acting in z-direction. The forces F = ± 6.44 kN are acting in x-direction and applied as load cases 3 and 4, respectively. The sum of the compliance of each load case is considered as the objective function g0. The volume is constrained to remain below or equal to 12.5%. Clamping boundary conditions are applied to the eight connector elements representing the stiffness of bolts at the bottom of the bracket. The bolt connectors are attached to the bracket using rigid distribution couplings. Preliminary numerical studies showed that the stiffness of the four corner bolts is the most sensitive for the optimization as these counteract the bending moments caused by the external forces applied in load case 3 and 4, respectively. Accordingly, the stiffnesses of the four corner bolts are chosen as random parameters for the robust design optimization. The random parameters xi = RVi are implemented as scale factors of the bolt stiffness.
Figure 9 shows the optimized designs for the deterministic and the robust optimization. Histograms for the relative elemental density distributions are provided in Fig. 16. For the deterministic optimization all random variables are fixed at xi = 1. For robust design optimization and evaluation, the random parameters are chosen to have a mean value of μRVi = 1 and a standard deviation of σRVi = 0.57. This standard deviation corresponds to a uniform distribution in the interval [0.01, 1.99]. The scatter was chosen that large because previous numerical studies show that the compliance is not very sensitive with respect to local structural stiffness properties, as also shown in (Kriegesmann and Lüdeker 2019). Considering a scatter that practically allows failure of one bolt can be interpreted as a worst-case or fail-safe approach. The finite difference step size for the gradient approximation is \(\Delta RV =1.5\times {\sigma }_{R{V}_{i}} =0.86\). The factor κ is κ0 = 3 for the robust design optimization objective in Eq. (2). For smaller variations of the random parameters and κ0 = 1 as in the previous section, the robust design optimization does not provide different results than a deterministic optimization. Despite the large scatter of the random parameters, the robust design shows only little differences compared to the deterministic design both in optimized material layout shown in Fig. 9b and numerical results listed in Table 3. This indicates, as additional numerical experiments also show, that the mixed sensitivities have a low dependency upon the present variations of the connector stiffness both for the initial design and optimized design. The FOSM approximation for the robust optimized design indicates a slightly decreased sensitivity with respect to the random variables which is validated by the Monte Carlo simulation. The improved robustness is a result of the additional connections of bolts to the optimized structure. Table 3 shows that the FOSM approximation is not accurate compared to the Monte Carlo validation results for the optimized designs. Especially the standard deviation is underestimated by approximately a factor of two. As stated in Sect. 2.2, the FOSM approximation is based upon a linearization assumption. For the present case this is not valid, since the compliance is a reciprocal function of the bolt stiffness representing the random variables. Thereby, the gradient approximation by finite differences fails to deliver a proper approximation of the nonlinear design response for the FOSM approximation. The limited applicability of FOSM is due to the scatter of the random variables being as significantly large as anticipated for the present example. The assumption of linearity is less problematic for random variables having small variations and consequently causing less variations in the design responses.
Stiffness optimized aircraft bracket designs for compliance topology optimization subject to a volume constraint of 12.5%. The robust optimization objective is to minimize the compliance (μc + 3σc) considering uncorrelated variation of the stiffness of the four corner bolts indicated in Fig. 8b
The robust optimized design shown in Fig. 9b is based on the assumption of uncorrelated random parameters. Therefore, another robust design optimization is performed where correlation between random parameters is assumed. The correlation of the stiffness of adjacent bolts is chosen equal to 0.5. The covariance required for Eq. (8) is given by cov(RVi, RVj) = ρij σ2, where ρij is an entry of the correlation matrix P. Hence, the correlation matrix P is defined as
Table 4 shows an increased standard deviation of the compliance for the deterministically optimized design due to the correlation of random variables defined by Eq. (14). Figure 9c shows the robust optimized design considering correlated random variables alongside the robust design considering uncorrelated random variables (Fig. 9b). The material layout for the robust optimized design considering correlated random variables has an additional connection between the bolts in the middle of the optimized structure to compensate for the increased sensitivity with respect to the correlated scatter of the bolt stiffness. The FOSM approximation in Table 4 is inaccurate again for the case of correlated variables when compared to the values obtained using Monte Carlo simulations. However, the robust optimized design shows a reduced standard deviation in comparison to the deterministically optimized design. The improvement in robustness is validated by the Monte Carlo estimation given in Table 4. Note that for all cases the FOSM approximation indicates a slightly increased mean value while the Monte Carlo simulations show an improvement of the mean compliance. Thereby, the FOSM approximation might be quantitatively inconsistent as discussed in Sect. 2.2, but qualitatively the robust design optimization using FOSM still introduces designs having a reinforcement in the material layout for robustness against variations in the stiffness of the bolts.
Concluding on the stiffness optimization results shown in Fig. 9 and validated in Tables 3 and 4, it is shown that large variations in the stiffness of the bolts are required for impacting the optimized designs, and the changes in the optimized designs are still small considering the large variations of the random variables. Generally, we can conclude that three-dimensional compliance optimized designs for multiple load cases are rather insensitive to variations of random parameters. This conclusion is rather similar to previous findings in the literature for two-dimensional compliance optimization subject to variation of the Young’s modulus or geometrical properties (Kriegesmann and Lüdeker 2019; Lazarov et al. 2012b). The present work confirms this observation for a three-dimensional application.
4.3 Strength optimization of an aircraft bracket
The present section addresses strength optimization of the aircraft bracket presented in the previous section by minimizing the mass subject to a stress constraint. The FE-model is identical to the model in Sect. 4.2 and the optimization setup is identical to the strength optimization of the L-bracket in Sect. 4.1 except for a stress constraint per load case. The maximum von Mises stress value over the elemental integration points per load case are introduced as the design responses g1, g2, g3 and g4, and constrained separately by \(\overline{{g}}_{i}\) = 300 MPa for Eq. (2). The finite difference step size is increased to ΔRV = 1.5 × σRV = 0.86 (based on the findings in (Kriegesmann et al. 2011)) and κ is set to κ = 1.
The deterministically optimized design and the robust design are shown in Fig. 10a and b, respectively. Again, histograms for the relative elemental density distributions are included in Appendix C in Fig. 17 and show clear solid/void material distribution for both the deterministically and robust optimized design. Even though the smoothed results are not perfectly symmetrical with respect to the z-y-plane, the stresses for the forces acting in the opposite directions are practically identical, and therefore considered to be the same when discussing numerical results in the following. The stresses are referred to as σLC 1,2 and σLC 3,4, respectively. The robust optimization yields a design slightly different to the deterministically optimized design. The stress constraint for load cases 1 and 2 is not active for the robust optimal design as shown in the optimization iteration history in Fig. 11b.
The numerical results are listed in Table 5. In contrast to the bracket design optimized for stiffness, the robustness with respect to strength is of concern for the optimized bracket design. The standard deviation of the maximum stress is approximately 1/3 of its mean value based on the Monte Carlo analysis, which is quite large. The reason for this large scatter is that the same distribution of the random variables is considered as in the previous section for stiffness optimization, but the maximum stress is much more sensitive with respect to the random variables than the compliance. Again, FOSM yields an inaccurate approximation of the stochastic moments. The standard deviations are underestimated significantly for both optimized designs and thereby, implying a low sensitivity with respect to the random variables. This causes the structural difference between optimized designs to be minor. However, the qualitative tendency provided by FOSM in terms of standard deviation is correct and therefore, the robust design optimization using FOSM indeed has a lower scatter for the active constraint (load case 3 and 4) as is shown by the results of the Monte Carlo simulation.
As observed in the previous section, the significant scatter of the random variables yields a large and highly nonlinear variation of the stress design response. The maximum stresses of each load case resulting from the Monte Carlo analysis of the robust design are shown in Fig. 12. All four random variables are varied at the same time following a uniform distribution in an interval of [0.01, 1.99]. Four configurations of random variables are marked in each of these plots. The corresponding values for each random parameter are listed in Table 6. The data illustrates the nonlinearity of the design response with respect to the variation of the random variables. Especially the third configuration of the random design variables demonstrates that low values for the random variables do not necessarily yield high stresses, as the stress distribution does not depend solely on the individual random variables, but also highly on the ratio between the random variables.
Stress is a local measure in contrast to global stiffness (represented by compliance). As a result, the maximum stress location does not move continuously but frequently occurs at arbitrary locations in the model when varying the random variables for the bolt stiffness. Therefore, the maximum element stress is generally non-differentiable. For illustration, stress plots of load case 3 for the four configurations of the random variables marked in Fig. 12 are shown in Fig. 13. The location of maximum stress is always in the bottom area of the model close to the bolts, but the location changes non-continuously depending on the individual random variables and their mutual ratio. Consequently, the local approximation, that the FOSM method is based on, fails to provide feasible approximations of the stochastic behavior of the maximum stress measure. Numerical studies using SOFM and a reciprocal approximation for FOSM [see (Kriegesmann and Lüdeker 2021)] did not yield a better approximation of the stochastic moments, and therefore the numerical results are not discussed separately. Consequently, the Taylor-based approximation of stochastic moments fails because of the severe non-linearity of the stress response introduced by the large scatter of the random variables. Again, a limitation of the approach to robust design optimization is shown when large scatter is considered for the random parameters.
Stress plots for robust design having different configurations for the random variables as marked in Fig. 12. Stress distribution is shown for load case 3 and the maximum stress location for the model is marked with a circle
The efficiency of Monte Carlo simulations can be increased by using surrogates models, see for instance (Balokas et al. 2021). We trained two different types of surrogate models, namely Kriging and Polynomial Chaos Expansion, for estimating the maximum stress as a function of the random parameters. However, even when training these surrogate models using the same 100 samples as considered for the plain Monte Carlo simulation using descriptive sampling for the random parameters, the estimated stochastic moments of the maximum stress deviate significantly. The reason is the non-smooth and highly non-linear stress response as shown in Fig. 12.
4.3.1 Small scatter of random variables
As previously discussed, robust design optimization considering heavily scattering random variables and design responses is a limitation of the present Taylor-based approach. Therefore, the scatter of the random parameters is reduced and a smaller standard deviation of σRVi = 0.1 is applied. The reduced standard deviation corresponds to a uniform distribution in the interval [0.83, 1.17]. The finite difference step size is chosen to ΔRV = 1.5 × σRV = 0.15 and the factor κ for the robustness constraint remains at κ = 1.
The optimized robust design is shown in Fig. 14b next to the deterministically optimized aircraft bracket. The corresponding histograms of the relative elemental material distributions are shown in Fig. 17 in Appendix C. The difference in topologies of the two optimized designs is now more pronounced even though the scatter of the random parameters considered is smaller compared to the scatter applied in the previous section. The numerical performance of both designs listed in Table 7 shows that the robustness regarding maximum stress is not of concern when the scatter of the bolt stiffness is small. The robust design optimization yields a design that satisfies the robustness constraints in Eq. (2). However, this result is only obtained by improving the mean performance of the design while the robustness is actually decreased. Still, the method yields a clear converged design with respect to the.solid/void material distribution, and the approximation of stochastic moments is successfully validated by Monte Carlo simulations.
4.3.2 Robust design optimization using design of experiments
Due to the computational cost of embedding Monte Carlo simulations in a RDO and due to the lack of accuracy of FOSM in presence of large input scatter, another approach for robustness in strength optimization is tested. Instead of performing a full Monte Carlo simulation, only designs considering possible combinations of extreme values for the random variables may be considered for the optimization. Two different Designs of Experiments (DOE) are applied in order to use the results of each evaluation as individual constraints for the robust design optimization. This approach resembles a worst-case optimization by means of DOE.
One DOE is a reduced axial point design and the other is a central composite design, combining a full factorial with the axial point design for the random variables (Dean 2017). The individual designs are generated by considering a mean value of μRVi = 1 and axial points of μRVi ± ΔRV = 1 ± 0.86, correlating to the large scatter of the random variables considered in Sect. 4.2 and 4.3, respectively. The maximum stresses of each design are considered as individual constraints for the optimization. The axial point design yields constraints for each pair of load cases and therefore, eight constraints in total. The central composite design considers a full 24 factorial design as well as the four axial points for the random variables yielding 20 constraints for each pair of load cases and a total of 40 constraints (see Appendix D for the corresponding design matrices). The designs obtained using these two approaches are shown in Fig. 15. The final designs are evaluated using a Monte Carlo simulation, and the stochastic moments listed in Table 8 show that the variability of maximum stress is reduced compared to the deterministically optimized design. The central composite design yields a design having a lower standard deviation than the robust optimized design in Sect. 4.3, even though the standard deviation is not explicitly considered in the optimization. The computational cost of the central composite DOE using 20 function calls per iteration is significantly larger than for the axial point DOE (4 function calls) and the RDO using FOSM (5 function calls). This discrepancy increases with the number of random parameters considered. For structures subject to large scatter of the random parameters, the central composite worst-case approach is an alternative to the Taylor-based approach only if the number of random variables is very small. The computational cost of this DOE-based approach increases rapidly and nevertheless, a Monte Carlo simulation has to be performed to determine the stochastic performance of the optimized design. The Taylor-based FOSM method provides a more cost-efficient approach to determine robust designs for problems having a moderate amount of random variables as shown in the present work.
5 Conclusions and outlook
A new semi-intrusive approach for robust topology optimization is presented. The semi-intrusive approach has two motivations. Firstly, it allows an arbitrary choice of design responses and random parameters. Secondly, the approach approximates the mean and standard deviation of design responses with respect to the random variables using the Taylor series-based first-order second-moment (FOSM) method or the second-order fourth-moment (SOFM) method, because using Monte Carlo simulations for determining the robustness in each optimization iteration is infeasible due to high computational cost. The numerical implementation for the mixed gradients combines existing adjoint derivatives with respect to the topology design variables and derivatives with respect to the random variables using finite differences. The adjoint sensitivities with respect to the design variables are assumed to be implemented intrusively in a given finite element solver, while the finite differences for the gradient approximation with respect to the random variables are implemented non-intrusively using additional mathematical programming. When the number of random variables is significantly lower than the number of topology design variables, the gradient calculations using finite differences can be parallelized using a HPC cluster environment to reduce the runtime significantly. The gradients are then applied in a mathematical optimization.
Consequently, the present semi-intrusive robust design optimization approach has a moderately low runtime and is easy to implement for an arbitrary choice of random parameter types. However, it has the drawback that the robustness is approximated linearly. This is presented using numerical examples for both academic and industrial models, showing the approach is practically feasible with respect to the computational cost, and that the FOSM method yields similar responses compared to those obtained using Monte Carlo simulations for small scatter of the random variables. For larger scatter of the random variables, the stochastic moments approximated using the FOSM method are different in comparison with a Monte Carlo simulation. Therefore, the linearization for calculating the FOSM method is not validated generally. However, the robust optimized topology can still be driven to a more robust design compared to a deterministically optimized design. All examples show a clear solid/void material distribution while having low volume fractions compared to the design domain. Thus, the method yields clear converged solid/void material distributions when robustness is included in the optimization formulation for these challenging cases.
The semi-intrusive approach is used for examining the design impact of uncertainties on both stiffness optimized designs and strength optimized designs. Some of the observations previously reported in the literature for two-dimensional stiffness optimization under uncertainty can similarly be observed in the present three-dimensional stiffness optimization under uncertainty. Practically, robustness is of no concern for stiffness optimization (compliance minimization) when having more than two load cases. This has now been shown for three-dimensional examples. Furthermore, the FOSM method and the SOFM method provide feasible results within the limitations discussed, while the evaluation of the Taylor-based methods is computationally inexpensive compared with sampling-based probabilistic methods.
In contrast to stiffness topology optimization, robustness is of practical concern for strength topology optimization. However, the approximation of stochastic moments using Taylor-based methods fails, because the locations of the maximum stress are frequently relocating positions location-wise subject to variations of the random variables. Thereby, the stress responses are highly discontinuous for large scatter of the random variables, and approximation methods for Taylor-based (e.g., FOSM) or sampling-based (e.g., Kriging) determination of stochastic moments fail due to the discontinuity in the stress responses with respect to large variations of the random variables. Consequently, only the computationally very expensive Monte Carlo simulation is feasible for robust design optimization subject to large scatter of random variables in strength topology optimization. Nonetheless, the Taylor-based approximation methods for the robustness work mathematically well when having small scatter of the random variables
6 Replication of results
All optimizations in this work are performed using penalty factor of 3 for the SIMP approach and a filter radius of 1.3 relative to the mesh size. Additional scripts generated during the study that extend the functionality of SIMULA Abaqus and Tosca are available from the corresponding author on reasonable request.
References
Abaqus (2021) SIMULIA User Assistance. Dassault Systèmes
Balokas G, Kriegesmann B, Czichon S, Rolfes R (2021) A variable-fidelity hybrid surrogate approach for quantifying uncertainties in the nonlinear response of braided composites. Comput Methods Appl Mech Eng 381:113851. https://doi.org/10.1016/j.cma.2021.113851
Bendsøe MP, Sigmund O (2004) Topology optimization theory, methods, and applications, 2nd edn. Springer, Heidelberg
Ben-Tal A, Ghaoui LE, Nemirovski A (2009) Robust Optimization. Princeton University Press. https://doi.org/10.1515/9781400831050
Bruggi M (2008) On an alternative approach to stress constraints relaxation in topology optimization. Struct Multidisc Optim 36:125–141. https://doi.org/10.1007/s00158-007-0203-6
Dean AM (2017) Design and analysis of experiments. Springer
Doltsinis I, Kang Z (2004) Robust design of structures using optimization methods. Comput Methods Appl Mech Eng 193:2221–2237. https://doi.org/10.1016/j.cma.2003.12.055
Duysinx P, Bendsøe MP (1998) Topology optimization of continuum structures with local stress constraints. Int J Numer Meth Eng 43:1453–1478
Elishakof I, Ohsaki M (2010) Optimization and anti-optimization of structures under uncertainty. Imperial College Press, London
Haldar A, Mahadevan S (1999) Probability, reliability and statistical methods in engineering design. Wiley, New York
Holmberg E, Torstenfelt B, Klarbring A (2013) Stress constrained topology optimization. Struct Multidisc Optim 48:33–47
Isight (2021.) , SIMULIA User Assistance. Dassault Systèmes
Jung H-S, Cho S (2004) Reliability-based topology optimization of geometrically nonlinear structures with loading and material uncertainties. Finite Elem Anal Des 41:311–331. https://doi.org/10.1016/j.finel.2004.06.002
Kanno Y (2020) On three concepts in robust design optimization: absolute robustness, relative robustness, and less variance. Struct Multidisc Optim. https://doi.org/10.1007/s00158-020-02503-9
Kharmanda G, Olhoff N, Mohamed A, Lemaire M (2004) Reliability-based topology optimization. Struct Multidiscip Optim 26:295–307. https://doi.org/10.1007/s00158-003-0322-7
Kriegesmann B, Lüdeker JK (2019) Robust compliance topology optimization using the first-order second-moment method. Struct Multidisc Optim 60:269–286. https://doi.org/10.1007/s00158-019-02216-8
Kriegesmann B, Rolfes R, Hühne C, Kling A (2011) Fast probabilistic design procedure for axially compressed composite cylinders. Compos Struct 93:3140–3149. https://doi.org/10.1016/j.compstruct.2011.06.017
Kriegesmann B, Lüdeker JK (2021) Reciprocal first-order second-moment method. arXiv:2105.12230 [stat].
Kriegesmann B (2021) On the applicability of first‐order approximations for design optimization under uncertainty. In: Challamel N, Kaplunov J, Takewaki I (eds) Modern trends in structural and solid mechanics 3: non‐deterministic mechanics. Wiley, pp 39–60. https://doi.org/10.1002/9781119831839.ch3
Krumscheid S, Nobile F, Pisaroni M (2020) Quantifying uncertain system outputs via the multilevel Monte Carlo method: part I: central moment estimation. J Comput Phys 414:109466. https://doi.org/10.1016/j.jcp.2020.109466
Lazarov BS, Schevenels M, Sigmund O (2012a) Topology optimization with geometric uncertainties by perturbation techniques. Int J Numer Meth Engng 90:1321–1336. https://doi.org/10.1002/nme.3361
Lazarov BS, Schevenels M, Sigmund O (2012b) Topology optimization considering material and geometric uncertainties using stochastic collocation methods. Struct Multidisc Optim 46:597–612. https://doi.org/10.1007/s00158-012-0791-7
Le C, Norato J, Bruns T, Ha C, Tortorelli D (2009) Stress-based topology optimization for continua. Struct Multidisc Optim 41:605–620. https://doi.org/10.1007/s00158-009-0440-y
Maute K, Frangopol DM (2003) Reliability-based design of MEMS mechanisms by topology optimization. Comput Struct 81:813–824. https://doi.org/10.1016/S0045-7949(03)00008-7
Michaleris P, Tortorelli DA, Vidal CA (1994) Tangent operators and design sensitivity formulations for transient non-linear coupled problems with applications to elastoplasticity. Int J Numer Meth Engng 37:2471–2499. https://doi.org/10.1002/nme.1620371408
Mogami K, Nishiwaki S, Izui K, Yoshimura M, Kogiso N (2006) Reliability-based structural optimization of frame structures for multiple failure criteria using topology optimization techniques. Struct Multidiscip Optim 32:299–311. https://doi.org/10.1007/s00158-006-0039-5
Oest J, Lund E (2017) Topology optimization with finite-life fatigue constraints. Struct Multidisc Optim 56:1045–1059. https://doi.org/10.1007/s00158-017-1701-9
Papadrakakis M, Papadopoulos V, Lagaros ND (1996) Structural reliability analyis of elastic-plastic structures using neural networks and Monte Carlo simulation. Comput Methods Appl Mech Eng 136:145–163. https://doi.org/10.1016/0045-7825(96)01011-0
Papoutsis-Kiachagias EM, Papadimitriou DI, Giannakoglou KC (2012) Robust design in aerodynamics using third-order sensitivity analysis based on discrete adjoint. Application to quasi-1D flows. Int J Numer Meth Fluids 69:691–709. https://doi.org/10.1002/fld.2604
Park G-J, Lee T-H, Lee KH, Hwang K-H (2006) Robust design: an overview. AIAA J 44:181–191. https://doi.org/10.2514/1.13639
Schevenels M, Lazarov BS, Sigmund O (2011) Robust topology optimization accounting for spatially varying manufacturing errors. Comput Methods Appl Mech Eng 200:3613–3627. https://doi.org/10.1016/j.cma.2011.08.006
Schuëller GI, Valdebenito MA (2010) Reliability-based optimization: an overview. Comput Technol Rev 1:121–155
Shapiro A (2008) Stochastic programming approach to optimization under uncertainty. Math Program 112:183–220. https://doi.org/10.1007/s10107-006-0090-4
Sigmund O, Maute K (2013) Topology optimization approaches: a comparative review. Struct Multidisc Optim 48:1031–1055. https://doi.org/10.1007/s00158-013-0978-6
Sudret B, Marelli S, Wiart J (2017) Surrogate models for uncertainty quantification: An overview. In: 2017 11th European Conference on Antennas and Propagation (EUCAP). Presented at the 2017 11th European Conference on Antennas and Propagation (EUCAP), pp 793–797. https://doi.org/10.23919/EuCAP.2017.7928679
Tosca (2021) SIMULIA User Assistance. Dassault Systèmes
Verbart A, Langelaar M, van Keulen F (2016) Damage approach: a new method for topology optimization with local stress constraints. Struct Multidisc Optim 53:1081–1098. https://doi.org/10.1007/s00158-015-1318-9
Zhang S, Le C, Gain AL, Norato JA (2019) Fatigue-based topology optimization with non-proportional loads. Comput Methods Appl Mech Eng 345:805–825. https://doi.org/10.1016/j.cma.2018.11.015
Acknowledgements
The work presented was supported through the program Calls for Transfer (reference number C4T532) funded by the Behörde für Wissenschaft, Forschung, Gleichstellung und Bezirke der Freien und Hansestadt Hamburg (BWFGB). The financial support is gratefully acknowledged.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Second-order approximation
Using a second-order Taylor series, the approximation of the variance is given by
This is referred to as second-order fourth-moment approach. All derivatives are evaluated at the mean vector of the random vector μX. The stochastic moments μij refer to the covariance of Xi and Xj, μijk is the third joint central moment of Xi, Xj and Xk, and μijkl is the fourth joint central moment, i.e.
Assuming independence of the random variables, Eq. (15) can be simplified to
Here, only joint central moments of a random parameter with itself are considered. For instance, the fourth central moment of Xi is now written as μiiii = μi,4. If the random variables are not independent, the transformation discussed in Appendix B needs to be applied.
The second order derivatives are determined with central differences
Determining mixed derivatives requires several function calls. The number of required function calls increases quadratically with the number of random parameters, namely 2n + 1 + ½ (n2 ˗ n).
Appendix B: Transformation to independent random parameters and parameter reduction
In general, random parameters may be dependent and hence, Eq. (15) has to be used for the second-order approach instead of Eq. (17). However, a random vector X having correlated entries can be transformed to a vector with uncorrelated entries Z using the transformation
Here, μX is the mean vector and ΣX the covariance matrix of X. The random vector Z has zero mean and its covariance matrix is the identity matrix. Hence, the entries of Z are uncorrelated and the second moments evaluate to μii = 0 for I ≠ j. However, the entries of Z are not independent, and their higher-order joint moments may be different from zero. If X follows Gauss distribution, then the entries of Z are indeed independent. So in order to obtain independent parameters, the entries of X first have to be transformed to Gauss distribution by using the Rosenblatt transformation (see e.g. (Haldar and Mahadevan 1999)) and also the mean vector and covariance matrix of this transformed vector have to be determined. Then, the transformation Eq. (19) can be applied to obtain independent parameters. Afterwards, the Taylor series in Eq. (6) is expanded in terms of the transformed parameters Zi and hence, also the finite difference steps in Eqs. (12), (13) and (18) are carried out for Zi.
The transformation Eq. (19) may also be applied for reducing the number of random parameters. Especially when a spatially varying quantity (e.g. when material parameters change within a structure) is considered, the number of random parameters equals the number of elements of the discretized random field (which typically, but not necessarily, equals the number of finite elements). The entries of adjacent elements are typically strongly correlated and the correlation in space is described by the correlation length. In this scenario, the covariance matrix ΣX is very large, but has very few eigenvalues significantly different from zero. The root of ΣX in this case can be determined from its spectral decomposition, i.e.
where Q is a matrix with eigenvectors qi of ΣX and Λ is a diagonal matrix with the eigenvalue λi of ΣX. Then the transformation Eq. (19) yields
By restricting the number n of considered eigenvalues and eigenvectors, the length of the transformed vector Z, i.e. the number of random variables, is reduced. This procedure is also referred to as principal component analysis or discrete Karhunen-Loève transformation. It has been demonstrated that one can reduce the number of random variables describing a random field by orders of magnitude without significant loss of accuracy (Kriegesmann et al. 2011; Lazarov et al. 2012a).
Appendix C: Histograms for relative elemental densities
The following histograms show the material distribution of the relative elemental densities.
Appendix D: Design of experiment
For the Design of Experiment the combinations of random variable RVi shown in Tables
9 and
10 are used. The central composite design combines both, the axial point and the full factorial design.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Steltner, K., Pedersen, C.B.W. & Kriegesmann, B. Semi-intrusive approach for stiffness and strength topology optimization under uncertainty. Optim Eng 24, 2181–2211 (2023). https://doi.org/10.1007/s11081-022-09770-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-022-09770-z