Acceleration of iterative refinement for singular value decomposition

Abstract

We propose fast numerical algorithms to improve the accuracy of singular vectors for a real matrix. Recently, Ogita and Aishima proposed an iterative refinement algorithm for singular value decomposition that is constructed with highly accurate matrix multiplications carried out six times per iteration. The algorithm runs for the problem that has no multiple and clustered singular values. In this study, we show that the same algorithm can be run with highly accurate matrix multiplications carried out five times. Also, we proposed four algorithms constructed with highly accurate matrix multiplications, two algorithms with the multiplications carried out four times, and the other two with the multiplications carried out five times. These algorithms adopt the idea of a mixed-precision iterative refinement method for linear systems. Numerical experiments demonstrate speed-up and quadratic convergence of the proposed algorithms. As a result, the fastest algorithm is 1.7 and 1.4 times faster than the Ogita-Aishima algorithm per iteration on a CPU and GPU, respectively.

1 Introduction

This study investigates the singular value decomposition for $A \in \mathbb {R}^{m \times n}$:

$$\begin{aligned} A = U \Sigma V^T, \end{aligned}$$

(1)

where $U \in \mathbb {R}^{m \times m}$ and $V \in \mathbb {R}^{n \times n}$ are orthogonal matrices whose ith columns are the left singular vectors $u_{(i)} \in \mathbb {R}^{m}$ for $i=1,\dots ,m$ and the right singular vectors $v_{(i)} \in \mathbb {R}^{n}$ for $i=1,\dots ,n$, respectively and $\Sigma \in \mathbb {R}^{m \times n}$ is a rectangular diagonal matrix whose ith diagonal elements are the singular values $\sigma _i \in \mathbb {R}$ for $i=1,\dots ,n$. Throughout the paper, we assume that $m \ge n$. The approximation $\hat{u}_{(i)} \approx u_{(i)}$, $\hat{\sigma }_i \approx \sigma _i$, and $\hat{v}_{(i)} \approx v_{(i)}$ for all i can be obtained by using various numerical solvers for singular value decomposition, e.g., gesdd, gesvd, gesvdx in LAPACK [1] and svd, svds, or svdsketch in MATLAB.

Now, for $k \le n$, let

$$\begin{aligned} U_{1:k}&:= (u_{(1)},\dots ,u_{(k)}),&\quad \hat{U}'_{1:k}&:= (\hat{u}'_{(1)},\dots ,\hat{u}'_{(k)}){} & {} \in \mathbb {R}^{m \times k},\\ V_{1:k}&:= (v_{(1)},\dots ,v_{(k)}),&\quad \hat{V}'_{1:k}&:= (\hat{v}'_{(1)},\dots ,\hat{v}'_{(k)}){} & {} \in \mathbb {R}^{n \times k} \end{aligned}$$

with $\hat{u}'_{(i)}:= \hat{u}_{(i)}/\Vert \hat{u}_{(i)}\Vert _2$ and $\hat{v}'_{(i)}:= \hat{v}_{(i)}/\Vert \hat{v}_{(i)}\Vert _2$, and $\hat{\Sigma }'_{k}:= \textrm{diag}(\hat{\sigma }'_1,\dots ,\hat{\sigma }'_k) \in \mathbb {R}^{k \times k}$ with $\hat{\sigma }'_i:= (\hat{u}'_{(i)})^TA\hat{v}'_{(i)}$. The residuals are defined as

$$\begin{aligned} R_{1:k} := A\hat{V}'_{1:k}-\hat{U}'_{1:k}\hat{\Sigma }'_{k} ,\quad S_{1:k} := A^T\hat{U}'_{1:k}-\hat{V}'_{1:k}\hat{\Sigma }'_{k}, \end{aligned}$$

and the gap of the singular values is given by

$$\begin{aligned} \delta _k:=\min _{\begin{array}{c} 1 \le i\le k\\ k<j\le \max (n,k+1) \end{array}}|\hat{\sigma }'_i-\sigma _j|, \end{aligned}$$

(2)

where $\sigma _{n+1}:= 0$ for the sake of convenience. Wedin [2] proposed the sin$\Theta$ theorem for singular value decomposition extending the sin$\Theta$ theorems for Hermitian matrices proposed by Davis and Kahan in [3]. If $\delta _k > 0$, then from [2], it holds that

$$\begin{aligned} \sqrt{\Vert \sin \Theta (U_{1:k},\hat{U}'_{1:k})\Vert _F^2+\Vert \sin \Theta (V_{1:k},\hat{V}'_{1:k})\Vert _F^2} \le \frac{\sqrt{\Vert R_{1:k}\Vert _F^2+\Vert S_{1:k}\Vert _F^2}}{\delta _k}, \end{aligned}$$

(3)

where $\Theta (U_{1:k},\hat{U}'_{1:k})$ and $\Theta (V_{1:k},\hat{V}'_{1:k})$ are matrices of canonical angles (see [4]) between $U_{1:k}$ and $\hat{U}'_{1:k}$ and between $V_{1:k}$ and $\hat{V}'_{1:k}$, respectively, and $\Vert \cdot \Vert _F$ denotes the Frobenius norm. Note that Dopico [5] also proposed a similar theorem. From (3), the smaller the value of $\delta _k$ in (2), the lower the accuracy of the computed singular vectors. Thus, iterative refinement methods are useful for obtaining sufficiently accurate results in singular value decomposition.

Let $\hat{U}:= (\hat{u}_{(1)},\dots ,\hat{u}_{(m)})$ and $\hat{V}:= (\hat{v}_{(1)},\dots ,\hat{v}_{(n)})$. Davies and Smith proposed an iterative refinement algorithm for singular value decomposition of $\hat{U}^TA\hat{V}$ in [6]. However, the singular values for $\hat{U}^TA\hat{V}$ are slightly perturbed compared to the exact singular values for the original matrix A. Convergence to results that include perturbations indicates a limitation of the achievable accuracy using the Davies-Smith algorithm. Recently, Ogita and Aishima proposed an iterative refinement algorithm for singular value decomposition of A constructed with highly accurate matrix multiplications carried out six times per iteration in [7]. That algorithm converges to exact singular vectors of A when $\hat{U}$ and $\hat{V}$ are moderately accurate.

The main contributions of this study are

• speeding up the Ogita-Aishima algorithm and

• performance evaluation of the proposed methods on a CPU and GPU when improving the accuracy of $\hat{U}$ and $\hat{V}$ from double-precision to quadruple-precision or from single-precision to double-precision.

We use the following environments for numerical experiments in this paper:

• Env. 1) MATLAB R2021a on a personal computer with an Intel Core i9-10900X CPU (3.70 GHz) with 128 GB main memory, a GeForce RTX 3090 GPU with CUDA 11.6, and Windows 10 operating system

• Env. 2) MATLAB R2021b on a personal computer with four AMD EPYC 7542 CPUs (2.90 GHz) with 512 GB shared main memory, a A100 Tensor Core GPU with CUDA 11.3, and Ubuntu 20.04.2 LTS operating system

Table 1 Computing time in seconds for matrix multiplication of $A \in \mathbb {R}^{n \times n}$ and $B \in \mathbb {R}^{n \times n}$ for $n = 10000$ using Env. 1

Generally, double-precision arithmetic is faster than arbitrary precision arithmetic implemented in software or arithmetic for multiple-component format values, such as double-double arithmetic [8, 9]. Moreover, on an enthusiast-class GPU, such as the GeForce RTX 3090, single-precision arithmetic is much faster than double-precision arithmetic. For example, using Env. 1, we obtain the results shown in Table 1. The table indicates double-precision matrix multiplication is 1353 times faster than quadruple-precision on CPU and single-precision matrix multiplication is 34 times faster than double-precision on GPU. Note that for quadruple-precision arithmetic in Table 1, we use the Advanpix Multiprecision Computing Toolbox for MATLAB [10]. Hence, lower-precision computations are much faster than higher-precision computations. Thus, we consider algorithms that reduce the cost of higher-precision computations at the expense of increasing the cost of lower-precision computations.

The computing time ratio, (single-precision arithmetic) : (double-precision arithmetic), for singular value decomposition is about 1 : 2 to 2 : 3 on a CPU and GPU in Env. 1 and 2, respectively. Moreover, matrix multiplication can be performed much faster than singular value decomposition. For example, from Table 2, using the single-precision results as the initial guess, the Ogita-Aishima algorithm with double-precision matrix multiplication can be run for $(22.7-15.4)/(0.11 \cdot 6) \approx 11$ iterations within the double-precision computing time. For a linear system, LAPACK provides a routine dsgesv that computes an initial guess for the solution using single-precision arithmetic and obtains double-precision equivalent results by using the mixed-precision iterative refinement method. Our study will enable the development of a similar routine for singular value decomposition.

Table 2 Computing time in seconds for matrix multiplication of A and B and the singular value decomposition of A for $A \in \mathbb {R}^{n \times n}$ and $B \in \mathbb {R}^{n \times n}$ for $n = 10000$ using GPU using Env. 2

In this study, we first show that the Ogita-Aishima algorithm can be executed with highly accurate matrix multiplications carried out four times per iteration, that is, with one fewer multiplication than in their original paper. Next, we propose four iterative refinement algorithms for singular value decomposition, combining the idea of a mixed-precision iterative refinement method for a linear system with the Ogita-Aishima algorithm. Those algorithms are constructed with highly accurate matrix multiplications carried out either four or five times per iteration. The Ogita-Aishima algorithm and proposed algorithms (Algorithms 5, 6, and 8 in the paper) are the same in exact arithmetic, their limiting accuracy in finite precision is different, and will be explored experimentally in this work. Numerical experiments are conducted to demonstrate speed-up and quadratic convergence of the proposed algorithms on a CPU and GPU.

The remainder of this paper is organized as follows: Section 2 introduces results obtained in previous studies; Section 3 presents the proposed iterative refinement algorithms for singular value decomposition; Section 4 presents numerical examples to illustrate the efficiency of the proposed algorithms; and Section 5 provides final remarks.

2 Notation and previous work

2.1 Notation

Let $(\cdot )_h$ and $(\cdot )_{\ell }$ denote the results of numerical arithmetic, where all operations inside the parentheses are executed at higher- and lower-precision, respectively. The combinations of precision [higher precision and lower precision] using in this study are [quadruple-precision and double-precision] and [double-precision and single-precision]. For simplicity, we will omit terms less than $\mathcal {O}(m^kn^\ell )$, $k+\ell = 3$ from the operations count. For example, we will write $s_1m^3+s_2m^2n+s_3mn^2+s_4n^3+s_5m^2+s_6mn+s_7n^2+\cdots$ operations for $s_i \in \mathbb {N}$ as $s_1m^3+s_2m^2n+s_3mn^2+s_4n^3$ operations.

2.2 Mixed-precision iterative refinement technique

We consider a linear system $Ax = b$ for $x,b \in \mathbb {R}^n$ and a non-singular matrix $A \in \mathbb {R}^{n \times n}$. Let $\hat{x} \approx x$ be a computed solution to $Ax=b$. There is an iterative refinement algorithm with mixed-precision arithmetic to improve the accuracy of $\hat{x}$. The process is shown in Algorithm 1.

Iterative refinement for the approximate solution $\hat{x}$ of a linear system $Ax=b$. The initial $\hat{x}$ is obtained using lower-precision arithmetic.

Note that if the matrix decomposition of A is already obtained for the initial approximation $\hat{x}$, the cost of line 4 is almost negligible. For using a solver based on LU factorization, Wilkinson [11] gave the error analysis for fixed-point arithmetic, and Moler [12] extended that for floating-point arithmetic. Jankowski and Woźniakowski [13] showed that the algorithm with an arbitrary solver could be made stable in the usual sense by normwise error analysis. Skeel [14] also showed that with a solver based on LU factorization by elementwise error analysis. Higham [15,16,17] extended Skeel’s analysis to an arbitrary solver. Langou et al. [18] showed the maximum number of iterations to convergence on the method with a solver based on LU factorization using single- and double-precision arithmetic. Carson and Higham [19] gave an error analysis for ill-conditioned A. In addition, Algorithm 1 has been accelerated using three precisions [20,21,22]. We focus on the lower-precision solution of the linear system in line 4 in Algorithm 1. Based on this principle, this study aims to reduce the number of higher-precision matrix multiplications of the iterative refinement algorithm for singular value decomposition proposed by Ogita and Aishima.

2.3 Iterative refinement for symmetric eigenvalue decomposition

In this subsection, we introduce the iterative refinement algorithms for symmetric eigenvalue decomposition proposed by Ogita and Aishima in [23] and Uchino, Ozaki, and Ogita in [24]. We will write $I_n$ to denote the $n \times n$ identity matrix. Now, we assume $A=A^T \in \mathbb {R}^{n \times n}$. Let $X \in \mathbb {R}^{n \times n}$ be orthogonal, $D \in \mathbb {R}^{n \times n}$ be diagonal, and $A = XDX^T$. The ith columns of X are the eigenvectors $x_{(i)} \in \mathbb {R}^n$ and the ith diagonal elements of D are the eigenvalues $\lambda _i \in \mathbb {R}$ for $i=1,\dots ,n$. Here, we assume that $\lambda _i \ne \lambda _j$ for $i \ne j$. For $\hat{X} \approx X$, we define the error matrix $E \in \mathbb {R}^{n \times n}$ such that $X = \hat{X}(I_n + E)$. Ogita and Aishima proposed an algorithm to compute $\tilde{E} \approx E$ and update $\hat{X}$ into $\tilde{X}$ as $\tilde{X} \leftarrow \hat{X}(I_n+\tilde{E})$. The algorithm converges quadratically, provided that the error matrix E satisfies the following conditions from [25, Theorem 3.4]:

$$\begin{aligned} \Vert E\Vert _2< \min \left( \frac{\displaystyle \min _{1 \le i < j \le n}|\lambda _i - \lambda _j|}{10\sqrt{n}\Vert A\Vert _2},\frac{1}{100} \right) . \end{aligned}$$

(4)

This process is shown in Algorithm 2. Note that Algorithm 2 is simplified from the original algorithm [23, Algorithm 1] because multiple eigenvalues are not considered.

Refinement of approximate eigenvectors $\hat{X} \in \mathbb {R}^{n \times n}$ for a real symmetric matrix $A \in \mathbb {R}^{n \times n}$ from [23]. Assume $\tilde{\lambda }_i \ne \tilde{\lambda }_j$ for $i \ne j$. The total cost is $6n^3$ to $8n^3$ operations.

Since $\hat{X}^T\hat{X}$ and $\hat{X}^T(A\hat{X})$ are symmetric, only the upper or lower triangular part needs to be computed. Thus, the total cost of Algorithm 2 is $6n^3$ operations. However, if the matrix product is obtained by using highly accurate algorithms, e.g., Ozaki’s scheme [26] or a subroutine in an arbitrary precision arithmetic library, such as MPLAPACK [27]¹, XBLAS (extra precise BLAS) [28], or Advanpix Multiprecision Computing Toolbox for MATLAB, the total cost is up to $8n^3$ operations since the symmetry of the matrix product may not be considered. The cost is divided into

$2n^3$::

$A\hat{X}$ and $\hat{X}\tilde{E}$,

$n^3$::

$\hat{X}^T\hat{X}$ and $\hat{X}^T(A\hat{X})$ after computing $A\hat{X}$ (exploiting symmetry),

$2n^3$::

$\hat{X}^T\hat{X}$ and $\hat{X}^T(A\hat{X})$ after computing $A\hat{X}$ (no exploiting symmetry).

Let $e:=\lceil \log _{10} (\Vert \tilde{E}\Vert _2) \rceil$. It is reported in [24] that the required arithmetic precision of high-accuracy matrix multiplications is 2e decimal digits for $\hat{X}^T\hat{X}$ and $\hat{X}^TA\hat{X}$ and e decimal digits for $\hat{X}\tilde{E}$ in Algorithm 2, i.e., line 8 in Algorithm 2 can be replaced by $\tilde{X} \leftarrow (\hat{X} + (\hat{X}\tilde{E})_{\ell })_h$. Thus, the total cost of 2e decimal digit computations is $4n^3$ to $6n^3$ operations.

Uchino, Ozaki, and Ogita [24] proposed an algorithm to reduce the required arithmetic precision of Algorithm 2. It is based on iterative refinement for the solution of linear systems using mixed-precision arithmetic. From $R= I_n-\hat{X}^T\hat{X}$ and $S = \hat{X}^TA\hat{X}$ in Algorithm 2, F at line 6 satisfies

$$ F = S+R\tilde{D} = \hat{X}^TA\hat{X}+(I_n-\hat{X}^T\hat{X})\tilde{D} = \hat{X}^T(A\hat{X}-\hat{X}\tilde{D}) + \tilde{D}. $$

Since the diagonal part of F is not referenced, it can be computed as

$$\begin{aligned} F := \hat{X}^TW, \end{aligned}$$

(5)

where $W:= A\hat{X}-\hat{X}\tilde{D}$. From line 4 in Algorithm 1, (5) can be computed with lower-precision. Moreover, the off-diagonal parts of R and S are not necessary. Finally, a variant equivalent of Algorithm 2 in exact arithmetic is obtained. The condition for convergence is the same as (4) for Algorithm 2.

Refinement of approximate eigenvectors $\hat{X} \in \mathbb {R}^{n \times n}$ for a real symmetric matrix $A \in \mathbb {R}^{n \times n}$ from [24]. Assume $\tilde{\lambda }_i \ne \tilde{\lambda }_j$ for $i \ne j$. The total cost is $6n^3$ operations.

The total cost of Algorithm 3 is $6n^3$ operations divided into

$2n^3$::

$A\hat{X}$, $\hat{X}^{T}W$, and $\hat{X}\tilde{E}$,

among which there are no matrix multiplications whose result is symmetric. It is reported in [24] that the required arithmetic precision of high-accuracy matrix multiplications is 2e decimal digits for $A\hat{X}$ and e decimal digits for $\hat{X}^TW$ and $\hat{X}\tilde{E}$ in Algorithm 3. Thus, the total cost of 2e decimal digit computations is $2n^3$ operations.

2.4 Iterative refinement for singular value decomposition

In this subsection, we introduce an iterative refinement for full singular value decomposition proposed by Ogita and Aishima in [7]. Hereafter, we assume that

$$\begin{aligned} \sigma _1> \sigma _2> \dots > \sigma _n \end{aligned}$$

and the approximation $\tilde{\sigma }_i$ of $\sigma _i$ satisfies $\tilde{\sigma }_i \ne \tilde{\sigma }_j$ for $i \ne j$. Let $\hat{U} \approx U$ and $\hat{V} \approx V$ for U and V in (1). Define the error matrices $F \in \mathbb {R}^{m \times m}$ and $G \in \mathbb {R}^{n \times n}$ such that

$$\begin{aligned} U = \hat{U}(I_m + F)\quad \text {and}\quad V = \hat{V}(I_n+G), \end{aligned}$$

(6)

respectively. Ogita and Aishima proposed an algorithm which is based on the same idea as Algorithm 2. It computes $\tilde{F} \approx F$ and $\tilde{G} \approx G$, which hold from [7, Lemma 2], and updates $\hat{U}$ and $\hat{V}$ to $\tilde{U}$ and $\tilde{V}$ as $\tilde{U} \leftarrow \hat{U}(I_m + \tilde{F})$ and $\tilde{V} \leftarrow \hat{V}(I_n+\tilde{G})$, respectively. This process is shown in Algorithm 4. Note that for $T,\hat{U},\tilde{U},R \in \mathbb {R}^{m \times m}$, we have

$$ T = (T_1\ T_2),\quad \hat{U} = (\hat{U}_1\ \hat{U}_2),\quad \tilde{U} = (\tilde{U}_1\ \tilde{U}_2),\quad \text {and}\quad R = \begin{pmatrix} R_{11} &{} R_{12}\\ R_{21} &{} R_{22} \end{pmatrix} $$

with $T_1,\hat{U}_1,\tilde{U}_1 \in \mathbb {R}^{m\times n}$, $T_2,\hat{U}_2,\tilde{U}_2 \in \mathbb {R}^{m\times (m-n)}$, $R_{11} \in \mathbb {R}^{n\times n}$, $R_{12},R_{21}^T \in \mathbb {R}^{n\times (m-n)}$, and $R_{22} \in \mathbb {R}^{(m-n)\times (m-n)}$.

Let $\tilde{U}$ and $\tilde{V}$ be obtained from $\hat{U}$ and $\hat{V}$ using Algorithm 4. Define $F' \in \mathbb {R}^{m \times m}$ and $G' \in \mathbb {R}^{n \times n}$ as $U = \tilde{U}(I_m + F')$ and $V = \tilde{V}(I_n + G')$, respectively, and $\varepsilon := \max (\Vert F\Vert _2,\Vert G\Vert _2)$, $\varepsilon ':= \max (\Vert F'\Vert _2,\Vert G'\Vert _2)$. If $\varepsilon$ satisfies

$$\begin{aligned} \varepsilon < \frac{\displaystyle \min _{1 \le i \le n-1}(\sigma _i - \sigma _{i+1})}{30m\Vert A\Vert _2}, \end{aligned}$$

(7)

then

$$\begin{aligned} \varepsilon '<\frac{7}{10}\varepsilon \quad \text {and} \quad \limsup _{\varepsilon \rightarrow 0}\frac{\varepsilon '}{\varepsilon ^2} \le \frac{18m\Vert A\Vert _2}{\displaystyle \min _{1 \le i \le n-1}(\sigma _i - \sigma _{i+1})} \end{aligned}$$

(8)

hold from [7, Theorem 1], and (8) implies that Algorithm 4 converges quadratically. For Algorithm 4, we assume that these are clustered singular values if (7) is not satisfied.

Refinement of approximate singular vectors $\hat{U} \in \mathbb {R}^{m \times m}$ and $\hat{V} \in \mathbb {R}^{n \times n}$ for a real matrix $A \in \mathbb {R}^{m \times n}$ from [7]. Assume $\tilde{\sigma }_i \ne \tilde{\sigma }_j$ for $i \ne j$. The total cost is $3m^3 + 2m^2n + 2mn^2 + 3n^3$ to $4m^3 + 2m^2n + 2mn^2 + 4n^3$ operations.

The total cost of Algorithm 4 is $3m^3 + 2m^2n + 2mn^2 + 3n^3$ operations; however, the cost can be up to $4m^3 + 2m^2n + 2mn^2 + 4n^3$ operations due to the computational problem of symmetry of the result of $\hat{U}^T\hat{U}$ and $\hat{V}^T\hat{V}$. The cost is divided into

$m^3$:	$\hat{U}^T\hat{U}$ (exploiting symmetry),
$2m^3$:	$\hat{U}^T\hat{U}$ (no exploiting symmetry),
$n^3$:	$\hat{V}^T\hat{V}$ (exploiting symmetry),
$2n^3$:	$\hat{V}^T\hat{V}$ (no exploiting symmetry),
$2mn^2$:	$A\hat{V}$,
$2m^2n$:	$\hat{U}^T(A\hat{V})$ after computing $A\hat{V}$,
$2m^3$:	$\hat{U}\tilde{F}$,
$2n^3$:	$\hat{V}\tilde{G}$.

Here, we define $\tilde{\varepsilon }:= \max (\Vert \tilde{F}\Vert _2,\Vert \tilde{G}\Vert _2)$ and

$$\begin{aligned} d :=\lceil -\log _{10} \tilde{\varepsilon } \rceil . \end{aligned}$$

(9)

Then, using (6) and $\varepsilon \approx \tilde{\varepsilon }$ from $F \approx \tilde{F}$ and $G \approx \tilde{G}$ yields

$$\begin{aligned} \max \left( \frac{\Vert U-\hat{U}\Vert _2}{\Vert \hat{U}\Vert _2},\frac{\Vert V-\hat{V}\Vert _2}{\Vert \hat{V}\Vert _2}\right) \le \varepsilon \approx \tilde{\varepsilon } \approx \mathcal {O}(10^{-d}). \end{aligned}$$

(10)

Since (8) holds,

$$\begin{aligned} \max \left( \frac{\Vert U-\tilde{U}\Vert _2}{\Vert \tilde{U}\Vert _2},\frac{\Vert V-\tilde{V}\Vert _2}{\Vert \tilde{V}\Vert _2}\right)&\le \varepsilon '\\&\le \frac{18m\Vert A\Vert _2}{\displaystyle \min _{1 \le i \le n-1}(\sigma _i - \sigma _{i+1})} \varepsilon ^2\\&\approx \frac{18m\Vert A\Vert _2}{\displaystyle \min _{1 \le i \le n-1}(\sigma _i - \sigma _{i+1})} \tilde{\varepsilon }^2 \approx \mathcal {O}(10^{-2d}) \end{aligned}$$

as $\varepsilon \rightarrow 0$. Thus, the required arithmetic precision of Algorithm 4 is almost 2d decimal digits. However, that for the computations of $\hat{U}\tilde{F}$ and $\hat{V}\tilde{G}$ at line 12 in Algorithm 4 is about d decimal digits. The reason for this is the same as for the required arithmetic precision for $\hat{X}\tilde{E}$ in Algorithm 2 and 3—since the first d decimal digits or so of $\hat{U}$ and $\hat{V}$ are correct from (10), only the first d decimal digits or so of $\hat{U}\tilde{F}$ and $\hat{V}\tilde{G}$ can affect the results. This situation is depicted in Fig. 1. From the above considerations, line 12 in Algorithm 4 is replaced by $\tilde{U} \leftarrow (\hat{U}+(\hat{U}\tilde{F})_{\ell })_h;\ \tilde{V} \leftarrow (\hat{V}+(\hat{V}\tilde{G})_{\ell })_h$. Therefore, the total cost of 2d and d decimal digit computations is $m^3 + 2m^2n + 2mn^2 + n^3$ to $2m^3 + 2m^2n + 2mn^2 + 2n^3$ operations and $2m^3 + 2n^3$ operations, respectively.

Fig. 1

Diagram representing $\tilde{U} \leftarrow \hat{U}+\hat{U}\tilde{F}$ and $\tilde{V} \leftarrow \hat{V}+\hat{V}\tilde{G}$ from Algorithm 4

2.5 Highly accurate matrix multiplication

We assume floating-point operations in rounding to nearest value according to IEEE Std. 754 [29] and no overflow or underflow. Let $\mathbb {F}$ be a set of floating-point numbers and $\textrm{fl}(\cdot )$ denote the result of a floating-point operation, where all operations inside the parentheses are executed in ordinary precision. Ozaki, Ogita, Oishi, and Rump proposed an algorithm for error-free transformation of matrix multiplication called Ozaki’s scheme [26]. Their algorithm transforms $A \in \mathbb {R}^{m \times k}$ and $B \in \mathbb {R}^{k \times n}$ into

$$\begin{aligned} A&= \sum _{p=1}^{n_A-1}A^{(p)} + \underline{A}^{(n_A)},\quad A^{(p)},\underline{A}^{(n_A)} \in \mathbb {F}^{m \times k}\\ B&= \sum _{q=1}^{n_B-1}B^{(q)} + \underline{B}^{(n_B)},\quad B^{(q)},\underline{B}^{(n_B)} \in \mathbb {F}^{k \times n}, \end{aligned}$$

where

$$ \underline{A}^{(s)}:= A-\sum _{p=1}^{s-1}A^{(p)}, \quad \underline{B}^{(s)}:= B-\sum _{p=1}^{s-1}B^{(p)}, $$

and

$$\begin{aligned} |a_{ij}^{(s)} |&\ge |a_{ij}^{(t)} |\qquad \text {if}\ a_{ij}^{(s)} \ne 0 \qquad \text {for}\ s< t,\\ \qquad |b_{ij}^{(s)} |&\ge |b_{ij}^{(t)} |\qquad \text {if}\ b_{ij}^{(s)} \ne 0 \qquad \text {for}\ s < t \end{aligned}$$

as described in [26, Algorithm 3]. In this case, there is no rounding error in $\textrm{fl}(A^{(p)}B^{(q)})$ for all (p, q) pairs. In this study, we compute $(AB)_h$ as

$$\begin{aligned} \left( \sum _{p+q \le \max (nA,nB)} (A^{(p)}B^{(q)})_{\ell } + \sum _{p=1}^{n_A-1}(A^{(p)}\underline{B}^{(n_B-p+1)})_{\ell } + (\underline{A}^{(n_A)}B)_{\ell }\right) _h. \end{aligned}$$

(11)

We set $n_A=n_B=4$ in this paper.

3 Proposed algorithms

In this section, we propose four faster algorithms for the iterative refinement of singular vectors.

3.1 Proposed algorithms based on iterative refinement for singular value decomposition

Here, we propose two algorithms based on Algorithm 4. From $R = I_m - \hat{U}^T\hat{U}$, $S = I_n-\hat{V}^T\hat{V}$, and $T = \hat{U}^TA\hat{V}$ in Algorithm 4, $C_{\alpha }$ and $C_{\beta }$ at line 7 satisfy

$$\begin{aligned} C_{\alpha }&= T_1 + R_{11}\tilde{\Sigma }_n \\&= \hat{U}_1^TA\hat{V} + (I_n-\hat{U}_1^T\hat{U}_1)\tilde{\Sigma }_n\\&= \hat{U}_1^T(A\hat{V}-\hat{U}_1\tilde{\Sigma }_n) + \tilde{\Sigma }_n,\\ C_{\beta }&= T_1^T+S\tilde{\Sigma }_n \\&= \hat{V}^TA^T\hat{U}_1 + (I_n-\hat{V}^T\hat{V})\tilde{\Sigma }_n \\&= \hat{V}^T(A^T\hat{U}_1-\hat{V}\tilde{\Sigma }_n) + \tilde{\Sigma }_n. \end{aligned}$$

Since the diagonal parts of $C_{\alpha }$ and $C_{\beta }$ are not necessary because the diagonal parts of D and E are not used, they can be computed as

$$\begin{aligned} C_{\alpha }&= \hat{U}_1^T(A\hat{V}-\hat{U}_1\tilde{\Sigma }_n), \\ C_{\beta }&= \hat{V}^T(A^T\hat{U}_1-\hat{V}\tilde{\Sigma }_n). \end{aligned}$$

Let $\tilde{F}_{11} \in \mathbb {R}^{n \times n},\tilde{F}_{12} \in \mathbb {R}^{n \times (m-n)},\tilde{F}_{21} \in \mathbb {R}^{(m-n) \times n},\tilde{F}_{22} \in \mathbb {R}^{(m-n) \times (m-n)}$ such that

$$ \tilde{F} = \begin{pmatrix} \tilde{F}_{11}&{} \tilde{F}_{12}\\ \tilde{F}_{21}&{} \tilde{F}_{22} \end{pmatrix}. $$

Then, from line 11 in Algorithm 4, the following holds:

$$\begin{aligned} (\tilde{F}_{11})_{ij}&= {\left\{ \begin{array}{ll} \frac{e_{ij}}{\tilde{\sigma }_j - \tilde{\sigma }_i} &{} (i \ne j)\\ \frac{r_{ij}}{2} &{} (\textrm{otherwise}) \end{array}\right. } \quad (\textrm{for}\ 1 \le i,j \le n),\\ \tilde{F}_{12}&= -\tilde{\Sigma }_n^{-1}T_2^T = -\tilde{\Sigma }_n^{-1}\hat{V}^TA^T\hat{U}_2,\\ \tilde{F}_{21}&= R_{21}-\tilde{F}_{12}^T = -\hat{U}_2^T\hat{U}_1 + \hat{U}_2^T A \hat{V} \tilde{\Sigma }_n^{-1} = \hat{U}_2^T (A \hat{V}-\hat{U}_1\tilde{\Sigma }_n)\tilde{\Sigma }_n^{-1},\\ \tilde{F}_{22}&= \frac{1}{2}R_{22} = \frac{1}{2}(I_{m-n}-\hat{U}_2^T\hat{U}_2). \end{aligned}$$

Thus, only the computations for $\textrm{diag}(R_{11})$, $R_{22}$, and $T_2$ are necessary. Finally, we obtain the following algorithm, which is a variant equivalent to Algorithm 4 in exact arithmetic.

Refinement of approximate singular vectors $\hat{U} \in \mathbb {R}^{m \times m}$ and $\hat{V} \in \mathbb {R}^{n \times n}$ for a real matrix $A \in \mathbb {R}^{m \times n}$. Assume $\tilde{\sigma }_i \ne \tilde{\sigma }_j$ for $i \ne j$. The total cost is $3m^3 + 2m^2n + 3mn^2 + 4n^3$ to $4m^3 + 4mn^2 + 4n^3$ operations. Bold font indicates differences from Algorithm 4.

The total cost of Algorithm 5 is $3m^3 + 2m^2n + 3mn^2 + 4n^3$ to $4m^3 + 4mn^2 + 4n^3$ operations divided into

$2n^3$:	$\hat{V}^TC_\delta$,
$2mn^2$:	$A\hat{V}$, $A^T\hat{U}_1$, $\hat{U}_1^TC_\gamma$,
$2mn(m - n)$:	$P^T\hat{U}_2$, $\hat{U}_2^TC_\gamma$,
$m(m - n)^2$:	$\hat{U}_2^T\hat{U}_2$ (exploiting symmetry),
$2m(m - n)^2$:	$\hat{U}_2^T\hat{U}_2$ (no exploiting symmetry),
$2m^3$:	$\hat{U}\tilde{F}$,
$2n^3$:	$\hat{V}\tilde{G}$

and is more expensive than that of Algorithm 4. The difference between the cost of Algorithms 4 and 5 is $mn^2 + n^3$ to $2m^2n - 2mn^2$ operations. For d in (9), the required arithmetic precision for the computations of $\hat{U}_1^TC_{\gamma }$, $\hat{V}^TC_{\delta }$, $\hat{U}_2^TC_{\gamma }$, $\hat{U}\tilde{F}$, and $\hat{V}\tilde{G}$ is d decimal digits, while that for the other computations is 2d decimal digits. Therefore, the total cost of 2d and d decimal digits higher-precision computations is $m^3 + 3mn^2$ to $2m^3 - 2m^2n + 4mn^2$ operations and $2m^3 + 2m^2n + 4n^3$ operations, respectively. The cost of 2d decimal digit computations in Algorithm 5 is $2m^2n -mn^2 + n^3$ to $4m^2n - 2mn^2 + 2n^3$ operations less than that of Algorithm 4.

We propose another algorithm with lower total cost than Algorithm 5. From $C_{\alpha }$ and $C_{\beta }$ at line 7 in Algorithm 4 and $R = R^T$, the following holds:

$$\begin{aligned} C_{\beta }&= T_1^T + S\tilde{\Sigma }_n\nonumber \\&= \hat{V}^TA^T\hat{U} + S\tilde{\Sigma }_n\nonumber \\&= \hat{V}^TA^T\hat{U} + \tilde{\Sigma }_nR - \tilde{\Sigma }_nR + S\tilde{\Sigma }_n\nonumber \\&= (\hat{U}^TA\hat{V} + R\tilde{\Sigma }_n)^T - \tilde{\Sigma }_nR + S\tilde{\Sigma }_n\nonumber \\&= C_{\alpha }^T - \tilde{\Sigma }_nR + S\tilde{\Sigma }_n. \end{aligned}$$

(12)

Thus, we obtain the following algorithm combining Algorithms 4, 5, and (12).

Refinement of approximate singular vectors $\hat{U} \in \mathbb {R}^{m \times m}$ and $\hat{V} \in \mathbb {R}^{n \times n}$ for a real matrix $A \in \mathbb {R}^{m \times n}$. Assume $\tilde{\sigma }_i \ne \tilde{\sigma }_j$ for $i \ne j$. The total cost is $3m^3 + 2m^2n + 2mn^2 + 3n^3$ to $4m^3 + 4mn^2 + 4n^3$ operations. Bold font indicates differences from Algorithm 5.

The total cost of Algorithm 6 is $3m^3 + 2m^2n + 2mn^2 + 3n^3$ to $4m^3 + 4mn^2 + 4n^3$ operations divided into

$n^3$:	$\hat{V}^T\hat{V}$ (exploiting symmetry),
$2n^3$:	$\hat{V}^T\hat{V}$ (no exploiting symmetry),
$2mn^2$:	$A\hat{V}$, $\hat{U}_1^T\hat{U}_1$, $\hat{U}_1^TC_\gamma$,
$2mn(m - n)$:	$P^T\hat{U}_2$, $\hat{U}_2^TC_\gamma$,
$m(m - n)^2$:	$\hat{U}_2^T\hat{U}_2$ (exploiting symmetry),
$2m(m - n)^2$:	$\hat{U}_2^T\hat{U}_2$ (no exploiting symmetry),
$2m^3$:	$\hat{U}\tilde{F}$,
$2n^3$:	$\hat{V}\tilde{G}$,

which is a little more expensive than Algorithm 4. The difference between the costs of Algorithms 4 and 6 is 0 to $2m^2n - 2mn^2$ operations, i.e., the minimum costs of Algorithm 4 and 6 are the same. For d in (9), the required arithmetic precision for the computations of $\hat{U}_1^TC_{\gamma }$, $\hat{U}_2^TC_{\gamma }$, $\hat{U}\tilde{F}$, and $\hat{V}\tilde{G}$ is d decimal digits, while that for the other computations is 2d decimal digits. Therefore, the total cost of 2d and d decimal digit computations is $m^3 + 2mn^2 + n^3$ to $2m^3 - 2m^2n + 4mn^2 + 2n^3$ operations and $2m^3 + 2m^2n + 2n^3$ operations, respectively. The cost of 2d decimal digit computations in Algorithm 6 is $2m^2n$ to $4m^2n - 2mn^2$ operations less than that of Algorithm 4.

3.2 Proposed algorithms based on iterative refinement for symmetric eigenvalue decomposition

Here, we propose two algorithms based on Algorithm 3. The singular value decomposition is easily extended to eigenvalue decomposition. From (1),

$$\begin{aligned} A^TA&= V \Sigma ^T\Sigma V^T\quad \text {and}\nonumber \\ AA^T&= U \Sigma \Sigma ^T U^T \end{aligned}$$

(13)

are satisfied, and these represent the eigenvalue decomposition of $A^TA$ and $AA^T$, respectively. From Algorithms 3, 5, and (13), we immediately obtain the following algorithm. Note that $\tilde{V}$ obtained using Algorithm 7 may not converge as well as Algorithm 4 because Algorithm 7 does not use $\hat{V}$.

Refinement of approximate singular vectors $\hat{U} \in \mathbb {R}^{m \times m}$ and $\hat{V} \in \mathbb {R}^{n \times n}$ for a real matrix $A \in \mathbb {R}^{m \times n}$. Assume $\tilde{\sigma }_i \ne \tilde{\sigma }_j$ for $i \ne j$. The total cost is $3m^3 + 4m^2n - mn^2$ to $4m^3 + 2m^2n$ operations. Bold font indicates differences from Algorithm 5.

We can obtain $\tilde{V}$ as $\tilde{V} \leftarrow A^T\tilde{U}_1\tilde{\Sigma }_n^{-1}$. The costs for $B \leftarrow AA^T$ and $\tilde{V} \leftarrow A^T\tilde{U}_1\tilde{\Sigma }_n^{-1}$ are $m^2n$ to $2m^2n$ and $2mn^2$, respectively. Thus, the total cost of $\nu$ iterations of Algorithm 7 is $(3m^3 + 4m^2n - mn^2)\nu + m^2n+2mn^2$ to $(4m^3 + 2m^2n)\nu + 2m^2n+2mn^2$ operations divided into

$m^2n$:	$AA^T$ (exploiting symmetry),
$2m^2n$:	$AA^T$ (no exploiting symmetry),
$2mn^2$:	$A^T\tilde{U}_1$,
$2m^2n\nu$:	$B\hat{U}_1$,
$2mn^2\nu$:	$\hat{U}_1^TC_\gamma$,

$2mn(m-n)\nu$:	$P^T\hat{U}_2$, $\hat{U}_2^TC_\gamma$,
$m(m - n)^2$:	$\hat{U}_2^T\hat{U}_2$ (exploiting symmetry),
$2m(m - n)^2$:	$\hat{U}_2^T\hat{U}_2$ (no exploiting symmetry),
$2m^3\nu$:	$\hat{U}\tilde{F}$,

which is less expensive than Algorithm 4. The difference between the costs of Algorithms 4 and 7 is $(2m^2n - 3mn^2 - 3n^3)\nu + m^2n+2mn^2$ to $(-2mn^2-4n^3)\nu + 2m^2n+2mn^2$ operations. For d in (9), the required arithmetic precision for the computations of $\hat{U}_1^TC_{\gamma }$, $\hat{U}_2^TC_{\gamma }$, and $\hat{U}\tilde{F}$ is d decimal digits, while that for the other computations is 2d decimal digits. Therefore, the total cost of 2d and d decimal digit computations is $(m^3 + 2m^2n - mn^2)\nu + m^2n+2mn^2$ to $2m^3\nu + 2m^2n+2mn^2$ operations and $(2m^3+2m^2n)\nu$ operations, respectively. The cost of 2d decimal digit computations in Algorithm 7 is $(n^3 + 3mn^2)\nu - m^2n-2mn^2$ to $(2m^2n + 2mn^2 + 2n^3)\nu - 2m^2n-2mn^2$ operations less than that of Algorithm 4.

We now introduce another extension of the singular value decomposition to the eigenvalue decomposition. We will write $O_{m,n}$ to denote the $m \times n$ zero matrix. Let $\Sigma _n:= \textrm{diag}(\sigma _1,\dots ,\sigma _n) \in \mathbb {R}^{n \times n}$. The eigenvalues of

$$\begin{aligned} B := \begin{pmatrix} O_{n,n} &{} A^T\\ A &{} O_{m,m} \end{pmatrix} \in \mathbb {R}^{(m+n)\times (m+n)} \end{aligned}$$

(14)

are $\sigma _1,\dots ,\sigma _n,-\sigma _1,\dots ,-\sigma _n, 0,\dots ,0$ from [30], and for $X,D \in \mathbb {R}^{(m+n)\times (m+n)}$ such that

$$\begin{aligned} X:= \frac{1}{\sqrt{2}}\begin{pmatrix} V &{} V &{} O_{n,m-n}\\ U_1 &{} -U_1 &{} \sqrt{2}U_2 \end{pmatrix},\quad D := \begin{pmatrix} \Sigma _n &{} O_{n,n} &{} O_{n,m-n}\\ O_{m,n} &{} -\Sigma &{} O_{m,m-n} \end{pmatrix}, \end{aligned}$$

it holds that

$$\begin{aligned} B = XDX^T \end{aligned}$$

(15)

from [31].

We consider transforming the singular value decomposition into the symmetric eigenvalue decomposition as (15) and improving the approximate results using Algorithm 3. Hereafter, we discuss omitting unnecessary computations to improve efficiency because the matrix size is increased. Assume that $\tilde{\Sigma }_n$ is obtained by the same computation as in Algorithm 5. Let $\hat{X},\tilde{D}= (\tilde{d}_{ij}) \in \mathbb {R}^{(m+n) \times (m+n)}$ be

$$\begin{aligned} \hat{X} := \frac{1}{\sqrt{2}}\begin{pmatrix} \hat{V} &{} \hat{V} &{} O_{n,m-n}\\ \hat{U}_1 &{} -\hat{U}_1 &{} \sqrt{2}\hat{U}_2 \end{pmatrix},\quad \tilde{D} := \begin{pmatrix} \tilde{\Sigma }_n &{} O_{n,n} &{} O_{n,m-n}\\ O_{m,n} &{} -\tilde{\Sigma } &{} O_{m,m-n} \end{pmatrix}. \end{aligned}$$

Then, for $B \in \mathbb {R}^{(m+n) \times (m+n)}$ in (14),

$$\begin{aligned} B\hat{X}&= \frac{1}{\sqrt{2}}\begin{pmatrix} A^T\hat{U}_1 &{} -A^T\hat{U}_1 &{} \sqrt{2}A^T\hat{U}_2\\ A\hat{V} &{} A\hat{V} &{} O_{m,m-n} \end{pmatrix},\\ \hat{X}\tilde{D}&= \frac{1}{\sqrt{2}}\begin{pmatrix} \hat{V}\tilde{\Sigma }_n &{} -\hat{V}\tilde{\Sigma }_n &{} O_{n,m-n}\\ \hat{U}_1\tilde{\Sigma }_n &{} \hat{U}_1\tilde{\Sigma }_n &{} O_{m,m-n} \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} B\hat{X}-\hat{X}\tilde{D} = \frac{1}{\sqrt{2}}\begin{pmatrix} P_1 &{} -P_1 &{} \sqrt{2}A^T\hat{U}_2\\ P_2 &{} P_2 &{} O_{m,m-n} \end{pmatrix}, \end{aligned}$$

where

$$ {\left\{ \begin{array}{ll} P_1:= A^T\hat{U}_1-\hat{V}\tilde{\Sigma }_n,\\ P_2:= A\hat{V}-\hat{U}_1\tilde{\Sigma }_n \end{array}\right. } $$

are satisfied. Therefore,

$$\begin{aligned} H =(h_{ij}) := \hat{X}^T(B\hat{X}-\hat{X}\tilde{D}) = \frac{1}{2}\begin{pmatrix} Q_1 &{} -Q_2 &{} \sqrt{2}\hat{V}^TA^T\hat{U}_2\\ Q_2 &{} -Q_1 &{} \sqrt{2}\hat{V}^TA^T\hat{U}_2\\ \sqrt{2}\hat{U}_2^TP_2 &{} \sqrt{2}\hat{U}_2^TP_2 &{} O_{m-n,m-n} \end{pmatrix}, \end{aligned}$$

where

$$ {\left\{ \begin{array}{ll} Q_1:= \hat{V}^TP_1 + \hat{U}_1^TP_2,\\ Q_2:= \hat{V}^TP_1 - \hat{U}_1^TP_2 \end{array}\right. } $$

holds. From the 8th line of Algorithm 3, we can write the approximate error matrix $\tilde{E} = (\tilde{e}_{ij})$ for $\hat{X}$ as

$$ \tilde{e}_{ij}:= {\left\{ \begin{array}{ll} \frac{r_{ij}}{2} &{} (i = j\ \textrm{or}\ i,j > 2n)\\ \frac{h_{ij}}{\tilde{d}_{jj}-\tilde{d}_{ii}} &{} (\textrm{otherwise}) \end{array}\right. } $$

for $R = (r_{ij}) = I_{m+n}-\hat{X}^T\hat{X}$. Now, let $\tilde{E}_1,\tilde{E}_2 \in \mathbb {R}^{n \times n}$, $\tilde{E}_3 \in \mathbb {R}^{n \times (m-n)}$, $\tilde{E}_4 \in \mathbb {R}^{(m-n) \times n}$, and $\tilde{E}_5 \in \mathbb {R}^{(m-n) \times (m-n)}$ such that

$$ \tilde{E} = \begin{pmatrix} \tilde{E}_{1} &{} \tilde{E}_{2} &{} -\tilde{E}_{3}\\ \tilde{E}_{2} &{} \tilde{E}_{1} &{} \tilde{E}_{3}\\ \tilde{E}_{4} &{} -\tilde{E}_{4} &{} \tilde{E}_{5} \end{pmatrix}. $$

Then, it holds that

$$ \hat{X}\tilde{E} =\frac{1}{\sqrt{2}}\begin{pmatrix} \tilde{G} &{}\tilde{G} &{} O_{n,m-n}\\ \tilde{F}_1 &{} -\tilde{F}_1 &{} \sqrt{2}\tilde{F}_2 \end{pmatrix}, $$

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{G} := \hat{V}(\tilde{E}_1 + \tilde{E}_2),\\ \tilde{F}_1 := \hat{U}_1(\tilde{E}_1-\tilde{E}_2)+\sqrt{2}\hat{U}_2\tilde{E}_4,\\ \tilde{F}_2 := \hat{U}_2\tilde{E}_5-\sqrt{2}\hat{U}_1\tilde{E}_3. \end{array}\right. } \end{aligned}$$

Thus, we can update $\hat{V},\hat{U}_1$, and $\hat{U}_2$ as

$$ \tilde{V} \leftarrow \hat{V} + \tilde{G},\quad \tilde{U}_1 \leftarrow \tilde{U}_1 + \tilde{F}_1,\quad \tilde{U}_2 \leftarrow \tilde{U}_2 + \tilde{F}_2. $$

Finally, we obtain the following algorithm to improve the accuracy of the approximation of singular vectors of A.

The total cost of Algorithm 8 is $3m^3 + 2m^2n + 3mn^2 + 4n^3$ to $4m^3 + 4mn^2 + 4n^3$ operations divided into

$2n^3$:	$\hat{V}^TP_1$,
$2mn^2$:	$A\hat{V}$, $A^T\hat{U}_1$, $\hat{U}_1^TP_2$, $\hat{U}_1(\tilde{E}_1-\tilde{E}_2)$
$2mn(m - n)$:	$P^T\hat{U}_2$, $\hat{U}_2^TP_2$, $\hat{U}_2\tilde{E}_4$, $\hat{U}_1\tilde{E}_3$
$m(m - n)^2$:	$\hat{U}_2^T\hat{U}_2$ (exploiting symmetry),
$2m(m - n)^2$:	$\hat{U}_2^T\hat{U}_2$ (no exploiting symmetry),
$2m(m - n)^2$:	$\hat{U}_2\tilde{E}_5$,
$2n^3$:	$\hat{V}(\tilde{E}_1+\tilde{E}_2)$,

which is more expensive than Algorithm 4. The difference between the costs of Algorithms 4 and 8 is $- mn^2-n^3$ to $2m^2n - 2mn^2$ operations. For d in (9), the required arithmetic precision for the computations of multiplications $\hat{V}^TP_1$, $\hat{U}_1^TP_2$, $\hat{U}_2^TP_2$, $\hat{U}_1(\tilde{E}_1-\tilde{E}_2)$, $\hat{U}_2\tilde{E}_4$, $\hat{U}_2\tilde{E}_5$, $\hat{U}_1\tilde{E}_3$, and $\hat{V}(\tilde{E}_1+\tilde{E}_2)$ is d decimal digits, while that for the other computations is 2d decimal digits. Therefore, the total costs of 2d and d decimal digit computations is $m^3 + 3mn^2$ to $2m^3 - 2m^2n + 4mn^2$ operations and $2m^3 + 2m^2n + 4n^3$ operations, respectively. The cost of 2d decimal digit computations in Algorithm 8 is $2m^2n - mn^2 + n^3$ to $4m^2n - 2mn^2 + 2n^3$ operations less than that of Algorithm 4. Moreover, the costs of Algorithms 5 and 8 are the same.

3.3 Comparison of the algorithms costs

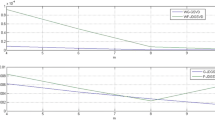
Here, we compare the costs of Algorithms 4, 5, 6, 7, and 8. Let $\nu$ denote the number of iterations. Define Case 1 and 2 as the cases when the symmetry of the matrix product is considered and not, respectively. We first focus on Case 1. Table 3 shows the total cost of higher-precision computations for all algorithms, and Figs. 2 and 3 indicate their ratios to the cost of Algorithm 4. From Fig. 3, the efficiency of Algorithm 7 increases with $\nu$. For $m/n \gtrsim 1.5$ or $\nu \le 2$, the costs of Algorithms 6 and 8 are the lowest from Fig. 2, while for other cases, the cost of Algorithm 7 is the lowest, as shown in Fig. 3.

Refinement of approximate singular vectors $\hat{U} \in \mathbb {R}^{m \times m}$ and $\hat{V} \in \mathbb {R}^{n \times n}$ for a real matrix $A \in \mathbb {R}^{m \times n}$. Assume $\tilde{\sigma }_i \ne \tilde{\sigma }_j$ for $i \ne j$. The total cost is $3m^3 + 2m^2n + 3mn^2 + 4n^3$ to $4m^3 + 4mn^2 + 4n^3$ operations. Bold font indicates differences from Algorithm 5.

Table 3 Total cost (number of operations) of higher-precision computations for $\nu$ iterations for Case 1

Fig. 2

Ratio of total cost of Algorithms 5, 6, and 8 to that of Algorithm 4 for any $\nu$ for Case 1

Fig. 3

Ratio of total cost of Algorithm 7 to that of Algorithm 4 for $\nu \in \{2,4,6,8,10\}$ for Case 1

Table 4 Total cost (number of operations) of higher-precision computations for $\nu$ iterations for Case 2

Fig. 4

Ratio of total costs of Algorithms 5, 6, and 8 to that of Algorithm 4 for any $\nu$ for Case 2

Next, we focus on Case 2. Table 4 shows the total costs of higher-precision computations for all algorithms, and Figs. 4 and 5 indicate the ratio to the cost of Algorithm 4. From Fig. 5, the efficiency of Algorithm 7 increases with $\nu$. For small m/n or $\nu = 1$, the costs of Algorithms 6 and 8 are the lowest, as shown in Fig. 4, while for other cases, the cost of Algorithm 7 is the lowest, as shown in Fig. 5.

Fig. 5

Ratio of total cost of Algorithm 7 to that of Algorithm 4 for $\nu \in \{2,4,6,8,10\}$ for Case 2

Table 5 Necessary performance ratio of higher- and lower-precision computations for Algorithms 5, 6, 7, and 8 to be comparable to the speed of Algorithm 4 for $\nu$ iterations

Next, we show that the performance ratio thresholds for higher- and lower-precision computations for each algorithm are lower than or comparable to Algorithm 4. We assume the performance of lower-precision arithmetic is r times faster than that of higher-precision arithmetic. Note that r means the ratio of hardware’s actual measured computation speed between higher- and lower-precision computations, not the hardware peak performance ratio. The performance ratio threshold t is defined as follows:

$$\begin{aligned} t := \frac{\text {Alg.~*}\ (r \cdot \text {(higher-precision costs)} + \text {(lower-precision costs)})}{\text {Alg.~4}\ (r\cdot \text {(higher-precision costs)} + \text {(lower-precision costs)})}. \end{aligned}$$

(16)

Table 5 indicates r when $t=1$ in (16) for each algorithm for $\nu$ iterations. If the performance ratio is greater than one, the algorithm is faster than Algorithm 4. The values for Algorithms 5, 6, and 8 in the table are less than or equal to 2. For example, in Env. 1, Algorithms 5, 6, and 8 are expected to be faster than Algorithm 4 because the performance ratio of double- and quadruple-precision arithmetic is 1353 on CPU and that of single- and double-precision arithmetic is 34 on GPU from Table 1. In Env. 2, Algorithms 5, 6, and 8 are expected to be slower than or comparable to the speed of Algorithm 4 because the performance ratio of single- and double-precision arithmetic is 1. The performance ratio thresholds for Algorithm 7 depend on $\nu$, and Algorithm 7 to be faster than Algorithm 4 for larger $\nu$.

4 Numerical experiments

In this section, we present the results of numerical experiments showing the performance of Algorithms 4, 5, 6, 7, and 8. We generate $A \in \mathbb {F}^{m \times n}$ using the MATLAB built-in function $\texttt {gallery}$ as

A = gallery(’randsvd’,[m n],cnd,mode,m,n,1),

where $\texttt {cnd}$ denotes the approximate condition number of A, and $\texttt {mode}$ is a variable that specifies

• 1. one large and $n-1$ small singular values: $\sigma _1 \approx 1$, $\sigma _i \approx \texttt {cnd}^{-1}$, $i=2,\dots ,n$,

• 2. one small and $n-1$ large singular values: $\sigma _n \approx \texttt {cnd}^{-1}$, $\sigma _i \approx 1$, $i=1,\dots ,n-1$,

• 3. geometrically distributed singular values: $\sigma _i \approx \texttt {cnd}^{-(i-1)/(n-1)}$, $i=1,\dots ,n$,

• 4. arithmetically distributed singular values: $\sigma _i \approx 1-(1-\texttt {cnd}^{-1})(i-1)/(n-1)$, $i=1,\dots ,n$, and

• 5. random singular values with uniformly distributed logarithm: $\sigma _i \approx \texttt {cnd}^{-r(i)}$, $r(i) \in (0,1)$, $i=1,\dots ,n$.

Figure 6 shows the singular value distribution for $n=100$ and $\texttt {cnd}=10^5$.

Fig. 6

Distribution of the singular values for $n=100$ and $\texttt {cnd}=10^5$

We fix $\texttt {mode}=4$ to satisfy (7). Note that for $\texttt {mode}=3$, (7) is satisfied if A is very well-conditioned; otherwise, clustered singular values appear and all algorithms do not work well. We regard the approximate singular values of A obtained by using the built-in function $\texttt {svd}$ in the Advanpix Multiprecision Computing Toolbox for MATLAB with 68 decimal digits as the exact singular values.

4.1 Convergence of algorithms

We show the results of convergence of Algorithms 4, 5, 6, 7, and 8 computed in 340 decimal digits arithmetic in order to simulate exact arithmetic. Here, we regard the approximate singular values of A obtained by using the built-in function $\texttt {svd}$ in 340 decimal digits as the exact singular values. Figures 7 and 8 show the convergence of all algorithms for $\texttt {cnd} = 10^{10}$ and $m = 1000$. Among the results, the convergence for Algorithms 4, 5, 6, and 8 are the same, while that for Algorithm 7 is worse. The reason for this is that the condition number of $AA^T$ is squared compared to that of A and Algorithm 7 does not consider the improvement of $\hat{V}$.

Fig. 7

Convergence of all algorithms for $m=2n=1000$ and $\texttt {cnd}=10^{10}$

Fig. 8

Convergence of all algorithms for $m=n=1000$ and $\texttt {cnd}=10^{10}$

4.2 Numerical experiments on CPU

Here, we show the numerical results obtained using a CPU. The numerical experiments are run using Env. 1. Assume that the results of the approximate singular value decomposition of A obtained using the MATLAB built-in function $\texttt {svd}$ with double-precision arithmetic are the initial values $\hat{U}$ and $\hat{V}$ of U and V, respectively. Additionally, all operations inside the parentheses of $(\cdot )_h$ and $(\cdot )_{\ell }$ are executed in double-double- and double-precision, respectively.

Tables 6 and 7 show the computing time in seconds for all algorithms for $\texttt {cnd} = 10^2$. Note that $\texttt {svd}$ in the following tables is executed as $\texttt {[U,S,V]=svd(A)}$. Also, the results of Algorithm 7 include the computing time for $AA^T$ and $A^T\tilde{U}_1\tilde{\Sigma }_n^{-1}$. Figures 9 and 10 show the convergence of all algorithms for $\texttt {cnd} = 10^2$ and $m = 5000$. Note that $\textrm{offdiag}(\tilde{U}^TA\tilde{V})$ denotes the off-diagonal part of $\tilde{U}^TA\tilde{V}$, that is, the diagonal elements are set to zero. The results indicate that Algorithms 5 and 8 are comparable. More specifically, they are 1.5 and 1.7 times faster than Algorithm 4 for $m = 2n$ and $m = n$ per iteration, respectively. Moreover, Algorithm 7 is the fastest; however, the convergence is a little worse than the others. Figures 11 and 12 show the convergence for all algorithms for $\texttt {cnd} = 10^6$ and $m = 5000$. Among the results, the convergence for Algorithms 4, 5, 6, and 8 are similar for the case of $\texttt {cnd} = 10^2$, while that for Algorithm 7 is worse. The reason for this is that the condition number of $AA^T$ is squared compared to that of A. Figures 13 and 14 show the convergence for all algorithms for $\texttt {cnd} = 10^{10}$ and $m = 5000$. From Figs. 9, 10, 11, 12, 13, and 14, we can see the tendency of bounds on the limiting accuracy for each $\texttt {cnd}$.

Table 6 Cumulative computing time in seconds for all algorithms for $m=2n$ on CPU

Table 7 Cumulative computing time in seconds for all algorithms for $m=n$ on CPU

Fig. 9

Convergence of all algorithms for $m=2n=5000$ and $\texttt {cnd}=10^2$ on CPU

Fig. 10

Convergence of all algorithms for $m=n=5000$ and $\texttt {cnd}=10^2$ on CPU

Fig. 11

Convergence of all algorithms for $m=2n=5000$ and $\texttt {cnd}=10^6$ on CPU

Fig. 12

Convergence of all algorithms for $m=n=5000$ and $\texttt {cnd}=10^6$ on CPU

Fig. 13

Convergence of all algorithms for $m=2n=5000$ and $\texttt {cnd}=10^{10}$ on CPU

Fig. 14

Convergence of all algorithms for $m=n=5000$ and $\texttt {cnd}=10^{10}$ on CPU

4.3 Numerical experiments on GPU

Next, we show the numerical results obtained using a GPU. The numerical experiments are run using the environments Env. 1 and 2. Let $B \in \mathbb {F}^{m \times n}$ be the conversion of A to a single-precision floating-point matrix as $\texttt {B=single(A)}$, where $\texttt {single}$ is the built-in function in MATLAB. Assume that the results of the approximate singular value decomposition of B obtained by using the MATLAB built-in function $\texttt {svd}$ with single-precision arithmetic are the initial values $\hat{U}$ and $\hat{V}$ of U and V, respectively. Here, all operations inside the parentheses of $(\cdot )_h$ and $(\cdot )_{\ell }$ are executed in double- and single-precision, respectively.

Tables 8 and 9 show the computing time in seconds for all algorithms for $\texttt {cnd} = 10^2$ using Env. 1. Figures 15 and 16 show the convergence for all algorithms for $\texttt {cnd} = 10^2$ and $m = 10000$. The results show that Algorithm 5 and 8 are comparable. More specifically, these algorithms are 1.2 times faster than Algorithm 4 for $m = 2n$ and $m = n$ per iteration. Moreover, Algorithm 7 is the fastest; however, the convergence is worse than the others. Figures 17 and 18 show the convergence of all algorithms for $\texttt {cnd} = 10^4$ and $m = 10000$. Among these, the convergence of Algorithms 4, 5, 6, and 8 are similar for the case of $\texttt {cnd} = 10^2$, while that of Algorithm 7 is worse. This result is due to the condition number of $AA^T$. For $\texttt {cnd} = 10^2$, the approximate singular values obtained by using two iterations of Algorithms 5 and 8 are as accurate as or more accurate than those obtained by using $\texttt {svd(A)}$. Also, the computing time for two iterations using Algorithms 5 or 8 is faster than that of $\texttt {svd(A)}$. Thus, for a well-conditioned matrix, iterative refinement with Algorithms 5 and 8 for the results of $\texttt {svd(B)}$ is superior to $\texttt {svd(A)}$ in terms of computation speed and accuracy of the approximate singular values.

Table 8 Cumulative computing time in seconds for all algorithms for $m=2n$ using Env. 1

Table 9 Cumulative computing time in seconds for all algorithms for $m=n$ using Env. 1

Fig. 15

Convergence of all algorithms for $m=2n=10000$ and $\texttt {cnd}=10^2$ using Env. 1

Fig. 16

Convergence of all algorithms for $m=2n=10000$ and $\texttt {cnd}=10^4$ using Env. 1

Fig. 17

Convergence of all algorithms for $m=n=10000$ and $\texttt {cnd}=10^4$ using Env. 1

Table 10 Cumulative computing time in seconds and ratio for all algorithms for $m=2n$ using Env. 2

Table 11 Cumulative computing time in seconds and ratio for all algorithms for $m=n$ using Env. 2

Tables 10 and 11 show the computing time in seconds for all algorithms for $\texttt {cnd} = 10^2$ using Env. 2. Using Env. 1 and 2, the convergence for all algorithms is almost the same. In the results, using Env. 2, all algorithms are much faster than the functions for singular value decomposition. In particular, Algorithm 7 is the fastest but has the worst convergence. For a well-conditioned matrix, iterative refinement with Algorithms 4, 5, 6 and 8 of the results of $\texttt {svd(B)}$ is superior to the same method applied to those of $\texttt {svd(A)}$ in terms of computation speed and accuracy of the approximate singular values.

5 Conclusion

In this paper, we showed that the Ogita-Aishima algorithm can be executed with highly accurate matrix multiplications carried out five times per iteration. Moreover, we proposed four iterative refinement algorithms for singular value decomposition constructed with highly accurate matrix multiplications carried out either four or five times per iteration. In an environment where lower-precision arithmetic is much faster than higher-precision arithmetic, the proposed algorithms are faster than the Ogita-Aishima algorithm. However, in an environment where the performance of lower-precision arithmetic is comparable to that of higher-precision arithmetic, the computing time for all algorithms is comparable.

All iterative refinement algorithms introduced in this paper do not work when multiple or clustered singular values are present. In the future, we will consider methods to overcome this problem. We also need to analyze the bounds on the limiting accuracy based on the precisions used and the convergence conditions.