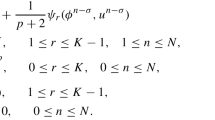An efficient numerical method on modified space-time sparse grid for time-fractional diffusion equation with nonsmooth data

Abstract

In this paper, we focus on developing a high efficient algorithm for solving d-dimension time-fractional diffusion equation (TFDE). For TFDE, the initial function or source term is usually not smooth, which can lead to the low regularity of exact solution. And such low regularity has a marked impact on the convergence rate of numerical method. In order to improve the convergence rate of the algorithm, we introduce the space-time sparse grid (STSG) method to solve TFDE. In our study, we employ the sine basis and the linear element basis for spatial discretization and temporal discretization, respectively. The sine basis can be divided into several levels, and the linear element basis can lead to the hierarchical basis. Then, the STSG can be constructed through a special tensor product of the spatial multilevel basis and the temporal hierarchical basis. Under certain conditions, the function approximation on standard STSG can achieve the accuracy order $\mathcal {O}(2^{-J}J)$ with $\mathcal {O}(2^{J}J)$ degrees of freedom (DOF) for $d=1$ and $\mathcal {O}(2^{Jd})$ DOF for $d>1$, where J denotes the maximal level of sine coefficients. However, if the solution changes very rapidly at the initial moment, the standard STSG method may reduce accuracy or even fail to converge. To overcome this, we integrate the full grid into the STSG, and obtain the modified STSG. Finally, we obtain the fully discrete scheme of STSG method for solving TFDE. The great advantage of the modified STSG method can be shown in the comparative numerical experiment.

1 Introduction

Consider the d-dimensional ($d=1,2,3$) TFDE

$$\begin{aligned} \textrm{D}_t^{\alpha }u=a\Delta u+f\big (u,\textbf{x},t\big ), \qquad (\textbf{x},t)\in \varOmega \times (0,T] \end{aligned}$$

(1)

with the homogeneous boundary condition

$$\begin{aligned} u(\textbf{x},t)=0, \qquad (\textbf{x},t)\in \partial \varOmega \times (0,T] \end{aligned}$$

(2)

and the initial condition

$$\begin{aligned} u(\textbf{x},0)=u_0(\textbf{x}),\qquad \textbf{x}\in \varOmega , \end{aligned}$$

where $T>0$ is a fixed final time, $a>0$ is the diffusion coefficient, $\Delta$ is the Laplacian, $f\big (u,\textbf{x},t\big )$ is the source term or reaction term, and $\partial \varOmega$ denotes the boundary of the rectangular domain $\varOmega$. Without loss of generality, we always assume

$$\begin{aligned} \varOmega =(0,1)^d \end{aligned}$$

in this paper. Here the operator $\textrm{D}_t^{\alpha }$ denotes the Caputo fractional derivative of order $\alpha \in (0,1)$ in temporal direction

$$\begin{aligned} \textrm{D}_t^{\alpha }u(\cdot ,t)=\frac{1}{\varGamma (1-\alpha )} \int _0^t(t-s)^{-\alpha }\frac{\partial }{\partial s} u(\cdot ,s)\textrm{d}s, \end{aligned}$$

(3)

where $\varGamma (z)$ is the Gamma function defined by

$$\begin{aligned} \varGamma (z)=\int _0^{+\infty }s^{z-1}\textrm{e}^{-s}\textrm{d}s,\qquad \textrm{Re}(z)>0. \end{aligned}$$

The classical diffusion model is based on the assumption of Brownian motion. In Brownian motion, the distribution of substance has linear growth of the mean squared particle displacement with the time t. However, a lot of physical processes [6, 28] cannot be accurately described by Brownian motion, and they have superlinear or sublinear mean square particle displacements with the time t. In contrast, the fractional diffusion equation can describe these problems more accurately than integer-order diffusion equation, and it has great application value. In particular, for TFDE, it has been used to describe many models of practical applications, such as the electron transport in Xerox photocopier [28], Modeling the epidemic control measures in overcoming COVID-19 outbreaks [34], simulating the viscoelastic liquid [16], the dynamics of latent liquidity in financial markets [2], and so on.

In recent years, there many researches about the numerical methods for fractional problem. The key for solving TFDE is how to discretize the time-fractional derivative. A classical discrete method is L1 difference method [17]. Kopteva [14] gave a complete convergence analysis of L1 difference method for standard TFDE. Mehandiratta et al. [19,20,21,22] extended the method to TFDE on metric star graph. Ali et al. [1] consider the variable-order fractional modified sub-diffusion equation. Moreover, other discretization of time-fractional derivative such as generalized Jacobi spectral method [4, 18] has also been used for solving TFDE. The time memory property of TFDE imply that it requires a lot of computational cost to approximate the time-fractional derivative, and so the research of fast algorithm is important. Jiang et al. [11] used the sum of exponentials approximation to obtain the fast convolution algorithm. Salama et al. [24,25,26,27] used hybrid Laplace transform-finite difference method to obtain the high efficient scheme.

In this paper, we mainly consider the TFDE with nonsmooth data, and there are two considerable problems. One problem is the memory of time-fractional derivatives, which means that the nonsmooth data will affect the spatial regularity of solutions for a long time. Thus, some spatial discrete methods, such as spectral method, high-order finite element method, etc, will be difficult to give full play to their high-accuracy advantages. The other problem is that the solution has singularity at the initial time if the source term $f\big (u,\textbf{x},t\big )$ is not compatible with the initial function [31]. For general cases, the direct difference discretization cannot exceed the first-order accuracy in temporal direction, even if the higher-order temporal basis function is selected. Therefore, many researches are interested in the improved method of temporal discretization. A famous method is to use the graded meshes instead of uniform meshes [14, 32, 37], and such method can effectively deal with the initial singularity by using the non-equidistant time stepsize. More recently, Yan et al. [35] developed the corrected L1 difference method, and this method corrects the first step of the standard L1 difference scheme and effectively overcomes the influence of initial singularity on the accuracy of the algorithm. Based on such idea, the high-order BDF method can also be obtained [12]. These corrected schemes are also introduce in [13]. However, the algorithm with high-order accuracy requires that the solution of the equation satisfy the corresponding regularity. For some cases, for example, if the source term $f(u,\textbf{x},t)$ is singular in the temporal direction, the advantages of the higher-order algorithm may be greatly weakened.

For the conventional time-stepping algorithm, which is called the full grid (FG) method in this paper, the total DOF is equal to the spatial DOF multiplied by the temporal DOF. When the convergence rate of the algorithm in spatial direction and temporal direction is seriously limited, the high-accuracy computation of FG method implies the expensive computational cost. In order to reduce the total DOF of high-accuracy computation, we introduce the STSG method.

The sparse grid method is presented by Smolyak [30], and it has been used to break “the curse of dimensionality” [3]. For sparse grid method, the selection of multilevel basis is necessary. The difference among different levels can be represented by hierarchical basis [36], which can lead to the hierarchical transform and hierarchical coefficients. The hierarchical coefficients are generally decay from level to level, and the decaying rate depends on the regularity of function and on the selection of basis functions. The numerical approximation requires a proper truncation of hierarchical coefficients indices. If the decaying rate of hierarchical coefficients is slow and anisotropic, the hyperbolic-type truncation may achieve nice results, and such hyperbolic-type approximation can lead to the construction of sparse grid. In particular, for time-dependent problems, if the decaying rate of hierarchical coefficient is anisotropic between spatial direction and temporal direction, then the STSG method can be considered in approximating these problems [8, 9]. The STSG method does not directly improve the convergence order in spatial or temporal direction. It only makes an appropriate choice for the basis functions of tensor product type (the product of spatial basis function and time basis function), so as to reduce the total DOF of the fully discrete scheme.

As far as we know, although there are a few researches about sparse grid method for space-fractional problems [10], there is no literature about STSG method for time-fractional problems or other time memory problems. Therefore, our purpose is to introduce the STSG method into the evolution equations with time memory property, and the TFDE considered in this paper is an important class of these equations. In the work of this paper, we combine the STSG method with the conventional algorithm of TFDE, and obtain a new scheme for solving TFDE. When the regularity of TFDE in the spatial direction is relatively weak, the STSG method has great advantages over the FG method. Compared with some temporal higher-order algorithms for solving TFDE, such as corrected L1 difference method, the comparative advantages of STSG are reflected when the value of $\alpha$ is relatively large or the source term has strong singularity in temporal direction. Moreover, if the solution changes very rapidly at the initial moment, the standard STSG method may reduce accuracy or even fail to converge. Therefore, we constructed the modified STSG. The numerical results show that the modified STSG method has wider applicability than the standard STSG method.

Besides, the sine pseudospectral method is used for spatial discretization in our research. For low regularity problem, although the high-accuracy advantage is greatly weakened, the sine pseudospectral method still has its value, because the obtained algebraic equations are more convenient for computation. Moreover, we use the hierarchical basis of linear element for temporal discretization. Such selection of spatial basis and temporal basis is very common in FG method, but it is very rare in the existing literatures about STSG researches. Therefore, the algorithm of function approximation is also a research point of this paper.

The rest of the paper is organized as follows. In Section 2, we illustrate why it is necessary to use STSG method for solving TFDE. In Section 3, by introducing the temporal hierarchical basis and the spatial multilevel basis, the standard STSG is constructed. Then, we obtain the discrete sine transform (DST) algorithm and the function approximation error estimate on STSG. In Section 4, we obtain the modified STSG, and the L1 difference method is used to obtain the algorithm for computing the Caputo derivative. In Section 5, by using the L1 difference/sine pseudospectral method on modified STSG, we obtain the fully discrete scheme for solving TFDE. In Section 6, several numerical experiments are given to show the great advantage of STSG method.

2 Motivation

Let v(x) be a periodic odd function with a period of 2, and $v\in \mathcal {L}^2_0(0,1)$. Then, the sine coefficients are defined as

$$\begin{aligned} \hat{v}_k=2\int _0^1 v(x)\sin k\pi x\textrm{d}x,\qquad k\in \mathbb {N}_+, \end{aligned}$$

where $\mathbb {N}_+$ denotes the set of positive integer numbers. Here the absolute value of the k-th coefficient $\mid \hat{v}_k\mid$ is also called the k-th frequency spectrum for $k\in \mathbb {N}_+$. It is well-known that the decaying rate of the frequency spectrum is directly related to the regularity of the function in periodic domain. Then, we consider the following problem.

Example 1

Consider the one-dimensional TFDE

$$\begin{aligned} \textrm{D}_t^{\alpha }u=0.1\frac{\partial ^2}{\partial x^2}u, \qquad (x,t)\in (0,1)\times (0,1], \end{aligned}$$

with the homogeneous boundary condition (2) and the initial function

$$\begin{aligned} u_0(x)=\delta (x-0.5),\qquad x\in (0,1), \end{aligned}$$

where $\delta (x)$ denotes the Dirac $\delta$ function.

The diffusion equation with Dirac $\delta$ initial function is very common in practical problems, and it means that the diffusing substance is concentrated in one point at the initial time. From the mathematical point of view, the Dirac $\delta$ function can be defined as an element of dual space. According to Theorem 2.1 of [13], the weak solution of Example 1 satisfies a certain regularity. For integer-order diffusion equation ($\alpha =1$), the solution becomes a smooth function (infinitely differentiable function) after a short moment. But for fractional problem ($0<\alpha <1$), because the Caputo fractional derivative (3) has the property of time memory, the singularity of the initial function will have a lasting effect on the regularity of the solution. Figure 1 clearly shows that the solution of equation in the case $\alpha =0.5$ is not smooth. Here we are very concerned about the decaying property of frequency spectrum. Figure 2 shows the decaying property of frequency spectrum at $t=0.1$. For integer-order diffusion equation, the frequency spectrum has exponentially decaying rate, and it implies that we can achieve very high spatial approximation accuracy with only a few spatial basis functions. But for TFDE, the decaying rate of frequency spectrum is greatly affected by the low regularity of solution. Therefore, if the conventional algorithm is used to solve such problem, the high-accuracy approximation requires a large number of spatial basis functions, which may bring an expensive computational cost.

Fig. 1

The solution at different time in Example 1 with $\alpha =1$ and $\alpha =0.5$

Fig. 2

The frequency spectrum at $t=0.1$ in Example 1

However, the algebraically decaying rate of frequency spectrum also implies that the high-frequency coefficients are relatively small. For high-accuracy approximation, although the high-frequency coefficients cannot be ignored, their computation can allow larger relative error. The main idea of STSG method is to discretize the lower-frequency coefficients with smaller time stepsize and to discretize the higher-frequency coefficients with larger time stepsize, whereas the accuracy is close to that by discretizing all coefficients with smallest time stepsize. In this way, the computational cost of high-accuracy computation can be greatly reduced.

3 Standard space-time sparse grid

Without loss of generality, we only consider the function defined on time interval [0, 1] in this section. Let $\theta _{s,\tau }(t)$ be a linear element with center point s and width $2\tau$, i.e.,

$$\begin{aligned} \theta _{s,\tau }(t)=\left\{ \begin{array}{ll} 1-\frac{1}{\tau }\vert t-s\vert , &{} \text {for}~t\in \big (s-\tau ,s+\tau \big ), \\ 0, &{} \text {for else}, \end{array} \right. \qquad s\in \mathbb {R},~\tau \in \mathbb {R}_+. \end{aligned}$$

For any level $J\in \mathbb {N}_0$ ($\mathbb {N}_0$ denotes the natural number including zero), let $\{\theta _{s,2^{-J}}\}_{s\in \mathcal {T}_J}$ be temporal basis of level J, where

$$\begin{aligned} \mathcal {T}_J=\{n2^{-J}\}_{n=0}^{2^J}. \end{aligned}$$

Obviously, the basis functions of adjacent levels satisfy the relation

$$\begin{aligned} \theta _{s,2^{1-J}}(t)=\theta _{s,2^{-J}}(t)+\frac{1}{2}\theta _{s-2^{-J},2^{-J}}(t)+\frac{1}{2}\theta _{s+2^{-J},2^{-J}}(t),\qquad s\in \mathcal {T}_{J-1}. \end{aligned}$$

(4)

Then, we can define the temporal linear element spaces $\mathcal {W}_J$ and their hierarchical increment spaces $\check{\mathcal {W}}_J$ as

$$\begin{aligned} \mathcal {W}_J=\textrm{span}\left\{ \theta _{s,2^{-J}}\right\} _{s\in \mathcal {T}_{J}},\qquad \check{\mathcal {W}}_J=\textrm{span}\left\{ \theta _{s,2^{-J}}\right\} _{s\in \check{\mathcal {T}}_{J}}, \qquad J\in \mathbb {N}_0, \end{aligned}$$

where

$$\begin{aligned} \check{\mathcal {T}}_{J}= \left\{ \begin{array}{ll} \mathcal {T}_{0}, &{} \textrm{for}~J=0, \\ \mathcal {T}_{J}\backslash \mathcal {T}_{J-1},\quad &{} \textrm{for}~J>0. \end{array}\right. \end{aligned}$$

Here $\{\theta _{s,2^{-J}}\}_{s\in \check{\mathcal {T}}_J}$ is the temporal hierarchical basis of level J. For any function $W\in \mathcal {W}_J$, we have

$$\begin{aligned} W(t)=\sum _{s\in \mathcal {T}_{J}}W(s)\theta _{s,2^{-J}}(t). \end{aligned}$$

Then, using the relation (4), we can easily prove that the function W(t) can be written as the linear combination of multilevel hierarchical basis

$$\begin{aligned} W(t)=\sum _{j=0}^{J}\sum _{s\in \check{\mathcal {T}}_{j}}\check{W}_{s}\theta _{s,2^{-j}}(t), \end{aligned}$$

(5)

where the hierarchical coefficients are given by the hierarchical transform

$$\begin{aligned} \check{W}_{s}= \left\{ \begin{array}{ll} W(s), &{} \textrm{for}~s\in \mathcal {T}_{0}, \\ W(s)-\frac{1}{2}\left( W(s-2^{-j}) +W(s+2^{-j})\right) ,\quad &{} \textrm{for} ~s\in \check{\mathcal {T}}_{j},~j>0. \end{array}\right. \end{aligned}$$

(6)

Let $\{\varphi _{\textbf{k}}\}_{\textbf{k}\in \mathbb {N}_+^d}$ be the d-dimensional sine basis, i.e.,

$$\begin{aligned} \varphi _{\textbf{k}}(\textbf{x})=\prod _{j=1}^d \sin \pi k_j x_j,\qquad \textbf{k}\in \mathbb {N}_+^d,~\textbf{x}\in \varOmega , \end{aligned}$$

where $\mathbb {N}_+$ denotes the set of positive integers. Then, any function $v\in \mathcal {L}^2_0=\mathcal {L}^2_0(\varOmega )$ can be expanded as

$$\begin{aligned} v(\textbf{x})=\sum _{\textbf{k}\in \mathbb {N}_+^d}\hat{v}_{\textbf{k}}\varphi _{\textbf{k}}(\textbf{x}), \qquad \textbf{x}\in \varOmega , \end{aligned}$$

where the multi-dimensional sine coefficients are given by

$$\begin{aligned} \hat{v}_\textbf{k}=2^d\int _{\varOmega } v(\textbf{x})\varphi _{\textbf{k}}(\textbf{x})\textrm{d}\textbf{x},\qquad k\in \mathbb {N}_+^d. \end{aligned}$$

(7)

For any level $J\in \mathbb {N}_0$, we can define the index set

$$\begin{aligned} \mathcal {K}_{J}=\left\{ 1,2,\cdots ,2^J-1\right\} ^d, \end{aligned}$$

the spatial grid points

$$\begin{aligned} \mathcal {X}_{J}=\left\{ 2^{-J},2\cdot 2^{-J},\cdots ,(2^J-1)2^{-J}\right\} ^d, \end{aligned}$$

and the spatial function space

$$\begin{aligned} \mathcal {V}_{J}=\textrm{span}\{\varphi _{\textbf{k}}\}_{\textbf{k}\in \mathcal {K}_J}. \end{aligned}$$

In particular, we assume that

$$\begin{aligned} \mathcal {K}_0=\varnothing ,\qquad \mathcal {X}_0=\varnothing ,\qquad \mathcal {V}_0=\{0\}. \end{aligned}$$

Then, the projection operator and the interpolation operator are defined as

$$\begin{aligned} \mathcal {P}_J~&:~\mathcal {L}_0^2\varOmega ~\rightarrow ~ \mathcal {V}_J\nonumber \\&: ~v(\textbf{x})~\mapsto ~\mathcal {P}_Jv(\textbf{x})=\sum _{\textbf{k}\in \mathcal {K}_J} \hat{v}_{\textbf{k}}\varphi _{\textbf{k}}(\textbf{x}), \end{aligned}$$

(8)

and

$$\begin{aligned} \mathcal {I}_J~&:~\mathcal {L}_0^2\varOmega ~\rightarrow ~ \mathcal {V}_J\nonumber \\&: ~v(\textbf{x})~\mapsto ~V(\textbf{x})=\mathcal {I}_Jv(\textbf{x})=\sum _{\textbf{k}\in \mathcal {K}_J} \hat{V}_{\textbf{k}}\varphi _{\textbf{k}}(\textbf{x}), \end{aligned}$$

(9)

respectively, where $\{\hat{v}_{\textbf{k}}\}_{\textbf{k}\in \mathcal {K}_J}$ is given by (7), and the discrete sine coefficients $\{\hat{V}_{\textbf{k}}\}_{\textbf{k}\in \mathcal {K}_J}$ are given by the DST

$$\begin{aligned} \hat{V}_{\textbf{k}}=2^{-Jd}\sum _{\varvec{\xi }\in \mathcal {X}_J}v(\varvec{\xi })\varphi _\textbf{k}(\varvec{\xi }). \end{aligned}$$

It is well-know that the algorithm of fast Fourier transform can be used in the computation of DST, so the computational cost of DST is of order $\mathcal {O}(2^{Jd}J)$.

Using the tensor product construction of the multilevel basis in space and the hierarchical basis in time, we can construct the standard STSG as

$$\begin{aligned}&\text {index set:}\qquad \mathcal {C}_J=\bigcup _{j=0}^{J-1}\mathcal {K}_{J-j}\times \check{\mathcal {T}}_{j},\nonumber \\&\text {grid points:}\qquad \mathcal {G}_J=\bigcup _{j=0}^{J-1}\mathcal {X}_{J-j}\times \check{\mathcal {T}}_{j},\nonumber \\&\text {function space:}\qquad \mathcal {U}_J=\bigoplus _{j=0}^{J-1}\mathcal {V}_{J-j}\times \check{\mathcal {W}}_{j}, \end{aligned}$$

(10)

with the level J. Figure 3 gives an example of STSG.

Fig. 3

Grid points (left) and index set (right) of STSG with $d=1$ and $J=5$

Any function $U\in \mathcal {U}_J$ can be written as the form

$$\begin{aligned} U(\textbf{x},t)= \sum _{j=0}^{J-1} \sum _{s\in \check{\mathcal {T}}_{j}}\theta _{s,2^{-j}}(t) \sum _{\textbf{k}\in {\mathcal {K}}_{J-j}}\varphi _{\textbf{k}}(\textbf{x})\check{\hat{U}}_{\textbf{k},s}, \end{aligned}$$

(11)

where $\big \{\check{\hat{U}}_{\textbf{k},s}\big \}_{\textbf{k}\in {\mathcal {K}}_{J-j},s\in \check{\mathcal {T}}_{j}}$ are the sine coefficients of $U(\textbf{x},t)$ on the space $\mathcal {V}_{J-j}\times \check{\mathcal {W}}_{j}$ for $j=0,1,\cdots ,J-1$. Let

$$\begin{aligned} \check{\mathcal {K}}_j=\mathcal {K}_{j}\backslash \mathcal {K}_{j-1},\qquad j=1,2,\cdots ,J, \end{aligned}$$

then

$$\begin{aligned} U(\textbf{x},t)=&\sum _{j=0}^{J-1} \sum _{s\in \check{\mathcal {T}}_{j}}\theta _{s,2^{-j}}(t)\sum _{j'=1}^{J-j} \sum _{\textbf{k}\in \check{\mathcal {K}}_{j'}}\varphi _{\textbf{k}}(\textbf{x}) \check{\hat{U}}_{\textbf{k},s}\nonumber \\ =&\sum _{j'=1}^J\sum _{\textbf{k}\in \check{\mathcal {K}}_{j'}}\varphi _{\textbf{k}}(\textbf{x}) \sum _{j=0}^{J-j'} \sum _{s\in \check{\mathcal {T}}_{j}} \theta _{s,2^{-j}}(t)\check{\hat{U}}_{\textbf{k},s}\nonumber \\ =&\sum _{\textbf{k}\in \mathcal {K}_{J}}\varphi _{\textbf{k}}(\textbf{x})\hat{U}_{\textbf{k}}(t). \end{aligned}$$

(12)

Therefore, the sine coefficients of $U(\textbf{x},t)$ satisfy

$$\begin{aligned} \hat{U}_{\textbf{k}}(t)=\sum _{j=0}^{J-j'} \sum _{s\in \check{\mathcal {T}}_{j}} \theta _{s,2^{-j}}(t)\check{\hat{U}}_{\textbf{k},s},\qquad \textbf{k}\in \check{\mathcal {K}}_{j'},~ j'=1,2,\cdots ,J. \end{aligned}$$

From (5) and (6), it follows from (12) that

$$\begin{aligned} \check{\hat{U}}_{\textbf{k},s}= \left\{ \begin{array}{ll} \hat{U}_{\textbf{k}}(s), &{} \textrm{for}~s\in \mathcal {T}_{0}, \\ \hat{U}_{\textbf{k}}(s)-\frac{1}{2}\big (\hat{U}_{\textbf{k}}(s-2^{-j}) +\hat{U}_{\textbf{k}}(s+2^{-j})\big ), &{} \textrm{for} ~s\in \check{\mathcal {T}}_{j},~j>0. \end{array}\right. \end{aligned}$$

(13)

Moreover, let

$$\begin{aligned} \check{U}_{s}(\textbf{x})=\sum _{\textbf{k}\in {\mathcal {K}}_{J-j}}\varphi _{\textbf{k}}(\textbf{x}) \check{\hat{U}}_{\textbf{k},s},\qquad s\in \check{\mathcal {T}}_{j},~j=0,1,\cdots ,J-1. \end{aligned}$$

Then, (11) yields

$$\begin{aligned} U(\textbf{x},t)=\sum _{j=0}^{J-1}\sum _{s\in \check{\mathcal {T}}_{j}}\check{U}_{s}(\textbf{x})\theta _{s,2^{-j}}(t) =\sum _{s\in \mathcal {T}_{J-1}}U(\textbf{x},s)\theta _{s,2^{1-J}}(t), \end{aligned}$$

(14)

and it is easy to obtain the hierarchical transform on grid function as

$$\begin{aligned} \check{U}_{s}(\textbf{x})= \left\{ \begin{array}{ll} U(\textbf{x},s), &{} \textrm{for}~s\in \mathcal {T}_{0}, \\ U(\textbf{x},s)-\frac{1}{2}\left( U(\textbf{x},s-2^{-j})+U(\textbf{x},s+2^{-j})\right) ,~ &{} \textrm{for} ~s\in \check{\mathcal {T}}_{j},~j>0, \end{array}\right. \end{aligned}$$

(15)

For simplicity, we use the form of vector to represent the relevant data. Let

$$\begin{aligned} \textbf{U}=(U(\varvec{\xi },s))_{(\varvec{\xi },s)\in \mathcal {G}_J},\qquad \hat{\textbf{U}}=(\hat{U}_{\textbf{k}}(s))_{(\textbf{k},s)\in \mathcal {C}_J}. \end{aligned}$$

Then, the derivations (11), (12) and (14) show a way to compute the coefficients $\hat{\textbf{U}}$ from the grid function $\textbf{U}$. Such process is called the DST on standard STSG, and it is specifically described by Algorithm 1. Here we use the following linear operators to represent the DST on standard STSG

$$\begin{aligned} \textbf{F}~&:~\mathbb {R}^{\mathcal {G}_J}~\rightarrow ~ \mathbb {R}^{\mathcal {C}_J}\nonumber \\&: ~\textbf{U}~\mapsto ~\hat{\textbf{U}}=\textbf{F}\textbf{U}. \end{aligned}$$

(16)

Algorithm 1 is obviously reversible, and so there exists an operator $\textbf{F}^{-1}$ such that

$$\begin{aligned} \textbf{U}=\textbf{F}^{-1}\hat{\textbf{U}}. \end{aligned}$$

Thanks to Lemma 2.5 in [9], the DOF of STSG is of order $\mathcal {O}(2^JJ)$ and $\mathcal {O}(2^{Jd})$ for $d=1$ and $d>1$, respectively. Moreover, the computational cost of Algorithm 1 can be estimated by the following theorem.

Theorem 1

The computational cost of Algorithm 1 is of order $\mathcal {O}(2^JJ^2)$ for $d=1$ and $\mathcal {O}(2^{Jd}J)$ for $d>1$.

Proof

For Algorithm 1, the computational costs of step 1 and step 3 have the same order as the number of grid points, and so we just need to care about step 2. The number of elements in $\check{T}_j$ is 2 and $2^{j-1}$ for $j=0$ and $j=1,2,\cdots ,J-1$, respectively. The computational cost of spatial DST in grid $\mathcal {X}_{J-j}$ is less than $C2^{(J-j)d}(J-j)$, where C is a constant independent of J and j.

Then, for one-dimensional case, the computational cost is less than

$$\begin{aligned} C2^{J+1}J+C\sum _{j=1}^{J-1}2^{j-1}2^{J-j}(J-j)=C2^{J+1}J+C2^{J-1}\sum _{j=1}^{J-1}(J-j), \end{aligned}$$

and for multi-dimensional case, the computational cost is less than

$$\begin{aligned} C2^{Jd+1}J+C\sum _{j=1}^{J-1}2^{j-1}2^{(J-j)d}(J-j)\le C2^{Jd+1}J+C2^{Jd-1}J\sum _{j=1}^{J-1}2^{j(1-d)}. \end{aligned}$$

Note that $\sum _{j=1}^{J-1}(J-j)=\mathcal {O}(J^2)$ and $\sum _{j=1}^{J-1}2^{j(1-d)}=\mathcal {O}(1)$, and we can obtain the result of original proposition. $\square$

Define the Hilbert space

$$\begin{aligned} \mathcal {H}_0^\beta =\{v~:~\Vert v\Vert _\beta <\infty \},\quad \textrm{where}~\Vert v\Vert _{\beta }=\bigg (\sum _{\textbf{k}\in \mathbb {N}_+^d}\mid \textbf{k}\mid ^{2\beta } \mid \hat{v}_\textbf{k}\mid ^2\bigg )^{\frac{1}{2}}. \end{aligned}$$

(17)

Especially, it is obvious that $\mathcal {H}_0^0=\mathcal {L}_0^2$ since

$$\begin{aligned} \Vert v\Vert _0=\sum _{\textbf{k}\in \mathbb {N}_+^d} \mid \hat{v}_\textbf{k}\mid ^2=\int _{\varOmega } \mid v(\textbf{x})\mid ^2\textrm{d}\textbf{x}=\Vert v\Vert _{\mathcal {L}^2}. \end{aligned}$$

Then, the function approximation on STSG is defined as

$$\begin{aligned} \widetilde{\mathcal {I}}_J~&:~\mathcal {L}^2([0,1],\mathcal {H}_0^0)~\rightarrow ~ \mathcal {U}_J\nonumber \\&: ~u(\textbf{x},t)~\mapsto ~U(\textbf{x},t)=\widetilde{\mathcal {I}}_Ju(\textbf{x},t)=\sum _{j=0}^{J-1} \sum _{s\in \check{\mathcal {T}}_{j}}\theta _{s,2^{-j}}(t)\mathcal {I}_{J-j}\check{u}_{s}(\textbf{x}), \end{aligned}$$

(18)

where the notation $\check{u}_{s}(\textbf{x})$ is given by (15). For (18), it is easy to prove

$$\begin{aligned} U(\varvec{\xi },s)=u(\varvec{\xi },s),\qquad \forall (\varvec{\xi },s)\in \mathcal {G}_J. \end{aligned}$$

Theorem 2

Suppose that $u\in \mathcal {L}^2([0,1],\mathcal {H}_0^\beta )$ for a fixed real number $\beta >\frac{d}{2}$, and the approximation $U=\widetilde{\mathcal {I}}_{J}u$ is shown in (18). Then,

$$\begin{aligned} \left| \left| \left| {u-U}\right| \right| \right| _0\lesssim 2^{-J\min \{\beta ,1\}}J\bigg \vert \bigg \vert \bigg \vert \frac{\partial }{\partial t}u\bigg \vert \bigg \vert \bigg \vert _\beta +2^{-J\beta }\big (\Vert u(\cdot ,0)\Vert _\beta +\Vert u(\cdot ,1)\Vert _\beta \big ) \end{aligned}$$

(19)

if $\frac{\partial }{\partial t}u\in \mathcal {L}^2([0,1],\mathcal {H}_0^\beta )$, and

$$\begin{aligned} \left| \left| \left| {u-U}\right| \right| \right| _0\lesssim 2^{-J\min \{\beta ,2\}}J\bigg \vert \bigg \vert \bigg \vert \frac{\partial ^2}{\partial t^2}u\bigg \vert \bigg \vert \bigg \vert _\beta +2^{-J\beta }\big (\Vert u(\cdot ,0)\Vert _\beta +\Vert u(\cdot ,1)\Vert _\beta \big ) \end{aligned}$$

(20)

if $\frac{\partial ^2}{\partial t^2}u\in \mathcal {L}^2([0,1],\mathcal {H}_0^\beta )$, where

$$\begin{aligned} \left| \left| \left| {u}\right| \right| \right| _\beta =\bigg (\int _0^1\Vert u(\cdot ,t)\Vert _\beta ^2\textrm{d}t\bigg )^{\frac{1}{2}}, \end{aligned}$$

and the notation $A\lesssim B$ means that there exists a number C independent of $u(\textbf{x},t)$ and J, such that $A\le CB$.

Proof

Here we only prove (20), because the proof of (19) is similar.

At first, the conditions $u\in \mathcal {L}^2([0,1],\mathcal {H}_0^\beta )$ and $\frac{\partial ^2}{\partial t^2}u\in \mathcal {L}^2([0,1],\mathcal {H}_0^\beta )$ can easily yield

$$\begin{aligned} \max _{0\le t\le 1}\Vert u(\cdot ,t)\Vert _\beta<\infty ,\qquad \max _{0\le t\le 1}\left\| \frac{\partial }{\partial t}u(\cdot ,t)\right\| _\beta <\infty . \end{aligned}$$

Let $u^*$ be the temporal discretization of u, i.e.,

$$\begin{aligned} u^*(\textbf{x},t)=\sum _{s\in \mathcal {T}_{J-1}}\theta _{s,2^{1-J}}(t)u(\textbf{x},s). \end{aligned}$$

Through the error estimate of linear element approximation [15], we can obtain

$$\begin{aligned} \left| \left| \left| {u-u^*}\right| \right| \right| _0 \lesssim 2^{-2J}\left| \left| \left| {\frac{\partial ^2u}{\partial t^2}}\right| \right| \right| _0. \end{aligned}$$

(21)

Using the similar proof of Theorem 2.3 in [29], we can obtain the error estimate of sine interpolation

$$\begin{aligned} \Vert v-\mathcal {I}_{j}v\Vert _0\lesssim 2^{-j\beta }\Vert v\Vert _\beta ,\qquad \forall j>0,~\beta >\frac{d}{2}. \end{aligned}$$

Thus,

$$\begin{aligned} \left| \left| \left| {u^*-U}\right| \right| \right| _0\le&\sum _{j=0}^{J-1}\bigg \vert \bigg \vert \bigg \vert \sum _{s\in \check{\mathcal {T}}_{j}} \theta _{s,2^{-j}} (\check{u}_{s}-\mathcal {I}_{J-j}\check{u}_{s}) \bigg \vert \bigg \vert \bigg \vert _0\nonumber \\ =&\sum _{j=0}^{J-1}\bigg (\sum _{s\in \check{\mathcal {T}}_{j}}\int _{s-2^{-j}}^{s+2^{-j}}\big \Vert \theta _{s,2^{-j}}(t) \big (\check{u}_{s}-\mathcal {I}_{J-j} \check{u}_{s} \big )\big \Vert _0^2\textrm{d}t \bigg )^{\frac{1}{2}}\nonumber \\ =&\sum _{j=0}^{J-1}\bigg (\sum _{s\in \check{\mathcal {T}}_{j}}\big \Vert \check{u}_{s}-\mathcal {I}_{J-j} \check{u}_{s} \big \Vert _0^2\int _{s-2^{-j}}^{s+2^{-j}}\mid \theta _{s,2^{-j}}(t)\mid ^2\textrm{d}t \bigg )^{\frac{1}{2}}\nonumber \\ \le&\sum _{j=0}^{J-1}2^{-\frac{j}{2}}\bigg (\sum _{s\in \check{\mathcal {T}}_{j}}\big \Vert \check{u}_{s}-\mathcal {I}_{J-j} \check{u}_{s} \big \Vert _0^2\bigg )^{\frac{1}{2}}\nonumber \\ \lesssim&\sum _{j=0}^{J-1}2^{-\frac{j}{2}-2(J-j)\beta }\bigg (\sum _{s\in \check{\mathcal {T}}_{j}}\big \Vert \check{u}_{s}\big \Vert _\beta ^2\bigg )^{\frac{1}{2}}. \end{aligned}$$

(22)

For $j\ge 1$, from the Taylor expansion of integral remainder, we have

$$\begin{aligned} \check{u}_{s}(\textbf{x})=&\frac{1}{2}\int _{s-2^{-j}}^{s+2^{-j}}\big (\vert s-t\vert -2^{-j}\big )\frac{\partial ^2}{\partial t^2}u(\textbf{x},t) \textrm{d}t\\ =&\frac{1}{2}\sum _{\textbf{k}\in \mathbb {N}_+^d}\varphi _{\textbf{k}}(\textbf{x})\int _{s-2^{-j}}^{s+2^{-j}} \big (\vert s-t\vert -2^{-j}\big ) \hat{u}_{\textbf{k}}^{\prime \prime }(t)\textrm{d}t, \end{aligned}$$

and so

$$\begin{aligned} \big \Vert \check{u}_{s}\big \Vert _{\beta }=&\frac{1}{2}\bigg (\sum _{\textbf{k}\in \mathbb {N}_+^d}\mid \textbf{k}\mid ^{2\beta } \bigg \vert \int _{s-2^{-j}}^{s+2^{-j}} \big (\vert s-t\vert -2^{-j}\big )\hat{u}_{\textbf{k}}^{\prime \prime }(t) \textrm{d}t\bigg \vert ^2\bigg )^{\frac{1}{2}}\\ \le&\frac{1}{2}\bigg (\sum _{\textbf{k}\in \mathbb {N}_+^d}\mid \textbf{k}\mid ^{2\beta } \int _{s-2^{-j}}^{s+2^{-j}} \big \vert \mid s-t\mid -2^{-j}\big \vert ^2\textrm{d}t \int _{s-2^{-j}}^{s+2^{-j}}\big \vert \hat{u}_{\textbf{k}}^{\prime \prime }(t)\big \vert ^2 \textrm{d}t\bigg )^{\frac{1}{2}}\\ \le&\frac{1}{2}\bigg (2^{-3j}\sum _{\textbf{k}\in \mathbb {N}_+^d}\vert \textbf{k}\vert ^{2m} \int _{s-2^{-j}}^{s+2^{-j}}\big \vert \hat{u}_{\textbf{k}}^{\prime \prime }(t)\big \vert ^2 \textrm{d}t\bigg )^{\frac{1}{2}}. \end{aligned}$$

Substituting the above inequality into (22), it follows that

$$\begin{aligned} \left| \left| \left| {u^*-U}\right| \right| \right| _0 \lesssim&\sum _{j=1}^{J-1} 2^{-2j-(J-j)\beta } \bigg (\sum _{s\in \check{\mathcal {T}}_{j}}\sum _{\textbf{k}\in \mathbb {N}_+^d}\vert \textbf{k}\vert ^{2\beta } \int _{s-2^{-j}}^{s+2^{-j}}\big \vert \hat{u}_{\textbf{k}}^{\prime \prime }(t)\big \vert ^2 \textrm{d}t\bigg )^{\frac{1}{2}}\nonumber \\&+2^{-J\beta }\big (\Vert u(\cdot ,0)\Vert _\beta +\Vert u(\cdot ,1)\Vert _\beta \big )\nonumber \\ =&2^{-J\beta }\bigg \vert \bigg \vert \bigg \vert \frac{\partial ^2u}{\partial t^2} \bigg \vert \bigg \vert \bigg \vert _\beta \sum _{j=1}^{J-1} 2^{j(\beta -2)}+2^{-J\beta }\big (\Vert u(\cdot ,0)\Vert _\beta +\Vert u(\cdot ,1)\Vert _\beta \big )\nonumber \\ \le&2^{-J\min \{\beta ,2\}}J\bigg \vert \bigg \vert \bigg \vert \frac{\partial ^2u}{\partial t^2}\bigg \vert \bigg \vert \bigg \vert _\beta +2^{-J\beta }\big (\Vert u(\cdot ,0)\Vert _\beta +\Vert u(\cdot ,1)\Vert _\beta \big ). \end{aligned}$$

(23)

From (21), (23) and the norm inequality

$$\begin{aligned} \left| \left| \left| {u-U}\right| \right| \right| _0\le \left| \left| \left| {u-u^*}\right| \right| \right| _0+\left| \left| \left| {u^*-U}\right| \right| \right| _0, \end{aligned}$$

the conclusion of the original proposition can be obtained. $\square$

Compare the discretization (18) with the FG discretization

$$\begin{aligned} U^*(\textbf{x},t)=\sum _{m=0}^{M}\theta _{\frac{m}{M},\frac{1}{M}}(t)\mathcal {I}_Ju\Big (\textbf{x},\frac{m}{M}\Big ). \end{aligned}$$

The FG approximation requires $\mathcal {O}(2^{Jd}M)$ DOF, and it is easy to prove the error estimate

$$\begin{aligned} \left| \left| \left| {u-U^*}\right| \right| \right| _0\lesssim \frac{1}{M^2}\left| \left| \left| {\frac{\partial ^2u}{\partial t^2}}\right| \right| \right| _0+2^{-J\beta }\max _{0\le t\le 1}\Vert u(\cdot ,t)\Vert _\beta . \end{aligned}$$

(24)

If the function $u(\textbf{x},t)$ has low regularity in spatial direction, the constant $\beta$ shown in Theorem 2 or in inequality (24) cannot be too large. In particular, if $\beta$ is equal to 2 and M is chosen to be proportional to $2^{J}$, then the accuracy order in (24) is the same to that in (20). But the FG approximation requires $\mathcal {O}(2^{J(d+1)})$ DOF, whereas the STSG approximation only requires $\mathcal {O}(2^{J}J)$ DOF for $d=1$ and $\mathcal {O}(2^{Jd})$ DOF for $d>1$. When $\beta$ is not equal to 2, the approximation effects for such two kinds of grids need to be discussed in detail. In general, the advantages of STSG method in saving DOF are very significant if $\beta$ is not too far from 2. However, it should be noted that the additional condition $\frac{\partial }{\partial t}u\in \mathcal {L}^2([0,1],\mathcal {H}_0^\beta )$ or $\frac{\partial ^2}{\partial t^2}u\in \mathcal {L}^2([0,1],\mathcal {H}_0^\beta )$ shown in Theorem 2 is necessary. Such condition implies that the spatial regularity is not very related to the temporal derivative, and it is an important factor for STSG method to reflect its advantages.

4 Approximating Caputo derivative on modified space-time sparse grid

Unfortunately, for TFDE (1), the condition $\frac{\partial }{\partial t}u\in \mathcal {L}^2([0,T],\mathcal {H}_0^\beta )$ or $\frac{\partial ^2}{\partial t^2}u\in \mathcal {L}^2([0,T],\mathcal {H}_0^\beta )$ in Theorem 2 is usually not satisfied, because the solution $u(\textbf{x},t)$ usually has the singularity at the initial time [31]. From another point of view, the high-frequency coefficients of the exact solution may change rapidly at the initial moment. In the construction of standard STSG (10), the large time stepsizes are employed to approximate the high-frequency coefficients, and the computation of large time stepsizes is not suitable to simulate the rapid change. In fact, the advantage of the standard STSG is reflected in simulating the spatial low regularity, but it is worse than FG in dealing with the singularity of initial time. Therefore, for some cases of TFDE, the standard STSG method may bring bad results.

For this problem, our approach is to compute the TFDE through the FG method in the first time step, and then the standard STSG is used to compute the equation in the remaining time intervals. And such approach can lead to the modified STSG, which will be introduced later.

The time interval [0, T] can be divided as

$$\begin{aligned} 0\le T_0<T_1<\cdots <T_L=T, \end{aligned}$$

(25)

where L is a given positive integer. For the approach of modified STSG, we select $T_0$ as the minimum time stepsize in STSG. Then, for any given maximal level J, we have

$$\begin{aligned}&T_n-T_{n-1}=\Delta T,\qquad n=1,2,\cdots ,L,\nonumber \\&T_0=\frac{\Delta T}{2^{J-1}}. \end{aligned}$$

(26)

Then, $T_0$ and $\Delta T$ can be solved as

$$\begin{aligned} T_0=\frac{T}{2^{J-1}L+1},\qquad \Delta T=\frac{2^{J-1}T}{2^{J-1}L+1}. \end{aligned}$$

According to the related definitions of standard STSG (10), we can define the index set and the grid points of the modified STSG as

$$\begin{aligned}&\text {index set:}\qquad \mathcal {C}^{(J,L)}=\bigcup _{n=0}^L\mathcal {C}^n_J,\nonumber \\&\text {grid points:}\qquad \mathcal {G}^{(J,L)}=\bigcup _{n=0}^L\mathcal {G}^n_J, \end{aligned}$$

(27)

where

$$\begin{aligned}&\mathcal {C}^0_J=\big \{(\textbf{k},s):~\textbf{k}\in \mathcal {K}_J,~s=0~\textrm{or}~T_0\big \},\\&\mathcal {G}^0_J=\big \{(\varvec{\xi },s):~\varvec{\xi }\in \mathcal {X}_J,~s=0~\textrm{or}~T_0\big \}, \end{aligned}$$

and

$$\begin{aligned} \begin{array}{l} \mathcal {C}^n_J=\left\{ \big (\textbf{k},s\Delta T+T_{n-1}\big ):~(\textbf{k},s)\in \mathcal {C}_J\right\} ,\\ \mathcal {G}^n_J=\left\{ \big (\varvec{\xi },s\Delta T+T_{n-1}\big ):~(\varvec{\xi },s)\in \mathcal {G}_J\right\} , \end{array}\qquad n=1,2,\cdots ,L. \end{aligned}$$

It is obvious that $\mathcal {G}^0_J$ is the FG with only one time step, and $\mathcal {G}^n_J~(n=1,2,\cdots ,L)$ are a group of standard STSG. Figure 4 proposes an example of the modified STSG.

Fig. 4

Grid points (left) and index set (right) of the modified STSG with $d=1$, $J=5$, $L=2$ and $T=1$

To ensure the feasibility of the modified STSG (27), we need to assume that the exact solution $u(\textbf{x},t)$ is singular only at the initial time, and so the norm $\left\| \frac{\partial }{\partial t}u(\cdot ,t)\right\| _\beta$ or $\left\| \frac{\partial ^2}{\partial t^2}u(\cdot ,t)\right\| _\beta$ is bounded with respect to $t\in [T_0,T]$. For the computation of interval $[0,T_0]$, we employ the FG method with maximal spatial level. And the FG method only needs to be used in the computation of the first time step, because the solution is no longer singular after the first time step.

Let

$$\begin{aligned} \mathcal {U}_J^{(0)}=\textrm{span}\big \{\varphi _{\textbf{k}}(\textbf{x})\theta _{s,T_0}(t): ~(\textbf{k},s)\in \mathcal {C}^0_J\big \}. \end{aligned}$$

Then, we say

$$\begin{aligned} U\in \mathcal {U}^{(J,L)}, \end{aligned}$$

if there exists $U^0\in \mathcal {U}_J^{(0)}$ and $U^1,U^2,\cdots ,U^L\in \mathcal {U}_J$ such that

$$\begin{aligned} U^{n-1}(\textbf{x},1)=U^n(\textbf{x},0),\qquad n=1,2,\cdots ,L \end{aligned}$$

and

$$\begin{aligned} U(\textbf{x},t)= \left\{ \begin{array}{ll} U^0(\textbf{x},t),\quad &{} \textrm{for}~t\in [0,T_0], \vspace{1ex}\\ U^n\left( \textbf{x},\frac{t-T_{n-1}}{\Delta T}\right) ,\quad &{} \textrm{for}~t\in [T_{n-1},T_n],~n=1,2,\cdots ,L. \end{array} \right. \end{aligned}$$

Any function $U\in \mathcal {U}^{(J,L)}$ can be written as the form

$$\begin{aligned} U(\textbf{x},t)=\sum _{\textbf{k}\in \mathcal {K}_J} \hat{U}_{\textbf{k}}(t)\varphi _{\textbf{k}}(\textbf{x}). \end{aligned}$$

Let

$$\begin{aligned} \begin{array}{l} \textbf{U}^n=\big (U(\varvec{\xi },s)\big )_{(\varvec{\xi },s)\in \mathcal {G}_J^n}, \\ \hat{\textbf{U}}^n=\big (\hat{U}_{\textbf{k}}(s)\big )_{(\textbf{k},s)\in \mathcal {C}_J^n}, \end{array}\qquad n=0,1,\cdots ,L. \end{aligned}$$

(28)

Similar to Algorithm 1, we can also obtain the DST on general STSG

$$\begin{aligned} \hat{\textbf{U}}^n=\textbf{F}\textbf{U}^n,\qquad n=1,2,\cdots ,L. \end{aligned}$$

Then, we will discuss the solution of the Caputo derivative $\textrm{D}_t^{\alpha }\hat{U}_{\textbf{k}}(t)$ for $\textbf{k}\in \mathcal {K}_J$ in this paragraph. Let

$$\begin{aligned} \tau _j=\frac{\Delta T}{2^j},\qquad j=0,1,\cdots ,J-1. \end{aligned}$$

According to the index set in (27), $\hat{U}_{\textbf{k}}(t)$ can be expanded as

$$\begin{aligned} \hat{U}_{\textbf{k}}(t)= \left\{ \begin{array}{ll} \hat{U}_{\textbf{k}}(0)\theta _{0,T_0}(t)+\hat{U}_{\textbf{k}}(T_0)\theta _{T_0,T_0}(t),\quad &{} \textrm{for}~t\in [0,T_0], \vspace{1ex}\\ \sum \limits _{m=0}\limits ^{2^{J-j}L}\hat{U}_{\textbf{k}}(T_0+m\tau _{J-j}) \theta _{T_0+m\tau _{J-j},\tau _{J-j}}(t),\quad &{} \textrm{for}~t\in [T_0,T], \end{array}\right. \end{aligned}$$

for $\textbf{k}\in \check{\mathcal {K}}_j$. Note that

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\hat{U}_{\textbf{k}}(t)=\frac{\hat{U}_{\textbf{k}}(T_0)}{T_0} -\frac{\hat{U}_{\textbf{k}}(0)}{T_0} \end{aligned}$$

for $t\in (0,T_0)$, and

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\hat{U}_{\textbf{k}}(t)=\frac{\hat{U}_{\textbf{k}}(T_0+m\tau _{J-j})}{\tau _{J-j}}- \frac{\hat{U}_{\textbf{k}}(T_0+(m-1)\tau _{J-j})}{\tau _{J-j}} \end{aligned}$$

for $t\in (T_0+(m-1)\tau _{J-j},T_0+m\tau _{J-j})$, $m=1,2,\cdots ,2^{J-j}L$ and $\textbf{k}\in \check{\mathcal {K}}_j$. Thus, by substituting the expression of $\frac{\textrm{d}}{\textrm{d}t}\hat{U}_{\textbf{k}}(t)$ into the Caputo fractional derivative (3), we can obtain

$$\begin{aligned}{} & {} \left. {}\textrm{D}_t^{\alpha }\hat{U}_{\textbf{k}}(t)\right| _{t=T_0+M\tau _{J-j}}\nonumber \\{} & {} \quad =\frac{1}{\varGamma (1-\alpha )} \int _0^{T_0}(T_0+M\tau _{J-j}-r)^{-\alpha }\frac{\textrm{d}}{\textrm{d}r}\hat{U}_{\textbf{k}}(r)\textrm{d}r\nonumber \\{} & {} \qquad +\sum _{m=1}^M\frac{1}{\varGamma (1-\alpha )} \int _{T_0+(m-1)\tau _{J-j}}^{T_0+m\tau _{J-j}} (T_0+M\tau _{J-j}-r)^{-\alpha }\frac{\textrm{d}}{\textrm{d}r}\hat{U}_{\textbf{k}}(r)\textrm{d}r\nonumber \\{} & {} \quad =\frac{(T_0+M\tau _{J-j})^{1-\alpha }-(M\tau _{J-j})^{1-\alpha }}{\varGamma (2-\alpha )T_0} \big (\hat{U}_{\textbf{k}}(T_0)-\hat{U}_{\textbf{k}}(0)\big )\nonumber \\{} & {} \qquad +\sum _{m=1}^M\frac{b_{M-m}}{\tau _{J-j}^\alpha } \big (\hat{U}_{\textbf{k}}(T_0+m\tau _{J-j})-\hat{U}_{\textbf{k}}(T_0+(m-1)\tau _{J-j})\big )\nonumber \\{} & {} \quad =\frac{(T_0+M\tau _{J-j})^{1-\alpha }-(M\tau _{J-j})^{1-\alpha }}{\varGamma (2-\alpha )T_0}\big (\hat{U}_{\textbf{k}}(T_0) -\hat{U}_{\textbf{k}}(0)\big )-\frac{b_{M-1}}{\tau _{J-j}^\alpha } \hat{U}_{\textbf{k}}(T_0)\nonumber \\{} & {} \qquad +\sum _{m=1}^{M-1}\frac{b_{M-m}-b_{M-m-1}}{\tau _{J-j}^\alpha } \hat{U}_{\textbf{k}}(T_0+m\tau _{J-j})+\frac{b_0}{\tau _{J-j}^\alpha }\hat{U}_{\textbf{k}}(T_0+M\tau _{J-j}) \end{aligned}$$

(29)

for $M=1,2,\cdots ,2^{J-j}L$, where

$$\begin{aligned} b_{l}=\frac{(l+1)^{1-\alpha }-l^{1-\alpha }}{\varGamma (2-\alpha )},\qquad l\in \mathbb {N}_0. \end{aligned}$$

The formula (29) is called the L1 difference method [17]. For convenience of computation, we assume that $2^{J-j}(n-1)\le M\le 2^{J-j}n$ for $n=1,2,\cdots ,L$, and (29) can be written as

$$\begin{aligned} \left. \textrm{D}_t^{\alpha }\hat{U}_{\textbf{k}}(t)\right| _{t=s=T_0+M\tau _{J-j}}= L^\alpha \hat{U}_{\textbf{k}}(s) +\hat{R}_{\textbf{k},s}, \end{aligned}$$

(30)

where

$$\begin{aligned} L^\alpha \hat{U}_{\textbf{k}}(s)=&\sum _{m=2^{J-j}n}^{M-1}\frac{b_{M-m}-b_{M-m-1}}{\tau _{J-j}^\alpha } \hat{U}_{\textbf{k}}(T_0+m\tau _{J-j})+\frac{b_0}{\tau _{J-j}^\alpha }\hat{U}_{\textbf{k}}(T_0+M\tau _{J-j})\\ \hat{R}_{\textbf{k},s}=&\frac{(T_0+M\tau _{J-j})^{1-\alpha }-(M\tau _{J-j})^{1-\alpha }}{\varGamma (2-\alpha )T_0} \big (\hat{U}_{\textbf{k}} (T_0)-\hat{U}_{\textbf{k}}(0)\big )-\frac{b_{M-1}}{\tau _{J-j}^\alpha } \hat{U}_{\textbf{k}} (T_0)\\&+\sum _{m=1}^{2^{J-j}n-1}\frac{b_{M-m}-b_{M-m-1}}{\tau _{J-j}^\alpha } \hat{U}_{\textbf{k}}(T_0+m\tau _{J-j}). \end{aligned}$$

Using the definition of the vector (28), the discretization of the Caputo derivative (30) in the function space $\mathcal {U}^{(J,L)}$ can be written in the form of vector as

$$\begin{aligned} \textbf{D}^\alpha _t\hat{\textbf{U}}^n=\textbf{L}^\alpha \hat{\textbf{U}}^n+\hat{\textbf{R}}^n, \end{aligned}$$

where

$$\begin{aligned} \textbf{D}^\alpha _t\hat{\textbf{U}}^n=\big ({}\textrm{D}_t^{\alpha }\hat{U}_{\textbf{k}}(s)\big )_{(\textbf{k},s) \in \mathcal {C}_J^n},\quad \textbf{L}^\alpha \hat{\textbf{U}}^n=\big (L^\alpha \hat{U}_{\textbf{k}}(s)\big )_{(\textbf{k},s) \in \mathcal {C}_J^n},\quad \hat{\textbf{R}}^n=\big (\hat{R}_{\textbf{k},s}\big )_{(\textbf{k},s) \in \mathcal {C}_J^n}, \end{aligned}$$

for $n=1,2,\cdots ,L$. And it is obvious that $\hat{\textbf{R}}^n$ is independent of $\hat{\textbf{U}}^n$.

5 Fully discrete algorithm

In this section, the fully discrete algorithm of TFDE (1) is obtained. As described in the previous section, the time interval [0, T] can be divided as (25). We construct a FG with only one time step on $[0,T_0]$ if $T_0>0$, and we construct several standard STSGs on $[T_0,T]$. Therefore, the numerical solution $U\in \mathcal {U}^{(J,L)}$ of TFDE (1) can be obtained via the following three steps:

• 1. Compute $\hat{U}_{\textbf{k}}(0)$ for $\textbf{k}\in \mathcal {K}_J$;

• 2. Compute $\hat{U}_{\textbf{k}}(T_0)$ for $\textbf{k}\in \mathcal {K}_J$, if $T_0>0$;

• 3. Compute $\hat{U}_{\textbf{k}}(s)$ for $(\textbf{k},s)\in \mathcal {C}_J^n$, $n=1,2,\cdots ,L$.

Step 1 can be obtained by the projection (8) or the interpolation (9) of initial function $u_0(\textbf{x})$. Step 2 can be obtained by L1 difference method with only one time step, and the scheme is

$$\begin{aligned} \frac{\hat{U}_{\textbf{k}}(T_0)-\hat{U}_{\textbf{k}}(0)}{T_0^\alpha \varGamma (2-\alpha )}+ a\pi ^2\vert \textbf{k}\vert _2^2\hat{U}_{\textbf{k}}(T_0)=\hat{f}_{\textbf{k}}(T_0), \end{aligned}$$

where $\{\hat{f}_{\textbf{k}}(t)\}_{\textbf{k}\in \mathcal {K}_J}$ are the discrete sine coefficients of function $f(u(\textbf{x},t),\textbf{x},t)$.

Thus we mainly discuss step 3. the negative Laplacian $-\Delta$ corresponds to the linear operator $\varvec{\Lambda }$ as

$$\begin{aligned} \varvec{\Lambda }\hat{\textbf{U}}^n =\big (\pi ^2\vert \textbf{k}\vert _2^2\hat{U}_{\textbf{k}}(s) \big )_{(\textbf{k},s)\in \mathcal {C}_J^n},\qquad n=1,2,\cdots ,L, \end{aligned}$$

where $\vert \textbf{k}\vert _2=\left( k_1^2+k_2^2+\cdots +k_d^2\right) ^{\frac{1}{2}}$, and $\hat{\textbf{U}}^n$ is defined in (28). Let

$$\begin{aligned} \textbf{f}^n(\textbf{U}^n)=\big (f(U(\varvec{\xi },s),\varvec{\xi },s)\big )_{(\varvec{\xi },s)\in \mathcal {C}_J^n}, \end{aligned}$$

then the numerical scheme of STSG method for TFDE (1) is

$$\begin{aligned} \textbf{L}^\alpha \hat{\textbf{U}}^n+a\varvec{\Lambda }\hat{\textbf{U}}^{n}= \textbf{F}\textbf{f}^n(\textbf{F}^{-1}\hat{\textbf{U}}^n)-\hat{\textbf{R}}^n, \qquad n=1,2,\cdots ,L, \end{aligned}$$

(31)

where $\textbf{L}^\alpha$ and $\hat{\textbf{R}}^n$ are given by (30). The algebraic equations of the scheme (31) can be solved by the iteration method

$$\begin{aligned} \left( \textbf{L}^\alpha +a\varvec{\Lambda }+c_{\textrm{opt}}^{n,p}\textbf{I} \right) \hat{\textbf{U}}^{n,p}= \textbf{F}\tilde{\textbf{f}}^{n,p}(\textbf{F}^{-1}\hat{\textbf{U}}^{n,p-1})-\hat{\textbf{R}}^n,\qquad p=1,2,\cdots , \end{aligned}$$

(32)

where $\hat{\textbf{U}}^{n,p}=\big (\hat{U}^p_{\textbf{k},s}\big )_{(\textbf{k},s)\in \mathcal {C}_J^n}$ is the approximation of $\textbf{U}^n$ obtained by the p-th iteration, $c_{\textrm{opt}}^{n,p}$ is an optimal factor given by

$$\begin{aligned} c_{\textrm{opt}}^{n,p}=\max \left\{ 0,\max _{\varvec{\xi }\in \mathcal {X}_{J}}\left\{ -\frac{\partial }{\partial u}f\big (u,\varvec{\xi },T_n\big )\Big \vert _{u=U^{p}(\varvec{\xi },T_n)}\right\} \right\} , \end{aligned}$$

and

$$\begin{aligned} \tilde{\textbf{f}}^{n,p}\big (\textbf{F}^{-1}\hat{\textbf{U}}^{n,p-1}\big )= \textbf{f}^n\big (\textbf{F}^{-1}\hat{\textbf{U}}^{n,p-1}\big ) +c_{\textrm{opt}}^{n,p}\textbf{F}^{-1}\hat{\textbf{U}}^{n,p-1}. \end{aligned}$$

The initial vector $\hat{\textbf{U}}^{n,0}$ of the iteration (32) is computed by

$$\begin{aligned} \textbf{L}^\alpha \hat{\textbf{U}}^{n,0}+a\varvec{\Lambda }\hat{\textbf{U}}^{n,0}=-\hat{\textbf{R}}^n, \end{aligned}$$

and the termination condition is given by

$$\begin{aligned} \bigg (\sum _{\textbf{k}\in \mathcal {K}_J}\big \vert \hat{U}^p_{\textbf{k},T_n}-\hat{U}^{p-1}_{\textbf{k},T_n} \big \vert ^2\bigg )^\frac{1}{2}\le \epsilon \end{aligned}$$

(33)

with a fixed threshold $\epsilon$.

For the numerical scheme (31), the corresponding stability analysis and convergence analysis can be carried out in three cases. These three cases correspond to the three forms of the source term $f(u,\textbf{x},t)$, and that is the form without u, the general linear form and the nonlinear form. For the first case, the analysis is relatively simple since the basis function in the equation is separable. For the second case, the stability of the numerical solution can be obtained by proving the positive definiteness of the fully discrete matrix, and then the convergence can be proved by using the results obtained in the first case. For the third case, we mainly focus on several special problems, and the analysis strategy depends on the specific form of each problem. By using such analysis method, we can prove that the scheme (31) is stable and convergent of order $\mathcal {O}(2^{-J}J)$. The detailed proving process is relatively complicated, and it will be given elsewhere. In the present paper, we only concentrate on the algorithm design and the numerical tests of the STSG method.

6 Numerical experiment

In this section, we present several numerical examples to show the advantage of modified STSG method in solving TFDE (1). All simulations of this section are accomplished with C++ programming language (Microsoft Visual Studio 2010 development environment), and run on the computer with an Intel (R) Core (TM) i5-4590 CPU and 8.00 GB of RAM. We both consider the standard STSG method and the modified STSG method, which are characterized as $T_0=0$ and $T_0$ satisfies (26) in the division of time interval (25). For comparison, we also consider the results computed by the standard L1 difference [13, 35]/sine pseudospectral method and the corrected L1 difference/sine pseudospectral method on FG, and these two methods are referred to as standard FG method and corrected FG method respectively in the following content. For FG method, we select the index set

$$\begin{aligned} (1,2,\cdots ,K)^d \end{aligned}$$

for spatial discretization and the grid points

$$\begin{aligned} \{0,T/M,\cdots ,T(M-1)/M,T\} \end{aligned}$$

for temporal discretization, where K and M are given positive integers. Moreover, for the iterative termination condition (33) of algebraic equations, we apply the threshold $\epsilon =10^{-10}$ in all numerical experiments, and this threshold is also used for the corresponding FG method.

For the error results, we mainly consider the relative error at the final time T, which is computed by

$$\begin{aligned} E_T=\frac{\left\| u_{\textrm{ref}}(\cdot ,T)-u^*(\cdot ,T)\right\| _{0}}{\left\| u_{\textrm{ref}}(\cdot ,T) \right\| _{0}}, \end{aligned}$$

where the norm $\Vert \cdot \Vert _0$ is defined in (17), $u^*$ is test solution, and $u_{\textrm{ref}}$ is the reference solution solved by the numerical method with enough accuracy. We also concerned about the convergence order. For an algorithm with two sets of computational parameters, suppose that $E_1,E_2$ and $N_1,N_2$ are the relative errors and the total DOFs, respectively. Then, the convergence order is calculated by

$$\begin{aligned} \textrm{Order}=\frac{\ln E_1-\ln E_2}{\ln N_2-\ln N_1}. \end{aligned}$$

Example 2

Consider the one-dimensional TFDE

$$\begin{aligned} \textrm{D}_t^{\alpha }u=0.1\frac{\partial ^2}{\partial x^2} u+(1-t^{\gamma })(1-u)(1-\cos 2\pi x), \qquad \gamma >0,~ (x,t)\in (0,1)\times (0,1] \end{aligned}$$

with the homogeneous boundary condition (2) and the linear element initial function

$$\begin{aligned} u_0(x)=\left\{ \begin{array}{ll} 2x, &{} \text {for}~0\le x\le 0.5, \\ 2(1-x), &{} \text {for}~0.5< x\le 1. \end{array} \right. \end{aligned}$$

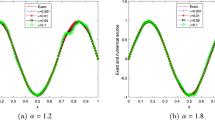
We firstly consider the case of $\gamma =1$. Figure 5 shows that the solutions at $t=1$ are similar in the case of $\alpha =0.5$ and $\alpha =0.2$. From Fig. 6, their frequency spectrum is about fourth-power decaying rate, and this implies that the solutions are not infinitely smooth.

Fig. 5

The solution at $t=1$ in Example 2 ($\gamma =1$)

In this example, we test the error of the numerical method through the reference solutions obtained by modified STSG method with $J=17$, $L=16$. Figure 7 shows the convergence behavior. For the standard FG method, the convergence rate is very slow for $M/K=1$, whereas the starting accuracy is too low for $M/K=16$. On the whole, the accuracy of modified STSG method is significantly higher than that of standard FG method for similar DOF. Figure 8 shows the relationship between the DOF and the CPU time cost. When the DOF are similar, the CPU time cost of modified STSG method may be more. This is because the algebraic system obtained modified STSG method is more complex than that obtained by standard FG method, and such algebraic system requires more iterative steps to compute.

We subjectively select some “optimized” computational parameters in the numerical method. Tables 1 and 2 give the representative results in the case of $\alpha =0.2$ and $\alpha =0.8$, respectively. From the whole convergence process, the convergence order of STSG method is close to first order, and such order is similar to that of L1 difference approximation. In contrast, the convergence order of standard FG method is significantly lower than first order. In this example, we give the comparison of the STSG method and the corrected FG method. For the case of $\alpha =0.2$, the STSG method requires fewer DOF to achieve similar accuracy, but the corrected FG method requires less CPU time cost, so the advantages of STSG method are not significant. But for the case of $\alpha =0.8$, the advantage of corrected FG method is greatly weakened, this is because the corrected L1 difference scheme is of order $\mathcal {O}(\tau ^{2-\alpha })$, which decrease with the increase of $\alpha$. By comparison, the convergence behavior of STSG method is basically not affected by the value of $\alpha$. Moreover, the convergence behavior of the standard STSG method and the modified STSG method is very similar for both $\alpha =0.2$ and $\alpha =0.8$.

Fig. 6

The frequency spectrum at $t=1$ in Example 2 ($\gamma =1$)

Fig. 7

Convergence behavior of modified STSG method and standard FG method in Example 2 ($\gamma =1$) with $\alpha =0.2$ (left) and $\alpha =0.8$ (right)

Fig. 8

The CPU time cost of modified STSG method and standard FG method in Example 2 ($\gamma =1$) with $\alpha =0.2$ (left) and $\alpha =0.8$ (right)

Table 1 Representative numerical results in Example 2 with $\alpha =0.2$, $\gamma =1$

Table 2 Representative numerical results in Example 2 with $\alpha =0.8$, $\gamma =1$

Then, we consider the smaller value of $\gamma$. Many numerical experiments show that the STSG method is better than the Corrected FG method when $\gamma <0.5$. In particular, the result of the case $\alpha =0.2,\gamma =0.1$ can be seen in Table 3. Indeed, when the source term is singularity at $t=0$, the regularity of the solution in temporal direction becomes very low. In this way, the high-order accuracy algorithm in temporal direction will not give full play to its effect, and so the corrected FG method has no obvious advantages. In contrast, the STSG method can show nice convergence behavior in the case of low regular solution. Besides, in this case, the accuracy of the modified STSG method is slightly better than the standard STSG method. This is because the source term changes quickly at the initial moment, which reduces the accuracy of the standard STSG method.

Table 3 Representative numerical results in Example 2 with $\alpha =0.2$, $\gamma =0.1$

Example 3

Consider the one-dimensional homogeneous problem

$$\begin{aligned} \textrm{D}_t^{\alpha }u=0.1\frac{\partial ^2}{\partial x^2} u+(1-t)(1-u)(1-\cos 2\pi x), \qquad (x,t)\in (0,1)\times (0,1], \end{aligned}$$

with the homogeneous boundary condition (2) and the Dirac $\delta$ initial function

$$\begin{aligned} u_0(x)=\delta (x-0.5). \end{aligned}$$

Note that the Dirac $\delta$ function cannot be interpolated, so we choose its projection $\mathcal {P}_Ju_0$ (8) as the initial vector of numerical solution. Figures 9 and 10 show the information of solution at $t=1$. The regularity of the solution in Example 3 is obviously weaker than that in Example 2, and the frequency spectrum is about second-power decaying. In contrast, the regularity of the solution in the case of $\alpha =0.2$ is slightly lower than that in the case of $\alpha =0.5$.

Fig. 9

The solution at $t=1$ in Example 3

Fig. 10

The frequency spectrum at $t=1$ in Example 3

In this example, we use the same reference solution as that in Example 2. At first, we observe the relative error results of the standard STSG method, which are shown in Fig. 11. In this example, the standard method even fails to converge. This is because the solution changes very quickly at the initial moment, and the convergence of the standard STSG method will become extremely difficult. In contrast, from Fig. 12 and Table 4, the modified STSG method can still achieve convergence of about first order, and its convergence behavior is still significantly better than the standard FG method. Therefore, for some special cases, modified technology of STSG can play a decisive role. On the other hand, for general cases, the modified STSG method is not weaker than the standard STSG method, so we can completely replace the standard STSG method with the modified STSG method.

Fig. 11

Relative error of standard STSG method in Example 3 with $\alpha =0.2$ (left) and $\alpha =0.5$ (right)

Fig. 12

Convergence behavior of modified STSG method and standard FG method in Example 3 with $\alpha =0.2$ (left) and $\alpha =0.5$ (right)

Table 4 Representative numerical results in Example 3 with $\alpha =0.2$

Example 4

Extending the problem of Example 3 to two-dimensional case, and we have

$$\begin{aligned} \textrm{D}_t^{0.5}u= & {} 0.1\Delta u+(1-t)(1-u)(1-\cos 2\pi x)(1-\cos 2\pi y), \\ u_0(x,y)= & {} \delta (x-0.5)\delta (y-0.5),\\ \end{aligned}$$

for $(x,y,t)\in (0,1)^2\times (0,1]$.

Multi-dimensional problems with Dirac $\delta$ initial function will encounter greater difficulties in computation. On the one hand, multi-dimensional problems require much more DOF in spatial direction; on the other hand, the singularity of solution caused by multi-dimensional Dirac $\delta$ function is stronger than that caused by one-dimensional Dirac $\delta$ function. From Fig. 13, although after a time of length 1, the solution still has a marked singularity at the point $(x,y)=(0.5,0.5)$.

Fig. 13

The solution at $t=1$ in Example 4

In this example, we consider the reference solution obtained by modified STSG method with $J=13$, $L=2$. From Fig. 14, the convergence behavior of modified STSG method is still significantly better than that of standard FG method. From Table 5, the standard FG method needs more than 500 million DOF to reach the relative error of about $9\cdot 10^{-4}$, and the required storage is close to the upper limit of our computer memory. For achieving such accuracy, The modified STSG method requires only one percent of the DOF. Moreover, the convergence order obtained by computing two-dimensional problems is about half of that in computing one-dimensional problems, which is true for both the modified STSG method and the standard FG method.

Fig. 14

The convergence behavior (left) and the CPU time cost (right) of modified STSG method and standard FG method in Example 4

Table 5 Representative numerical results in Example 4

Fig. 15

The solution at different time in Example 5

Example 5

Consider the time-fractional Allen-Cahn equation

$$\begin{aligned} \textrm{D}_t^{\alpha }u=0.01\frac{\partial ^2}{\partial x^2} u+u-u^3, \quad (x,t)\in (0,1)\times (0,100], \end{aligned}$$

with the homogeneous boundary condition (2) and the bidirectional pulse initial function

$$\begin{aligned} u_0(x)=\left\{ \begin{array}{ll} 0.1, &{} \text {for}~\dfrac{1}{8}\le x\le \dfrac{3}{8}, \vspace{1ex}\\ -0.1, &{} \text {for}~\dfrac{5}{8}\le x\le \dfrac{7}{8},\vspace{1ex}\\ 0, &{} \text {for}~0<x<\dfrac{1}{8}~\text {or}~\dfrac{3}{8}< x<\dfrac{5}{8}~\text {or}~\dfrac{7}{8}< x<1. \end{array} \right. \end{aligned}$$

The Allen-Cahn equation is an important kind of reaction-diffusion equation, and it is also one of basic equations in phase-field theory. The numerical method of time-fractional Allen-Cahn equation has also been studied in recent years [5, 33]. Figure 15 shows the snapshots of solutions at different times. In the beginning, the change is faster for smaller $\alpha$. However, for long time observation, the change with smaller $\alpha$ is obviously slower. The solution of the integer-order case has basically arrived at the steady state when $t=10$, but the solution of the case $\alpha =0.2$ is still far from the steady state when $t=100$. Figure 16 shows the frequency spectrum at $t=100$. The frequency spectrum is exponentially decaying in the integer-order case. But in the fractional case of $\alpha =0.8$ or $\alpha =0.5$, although their solution functions look similar to that in the integer-order case, their frequency spectrums are not exponentially decaying. Therefore, the solutions at $t=100$ in the fractional case are not infinitely smooth.

Fig. 16

The frequency spectrum at $t=100$ in Example 5

Then, we consider the convergence behavior of numerical method for $\alpha =0.5$, and the reference solution is obtained by modified STSG method with $J=19$, $L=2$. From Fig. 17, the modified STSG method can still greatly reduce DOF in high-accuracy approximation. However, the CPU time costs of modified STSG method in this example are obviously more than those in Examples 2 and 3. The nonlinear property brings more difficult to solve the algebraic system, which is more obvious in the modified STSG method. Nevertheless, from Table 6, the modified STSG method still has obvious advantages in time efficiency and storage efficiency. In particular, when the required relative error is not more than $3\cdot 10^{-7}$, the DOF and the CPU time cost saved by the modified STSG method are about 500 times and 100 times, respectively. Therefore, the modified STSG method is still suitable for nonlinear problems.

Fig. 17

The convergence behavior (left) and the CPU time cost (right) of modified STSG method and standard FG method in Example 5 with $\alpha =0.5$

Table 6 Representative numerical results in Example 5 with $\alpha =0.5$

Example 6

Consider the TFDE

$$\begin{aligned} \textrm{D}_t^{0.5}u=0.1\frac{\partial ^2}{\partial x^2} u+f(u,x,t), \quad (x,t)\in (0,1)\times (0,1], \end{aligned}$$

with the homogeneous boundary condition (2) and the sine initial function $u_0(x)=\sin \pi x$, where the source term is

$$\begin{aligned} f(u,x,t)=\left\{ \begin{array}{ll} (1-u)(2xt)^2, &{} \text {for}~0\le x\le 0.5, \vspace{1ex}\\ (1-u)\big (2(1-x)t\big )^2, &{} \text {for}~0.5< x\le 1. \end{array}\right. \end{aligned}$$

Different from the previous examples, we consider smooth initial function and nonsmooth source term in this example. Figure 18 shows that the frequency spectrums are about fourth-power decaying rate at different time. Note that the sine coefficient of the initial function is equal to 0 for $k>1$, and it implies that the frequency spectrums of index $k>1$ have a fast growth at the initial moment.

Fig. 18

The frequency spectrum at different time in Example 6

In this example, the reference solution is obtained by the modified STSG method with $J=17$, $L=32$. Figure 19 and Table 7 show the results of numerical comparison. When the required relative error is not more than $1\cdot 10^{-6}$, the modified STSG method saves more than 100 times of total DOF.

Fig. 19

The convergence behavior (left) and the CPU time cost (right) of modified STSG method and standard FG method in Example 6

Table 7 Representative numerical results in Example 6

7 Conclusion

In this paper, the modified STSG method is constructed for solving TFDE (1). In numerical experiments, we give the comparison for different cases (one-dimensional problem or multi-dimensional problem, linear problem or nonlinear problem, nonsmooth initial function or nonsmooth source term). When the solution is not smooth enough in spatial direction, the modified STSG method has obvious advantages over the standard FG method. Furthermore, if the value of $\alpha$ is relatively large or the source term has strong singularity at the initial point, the modified STSG method is also obviously better than the corrected FG method. In addition, compared with the standard STSG method, the modified STSG method can well deal with the fast change at the initial moment. To sum up, we can determine that the modified STSG method has special advantages in solving TFDE.

Moreover, the STSG method has great promotion value. On the one hand, the idea of STSG method can be extended to other evolution equation with time memory property, such as delay diffusion equation [7], Volterra diffusion equation [23], and so on. On the other hand, the STSG technique is also feasible for most spatial discretization method, such as finite difference method, finite element method and other Fourier-like spectral method. Besides, in order to improve further the efficiency of the algorithm, the STSG method can also be combined with other fast algorithm or high-order accuracy method for solving TFDE.