Explicit frictional stick–slip dynamics of elastic contact problem incorporating the LuGre model

Abstract

Dynamical contact problem with friction is of continuous concern and have been investigated over the years. The effective and accurate description of the development of the friction force is the key to this problem. However, the stick–slip phenomenon, as typical dynamical behaviour, has rarely been considered when developing contact algorithms for frictional contact problems of elastic bodies. The conventionally used Coulomb’s model, with differentiating the static and kinetic coefficient of friction, can lead to inaccurate results due to errors generated when switch between the stick or slip states. In this work, a three-dimensional mortar-based frictional contact algorithm is proposed in an explicit scheme. The proposed algorithm incorporates the LuGre model to account for dynamical frictional behaviours such as stick–slip. The effectiveness and accuracy of the proposed algorithm are validated through several simplified two-dimensional cases. The sticking time ratio and the evolution of the global coefficient of friction with time of a three-dimensional contact problem with a randomly rough contact interface are investigated as an application.

1 Introduction

Frictional contact problems have widespread applications in industry and have become a promising research field for decades. It has been recognised that dealing with frictional contact problems in a finite deformation regime is one of the most challenging tasks in computational mechanics. A workable solution must contain efficient contact detection algorithms, enforcement of contact constraints and iterative schemes for solving non-linear problems. The effective and accurate employment of contact constraints is recognised as problematic due to its numerically stiff, strongly non-smooth and non-linear nature. In static analysis, effective and robust algorithms have been successfully developed to tackle the frictional contact condition, such as the surface-to-surface scheme and mortar methods [1, 2], which passed the patch test, preserving consistent contact stress between the contact bodies. One can find extensive reviews of the recent development of the contact algorithms using Finite Element Method (FEM) and Isogeometric analysis (IGA) framework respectively in [3] and [4]. In dynamical analysis, however, contact problems are much more complicated. In addition to the demanding tasks mentioned in the static analysis, requirements related to stability, energy conservation and contact persistency condition should also be satisfied concerning the specific topic on which the study is focused. For example, investigations on contact-impact problems pay particular attention to the proper treatment of impact forces during contact [5,6,7,8] and the energy conservation during contact and separation [9,10,11]. As an extension to involve the frictional effect, dissipative algorithms were proposed to account for the energy loss caused by friction [8, 12]. Implicit [11, 13] and explicit [14, 15] schemes were investigated by various researchers to address the stability of the methods.

These algorithms, effective as they are in dealing with frictional contact problems in some restricted scenarios, usually have little concern about the dynamical stick–slip effect, which is a typical phenomenon when the contacting body is experiencing a series of repeated stick and slip motions under the driving source. The reason for such a restriction is that the algorithmic design for friction development generally uses the classical/modified Coulomb’s model. The classical Coulomb’s model does not differentiate the static and kinetic coefficients of friction (COF) and thus can not replicate the stick–slip effect. Consequently, it is mostly used in the static or quasi-static analysis [3]. The modified Coulomb’s model, where a reduced kinetic COF is defined compared with the static one, has been proved to replicate the stick–slip effect [16]. However, since the Coulomb’s model belongs to the category of the static friction model, a stick–slip transition criterion is required. In each time step, the violation of this criterion has to be checked and the status of motion is correspondingly updated. Such an update is usually performed following a return-mapping scheme [17, 18]. In this scheme, the friction force is firstly approximated using a trial value and then compared with the maximum allowable value and is modified to a proper value if it violates the criterion. The continuous demand of this ’checking and updating’ procedure will firstly deteriorate the algorithm efficiency. Secondly, it will also cause errors to accumulate and produce inaccurate results. However, an accurate description of the stick–slip behaviours is vital in many applications, for instance, the precise prediction of positions of robotic manipulator joints and cutter-head control of drilling engineering management.

In this work, focusing on modeling the dynamical stick–slip effect, the authors propose a new explicit frictional contact algorithm that incorporates the LuGre model. The LuGre model [19] is constructed using a few parameters and a state variable that is well suited for theoretical analysis and can be matched well with experimental results [20, 21]. The LuGre model is an extension of the Dahl model [22], including the Stribeck effect so that the stick–slip effect can be properly described, and it is easy to implement compared with its extensions, such as the elastoplastic model [23] and the Leuven model [24]. This work will show that using the LuGre model, the friction force is not determined accumulatively but depends on the development of the state variable and the local tangential velocity, by which repetitive stick–slip motion can result.

The authors would like to note related literature that uses dynamic-type interface constitutive models. Tonazzi et al. [25] studied frictional phenomena such as stick–slip and mode coupling instabilities using explicit Forward Lagrangian method and adherence time-related friction law. Oancea and Laursen [26, 27] used a state- and rate-dependent frictional model [28, 29], in which a state variable is introduced to quantify the steady-state slipping and a viscoplastic regularisation is adopted to depict viscous frictional behaviour stemming from rapid slip rate changes. Araki and Hjelmstad [30] developed Maxwell-type rate-dependent regularisation approaches for 3D frictional contact constraints that can avoid convergence issues. Moreover, there have been successful attempts to incorporate rate- and state-dependent friction laws into the exploration of dynamics of shear rupture for the elastic contact interfaces [31, 32].

The rest of the paper is dedicated to presenting this algorithm and giving a few 2D & 3D numerical examples for validation and investigation. Section 2 details the new dynamical frictional contact algorithm including instructions for implementation. Section 3 presents three 2D numerical cases to demonstrate the stick–slip effect under flat contact profiles. Specifically, in Sect. 3.1 a spring-slider model is studied as a validation case; in Sect. 3.2 a slider model with top layer velocity control is presented to study the impact of mesh size on the stick–slip effect; in Sect. 3.3 the case of a slider model applied by a harmonic cyclic force is studied to demonstrate the pre-sliding behaviours. Finally, Sect. 4 demonstrates the stick–slip effect of 3D contact with a randomly rough surface with particular interest in the sticking time ratio and the global coefficient of friction (COF).

2 An explicit three dimensional frictional contact algorithm incorporating the LuGre model

This section starts with the problem definition of the 3D contact problem under consideration, followed by the proposed frictional contact algorithm emphasising the incorporation of the LuGre model. Then, the contact virtual work and discretisation details are briefly addressed. Finally, the lumped mass method is introduced to complete the explicit solution procedure. For simplicity, only an elastic body in contact with a fixed ground with a flat and rigid surface will be included in this paper. However, an extension to contact between elastic bodies with diverse contact interface conditions is achievable when combining with suitable contact detection algorithms.

2.1 Problem definition

Fig. 1

Initial and current configuration of the contact problem

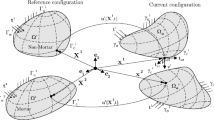
A 3D contact problem is investigated between an elastic body and a fixed, rigid ground with finite deformations and finite sliding, as shown in Fig. 1. The elastic body is represented by the open set ${\mathcal {B}}^0\in {\mathbb {R}}^3$ in the reference configuration and by ${\mathcal {B}}^t$ in the current configuration. The boundary of the elastic body $\partial {\mathcal {B}}$ is formed by three disjoint parts: $\partial {\mathcal {B}}^0=\Gamma _u\cup \Gamma _\sigma \cup \Gamma _c$ and $\partial {\mathcal {B}}^t=\gamma _u\cup \gamma _\sigma \cup \gamma _c$, where the subscript ’u’, ’$\sigma$’ and ’c’ denote the Dirichlet, the Neumann and the contact boundary condition respectively. The deformation of the elastic body can be expressed as

$$\begin{aligned} {\textbf{x}}=\varvec{\Phi }({\textbf{X}})={\textbf{X}}+{\textbf{u}}, \end{aligned}$$

(1)

where ${\textbf{x}}$ and ${\textbf{X}}$ indicate the coordinates of the material points in the current and reference configurations, respectively. ${\textbf{u}}$ is the displacement field of the elastic body. $\varvec{\Phi }(\cdot )$ is the deformation mapping from the reference configuration to the current configuration. The strong form of this initial boundary value problem without contact constraints can be stated as [33]

$$\begin{aligned} \textrm{div}(\textbf{FS})+{\textbf{b}}_0&= \rho _0\,\ddot{{\textbf{u}}},\ {}&\textrm{in}\ {\mathcal {B}}^t, \times [0, T] \end{aligned}$$

(2)

$$\begin{aligned} {\textbf{u}}&= \hat{{\textbf{u}}},\ {}&\text { on }\ \Gamma _u\times [0, T] \end{aligned}$$

(3)

$$\begin{aligned} {\textbf{P}}\cdot {\textbf{N}}&= \hat{{\textbf{t}}}\,&\text { on }\ \Gamma _\sigma \times [0, T] \end{aligned}$$

(4)

$$\begin{aligned} {\textbf{u}}({\textbf{X}}, 0)&= \hat{{\textbf{u}}}_0({\textbf{X}}),\ {}&\text {in}\ {\mathcal {B}}^0 \end{aligned}$$

(5)

$$\begin{aligned} \dot{{\textbf{u}}}({\textbf{X}}, 0)&= \dot{\hat{{\textbf{u}}}}_0({\textbf{X}}),\ {}&\text {in}\ {\mathcal {B}}^0 \end{aligned}$$

(6)

where ${\textbf{F}}=\frac{\partial {\textbf{x}}}{\partial {\textbf{X}}}$ is the material deformation gradient. ${\textbf{P}}$ and ${\textbf{S}}$ are respectively the first and second Piola-Kirchhoff stress tensors. Vectors $\hat{{\textbf{u}}}$ and $\hat{{\textbf{t}}}$ are the prescribed displacements and prescribed tractions on the corresponding Dirichlet boundary $\Gamma _u$ and Neumann boundary $\Gamma _\sigma$. $\hat{{\textbf{u}}}_0$ and $\dot{\hat{{\textbf{u}}}}_0$ are the initial conditions for the displacements and velocities of the elastic body. Moreover, ${\textbf{b}}_0$ and $\rho _0$ are respectively the body force and mass density per unit of undeformed volume, and ${\textbf{N}}$ is the reference unit outward normal on $\Gamma _\sigma$. For the representation purpose, the incompressible Neo-Hookean (hyperelastic) material is used throughout this work, of which the hyperelastic strain energy function is denoted by $\mathbf {\Psi }$. Consequently, the second Piola-Kirchhoff stress ${\textbf{S}}$ and the fourth-order constitutive tensor ${\mathbb {C}}$ can be derived as

$$\begin{aligned} {\textbf{S}} = \frac{\partial \mathbf {\Psi }}{\partial {\textbf{E}}},\ \ {\mathbb {C}} = \frac{\partial ^2\mathbf {\Psi }}{\partial {\textbf{E}}^2}, \end{aligned}$$

(7)

where ${\textbf{E}}=\frac{1}{2}({\textbf{F}}^\textrm{T}{\textbf{F}}-{\textbf{I}})$ is the Green-Langrange strain tensor and ${\textbf{I}}$ is the second-order identity tensor.

2.2 Contact constraints

In order to enforce contact constraints, the rigid ground surface is parameterised with the convective coordinate pair $(\xi , \eta )$. Define covariant vectors $\varvec{\tau }_\alpha = {\textbf{x}}^g_{,\alpha }$, $\alpha =\{\xi , \eta \}$, where ${\textbf{x}}^g$ denotes the coordinate of the rigid ground surface. The coordinates of points on the ground surface are the same whether in the reference or current configuration, e.g. ${\textbf{X}}^g = {\textbf{x}}^g$ since the ground is rigid and fixed. The corresponding contravariant vectors are defined as $\varvec{\tau }^\alpha :=m^{\alpha \beta }\varvec{\tau }_\beta$, where $m_{\alpha \beta }=(m^{\alpha \beta })^{-1}=\varvec{\tau }_\alpha \cdot \varvec{\tau }_\beta$ is the metric matrix and $\alpha , \beta = \{\xi , \eta \}$. The curvature is defined as $k_{\alpha \beta }={\textbf{x}}^g_{,\alpha \beta }\cdot {\textbf{n}}$, where ${\textbf{n}} = \frac{\varvec{\tau }_\alpha \times \varvec{\tau }_\beta }{\Vert \varvec{\tau }_\alpha \times \varvec{\tau }_\beta \Vert }$ is the unit normal vector.

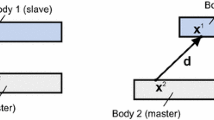
For the determination of the contact interface $\gamma _c$ in the current configuration, the distance function $d({\textbf{x}}^e, {\textbf{x}}^g)$ is introduced as

$$\begin{aligned} d({\textbf{x}}^e, {\textbf{x}}^g):=\Vert {\textbf{x}}^e-{\textbf{x}}^g(\xi ,\,\eta )\Vert , \end{aligned}$$

(8)

which describes the distance between a fixed point ${\textbf{x}}^e$ of the elastic body on $\gamma _c$ and an arbitrary point ${\textbf{x}}^g(\xi , \eta )$ on the ground surface. Among all arbitrary points, denote $\bar{{\textbf{x}}}^g={\textbf{x}}^g({\bar{\xi }}, {\bar{\eta }})$ that minimises d as the projection of ${\textbf{x}}^e$, the determination of which usually entails the Closest Point Projection (CPP) method [34, 35]. In this method, the solution can be found by solving the following equations

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} \varvec{\tau }_\xi \cdot [{\textbf{x}}^e-{\textbf{x}}^g(\xi ,\,\eta )] = 0 \\ &{} \varvec{\tau }_\eta \cdot [{\textbf{x}}^e-{\textbf{x}}^g(\xi ,\,\eta )] = 0 \end{array}\right. }. \end{aligned}$$

(9)

Fig. 2

Illustration of the return-mapping scheme. A reduction of tangential force is considered in the state of slip

Since $\varvec{\tau }_\alpha$ also depends on $(\xi , \eta )$, the solutions to (9) often require iterations, e.g. Newton’s method. For highly smooth ground surfaces, the existence and uniqueness of the solutions can be guaranteed, but otherwise (e.g. the ground surface is of locally high curvatures and singularities), severe numerical difficulties often occur to the problem and more advanced contact searching techniques [36, 37] must be applied. The gap vector can then be represented as

$$\begin{aligned} {\textbf{g}} = {\textbf{x}}^e - \bar{{\textbf{x}}}^g. \end{aligned}$$

(10)

The normal gap is simply defined as $g_N = {\textbf{g}}\cdot \bar{{\textbf{n}}}=({\textbf{x}}^e - \bar{{\textbf{x}}}^g)\cdot \bar{{\textbf{n}}}$, where $\bar{{\textbf{n}}}$ is the unit normal vector at $\bar{{\textbf{x}}}^g$. The tangential gap rate can be defined similarly as ${\dot{g}}_{T\alpha } = (\dot{{\textbf{x}}}^e - \dot{\bar{{\textbf{x}}}}^g)\cdot \bar{\varvec{\tau }}_\alpha$, where $\bar{\varvec{\tau }}_\alpha = \bar{{\textbf{x}}}^g_{,\alpha }$. The contact force vector of the current configuration can be decomposed into the normal and tangential components as

$$\begin{aligned} {\textbf{t}}_c = {\textbf{t}}_N + {\textbf{t}}_T = t_N\,\bar{{\textbf{n}}}+t_{T\alpha }\bar{\varvec{\tau }}^\alpha , \end{aligned}$$

(11)

where $t_N$ denotes the normal contact force and $t_{T\alpha }$ the covariant components of the tangential forces. Concerning unilateral contact with dry friction only, the Karush-Kuhn-Tucker (KKT) conditions for impenetrability in the normal direction are expressed as

$$\begin{aligned} g_N\ge 0,\ t_N\le 0,\ g_N t_N=0,\ {\dot{g}}_N t_N=0, \end{aligned}$$

(12)

where the last equation denotes the persistency condition [8, 13]. The normal contact force are here regularised with the penalty method as

$$\begin{aligned} t_N=\varepsilon _N \langle g_N \rangle _{-}\,\ \langle g_N \rangle _{-}= {\left\{ \begin{array}{ll} g_N &{} \text { if }\ g_N\le 0 \\ 0 &{} \text {otherwise} \end{array}\right. }, \end{aligned}$$

(13)

where $\varepsilon _N$ is the penalty parameter. For the tangential contact forces, the commonly used history-dependent return mapping algorithm based on Coulomb’s model by researchers of computational contact mechanics becomes inappropriate for dynamic contact problems. In that algorithm, as shown in the next section, the tangential contact forces are first approximated as the accumulated contact forces in addition to the change of the covariant variable regularised by a tangential penalty parameter. Then these trial tangential contact forces are compared with the maximum allowable value defined using the local COF times local normal contact force. The trial values are then reset to the full value if they exceed that value. The problem with that method in the dynamic regime lies in its dependence on the history rather than on the current state. For instance, once the trial tangential contact forces saturate, the elastic body starts to slip and may hardly stick again. Such a property prevents important dynamical frictional behaviours, such as the stick–slip effect, from being appropriately simulated. In this work, the authors advocate using the LuGre model to better address dynamical frictional responses.

2.3 Interface friction law

2.3.1 Coulomb’s model

Coulomb’s model is the most widely used frictional interface law in contact problems. This model uses assumptions that two bodies in contact stay still relatively to each other on macroscopic scale until the maximum tangential force has been reached. The KKT conditions for Coulomb friction are stated as [38]

$$\begin{aligned} \begin{aligned}&{\hat{\Phi }}:= \Vert {\textbf{t}}_T\Vert -\mu _s t_N \le 0, \\&\dot{{\textbf{g}}}_T = {\dot{\xi }}\frac{\partial }{\partial {\textbf{t}}_T}{\hat{\Phi }}, \\&\xi \ge 0,\\&\xi {\hat{\Phi }} = 0, \end{aligned} \end{aligned}$$

(14)

where $\mu _s>0$ represents the static COF ($\mu _k$ the kinetic COF), $\xi$ is the amount of slip. On microscopic scale, tangential micro-sliding can occur within the contact area and is often assumed proportional to the tangential force. Under such an assumption, the tangential displacement and velocity can be decomposed as

$$\begin{aligned} \begin{aligned} {\textbf{g}}_T&= {\textbf{g}}_T^{el} + {\textbf{g}}_T^{pl}, \\ \dot{{\textbf{g}}}_T&= \dot{{\textbf{g}}}_T^{el} + \dot{{\textbf{g}}}_T^{pl}, \end{aligned} \end{aligned}$$

(15)

where the superscripts, el and pl, denote respectively the elastic (reversible) part and the plastic (irreversible) part. The elastic tangential force can then be obtained by ${\textbf{t}}_T=\varepsilon _T\,{\textbf{g}}_T^{el}$ and the slip rule in (14) becomes $\dot{{\textbf{g}}}_T^{pl} = {\dot{\xi }}\frac{\partial }{\partial {\textbf{t}}_T}\phi$, where $\varepsilon _T$ is a penalty-regularised term also being interpreted as tangential stiffness. Practically, the determination of tangential force entails integrating (14) with the backward Euler scheme and the return-mapping strategy. Supposing a time step $\{t_n, t_{n+1}\}$ where the contact-related terms $\{{\textbf{g}}_n, {\textbf{t}}_{Nn}, {\textbf{t}}_{Tn}\}$ at $t_n$ are fully known while their values are to be calculated at $t_{n+1}$. Following the return-mapping procedure, the trial tangential force is defined as

$$\begin{aligned}&{\textbf{t}}_{T_{n+1}}^\textrm{trial} = {\textbf{t}}_{T_n}+\varepsilon _T({\textbf{g}}_{T_{n+1}}-{\textbf{g}}_{T_{n}}), \end{aligned}$$

(16)

$$\begin{aligned}&{\hat{\Phi }}^\textrm{trial} = \Vert {\textbf{t}}_{T_{n+1}}^\textrm{trial}\Vert -\mu _s t_{N_{n+1}}.\nonumber \\ \end{aligned}$$

(17)

Then the true value of tangential force is return-mapped back as

$$\begin{aligned} {\textbf{t}}_{T_{n+1}} = {\textbf{t}}_{T_{n+1}}^\textrm{trial} - \Delta \xi \frac{{\textbf{t}}_{T_{n+1}}^\textrm{trial}}{\Vert {\textbf{t}}_{T_{n+1}}^\textrm{trial}\Vert }, \end{aligned}$$

(18)

where

$$\begin{aligned} \Delta \xi = {\left\{ \begin{array}{ll} 0 &{} \textrm{if}\, {\hat{\Phi }}^\textrm{trial}\le 0 \ \ \textrm{stick}, \\ {\hat{\Phi }}^\textrm{trial}+(\mu _s-\mu _k)t_{N_{n+1}} &{} \textrm{if}\, {\hat{\Phi }}^\textrm{trial}> 0 \ \ \textrm{slip}. \end{array}\right. }\nonumber \\ \end{aligned}$$

(19)

Equations (16)$\sim$(19) ensure that the friction force changes linearly with the incremental tangential gap within the sticking zone, and satisfies $\Vert {\textbf{t}}_{T_{n+1}}^\textrm{trial}\Vert = \mu _k t_{N_{n+1}}$ when the criterion ${\hat{\Phi }} \le 0$ is violated. The classical Coulomb’s model assumes no differentiation between $\mu _s$ and $\mu _k$, which is commonly seen in computational contact mechanics when stick–slip effect is not concerned. In the modified Coulomb’s model, a kinetic COF $\mu _k < \mu _s$ is often assigned enabling the replication of stick–slip effect (Fig. 2).

2.3.2 The LuGre model

The LuGre model [19] is a state-variable friction model able to describe several dynamical friction characteristics, e.g. Stribeck effect and presliding, within a simple structure. A typical depiction of the LuGre model can be seen in Fig. 3. In this model, the microscopic interactions between contacting asperities are considered and modelled as elastic spring-like bristles with damping. These bristles are under deflection by the enforcement of the external load.

Fig. 3

The LuGre model

Fig. 4

Velocity-dependent function

In the amended form of the LuGre model [39], the local COF is determined by the deflection of averaged deflection of bristles, indicated by an auxiliary state vector, ${\textbf{z}}$, and the associated micro- and macro-damping terms. The rate of ${\textbf{z}}$ is modelled as

$$\begin{aligned} \dot{{\textbf{z}}} = {\textbf{v}}_r - {\textbf{z}}\,\frac{\sigma _0|{\textbf{v}}_r|}{G({\textbf{v}}_r)}, \end{aligned}$$

(20)

where ${\textbf{v}}_r={\dot{g}}_{T\alpha }\bar{\varvec{\tau }}^\alpha$ is the relative tangential velocity between two contact nodes, $\sigma _0$ is a constant parameter denoting the stiffness coefficient of the bristle. $G({\textbf{v}}_r)$ is a velocity-dependent function defined as

$$\begin{aligned} G({\textbf{v}}_r) = \mu _\textrm{k}+(\mu _\textrm{s}-\mu _\textrm{k})\,\textrm{e}^{-|{\textbf{v}}_r/v_s|^\theta }, \end{aligned}$$

(21)

where $v_s$ is the Stribeck velocity controlling the decay rate of the effective COF from the static one ($\mu _s$) to the kinetic one ($\mu _k$), as shown in Fig. 4, and $\theta$ is a constant exponent. Finally, the friction force generated due to the deflection of bristles is described as

$$\begin{aligned} {\textbf{F}}_T = (\sigma _0{\textbf{z}}+\sigma _1\dot{{\textbf{z}}}+\sigma _2{\textbf{v}})\,N, \end{aligned}$$

(22)

where $\sigma _1$ and $\sigma _2$ represent the microscopic and macroscopic (viscous) damping coefficients, respectively. N is the local normal load and ${\textbf{F}}_T$ the corresponding local tangential contact forces. As a rate- and state-dependent friction model, the LuGre model can successfully describe complex dynamical frictional behaviours, such as the Stribeck effect and stick–slip effect, and has intuitive conceptualisation that is convenient to be understood and implemented. Relating to (11), the following equation can be derived straightforwardly as

$$\begin{aligned} {\textbf{F}}_T = {\textbf{t}}_T = t_{T\alpha }\bar{\varvec{\tau }}^\alpha . \end{aligned}$$

(23)

Therefore, the covariant component of the tangential contact force can be obtained immediately as

$$\begin{aligned} t_{T\alpha } = {\textbf{F}}_T \cdot \bar{\varvec{\tau }}_\alpha . \end{aligned}$$

(24)

2.4 Contact virtual work and discretisations

The contribution of the contact forces to the virtual work can be expressed as

$$\begin{aligned} \delta W_c{} & {} =\int _{\gamma _c} \Big [t_N\delta g_N+{\textbf{t}}_T \cdot \delta {\textbf{g}}_T\Big ]\textrm{d}\gamma \nonumber \\{} & {} =\int _{\gamma _c} \Big [t_N\delta g_N+t_{T_\alpha }\delta {\bar{\xi }}^\alpha \Big ]\textrm{d}\gamma , \end{aligned}$$

(25)

where $\delta g_N = (\delta {\textbf{x}}^e -\delta \bar{{\textbf{x}}}^g)\cdot \bar{{\textbf{n}}} = \delta {\textbf{u}}^e\cdot \bar{{\textbf{n}}}$ and $\delta {\bar{\xi }}^\alpha = H^{\alpha \beta }(\delta {\textbf{x}}^e\cdot {\bar{\tau }}_\beta +g_N\bar{{\textbf{n}}}\cdot \delta \bar{{\textbf{x}}}^g_{,\beta })=H^{\alpha \beta }(\delta {\textbf{u}}^e\cdot {\bar{\tau }}_\beta )$, $H^{\alpha \beta }=H_{\alpha \beta }^{-1}$ and $H_{\alpha \beta } = m_{\alpha \beta }-g_N\,k_{\alpha \beta }$.

The elastic body can be discretised using either the Finite Element framework [1] or the Isogeometric analysis (IGA) framework [40]. Define the following matrices

$$\begin{aligned} \delta {\textbf{u}}={} & {} \begin{bmatrix} \delta {\textbf{u}}_1^e \\ \delta {\textbf{u}}_2^e \\ \vdots \\ \delta {\textbf{u}}_{n_e}^e \\ \end{bmatrix},\ \ {\textbf{N}} = \begin{bmatrix} R_1({\textbf{x}}_1^e)\bar{{\textbf{n}}} \\ R_2({\textbf{x}}_2^e)\bar{{\textbf{n}}} \\ \vdots \\ R_{n_e}({\textbf{x}}_{n_e}^e)\bar{{\textbf{n}}} \\ \end{bmatrix},\ \ \nonumber \\{} & {} {\textbf{T}}_\alpha = \begin{bmatrix} R_1({\textbf{x}}_1^e)\bar{\varvec{\tau }}_\alpha \\ R_2({\textbf{x}}_2^e) \bar{\varvec{\tau }}_\alpha \\ \vdots \\ R_1({\textbf{x}}_{n_e}^e)\bar{\varvec{\tau }}_\alpha \\ \end{bmatrix},\ \ \hat{{\textbf{T}}} = [{\textbf{T}}_1, {\textbf{T}}_2]\ (\text { in 3D}),\nonumber \\{} & {} {\textbf{D}} = [{\textbf{D}}_1, {\textbf{D}}_2] = \hat{{\textbf{T}}}{\textbf{H}}^{-1}, \end{aligned}$$

(26)

where ${\textbf{u}} = \sum _{i=1}^{n_e} R_i({\textbf{x}}^e_i){\textbf{u}}^e_i$ means that the displacement is formed by the $n_e$ non-zero shape functions (or NURBS basis functions in IGA) $\{R_i\}$ in the corresponding element multiplied by the displacements at nodes (or control points in IGA), and ${\textbf{H}} = \{H_{\alpha \beta }\}$. In the 2D case, simply let $\hat{{\textbf{T}}} = {\textbf{T}}_1$ and ${\textbf{D}} = {\textbf{D}}_1$. Note that a few matrices have been simplified or even eliminated compared with their original form due to the rigid assumption for the ground surface. Some aforementioned quantities can be represented using (26) as

$$\begin{aligned} \delta g_N = \delta {\textbf{u}}^\textrm{T}\,{\textbf{N}},\ \delta {\bar{\xi }}^\alpha = \delta {\textbf{u}}^\textrm{T}\,{\textbf{D}}_\alpha . \end{aligned}$$

(27)

Therefore, rewrite (25) into matrix form taking into account the contact forces, the following equation can be obtained as

$$\begin{aligned} \delta W_c{} & {} = \delta {\textbf{u}}^\textrm{T} \int _{\gamma _c} [\varepsilon _N \langle g_N \rangle _{-}\,{\textbf{N}}+{\textbf{F}}_T\cdot \bar{\varvec{\tau }}_\alpha \,{\textbf{D}}_\alpha ]\,\textrm{d}\gamma \nonumber \\ {}{} & {} = \delta {\textbf{u}}^\textrm{T}\,{\textbf{F}}^c, \end{aligned}$$

(28)

where ${\textbf{F}}^c$ can be deemed as the residual force vector related to contact.

2.5 Mortar treatment

In this section, the Mortar-based method is performed on the contact integral in (25) to produce a more robust algorithm deriving the contact forces. Mortar treatment is essentially weak enforcement of the contact constraints by projecting the constraints to the nodes or control points through the integration over the local element. Such a treatment can effectively alleviate the spurious oscillations in the contact forces computed via the conventional Gauss-point-to-surface (GPTS) method [41]. It can also significantly reduce the number of auxiliary state variables of the incorporated LuGre model. Moreover, the contact integral is evaluated in an element-based manner, although options like segmentation method [42] and hybrid method [43] are more accurate but less convenient alternatives. The Mortar treatment to (25) can be expressed as

$$\begin{aligned} \delta W_c = \sum _A(t_{NA}\delta g_{NA}+t_{T\alpha A}\delta {\bar{\xi }}^\alpha _A)\,A_A, \end{aligned}$$

(29)

where the subscript A indicates the active nodes (or control points) and $A_A=\int _{\gamma _c}\,R_A\textrm{d}\gamma$ is the tributary area. The weighted averaged normal gap and projected parametric coordinates and their variations are defined as

$$\begin{aligned} g_{NA}{} & {} = \frac{\int _{\gamma _c} R_A\,g_N\,\textrm{d}\gamma }{\int _{\gamma _c}\,R_A\,\textrm{d}\gamma },\ {\bar{\xi }}^\alpha _A = \frac{\int _{\gamma _c}R_A\,{\bar{\xi }}^\alpha \,\textrm{d}\gamma }{\int _{\gamma _c}\, R_A\,\textrm{d}\gamma },\ \delta g_{NA} \nonumber \\ {}{} & {} = \frac{\int _{\gamma _c} R_A\, g_N\,\textrm{d}\gamma }{\int _{\gamma _c}\,R_A\,\textrm{d}\gamma },\ \delta {\bar{\xi }}^\alpha _A= \frac{\int _{\gamma _c}R_A\,\delta {\bar{\xi }}^\alpha \,\textrm{d}\gamma }{\int _{\gamma _c}\, R_A\,\textrm{d}\gamma }. \end{aligned}$$

(30)

The weighted averaged normal contact force can thus be defined as

$$\begin{aligned} t_{NA} = \frac{\int _{\gamma _c} R_A\,t_T\,\textrm{d}\gamma }{\int _{\gamma _c} R_A\,\textrm{d}\gamma } = \varepsilon \,\langle g_{NA} \rangle _{-}, \end{aligned}$$

(31)

and its tangential counterparts can be obtained through the following equations

$$\begin{aligned} {\left\{ \begin{array}{ll} {\textbf{v}}_A = \frac{\int _{\gamma _c}R_A{\textbf{v}}\,\textrm{d}\gamma }{\int _{\gamma _c}R_A\,\textrm{d}\gamma } \\ \dot{{\textbf{z}}}_A = {\textbf{v}}_A - {\textbf{z}}_A\frac{\sigma _0|{\textbf{v}}_A|}{G({\textbf{v}}_A)} \\ G({\textbf{v}}_A) = \mu _k+(\mu _s-\mu _k)\,\textrm{e}^{-|{\textbf{v}}_A/v_s|^\theta } \\ {\textbf{F}}_{TA} = (\sigma _0{\textbf{z}}_A+\sigma _1\dot{{\textbf{z}}}_A+\sigma _2{\textbf{v}}_A)\, t_{NA} \\ t_{T\alpha A} = {\textbf{F}}_{TA}\cdot \frac{\int _{\gamma _c}R_A\bar{\varvec{\tau }}_\alpha \,\textrm{d}\gamma }{\int _{\gamma _c}R_A\,\textrm{d}\gamma } \end{array}\right. }. \end{aligned}$$

(32)

Finally, substituting (30)-(32) into (29) and making use of (27), one gets the discretised form of the contact virtual work after Mortar treatment as

$$\begin{aligned} \begin{aligned} \delta W_c&= \sum _A\big (\varepsilon \,\langle g_{NA} \rangle _{-}\int _{\gamma _c}R_A\,\delta {\bar{\xi }}^\alpha \,\textrm{d}\gamma \\&\quad + t_{T\alpha A}\int _{\gamma _c}R_A\,\delta {\bar{\xi }}^\alpha \,\textrm{d}\gamma \big ) \\&= \delta {\textbf{u}}^\textrm{T} \int _{\gamma _c}\big [ \big (\varepsilon \sum _A\,R_A\langle g_{NA}\rangle _{-}\big ){\textbf{N}}\\&\quad +\big (\sum _A R_A t_{T\alpha A}\big ){\textbf{D}}_\alpha \big ]\,\textrm{d}\gamma \\&= \delta {\textbf{u}}^\textrm{T}\,{\textbf{F}}^{cA}, \end{aligned} \end{aligned}$$

(33)

where ${\textbf{F}}^{cA} {=} \int _{\gamma _c}\big [ \big (\varepsilon \sum _A\,R_A\langle g_{NA}\rangle _{-}\big ){\textbf{N}}+\big (\sum _A R_A t_{T\alpha A}\big )$ ${\textbf{D}}_\alpha \big ]\,\textrm{d}\gamma$ is the Mortar-based contact residual force. The numerical evaluation of ${\textbf{R}}_{cA}$ entails Gauss quadrature method, such that

$$\begin{aligned} {\textbf{F}}^{cA}{} & {} = \sum _{GP}\bigg [ \bigg (\varepsilon \sum _A\,R_{Ag}\langle g_{NA}\rangle _{-}\bigg ){\textbf{N}}_g\nonumber \\{} & {} \quad +\bigg (\sum _A R_{Ag} t_{T\alpha A}\bigg ){\textbf{D}}_{\alpha g}\bigg ]\,w_g J_g, \end{aligned}$$

(34)

where the subscript ’g’ means evaluating the value at the gth Gauss integration point, and $w_g$ and $J_g$ are respectively the weight and Jacobian associated with that integration point.

2.6 Explicit dynamics algorithm

With the residual contact force derived, the solution is sought for the time-dependent solid mechanics problem. Implicit and explicit integration methods stand as two optional schemes for solving such problems. The implicit methods are unconditionally stable and pose no requirement for the minimum time step. However, in an implicit scheme, the time step has to be adapted to the highest frequency of interest of the elastic body to ensure the accuracy of the results. Moreover, due to finite deformations and non-linear contact constraints, convergence issues may occur as the structural configurations can notably differ between adjacent time steps. Besides, the efforts are often not trivial for deriving a workable tangent stiffness matrix required in the Newton–Raphson procedure leading to a converged result. As a result, the small time steps satisfying the accuracy requirement and the iterations required to achieve convergence mean demanding computational resources, hindering the use of implicit schemes in solving dynamical frictional contact problems. Conversely, explicit methods are conditionally stable, for the time step should be kept small to satisfy the classical Courant-Friedrichs-Lewy (CFL) condition [44]. The CFL condition requires a stable time step $\Delta t$ to have the following relationship with the critical time step $\Delta t_{\text {cr}}$

$$\begin{aligned} \Delta t < \Delta t_{\text {cr}} = \frac{2}{\omega _{\text {max}}} \le \min _{e, I}\frac{2}{\omega _I^e} = \min _{e}\frac{l_e}{c_e}, \end{aligned}$$

(35)

where $\omega _{\text {max}}$ is the maximum frequency of interest, $l_e$ is the characterised length of an element, and $c_e$ is the longitudinal wave speed in this element [45]. With a proper choice of the time step, explicit methods are more efficient and ready-to-implement than their implicit counterparts, at the same time yielding accurate results. The present work adopts an explicit scheme in which the central difference method is used to approximate the acceleration. The solution procedure can be briefly stated as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{{\textbf{u}}}_t = \frac{1}{2\Delta t}({\textbf{u}}_{t+\Delta t}-{\textbf{u}}_{t-\Delta t}) \\ \ddot{{\textbf{u}}}_t = \frac{1}{\Delta t^2}({\textbf{u}}_{t+\Delta t}-2{\textbf{u}}_t+{\textbf{u}}_{t-\Delta t}) \\ {\textbf{M}}\,\ddot{{\textbf{u}}}_t = {\textbf{F}}^{\text {ext}}_t - {\textbf{F}}^\text {int}_t - {\textbf{F}}^{cA} \\ \end{array}\right. }, \end{aligned}$$

(36)

Fig. 5

The spring-slider model

where ${\textbf{M}}$, ${\textbf{F}}^\text {ext}$ and ${\textbf{F}}^\text {int}$ are respectively the mass matrix, the external force vector and the internal force vector obtained in a large deformation regime. The displacement vector in a forward time step ${\textbf{u}}_{t+\Delta t}$ is readily obtained by substituting (36)$_{1-2}$ into (36)$_{3}$ with the following starting procedure

$$\begin{aligned} {\textbf{u}}_{-\Delta t} = {\textbf{u}}_0-\dot{{\textbf{u}}}_0+\frac{1}{2}\ddot{{\textbf{u}}}_0\Delta t^2.\nonumber \\ \end{aligned}$$

(37)

To facilitate the efficiency and practicability of the algorithm, the lumped mass method [46] is adopted and is derived as

$$\begin{aligned} ({\textbf{M}})_{mn} = \delta _{mn}\sum _i\int _{{\mathcal {B}}^0}\rho _0 R_m({\textbf{x}})R_i({\textbf{x}})\,\textrm{d}{\mathcal {B}}^0 = m_m\delta _{mn}, \nonumber \\ \end{aligned}$$

(38)

where $\delta _{mn}$ is the Kronecher delta and $m_m = \int _{{\mathcal {B}}^0}\rho ^0 R_m({\textbf{x}})\,\textrm{d}{\mathcal {B}}$. The last equation of (38) makes use of the partition of unity of the basis functions, namely

$$\begin{aligned} \sum _i R_i({\textbf{x}}) = 1, \end{aligned}$$

(39)

which is usually satisfied in both FEM and IGA frameworks. As a result, only the diagonal elements of mass matrix ${\textbf{M}}$ are not zero, which improves the speed greatly in solving (36)$_3$.

3 2D stick–slip effect for flat contact profiles

3.1 Spring-slider model

As a widely used model for studying the stick–slip effect, the classical spring-slider model is investigated in this section in both rigid and elastic body settings. The model is depicted in Fig. 5 where the slider is connected with a horizontal spring, of which the other endpoint is driven with a constant velocity. Due to the difference between static and kinetic friction, the slider is subjected to a periodic stick–slip motion.

Both the rigid and deformable cases use the LuGre friction model, of which the parameters are shown in Table 1. In the deformable case, the material parameters are used as follows: Young’s modulus $E = 1$ [MPa] and Poisson’s ratio $\nu = 0.25$. Other parameters are the same as indicated in Fig. 5 in both cases. The total simulation time is 6 [s]. The deformable case is solved using the IGA framework, and the mesh size for the elastic body is set as $h = 0.2$. In the simulation of the deformable case, a set of distributed springs are installed with an equivalent overall stiffness as the single spring, over the right edge to mitigate stress concentration and any singularity brought with it, but only one spring is shown for illustration purpose. The authors would like to note that the vertical degrees of freedom of the top layer are restricted once the gravity force is enforced to the elastic body, so that vertical oscillations are prevented and contact separation [47, 48] in most cases does not occur.

Table 1 Parameters used in the LuGre model

Fig. 6

Comparison of rigid and elastic contact results. a Displacements; b friction forces

The results are shown in Fig. 6 where good agreement of displacements (of the mass centre) and the global friction forces in both cases can be observed. The slider macroscopically rests at the first two seconds when the friction force gradually builds up. Once it reaches the maximum static friction force, the state of stick breaks and gross sliding occurs. In the meantime, the friction force drops due to the smaller value of the kinetic COF, and the elastic energy stored in the springs is released, at which time the driving force becomes lower than the friction force so that the slider starts to decelerate. When the slider has zero velocity, it enters into the state of stick again, and the friction force rebuilds as a balance to the external load, which completes a typical periodic stick–slip motion. As a comparison, the results of the deformable case with classical/modified Coulomb’s model are also provided. These results indicate that the proposed contact algorithm can adequately handle the dynamic friction in the spring-slider model. Both displacement and the friction force can be well described, and the stress distribution during the motion is also properly depicted, e.g. in Fig. 7. On the other side, the classical Coulomb’s model fails to address the stick–slip effect due to the negligence of the coefficient of friction reduction during slipping, and the modified Coulomb’s model shows low computational efficiency due to repeatedly checking and updating the friction force, during which the error accumulates.

Fig. 7

A snapshot of the stress distribution of the elastic body. A set of springs is distribute across the right edge to mitigate stress concentration but only one is shown. Unit: [Pa]

3.2 Slider model with top layer velocity control

The second 2D example relates to a simulation in which an elastic body is in contact with the rigid ground. The motion of the elastic body is triggered by dragging the top layer of the elastic body at a constant speed. The motion of the top layer is supposed to propagate downwards in the elastic body through deformation until it reaches the bottom layer, where frictional contact occurs. The initial configuration and key parameters are shown in Fig. 8 where a potential deformed configuration is also illustrated in the figure. The parameters of the LuGre model used in the simulation are the same as shown in Table 1. The total simulation time is 5 [s] and the time step is set as $\Delta t = 10^{-5}$ [s].

Fig. 8

The slider model for elastic contact with friction and top-layer velocity control

Fig. 9

Displacements of midpoint contact layer with IGA and FEM framework for a $h = 0.5$; b $h = 0.15$

As an initial validation case, simulations have been conducted using both IGA and FEM frameworks for a very coarse mesh ($h = 0.5$) to show the consistency of results using two different frameworks, as depicted in Fig. 9a. The reason to use a coarse mesh is to simplify the problem since the stick–slip behaviours are extremely sensitive to the fluctuations in the friction force. As time develops, more state variables will result in significant variabilities in the friction force. These variabilities accumulate and lead to varying stick–slip patterns, as shown in Fig. 9b, where the results are obtained using a mesh size $h = 0.15$. So using such a coarse mesh and simplified setting, the consistency of results using different frameworks can be demonstrated, validating the robustness of the proposed algorithm.

In addition, four mesh sizes $h=\{0.250, 0.160,$ $0.125, 0.100\}$ in the IGA framework are employed in the simulations, and the displacements of the midpoint bottom layer of the elastic body are presented in Fig. 10. The results follow the same path but with subtle differences in the stick–slip transition points because of finer meshes of the contact layer which require more state variables in the algorithm. These state variables, as well as the local points where friction is present, can interact with each other so that more detailed dynamical behaviours of the contact interface can be considered. However, from a global viewpoint, the total sticking time shows no significant difference among cases using various mesh sizes. The sticking time ratio is computed as a summation of sticking time where the velocity of the point of interest under the Stribeck velocity $v_s$ is considered sticking, divided by the total simulation time. Therefore, the sticking time ratio can be deemed a quantity of interest to quantify the stick–slip behaviours of the system.

Fig. 10

Displacements of midpoint contact layer with various mesh sizes

Moreover, to get a better understanding of such a phenomenon, consider the well-known Burridge-Knopoff (BK) model [49], which has a similar setting as shown in Fig. 11 but in the rigid body regime. The BK model was initially proposed to investigate the seismicity of earthquake events, but the theoretical results can be heuristic for the current work. In this model, multiple equivalent blocks of mass m, subjected to gravity, are connected to a rigid support, which moves horizontally with a constant speed v, with vertical springs of the same stiffness $k_v$. These masses are also connected in sequence with horizontal springs of the same stiffness $k_h$. In an ideal case, when the initial condition for all the blocks is the same, all blocks should have the same trajectory. However, a small perturbation in the friction force or displacement could break such balance so that the blocks will interact with each other through the horizontal springs. Consequently, the trajectories of blocks, especially their stick–slip behaviours, can be very different. In addition, when the number of blocks increases, the trajectories of their mass centre can also be different since more block interactions are involved in the simulation. In an exemplified case, the parameters shown in Table 2 are used, and the number of blocks is varied as $n = \{3, 5, 10, 15\}$. The friction is modelled using the LuGre model with parameters in Table 1. The total simulation time is 15 [s] using a stiff differential equation solver with variable orders and variable time steps. The local results for $n=5$ are shown in Fig. 12, indicating a state synchronisation for the blocks. Therefore, the mean value of the results, representing the displacements of the mass centre is used and compared in Fig. 13 for various DOFs. These displacements show clear inconsistency after some time of development, which explains that the dynamical behaviours of the system can be very sensitive to the number of degrees of freedom (DOF) involved due to the interactions between these DOFs.

Fig. 11

The Burridge–Knopoff model

Table 2 Parameters used in the BK model

Fig. 12

The local results of the Burridge–Knopoff model $n=5$

Fig. 13

The displacement of the Burridge–Knopoff model with various DOFs

Another quantity of interest under inspection is the global COF, which can be computed as integration of frictional traction along the contact layer divided by the normal force. The development of the global COF can also indicate the state of the elastic body and reveal the stick–slip transition as a sudden decrease of COF in the slipping state can be expected. For the most refined mesh case ($h = 0.1$), the global COF is depicted in Fig. 14, where fluctuations around $\mu _k$ can be observed. The authors would like to note that the local COF relates to the state and the location on the contact layer and may not present the same pattern as the global COF as some local points may be sticking while others are slipping. The global COF, however, can be seen as an overall reflection of the state of the elastic body.

3.3 Slider model applied by a harmonic cyclic force

In the third example, consider the slider model again, but a cyclic force is applied uniformly to its right edge, as shown in Fig. 15. The exact parameters of the LuGre model, as shown in previous sections, are adopted to model the friction forces. The cyclic force is modelled in a sinusoidal form with an amplitude slightly lower than the gross maximum static friction force. In this case, the pre-sliding behaviours of the elastic body can be investigated since the applied external force does not exceed the break-away force, which is assumed to be the maximum static friction force. As a result, the elastic body will stay in the state of stick. However, it is theoretically believed [24, 50] and experimentally proved [51, 52] that the body under frictional contact will not stay still when the external force is less than the break-away force but will be subjected to a minor sliding according to the external force, which is termed as the pre-sliding behaviour.

The simulations are conducted in a time span [0, 8] [s] with a time step $\Delta t = 10^{-5}$ [s]. On the global scale, the block is under equilibrium during the simulation as the generated friction force is always equal to the applied force (but in the opposite direction). However, the local points can have minor sliding on a smaller scale. Taking an inspection of the displacements and velocities at some points on the bottom layer, which have x coordinate $\{0.00, 0.25, 0.50, 0.75, 1.00\}$ during the simulation, pre-sliding behaviours can be detected, as illustrated in Fig. 16. It can also be observed that the points closer to the edge acted on by the external force have a higher amplitude in both displacement and velocity, indicating that the applied force has a higher impact on those points closer to the slip front, at which these points are supposed to break the interlocking earlier than other points and thus enter into the state of slip earlier. On the other hand, for those points located far away from the slip front, the responses are less intensive, and it usually takes longer to reach the critical stick–slip transition point. The results also show that following the removal of external force, the drift of the elastic body is almost zero, a testament to the effectiveness of the proposed approach.

4 Stick–slip effect of 3D contact with randomly rough surface

This section addresses the application of the proposed frictional contact algorithm on the 3D elastic contact problem with randomly rough contact interfaces. To simplify the situation without loss of generality, consider a square plate moving on a flat plane with its bottom surface assigned with random roughness, as shown in Fig. 17a. The random roughness is realised using the IGA-based random geometry framework proposed in [53], which integrates the collocation-based random field modelling method [54] and the NURBS surface interpolation method [55]. The authors would like to note that other ways of rough surface modelling can also be deployed, for instance, the random midpoint displacement method [56, 57], which characterises the fractal properties of the surface. As depicted in Fig. 17b, the red dots in the figure are sampled from the random field by a 20$\times$20 grid, which satisfies the prescribed spatial property, e.g. Root Mean Square (RMS) roughness and spectral property, e.g. correlation length.

Fig. 14

The development of global COF for the elastic contact problem

Fig. 15

The slider model driven by a cyclic force

Fig. 16

Responses of the cyclic force a displacement; b velocity

Fig. 17

a Square plate moving on a flat plane; b bottom surface with random roughness

The random surface is constructed based on these sampling points with NURBS basis functions so that the surface becomes at least $C^1$ continuous. The top layer of the plate is enforced by a small constant driving velocity $v_d$ in the x-direction. Under this condition, the plate starts to deform correspondingly, and meanwhile, local friction forces between the bottom surface and the plane grow until they reach the break-away force. The numerical experiments are conducted in the Monte-Carlo (MC) approach with 100 realisations for three different correlation lengths $l_c = \{0.1, 1, 10\}$. The parameters shown in Table 3 are used in the simulation, where L is the side length of the square plate, RMS is the roughness property, T is the total simulation time, and $\textrm{d}t$ is the time step adopted. The same mesh size $h=0.05$ is used for the three cases. The LuGre model parameters are the same as in Table 1 except for the Stribeck velocity in this case being $v_s = 0$. The number of realisations was determined through a convergence study concerning the statistical properties of the responses. The simulations were run on a High Performance Computing cluster with 40 cores of Intel Xeon Gold Skylake processors and 384 GB of memory. The total simulation time is around 150 h.

In each realisation, the sticking states of the points in the bottom surface are tracked and represented as the sticking time ratio, which is the ratio of the total sticking time to the total simulation time. The total sticking time for a local point is computed as the sum of all time segments in which its velocity is under the Stribeck velocity. The statistical properties of the sticking time ratio obtained through MC simulations have been presented in Fig. 18. It can be observed that the sticking time ratio is distributed non-uniformly on the bottom surface. Those points close to the slip front (in this case close to $x=1$) experience a higher proportion of the sticking state than other parts. Besides, it shows a downfall in the sticking time during the motion for points on the four corners. In the case where the correlation length is 10.0, the proportion of high sticking time area is more prominent than in the other two cases, and the standard deviations at the same time are the lowest. The results imply that the whole bottom surface being smooth and consequently having more real contact area with the plane will result in a higher sticking area. In comparison, in the case where the correlation length and side length are comparable, the high sticking time area is the smallest among the three cases. In the case where $l_c = 0.1$, the roughness is scattered most prominently due to the small correlation length compared with L, the high sticking time area is the second largest in the three cases, for which real contacts can be established as an effect of homogenisation. However, the standard deviations for this case are the largest among the three cases because these contacts are not stable and can be significantly affected by local deformations.

The global COF, computed as the integration of friction traction over the whole contact interface divided by the normal contact force, is illustrated in Fig. 19. The global COF develops into a steady state for all three cases after around 1 [s]. The main difference lies in the oscillatory behaviours in the global COF, as it can be detected in the case $l_c = 10.0$ but not in the other two cases. The results imply that global oscillatory behaviours caused by the stick–slip effect can be observed when the surface roughness is not prominent, while otherwise oscillatory behaviours can only be found locally. The authors finally note that the scale dependency of the surface roughness and the COF [58, 59] is not taken into account in the current model and will be pursued in future work.

Table 3 Simulation parameters for the 3D contact case

Fig. 18

Statistical properties of the sticking time ratio for the points on the bottom surface. Mean values for a $l_c = 0.1$, c $l_c = 1.0$ and e $l_c = 10.0$. Standard deviations for b $l_c = 0.1$, d $l_c = 1.0$ and f $l_c = 10.0$

Fig. 19

The global COF for a $l_c = 0.1$; b $l_c = 1.0$; c $l_c = 10.0$. Solid line - mean value; shaded area - standard deviation

5 Conclusions

An explicit dynamical frictional contact algorithm is proposed in this paper. The algorithm is based on the mortar method and incorporates the LuGre model to take into account frictional dynamics. In such a way, the typical dynamical frictional behaviour such as the stick–slip effect can be effectively accounted for, for which the conventional contact algorithms usually overlook or address with limited accuracy. The effectiveness and accuracy of the proposed algorithm are demonstrated through a simplified 2D spring-slider model. The influence of the mesh size is investigated using a slider model with top layer velocity control. The results are validated in comparison with those of the Burridge–Knopoff model. The presliding behaviour is addressed utilising a slider model applied by a harmonic cyclic force. It is found that the points of the contact interface closer to the edge where an external force is enforced will break the interlocking earlier than others. A 3D elastic contact with a randomly rough surface is also studied. The contact interface with a large correlation length tends to have a large area of high sticking time ratio and a prominent global stick–slip effect. The contact interface where the correlation length and characterised geometry length are comparable has the smallest area of high sticking time ratio, and the global stick–slip behaviour is also suppressed.