Friction-induced vibration of an elastic disc and a moving slider with separation and reattachment

Abstract

The transverse vibration of an elastic disc, excited by a preloaded mass–damper–spring slider dragged around on the disc surface at a constant rotating speed and undergoing in-plane stick–slip oscillation due to friction, is studied. As the vertical vibration of the slider grows at certain conditions, it can separate from the disc and then reattach to the disc. Numerical simulation results show that separation and reattachment between the slider and the disc could occur in a low speed range well below the critical disc speed in the context of a rotating load. Rich nonlinear dynamic behaviour is discovered. Time–frequency analysis reveals the time-varying properties of this system and the contributions of separation and in-plane stick–slip vibration to the system frequencies. One major finding is that ignoring separation, as is usually done, often leads to very different dynamic behaviour and possibly misleading results.

1 Introduction

Elastic discs are key components in a wide range of mechanical applications such as rotors and stators in some engines, brakes and clutches, computer hard disc drives, and saws. During the operation of these mechanical devices, dry friction plays an important role on the dynamic behaviour. Generally speaking, dry friction dissipates energy and thus reduces vibration, but it can also sustain self-excited oscillation and even cause vibration to grow under certain conditions. For example, brake squeal is a well-known friction-induced vibration phenomenon in car brakes. The annoying noise can cause customers to doubt the quality of their automobiles. Friction-induced vibration has been generally accepted as the main reason for brake squeal [1–4]. Another consequence of friction-induced disc vibration is data losses of a computer hard disc drive because of its undesirable vibration.

Several physical mechanisms that attempt to explain unstable friction-induced vibration have been proposed in the literature and were reviewed in [5]: the negative friction slope [6], sprag-slip instability [7], mode-coupling instability [8], and stick–slip instability [9]. However, there has been no universal acceptance of an explanation for brake squeal [10], and the dynamic behaviour of friction-induced vibration is not fully understood.

Stick–slip vibration occurs when the static friction coefficient is greater than the kinetic friction coefficient [9]. Numerous investigations have focused on dry friction-induced stick–slip instability [11–14]. Popp and Stelter [9] studied the chaotic behaviour of several simple systems, which provided an insight into stick–slip instability. In [15], the critical speed for the initiation of stick–slip oscillation from pure sliding oscillation was derived by an analytical method. The results indicated that stick–slip motion took place in a wide speed range of the moving belt. Kinkaid et al. [16] examined the dynamics behaviour of a four-degree-of-freedom model with friction force in two orthogonal directions at the contact interface. Since the friction in [16] followed the Amontons–Coulomb’s law of friction, a new mechanism due to the combination of the stick–slip instability in both directions was presented. Stelter [17] investigated the nonlinear stick–slip behaviour of a cantilever beam excited by dry friction via numerical analyses and experiments. In [18], the influences of the non-smooth Coulomb’s law of friction on the stability of the self-excited vibration of a one-degree-of-freedom model with negative damping were studied. Pascal [19] explored the sticking and non-sticking orbits of a two-degree-of-freedom model with dry friction under harmonic excitation. Feeny et al. [20] presented a very interesting review of stick–slip vibration.

Research on the vibration of an elastic disc excited by a rotating slider system has been reported in [21–25]. Mottershead [21] reviewed vibration of stationary and rotating discs under various loads, including friction. In [26], parametric resonances in a disc with a rotating mass–spring–damper system were studied in the subcritical speed range, in which friction force was treated as a follower force. Ouyang et al. [23] examined the transverse instability of an elastic disc under the action of a rotating friction slider with stick–slip vibration. The influence of system parameters on the disc’s transverse vibration and the slider’s horizontal stick–slip vibration was investigated through numerical simulations. In a later paper [27], a model consisting of an elastic disc with two rotating oscillators acting on each side of the disc was developed. In that model, a bending couple was produced by the unbalanced friction forces on the lower and upper surfaces of the disc. The instability of the disc due to the friction couple was studied. The rotating speed of the mass–spring–damper slider system studied in these papers is in the subcritical range.

Other work on friction-induced vibration in discs was reported in [28–34]. Spelsberg-Korspeter et al. [29] proposed a new model containing a rotating Kirchhoff plate and an idealised elastic pad, which was in friction contact with the rotating plate. In that paper, both the in-plane and bending vibration of the rotating plate due to distributed friction forces were investigated. In [32], the wave pattern and the limit cycle of the stick–slip motion of a rotating disc, which was in frictional contact with a pad under uniform pressure, in a simplified brake system were analysed.

Loss of contact at the friction interface of the disc has been neglected in most of the studies mentioned above. Sinou [33] investigated the transient and stationary dynamics of a nonlinear automotive disc brake model due to friction. He showed that more unstable modes took part in the transient vibration because of the nonlinearity and loss of contact at the friction surface. However, the specific roles of separation and its importance to the friction-induced vibration have not been studied. The main purpose of the current paper is to investigate the friction-induced transverse vibration of a disc subjected to a rotating slider undergoing vertical vibration and in-plane stick–slip vibration.

In the present paper, a model containing an elastic disc in friction contact with a rotating oscillator is developed. Stick–slip motion of the slider takes place on the disc surface due to friction governed by the Coulomb’s law of friction, which leads to the coupling between the transverse vibration of the disc and the horizontal (in-plane) vibration of the rotating slider. Theoretical formulations of the system in stick and slip states are derived, and the conditions for staying in individual motion states are discussed in Sect. 2. In Sect. 3, the conditions and equations of motion for separation and reattachment are given; meanwhile, impact at the instant of reattachment is considered. In Sect. 4, dynamic behaviour of the model is analysed and numerical results show that separation can happen during unstable vibration at a low rotating speed level. Moreover, comparisons between the dynamic behaviour of the disc considering and ignoring separation indicate the importance of considering separation. Then, the effects of key system parameters on the friction-induced vibration of the system are examined via a numerical parametric analysis. Finally, the evolutions of the frequencies of the system with time are studied through the short-time Fourier transform that reveals the time-varying nature of the whole system due to the transverse separation–reattachment and in-plane stick–slip events.

2 Disc model and theoretical development

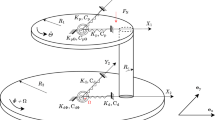
Figure 1 presents the mechanical model studied in this paper. The system contains an elastic annular disc, which is clamped at its inner radius a and free at its outer radius b, and a slider system in friction contact with the disc. The annular disc is a Kirchhoff plate which exhibits only transverse motion. The mass (slider) has a vertical branch and a horizontal (in-plane) branch, each having a spring and a damper in parallel. A vertical displacement $\varDelta$ is applied on the top of the vertical branch and is kept constant throughout the subsequent vibration, so that a vertical pre-load is generated and is always present. The horizontal branch is connected with a drive point that moves around on the surface of the elastic annular plate at a constant rotating speed $\varOmega$. In this paper, the Coulomb’s law of friction is used with a static friction coefficient $\mu _{\mathrm{s}}$ and kinetic friction coefficient $\mu _{\mathrm{k}}$. The slider is capable of stick–slip oscillation in the horizontal direction. Such a system was studied in [22] in which loss of contact and subsequent reattachment were excluded.

Fig. 1

Annular plate and slider system in the cylindrical coordinate system (top view from the side; bottom view from the top)

2.1 In-plane stick–slip motion of the slider

As the friction coefficient $\mu _{\mathrm{s}}$ is assumed to be greater than $\mu _{\mathrm{k}}$ in this work, the slider can undergo stick–slip oscillation in the horizontal direction. When the slider is sliding, its in-plane equation of motion is expressed in Eq. (1):

$$\begin{aligned} {r_0}\left( {m\ddot{\psi } + {c_{\mathrm{p}}}\dot{\psi } + {k_\mathrm{p}}{\psi } } \right) = {\mu _\mathrm{{k}}}{\mathrm{sgn}}\left( {\dot{\varphi }} \right) P \end{aligned}$$

(1)

in which $\psi$ denotes the circumferential angular position of the slider relative to the drive point and $\varphi$ is the absolute circumferential angular position of the slider, $r_{0}$ is the radial position of the slider, $c_{\mathrm{p}}$ is the in-plane damping coefficient of the slider, $k_{\mathrm{p}}$ is the in-plane stiffness of the slider, and P is the (total) contact force between the disc and the slider.

The sliding motion can be maintained if the following conditions are satisfied:

$$\begin{aligned} {r_0}|{c_\mathrm{p}}\dot{\psi } + {k_\mathrm{p}}\psi | \ge {\mu _\mathrm{s}}P \end{aligned}$$

(2)

or

$$\begin{aligned} \dot{\psi } \ne \varOmega \end{aligned}$$

(3)

The relation between the relative motion represented by $\psi$ and absolute motion $\varphi$ is:

$$\begin{aligned} \varphi = \varOmega t - \psi , \dot{\varphi } = \varOmega t - \dot{\psi } , \ddot{\varphi } = - \ddot{\psi } \end{aligned}$$

(4)

where t is time.

Otherwise, the slider sticks to the plate. In this motion phase, the slider’s absolute circumferential velocity $\dot{\varphi }$ and its acceleration $\ddot{\varphi }$ are equal to zero, and its circumferential position is referred to as $\varphi _{\mathrm {stick}}$. The relative motion of the slider is given by Eq. (5):

$$\begin{aligned} \psi =\varOmega t-\varphi _{\mathrm{stick}} \end{aligned}$$

(5)

The condition for the slider staying in the stick phase is:

$$\begin{aligned} {r_0}|{c_\mathrm{p}}\dot{\psi } + {k_\mathrm{p}}\psi | < {\mu _\mathrm{s}}P \end{aligned}$$

(6)

2.2 Transverse vibration of the disc

The equation of transverse motion of the disc under the action of the moving slider is given by Eq. (7):

$$\begin{aligned} \rho h{{{\partial ^2}w} \over {\partial {t^2}}} + {D^*}{\nabla ^4} \dot{w} + D{\nabla ^4}w= & {} - {1 \over r}\delta \left( {r - {r_0}} \right) \nonumber \\&\delta \left( {\theta - \varphi } \right) P \end{aligned}$$

(7)

where w denotes the transverse displacement of the plate, r and $\theta$ are the radial and circumferential coordinates in the cylindrical coordinate system, respectively, $D^*$ is the damping coefficient of the disc, $\rho$ is the mass density of the disc, D is the flexural rigidity of the disc, and $\delta (\bullet )$ is the Dirac delta function.

P can be obtained from the equation of vertical motion of slider m:

$$\begin{aligned} P = N + m\ddot{u} + c\dot{u} + k\left( {u - {u_0}} \right) \end{aligned}$$

(8)

where u and $\dot{u}$ are the vertical motion and vertical velocity of the slider, $u_0$ is the initial vertical displacement of the slider, c is the damping coefficient, k is the stiffness of the vertical branch of the slider, and N is the pre-load as a result of the vertical displacement $\varDelta$ applied.

In this paper, contact force P is defined as positive when there is contact (so that P is a compressive force). Thus, the condition for maintaining contact is:

$$\begin{aligned} P>0 \end{aligned}$$

(9)

If there is contact between the slider and the plate, the relationship between the transverse displacement w of the plate and the vertical displacement u of the slider is [35]:

$$\begin{aligned} u\left( t \right) =w(r_0 ,\varphi \left( t \right) ,t) \end{aligned}$$

(10)

and therefore

$$\begin{aligned} \dot{u}= & {} \dot{\varphi }{{\partial w} \over {\partial \theta }} + {{\partial w} \over {\partial t}} \end{aligned}$$

(11)

$$\begin{aligned} \ddot{u}= & {} \ddot{\varphi }{{\partial w} \over {\partial \theta }} + {{\dot{\varphi } }^2}{{{\partial ^2}w} \over {\partial {\theta ^2}}} + 2\dot{\varphi } {{{\partial ^2}w} \over {\partial \theta \partial t}} + {{{\partial ^2}w} \over {\partial {t^2}}} \end{aligned}$$

(12)

By substituting Eqs. (8) and (10)–(12) into Eq. (7), the equation of transverse motion of the disc can be derived as:

$$\begin{aligned}&\rho h{{{\partial ^2}w} \over {\partial {t^2}}} + {D^*}{\nabla ^4}\dot{w} + D{\nabla ^4}w = - {1 \over r}\delta \left( {r - {r_0}} \right) \delta \left( {\theta - \varphi } \right) \nonumber \\&\quad \left( N + m\left( {\ddot{\varphi } {{\partial w} \over {\partial \theta }} + {{\dot{\varphi } }^2}{{{\partial ^2}w} \over {\partial {\theta ^2}}} + 2\dot{\varphi } {{{\partial ^2}w} \over {\partial \theta \partial t}} + {{{\partial ^2}w} \over {\partial {t^2}}}} \right) \right. \nonumber \\&\quad \left. +\, c\left( {\dot{\varphi } {{\partial w} \over {\partial \theta }} + {{\partial w} \over {\partial t}}} \right) + k\left( {w - {w_0}} \right) \right) \end{aligned}$$

(13)

where $w_{0}$ is initial transverse displacement of the disc as a result of applying $\varDelta$ to the vertical branch of the slider.

Although Eq. (13) is applicable to both stick and slip motion states, as $\dot{\varphi }$ and $\ddot{\varphi }$ are zero in the stick phase, Eq. (13) is simplified to Eq. (14) which represents the equation of motion when the slider sticks to the disc.

$$\begin{aligned}&\rho h{{{\partial ^2}w} \over {\partial {t^2}}} + {D^*}{\nabla ^4}\dot{w} + D{\nabla ^4}w = - {1 \over r}\delta \left( {r - {r_0}} \right) \nonumber \\&\quad \delta \left( {\theta - \varphi } \right) \left( {N + m{{{\partial ^2}w} \over {\partial {t^2}}} + c{{\partial w} \over {\partial t}} + k\left( {w - {w_0}} \right) } \right) \nonumber \\ \end{aligned}$$

(14)

2.3 Coupled equations of motion of the whole system in modal coordinates

The transverse displacement of the disc can be expressed as an infinite series in modal coordinates:

$$\begin{aligned} w\left( {r,\theta ,t} \right) = \sum \limits _{k=0}^\infty \sum \limits _{l=-\infty }^\infty \varPsi _{kl} \left( {r,\theta } \right) q_{kl} \left( t \right) \end{aligned}$$

(15)

where $\varPsi _{kl} \left( {r,\theta } \right)$ is the mode shape of the plate given by Eq. (16):

$$\begin{aligned} \varPsi _{kl} \left( {r,\theta } \right) =\frac{1}{\sqrt{\rho hb^{2}}}R_{kl} \left( r \right) \mathrm{e}^{{\mathrm{i}}l\theta } \end{aligned}$$

(16)

in which $R_{kl} \left( r \right)$ is a combination of the Bessel functions and the modified Bessel functions. Subscript k denotes the number of nodal circles, and l denotes the number of nodal diameters; $\hbox {i}=\sqrt{-1}$.

The ortho-normality conditions of modal functions are:

$$\begin{aligned}&\int _a^b \int _0^{2\pi } \rho h\bar{\varPsi }_{kl} \varPsi _{rs} r\mathrm{d}r\mathrm{d}\theta =\delta _{kr} \delta _{ls}, \nonumber \\&\quad \int _a^b \int _0^{2\pi }\bar{\varPsi }_{kl} \nabla ^{4}\varPsi _{rs} r\mathrm{d}r\mathrm{d}\theta =\delta _{kr} \delta _{ls} , \end{aligned}$$

(17)

in which $\bar{\varPsi }_{kl}$ is the complex conjugate of $\varPsi _{kl}$.

Then, by multiplying $\bar{\varPsi }_{kl}$ on both sides of Eqs. (13) and (14), then integrating them over the whole disc surface, and by using the ortho-normality conditions shown in Eq. (17), Eqs. (13) and (14) are rewritten in terms of modal coordinates $q_{kl} \left( t \right)$ shown below.

In the stick phase, the equation of transverse motion of the disc in terms of modal coordinates is expressed as:

$$\begin{aligned}&{{\ddot{q}}_{kl}} + 2\xi {\omega _{kl}}{{\dot{q}}_{kl}} + \omega _{kl}^2{q_{kl}} = - {{N - k{w_0}} \over {\sqrt{\rho h{b^2}} }}\nonumber \\&\quad {R_{kl}}\left( {{r_0}} \right) \exp \left( { - \mathrm{{i}}l\varphi } \right) \nonumber \\&\quad - {1 \over {\rho h{b^2}}}\sum \limits _{r = 0}^\infty \sum \limits _{s = - \infty }^\infty {R_{rs}}\left( {{r_0}} \right) {R_{kl}}\left( {{r_0}} \right) \nonumber \\&\quad {{\exp }}\left( {{\mathrm{i}}\left( {s - l} \right) \varphi } \right) \left( {m{{\ddot{q}}_{rs}} + c{{\dot{q}}_{rs}} + k{q_{rs}}} \right) \end{aligned}$$

(18)

in which

$$\begin{aligned} \varphi =\varphi _{\mathrm{stick}} \end{aligned}$$

(19)

and the relative motion of the slider in the stick phase has been given by Eq. (6).

The condition for remaining in stick phase given by Eq. (6) is transformed into Eq. (20):

$$\begin{aligned} {r_0}|{c_\mathrm{p}}\dot{\psi } + {k_\mathrm{p}}\psi |< & {} {\mu _\mathrm{s}}\left( N - k{w_0} + {1 \over {\sqrt{\rho h{b^2}} }}\sum \limits _{r = 0}^\infty \right. \nonumber \\&\left. \sum \limits _{s = - \infty }^\infty {R_{rs}}\left( {{r_0}} \right) {{\exp }}\left( {{\mathrm{i}}s\varphi } \right) \right. \nonumber \\&\left. \left( {m{{\ddot{q}}_{rs}} + c{{\dot{q}}_{rs}} + k{q_{rs}}} \right) \right) \end{aligned}$$

(20)

During the sliding motion, the equations of transverse motion of the disc and the equation of horizontal motion of the slider are given by Eqs. (21) and (22):

$$\begin{aligned}&\ddot{q}_{kl} + 2\xi {\omega _{kl}}{\dot{q}_{kl}} + \omega _{kl}^2{q_{kl}} = - {{N - k{w_0}} \over {\sqrt{\rho h{b^2}} }}\nonumber \\&\quad {R_{kl}}\left( {{r_0}} \right) \exp \left( { - {\mathrm{i}}l\varphi } \right) - {1 \over {\rho h{b^2}}}\nonumber \\&\quad \sum \limits _{r = 0}^\infty \sum \limits _{s = - \infty }^\infty {R_{rs}}\left( {{r_0}} \right) {R_{kl}}\left( {{r_0}} \right) \exp \left( {{\mathrm{i}}\left( {s - l} \right) \varphi } \right) \nonumber \\&\quad \left\{ m\left[ {{{\ddot{q}}_{rs}} + {\mathrm{i}}2s\dot{\varphi } {{\dot{q}}_{rs}} + \left( {{\mathrm{i}}s\ddot{\varphi } - {s^2}{{\dot{\varphi } }^2}} \right) {q_{rs}}} \right] \right. \nonumber \\&\quad +\left. c\left( {{{\dot{q}}_{rs}} + {\mathrm{i}}s\dot{\varphi } {q_{rs}}} \right) + k{q_{rs}} \right\} \end{aligned}$$

(21)

and

$$\begin{aligned}&{r_0}\left( {m\ddot{\varphi } + {c_{\mathrm{p}}}\dot{\varphi } + {k_{\mathrm{p}}}\varphi } \right) = {r_0}\left( {{c_{\mathrm{p}}}\Omega + {k_{\mathrm{p}}}\Omega t} \right) \nonumber \\&\quad - {\mu _\mathrm{{k}}}{\mathrm{sgn}}\left( {\dot{\varphi } } \right) \left( N - k{w_0} + {1 \over {\sqrt{\rho h{b^2}} }}\sum \limits _{r = 0}^\infty \sum \limits _{s = - \infty }^\infty \right. \nonumber \\&\quad {R_{rs}}\left( {{r_0}} \right) {\exp }\left( {{\mathrm{i}}s\varphi } \right) \left\{ m\left[ {{\ddot{q}}_{rs}} + {\mathrm{i}}2s\dot{\varphi } {{\dot{q}}_{rs}}\right. \right. \nonumber \\&\quad \left. \left. \left. + \left( {{\mathrm{i}}s\ddot{\varphi } - {s^2}{{\dot{\varphi } }^2}} \right) {q_{rs}} \right] + c\left( {{{\dot{q}}_{rs}} + {\mathrm{i}}s\dot{\varphi } {q_{rs}}} \right) + k{q_{rs}} \right\} \right) \nonumber \\ \end{aligned}$$

(22)

And because of the axial symmetry of the annular disc, the relationships in Eq. (23) are satisfied [25]:

$$\begin{aligned} R_{{r,s}} \left( r \right)= & {} R_{{r, - s}} \left( r \right) ,\,\,\omega _{{r,s}} \left( r \right) \nonumber \\= & {} \omega _{{r, - s}} \left( r \right) ,\,\,q_{{r,s}} \left( t \right) = \bar{q}_{r, - s} \left( t \right) \end{aligned}$$

(23)

The conditions for staying in the slip phase [(Eqs. (2) and (3)] can be expressed in modal coordinates as:

$$\begin{aligned}&r_{0} |c_{{\text {p}}} \dot{\psi } + k_{{\text {p}}} \psi | < \mu _\mathrm{s} \left( N - kw_{0} + \frac{1}{{\sqrt{\rho hb^{2} } }} \sum \limits _{{r = 0}}^{\infty } \right. \nonumber \\&\quad \sum \limits _{{s = - \infty }}^{\infty } R_{{rs}} \left( {r_{0} } \right) {{\exp }}\left( {{\mathrm{i}}s\varphi } \right) \nonumber \\&\quad \left\{ m\left[ \ddot{q}_{{rs}} + {\mathrm{i}}2s\dot{\varphi }\dot{q}_{{rs}}. + \left( {{\mathrm{i}}s\ddot{\varphi } - s^{2} \dot{\varphi }^{2} } \right) q_{{rs}} \right] \right. \nonumber \\&\quad \left. \left. + c\left( {\dot{q}_{{rs}} + {\mathrm{i}}s\dot{\varphi }q_{{rs}} } \right) + kq_{{rs}} \right\} \right) \end{aligned}$$

(24)

3 Separation and reattachment

In this paper, separation takes place when contact force P(t) drops to zero. During the numerical calculations, it is important to monitor P(t) at each time step, because if separation happens, a new set of equations of motion of the slider and disc needs to be used. When P(t) becomes negative, the bisection method is used to find the critical point at which P(t) satisfying ${\vert }P(t){\vert }\,\le \,\varepsilon$, in which $\varepsilon$ is a small tolerance defined in the MATLAB codes. During separation, the contact force is zero and the sliding friction force vanishes.

The transverse motion of the disc and the vertical motion of the slider during separation are governed by Eqs. (25) and (26), respectively:

$$\begin{aligned} \rho h\frac{{\partial ^{2} w}}{{\partial t^{2} }} + D^{*} \nabla ^{4} \dot{w} + D\nabla ^{4} w = 0 \end{aligned}$$

(25)

$$\begin{aligned} m\ddot{u} + c\dot{u} + k\left( {u - u_{0} } \right) + N = 0 \end{aligned}$$

(26)

The new equation of horizontal motion of the slider is expressed in Eq. (27):

$$\begin{aligned} m\ddot{\psi } + c_{{\mathrm{p}}} \dot{\psi } + k_{{\mathrm{p}}} \psi = 0 \end{aligned}$$

(27)

Separation can be maintained when Eq. (28) is satisfied:

$$\begin{aligned} u > ~w \end{aligned}$$

(28)

After separation, the slider may get into contact with the disc again. Reattachment takes place when the displacement of the slider u equals to the displacement w of a point on the disc having the same coordinate as the slider. During the very short time interval of reattachment, denoted by ($t_{\mathrm{r}}^- ,t_{\mathrm{r}}^+ )$, impact may happen. $t_{\mathrm{r}}^-$ and $t_{\mathrm{r}}^+$ are the starting and the ending time moments of the impact. The states of the disc and the slider at time $t_{\mathrm{r}}^+$ are determined based on the momentum theory. The procedure for determining the dynamic states immediately after reattachment, which was presented in [36] for a moving-mass-on-beam problem, is derived for the present problems below.

For simplification, a simple perfectly plastic impact is assumed, and slider sticks onto the disc after the impact. Thus, the slider takes the displacement and the velocity of the disc at time $t_{\mathrm{r}}^+$. Suppose the impulse at $t_{\mathrm{r}}$ is p, the equation of motion of the disc is:

$$\begin{aligned}&\rho h\frac{{\partial ^{2} w}}{{\partial t^{2} }} + D^{*} \nabla ^{4} \dot{w} + D\nabla ^{4} w = - \frac{p}{r}\delta \nonumber \\&\quad \left( {r - r_{0} } \right) \delta \left( {\theta - \varphi } \right) \delta \left( {t - t_{{\mathrm{r}}} } \right) \end{aligned}$$

(29)

By using the same modal expansion process described in Sect. 2.3, Eq. (29) can be converted to Eq. (30) in modal coordinates:

$$\begin{aligned}&\ddot{q}_{{kl}} \!+\! 2\xi \omega _{{kl}} \dot{q}_{{kl}} \!+\! \omega _{{kl}}^{2} q_{{kl}} \!=\! -\! p \bar{\varPsi }_{{kl}} \left( {r_{0} ,~\varphi \left( {t_{{\mathrm{r}}} } \right) } \right) \delta \left( {t \!-\! t_{{\mathrm{r}}} } \right) \end{aligned}$$

(30)

The velocity jump as a result of the impact can be solved from Eq.  (30) and given by Eq. (31):

$$\begin{aligned} \dot{q}_{{kl}} \left( {t_{{\mathrm{r}}}^{ + } } \right) \!-\! \dot{q}_{{kl}} \left( {t_{{\mathrm{r}}}^{ - } } \right) \!= \!-\! \frac{p}{{\sqrt{\rho hb^{2} } }}R_{{kl}} \left( {r_{0} } \right) \exp \left( { \!-\! {\mathrm{i}}l\varphi \left( {t_{{\mathrm{r}}} } \right) } \right) \end{aligned}$$

(31)

Similarly, the velocity jump of the slider can be acquired:

$$\begin{aligned} \dot{u}\left( {t_{{\mathrm{r}}}^{ + } } \right) - \dot{u}\left( {t_{{\mathrm{r}}}^{ - } } \right) = \frac{p}{m} \end{aligned}$$

(32)

The combination of Eqs. (31) and (32) gives:

$$\begin{aligned} \dot{q}_{{kl}} \left( {t_{{\mathrm{r}}}^{ + } } \right) - \dot{q}_{{kl}} \left( {t_{{\mathrm{r}}}^{ - } } \right)= & {} - m\left( {\dot{u}\left( {t_{{\mathrm{r}}}^{ + } } \right) - \dot{u}\left( {t_{{\mathrm{r}}}^{ - } } \right) } \right) \nonumber \\&{\bar{\varPsi }}_{{kl}} \left( {r_{0} ,~\varphi \left( {t_{{\mathrm{r}}} } \right) } \right) \end{aligned}$$

(33)

For perfectly plastic impact, the slider takes the displacement and the velocity of the disc at time $t_{\mathrm{r}}^+. \dot{u}(t_{\mathrm{r}}^+)$ can be expressed as Eq. (34):

$$\begin{aligned} \dot{u}\left( {t_{{\mathrm{r}}}^{ + } } \right)= & {} \left( {\dot{\varphi }\frac{{\partial w}}{{\partial \theta }} + \frac{{\partial w}}{{\partial t}}} \right) |_{{\theta = \varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) }} \nonumber \\= & {} \sum \limits _{{k = 0}}^{\infty } \sum \limits _{{l = - \infty }}^{\infty } \left( \varPsi _{{kl}} \left( {r_{0} ~,~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) {q_{{kl}} } \left( {t_{{\mathrm{r}}}^{ + } } \right) \right. \nonumber \\&\left. + \dot{\varphi }\left( {t_{{\mathrm{r}}}^{ + } } \right) \frac{{\partial \varPsi _{{kl}} \left( {r_{0} ~,~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) }}{{\partial \theta }}q_{{kl}} \left( {t_{{\mathrm{r}}}^{ + } } \right) \right) \end{aligned}$$

(34)

Because the transverse displacement is continuous and in-plane motion of the slider does not change by the vertical impact, one gets:

$$\begin{aligned} q_{{kl}} \left( {t_{{\mathrm{r}}}^{ + } } \right)= & {} q_{{kl}} \left( {t_{{\mathrm{r}}} } \right) = q_{{kl}} \left( {t_{{\mathrm{r}}}^{ - } } \right) ,\,\,~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) \nonumber \\= & {} \varphi \left( {t_{{\mathrm{r}}} } \right) ,\,\,\dot{\varphi }\left( {t_{{\mathrm{r}}}^{ + } } \right) = \dot{\varphi }\left( {t_{{\mathrm{r}}} } \right) \end{aligned}$$

(35)

By substituting Eq. (34) into (33), and combining Eq. (35), then modal velocity $\dot{q}_{kl}$ and vertical velocity $\dot{u}$ at time $t_{\mathrm{r}}^+$ are derived as:

$$\begin{aligned}&\dot{u}\left( {t_{{\mathrm{r}}}^{ + } } \right) = \frac{{ \sum \nolimits _{{k = 0}}^{\infty } \sum \nolimits _{{l = - \infty }}^{\infty } \left( {m\dot{u}\left( {t_{{\mathrm{r}}}^{ - } } \right) {\varPsi }_{{kl}} \left( {r_{0} ~,~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) \bar{\varPsi }_{{kl}} \left( {r_{0} ,~\varphi \left( {t_{{\mathrm{r}}} } \right) } \right) \!+\! {{\varPsi }} _{{kl}} \left( {r_{0} ~,~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) \dot{q}_{{kl}} \left( {t_{{\mathrm{r}}}^{ - } } \right) \!+\! \dot{\varphi }\left( {t_{{\mathrm{r}}}^{ + } } \right) \frac{{\partial \varPsi _{{kl}} \left( {r_{0} ~,~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) }}{{\partial \theta }}q_{{kl}} \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) }}{{1 + m \sum \nolimits _{{k = 0}}^{\infty } \sum \nolimits _{{l = - \infty }}^{\infty } \left( {\varPsi _{{kl}} \left( {r_{0} ~,~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) {\bar{\varPsi }}_{{kl}} \left( {r_{0} ,~\varphi \left( {t_{{\mathrm{r}}} } \right) } \right) } \right) }} \nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned}&\dot{q}_{{kl}} \left( {t_{{\mathrm{r}}}^{ + } } \right) = \dot{q}_{{kl}} \left( {t_{{\mathrm{r}}}^{ - } } \right) - m\left( {\frac{{\sum \nolimits _{{k = 0}}^{\infty } \sum \nolimits _{{l = - \infty }}^{\infty } \left( {\varPsi _{{kl}} \left( {r_{0} ,~~~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) \dot{q}_{{kl}} \left( {t_{{\mathrm{r}}}^{ - } } \right) + \dot{\varphi }\left( {t_{{\mathrm{r}}}^{ + } } \right) \frac{{\partial \varPsi _{{kl}} \left( {r_{0} ,~~~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) }}{{\partial \theta }}q_{{kl}} \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) - \dot{u}\left( {t_{{\mathrm{r}}}^{ - } } \right) }}{{1 + m\mathop \sum \nolimits _{{k = 0}}^{\infty } \sum \nolimits _{{l = - \infty }}^{\infty } \left( {{\varPsi } _{{kl}} \left( {r_{0} ,~~~\varphi \left( {t_{{\mathrm{r}}}^{ + } } \right) } \right) \bar{\varPsi }_{{kl}} \left( {r_{0} ,~~~\varphi \left( {t_{{\mathrm{r}}} } \right) } \right) } \right) }}} \right) {\bar{\varPsi }} _{{kl}} \left( {r_{0} ,~\varphi \left( {t_{{\mathrm{r}}} } \right) } \right) \nonumber \\ \end{aligned}$$

(37)

4 Numerical study

As the state of the system switches between stick and slip phases, and between separation and contact phases, the dynamic behaviour of the system needs to be obtained by solving three different sets of governing equations, which brings out some difficulties in the numerical computations. In this paper, Runge–Kutta method appropriate for the second-order differential equations [37] is used to solve this non-smooth dynamic problem. The states of the disc and the slider during vibration, including the contact force, the absolute circumferential speed of the slider, and the force in the horizontal spring and damper, are monitored at each time step. If the results at the end of a time step do not satisfy the conditions for the system to stay in the same motion phase as at the start of the time step, then the bisection method is used to find the critical point where the dynamics switches from one phase to another phase. After getting the critical point, the current set of equations of motion changes to another set. Rich dynamic behaviour, some of which has not been seen in the literature, is found. Due to the limited space, however, only some distinct and interesting results are presented in this paper. The basic parameter values used in the numerical examples are listed in Table 1.

Table 1 Values of system parameters

Fig. 2

Time response of the contact force when $N=200\hbox { N}$ and $\varOmega =20\hbox { rad}/\hbox {s}$. a In the entire time duration. b Its zoom-in plot during $t=[602.115, 602.15]$ s

To avoid expensive computations, truncated modal series of the disc’s displacement is used in this paper. The first five distinct natural frequencies are obtained: 1491.92, 1516.76, 1823.88, 2774.19, and 4383.04 rad/s, which are 237.45, 241.40, 290.28, 441.53, and 697.58 in Hz, respectively. Except for the zero nodal circle mode (indices $k=0$ and $l=0$) which is a single mode, all other frequencies each have two natural (nodal diameter) modes. In order to obtain more dynamic information, long time calculations are carried out. It is found that nine disc modes are good enough since more modes do not lead to noticeable change in vibration behaviour.

Fig. 3

Enlarged time response of the transverse displacement of the disc and the vertical displacement of the slider

Fig. 4

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right) when separation is ignored($N=200\hbox { N}, \varOmega =20$ rad/s)

Fig. 5

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right) when separation is considered$(N=200\hbox { N}, \varOmega =20\hbox { rad}/\hbox {s})$

4.1 Separation during vibration

Firstly, the occurrence of separation is illustrated by a numerical example. The time response of the contact force and transverse vibration of the disc are shown in Figs. 2 and 3. In this example, the rotating speed of the driving point is $\varOmega =20$  rad/s, and the pre-load is $N=200\,\hbox {N}$. A long time calculation is run. Figure 2a shows the time response of the contact force during the entire calculation time. Although details of the vibration cannot be observed easily in Fig. 2a, it can be observed that the oscillating range of the contact force grows, and the contact force can drop to zero, which means that separation can occur during the vibration. Then, for a clearer observation, the zoom-in view of Fig. 2a within a short time interval is given in Fig. 2b. It shows that when the contact force decreases to zero, separation takes place, and then, contact force remains zero during separation. Moreover, multiple separation events can happen. The results of transverse vibration of the disc and the vertical vibration of the slider during one full event of the separation and reattachment process are shown in Fig. 3. As shown in Fig. 3, separation happens while the disc moves upward; therefore, the growing vibration of the disc is bounded due to loss of contact. It shows that the duration of the separation is very short, which can be explained as follows: the pre-load acts on the slider all the time even during separation, so the slider quickly gets into contact with the disc again under these parameter values.

Fig. 6

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right) when separation is ignored$(N=300\hbox { N}, \varOmega =20\hbox { rad}/\hbox {s})$

Fig. 7

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right) when separation is considered ($N=300\,\mathrm{N}, \varOmega =20$ rad/s)

Fig. 8

Poincare maps of the relative horizontal motion of the slider (left) and the vertical motion of the disc (right) when separation is ignored$(N=200\hbox { N}, \varOmega =50 \hbox { rad}/\hbox {s})$

Fig. 9

Poincare maps of the relative horizontal motion of the slider (left) and the vertical motion of the disc (right) when separation is considered($N=200\, \mathrm{N}, \varOmega =50$ rad/s)

Secondly, the influences of the separation on the in-plane vibration of the slider and the transverse vibration of the disc are studied by comparing the results of the system with considering and ignoring separation. The transverse vibration of the disc is observed at a fixed point on the disc at $r=r_{0}$ and $\varphi =1$. Three sets of examples, at different values of pre-load N and driving speed $\varOmega$ , are illustrated in Figs. 4, 5, 6, 7, 8, and 9 in terms of Poincare maps in order to reveal the dynamic behaviour. For clear observation, the results of the entire simulated time duration are divided and shown in several stages. As to the results of ignoring separation, shown in Figs. 4, 6, and 8, the entire time interval is divided into two stages. Blue crosses denote the motion of the first half of the total computing time, and the green dots denote the motions of the next half. In the results with separation, shown in Figs. 5, 7, and 9, blue crosses denote the motion before the first separation which is called ‘In contact-period 1’; green dots denote the motion that occurs when contact reoccurs and is maintained after the first separation, which is called ‘In contact-period 2’; and red triangles denote the motion during separation.

It can be seen from the Poincare maps (the sampling rate is the driving point’s speed) in these comparison cases shown in Figs. 4 and 5, Figs. 6 and 7, and Figs. 8 and 9 that ignoring and considering separation result in different dynamic behaviour. In the Poincare maps of the in-plane motion of the slider, the dots or crosses forming the horizontal straight line represent motion in the stick phase and those dots and crosses away from this line represent motion in the slip phase. In all the cases when the contact is assumed to be maintained during vibration, shown in Figs. 4, 6 and 8, the trajectories of horizontal stick–slip motion exhibit transient behaviour initially, but finally settle down to a steady state of stick and slip motion (given by the green dots). The stick and slip motion can be always maintained during the steady state, which are not affected by the values of the pre-load and the rotating speed. However, when separation is considered, shown in Figs. 5, 7, and 9, separation changes the patterns of the trajectories formed by the Poincare points, which indicates that a variety of complex dynamic behaviour of the system can be produced, depending on system parameters like the pre-load and the rotating speed. With respect to the transverse vibration of the disc, more frequencies actually join in during the steady state when separation is considered, as there are more points on the Poincare plane in Figs. 5 and 7 (considering separation) compared with Figs. 4 and 6 (ignoring separation). As to the horizontal vibration of the slider, it is periodic at the steady state (in stage 2) when separation is ignored (Figs. 4, 6), as confirmed by their phase portraits. However, it is quasi-periodic at steady state (in contact-period 2 and during separation) in Figs. 5 and 7 as new non-commensurate frequencies take part when separation is considered, which is also confirmed by their phase portraits. The phase portraits of the transverse vibration of the disc in Figs. 4 and 5 are shown in ‘Appendix’. Further investigations on the vibration frequencies of the system are carried out in Sect. 4.4.

Fig. 10

Time history of the transverse vibration of the disc for $N=200$ N and $\varOmega =20$ rad/s. a Separation is ignored. b Separation is considered

Fig. 11

Transient responses ($N=385$ N, $\varOmega =$15 rad/s). a Time history of the contact force. b Time history of the disc’s transverse vibration

Fig. 12

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right)($N=385$  N, $\varOmega =15$ rad/s)

Additionally, the vibration ranges of the disc when considering separation are much smaller than those when ignoring separation, shown in Fig. 10. The reason for this can be explained. Because of separation, the disc cannot get further excitation from the slider (note that the rotating slider is the source of excitation), unlike the cases when contact is assumed to be always maintained even though the contact force has dropped to a negative value. Therefore, separation serves to contain the vibration in a smaller range of magnitude.

Consequently, the necessity of considering separation in friction-induced vibration of this system is obvious. As this paper focuses on the dynamic behaviour of friction-induced vibration with separation, more numerical results with separation for various parameter values are provided in Sect. 4.3.

4.2 The critical speed for separation

Firstly, two numerical examples are shown to give a brief description of the critical rotating speed $\varOmega _{\mathrm{c}}$ for separation. Figures 11, 12, 13, and 14 illustrate the dynamic responses of the system in cases with different but close driving rotating speeds: $\varOmega =15$ rad/s and $\varOmega =15.1$ rad/s. Figure 11 clearly indicates that separation does not happen at $\varOmega =15$ rad/s, and the disc vibration does not grow and only oscillates in a small constant range. However, at a slightly higher rotating speed of $\varOmega =15.1$ rad/s, the oscillation range of the contact force grows, as shown in Fig. 13a, and then, several separation events take place. In this case, the disc vibrates in a larger range in Fig. 13b. The Poincare maps of these two cases shown in Figs. 12 and  14 indicate that the dynamic behaviour of the system can be very different when the system becomes unstable. This rotating speed is referred to as the critical speed for separation.

Fig. 13

Transient responses($N=385$ N, $\varOmega =15.1$ rad/s). a Time history of the contact force. b Time history of the disc’s transverse vibration

Fig. 14

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right)($N=385$ N, $\varOmega =15.1$ rad/s)

Fig. 15

Critical speed for separation

Fig. 16

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right)  ($N=50$ N, $\varOmega =15$ rad/s)

In order to study the critical speed range of this system, numerical calculations for various values of initial pre-load and rotating speed are carried out. Figure 15 shows the changes in critical rotating speed $\varOmega _{\mathrm{c}}$ for the occurrence of separation with pre-load N. When the rotating speed is smaller than the critical speed, the contact is always maintained during vibration. Otherwise, when the rotating speed is greater than $\varOmega _{\mathrm{c}}$, the slider can lose contact with the disc along with growing vibration. It can be seen that the critical speed for the loss of contact of this system can be low, which is much lower than the conventional critical speed (defined as the speed value of a rotating constant load which causes the resonance of the disc). Moreover, with the initial increase in pre-load N, the system becomes unstable and separation occurs at a lower rotating speed; from a certain value of N, with further increase in N, the system becomes unstable and separation takes place at a higher rotating speed.

4.3 Influences of significant parameters

To reveal various dynamic behaviour of the system when separation is considered, parametric studies are carried out. In this section, the effects of the pre-load N are examined firstly. The results of three pre-load cases ($N=385$, 50 and 200 N) are illustrated in Fig. 12, 16, and 17, respectively. The rotating speed in these examples is fixed at 15 rad/s. When the initial pre-load is small ($N=50$ N), the disc vibrates periodically at a small amplitude and there is no separation during the vibration; the in-plane vibration is periodic as well, shown in Fig 16. At a larger pre-load (N =200 N), both of the slider’s in-plane vibration and disc’s transverse vibration become unstable and separation occurs, as shown in Fig. 17. As to the in-plane motion of the slider, the stick phase gets longer because of the larger pre-load, but then due to separation, the stick–slip vibration becomes very complicated. However, with further increase in the normal force ($N=385$ N), the vibration of the system becomes stable again and no separation occurs, as shown in Fig. 12 in Sect. 4.2. Therefore, pre-load N plays a complex role in the stability of this system and does not have a monotonous effect on the friction-induced disc vibration. Initial increase in N destabilises the system, while further increase in N leads to a stable system.

Fig. 17

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right)($N=200$ N, $\varOmega$ =15 rad/s)

Fig. 18

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right)(D*=0, $N=200$ N, $\Omega =10$ rad/s)

Although the specific reasons for its complex role in this model is difficult to identify because of coupling of non-smooth in-plane vibration of the slider with out-of-plane vibration of the slider, two extreme situations can shed some light onto this matter. One extreme situation is: when N is zero, there is no friction force, and thus, the slider undergoes pure sliding motion in the horizontal direction; as the running speed in this case ($\varOmega =15$  rad/s) is far below the critical speed ($\varOmega =608$ rad/s) for the unstable vibration of the disc in the moving load problem, the system is stable when the normal force is zero at low rotating speed. The other extreme situation is: when N is extremely large, the slider can hardly move, which means that the slider sticks to the disc within the time duration of observation and the system is also stable. Between the two extreme situations, horizontal stick–slip motion appears and is affected by the value of the normal force N; as the horizontal motion of the slider is coupled with the vertical motion of the slider and the transverse motion of the disc, the whole system dynamics is affected by the normal force in a complicated way.

Fig. 19

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right)($c_{\mathrm{p}}$=0.5, $N=385$ N, $\varOmega =15$  rad/s)

Fig. 20

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right)($c=0.5$, $N=200$ N, $\varOmega =20$ rad/s)

Secondly, the effects of damping, including the disc’s damping, damping of the horizontal and vertical dampers, are examined. When pre-load N is at 200 N and the disc’s damping D* is 10$^{-5}$, critical rotating speed $\varOmega _{\mathrm{c} }$ for separation is 12.6  rad/s. When there is no disc’s damping (D* $=$ 0), the vibration of the system becomes unstable and separation occurs at a lower rotating speed shown in Fig. 18, $\varOmega =10$ rad/s, at $N=200$ N. The trajectory of the in-plane motion of the slider changes after the first separation, which is shown by the green dots in the left Poincare map of Fig. 18. Additionally, when D* is at $2\times 10^{-5}$, both the horizontal vibration of the slider and the transverse vibration of the disc become stable.

It is found that the influences of the in-plane damping on the transverse vibration of the disc are more complicated, as contact force P is changing during the vibration. The in-plane damping can destabilise the system, in a large pre-load range, shown in Fig. 19, in comparison with the vibration of this system when the in-plane damping is zero, shown in Fig. 12, which indicates that the system is stable at $c_{\mathrm{p}}=0, N=385\hbox { N}$ and $\varOmega =15$ rad/s. However, when there is in-plane damping $(c_{\mathrm{p}}=0.5)$, the vibration of the disc increases and it becomes unstable, and loss of contact happens as a consequence of the increase in vibration. From the Poincare map in Fig. 19, after separation both of the slider’s in-plane stick–slip motion and disc’s transverse vibration are unstable periodic motion.

The influences of the vertical damping coefficient are also studied. When there is vertical damping, as shown in Fig. 20, the slider’s in-plane motion is a periodic stable stick–slip motion; the vibration of the disc is also stable, and it oscillates within a small range around its static equilibrium position. Therefore, vertical damping coefficient appears as a stabilising factor to the system.

Fig. 21

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right) ($E=100$ GPa, $\varOmega =11$ rad/s)

Fig. 22

Poincare maps of the relative horizontal motion of the slider (left) and the transverse motion of the disc (right)($k_{\mathrm{p}}=2\times 10^{3}$ N/m, $N=300$ N, $\varOmega =50$ rad/s)

Then, the effects of the stiffness of the disc and the stiffness of the vertical and horizontal springs on the vibration of the system when separation is considered are studied. Increasing the elasticity of the disc and the stiffness of the vertical spring stabilises the unstable transverse vibration of the disc. On the other hand, decreasing the value of the elasticity and the vertical stiffness makes the vibration more unstable. At sufficiently small value of E, the transverse vibration of the disc seems quasi-periodic with irregular Poincare points, but separation does not happen during the vibration, shown in Fig. 21 ($E=100$ GPa, $\varOmega =11$ rad/s) in which blue crosses denote the motions of the first half of the total computing time (stage 1), and the green dots denote the motions of the last half (stage 2).

When k becomes smaller, the system becomes unstable sooner and separation takes place more easily. The system becomes stable when k is large enough (i.e. $k=2\times 10^{5}$ N/m).

The role of the in-plane stiffness of the slider on the vibration of the system is complex. When $k_{\mathrm{p}}=2\times 10^{3}$ N/m, the vibration of the disc initially vibrates quasi-periodically. However, after separation occurs, the points, shown by green dots, on the Poincare section of the disc wander within a certain range and become unpredictable, shown in Fig. 22. When $k_{\mathrm{p}}=2\times 10^{4}$ N/m, the unstable vibration grows faster and separation takes place earlier. However, a large enough $k_{\mathrm{p}}(2\times 10^{5}$ N/m) then appears to stabilise the system.

Finally, the value of the slider’s mass is found to affect the separation location in the vertical direction. In all the results shown above, separation happens while the disc is moving upward. In Fig. 23, however, the position of separation is changed if the mass is small ($m=0.01$). In this example, separation happens when the mass reaches its lowest vertical position. This information is not available from Poincare maps and can only be obtained from the time response of vibration.

Fig. 23

Enlarged time response of the transverse displacement of the disc ($m=0.01$, $N=200$ N, $\varOmega =20$ rad/s)

Therefore, the vibration of the disc induced by the frictional moving slider is quite complex. Unstable vibration of the disc happens in a low speed range, and separation takes place along with the growing vibration of the disc. After separation, the transverse vibration of the disc becomes bounded; the horizontal slider exhibits pure slip vibration, and the stick phase disappears under some parameter values. The different dynamic behaviour between the situations when separation is considered and when separation is ignored can be seen. Numerical results through a parametric analysis reveal the roles of key system parameters on the vibration of the system. It is notable that small and large values of the pre-load appear as stabilising factors to the system, but the intermediate values are destabilising. However, when the normal pre-load is large enough, the in-plane damping then appears as a destabilising factor to the system.

4.4 Non-stationary dynamic behaviour

As the system actually experiences distinct motion states during vibration, the vibration frequencies in these motion states can be different, and thus, the system is non-stationary and FFT analysis is no longer suitable. In this subsection, time–frequency analysis through the short-time Fourier transform is carried out to explore evolution of the vibration frequency of the system studied in this paper.

In the following, the time–frequency analysis of three examples is carried out. The results of the first example are shown in Figs. 24 and 25. The time history of the contact force, shown in Fig. 13 in Section 4.2, indicates that separation starts to take place at 54.5s, followed by events of repeated reattachment and separation. Figure 24 shows that there are roughly three kinds of behaviour during transverse vibration of the disc. Its vibration frequency during four time segments, marked as (a), (b), (c), and (d) in Fig. 24, are calculated, and the corresponding time–frequency results are shown in Fig. 25a–d, respectively.

Fig. 24

Time history of the transverse displacement of the disc ($E=150$ Gpa, $N=385$ N, $\varOmega =15.1$ rad/s)

Fig. 25

Time–frequency spectrum of the transverse vibration of the disc ($E=150$ Gpa, $N=385$ N, $\varOmega =15.1$ rad/s)

Firstly, in the starting stage of the transient vibration, the vibration amplitude grows, and the main frequencies of the unstable modes are indicated in Fig. 25a. It can be seen that there are several frequencies involved in the vibration. The values of the main frequencies, shown in the time–frequency power spectrum, making significant contributions to the vibration during t = [0, 10] s are listed in Table 2.

Table 2 Significant frequencies (Hz)found through the time–frequency analysis

Among these frequencies, $f_{\varOmega }$ is the predominant frequency, which comes from the rotating driving point, and its superharmonic components 2$f_{\varOmega }$ and $3f_{\varOmega }$ also take part in the vibration. Additionally, frequencies $f_{\mathrm{h}1 }$ and $f_{\mathrm{h}2 }$ are associated with the in-plane vibration of the slider whose frequency is 70Hz and splits into the two frequencies due to the rotation of the slider.

The main frequencies for the transverse vibration of the disc when the slider and the driving point are not rotating are calculated by solving the corresponding eigenvalues. The natural frequencies of the first nine modes are 850.86, 1492.55, 1516.76, 1814.90, 1823.88, 2758.02, 2774.19, 4360.49, and 4383.04 rad/s, which are 135.42, 237.55, 241.40, 288.85, 290.28, 441.53, 438.95, 693.99, and 697.58 in Hz, respectively. It is notable that any pairs of natural frequencies corresponding to modes of the same number of nodal diameters of this disc with a stationary slider are not at the same values as the natural frequencies of the corresponding modes of the symmetrical disc given at the beginning of Sect. 4.

Fig. 26

Horizontal response of the slider ($E=150$ Gpa, $N=385$ N, $\varOmega =15.1$ rad/s). a The time history of $\psi$. b Its time–frequency spectrum for $t= [50, 60]$ s

Fig. 27

Transient response of the disc ($E=150$ Gpa, $N=300$ N, $\varOmega =20$ rad/s). a The time history of the transverse displacement. b Its time–frequency spectrum for $t= [143, 153]$ s

Fig. 28

Horizontal response of the slider $(E=150\,\hbox {Gpa}, N=300\,\hbox {N}, \varOmega =20\,\hbox {rad}/\hbox {s})$. a The time history of $\psi$. b Its time–frequency spectrum for $t= [143, 153]$ s

Fig. 29

Transient responses of the disc ($E=100$ GPa, $N=200$ N, $\varOmega =11$ rad/s). a The time history of the transverse displacement. b Its time–frequency spectrum for $t= [465, 475]$ s

$f_{1}$ to $f_{6}$ in Fig. 25 and in Table 2 are close to but not the same as some natural frequencies of the static system (135.42, 237.55 and 288.85 Hz). This is due to the effect of the in-plane rotation of the slider.

Figure 25b indicates that, in addition to the main frequencies ($f_{\varOmega }, f_{\mathrm{h}1}, f_{\mathrm{h}2}$, and $f_{1}$ to $f_{6})$, new vibration frequencies emerge during the transient vibration of the system due to unstable horizontal vibration of the slider, which are shifted from the main frequencies ($f_{\varOmega }, f_{\mathrm{h}1}, f_{\mathrm{h}2}$, and $f_{1}$ to $f_{6})$. Figure 25c shows that when separation takes place at 54.5s, the frequency spectrum has a sudden change. Higher frequencies show up after separation. At the same time, the fuzzy frequencies (in Fig. 25b, c) in the midst of the main frequencies disappear in Fig. 25d, which can be explained by the horizontal responses of the slider shown in Fig. 26. Figure 26a is the time history of $\psi$ which is very complex as the switching between stick and slip motion relies on not only the difference between the static and kinetic friction coefficients but also the oscillating contact force. Figure 26b gives the frequency spectrum during t = [50, 60] s which shows that the obviously irregular shifting between the horizontal vibration frequency of the slider $f_{\mathrm{h} }$ and its superharmonics $({nf}_{\mathrm{h}}, n=1, 2, 3{{\ldots }})$ disappear after separation, and the horizontal stick–slip motion becomes periodic which can be also seen from the Poincare map shown in Fig. 14 in Sect. 4.2. When the transverse disc vibration becomes steady long after the first separation event, it possesses constant values of frequencies (including the fundamental frequency and higher frequencies) due to separation, as shown in Fig. 25d.

The second example is computed using the following parameter values: $E=150$ GPa, $N=300$ N, $\varOmega =20$ rad/s. Figure 27a illustrates the time history of the transverse displacement of the disc. Firstly, the vibration grows gradually, then increases sharply for a while before the growth rate drops, and finally becomes bounded due to separation which firstly occurs around 149.5 s. A time–frequency analysis is conducted within the time interval of $t = [143, 153]$ s, since this time interval is very special which covers different stages of the vibration (transient vibration, transition to separation and steady-state vibration after separation). Figure 27b shows that the vibration of the disc is mainly governed by its natural frequencies; meanwhile, a number of fuzzy frequencies (shown by the dense red lines between the main system frequencies) start to make contributions to unstable transient vibration. After the transition point to separation, higher disc frequencies arise. On the other hand, the fuzzy frequencies maintain their contributions to the vibration, and in contrast, they disappear in the first example, which can be explained by the in-plane time–frequency results of the slider shown in Fig. 28b. Figure 28b is obtained during the same time interval t = [143, 153] s, and the time history of $\psi$ is illustrated in Fig. 28a. From the time–frequency results, it can be seen, in Fig. 28b, that the in-plane stick–slip vibration of the slider in steady state is quasi-periodic.

The dynamic response of the third example is shown in Fig. 29. The parameter values used are: $E=100$ GPa, $N=200$  N, $\varOmega =11$ rad/s. In this case, there is no separation during the vibration which is illustrated in Fig. 21. Although the vibration magnitude of the disc, in Fig. 29a, is bounded due to the nonlinearity of the in-plane stick–slip vibration, how the limit cycle of the vibration evolves is different from those cases in which the transverse disc vibration is non-smooth because of repeated events of separation and reattachment. Consequently, the time–frequency response in this case does not show any high frequency arising above the maximum natural frequency (4383.04 rad/s) of the system with slider being stationary, during steady-state vibration, after the transient phase of vibration (marked by ${\Delta }t$ in Fig. 29a). The vibration of the disc in this case is quite erratic as its frequency spectrum shows several prominent incommensurate frequencies and many low-amplitude frequencies emerge, vanish, or shift with time.

In conclusion, the time–frequency analysis of all three examples reveals that the frequencies of the non-smooth self-excited friction-induced vibration problem vary with time in a complicated manner. The power spectrum of system frequencies is non-stationary, and other frequencies arise and shift between the main system frequencies. Higher frequencies can arise due to separation. It also shows the importance of considering separation from the point of view of evolution of the frequency with time. Moreover, the unstable in-plane stick–slip vibration of the slider which couples with the vertical vibration of the slider can make significant contributions to the frequencies of the disc’s transverse vibration.

5 Conclusions

In this paper, the dynamic behaviour of a disc modelled as a thin elastic annular plate excited by a rotating oscillator which has a vertical branch normal to the disc and a horizontal branch in the plane of the disc is studied. Because of the non-smooth nature of friction between the slider and the disc, the slider undergoes stick–slip vibration in the circumferential direction on the disc. The variable in-plane location of the slider leads to a varying contact force at the interface between the disc and the slider, which affects the transverse vibration of the disc and makes the in-plane stick–slip vibration and vertical vibration of the slider system coupled and complicated. During vibration, the slider can lose contact (separation) with the disc and then reattach to the disc again.

The equations of motion of this discrete–continuous system at three motion states (stick motion, slip motion, and separation) are derived. The conditions for staying in each state are established, and impact at the moment of the reattachment is formulated. Then, numerical study is carried out at various values of the key parameters. The following conclusions can be drawn:

• 1. Separation can happen during the unstable vibration of the system caused by friction. The time duration of separation is very short. Reattachment naturally occurs following separation.

• 2. The system become unstable and separation occurs in low speed range of the driving point, which is much smaller than the critical speed of the disc in the corresponding moving load problem.

• 3. When separation is considered, the disc’s transverse vibration becomes bounded within a smaller range; and the in-plane motion of the slider may change to a trajectory which is totally different from its trajectory before separation, and the stick phase disappears under certain parameter values. On the other hand, if contact is assumed to be maintained during vibration (in cases of ignoring separation), both the in-plane stick–slip vibration of the slider and transverse vibration of the disc can be very different from those cases of considering separation.

• 4. More interesting dynamic behaviour of the disc and the slider when separation is considered is revealed through a parametric analysis. The relationship between the stability of the system and the pre-load in-plane damping and in-plane stiffness is not monotonous. A pre-load appears destabilising within a certain range but stabilising within another range. Disc damping and vertical damping of the slider stabilise the friction-induced disc vibration, while the in-plane damping of the slider destabilises the vibration at some large pre-load values. Within the range of the stiffness values of the vertical spring of the slider considered in this paper, the stiffness stabilises the system when it is large enough. Larger in-plane stiffness makes the vibration grow faster and separation occurs earlier, but it becomes a stabilising factor when it reaches a large enough value. Additionally, separation may not happen when the disc is soft enough. Where separation occurs during disc vibration can be affected by the mass of the slider.

• 5. The variation of the frequencies of the system over time is illustrated through a time–frequency analysis. The frequency of the rotating speed, the natural frequencies of the disc, and the horizontal and vertical branches of the slider all make contributions to the frequencies of the whole system. Frequencies higher than the main frequencies of the disc arise due to separation. The in-plane stick–slip vibration results in complex evolution of the frequencies of the transverse disc vibration.

The most important conclusion of this paper is that separation should be taken into account in many friction-induced vibration problems.

Appendix

Fig. 30

Phase portrait of the relative horizontal motion of the slider when separation is ignored ($N=200$ N, $\varOmega =20$ rad/s)

Fig. 31

Phase portrait of the relative horizontal motion of the slider when separation is considered ($N=200$ N, $\varOmega =20$ rad/s)

Figures 30 and 31 show the phase portraits of the relative horizontal motion of the slider under the same operation conditions when separation is ignored and considered, respectively, which serve as supplements to the discussion on the results presented in Figs. 4 and 5.

Figure 30 shows that the horizontal motion of the slider lies on a regular stick–slip limit cycle, during the steady state, when separation is ignored, which is periodic vibration. However, the actual horizontal vibration, when separation is considered, is quasi-periodic, as the regular stick–slip limit cycle breaks out, and an intricate phase portrait can be observed in Fig. 31.