1 Introduction

New designs of mechanical structures are increasingly lighter and more flexible and exhibit geometric nonlinearities due to the presence of large displacements and rotations. A popular formulation for modelling geometrically nonlinear beams is the von Kármán finite element (FE) model, which assumes Euler–Bernoulli bending and approximates the Green–Lagrange strain measures by including only quadratic terms pertaining to the rotations. The von Kármán model is used extensively in the literature in modelling beams, plates and shells [1,2,3,4,5,6,7]. Many model reduction methods also consider the von Kármán formulation as the full-order basis for model reduction [2, 3, 8,9,10]. Despite the extensive use of this formulation, the model is predicated on approximate kinematics, which makes it unsuited for studying complex and highly nonlinear systems with large displacements. Examples include numerical simulations with vibration amplitudes greatly exceeding the beam or plate thickness (up to 5–10 times), or cases including rotary inertia or shear effects [1]. Reduced-order models that are based on this formulation therefore will suffer from the same inaccuracies of the full-order model and will not be able to adequately describe complex nonlinear dynamic phenomena of highly flexible physical structures.

More accurate displacement-based FE methods can be developed using geometrically exact beam theories in order to model large deformations and nonlinearities. Geometrically exact beam models were initially developed by Simo [11] and later by Cardona and Geradin [12], Ibrahimbegović [13], and Betsch and Steinmann [14]. The geometric exactness of these methods comes from keeping the strain measures consistent with the equilibrium equations of a deformed configuration with finite rotations. However, parametrisation of the rotations is not trivial in these formulations and can lead to discretisations, which do not preserve the property of invariance of strains under rigid body motion [15]. To overcome this, additional local interpolations of rotations are required in the finite element model [16]. This, however, adds to the complexity of the discretised equations with increased nonlinearity in the equations of motion and makes the formulations numerically less convenient.

Amongst beam formulations that aim to address the difficulty of parametrising the rotations is the intrinsic beam theory developed by Hodges [17], in which the displacement and rotation terms are not included in the equations. Although the parametrisation of rotations therefore is no longer required, the application of boundary conditions as displacement constraints cannot be imposed explicitly that introduces further challenges to the method [18]. Other beam formulations based on the quaternion parametrisation of rotations [19], or based on velocities and angular velocities [20], have also been developed. Although these methods aim to avoid the difficulties of using spatial rotations as unknowns, they miss the opportunity to capitalise on the more appropriate description of the beam kinematics afforded by the special Euclidean group.

Beam formulations based on the special Euclidean Lie group SE(3) exploited here circumvent all these problems by coupling the rotations and positions and by adopting a local frame approach [21]. The invariance of the strains under rigid body motion comes naturally from this formulation, as the local frame formulation allows the relative description of the nodal motions and velocities. Additionally, the local frame derivatives are at most quadratically nonlinear, which reduces the overall complexity of the numerical model. The global parametrisation of frames is avoided by the time-integration method, which yields an efficient integration scheme that is guaranteed to be singularity-free [22]. Moreover, shear locking is avoided thanks to a nonlinear interpolation formula based on the exponential map that couples the rotation and position fields and governs the nonlinear configuration space. The geometrically exact formulation leads to the recovery of the exact displacements with no approximations in the curvature of the solution for pure bending [21].

The presence of nonlinearities can have significant effects on the dynamics of a system. The dependence of vibration frequency on the oscillation amplitude is a characteristic example of such effects. Other phenomena such as energy exchange between modes, internal resonances, harmonic distortion, and quasi-periodic or chaotic oscillations can also be present [23, 24]. NNMs provide a framework for investigating these phenomena and are therefore an invaluable tool in the study of nonlinear systems. In this study, NNMs are exploited as a mean to compare the nonlinear dynamics resulting from a von Kármán beam model and the SE(3) model. Each of the beam formulations has been independently validated on various numerical test cases [25,26,27,28]. The aim of the present work is not to replicate those validation works, but instead to investigate the changes that occur in the dynamics due to the use of a geometrically exact Lie group model. The choice of taking the von Kármán formulation, as opposed to other more accurate formulations, is based on the popularity of the von Kármán model when dealing with discretised flexible structures using the finite element method [8] and reduction of nonlinear models [2, 29, 30]. This model has also been the subject of comparison work in other research efforts focusing on computing nonlinear modes of geometrically exact beams [31, 32]. The shortcoming of the von Kármán beam model in giving a correct and accurate description of large deformations is indicated against the results from the Lie group model.

The NNMs considered here are defined as not-necessarily synchronous periodic oscillations of the conservative system as proposed in [33, 34]. The NNMs of a 2D doubly clamped beam, a shallow arch, and a cantilever beam formulated on the SE framework are computed numerically using a combination of shooting and pseudo-arclength continuation directly applied to the full-order finite element model of the structures. However, owing to the nonlinearity of the Lie group, the usual periodicity condition used in the shooting algorithm has been changed to one based on the group’s logarithm map in order to calculate the difference in the beam states over a period of oscillation. A further adaptation is introduced to the continuation algorithm, where prediction increments are made with respect to the previously converged solution and are thus smaller in magnitude. As the group’s exponential map is used to map the increments to the group, this adaptation makes the mapping less nonlinear and therefore speeds up the continuation process. Alternative approaches for obtaining NNMs, including analytical approximations [35,36,37,38], are not considered in this work (see [39, 40] for a review).

This paper is structured as follows: Section 2 gives a brief account of the FE beam model and the underlying Lie group theory, Sect. 3 explains the shooting and pseudo-arclength methods used, which is finally followed by results presented in Sect. 4 and the conclusions in Sect. 5.

2 Lie group beam model

A brief overview of the finite element beam equations derived under the SE(3) framework is presented in this section, which is accompanied by a short review of some background theory given in Appendix A.

2.1 Beam kinematics

We consider a straight beam of length L with the value \(s \in [0,L]\) defined as the longitudinal coordinate along its reference line, as depicted in Fig. 1. The position of any point p on the reference beam at time \(t=0\) can be written in the inertial frame as [21]

$$\begin{aligned} {{\textbf {x}}}_p^0(s, u, v) = {{\textbf {x}}}^0(s) + {{\textbf {O}}}_0(s)\varvec{y}(u, v), \end{aligned}$$
(1)

where \({{\textbf {x}}}(s)\) is the position vector along the neutral axis, \({{\textbf {O}}}_0(s)=\left[ {{\textbf {i}}}_s \;\; {{\textbf {i}}}_t \;\; {{\textbf {i}}}_u\right] \) is a constant rotation matrix accounting for the beam’s reference orientation relative to the inertial frame, and \(\varvec{y}(u,v) = \left[ 0 \;\; u \;\; v\right] ^T\) contains the coordinates of the point along the cross section axes. We assume the cross sections do not deform, and therefore, the point coordinates along the cross section axes remain unchanged.

Deformation of the beam will impose a translation and rotation of the cross sections relative to the fixed inertial frame. The position of the point p in the deformed configuration at time t, written in the inertial frame, will therefore be written as:

$$\begin{aligned} {{\textbf {x}}}_p(s, u, v) = {{\textbf {x}}}(s) + {{\textbf {R}}}(s){{\textbf {O}}}_0\varvec{y}(u, v), \end{aligned}$$
(2)

where \({{\textbf {R}}}(s)\) is the rotation vector accounting for the rotation of the cross section, which brings the vector \({{\textbf {O}}}_0\varvec{y}(u, v)\) from the local frame onto the global inertial frame.

Fig. 1
figure 1

Description of beam kinematics [21]

Full size image

The coordinate transformation between the frames can be represented by a homogenous transformation matrix \({{\textbf {H}}}(s)\) pertaining to a rigid body motion, given by

$$\begin{aligned} {{\textbf {H}}}(s) = \begin{bmatrix} {{\textbf {R}}}(s) &{}\quad {{\textbf {x}}}(s) \\ \varvec{0}_{1\times 3} &{}\quad 1 \end{bmatrix}, \end{aligned}$$
(3)

from which the position of point p can be found by matrix multiplication as

$$\begin{aligned} {{\textbf {H}}}_p(s, u, v)= & {} \quad {{\textbf {H}}}(s) \begin{bmatrix} {{\textbf {I}}}_{3\times 3} &{}\quad {{\textbf {O}}}_0\varvec{y}(u, v,) \\ \varvec{0}_{1\times 3} &{}\quad 1 \end{bmatrix} \nonumber \\= & {} \begin{bmatrix} {{\textbf {R}}}(s) &{}\quad {{\textbf {x}}}_p(s, u, v) \\ \varvec{0}_{1\times 3} &{}\quad 1 \end{bmatrix}. \end{aligned}$$
(4)

The matrix \({{\textbf {H}}}(s)\) belongs to the 3-dimensional set termed the Special Euclidean Lie group SE(3). (The 3 rotation and 3 position elements give this group 6 degrees of freedom in total.) By the composition rule of the group, the product of two such matrices results in another matrix of the group. The rotation matrix \({{\textbf {R}}}(s)\) belongs to the Special Orthogonal Lie group SO(3). All geometrically exact beam formulations include rotation terms and therefore follow a \({\mathbb {R}}^3 \times {\textit{SO}(3)}\) approach in their formulations. Beam kinematics formulated in the SE(3) framework, however, treat the positions and rotations simultaneously as a homogenous frame matrix (3) [21]. A local frame approach can then be adopted by attaching a frame to each material point of the beam.

2.2 Derivatives

The deformation gradient and time derivative of the material frame on the neutral axis are elements of the Lie algebra \({\mathfrak {se}}(3)\), which is defined as the tangent space at the group identity. The deformation gradient is denoted as \(\widetilde{{{\textbf {f}}}}(s) \in {\mathfrak {se}}(3)\) and is defined as

$$\begin{aligned} \frac{\textrm{d}{{\textbf {H}}}(s)}{\textrm{d}s}={{\textbf {H}}}^\prime (s)={{\textbf {H}}}(s)\widetilde{{{\textbf {f}}}}(s), \end{aligned}$$
(5)

where the matrix \(\widetilde{{{\textbf {f}}}}(s)\) can also be written without the \(\widetilde{(\bullet )}\) operator in vector form as \({{\textbf {f}}}(s)\) (see appendix Eq. (A.8) for an explanation of the tilde operator). The deformation gradient \({{\textbf {f}}}(s)\) can be split into those of the reference \({{\textbf {f}}}^0\) and current \(\varvec{\epsilon }\) configurations, and classical notations of position \(\varvec{\gamma }\) and rotation \(\varvec{\kappa }\) deformations can be introduced as:

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}(s)&= \begin{bmatrix} {{\textbf {f}}}_U(s) \\ {{\textbf {f}}}_\varOmega (s) \end{bmatrix} ={{\textbf {f}}}^0(s) + \varvec{\epsilon }(s), \quad \text {with} \\ \varvec{\epsilon }(s)&= \begin{bmatrix} \varvec{\gamma }(s) \\ \varvec{\kappa }(s) \end{bmatrix}. \end{aligned} \end{aligned}$$
(6)

As per the local frame representation of derivatives, these quantities are invariant under rigid body transformations, thus maintaining the objectivity of the strain measures under the beam formulation. From the representation of the derivatives on SE(3) (see appendix Eq. (A.15)), the deformations in Eq. (6) can be written as:

$$\begin{aligned} \begin{aligned} \varvec{\gamma }(s)&= {{\textbf {R}}}^T(s) {{\textbf {x}}}^\prime (s) - {{\textbf {f}}}_U^0(s), \\ \varvec{\kappa }(s)&= {{\textbf {R}}}^T(s) {{\textbf {R}}}^\prime (s) - {{\textbf {f}}}_\varOmega ^0(s). \end{aligned} \end{aligned}$$
(7)

The deformation at any point p on the cross section can then be evaluated as:

$$\begin{aligned} \frac{\partial {{\textbf {H}}}_p(s,u,v)}{\partial s} = {{\textbf {H}}}_p(s,u,v) \widetilde{{{\textbf {f}}}}_p(s,u,v), \end{aligned}$$
(8)

where the deformation can again be split into the reference and current configuration as \({{\textbf {f}}}_p(s,u,v) = {{\textbf {f}}}^0_p(s,u,v) + \varvec{\epsilon }_p(s,u,v)\). We then have

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}_p(s,u,v)&= \begin{bmatrix} {{\textbf {f}}}_{pU}(s,u,v) \\ {{\textbf {f}}}_\varOmega (s) \end{bmatrix}, \\ \varvec{\epsilon }_p(s,u,v)&= \begin{bmatrix} \varvec{\gamma }_p(s,u,v) \\ \varvec{\kappa }(s) \end{bmatrix}. \end{aligned} \end{aligned}$$
(9)

Due to the assumption of the cross sections remaining undeformed, the rotation components of the strains are the same as those of the neutral axis. The position components can be evaluated as \({{\textbf {f}}}_{pU}(s,u,v) = {{\textbf {f}}}_U(s) - \widetilde{{{\textbf {O}}}}_0\widetilde{\varvec{y}}(u,v){{\textbf {f}}}_\varOmega (s)\).

The time derivative of the material frames on the neutral axis can be written using a Lie algebra element as:

$$\begin{aligned} \dot{{{\textbf {H}}}}(s) ={{\textbf {H}}}(s) \widetilde{{{\textbf {v}}}}(s), \end{aligned}$$
(10)

where the velocities \(\widetilde{{{\textbf {v}}}}(s) \in {\mathfrak {se}}(3)\) are also expressed in the local frame, and writing them in vector form we have \({{\textbf {v}}}(s) = \left[ {{\textbf {v}}}_U^T(s) \; {{\textbf {v}}}_\varOmega ^T(s)\right] ^T\). The velocities at any point p on the beam cross section can be evaluated as:

$$\begin{aligned} \dot{{{\textbf {H}}}}_p(s,u,v) ={{\textbf {H}}}_p(s,u,v) \widetilde{{{\textbf {v}}}}_p(s,u,v), \end{aligned}$$
(11)

where

$$\begin{aligned} \widetilde{{{\textbf {v}}}}_p(s,u,v) = \begin{bmatrix} \widetilde{{{\textbf {v}}}}_{pU}(s,u,v) \\ {{\textbf {v}}}_\varOmega (s) \end{bmatrix}, \end{aligned}$$
(12)

and similar to the strains we have \({{\textbf {v}}}_{pU}(s,u,v) = {{\textbf {v}}}_U(s) - \widetilde{{{\textbf {O}}}}_0\widetilde{\varvec{y}}(u,v){{\textbf {v}}}_\varOmega (s)\).

2.3 Dynamic equilibrium equations

The components of the Green Lagrange strain tensor and the second Piola–Kirchhoff stress tensor can be evaluated using the deformation gradients and beam stiffness parameters. Assuming linear elastic behaviour, the strain energy can be computed as:

$$\begin{aligned} {\mathcal {W}}_{int} = \frac{1}{2}\int \limits _{0}^{L}\varvec{\epsilon }^T(s){{\textbf {K}}}\varvec{\epsilon }(s) \, \textrm{d}s, \end{aligned}$$
(13)

where \({{\textbf {K}}}\) is the diagonal stiffness matrix as

$$\begin{aligned} \begin{aligned} {{\textbf {K}}}&= \begin{bmatrix} {{\textbf {K}}}_U &{}\quad \varvec{0}_{3\times 3} \\ \varvec{0}_{3\times 3} &{}\quad {{\textbf {K}}}_\varOmega \end{bmatrix}, \\ {{\textbf {K}}}_U&= {{\textbf {O}}}_0 \begin{bmatrix} EA &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad GA_t &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad GA_u \end{bmatrix} {{\textbf {O}}}_0^T, \\ {{\textbf {K}}}_\varOmega&= {{\textbf {O}}}_0 \begin{bmatrix} GJ &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad EI_t &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad EI_u \end{bmatrix} {{\textbf {O}}}_0^T. \end{aligned} \end{aligned}$$
(14)

The kinetic energy can also be written using the velocities as

$$\begin{aligned} {\mathcal {K}} =\frac{1}{2}\int _{0}^{L}{{\textbf {v}}}^T(s){{\textbf {M}}}{{\textbf {v}}}(s)\,\textrm{d}s, \end{aligned}$$
(15)

where the mass matrix is calculated as

$$\begin{aligned} {{\textbf {M}}} = \begin{bmatrix} \frac{m}{L}{{\textbf {I}}}_{3\times 3} &{}\quad -{{\textbf {O}}}_0{{\textbf {J}}}_I{{\textbf {O}}}_0^T \\ -{{\textbf {O}}}_0{{\textbf {J}}}_I^T{{\textbf {O}}}_0^T &{}\quad {{\textbf {O}}}_0{{\textbf {J}}}{{\textbf {O}}}_0^T \end{bmatrix}, \end{aligned}$$
(16)

where m is the element mass and \({{\textbf {J}}}_I\) and \({{\textbf {J}}}\) are the first and second moments of inertia of the cross sections computed in the local frame. The energy equations only exhibit quadratic nonlinearity in strains and velocities. This is a convenient feature of the Lie group formulation, which leads to simple equations as the nonlinearity is embedded in the structure of the configuration space.

To obtain the dynamic equilibrium equations, the variations of the energies are computed and used in Hamilton’s principle given by

$$\begin{aligned} \int _{\tau _0}^{\tau _1} \delta ({\mathcal {K}}) - \delta ({\mathcal {W}}_{int}) \; \textrm{d}\tau = 0. \end{aligned}$$
(17)

The variations of the strain and kinetic energy are given by:

$$\begin{aligned} \begin{aligned}&\delta ({\mathcal {W}}_{int})=\int _{0}^{L}\delta (\varvec{\epsilon })^T{{\textbf {K}}}\varvec{\epsilon }\;\textrm{d}s, \\&\delta ({\mathcal {K}})=\int _{0}^{L}\delta ({{\textbf {v}}})^T{{\textbf {M}}}{{\textbf {v}}}\;\textrm{d}s. \end{aligned} \end{aligned}$$
(18)

Due to the Lie group structure and the non-commutativity of the derivatives on the group (see appendix Eq. (A.7)), the variations of the deformations and velocities are related to the state variables which are SE(3) elements by the following equations

$$\begin{aligned} \begin{aligned} \delta (\varvec{\epsilon })&= \delta ({{\textbf {f}}})= \frac{\text {d}}{{\text {d}}s}(\delta {{\textbf {h}}})+\hat{{{\textbf {f}}}}\delta {{\textbf {h}}}, \\ \delta ({{\textbf {v}}})&= \frac{\text {d}}{{\text {d}}\tau }(\delta {{\textbf {h}}})+\hat{{{\textbf {v}}}}\delta {{\textbf {h}}}, \end{aligned} \end{aligned}$$
(19)

where \(\widetilde{\delta {{\textbf {h}}}}={{\textbf {H}}}^{-1}\delta {{\textbf {H}}}\) is the Lie algebra element for virtual motions. The \(\hat{(\bullet )}\) is a linear operator, which maps a vector in \({\mathbb {R}}^k\) to a \(k \times k\) matrix (see appendix Eq. (A.11)). Inserting the variations (19) into (18) and integrating by parts yields

$$\begin{aligned} \begin{aligned} \delta ({\mathcal {W}}_{\text {int}})&= \left[ \delta {{\textbf {h}}}^T{{\textbf {K}}}\varvec{\epsilon }\right] _0^L \\&\quad - \int _{0}^{L}\delta {{\textbf {h}}}^T\left( {{\textbf {K}}}\frac{d}{ds}(\varvec{\epsilon })-\hat{{{\textbf {f}}}}^T{{\textbf {K}}}\varvec{\epsilon }\right) \; {\text {d}}s, \\ \int \limits _{\tau _0}^{\tau _1}\delta ({\mathcal {K}}) \; {\text {d}}\tau&= \left[ \int \limits _{0}^{L}\delta {{\textbf {h}}}^T{{\textbf {Mv}}} \; {\text {d}}s \right] _{\tau _0}^{\tau _1} \\&\quad - \int \limits _{\tau _0}^{\tau _1}\int \limits _{0}^{L} \delta {{\textbf {h}}}^T ({{\textbf {M}}}\dot{{{\textbf {v}}}} - \hat{{{\textbf {v}}}}^T{{\textbf {Mv}}}) \; {\text {d}}s \; {\text {d}}\tau . \end{aligned} \end{aligned}$$
(20)

Combining the expressions in equations (20) inside the Hamilton Eq. (17) gives the weak form of the dynamic equilibrium equations as:

$$\begin{aligned}{} & {} \left[ \delta {{\textbf {h}}}^T{{\textbf {K}}}\varvec{\epsilon }\right] _0^L - \int _{0}^{L}\delta {{\textbf {h}}}^T ({{\textbf {M}}}\dot{{{\textbf {v}}}} - \hat{{{\textbf {v}}}}^T{{\textbf {Mv}}} \nonumber \\{} & {} \quad + {{\textbf {K}}}\frac{{\text {d}}}{{\text {d}}s}(\varvec{\epsilon }) - \hat{{{\textbf {f}}}}^T{{\textbf {K}}}\varvec{\epsilon }) \; {\text {d}}s = 0, \end{aligned}$$
(21)

from which the strong form of the dynamic equation is given by the following second-order nonlinear PDE for the unknowns \(\varvec{\epsilon }\) and \({{\textbf {v}}}\)

$$\begin{aligned} {{\textbf {M}}}\dot{{{\textbf {v}}}} - \hat{{{\textbf {v}}}}^T{{\textbf {M}}}{{\textbf {v}}} + {{\textbf {K}}}\frac{{\text {d}}}{{\text {d}}s}(\varvec{\epsilon }) - \hat{{{\textbf {f}}}}^T {{\textbf {K}}}\varvec{\epsilon } = 0. \end{aligned}$$
(22)

It is noted that this equation is intrinsic, as it was obtained without introducing any frame parametrisation and is solved for velocities \({{\textbf {v}}}\) and deformations \(\varvec{\epsilon }\) only. A further compatibility equation between the second spatial and time derivatives due to the Lie group structure should also be solved (see appendix Eq. (A.7)), given by

$$\begin{aligned} \frac{{\text {d}}}{{\text {d}}s}({{\textbf {v}}}) - \dot{\varvec{\epsilon }} = \hat{{{\textbf {v}}}}\varvec{\epsilon } \Longleftrightarrow \frac{{\text {d}}}{{\text {d}}s}({{\textbf {v}}}) - \dot{\varvec{\epsilon }} = -\hat{\varvec{\epsilon }}{{\textbf {v}}}. \end{aligned}$$
(23)

Equations (22) and (23) do not depend on the position or the orientation of the beam and are solved together along with the boundary conditions

$$\begin{aligned} \delta {{\textbf {h}}}^T(L){{\textbf {K}}}(L)\varvec{\epsilon }(L) - \delta {{\textbf {h}}}^T(0){{\textbf {K}}}(0)\varvec{\epsilon }(0) = 0. \end{aligned}$$
(24)

The position and orientation of the beam are recovered afterwards by solving the kinematic equations Eq. (5) and (10).

2.4 Finite element discretisation

A finite element discretisation is introduced in order to solve the dynamic equilibrium Eq. (22). The discretisation along the neutral axis of the beam is achieved by means of an interpolation formula based on the SE(3) exponential map as follows. Let \({{\textbf {H}}}_A\) and \({{\textbf {H}}}_B\) denote the material frames on two end nodes A and B of a single element of the FE mesh with length l. We calculate the frame at any point x along the element by the following interpolation

$$\begin{aligned} {{\textbf {H}}}(x) = {{\textbf {H}}}_A \exp _{{\text {SE}}(3)} \left( \frac{x}{l} {{\textbf {d}}}\right) , \end{aligned}$$
(25)

where \(x \in [0, l]\), and \({{\textbf {d}}} = \left[ {{\textbf {d}}}_U^T \; {{\textbf {d}}}_\varOmega ^T \right] ^T\) is the relative configuration vector given by

$$\begin{aligned} {{\textbf {d}}} = \log _{{\text {SE}}(3)}({{\textbf {H}}}_A^{-1}{{\textbf {H}}}_{{{\textbf {B}}}}). \end{aligned}$$
(26)

By the above definition, \({{\textbf {d}}}\) is a Lie algebra element \(\in {\mathfrak {se}}(3)\) and thus belongs to a linear space. The exponential map acts as a local parametrisation which maps the linear space to the nonlinear space of the nodal frames (see appendix Eq. (A.17)). This interpolation satisfies the frame invariance requirement, as for any rigid body motion defined by applying the same group composition to \({{\textbf {H}}}_A\) and \({{\textbf {H}}}_B\), \({{\textbf {d}}}\) remains unchanged. Furthermore, the nonlinear coupling between the positions and rotations, which is retained in the discretisation, enables a geometrically exact representation of the beam curvature in pure bending with just a single element [21].

By the discretisation, a finite set of local nodal frames \(\varvec{q}_k(t) \in {\textit{SE}}(3)\) and their velocities \(\varvec{v}_k(t) \in {\mathbb {R}}^6\) are obtained, which together are termed the configuration of the beam. A spatial derivative of this configuration interpolation gives the discretised strains and velocities from which the discretised dynamic equilibrium equations can be formulated.

2.5 Time integration

The discretised dynamic equilibrium equations are solved using a Lie group version of the generalised-\(\alpha \) scheme, which preserves the Lie group structure of the problem [41]. Given the configuration state of the beam with the frame \(\varvec{q}\) and the velocity \(\varvec{v}\), the acceleration \(\dot{\varvec{v}}\), and the inertial and internal forces respectively, by \({{\textbf {g}}}_{ine}\) and \({{\textbf {g}}}_{int}\), the time integration relies on the discretised equations involving the exponential map as

$$\begin{aligned} \begin{aligned}&\varvec{q}_{n+1} = \varvec{q}_n \exp (\widetilde{{{\textbf {x}}}}_{n+1}), \\&{{\textbf {g}}}_{ine}(\varvec{v}_{n+1}, \dot{\varvec{v}}_{n+1}) + {{\textbf {g}}}_{int}(\varvec{q}_{n+1}) = {{\textbf {0}}}, \end{aligned} \end{aligned}$$
(27)

and the time-integration formulae

$$\begin{aligned} \begin{aligned}&{{\textbf {x}}}_{n+1} = h\varvec{v}_n + (0.5-\beta )h^2\varvec{a}_n + \beta h^2\varvec{a}_{n+1}, \\&\varvec{v}_{n+1} = \varvec{v}_n + (1-\gamma )h\varvec{a}_n + \gamma h \varvec{a}_{n+1}, \\&(1-\alpha _m)\varvec{a}_{n+1} + \alpha _m\varvec{a}_n = (1-\alpha _f)\dot{\varvec{v}}_{n+1} + \alpha _f\dot{\varvec{v}}_n, \end{aligned} \end{aligned}$$
(28)

where the usual numerical parameters of the generalised-\(\alpha \) scheme are used. These equations are solved for the unknown nodal frames using a Newton iterative procedure, which requires the linearisation of the equations. This is done under the Lie group framework, which means the algorithm involves operations on tangent vectors in the Lie algebra and derivatives of the exponential map. Further details about the time-integration scheme can be found in [41].

3 Computation of periodic solutions

3.1 Pseudo-arclength continuation with shooting

Families of periodic solutions along an NNM branch are found using pseudo-arclength continuation. In this work, we adopt the algorithm proposed originally by Keller [42], with some modifications on the correction procedure as introduced by Peeters et al. [34]. Let

$$\begin{aligned} \phi (\varvec{X}(0), T), \; \phi : {\mathbb {R}}^{2N} \times {\mathbb {R}} \rightarrow {\mathbb {R}}^{2N}, \end{aligned}$$
(29)

denote the result of the time integration of the equation of motion, over a time interval of length T, starting from the initial condition vector \(\varvec{X}(0)\). A periodic solution is one that satisfies the periodicity condition given by

$$\begin{aligned} \varvec{\psi }(\varvec{X}(0), T) = \phi (\varvec{X}(0), T) - \varvec{X}(0) = \varvec{0}. \end{aligned}$$
(30)

This periodic solution is found using a shooting method, which is an iterative scheme for finding the roots of a smooth boundary value problem using a sequence of initial value problems [43]. Finding the roots of the boundary value problem reduces to finding the set of initial values, for which the boundary conditions are satisfied under time integration of the system dynamic equations.

The periodicity condition does not have a unique solution. Indeed, as the system is autonomous, any point on the periodic orbit can be used as an initial condition. An additional equation termed the phase condition must be added to restrict the number of solutions to the shooting problem. Various choices for the phase condition exist, such as the Poincaré [44] or integral phase conditions [45]. In this work, the initial velocities across all system degrees of freedom are set to zero as in [34]. The resulting phase condition equation is therefore given by:

$$\begin{aligned} g(\varvec{X}(0)) = {{\textbf {B}}}\varvec{X}(0) = \varvec{0}, \end{aligned}$$
(31)

where \({{\textbf {B}}}\) is a \(N\times 2N\) sparse Boolean matrix with ones corresponding to the velocities.

Starting from a converged periodic solution \(\Big (\varvec{X}^\star _j(0), T^\star _j\Big )\), a prediction for the next point on the NNM branch is made along the tangent vector at the current solution, \(\varvec{P}_j = \left[ \varvec{u}_j^T \; \lambda _j\right] ^T\), which is found from solving the overdetermined linear system

(32)

where the subscript j indicates the continuation index. \(\varvec{P}_{j-1}\) is the tangent at the previous continuation step; for the first continuation point where no previous tangent vector is available, this is replaced by \(\left[ \varvec{0}_{2N} \;\; 1\right] \). It is noted that \({{\textbf {B}}}\) is the derivative of the phase condition (31) with respect to \(\varvec{X}(0)\). The tangent vector found from solving (32) is then normalised to unit length. The prediction can therefore be written as:

$$\begin{aligned} \begin{bmatrix} \varvec{X}^0_{j+1}(0) \\ T^0_{j+1} \end{bmatrix} = \begin{bmatrix} \varvec{X}^\star _j(0) \\ T^\star _j \end{bmatrix} + z_j \begin{bmatrix} \varvec{u}_j \\ \lambda _j \end{bmatrix}, \end{aligned}$$
(33)

where the superscript 0 indicates that this is the first prediction point, and \(z_j\) is the continuation step size. The prediction point is generally not a periodic solution of the system. Corrections are therefore required to the prediction, which are found iteratively using a Newton–Raphson scheme. The corrections are forced to remain orthogonal to the tangent vector, thereby ensuring the adherence of the solution to turns in the NNM branch [34]. The corrections are found by solving the following linear system

$$\begin{aligned}{} & {} \begin{bmatrix} \frac{\partial \varvec{\psi }}{\partial \varvec{X}^k_{j+1}(0)} &{}\quad \frac{\partial \varvec{\psi }}{\partial T^k_{j+1}} \\ {{\textbf {B}}} &{}\quad 0 \\ \varvec{u}_j^T &{}\quad \lambda _j \end{bmatrix} \begin{bmatrix} \varDelta \varvec{X}^k_{j+1}(0) \\ \varDelta T^k_{j+1} \end{bmatrix} \nonumber \\{} & {} \quad = - \begin{bmatrix} \varvec{\psi }(\varvec{X}^k_{j+1}(0), T^k_{j+1}) \\ h(\varvec{X}^k_{j+1}(0)) \\ \varvec{0} \end{bmatrix}. \end{aligned}$$
(34)

where the superscript is now k and indicates the correction iteration index. The periodic solution is updated iteratively after the corrections are found by

$$\begin{aligned} \begin{aligned} \varvec{X}^{k+1}_{j+1}(0)&= \varvec{X}^k_{j+1}(0) + \varDelta \varvec{X}^k_{j+1}(0), \\ T^{k+1}_{j+1}&= T^k_{j+1} + \varDelta T^k_{j+1}. \end{aligned} \end{aligned}$$
(35)

This continues until desired convergence is met and a new periodic solution is found along the continuation branch as \(\left( \varvec{X}^\star _{j+1}(0), \; T^\star _{j+1}\right) \).

As seen in the Newton–Raphson scheme, derivatives of the periodicity equation are required with respect to the initial conditions at each iteration step. This can be evaluated using the Monodromy matrix

$$\begin{aligned} M^\phi = \frac{\partial \phi (\varvec{X}(0), T)}{\partial \varvec{X}(0)}, \end{aligned}$$
(36)

which gives the variation in the solution of the system after time T with respect to the initial conditions [40]. This quantity is computed simultaneously with the time integration of the equation of motion of the mechanical system, as a differentiation of the time-integration method itself [46]. The underlying Lie group framework leads to the usage of the exponential and its derivative in the sensitivity equations.

As mentioned, a converged starting solution needs to exist to begin the continuation process. In the calculation of NNMs of mechanical systems, this usually comes from the solution to the shooting problem, starting with an initial guess corresponding to a particular linear normal mode of the system [40]. The modal amplitude is scaled to ensure a linear-like response at very low energy. The corrections to this starting point are made to be orthogonal to the linear mode to ensure the iterative process does not converge to the trivial zero solution.

It is noted that in Eq. (32), following the methodology proposed by Keller [42], the tangent is found by making it parallel to the normalised tangent from the previous continuation step. The last row of Eq. (32) can be written using the vector dot product and by taking \(\theta _j\) to be the angle between tangent vectors \(\varvec{P}_{j-1}\) and \(\varvec{P}_{j}\) as

$$\begin{aligned} \Vert \varvec{P}_{j-1} \Vert \Vert \varvec{P}_{j} \Vert \cos (\theta _j) = 1. \end{aligned}$$
(37)

Noting that \(\Vert \varvec{P}_{j-1} \Vert = 1\) as it has already been normalised, Eq. (37) implies the angle between consecutive tangent vectors cannot exceed \(\frac{\pi }{2}\) since the cosine must remain positive. This removes the necessity for computing the continuation step sign for following the NNM branch.

3.2 Adaptation to Lie group formulation

Some modifications are required to the pseudo-arclength method for calculating the NNMs of a system whose dynamic equations are obtained under the Lie group formulation outlined in Sect. 2.

First, the periodicity equation (30) is modified to account for the beam position belonging to the nonlinear space of the SE(3) group. \(\varvec{X}(0)\) is given by its constituent parts of initial state increments and velocities for the discretised beam as

$$\begin{aligned} \varvec{X}_{2N\times 1}(0) = \left[ \bar{\varvec{q}}^T_{N\times 1}(0) \;\; \varvec{v}^T_{N\times 1}(0)\right] ^T, \end{aligned}$$
(38)

where \(\bar{\varvec{q}}(0)\) indicates the increment required to map the reference beam configuration \({{\textbf {H}}}_0(s)\), to the deformed shape of the beam initial condition, given by the frame \(\varvec{q}(0)\) as

$$\begin{aligned} \varvec{q}(0) = {{\textbf {H}}}_0(s) \exp _{{\text {SE}}(3)}(\bar{\varvec{q}}(0)). \end{aligned}$$
(39)

The periodicity equation (30) is also modified and expressed as the following zero function:

$$\begin{aligned} \varvec{\psi }(\varvec{X}(0), T) = \begin{bmatrix} \log _{{\text {SE}}(3)}(\varvec{q}^{-1}(0)\varvec{q}(T)) \\ \varvec{v}(T) - \varvec{v}(0) \end{bmatrix} = \varvec{0}, \end{aligned}$$
(40)

where \(\varvec{q}\) and \(\varvec{v}\) are the vector of frame positions and velocities along the discretised beam. Due to the Lie group framework, the logarithm map is required to find the difference between the initial and final states in Eq. (40). This is not the case with the velocities that can be readily subtracted.

The second remark is concerned with the corrections made in the continuation process. As shown in Eq. (38), the vector \(\varvec{X}(0)\) includes the nodal increments mapping the reference beam configuration to the desired deformed configuration, and the nodal velocities. The increments belong to the linear space of the Lie algebra of the SE(3) group. As such, corrections can be added linearly to the increments during the continuation process, which is why the orthogonality condition used in Eq. (34) is valid. In contrast, Keller [42] proposes a different condition, which ensures the next continuation solution lies on the hyperplane orthogonal to the tangent vector, and at a distance away from the previous converged solution equal to the continuation step. This condition, which is effectively equivalent to the orthogonality condition in Eq. (34), can be written as:

$$\begin{aligned} \varvec{u}_j^T(\varvec{X}^{k}_{j+1}(0) - \varvec{X}_{j}(0)) + \lambda _j(T^{k}_{j+1} - T_{j}) = z_j. \end{aligned}$$
(41)

Keller’s method therefore requires the calculation of the difference between initial condition vectors \(\varvec{X}(0)\). However, owing to the nonlinear embedding of the Lie group manifold, Eq. (41) cannot be used in its current form. The elements of \(\varvec{X}(0)\) corresponding to the increments (see Eq. (38)) cannot be subtracted under a Euclidean vector operation. Instead, Eq. (41) will need to be adapted to include the exponential map to find the frame positions from the increments and the logarithm map to find the relative difference between the frames. This would therefore lead to a more complicated correction algorithm and is therefore not employed in this work.

The final remark concerns the adaptation of the continuation implementation to take full advantage of the Lie group framework. After a converged periodic solution is found at step j, the deformed beam configuration \(\varvec{q}_j(0)\) containing the beam initial position and orientation is stored. The initial condition vector \(\varvec{X}^{j+1}(0)\) for the next continuation step then stores the increment with respect to \(\varvec{q}_j(0)\), instead of the increment with respect to the undeformed beam configuration. Denoting this increment by \(\bar{\varvec{q}}_j(0)\), \(\varvec{q}_{j+1}(0)\) can then be found using the exponential map as

$$\begin{aligned} \varvec{q}_{j+1}(0) = \varvec{q}_{j}(0) \exp _{{\text {SE}}(3)}(\bar{\varvec{q}}_j(0)). \end{aligned}$$
(42)

The initial reference beam configuration remains unchanged, and the absolute deformed state in \(\varvec{q}_{j+1}(0)\) is still measured with respect to the reference configuration, maintaining the geometric nonlinearity of the system that arises from large deformations. However, as the state of a converged continuation solution is used as the basis of the increment vector for the next prediction point, the increment vector will therefore be smaller in magnitude. As the increment is used in the exponential map to find the new beam state in Eq. (42), the smaller magnitude of this vector results in reduced nonlinearity from the exponential map, which dramatically reduces the number of iterations required in the continuation correction process.

4 Comparison of SE & von Kármán beams on 2D cases

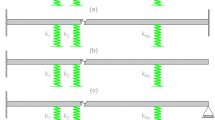
Three 2D test cases were chosen to compare NNMs found using the SE FE model and those from the von Kármán model. These are a straight clamped–clamped beam, a shallow arch, and a cantilever beam. In all cases, the beam is discretised with 30 elements, and its geometric and material properties are [47]: \(E=210 \, \textrm{GPa}\), \(\rho = 7850 \, \textrm{kg}/\textrm{m}^3\), \(L = 1 \, \textrm{m}\), \(A = 10^{-4} \, \textrm{m}^2\). As the cases are 2D, the Lie group formulation is made under the SE(2) framework.

4.1 Straight clamped–clamped beam: NNM1

The frequency-energy plot (FEP) for the first NNM of the clamped–clamped beam is shown in Fig. 2a, where the effects of nonlinearity can be observed in the increase of frequency with energy. The figure shows the occurrence of a thin loop, termed an internal resonance tongue, comprising of periodic solutions that indicate a 5:1 interaction between NNM1 and NNM3. The SE(2) and the von Kármán model agree well on this example, as the beam is not experiencing large deformations, and therefore, the von Kármán model can adequately predict the system dynamics. Figure 2b shows the maximum absolute in-plane displacement of the beam mid-point normalised with respect to the beam thickness, over the range of frequencies observed in the FEP. The maximum is taken as the largest displacement during the full period of the shooting solution. The backbone and tongue are observed, and again good agreement is noted between the models which continues through to larger-amplitude displacements.

Fig. 2
figure 2

First NNM of clamped–clamped beam. a Frequency–energy plot. b Max normalised amplitude at \(x/L = 0.5\). Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). (Color figure online)

Full size image

4.2 Straight clamped–clamped beam: NNM2

The frequency–energy plot corresponding to the second NNM is seen in Fig. 3a. Two resonance tongues appear on the solution curve, the first starting at approximately 160 Hz and corresponding to a 3:1 interaction with NNM4, and the second starting at approximately 207 Hz and corresponding to a 5:1 interaction with NNM6. Additional smaller secondary branches can be seen on the higher tongue, namely at approx. 221 Hz for the von Kármán model and at approx. 233 Hz for the SE(2) model. These correspond to higher-order harmonic interactions with NNM13 at a 17:1 ratio for both models. The backbones of NNM13 are included in Fig. 3a in grey for both models, where the frequency has been divided by the harmonic ratio of 17. It is seen that the backbones cross the curve near the regions where the secondary tongues are located. The linear natural frequencies for mode 13 for the von Kármán and the SE(2) model are 3672 Hz and 3928 Hz, respectively. This difference in the frequencies of the higher modes leads to the separation of the backbone curves and thus to the difference in the frequency at which the 17:1 interactions on the FEP occur. The differences in the higher modes could therefore have a significant effect on the location and shape of the interaction tongues. The difference between the NNMs can also be observed in the amplitude plots in Fig. 3b, which shows the maximum absolute in-plane displacement at the \(x/L = 0.3\) point along the beam, normalised with respect to the beam thickness.

Fig. 3
figure 3

Second NNM of clamped–clamped beam. a Frequency–energy plot. b Max normalised amplitude at \(x/L = 0.3\). Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). Dotted grey lines indicate NNM13 for both models with frequency divided by 17. Time history of displacement of point (a) green diamond depicted in Fig. 4. (Color figure online)

Full size image

The time evolution of the vertical displacement at the \(x/L=0.3\) point for the periodic solution (a) indicated in Fig. 3a can be seen in Fig. 4a. The 5:1 frequency ratio can clearly be seen, and a difference is observed between the solutions from the two models. This is also highlighted in Fig. 4b which shows the solutions in phase space. The difference in the solutions is due to a \(\pi /2\) phase shift in the 5th harmonic of the responses from the two models. It is noted that a direct comparison of solutions from points selected on the frequency-energy plot is extremely challenging, as the graph is a 2D projection of a high-dimensional state space. Selected points are here chosen based on their qualitative similarity (for instance, turning points on the FEP), bearing in mind that solutions may not be strictly identical.

Fig. 4
figure 4

Point a Green diamond in Fig. 3a, normalised vertical amplitude at \(x/L=0.3\) versus (a) time and (b) in phase space. Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). A 5:1 interaction between modes 2 and 6 is observed, and a \(\pi /2\) phase difference exists between the 5th harmonics of the two solutions. (Color figure online)

Full size image

4.3 Shallow arch: NNM1

A shallow arch is created by curving the doubly clamped beam such that the mid-point is displaced vertically by \(10 \textrm{mm}\), thus creating a curvature of radius \(R=12.5\,\textrm{m}\). The material properties of the beam are unchanged. The effects of curvature are manifested as the existence of both vertical and lateral displacements in the linear mode shapes of the model [47].

The FEP of the first NNM is shown in Fig. 5a. A softening–hardening behaviour is observed, which is characteristic of structures with initial curved geometries, and an internal resonance tongue is seen within the softening region. The tongue indicates a 4:1 resonance between NNM1 and NNM3. This is in contrast to the 5:1 resonance seen between these modes for the first NNM of the straight beam, which is due to the asymmetry of initial curvature promoting the occurrence of even interaction ratios [47]. The normalised absolute maximum vertical displacement of the beam mid-point is depicted in Fig. 5b. Despite displacement amplitudes larger than twice the beam thickness, the von Kármán model is able to make a correct prediction of the periodic solutions, due to the limited axial displacement of the doubly clamped configuration and the subsequent smaller coupling between the axial and transverse modes.

Fig. 5
figure 5

First NNM of shallow arch. a Frequency–energy plot. b Max normalised amplitude at x/L = 0.5. Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). Time history of displacement of point (a) green diamond depicted in Fig. 6. (Color figure online)

Full size image

The time history of the vertical displacement of the arch mid-point from the periodic solution at point (a) from Fig. 5a is presented in Fig. 6, which shows the 4:1 frequency ratio between the harmonics. Similar to the clamped–clamped beam, a \(\pi /2\) phase shift exists between the 4th harmonic of the responses, causing a difference in the time history of the two models.

Fig. 6
figure 6

Point a Green diamond in Fig. 5a, normalised vertical amplitude at \(x/L=0.5\). Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). A 4:1 interaction between modes 1 and 3 is observed, and a \(\pi /2\) phase difference exists between the 4th harmonics of the two solutions. (Color figure online)

Full size image

4.4 Shallow arch: NNM2

The FEP for the second NNM is presented in Fig. 7. Increasingly complex dynamics can be seen, with multiple interactions between various modes of the system. The main tongue spans a large frequency range between 160 and 180 Hz and corresponds to a 3:1 interaction between NNM2 and NNM4. Higher-order interactions are seen as secondary tongues which branch away from the main curve. The secondary tongue between 168–170 Hz (terminating at point (a) on the FEP) is captured by both solvers and indicates the presence of NNM7 at an 8:1 ratio with NNM2, along with static contributions from NNMs 1 and 3. Similar static contributions from additional modes were also reported by Sombroek et al. [47] for the arch. Figure 8 shows the time history of the periodic solution at point (a) depicting the normalised vertical displacement at the beam point \(x/L=0.36\). It is seen that for this point the models predict the same periodic solution corresponding to the same point on the FEP. The von Kármán and SE(2) solutions start to differ at higher-frequency ranges above this point. A smaller secondary tongue which emanates at approx. 172 Hz on the SE(2) curve indicates higher-order dynamic interaction through the 24th harmonic which is not captured by the von Kármán model. An additional interaction occurring at approx. 180 Hz on the main tongue is with NNM9 through the 12th harmonic and is found only by the von Kármán model. As seen previously with the doubly clamped beam, the differences in the higher modes between the models can lead to high-order interactions appearing at different frequencies, which is why these interactions are not captured by both models at the same locations on the FEP.

The periodic solution at point (b) in Fig. 7 is presented in Fig. 9, which shows the time series of the vertical displacement at the \(x/L=0.36\) point and its frequency spectrum, respectively. The 3:1 interaction between NNM2 and NNM4 is observed, where some static contribution is also present from NNM 1. There is good agreement between the time histories for both models, which is to be expected as higher-order dynamics are not manifested on the periodic solution at point (b).

Fig. 7
figure 7

FEP of second NNM of shallow arch, comparison between von Kármán (black solid line) and SE(2) (orange dashed line). Time history of displacement of points a Green diamond and b Blue diamond depicted in Figs. 8 and 9, respectively. (Color figure online)

Full size image
Fig. 8
figure 8

Point a Green diamond in Fig. 7, normalised vertical amplitude at \(x/L=0.36\). NNM7 present at 8:1 with NNM2. Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). (Color figure online)

Full size image
Fig. 9
figure 9

Point b Blue diamond in Fig. 7, normalised vertical amplitude at \(x/L=0.36\). a time history and b frequency content. Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). (Color figure online)

Full size image

4.5 Straight cantilever beam: NNM1

As a final test case, the straight beam was made free on one end to create a straight cantilever beam. The material properties of the beam remain unchanged.

The FEP of the first NNM is shown in Fig. 10. It is seen that the responses from the beam models are characteristically different, with the SE(2) model showing hardening behaviour in contrast to the softening behaviour from the von Kármán model. The hardening effect for the SE(2) model is in agreement with results obtained using an intrinsic beam model by Palacios [48] and a geometrically exact model by Debeurre et al. [31]. This supports the conclusion that the softening behaviour observed from the von Kármán model is incorrect. This softening behaviour is not observed if the von Kármán model is solved with full integration, as the effect of full integration is seen in an overall stiffening of the structure. This serves as strong motivation for not using the von Kármán model for modelling large deformations, as full integration can lead to shear locking [49], and reduced integration, as observed here, can lead to incorrect results.

The SE(2) model is able to trace the backbone of NNM1 up to larger energy levels, compared to the lower levels found by the von Kármán model. The highest energy point on the backbone is indicated by a green marker on the FEP for both models. The deformed shape of the beam corresponding to this point is given in Fig. 11. It is clearly seen that the SE(2) model is able to capture periodic responses with significantly larger displacements and rotations compared to the von Kármán model. Despite significant efforts, the continuation algorithm was not able to trace the von Kármán curve beyond the point already found in Fig. 10. At higher energies, solutions on the SE(2) backbone start showing contributions from NNM8, which is the first axial mode of the beam, due to the large deformations leading to axial motion. The frequency content of the solutions also shows vibrations at the third harmonic of the fundamental frequency of NNM1. As the contribution of NNM8 grows along the backbone, higher-order interaction tongues begin to appear. These correspond to mixed interactions with higher axial modes such as 14, 19, and 22, primarily at the 15th, 17th, and 19th harmonic. These interactions are at energy levels beyond the reach of the von Kármán model. The presence of the axial modes in the response points to a further motivation for using the SE(2) model to ensure the axial deformations and their effect on the periodic solution is captured correctly.

It was further found that the von Kármán model required a smaller time step by an order of magnitude in the shooting time integration for tracing the NNM curve compared to the SE(2) model, resulting in slower convergence of the continuation process. Though not systematically quantified here, it was observed that the SE(2) model can accurately produce the correct NNM solutions with fewer FE elements—an observation that is supported by other observations already made in the literature [21]. This indicates a further usable possibility for reducing the overall computational time. The cantilever therefore presents a case where there are starker differences between the NNMs obtained by the SE(2) and von Kármán models. A strong argument can therefore be made for using the SE(2) model over the von Kármán for modelling beams with large rotations and deformations such as the cantilever.

Fig. 10
figure 10

FEP of first NNM of straight cantilever. Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). Point Green diamond indicates highest energy point captured on the backbone for each model. (Color figure online)

Full size image
Fig. 11
figure 11

Deformed beam shape at points indicated by Green diamond in Fig. 10. Comparison between von Kármán (top black line) and SE(2) (bottom orange line). (Color figure online)

Full size image

4.6 Straight cantilever beam: NNM2

The FEP of the second NNM is shown in Fig. 12. Here, the backbones are in agreement, while various interaction tongues are observed on the SE(2) curve. A prominent tongue appears at around 51 Hz, which corresponds to a 41:1 interaction with NNM11. Smaller tongues corresponding to high-order harmonics also appear further along the backbone. The deformed beam shape at the lowest frequency point on the backbone (approx. 44.8 Hz) for both models is shown in Fig. 13. There is good agreement between the models, and the von Kármán beam shape does not show significant deviation from that of the reference SE(2) model. The presence of axial deformation is clearly seen in the beam shapes owing to contributions from axial modes in the response: mainly NNM 8, along with NNMs 14, 19, 22, and 24. The normalised vertical and axial displacements of the beam tip are depicted in Fig. 14. The presence of the third harmonic is seen in the vertical tip displacement, which manifests as double the frequency in the axial displacement. NNM3 begins to contribute to the response by means of excitation through the third harmonic of NNM2. The deformed beam shape in Fig. 13 also reveals the presence of the beam’s third mode shape, more prominently on the SE(2) beam where it is relatively stronger. Though the vertical tip displacements are in relatively close agreement between the two models, there is greater difference in the displacement in the axial direction. The importance of using a more accurate beam model is therefore highlighted once more, as the significant contribution from higher-order axial modes needs to be modelled correctly for the full dynamics to be captured.

Fig. 12
figure 12

FEP of second NNM of straight cantilever. Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). (Color figure online)

Full size image
Fig. 13
figure 13

Deformed beam shape for lowest frequency point on the backbone in Fig. 12 (approx. 44.8 Hz). Comparison between von Kármán (top black line) and SE(2) (bottom orange line). (Color figure online)

Full size image
Fig. 14
figure 14

Normalised a vertical and b axial amplitude versus time at beam tip for lowest frequency point on the backbone in Fig. 12 (approx. 44.8 Hz). Comparison between von Kármán (black solid line) and SE(2) (orange dashed line). (Color figure online)

Full size image

5 Conclusion

The constant drive to improve performance margins of structures is leading to lighter designs, which are increasingly flexible and exhibit geometric nonlinearity. The modelling of geometrically nonlinear structures currently relies on approaches that have approximate kinematic assumptions, require approximations when implemented, or are difficult to generalise to more complex (3D) examples. In this paper, all these issues were tackled by using models based on a two-dimensional SE(2) Lie group formulation. A doubly clamped straight beam, a shallow arch, and a cantilever beam were modelled using this formulation. To analyse the nonlinear dynamics of these structures, their nonlinear normal modes were computed using the shooting and pseudo-arclength continuation methods. However, the use of the underlying Lie group model required modifications to both methods to account for the non-Euclidean nature of the state space.

Comparison with the results obtained using the popular von Karman model highlighted several important observations:

  • The approximate kinematics of the von Karman model can lead to erroneous qualitative predictions (see Sect. 4.5). As anticipated, the geometrically exact nature of the SE(2) model captures the correct frequency–energy dependence of the NNMs. For large vibrations of the cantilever beam, the responses along the backbone of the NNM exhibit a relatively strong higher-harmonic content and the contribution of several high-frequency linear modes with significant axial components, which is not captured by the von Kármán model.

  • Differences in the kinematic assumptions between the two models lead to differences in the natural frequencies of the higher modes and can also affect their overall frequency–energy dependence. As such, mode interactions were seen to differ in location and shape between the two models. In principle, this could also affect the order of the interactions observed between the two models.

  • Finding periodic solutions is computationally less expensive with the SE(2) model, which generally requires fewer time steps during shooting. The number of finite elements in the SE(2) model can also be reduced compared to the von Karman model, while preserving the accuracy of the results.

Differences between the von Karman and Lie group formulations are expected to be even more important when considering 3D structures with larger rotations and displacements. Owing to the correct underlying kinematics of the Lie group model, and thanks to its local frame formulation, problems such as shear locking and rigid body strain are completely avoided. The higher efficiency of the Lie group model also results in needing fewer finite elements, which has a significant computational advantage in modelling 3D structures. The Lie group model considered, and the new shooting and continuation methods developed here, are thus expected to significantly benefit the modelling and analysis of vibrations of complex and highly flexible structures, such as those being increasingly developed by industry.