Nonlinear model order reduction for flexible multibody dynamics: a modal derivatives approach

Abstract

An effective reduction technique is presented for flexible multibody systems, for which the elastic deflection could not be considered small. We consider here the planar beam systems undergoing large elastic rotations, in the floating frame description. The proposed method enriches the classical linear reduction basis with modal derivatives stemming from the derivative of the eigenvalue problem. Furthermore, the Craig–Bampton method is applied to couple the different reduced components. Based on the linear projection, the configuration-dependent internal force can be expressed as cubic polynomials in the reduced coordinates. Coefficients of these polynomials can be precomputed for efficient runtime evaluation. The numerical results show that the modal derivatives are essential for the correct approximation of the nonlinear elastic deflection with respect to the body reference. The proposed reduction method constitutes a natural and effective extension of the classical linear modal reduction in the floating frame.

1 Introduction

The floating frame of reference (FFR), which follows a mean rigid body motion of an arbitrary flexible component, is widely applied in flexible multibody systems (FMBS) [1]. The major advantage of the floating reference, when compared with the corotational frame of reference (CFR), is the ability to naturally allow Model Order Reduction (MOR): the local generalized coordinates can be expressed as a linear combination of a small number of modes.

The traditional FFR approach combined with linear elastic finite element (FE) models was illustrated by Shabana [2]. This formulation has been used to numerous problems featuring large rigid body displacement but small deflections. However, nonlinear effects due to elastic geometric nonlinearities are not incorporated in this method, and cannot be ignored in many FMBS applications. In [3, 4], the classical geometric stiffness, obtained from an expression for the strain energy that includes only some higher-order terms of the strain tensor, was included in the motion equations. This approximation ignores the foreshortening displacement, and may lead to diverging solutions in applications involving large deflections and large axial forces [5]. Mayo [6] extended this formulation and obtained additional geometric stiffness matrix and nonlinear elastic force vectors. The inclusion of this effect improved both the axial and transverse response.

The FE discretization of the elastic bodies in FFR introduces a large number of degrees of freedom (dofs), and the simulation of the multibody system becomes computationally expensive, especially when the internal forces are nonlinear. Therefore, an essential step in the modeling of FMBS is the reduction of the elastic dofs. While the traditional linear MOR methods have been widely applied in FFR formulation [2, 3], some other non-modal model reduction techniques have also been used in large scale industrial models in the last few years [7–9]. However, efficient reduction techniques with elastic geometrical nonlinearities in FFR formulation still remain a relevant research topic, given the broad range of applications tackled by FMBS. One proposed approach, under the name of ad-hoc modes, is to specifically select some axial vibration modes, in addition to low-frequency bending and torsion modes, and include them in the reduction basis in order to properly account for the nonlinear membrane response [10, 11]. However, the frequencies of fundamental axial modes are normally much higher than the ones associated to bending modes. The extraction of such modes is difficult and expensive, and therefore not practical for realistic applications. Along this line, Holm-Jørgensen [12] extended the truncated modal basis with a quasi-static correction, assuming that the high-frequency elastic modes only cause quasi-static displacements. Similar approaches were previously proposed by Schwertassek [13, 14]. A set of suitable quasi-comparison function, by combining eigenfunctions and static modes, is used in the FFR formulation applying Ritz method. This method was further applied to the deployment of a solar panel array by Wallrapp [15].

Higher-order modes, also known as modal derivatives (MDs), have been proved to be an efficient approach to enrich the modal basis and represent the effects of nonlinearity [16–18]. This method has been successfully applied in the inertial frame description to solve nonlinear problems without large rigid body motion. Interesting applications are also found in computer graphics and haptics [19, 20]. Recently, this method has also been extended from the planar beam element to a general three-dimensional shell element implementation in an inertial frame [21].

In this paper, a reduction method based on the enrichment of reduction basis constituted of vibration modes with modal derivatives is presented. The FFR formulation is considered here. The elastic nonlinearity is modeled by employing the full quadratic Green strain expression, and the MDs can be interpreted as a static correction of the selected vibration modes that correctly represent the nonlinear forces with respect to the body reference. The proposed technique is implemented with the Craig–Bampton method on the floating frame [22, 23], to give an exact compatibility at boundaries. The effectiveness of the proposed method will be illustrated through several numerical examples.

2 Floating frame of reference formulation

The proposed method is illustrated by planar beam systems featuring multiple components. The following assumptions have been made:

• 1. We consider only Euler–Bernoulli beam theory;

• 2. The material nonlinearities are not taken into consideration;

• 3. Damping is neglected.

2.1 Kinematic description

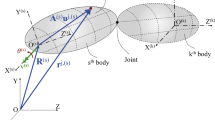
In the FFR description, the absolute motion of an arbitrary point on element $P_{j}$ of body $\mathcal{S}_{i}$ is described as the superposition of the motion of the body coordinate $X^{i}Y^{i}$ and the position of the points with respect to the body reference, as shown in Fig. 1. The definition of body coordinate $X^{i}Y^{i}$ is not unique, we adopt here the nodal fixed frame [24]: the origin of the body coordinate is fixed to one node of the body $\mathcal{S}_{i}$, and the $O^{i}X^{i}$ axis connects the origin to the end node. The position vector $\mathbf{r}^{ij}$ on body $\mathcal{S}_{i}$ can be defined in FFR formulation as

$$ \mathbf{r}^{ij}=\mathbf{R}^{i}+ \mathbf{A}^{i}\mathbf{N}^{ij}\bigl(\mathbf {e}_{0}^{ij}+\mathbf{q}_{f}^{ij}\bigr), $$

(1)

where $\mathbf{R}^{i}$ represents the position of origin of body system $X^{i}Y^{i}$ with respect to global system $XY$, $\mathbf{A}^{i}$ is the transformation matrix from $X^{i}Y^{i}$ to $XY$, $\mathbf{N}^{ij}$ are the FE shape functions, $\mathbf{e}_{0}^{ij}$ is the nodal coordinate vector in the undeformed state and $\mathbf{q}_{f}^{ij}$ is the vector of elastic deformation at the nodal points. In the presented 2D framework, the transformation matrix $\mathbf{A}^{i}$ depends only on the angle $\theta_{i}$. The kinetic energy $\mathcal{T}^{ij}$ for element $P_{j}$ on body $\mathcal{S}_{i}$ is defined as

$$ \mathcal{T}^{ij}=\frac{1}{2}\int_{V^{ij}} \rho^{ij}\dot{\mathbf {r}}^{ijT}\dot{\mathbf{r}}^{ij} \,\mathrm{d}V^{ij}, $$

(2)

where the velocity $\dot{\mathbf{r}}^{ij}$ is given by

$$ \dot{\mathbf{r}}^{ij}=\dot{\mathbf{R}}^{i}+\dot{ \mathbf{A}}^{i}\mathbf {N}^{ij}\bigl(\mathbf{e}_{0}^{ij}+ \mathbf{q}_{f}^{ij}\bigr)+\mathbf{A}^{i}\mathbf {N}^{ij}\dot{\mathbf{q}}_{f}^{ij}, $$

(3)

and $\dot{\mathbf{A}}^{i}=\dot{\theta_{i}}\mathbf{e}_{Z}\times\mathbf {R}^{i}$, $\mathbf{e}_{Z}$ is the unit vector associated with the global axis $Z$. Global quantities (therefore not equipped with index $j$) are obtained with standard FE assembly.

Fig. 1

Generalized coordinates expression in FFR

The equations of motion for the entire multibody system can be derived from Lagrange’s equations

$$ \frac{\mathrm{d}}{\mathrm{d}t} \biggl(\frac{\partial\mathcal{T}}{\partial\dot{\mathbf {q}}} \biggr)^{T}- \biggl( \frac{\partial\mathcal{T}}{\partial\mathbf {q}} \biggr)^{T}+ \biggl(\frac{\partial\mathcal{U}}{\partial\mathbf {q}} \biggr)^{T}+\mathbf{C}^{T}_{q}\boldsymbol{\lambda}= \mathbf{Q}_{e}, $$

(4)

where $\mathcal{T}$ and $\mathcal{U}$ are, respectively, the kinetic energy and strain energy for the entire system; $\mathbf{C}_{q}$ is the constraint Jacobian matrix, obtained from the constraint equation $\mathbf{C}(\mathbf{q})=\mathbf{0}$; $\boldsymbol{\lambda}$ is the vector of Lagrange multipliers, representing the constraint forces; $\mathbf{Q}_{e}$ is the vector of externally applied forces; $t$ indicates time; $\mathbf{q}$ is the vector of the body generalized coordinates, formed as $\mathbf{q}^{T} = [\mathbf{q}^{1^{T}}\ \dots\ \mathbf {q}^{N^{T}}]$. Here, $N$ is the number of bodies forming the system. Furthermore, $\mathbf{q}^{i}$ can be divided as

$$ \mathbf{q} ^{i^{T}}= \begin{bmatrix} \mathbf{q}^{i^{T}}_{r} & \mathbf{q}^{i^{T}}_{f} \\ \end{bmatrix} = \begin{bmatrix} \mathbf{R}^{i^{T}} & \theta_{i} & \mathbf{q}^{i^{T}}_{f}\\ \end{bmatrix} , $$

(5)

where $\mathbf{q}{^{i}}_{r}\in\mathbb{R}^{3}$ refers to the displacement and orientation of the body coordinate $\mathcal{S}_{i}$, $\mathbf {q}{^{i}}_{f}\in\mathbb{R}^{n}$ refers to the elastic displacement in the body coordinate $\mathcal{S}_{i}$, and $n$ is the corresponding number of elastic dofs. For the remainder of this paper, we drop the superscript $i$ for the sake of clarity.

The inertia coupling between the body coordinates $\mathbf{q}_{r}$ and elastic coordinates $\mathbf{q}_{f}$ leads to inertia terms which are configuration and velocity dependent

$$ \frac{\mathrm{d}}{\mathrm{d}t} \biggl(\frac{\partial\mathcal{T}}{\partial\dot{\mathbf {q}}} \biggr)^{T}- \biggl( \frac{\partial\mathcal{T}}{\partial\mathbf {q}} \biggr)^{T}=\mathbf{M}(\mathbf{q})\ddot{\mathbf{q}} - \mathbf {Q}_{v}(\mathbf{q},\dot{\mathbf{q}}), $$

(6)

where $\mathbf{M}$ is the configuration-dependent mass matrix, and $\mathbf{Q}_{v}$ is the quadratic velocity vector. The details of the derivation can be found in Appendix A.1.

2.2 Nonlinear strain expression

For a planar Euler–Bernoulli beam, the strain energy $\mathcal{U}$ could be written as [25]

$$ \mathcal{U}=\frac{1}{2}\int_{0}^{L} EA \varepsilon^{2}_{xx}\,\mathrm{d}x, $$

(7)

where $E$ is Young’s modulus; $A$ is the cross-sectional area of the beam; $L$ is the length, and $\varepsilon_{xx}$ is the axial strain.

The axial strain of an Euler–Bernoulli beam is given by Green–Lagrange strain expression [26]

$$ \varepsilon_{xx}=\frac{\partial{u}}{\partial x}+\frac{1}{2} \biggl[ \biggl( \frac{\partial{u}}{\partial x} \biggr)^{2}+ \biggl(\frac{\partial {v}}{\partial x} \biggr)^{2} \biggr], $$

(8)

where $u$ and $v$ are, respectively, the axial and transverse displacement at any point of the cross-section. Furthermore, the displacement field can be typically specified by the following linearized form

$$ \textstyle\begin{cases} u=u_{0}-y\dfrac{\partial{v_{0}}}{\partial x},\\ v=v_{0}, \end{cases} $$

(9)

where subscription $(\cdot )_{0}$ indicates the position at the centroid of the cross-section, and $y$ is the transverse coordinate. We adopt here the moderate rotations, von K$\acute{\text{a}}$rm$\acute {\text{a}}$n kinematic, which states that axial deformations and curvature are small compared to the bending rotation

$$ \frac{1}{2} \biggl(\frac{\partial{u}}{\partial x} \biggr)^{2} \ll \frac {\partial u}{\partial x} , \ \frac{1}{2} \biggl(\frac{\partial v}{\partial x} \biggr)^{2}. $$

(10)

Therefore, the quadratic strain expression applied in this work is suitable for the model with small to moderate deflections [27]

$$ \varepsilon_{xx}=\frac{\partial{u}}{\partial x}+\frac{1}{2} \biggl( \frac {\partial{v}}{\partial x} \biggr)^{2}=\frac{\partial{u_{0}}}{\partial x}-y\frac{\partial^{2}{v_{0}}}{\partial x^{2}}+ \frac{1}{2} \biggl(\frac{\partial {v_{0}}}{\partial x} \biggr)^{2}. $$

(11)

In case of isotropic linear elastic material, the strain energy could be expressed as

$$\begin{aligned} \mathcal{U} =&\frac{1}{2}\int_{0}^{L} EA \biggl(\frac{\partial u_{0}}{\partial x} \biggr)^{2}\,\mathrm{d}x+\frac{1}{2} \int_{0}^{L} EI \biggl(\frac{\partial^{2} v_{0}}{\partial x^{2}} \biggr)^{2}\,\mathrm{d}x \\ &{}+\frac{1}{2}\int_{0}^{L} EA \frac{\partial u_{0}}{\partial x} \biggl(\frac {\partial v_{0}}{\partial x} \biggr)^{2}\,\mathrm{d}x+ \frac{1}{2}\int_{0}^{L} \frac{EA}{4} \biggl(\frac{\partial v_{0}}{\partial x} \biggr)^{4}\,\mathrm{d}x, \end{aligned}$$

(12)

where $I$ is the moment of inertia.

The classical linear strain energy expression, which is commonly applied in the FFR, only contains first and second order integrals in (12). The last two integrals in (12) are cubic and quartic functions of displacements, respectively. Once the FE discretization and assembly are applied, the elastic forces here can be directly generated from the differentiation of strain energy $\mathcal{U}$ as

$$ \mathbf{Q}_{nl}= \biggl(\frac{\partial\mathcal{U}}{\partial\mathbf {q}} \biggr)^{T} = \begin{bmatrix} \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{K}_{L} \end{bmatrix} \begin{bmatrix} \mathbf{q}_{r} \\ \mathbf{q}_{f} \end{bmatrix} + \begin{bmatrix} \mathbf{0} \\ \mathbf{Q}_{f} \end{bmatrix} , $$

(13)

where the internal force vector $\mathbf{Q}_{nl}$ is a third-order polynomial function of the displacements $\mathbf{q}_{f}$, and it can be divided into two contributions: the first term contains the classical linear internal forces, while the second term $\mathbf{Q}_{f}$ contains the higher order geometrically nonlinear terms.

2.3 Equations of motion

The equations of motion could be obtained by simply substituting (6) and (13) into (4), and written as

$$ \mathbf{M}(\mathbf{q})\ddot{\mathbf{q}}-\mathbf{Q}_{v}(\mathbf{q}, \dot {\mathbf{q}})+\mathbf{Q}_{nl}(\mathbf{q})+\mathbf{C}_{q}^{T} \boldsymbol {\lambda}=\mathbf{Q}_{e}, $$

(14)

or more compactly,

$$ \mathbf{M}\ddot{\mathbf{q}}+\mathbf{Q}_{nl}+\mathbf{C}_{q}^{T} \boldsymbol {\lambda}=\mathbf{f}, $$

(15)

where $\mathbf{f}=\mathbf{Q}_{e}+\mathbf{Q}_{v}$. The explicit dependency on $\mathbf{q}$ is here dropped for clarity. Equation (15) can be conveniently written in a partitioned form in terms of a coupled set of reference and elastic coordinates:

$$ \begin{bmatrix} \mathbf{M}_{rr} & \mathbf{M}_{rf} \\ \mathbf{M}_{fr} & \mathbf{M}_{ff} \end{bmatrix} \begin{bmatrix} \ddot{\mathbf{q}}_{r} \\ \ddot{\mathbf{q}}_{f} \end{bmatrix} + \begin{bmatrix} \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{K}_{L} \end{bmatrix} \begin{bmatrix} \mathbf{q}_{r} \\ \mathbf{q}_{f} \end{bmatrix} + \begin{bmatrix} \mathbf{0} \\ \mathbf{Q}_{f} \end{bmatrix} + \begin{bmatrix} \mathbf{C}_{qr}^{T} \\ \mathbf{C}_{qf}^{T} \end{bmatrix} \boldsymbol{\lambda} = \begin{bmatrix} \mathbf{f}_{r}\\ \mathbf{f}_{f} \end{bmatrix} . $$

(16)

In multibody dynamics, the constraints are often differentiated twice with respect to time and incorporated in the inertial terms [2, 3]. Then, additional regularization for constraint equations is required to ensure that the constraints are satisfied on the displacement and velocity level. This constraint regularization could be avoided by solving the original constraints (usually nonlinear) together with the equations of motion

$$ \textstyle\begin{cases} \mathbf{r}(\mathbf{q},\boldsymbol{\lambda})=\mathbf{M}\ddot{\mathbf {q}}+\mathbf{Q}_{nl}+\mathbf{C}_{q}^{T}\boldsymbol{\lambda}-\mathbf {f}=\mathbf{0}, \\ \mathbf{C}(\mathbf{q})=\mathbf{0}. \end{cases} $$

(17)

Since the constraints will generally introduce infinite stiffness into the system, it is necessary to use unconditionally stable time integration schemes [12]. Usually, the constraints are acting only on specific boundary nodes. It is therefore convenient to further partition the elastic dofs as $\mathbf{q}_{f}^{T}=[\mathbf{q}_{b}^{T} \ \mathbf{q}_{i}^{T}]$, where the subscripts $(\cdot)_{b}$ and $(\cdot )_{i}$ replace $(\cdot)_{f}$ to represent boundary and internal dofs. $\mathbf{q}_{b}\in\mathbb{R}^{n_{b}}$, $\mathbf{q}_{i}\in\mathbb{R}^{n_{i}}$ and $n= n_{b}+n_{i}$. The constraint Jacobian matrix can then be written as

$$ \mathbf{C}_{q}= \begin{bmatrix} \mathbf{C}_{qr} & \mathbf{C}_{qb} & \mathbf{0}_{qi} \end{bmatrix} , $$

(18)

where the zero block matrix $\mathbf{0}_{qi}$ indicates that no constraints are acting on the internal dofs. Equation (16) can then be partitioned in the same fashion as

$$ \begin{bmatrix} \mathbf{M}_{rr} & \mathbf{M}_{rb} & \mathbf{M}_{ri} \\ \mathbf{M}_{br} & \mathbf{M}_{bb} & \mathbf{M}_{bi} \\ \mathbf{M}_{ir} & \mathbf{M}_{ib} & \mathbf{M}_{ii} \end{bmatrix} \begin{bmatrix} \ddot{\mathbf{q}}_{r} \\ \ddot{\mathbf{q}}_{b} \\ \ddot{\mathbf{q}}_{i} \end{bmatrix} + \begin{bmatrix} \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{K}_{bb} & \mathbf{K}_{bi} \\ \mathbf{0} & \mathbf{K}_{ib} & \mathbf{K}_{ii} \end{bmatrix} \begin{bmatrix} \mathbf{q}_{r} \\ \mathbf{q}_{b} \\ \mathbf{q}_{i} \end{bmatrix} + \begin{bmatrix} \mathbf{0} \\ \mathbf{Q}_{b} \\ \mathbf{Q}_{i} \end{bmatrix} + \begin{bmatrix} \mathbf{C}^{T}_{qr} \\ \mathbf{C}^{T}_{qb} \\ \mathbf{0} \end{bmatrix} \boldsymbol{\lambda} = \begin{bmatrix} \mathbf{f}_{r}\\ \mathbf{f}_{b}\\ \mathbf{f}_{i} \end{bmatrix} . $$

(19)

3 Nonlinear model order reduction

In the classical application of modal analysis in FFR [3], the elastic displacement field $\mathbf{q}_{f}$ is represented as a linear combination of mode shapes. In this section, we discuss the extension of the well-known Craig–Bampton method for the effective reduction of flexible multibody systems characterized by elastic geometric nonlinearities.

3.1 Craig–Bampton method

In order not to introduce any error in the constraints during the modal transformation, we adopt here the well known Craig–Bampton method [28] for the reduction of the internal elastic dofs. The reduction can be written as

$$ \mathbf{q}_{f}= \begin{bmatrix} \mathbf{q}_{b} \\ \mathbf{q}_{i} \end{bmatrix} = \begin{bmatrix} \mathbf{I} & \mathbf{0} \\ \boldsymbol{\Psi} & \boldsymbol{\Phi} \end{bmatrix} \begin{bmatrix} \mathbf{q}_{b} \\ \boldsymbol{\eta}\end{bmatrix} , $$

(20)

where constraint modes $\boldsymbol{\Psi} \in\mathbb{R}^{n_{i} \times n_{b}}$

$$ \boldsymbol{\Psi}=-\mathbf{K}_{ii}^{-1}\mathbf{K}_{ib} $$

(21)

are used to account for local effects at boundaries. In the linear modal analysis, the fixed interface modes $\boldsymbol{\Phi}$ only contains $m$ vibration modes (VMs) of the system when constrained at the interface (i.e., $\mathbf{q}_{b}=\mathbf{0}$), solution of the eigenvalue problem

$$ \bigl( \mathbf{K}_{ii} - \omega^{2}_{j} \mathbf{M}_{ii} \bigr)\boldsymbol{\phi}_{j}=\mathbf{0}, $$

(22)

where $\omega_{j}$ is the $j$th eigenfrequency and $\boldsymbol{\phi} _{j}$ is the associated VM. In (20), $\boldsymbol{\eta} \in\mathbb{R}^{m}$ is a vector of modal coordinates. The reduction will be achieved by forming $\boldsymbol{\Phi}$ only with $m\ll n_{i}$ internal VMs. In practice, the reduction is performed on each component of the multibody system independently.

3.2 Augmented reduction basis with modal derivatives

Although Craig–Bampton method has been successfully applied in the FFR formulation in [22], the reduction basis in (20) is usually linearized around a reference equilibrium position.

In geometrically nonlinear systems, linear VMs usually fail to accurately reproduce the motion because of their inability to account for bending–stretching coupling caused by finite deflections. Typically, low-frequency bending dominated VMs must be accompanied by axial modes to accommodate for such effects. Axial VMs can in principle be calculated. However, their extraction is expensive since they are typically associated to much higher frequencies with respect to the bending modes. In addition, for more complex and realistic components, the distinction between axial and bending/twisting dominated modes can be difficult to establish.

To overcome this difficulty, modal derivatives (MDs) stemming from VMs can be appended to the existing linear reduction basis $\boldsymbol{\Phi }$, as shown in [16, 17]. When the internal displacement $\mathbf{q}_{i}$ cannot be considered small, we first assume a nonlinear mapping $\boldsymbol{\Gamma}$ between the modal coordinate vector $\boldsymbol{\eta}$ and internal displacement vector $\mathbf{q}_{i}$,

$$ \mathbf{q}_{i}\approx \boldsymbol{\Psi}\mathbf{q}_{b}+ \boldsymbol{\Gamma }(\boldsymbol{\eta}), $$

(23)

which gives

$$ \mathrm{d} \mathbf{q}_{i}=\boldsymbol{\Psi}\, \mathrm{d} \mathbf{q}_{b}+\frac {\partial\boldsymbol{\Gamma}}{\partial\boldsymbol{\eta}} \,\mathrm{d} \boldsymbol{\eta}= \boldsymbol{\Psi} \,\mathrm{d} \mathbf{q}_{b}+\boldsymbol {X}(\boldsymbol{\eta}) \,\mathrm{d} \boldsymbol{\eta}, $$

(24)

where $\boldsymbol{X}(\boldsymbol{\eta})$ is a configuration-dependent matrix of modes. The mapping (23) can be expanded in Taylor series around the equilibrium position

$$ \mathbf{q}_{i}\approx \boldsymbol{\Psi}\mathbf{q}_{b}+\sum _{j=1}^{m} \frac{\partial\boldsymbol{\Gamma}}{\partial\eta_{j}}\bigg|_{\mathrm{eq}}\eta _{j}+\sum_{j=1}^{m} \sum_{k=1}^{m}\frac{1}{2} \frac{\partial^{2} \boldsymbol{\Gamma}}{\partial\eta_{j} \partial\eta_{k}}\biggr| _{\mathrm{eq}}\eta _{j}\eta_{k}, $$

(25)

where the derivatives of the displacement vector $\mathbf{q}_{i}$ with respect to the modal amplitudes $\eta_{j}$ around the equilibrium position can be computed from (24) as

$$ \frac{\partial\boldsymbol{\Gamma}}{\partial{\eta_{j}}}\bigg| _{\mathrm{eq}}=\boldsymbol{X}_{j}( \boldsymbol{0})=\boldsymbol{\phi}_{j} $$

(26)

and

$$ \frac{\partial^{2} \boldsymbol{\Gamma}}{\partial\eta_{j} \partial\eta _{k}}\biggr| _{\mathrm{eq}}=\frac{\partial\boldsymbol{X}_{j}}{\partial\eta _{k}} \biggr| _{\mathrm{eq}}=\boldsymbol{\theta}_{jk}, $$

(27)

where (26) represents the linear VM $\boldsymbol{\phi}_{j}$ (i.e., calculated at the equilibrium), and (27) gives the corresponding MD, denoted here as $\boldsymbol{\theta}_{jk}$, which represents how $\boldsymbol{X}_{j}$ changes because of an imposed perturbation in the shape $\boldsymbol{X}_{k}$, at equilibrium. Equation (25) can therefore be written as

$$ \mathbf{q}_{i}\approx \boldsymbol{\Psi}\mathbf{q}_{b}+\sum _{j=1}^{m}\boldsymbol{\phi}_{j} \eta_{j}+\sum_{j=1}^{m}\sum _{k=1}^{m}\frac {1}{2}\boldsymbol{ \theta}_{jk}\eta_{j}\eta_{k}. $$

(28)

The MDs can be computed analytically by differentiating the linearized eigenvalue problem with respect to the modal amplitudes:

$$ \biggl(\frac{\partial{\mathbf{K}_{ii}^{nl}}}{\partial{\eta _{k}}}\biggr| _{\mathrm{eq}}-\frac{\partial{\omega_{j}^{2}}}{\partial{\eta_{k}}} \mathbf {M}_{ii} \biggr)\boldsymbol{\phi}_{j}+ \bigl( \mathbf{K}_{ii}-\omega_{j}^{2}\mathbf {M}_{ii} \bigr)\boldsymbol{\theta}_{jk}=\mathbf{0}. $$

(29)

It has already been shown that the inertia related terms in (29) can be neglected [16–18]. In this case, the MDs could be interpreted as a static correction, and are calculated by solving the linear system

$$ \boldsymbol{\theta}_{jk}=-\mathbf{K}_{ii}^{-1} \frac{\partial{\mathbf {K}^{nl}_{ii}}}{\partial{\eta_{k}}}\biggr| _{\mathrm{eq}}\boldsymbol{\phi}_{j}. $$

(30)

Since the system is fixed at its boundary nodes by applying a nodal-fixed frame in FFR, the internal stiffness matrix $\mathbf{K}_{ii}$ is nonsingular. By neglecting all the inertia terms in (29), it can be proved that MDs are symmetric, i.e., $\boldsymbol{\theta}_{jk}=\boldsymbol{\theta}_{kj}$. Therefore, given $m$ VMs, $r=m(m+1)/2$ MDs can be calculated.

In order to properly capture the contribution of the nonlinearity, we now augment the reduction basis for the internal dofs with a set of MDs collected in the matrix $\boldsymbol{\Theta}$, by loosing the quadratic mapping (28) between VMs and MDs and adding additional modal coordinates $\boldsymbol{\xi}$,

$$ \mathbf{q}_{i}\approx \boldsymbol{\Psi}\mathbf{q}_{b}+ \boldsymbol{\Phi }\boldsymbol{\eta}+\boldsymbol{\Theta}\boldsymbol{\xi}. $$

(31)

Note that, although the number of MDs $r$ grows quadratically with the number of chosen VMs $m$, it is possible to use simple selection criteria that indicate the most significant $k$ MDs for the given analysis [29]. The reduction basis for an arbitrary body $\mathcal{S}_{i}$ is therefore written as

$$ \mathbf{q}= \begin{bmatrix} \mathbf{q}_{r} \\ \mathbf{q}_{b} \\ \mathbf{q}_{i} \end{bmatrix} = \begin{bmatrix} \mathbf{I} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{I} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{\Psi} & \boldsymbol{\Phi} & \boldsymbol {\Theta} \end{bmatrix} \begin{bmatrix} \mathbf{q}_{r} \\ \mathbf{q}_{b} \\ \mathbf{\boldsymbol{\eta}} \\ \mathbf{\boldsymbol{\xi}} \end{bmatrix} . $$

(32)

Once the reduction basis (32) has been derived, the equations of motion (19) can be evaluated and projected to obtain a model of greatly reduced dimensions. Unfortunately, this procedure is inefficient since the cost for the evaluation of the nonlinear terms (i.e., inertial and elastic forces) scales with the size of the nodal coordinates: the nonlinear terms have to be computed in nodal coordinates and then projected on the reduced subspace. In our case, the nonlinear terms are written directly in terms of the modal coordinates. This is discussed in detail in the next section.

3.3 Precomputing polynomial coefficients

The adopted kinematic model yields a multivariate third-order polynomial expression of the nonlinear elastic forces $\mathbf{Q}_{f}$. A generic component ${Q}_{f}^{I}$ can be written as

$$ {Q}_{f}^{I}=Q_{1}^{Iij}q_{f}^{i}q_{f}^{j}+Q_{2}^{Iijl}q_{f}^{i}q_{f}^{j}q_{f}^{l}, $$

(33)

where $\mathbf{Q}_{1} \in\mathbb{R}^{n\times n \times n}$ , $\mathbf {Q}_{2}\in\mathbb{R}^{n\times n \times n \times n}$ are constant third order and fourth order tensor coefficients with generic components $Q_{1}^{Iij}$ and $Q_{2}^{Iijl}$. We adopted here the Einstein summation convention over the repeated indexes in the superscript.

Consequently, with the modal transformation of the form $\mathbf {q}_{f}=\mathbf{V}\boldsymbol{\gamma}$, where

$$ \mathbf{V}= \begin{bmatrix} \mathbf{I} & \mathbf{0} & \mathbf{0} \\ \boldsymbol{\Psi} & \boldsymbol{\Phi} & \boldsymbol{\Theta} \end{bmatrix} $$

(34)

and

$$ \boldsymbol{\gamma}^{T}= \begin{bmatrix} \mathbf{q}_{b}^{T} & \boldsymbol{\eta}^{T} & \boldsymbol{\xi}^{T} \end{bmatrix} , $$

(35)

the reduced internal forces $\overline{\mathbf{Q}}_{f}=\mathbf {V}^{T}\mathbf{Q}_{f}(\mathbf{V}\boldsymbol{\gamma})$ is a multivariate cubic polynomial in reduced coordinates $\boldsymbol{\gamma}$,

$$\begin{aligned} \overline{Q}_{f}^{I} =& V^{iI}{Q}_{f}^{i}= V^{iI}{Q_{1}}^{ijl}{V}^{jp}{V}^{ls} \gamma^{p}\gamma ^{s}+{V}^{iI}{Q_{2}}^{ijlv}{V}^{jp}{V}^{ls}{V}^{vw} \gamma^{p}\gamma^{s}\gamma ^{w} \\ =&\overline{Q}_{1}^{Ips}\gamma^{p} \gamma^{s}+\overline{Q}_{2}^{Ipsw}\gamma ^{p}\gamma^{s}\gamma^{w}, \end{aligned}$$

(36)

where $\overline{\mathbf{Q}}_{1} \in\mathbb{R}^{v\times v \times v}$ , $\overline {\mathbf{Q}}_{2}\in\mathbb{R}^{v\times v \times v \times v}$ are constant third order and forth order tensor coefficients in the reduced coordinates with $v=n_{b}+m+k$. Similarly, each component of the reduced tangent stiffness matrix $\overline{\mathbf{K}}_{nl}$ is also a multivariate quadratic polynomial in $\boldsymbol{\gamma}$,

$$ \overline{K}^{IJ}_{nl}=\overline{K}_{L}^{IJ}+ \overline{K}_{3}^{IJl}\gamma ^{l}+ \overline{K}_{4}^{IJls}\gamma^{l} \gamma^{s}, $$

(37)

with constant tensor coefficients $\overline{\mathbf{K}}_{3} \in\mathbb {R}^{v\times v \times v}$ , $\overline{\mathbf{K}}_{4} \in\mathbb {R}^{v\times v \times v \times v}$. The constant linear stiffness can be expressed as

$$ \overline{\mathbf{K}}_{L}=\mathbf{V}^{T} \mathbf{K}_{L}\mathbf{V}. $$

(38)

The tensors $\overline{\mathbf{Q}}_{1}, \ \overline{\mathbf{Q}}_{2}, \ \overline{\mathbf{K}}_{3}, \ \overline{\mathbf{K}}_{4}$ and $\overline {\mathbf{K}}_{L}$ can be precomputed offline for efficient runtime evaluation.

3.4 Reduced equations

The reduced equations are obtained via a classical Galerkin projection, i.e., the residual obtained by introducing (32) in (16) is projected onto the same reduced basis used for the approximation of the displacements. As discussed in the previous section, it is possible to precompute the nonlinear terms to directly obtain modal terms rather than performing the full evaluation and projection. The resulting reduced equations are written as

$$ \begin{bmatrix} \mathbf{M}_{rr} & \overline{\mathbf{M}}_{rf}\\ \overline{\mathbf{M}}_{fr} & \overline{\mathbf{M}}_{ff} \end{bmatrix} \begin{bmatrix} \ddot{\mathbf{q}}_{r}\\ \ddot{\boldsymbol{\gamma}} \end{bmatrix} + \begin{bmatrix} \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \overline{\mathbf{K}}_{L} \end{bmatrix} \begin{bmatrix} \mathbf{q}_{r}\\ \boldsymbol{\gamma} \end{bmatrix} + \begin{bmatrix} \mathbf{0} \\ \overline{\mathbf{Q}}_{f} \end{bmatrix} + \begin{bmatrix} \mathbf{C}_{qr}^{T} \\ \overline{\mathbf{C}}_{qf}^{T} \end{bmatrix} \boldsymbol{\lambda}= \begin{bmatrix} \mathbf{f}_{r}\\ \overline{\mathbf{f}}_{f} \end{bmatrix} , $$

(39)

where

$$\overline{\mathbf{M}}_{rf}=\overline{\mathbf{M}}_{fr}^{T}= \mathbf {M}_{rf}\mathbf{V}; \qquad \overline{\mathbf{M}}_{ff}= \mathbf{V}^{T}\mathbf{M}_{ff}\mathbf{V}; \qquad \overline{ \mathbf{f}}_{f}=\mathbf{V}^{T}\mathbf{f}_{f}. $$

Note that $\overline{\mathbf{C}}_{qf}$ only contains nonzero terms on the column corresponding to the boundary dofs $\mathbf{q}_{b}$.

Because of the inertia coupling between the reference motion of the body and the elastic deformation of elements, also the inertia related terms $\overline{\mathbf{M}}_{rf}$, $\overline{\mathbf{M}}_{fr}$ and $\overline{\mathbf{f}}_{f}$ will be configuration-dependent. Similar to the elastic terms, the inertial terms can also be directly expressed in modal coordinates. The detailed formulation of the reduced mass matrix and quadratic velocity vector is reported in Appendix A.2.

The detailed MOR procedure proposed is illustrated in Fig. 2 on a flexible slider–crank mechanism. The end nodes in both crank and connecting rod are treated as boundary nodes: their corresponding dofs will not be transformed to modal coordinates. The material and geometrical properties are taken from the numerical example in Sect. 5.3. From Fig. 2 we can see that the first few VMs feature bending displacements only, while the corresponding MDs, which describe the second-order nonlinearities, exhibit only longitudinal displacement.

Fig. 2

Detailed modal transformation procedure for a slider–crank mechanism in FFR. To further highlight the MDs, the axial displacement DX (dotted line) is plotted here as a function of node position. The actual mesh deformation is shown as well. Note the axial-only contribution of the MDs that capture the necessary second order effect of the geometric nonlinearity associated to bending-only VMs

4 Computational cost estimation for reduced time integration

In this section, we present a complexity analysis to highlight the benefits of the proposed method in terms of computational cost. The number of dofs $N_{1}=3+n_{b}+n_{i}$ relative to the full analysis is reduced to $N_{2}=3+n_{b}+m+k$ where $m+k\ll n_{i}$. In the present work, the numerical solution of the second order differential equations resulting from the reduced order model is performed with the implicit Newmark method, with time integration parameters $\beta=0.25$ and $\alpha=0.5$. A similar scheme has already been successfully applied in FFR with full models [30], and now it will be applied to reduced models.

If we express the computational cost in terms of total number of dofs in the full and reduced models, i.e., $N_{1}$ and $N_{2}$, respectively, then a detailed comparison can be summarized in Table 1 for a single iteration step.

Table 1 Computational cost comparison: full and reduced system

For a fair estimation, the computational cost involved in this table also includes the time spent on the evaluation of the reduction basis and polynomial coefficients, sometimes also referred as offline cost (steps 1 and 2). The two most time-consuming operations are tangent stiffness and force assembly (steps 4 and 5), as well as the solution for displacement increment (step 6), which involves the factorization of large sparse symmetric matrices.

In this work, the effort in steps 4 and 5 is reduced by directly expressing the nonlinear force vector as a function of modal coordinates, with precomputing polynomial coefficients as shown in Sect. 3.3.

In addition, the reduced model here results in a much smaller system of equations to be solved for the displacement increment (step 6) during every corrector step in the time integration scheme. In Table 1, the cost of increment update for the full model and reduced model is indicated with $\mathcal{O}[s(N_{1})]$ and $\mathcal {O}[s(N_{2})]$, where $s(N_{1})$ and $s(N_{2})$ are functions depending on the solver characteristics. Table 1 clearly indicates the potential time savings if the number of reduced dofs $N_{2}$ grows much more slowly than the number of full dofs $N_{1}$.

5 Numerical examples

Three numerical examples are presented in this section to show the effectiveness of the proposed approach. The reduced solutions in the FFR are not only compared with the corresponding full solutions, but also with the response obtained by using a Corotational Frame of Reference (CFR) formulation. The CFR is a more general and expensive framework that is able to deal with an arbitrary large elastic deflection. This allows assessing that the magnitudes of the elastic deflections are within the validity of the adopted approximated von Kármán kinematic model. We considered here the CFR formulation discussed in [31] as a reference, where cubic shape functions are used to derive both the inertia and elastic terms. Recently, this formulation has also been successfully extended to the dynamic analysis of 3D flexible beam with good accuracy [32].

5.1 Test 1: rotating beam

The dynamic analysis of a rotating beam, which has been used as a benchmark in many papers dealing with flexible beams and geometric nonlinearities [33–36], is here presented. The geometry of the beam and the corresponding material properties are shown in Fig. 3. An imposed end rotation $\theta_{s}$ is applied as

$$ \theta_{s} = \textstyle\begin{cases} \frac{\omega_{s}}{T_{s}} [\frac{1}{2}t^{2}+ (\frac{T_{s}}{2\pi} )^{2} (\cos (\frac{2\pi t}{T_{s}} )-1 ) ], & t< T_{s}, \\ \omega_{s} ( t-\frac{T_{s}}{2} ), & t>T_{s}. \end{cases} $$

(40)

Fig. 3

The spin-up beam and two components of its tip displacement: U and V

The beam reaches steady state motion after $T_{s}$ seconds and then rotates at a constant angular velocity $\omega_{s}$. Transient responses are computed for $T_{s}=15$ s, and for angular velocity $\omega_{s}=$ 6 rad/s.

In order to make a comprehensive comparison, this example is analyzed by different approaches: (i) the CFR is taken as reference solution; (ii) the nonlinear floating frame is mentioned as the full analysis (denoted as NLFFR); (iii) the linear floating frame is performed by neglecting the nonlinear internal forces $\mathbf{Q}_{f}$ in equation of motion (denoted as LFFR); (iv) the MDs based reduction solution is applied in a nonlinear floating frame, where the modal basis is composed of the first 10 VMs and 10 MDs corresponding to the first 4 VMs (denoted as $10\ \mbox{VMs}+10\ \mbox{MDs}$); (v) a reduced solution obtained with the first 20 VMs (denoted as 20 VMs) is also calculated. The two components of the tip displacement vector are shown in Fig. 4.

Fig. 4

Time history for two components of the tip displacement relative to the spin-up beam. (a) Axial Tip Displacement U. (b) Vertical Tip Displacement V

The results obtained with the NLFFR are in very good agreement with the CFR solution and clearly differ from the LFFR response, to confirm that the adopted kinematic model is adequate for the problem at hand; see Fig. 4. Furthermore, the proposed modal derivatives based reduction method with 10 VMs and 10 MDs shows a good agreement with the reference solution. On the contrary, if only the first 20 VMs are applied in the reduced basis, a clear difference can be observed.

To offer further insight, some other reduced models with different modal basis are compared with the full analysis (NLFFR), as shown in Fig. 5. The comparison is performed between different reduction basis of the same size. The tip displacements components are shown. In addition, the root mean square (RMS) error $\epsilon_{\mathrm{RMS}}$ relative to the entire displacement vector is shown, calculated as

$$ \epsilon_{\mathrm{RMS}}=\sqrt{\frac{1}{n} \Biggl[\sum _{i=1}^{n} (u_{i}-\overline{u}_{i})^{2} + \sum_{i=1}^{n} (w_{i}-\overline{w}_{i})^{2} \Biggr]} $$

(41)

where $u_{i}, w_{i}$ and $\overline{u}_{i}, \overline{w}_{i}$ are the horizontal and vertical components of the node displacement from the full and reduced models, respectively.

Fig. 5

The comparison of the spin-up beam under different reduced models. (a) Axial Tip Displacement U. (b) Vertical Tip Displacement V. (c) RMS error of the displacement field

The reduced basis with 10 VMs enriched by 6 MDs (indicated as $10\ \mbox{VMs} + 6\ \mbox{MDs}$) yields much better results when compared to the reduced solution obtained with 16 VMs. In addition, by increasing the reduction basis with two additional MDs ($10\ \mbox{VMs} + 8\ \mbox{MDs}$), the results show a marked improvement, while the results are almost unchanged if two additional VMs are added in the 18 VMs cases. In some related work [10, 11], high-frequency axial vibration modes (AVMs) are specifically added to the basis in order to properly account for the nonlinear bending–stretching coupling. It is therefore interesting to compare this approach with the method proposed here. We form the reduction basis with first 10 VMs and the first 8 AVMs. The eigenfrequencies associated to the AVMs are reported in Table 2. Note that the frequency range of interest has to be extended from 145 Hz to almost 2100 Hz. In addition, the obtained results do not match the accuracy given by the $10\ \mbox{VMs} + 8\ \mbox{MDs}$ case. Therefore, we can conclude that in order to reproduce the nonlinear behavior, MDs based reduction basis provides better accuracy than an equal size reduction constructed with AVMs.

Table 2 Frequencies of the first 10 VMs and additional 8 AVMs

5.2 Test 2: swinging rubber bar

We consider here a slender rubber beam connected to a fixed inertial frame via a joint and exposed to a constant gravitational force. The beam is initially at rest in horizontal position. The material and geometric properties of the beam are taken from [37, 38]: $E=5 \times 10^{6}\ \mbox{N/m}^{2}$, $\rho=1.1\times 10^{3}\ \mbox{kg/m}^{3}$, $L=1.0\ \mbox{m}$. The cross-section is circular with a radius of 5 mm. The analysis is performed for a time interval of 1 second with a fixed time step $\Delta T$ of 0.001 seconds.

The dynamic response is shown in Fig. 6. The full response is compared with reduced basis formed with the first 5 VMs plus 10 MDs, as well as 15 VMs, respectively. As shown in Fig. 6, a reduction basis containing 5 VMs plus 10 MDs clearly outperforms a basis of the same size formed with 15 VMs only.

Fig. 6

Response of a swinging rubber beam during the first second: (a) $5\ \mbox{VMs} + 10\ \mbox{MDs}$ vs. full analysis; (b) 15 VMs vs. full analysis

The RMS error $\epsilon_{\mathrm{RMS}}$ of four reduced models with different modal basis is shown in Fig. 7. The number of VMs is fixed and equal to 5, while the number of MDs is increased to include the contribution of the first 2, 3 and 4 VMs, respectively. The error rapidly decreases as more MDs associated to the low frequency VMs are included in the basis.

Fig. 7

RMS error of the different modal basis in the swinging rubber bar example

5.3 Test 3: flexible slider–crank mechanism

In the third numerical example, a flexible slider–crank mechanism is analyzed. The system is depicted in Fig. 8 together with the material and geometric properties. The connection rod is constrained to the crank at the left end by a joint, and is fixed in vertical direction at the right end. A constant angular acceleration is prescribed to the crank such that the rotation $\theta_{s}$ reaches 270 degrees after 5 seconds, as shown in Fig. 9(a). At this point, the angular rotation of the crank is locked and the system starts to exhibit elastic oscillations in the geometrically nonlinear range.

Fig. 8

The deformed configuration of a slider–crank mechanism

Fig. 9

The elastic deflection of the flexible slider–crank mechanism using different formulations: (a) prescribed rotational angular during the 9 second time span; (b) the deflection $d_{1}$ of the middle point of the flexible crank; (c) the deflection $d_{2}$ of the middle point of the flexible rod. In (a), snapshots of the flexible crank–rod system are shown at 2, 4.5, 6, and 8.5 s

In the FFR model, two fixed nodal frames are attached to the crank and rod, respectively. The two end nodes of both crank and rod are set as the boundary nodes, and therefore 6 constraint modes are present in the reduced model for each substructure.

The elastic deflection of the middle point of both the crank and rod is shown in Fig. 9. The results obtained with the CFR have been set as a reference to check the accuracy of the full analysis in FFR. The reduction basis is formed with 5 VMs and 10 MDs (relative to the first 4 VMs) for both substructures, and the obtained results are compared with the case when only first 15 VMs are used.

The response of the system during the first 5 seconds (i.e., before the rotation locking) exhibits mainly rigid motion, and therefore both of the two reduced models show accurate results. After the locking, the elastic deflections are large and the reduction basis featuring only VMs is not able to reproduce the full solution, while the reduced basis formed with VMs and MDs yields very good results, as can be seen in Fig. 9.

The RMS error between the full and reduced solutions is computed also for this example in order to gain additional insight on the properties of the reduction basis, see Fig. 10. It can be noticed that, if not enough MDs are included in the reduction basis, the reduced solution is of poor accuracy. This could be attributed to the fact that the impulsive load generated by the rotation locking triggers the large response of the first few VMs, and therefore their interactions, which is given by the corresponding MDs, must be properly included in the basis.

Fig. 10

RMS error of the different modal basis in the flexible slider–crank example

5.4 Computational efficiency

In this subsection, the computational efficiency is compared between the nonlinear modal analysis with augmented basis $(\mathrm{VMs} + \mathrm{MDs})$ and the full nonlinear FEM analysis (NLFFR). The performance is measured in terms of computational time for Test 1: rotating beam. All the simulations are performed with MATLAB^® R2012b, on an Intel^® Core^TM i5-3470 @ 3.2 GHz and 16 GB RAM machine.

Table 3 compares the CPU time required for Test 1. The simulations are performed for 20 s with a time step $\Delta t=0.02\ \mbox{s}$. As shown in Table 3, the computational time in the case of nonlinear modal analysis mainly depends on the size of selected model reduction bases, and only slightly rises with the increase of element number owing to the time spend on modal transformation. Therefore, a substantial CPU time reduction can be achieved for application characterized by a large number of elements, which is typically the case for realistic applications.

Table 3 CPU time for the Test 1: rotating beam, between full model and reduced model

6 Conclusions

We propose a model order reduction method for the dynamic analysis of flexible multibody systems featuring large overall motion and nonlinear elastic deflection, which can be described with the von Kármán kinematic assumption in the body reference. The equations of motion are written in the floating frame of reference (FFR) for each flexible component. This enables the description of the elastic motion with an internal reduction basis complemented with interface modes, which allow the connection between the bodies via constraints. The internal basis of linear vibration modes (VMs) is enriched with modal derivatives (MDs), which describe the essential nonlinear contributions for the elastic geometric nonlinearities induced by the VMs.

The MDs can be obtained through a sensitivity analysis of the eigenvalue problem associated to the internal VMs for each component, with respect to the modal amplitudes. The reduced basis is formed by enriching a classical Craig–Bampton reduction with MDs relative to the VMs considered for each component. Subsequently, the reduced equations of motion are obtained with a Galerkin projection.

The reduction in computational time is obtained by the substantial reduction in size of the governing equations of motion. This results in the solution of a much smaller system during the time integration via the implicit scheme. Moreover, the polynomial form of the nonlinear elastic forces allows the offline computation of the reduced nonlinear terms directly in modal coordinates.

The presented numerical examples highlight the superior performance of the proposed approach with respect to classical reduction with VMs only. It is worth noting that the ad-hoc inclusion of axial vibration modes in the reduction basis does not provide results as accurate as those obtained with the proposed approach. The proposed method extends the common practice of linear modal analysis to systematically tackle geometrically nonlinear multibody problems. As a consequence, the proposed technique does not require expensive sampling of the full solution to form the reduction basis, as necessary in several model order reduction techniques based on the proper orthogonal decomposition.

The proposed approach does not pose additional conceptual difficulties for the extension into three dimensional cases. In this case, it is recommended to resort on the mean-axis definition for the floating frame of reference. This choice could be more practical than the nodal fixed frame, as the best choice of the specified fixed nodes in the nodal fixed frame is not straightforward in three dimensional cases. Also, the MDs have been successfully calculated for three dimensional models [29, 39] in the inertia frame, to solve nonlinear problems without large rigid body motion. It is worth mentioning that the benefits of the proposed technique will be even more apparent for three dimensional problems that would feature, in general, larger finite element meshes and therefore provide larger gains from the adopted modal approach.

Appendix:  The mass matrix and quadratic velocity vector

This Appendix contains a detailed formulation of the mass matrix and quadratic velocity vector. Appendix A.1 gives all the quantities in nodal formulation in Eq. (6), while Appendix A.2 refers to the reduced coordinates (i.e., modal) formulation in Eq. (39).

1.1 A.1 Precomputed offline quantities in nodal coordinates

The configuration-dependent mass matrix $\mathbf{M}$ and quadratic velocity vector $\mathbf{Q}_{v}$ can be written in a partitioned form as

$$ \mathbf{M} = \begin{bmatrix} \mathbf{M}_{rr} & \mathbf{M}_{rf} \\ \mathbf{M}_{fr} & \mathbf{M}_{ff} \end{bmatrix} = \begin{bmatrix} \mathbf{M}_{RR} & \mathbf{M}_{R\theta} & \mathbf{M}_{Rf} \\ & \mathbf{M}_{\theta\theta} & \mathbf{M}_{\theta f} \\ \mathit{sym} & & \mathbf{M}_{ff} \end{bmatrix} $$

(A.1)

and

$$ \mathbf{Q}_{v}= \begin{bmatrix} (\mathbf{Q}_{v})_{r} \\ (\mathbf{Q}_{v})_{f} \end{bmatrix} = \begin{bmatrix} (\mathbf{Q}_{v})_{R} \\ (\mathbf{Q}_{v})_{\theta} \\ (\mathbf{Q}_{v})_{f} \end{bmatrix} . $$

(A.2)

In the following, we define the components of (A.1)–(A.2) at element level as

$$\begin{gathered} \mathbf{M}_{RR}^{j}= \begin{bmatrix} m^{j} & 0 \\ 0 & m^{j} \end{bmatrix} , \end{gathered}$$

(A.3)

$$\begin{gathered} \mathbf{M}^{j}_{ff}=\overline{ \mathbf{C}}^{j T}\mathbf {S}_{ff}^{j}\overline{ \mathbf{C}}^{j}=\mathbf{D}_{1}^{j}, \end{gathered}$$

(A.4)

$$\begin{gathered} \mathbf{M}^{j}_{R\theta}=\mathbf{A}_{\theta} \mathbf{C}^{j}\overline {\mathbf{S}}^{j} \overline{C}^{j}\bigl(\mathbf{e}_{0}^{j}+\mathbf {q}_{f}^{j}\bigr)=\mathbf{A}_{\theta} \mathbf{D}_{2}^{j}\mathbf{e}_{0}^{j}+ \mathbf {A}_{\theta}\mathbf{D}_{2}^{j} \mathbf{q}_{f}^{j}, \end{gathered}$$

(A.5)

$$\begin{gathered} \mathbf{M}^{j}_{\theta\theta}=\bigl(\mathbf{e}_{0}^{j}+ \mathbf {q}_{f}^{j}\bigr)^{T}\mathbf{M}_{ff}^{j} \bigl(\mathbf{e}_{0}^{j}+\mathbf {q}_{f}^{j} \bigr)=\mathbf{e}_{0}^{jT}\mathbf{D}_{1}^{j} \mathbf {e}_{0}^{j}+2\mathbf{e}_{0}^{jT} \mathbf{D}_{1}^{j}\mathbf{q}_{f}^{j}+ \mathbf {q}_{f}^{jT}\mathbf{D}_{1}^{j} \mathbf{q}_{f}^{j}, \end{gathered}$$

(A.6)

$$\begin{gathered} \mathbf{M}^{j}_{Rf}=\mathbf{A}\mathbf{C}^{j} \overline{\mathbf {S}}^{j}\overline{\mathbf{C}}^{j}= \mathbf{A}\mathbf{D}^{j}_{2}, \end{gathered}$$

(A.7)

$$\begin{gathered} \mathbf{M}_{\theta f}^{j}=\bigl( \mathbf{e}_{0}^{j}+\mathbf{q}_{f}^{j} \bigr)^{T}\overline {\mathbf{C}}^{jT}\widetilde{ \mathbf{S}}^{j}\overline{\mathbf{C}}^{j}= \mathbf{e}_{0}^{jT}\mathbf{D}_{3}^{j}+ \mathbf{q}_{f}^{jT}\mathbf{D}_{3}^{j}, \end{gathered}$$

(A.8)

$$\begin{aligned} (\mathbf{Q}_{v})^{j}_{R} =&\dot{ \theta}^{2}\mathbf{A}\mathbf{C}^{j}\overline{\mathbf {S}}^{j}\overline{C}^{j}\bigl(\mathbf{e}^{j}_{0}+ \mathbf{q}^{j}_{f}\bigr)-2\dot{\theta }\mathbf{A}_{\theta} \mathbf{C}^{j}\mathbf{\overline{S}}^{j}\overline {\mathbf{C}}^{j}\dot{\mathbf{q}}^{j}_{f} \\ =&\dot{\theta}^{2}\mathbf{A}\mathbf{D}_{2}^{j} \bigl(\mathbf{e}_{0}^{j}+\mathbf {q}_{f}^{j} \bigr)-2\dot{\theta}\mathbf{A}_{\theta}\mathbf{D}_{2}^{j} \dot{\mathbf {q}}_{f}^{j} \end{aligned}$$

(A.9)

$$\begin{gathered} (\mathbf{Q}_{v})^{j}_{\theta}=-2 \dot{\theta}\dot{\mathbf{q}}^{jT}_{f}\mathbf {M}^{j}_{ff}\bigl(\mathbf{e}^{j}_{0}+ \mathbf{q}^{j}_{f}\bigr)=-2\dot{\theta}\dot {\mathbf{q}}^{jT}_{f}\mathbf{D}^{j}_{1}\bigl( \mathbf{e}^{j}_{0}+\mathbf{q}^{j}_{f} \bigr), \end{gathered}$$

(A.10)

$$\begin{gathered} (\mathbf{Q}_{v})^{j}_{f}= 2\dot{ \theta}\overline{\mathbf {C}}^{jT}\widetilde{\mathbf{S}}^{j} \overline{\mathbf{C}}^{j}\dot{\mathbf {q}}^{j}_{f}+ \dot{\theta}^{2}\mathbf{M}_{ff}^{j}\bigl( \mathbf{e}^{j}_{0}+\mathbf {q}^{j}_{f} \bigr)= 2\dot{\theta}\mathbf{D}_{3}^{j}\dot{ \mathbf{q}}^{j}_{f}+\dot {\theta}^{2} \mathbf{D}_{1}^{j}\bigl(\mathbf{e}^{j}_{0}+ \mathbf{q}^{j}_{f}\bigr), \end{gathered}$$

(A.11)

where the superscript $j$ refers to the element number of the corresponding body. $\mathbf{S}^{j}_{ff}\in\mathbb{R}^{6 \times6}, \overline{\mathbf{S}}^{j}\in\mathbb{R}^{2 \times6},\widetilde{\mathbf {S}}^{j} \in\mathbb{R}^{6 \times6}$ are inertia shape integrals defined for each element, $\mathbf{C}^{j}\in\mathbb{R}^{2 \times2}$, and $\overline{\mathbf{C}}^{j}\in\mathbb{R}^{6 \times6}$ are the orthogonal transformation matrix. All these quantities are constant and can be calculated offline. The details can be found in [2]. To simplify the expression, three constant matrices $\mathbf{D}_{1}^{j} \in\mathbb{R}^{6 \times6}, \mathbf{D}_{2}^{j} \in \mathbb{R}^{2\times6}, \mathbf{D}_{3}^{j} \in\mathbb{R}^{6 \times6}$ are defined as

$$ \mathbf{D}_{1}^{j}=\overline{\mathbf{C}}^{j T} \mathbf{S}_{ff}^{j}\overline {\mathbf{C}}^{j}, \qquad \mathbf{D}_{2}^{j}=\mathbf{C}^{j}\overline{ \mathbf{S}}^{j}\overline {C}^{j}, \qquad \mathbf{D}_{3}^{j}=\overline{\mathbf{C}}^{jT} \widetilde{\mathbf {S}}^{j}\overline{\mathbf{C}}^{j}. $$

(A.12)

After element assembly, the components of mass matrix $\mathbf{M}$ and quadratic velocity vector $\mathbf{Q}_{v}$ for the substructure can be expressed as

$$\begin{gathered} \mathbf{M}_{RR}= \underline{ \begin{bmatrix} m & 0 \\ 0 & m \end{bmatrix} }, \end{gathered}$$

(A.13)

$$\begin{gathered} \mathbf{M}_{ff}=\underline{\mathbf{D}_{1}}, \end{gathered}$$

(A.14)

$$\begin{gathered} \mathbf{M}_{R\theta}=\mathbf{A}_{\theta}\underline{ \mathbf{D}_{2}\mathbf {e}_{0}}+\mathbf{A}_{\theta} \underline{\mathbf{D}_{2}}\mathbf{q}_{f}, \end{gathered}$$

(A.15)

$$\begin{gathered} \mathbf{M}_{\theta\theta}=\underline{\mathbf{e}_{0}^{T} \mathbf {D}_{1}\mathbf{e}_{0}}+2\underline{ \mathbf{e}_{0}^{T}\mathbf {D}_{1}} \mathbf{q}_{f}+\mathbf{q}_{f}^{T}\underline{ \mathbf{D}_{1}}\mathbf{q}_{f}, \end{gathered}$$

(A.16)

$$\begin{gathered} \mathbf{M}_{Rf}=\mathbf{A}\underline{\mathbf{D}_{2}}, \end{gathered}$$

(A.17)

$$\begin{gathered} \mathbf{M}_{\theta f}=\underline{\mathbf{e}_{0}^{T} \mathbf{D}_{3}}+\mathbf {q}_{f}^{T}\underline{ \mathbf{D}_{3}}, \end{gathered}$$

(A.18)

$$\begin{gathered} (\mathbf{Q}_{v})_{R}=\dot{ \theta}^{2}\mathbf{A}\underline{\mathbf {D}_{2} \mathbf{e}_{0}}+\dot{\theta}^{2}\mathbf{A}\underline{\mathbf {D}_{2}}\mathbf{q}_{f}-2\dot{\theta}\mathbf{A}_{\theta} \underline{\mathbf {D}_{2}}\dot{\mathbf{q}}_{f}, \end{gathered}$$

(A.19)

$$\begin{gathered} (\mathbf{Q}_{v})_{\theta}=-2\dot{\theta}\dot{ \mathbf{q}}^{T}_{f}\underline {\mathbf{D}_{1} \mathbf{e}_{0}}-2\dot{\theta}\dot{\mathbf{q}}^{T}_{f} \underline{\mathbf{D}_{1}}\mathbf{q}_{f}, \end{gathered}$$

(A.20)

$$\begin{gathered} (\mathbf{Q}_{v})_{f}=2\dot{\theta} \underline{\mathbf{D}_{3}}\dot{\mathbf {q}}_{f}+\dot{ \theta}^{2}\underline{\mathbf{D}_{1}\mathbf{e}_{0}}+ \dot{\theta }^{2}\underline{\mathbf{D}_{1}} \mathbf{q}_{f}. \end{gathered}$$

(A.21)

All the underlined terms in equations (A.13)–(A.21) can be computed offline. The cost of their construction scales with the size of high-dimensional FE model.

1.2 A.2 Precomputed offline quantities in generalized modal coordinates

Referring to the reduced equation of motion in (39), the reduced mass matrix and quadratic velocity vector is written as

$$\begin{gathered} \overline{\mathbf{M}}= \begin{bmatrix} \mathbf{M}_{rr} & \overline{\mathbf{M}}_{rf} \\ \overline{\mathbf{M}}_{rf} & \overline{\mathbf{M}}_{ff} \end{bmatrix} = \begin{bmatrix} \mathbf{M}_{RR} & \mathbf{M}_{R\theta} & \overline{\mathbf{M}}_{Rf} \\ & \mathbf{M}_{\theta\theta} & \overline{\mathbf{M}}_{\theta f} \\ \mathit{sym} && \overline{\mathbf{M}}_{ff} \end{bmatrix} , \end{gathered}$$

(A.22)

$$\begin{gathered} \overline{\mathbf{Q}}_{v}= \begin{bmatrix} (\mathbf{Q}_{v})_{r}\\ (\overline{\mathbf{Q}}_{v})_{f} \end{bmatrix} = \begin{bmatrix} (\mathbf{Q}_{v})_{R}\\ (\mathbf{Q}_{v})_{\theta}\\ (\overline{\mathbf{Q}}_{v})_{f} \end{bmatrix} , \end{gathered}$$

(A.23)

where all the quantities can be directly expressed as:

$$\begin{gathered} \mathbf{M}_{R\theta}=\mathbf{A}_{\theta} \mathbf{D}_{2}\mathbf{e}_{0}+\mathbf {A}_{\theta} \mathbf{D}_{2}\mathbf{q}_{f}=\mathbf{A}_{\theta} \underline {\mathbf{D}_{2}\mathbf{e}_{0}}+ \mathbf{A}_{\theta}\underline{\mathbf {D}_{2}\mathbf{V}} \boldsymbol{\gamma}, \end{gathered}$$

(A.24)

$$\begin{gathered} \mathbf{M}_{\theta\theta}=\mathbf{e}_{0}^{T} \mathbf{D}_{1}\mathbf {e}_{0}+2\mathbf{e}_{0}^{T} \mathbf{D}_{1}\mathbf{q}_{f}+\mathbf {q}_{f}^{T} \mathbf{D}_{1}\mathbf{q}_{f}=\underline{ \mathbf{e}_{0}^{T}\mathbf {D}_{1} \mathbf{e}_{0}}+2\underline{\mathbf{e}_{0}^{T} \mathbf{D}_{1}\mathbf {V}}\boldsymbol{\gamma}+\boldsymbol{ \gamma}^{T}\underline{\mathbf {V}^{T}\mathbf{D}_{1} \mathbf{V}}\boldsymbol{\gamma}, \end{gathered}$$

(A.25)

$$\begin{gathered} \overline{\mathbf{M}}_{Rf}=\mathbf{M}_{Rf}\mathbf{V}= \mathbf {A}\underline{\mathbf{D}_{2}\mathbf{V}}, \end{gathered}$$

(A.26)

$$\begin{gathered} \overline{\mathbf{M}}_{\theta f}=\mathbf{M}_{\theta f}\mathbf {V}= \underline{\mathbf{e}_{0}^{T}\mathbf{D}_{3} \mathbf{V}}+\boldsymbol {\gamma}^{T}\underline{\mathbf{V}^{T} \mathbf{D}_{3}\mathbf{V}}, \end{gathered}$$

(A.27)

$$\begin{gathered} \overline{\mathbf{M}}_{ff}=\mathbf{V}^{T} \mathbf{M}_{ff}\mathbf {V}=\underline{\mathbf{V}^{T} \mathbf{D}_{1}\mathbf{V}}, \end{gathered}$$

(A.28)

$$\begin{gathered} (\mathbf{Q}_{v})_{R}=\dot{ \theta}^{2}\mathbf{A}\underline{\mathbf {D}_{2} \mathbf{e}_{0}}+\dot{\theta}^{2}\mathbf{A}\underline{\mathbf {D}_{2}\mathbf{V}}\boldsymbol{\gamma}-2\dot{\theta} \mathbf{A}_{\theta }\underline{\mathbf{D}_{2}\mathbf{V}}\dot{ \boldsymbol{\gamma}}, \end{gathered}$$

(A.29)

$$\begin{gathered} (\mathbf{Q}_{v})_{\theta}=-2\dot{\theta}\dot{ \boldsymbol{\gamma}}^{T}\underline{\mathbf{V}^{T} \mathbf{D}_{1}\mathbf{e}_{0}}-2\dot{\theta }\dot{\boldsymbol{\gamma}}^{T}\underline{\mathbf{V}^{T}\mathbf {D}_{1}\mathbf{V}}\boldsymbol{\gamma}, \end{gathered}$$

(A.30)

$$\begin{gathered} (\overline{\mathbf{Q}}_{v})_{f}= \mathbf{V}^{T}(\mathbf{Q}_{v})_{f}=2\dot {\theta} \underline{\mathbf{V}^{T}\mathbf{D}_{3}\mathbf{V}}\dot { \boldsymbol{\gamma}}+\dot{\theta}^{2}\underline{\mathbf{V}^{T} \mathbf {D}_{1}\mathbf{e}_{0}}+\dot{\theta}^{2} \underline{\mathbf{V}^{T}\mathbf {D}_{1}\mathbf{V}} \boldsymbol{\gamma}. \end{gathered}$$

(A.31)

Therefore, all the underlined terms in (A.24)–(A.31) can be computed offline during the modal analysis. Note that all the quantities can be expressed directly in reduced coordinates (i.e., not evaluated with respect to nodal coordinates and then projected) and lead therefore to a computationally efficient reduced order model.