1 Introduction

Microelectromechanical systems have been recently used in diverse applications due to their numerous advantages. Resonators [1], filters [2], various types of sensors [3] such as accelerometers and gyroscopes, different types of actuators [4, 5] are among the current applications of these systems. A comprehensive understanding of the nonlinear dynamic behavior of these systems is essential in their successful implementation in new technologies, especially those operating at frequencies near their resonance frequency. Microbeams are one of the most widely used microstructures in MEMS. Initial curvature may sometime occur in the microbeams upon the presence of a minimum defect in their production process. Therefore, consideration of the quadratic nonlinear effects of these initial curvatures is highly crucial. However, initially curved microbeams have shown several unique properties making them suitable for special research and application fields. Among these properties, bistability can be mentioned. Provided to a proper initial curvature, in contrast to the straight microbeams, these microbeams can exhibit two stable equilibrium states in specific ranges of their operation. They can jump from one equilibrium state to another, which is known as the snap-through phenomenon. No power consumption is required to maintain the bistable systems in any of the stable equilibrium states. Power is only required to transfer from one stable equilibrium state to another [6]. The other superiority of the initially curved microbeams over the straight or monostable ones is their high displacement range in addition to their high sensitivity. Thanks to their interesting and unique features, initially curved microbeams have been extensively employed in microelectromechanical systems such as actuators, sensors [7], switches [6], band-pass filters [8,9,10], non-volatile mechanical memories [11, 12] as well as applications requiring two separate stable states. Theoretical and experimental studies [13,14,15,16,17,18,19,20,21,22] have recently explored the nonlinear statics and dynamics of the initially curved microelectromechanical systems. In this regard, Zhang et al. [22] theoretically and experimentally investigated the snap-through and pull-in instabilities in the arch-shaped microbeams. Younis et al. [14] also investigated the effects of axial forces on the static behavior and fundamental natural frequency of the MEMS arches. The theoretical and experimental investigations of the nonlinear static and dynamic behavior of MEMS arches were reported by Ramini et al. [17]. They showed the softening behavior due to the quadratic nonlinear effect caused by the arch geometry and electrostatic force for the actuation close to the first resonant frequency. Ouakad et al. [13] also examined the static and dynamic behaviors of electrostatically actuated double-clamped microarches. Applying the method of multiple scales, they studied the forced vibration responses of the microarch near its natural frequency. A few papers have discussed period doubling bifurcation in curved microbeams. Najar et al. [7] studied the dynamics of a curved microbeam exposed to electrostatic actuation; they utilized the nonlinearity of the response to enhance the performance of the designed sensor.

Parallel-plates actuation is a common method for electrostatic actuation of the microbeams in the MEMS-based devices. The pull-in instability is one of the major concerns in the parallel-plate electrostatic actuation in which the fixed electrode is precisely below the microbeam and stiction may result in the collapse of the device. The key point in the design of most MEMS such as MEMS resonators and sensors is the adjustment of the applied electrostatic force to avoid pull-in. To prevent pull-in, the fringing-field out-of-plane actuation arrangement was first introduced by Rosa et al.[23]. In contrast to the parallel-plate actuation, in the out-of-plane case, the electrodes are placed on both sides of the microbeam. The fringing-field electrostatic actuation works in a contact-less manner, hence preventing pull-in instabilities. In this method, large amplitudes are not limited by pull-in instabilities and squeeze film damping. Therefore, this actuation arrangement can increase the lifelong of the devices with large-displacement ranges. Thanks to the mentioned advantages, fringing-field electrostatic actuation is highly useful for the MEMS. Ouakad [24] presented a numerical model to determine the electrostatic force in non-parallel electrodes for MEMS applications. In another study, Ouakad [25] numerically explored the nonlinear response of a CNT-based nanoactuator considering the fringing-field out-of-plane actuation arrangement. Krylov et al. [26] explored the efficient parametric excitation in microcantilever beams. Their actuation method relied on the electrostatic fringing fields. The presented resonators offer substantially large vibration amplitudes using tunable forces.

The initially curved microbeam model exposed to fringing-field electrostatic actuation offers the advantages of both the initially curved microbeam and the fringing-field electrostatic actuation, which could be highly promising for the MEMS. A limited number of studies have addressed the nonlinear dynamics of the initially curved microbeam under fringing-field electrostatic actuation. Krylov et al. [27] evaluated the possibility of two-dimensional switching of an initially curved microbeam under the fringing-field electrostatic actuation. Tausiff et al. [28] addressed a static analysis and eigenvalue problem of the MEMS arches under fringing-field electrostatic actuation. Tausiff et al.[29] also examined the nonlinear dynamic behavior of the microarches under fringing-field electrostatic actuation in the local vicinity of the fundamental natural frequency. Their results are only credible for weak nonlinearities and low amplitudes of excitation because perturbation analysis by the multiple scales method has been employed to explore the resonance behavior of the microbeam. So far, there has been no discussion in the literature about the determination of the bifurcation types and the branches that emanate from the period doubling bifurcation. Previous studies have shown the necessity of further investigation of the nonlinear behavior of initially curved microbeams under fringing-field electrostatic actuation.

The present research is aimed to comprehensively analyze the nonlinear behavior of MEMS resonators based on piezoelectrically laminated initially curved microbeam exposed to fringing-field electrostatic actuation. The adjustment of the resonance frequency is a prominent issue in MEMS resonators. In the present study, direct piezoelectric actuation is used for the adjustment of frequency and controlling the nonlinear behaviors of the structure for the first time. The nonlinear static and dynamic responses of the structure in the vicinity of primary resonance are studied, and the frequency–response curves are derived by means of shooting [30] and continuation [31] techniques; therefore, the results will be credible for strong nonlinearities and high amplitudes of excitation. The nonlinear behavior has been attributed to an appropriate source of nonlinearity, and the bifurcation points have been classified based on the associated Floquet multipliers. In this study, the period-doubled branches have been introduced by carrying out a separate study to capture the periodic solutions with a doubled period. The effects of the governing parameters including the viscous damping ratio, DC and AC electrostatic actuation as well as piezoelectric excitation on the response of the system have been examined and discussed.

2 Model description and mathematical modeling

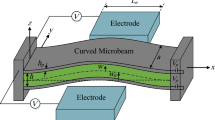
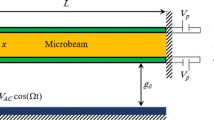
Figure 1 depicts a schematic of the curved beam along with the lateral electrodes. The double-clamped microbeam has the length, width and thickness of \(L\), \(a\) and \(h\), respectively. The initial curvature of the microbeam can be described by \(w_{0} \left( x \right) = b_{0} \left( {1 - \cos \left( {2\pi x/L} \right)} \right)/2\), in which \(b_{0}\) is the initial elevation of the midpoint of the microbeam. The material is silicon, which is considered to be isotropic and linearly elastic with Young’s modulus \(E_{b}\), Poisson’s ratio \(\upsilon_{b}\) and density \(\rho_{b}\). As the width of the microbeam is larger than its thickness \(\left( {a \ge 5h} \right)\), the effective modulus of elasticity (plane strain) is used as \(\tilde{E}_{b} = E_{b} /\left( {1 - \upsilon_{b}^{2} } \right)\)[27]. For simplicity, the sign of \(\sim\) is avoided on effective Young’s modulus. Two thin layers of PZT as a piezoelectric material are deposited throughout the length on the top and bottom surfaces of the microbeam. The thickness of the PZT layers is denoted by \(h_{{\text{p}}}\). The PZT layers are assumed to be homogenous and isotropic with the respective Young’s modulus, Poisson’s ratio and density of \(E_{{\text{p}}}\), \(\upsilon_{{\text{p}}}\) and \(\rho_{{\text{p}}}\), respectively. According to Fig. 1, the potential difference \(V_{{\text{p}}}\) is separately applied to each of the piezoelectric layers. Moreover, the lateral electrodes are symmetrically placed on either sides of the microbeam. The actuation electrodes have the length of \(L_{{\text{e}}}\), and their width and thickness are the same as the microbeam. The distance between the actuation electrodes and microbeam edge image on the \(xy\) plane is g. The potential difference \(V\) is also applied between the microbeam and actuation electrodes. The applied electrostatic voltage is a DC voltage superimposed by a single-frequency AC component.

Fig. 1
figure 1

Schematic model of a piezoelectrically laminated initially curved microbeam under fringing-field electrostatic actuation

Full size image

Application of DC voltage to the piezoelectric patches led to an axial force along the microbeam length. Such an axial force can alter the stiffness of the microbeam, hence adjusting its natural frequency. Here the electric field is only applied along the thickness of the piezoelectric \(\left(z\right)\). Based on the governing constitutive equations of the piezoelectric materials [32], the axial stress due to the piezoelectric actuation is expressed as:

$$ \sigma_{{\text{p}}} = - e_{31} E_{z} $$
(1)

in which \({E}_{z}\) is the electric field component along the z-axis and \({e}_{31}\) denotes the piezoelectric voltage constant. Considering \({E}_{z}={V}_{\mathrm{p}}/{h}_{\mathrm{p}}\), the axial force due to the piezoelectric actuation can be expressed by the following equation, which can be tensile or compressive depending on the polarity of the piezoelectric voltage:

$$ F_{{\text{p}}} = \int \sigma_{{\text{p}}} {\text{d}}A_{{\text{p}}} = - e_{31} E_{z} A_{{\text{p}}} = - e_{31} \frac{{V_{{\text{p}}} }}{{h_{{\text{p}}} }}A_{{\text{p}}} ;\quad A_{{\text{p}}} = 2ah_{{\text{p}}} $$
(2)

Having the axial force due to the piezoelectric actuation, the governing equation of the system and boundary conditions can be derived using the Hamilton’s principle. The microbeam is assumed to be long and thin \(\left(h\ll L\right)\) with shallow curvature \(\left({b}_{0}\ll L\right)\); therefore, the displacement field can be expressed by[33]:

$$ \begin{gathered} u_{x} \left( {x,z,t} \right) = u\left( {x,t} \right) - z\frac{{\partial u_{z} \left( {x,t} \right)}}{{\partial x}} \hfill \\ u_{y} \left( {x,z,t} \right) = 0 \hfill \\ u_{z} \left( {x,z,t} \right) = w_{0} \left( x \right) + w\left( {x,t} \right) \hfill \\ \end{gathered} $$
(3)

in which \(u\left(x,t\right)\) and \(w\left(x,t\right),\) respectively, represent the axial and transverse displacements of each point on the neutral axis. Von-Karman theory is also used to account for the geometrical nonlinear effects due to the mid-plane stretching [34]. Based on the Von-Karman assumptions, the only nonzero component of the strain tensor will be:

$$ \varepsilon_{xx} = u^{\prime} + \frac{{\left( {w^{\prime}} \right)^{2} }}{2} + w^{\prime}_{0} w^{\prime} - zw^{\prime\prime} $$
(4)

According to Hamilton’s principle [35, 36]:

$$ \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \left( {\delta T - \delta U + \delta W_{{{\text{ext}}}} + \delta W_{{{\text{damping}}}} } \right)dt = 0 $$
(5)

in which \(T\) and \(U\), respectively, show the total kinetic and strain potential energies, \(W_{{{\text{ext}}}}\) denotes the work done by the electrostatic force and \(W_{{{\text{damping}}}}\) is the work done by damping. By ignoring the rotational inertia, total kinetic energy can be determined as:

$$ T = T_{b} + T_{{\text{p}}} = \frac{1}{2}\left( {\rho A} \right)_{{{\text{eq}}}} \mathop \int \limits_{0}^{L} \left( {\dot{u}^{2} + \dot{w}^{2} } \right){\text{d}}x $$
(6)

where

$$ \left( {\rho A} \right)_{{{\text{eq}}}} = \rho_{b} A_{b} + \rho_{{\text{p}}} A_{{\text{p}}} = \rho_{b} ah + 2\rho_{{\text{p}}} ah_{{\text{p}}} $$
(7)

Moreover, the total strain potential energy can be determined by the following equation:

$$ U = U_{b} + U_{{\text{p}}} = \frac{1}{2}\int {\left( {\left( {\sigma_{xx} } \right)_{b} \varepsilon_{xx} } \right){\text{d}}V_{b} } + \frac{1}{2}\int {\left( {\left( {\sigma_{xx} } \right)_{{\text{p}}} \varepsilon_{xx} } \right){\text{d}}V_{p} } $$
(8)

where

$$ \left( {\sigma_{xx} } \right)_{b} = E_{b} \varepsilon_{xx} ,\quad \left( {\sigma_{xx} } \right)_{{\text{p}}} = E_{{\text{p}}} \varepsilon_{xx} - E_{z} e_{31} = E_{{\text{p}}} \varepsilon_{xx} - \frac{{V_{{\text{p}}} }}{{h_{{\text{p}}} }}e_{31} $$
(9)

It is to be noted that since a perfect bonding is assumed between the piezoelectric layers and the microbeam, the strain of the piezoelectric layer is equal to that of the microbeam at the interface. The work done by the fringing-field electrostatic force and damping is expressed as:

$$ W_{{{\text{ext}}}} = \int\limits_{0}^{L} {f_{{\text{e}}} w{\text{d}}x} ,\quad W_{{{\text{damping}}}} = - C_{{\text{d}}} \mathop \int \limits_{0}^{L} \frac{\partial w}{{\partial t}}w{\text{d}}x $$
(10)

in which \({f}_{\mathrm{e}}\) is the electrostatic force per unit of length and \({C}_{\mathrm{d}}\) denotes the viscose damping coefficient. By substituting the variation of the kinetic and potential energies and works done by the electrostatic force and damping in the Hamilton’s principle (Eq. 5), performing integration by parts and neglecting the effects of the longitudinal inertia compared with the transverse inertia, the governing equation of the transverse vibrations can be determined as:

$$ \left( {{\text{EI}}} \right)_{{{\text{eq}}}} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {\rho A} \right)_{{{\text{eq}}}} \frac{{\partial^{2} w}}{{\partial t^{2} }} + C_{{\text{d}}} \frac{\partial w}{{\partial t}} = \left[ {F_{{\text{p}}} + \frac{{\left( {{\text{EA}}} \right)_{{{\text{eq}}}} }}{2L}\mathop \int \limits_{0}^{L} \left( {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + 2\frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right){\text{d}}x} \right]\left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{{\text{d}}^{2} w_{0} }}{{{\text{d}}x^{2} }}} \right] + f_{{\text{e}}} $$
(11)

where

$$ \begin{gathered} \left( {{\text{EI}}} \right)_{{{\text{eq}}}} = E_{b} I_{b} + E_{{\text{p}}} I_{{\text{p}}} = E_{b} \frac{{ah^{3} }}{12} + E_{{\text{p}}} a\left( {h_{{\text{p}}} h\left( {\frac{h}{2} + h_{{\text{p}}} } \right) + \frac{{2h_{{\text{p}}}^{3} }}{3}} \right) \hfill \\ \left( {{\text{EA}}} \right)_{{{\text{eq}}}} = E_{b} A_{b} + E_{{\text{p}}} A_{{\text{p}}} = E_{b} ah + 2E_{{\text{p}}} ah_{{\text{p}}} \hfill \\ \end{gathered} $$
(12)

Furthermore, the electrostatic force per unit of length \(\left({f}_{e}\right)\) can be expressed as:

$$ f_{e} = - \frac{{r\sinh \left( {q\left( {w_{0} + w} \right)} \right) \times V^{2} }}{{\cosh^{s} \left( {q\left( {w_{0} + w} \right)} \right)}}H\left( {x - \frac{{L - L_{e} }}{2}} \right)H\left( {L_{e} + \frac{{L - L_{e} }}{2} - x} \right) $$
(13)

In the above equation, \(H\left(x\right)\) is the Heaviside step function and \(V = \left[ {V_{{{\text{DC}}}} + V_{{{\text{AC}}}} \cos \left( {\Omega t} \right)} \right]\). The boundary conditions associated with Eq. (11) are:

$$ w\left( {0,t} \right) = 0,\quad w\left( {L,t} \right) = 0,\quad \frac{{\partial w\left( {0,t} \right)}}{\partial x} = 0,\quad \frac{{\partial w\left( {L,t} \right)}}{\partial x} = 0 $$
(14)

The governing dimensionless equation and boundary conditions are determined by introducing the following nondimensional parameters:

$$ \hat{w} = \frac{w}{h},\quad \hat{w}_{0} = \frac{{w_{0} }}{h},\quad \hat{x} = \frac{x}{L},\quad \hat{L}_{{\text{e}}} = \frac{{L_{{\text{e}}} }}{L},\quad \hat{t} = \frac{t}{{\tilde{t}}},\quad {\tilde{\Omega }} = {\Omega }\tilde{t} $$
(15)

where \(\tilde{t} = \sqrt {\left( {\rho A} \right)_{{{\text{eq}}}} L^{4} /\left( {EI} \right)_{{{\text{eq}}}} }\). By substituting Eq. (15) in Eq. (11), the transverse vibration equation of the system can be obtained in the dimensionless form. The over hat (^) is eliminated for the sake of simplicity:

$$ \begin{aligned} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{2} w}}{{\partial t^{2} }} + C\frac{\partial w}{{\partial t}} & = \left[ {P + \alpha_{1} \mathop \int \limits_{0}^{1} \left( {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + 2\frac{\partial w}{{\partial x}}\frac{{dw_{0} }}{dx}} \right){\text{d}}x} \right]\left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{{\text{d}}^{2} w_{0} }}{{{\text{d}}x^{2} }}} \right] \\ \quad - \alpha_{2} \frac{{\sinh \left( {q\left( {w_{0} + w} \right)} \right)}}{{\cosh^{s} \left( {q\left( {w_{0} + w} \right)} \right)}}H\left( {x - \frac{{1 - L_{{\text{e}}} }}{2}} \right)H\left( {L_{{\text{e}}} + \frac{{1 - L_{{\text{e}}} }}{2} - x} \right) \\ \end{aligned} $$
(16)

where

$$ C = \frac{{C_{d} L^{4} }}{{\tilde{t}\left( {{\text{EI}}} \right)_{{{\text{eq}}}} }},\quad P = \frac{{F_{{\text{p}}} L^{2} }}{{\left( {{\text{EI}}} \right)_{{{\text{eq}}}} }},\quad \alpha_{1} = \frac{{h^{2} \left( {{\text{EA}}} \right)_{{{\text{eq}}}} }}{{2\left( {{\text{EI}}} \right)_{{{\text{eq}}}} }},\quad \alpha_{2} = \frac{{rL^{4} V^{2} }}{{\left( {{\text{EI}}} \right)_{{{\text{eq}}}} h}} $$
(17)

In Eq. (17), \(C=2\xi {\omega }_{\mathrm{n}}\) where \(\xi \) and \({\omega }_{\mathrm{n}}\) indicate the damping ratio and the natural frequency, respectively. The dimensionless boundary conditions for Eq. (16) are as follows:

$$ w\left( {0,t} \right) = 0,\quad w\left( {1,t} \right) = 0,\quad \frac{{\partial w\left( {0,t} \right)}}{\partial x} = 0,\quad \frac{{\partial w\left( {1,t} \right)}}{\partial x} = 0 $$
(18)

3 Reduced-order model based on the Galerkin decomposition method

In the Galerkin decomposition method, the solution of Eq. (16) is considered as follows:

$$ w\left( {x,t} \right) = \mathop \sum \limits_{i = 1}^{M} u_{i} \left( t \right)\varphi_{i} \left( x \right) $$
(19)

In Eq. (19), \({\varphi }_{i}\left(x\right)\) are admissible functions satisfying the boundary conditions in Eq. (18) and \({u}_{i}\left(t\right)\) are also unknown time-dependent generalized coordinates. Normalized mode shapes of the double-clamped straight microbeams considering the effect of the axial force due to the piezoelectric actuation, given in Eq. (20), can be used as the admissible functions in the Galerkin method:

$$ \begin{gathered} \varphi_{i}^{{\left( {iv} \right)}} = P\varphi^{\prime\prime}_{i} + \omega_{i}^{2} \varphi_{i} \hfill \\ \varphi_{i} \left( 0 \right) = 0,\quad \varphi_{i} \left( 1 \right) = 0,\quad \varphi^{\prime}_{i} \left( 0 \right) = 0,\quad \varphi^{\prime}_{i} \left( 1 \right) = 0 \hfill \\ \end{gathered} $$
(20)

where \({\omega }_{i}\) is the \(i\)-th natural frequency of the double-clamped straight microbeam under axial piezoelectric actuation. By substituting Eq. (19) into Eq. (16), multiplying both sides of the equation by \({\varphi }_{i}\left(x\right)\) and integrating the resultant over the interval \(x=\left[\mathrm{0,1}\right]\), the reduced-order model is obtained as:

$$ \begin{gathered} \ddot{u}_{n} + C\dot{u}_{n} + \mathop \sum \limits_{i = 1}^{M} u_{i} \left( t \right)\mathop \int \limits_{0}^{1} \varphi_{i}^{{\left( {iv} \right)}} \varphi_{n} dx - P\left( {\mathop \sum \limits_{i = 1}^{M} u_{i} \left( t \right)\mathop \int \limits_{0}^{1} \varphi^{\prime\prime}_{i} \varphi_{n} dx + \mathop \int \limits_{0}^{1} w^{\prime\prime}_{0} \varphi_{n} dx} \right) \hfill \\ - \alpha_{1} \left( \begin{gathered} \mathop \sum \limits_{i = 1}^{M} \mathop \sum \limits_{j = 1}^{M} \mathop \sum \limits_{k = 1}^{M} u_{i} u_{j} u_{k} \mathop \int \limits_{0}^{1} \varphi^{\prime}_{i} \varphi^{\prime}_{j} dx\mathop \int \limits_{0}^{1} \varphi^{\prime\prime}_{k} \varphi_{n} dx + \mathop \sum \limits_{i = 1}^{M} \mathop \sum \limits_{j = 1}^{M} u_{i} u_{j} \mathop \int \limits_{0}^{1} \varphi^{\prime}_{i} \varphi^{\prime}_{j} dx\mathop \int \limits_{0}^{1} w^{\prime\prime}_{0} \varphi_{n} dx \hfill \\ + 2\mathop \sum \limits_{i = 1}^{M} \mathop \sum \limits_{j = 1}^{M} u_{i} u_{j} \mathop \int \limits_{0}^{1} \varphi^{\prime}_{i} w^{\prime}_{0} dx\mathop \int \limits_{0}^{1} \varphi^{\prime\prime}_{j} \varphi_{n} dx + 2\mathop \sum \limits_{i = 1}^{M} u_{i} \mathop \int \limits_{0}^{1} \varphi^{\prime}_{i} w^{\prime}_{0} dx\mathop \int \limits_{0}^{1} w^{\prime\prime}_{0} \varphi_{n} dx \hfill \\ \end{gathered} \right) \hfill \\ = - \alpha_{2} \mathop \int \limits_{0}^{1} \frac{{\sinh \left( {q\left( {w_{0} + \mathop \sum \nolimits_{i = 1}^{M} u_{i} \varphi_{i} } \right)} \right)\varphi_{n} \left( x \right)}}{{\cosh^{s} \left( {q\left( {w_{0} + \mathop \sum \nolimits_{i = 1}^{M} u_{i} \varphi_{i} } \right)} \right)}}H\left( {x - \frac{{1 - L_{e} }}{2}} \right)H\left( {L_{e} + \frac{{1 - L_{e} }}{2} - x} \right)dx \hfill \\ \end{gathered} $$
(21)

Such that \(n=\mathrm{1,2},3,\dots ,M\). Equation (21) is the reduced order model of the transverse vibration of the initially curved double-clamped microbeam under simultaneous piezoelectric and fringing-field electrostatic actuation. The reduced-order model includes the system of nonlinear ordinary differential equations in terms of the generalized coordinates \({u}_{i}\left(t\right)\), which requires to be integrated over the time.

4 Static and dynamic solutions

For the static analysis, the time-dependent terms in Eq. (21) are set to be zero. Hence, the generalized coordinates are assumed to be unknown constant coefficients. The resultant system of algebraic equations is numerically solved for the generalized coordinates based on Newton–Raphson algorithm. For the dynamic analysis, the equations governing the reduced-order model are numerically integrated over time to capture the time response in a given time. The periodic solutions in the vicinity of the primary resonance are captured by applying the shooting technique to the motion equations. Shooting is a powerful numerical technique for capturing both stable and unstable periodic solutions. However, depending on the studied model, finding unstable periodic solutions may require numerous iterations or multiple initial guesses. The most important advantage of the shooting method is that it does not require integrating the equations over a long time to let the response settle on the stable limit cycle. In the case of nonautonomous systems as the model in this study is, the integration is carried out over one entire period \(T=2\pi /\Omega \) (for primary resonance), in which \(\Omega \) is the frequency of the excitation. Once the periodic solution is captured, its stability is examined by means of determination, the so-called Floquet exponents.

5 Results and discussion

5.1 Estimation of the electrostatic force

As illustrated in Fig. 2, the potential difference between the electrodes and the curved beam generates fringing-field lines, and accordingly due to each individual electrode, two forces along (z) and (y) directions are applied to the microbeam. In the symmetric configuration, both y and z components of the overall force are canceled out as the corresponding components of the forces due to each of the electrodes are in opposite directions and the same magnitude; this yields in zero net force applied on the microbeam; however, in the asymmetric configuration which is the case for the present study, though the y component of the total force vanishes, the out-of-plane component turns out to be nonzero.

Fig. 2
figure 2

Fringing-field electrostatic actuation method: (a): symmetric configuration, (b) asymmetric configuration

Full size image

The electrostatic force in the asymmetric excitation, in contrast to the parallel-plate case, cannot be analytically calculated in a closed form [27] and needs to be determined numerically. To compute the electrostatic force, a finite element simulation (Fig. 3) is carried out using the geometrical and material properties of the studied model in Table 1. Figure 4 shows the magnitude of the electrostatic force per unit of length versus the normalized vertical offset for a 1V electrostatic force. An appropriate fitting function based on least-square error is also applied to represent the electrostatic force per unit of length as follows:

$$ f_{e} = - \frac{{r\sinh \left( {q\left( {d/h} \right)} \right)}}{{\cosh^{s} \left( {q\left( {d/h} \right)} \right)}} $$
(22)

where \(d/h\) is the normalized vertical offset; \(r\), \(q\) and \(s\) are the fitting parameters given in Table 2.

Fig. 3
figure 3

Finite element simulation of the micro-resonator: (a) electric potential contour, (b) electric force distribution around the microbeam

Full size image
Table 1 Geometrical and material properties of the studied model
Full size table
Fig. 4
figure 4

Magnitude of the electrostatic force per unit of length versus the normalized vertical offset

Full size image
Table 2 Fitting parameters of the electrostatic force
Full size table

5.2 Static and dynamic analysis

To perform validation, the results of the current model are compared with those presented in reference [28]. For this purpose, the initially curved microbeam with geometrical and mechanical properties studied in reference [28] is considered. The variations of the microarch mid-point elevation with respect to the DC voltage for the present study, along with the results of Tausiff et al., are shown in Fig. 5. As observed, there is very good agreement between the results.

Fig. 5
figure 5

Variation of midpoint elevation with DC voltage: validation of the current model

Full size image

For static and dynamic analyses, a shallow initially curved microbeam with geometrical and material properties given in Table 1 is considered. Figure 6 illustrates the center deflection of the microbeam versus the applied DC electrostatic voltage. The computations are based on two different methods including Newton–Raphson algorithm and continuation method thanks to the Matcont Toolbox MATLAB. As depicted, there exists a reasonable convergency for one mode and it is confirmed by both approaches.

Fig. 6
figure 6

Center deflection of the microbeam by Newton–Raphson and continuation methods

Full size image

Figure 7a illustrates the static deflection of the mid-point of the microbeam for various initial curvatures in terms of the applied DC voltage; this reveals that the qualitative response of the microbeam strongly depends on the initial gap and microbeams with greater initial gaps are more likely to exhibit bistable behavior. Figure 7b shows the effect of the polarity of the piezoelectric actuation on the deflection of the midpoint of the microbeam. Positive and negative polarities are located in either sides VP = 0 V, which reveals the two-side tunability offered to the system thanks to the piezoelectric excitation.

Fig. 7
figure 7

Center deflection of the microbeam for a Vp = 0 V and various b0 s, b b0 = 4 μm and various Vp s

Full size image

Applying electrostatic force implicitly changes the stiffness of the microbeam as it superimposes additional stiffness to the structural stiffness, and accordingly, the natural frequency of the system varies. This is illustrated in Fig. 8.

Fig. 8
figure 8

Variation of the natural frequency versus the applied electrostatic voltage

Full size image

To discuss the variation of the natural frequency versus VDC, the linear stiffness due to the electrostatic voltage is computed and depicted in Fig. 9.

Fig. 9
figure 9

Variation of the linear stiffness versus the electrostatic voltage

Full size image

As VDC increases, the linear stiffness due to the electrostatic voltage slightly decreases in value and it softens the overall stiffness, and as a result, the natural frequency of the microbeam decreases. When the voltage exceeds 83.9 V, the linear stiffness of the electrostatic term becomes positive and causes the microbeam to stiffen. However, the curvature still has a softening effect. Once the voltage surpasses 90 V, the electrostatic voltage's hardening effect takes over and the natural frequency begins to increase. Comparing the effect of VDC on the natural frequency reveals that for the fringing-field excitation the natural frequency would either increase or decrease with VDC, which depends on the value of the applied electrostatic voltage; however, in case of parallel-plate excitation, the natural frequency has been reported to monotonically decreasing with the electrostatic voltage. Applying VP with positive polarity stiffens the microbeam and consequently increases the natural frequency; however, the negative polarity generates compressive axial force and accordingly the overall stiffness of the system reduces. Confrontation of the softening and hardening effects of the piezoelectric force and the electrostatic excitation brings about bifurcation and origination of multi-response solution regions, which is illustrated in Fig. 10.

Fig. 10
figure 10

The variation of the center deflection with versus VDC for various Vp s (SN: Saddle Node)

Full size image

For VP = − 0.37 V, by increasing the electrostatic voltage the equilibrium position moves further below the original equilibrium position. As the magnitude of the piezoelectric voltage increases, the mid-part of the solution curve bends backward and consequently a multi-response solution region emerges as a result of saddle node bifurcation, which yields in snap-through buckling. Existence of snap-through bifurcation in MEMS switches enables switching without sticking the structure to the substrate, which substantially limits the functionality of pull-in-based switches in MEMS [37, 38]. For VP = − 0.41 V and less than it, the system exhibits two stable and one unstable equilibrium points before the saddle node bifurcation point. As the bifurcation point is passed, the unstable solution disappears, and the stable solutions reduces to one which increases in amplitude as VDC increases (Fig. 10b).

The frequency response of the microbeam exposed to various VDC s and VP = 0 V is given in Fig. 11. As illustrated, in the absence of VDC, the excitation frequency is doubled [39, 40], and consequently, the primary resonance occurs at 29.12. Applying VDC prevents doubling of the excitation frequency, and as a result, the primary resonance occurs at 57.28. Further increase in the electrostatic voltage amplifies the nonlinearity and two bifurcations emerge on the frequency–response curve (Fig. 11c). The Floquet multipliers here at the cyclic fold bifurcation exit the unit circle through + 1. The corresponding eigenvalues of the periodic solutions are illustrated as inset in Fig. 11c. As the bifurcation parameter (\(\Omega \)) increases, the stable and unstable manifolds of the linearized system approach each other and intersect at the bifurcation point, beyond which both manifolds disappear. It is important to observe that eigenvalues having a magnitude larger than one represent unstable periodic solutions, whereas eigenvalues with a magnitude smaller than one are linked to stable periodic solutions. To comprehensively discuss the frequency–response curves, the coefficients of the quadratic and cubic nonlinear stiffness terms due to electrostatic excitation are computed in terms of VDC, as illustrated in Fig. 12. Starting from VDC = 0 V the linear stiffness dominates and accordingly the system exhibits a linear response (Fig. 11a). By increasing VDC, the amplitude of the motion increases and the nonlinear terms become strong enough to dominate the linear terms and accordingly the system undergoes bifurcation on the frequency–response curves (Fig. 11c). For small enough VDCs, the quadratic term softens; however, the cubic term confronts against and increases the stiffness. For VDC = 50 V, the frequency–response curve in the resonance region bends leftward and accordingly exhibits softening response which is attributed to the quadratic nonlinearity; however, in the vicinity of the peak point, a cyclic fold bifurcation occurs; beyond this bifurcation point, the cubic nonlinearity gets more prominent and the frequency response slightly returns back to the right and an unstable branch of solution originates, which eventually connects to the lower branch of the stable solution through another cyclic fold bifurcation. The slight hardening nature of the response in the vicinity of the peak is associated with the cubic nonlinearity of the electrostatic force. For VDC = 90 V, the cubic nonlinearity increases in value and the hardening nature of the response gets more pronounced. As illustrated in Fig. 11d, the backward hardening loop gets larger in size and the cyclic fold bifurcation points are symmetrically placed on either side of the primary resonance frequency. Further increase of the excitation frequency yields in the generation of two more period-doubling bifurcation points, which are represented by PD on the frequency–response curve. The loci of the Floquet multipliers are represented as an inset in Fig. 11 (d) where they exit the unit circle through − 1 and a new branch of period-doubled stable solution originates which is shown for both of the bifurcation points. We believe the nonlinear dynamics of the microbeam in this region requires further investigation as a period doubling route to chaos is likely to occur by increasing the amplitude of VAC [41]. We have introduced the period-doubled branch by carrying out a separate study to capture the associated periodic solutions. For VDC > 104.9, the cubic and quadratic electrostatic terms become negative, and consequently, they both soften the microbeam; this is depicted in Fig. 11e in which the frequency–response curve is bent leftward indicating the domination of softening nonlinearity.

Fig. 11
figure 11

Frequency–response curves for VP = 0 V, \(V_{{{\text{AC}}}} = 30\;{\text{V}}\) a VDC = 0 V, b VDC = 20 V, c VDC = 50 V, d VDC = 90 V, e VDC = 180 V

Full size image
Fig. 12
figure 12

The coefficients of nonlinear quadratic and cubic terms

Full size image

It is important to observe that eigenvalues having a magnitude larger than one represent unstable periodic solutions, whereas eigenvalues with a magnitude smaller than one are linked to stable periodic solutions.

The results of the shooting method are compared to those of the continuation method which for \(V_{{{\text{DC}}}} = 50\,{\text{V}}, \;V_{{{\text{AC}}}} = 30\;{\text{V}},\; V_{{\text{p}}} = 0.0\;{\text{V}}, \;\xi = 0.06\) and various excitation frequencies is given in Table 3.

Table 3 Amplitudes of the periodic solutions computed based on shooting and continuation methods
Full size table

Considering the parameters as of Fig. 11d, forward and backward frequency sweeps are carried out to explore the time response as the frequency passes over the period-doubling bifurcation point. Figure 13 illustrates the time response as the frequency is forward swept from \(\Omega =39\) up to Ω = 48; the period-doubling bifurcation remains within the scanned frequency (Fig. 11d) and the system response undergoes a period doubling and meanwhile a quick increase in amplitude as \(\Omega \) passes the bifurcation point; this is qualitatively justified by the topology of the frequency–response curve. Here the time rate of the frequency sweep is assumed to be small enough to avoid the transient responses due to the frequency change.

Fig. 13
figure 13

Forward frequency sweep considering VP = 0 V, VAC = 30 V, VDC = 90 V, a Frequency variation, b Time response

Full size image

Figure 14 illustrates backward sweep with the excitation voltages as of Fig. 13. The frequency is swept from \(\Omega =63\) to \(\Omega =55\); the second period doubling bifurcation point falls within the excitation range.

Fig. 14
figure 14

Backward frequency sweep considering VP = 0 V, VAC = 30V, VDC = 90V, a Frequency variation, b Time response

Full size image

Starting from the excitation frequency \(\Omega =63\), the time response settles on the associated limit cycle, and while decreasing the excitation frequency (Fig. 14a), the amplitude of the motion gradually increases while the frequency passes the period-doubling bifurcation where a catastrophic jump [42,43,44,45] occurs and the response settles into a high-amplitude period-doubled attractor.

Assuming \(\Omega =50\) and the excitation voltages as of Fig. 11d, the only stable attractor is a period-doubled limit cycle; the time response and the corresponding phase planes are depicted in Fig. 15.

Fig. 15
figure 15

Response for VP = 0V, VAC = 30 V, VDC = 90V, \(\Omega = 50\) a Time response, b Phase plane

Full size image

Considering VP = 0V, VDC = 50 V, the effect of \(V_{{{\text{AC}}}}\) for \(\xi = 0.06\) and damping for VAC = 30 V on the frequency–response curves is shown in Figs. 16 and 17, respectively.

Fig. 16
figure 16

Frequency response for VP = 0V, VDC = 50V, \(\xi = 0.06\), a \(V_{{{\text{AC}}}} = 40{\text{V}}\), b \(V_{{{\text{AC}}}} = 50{\text{V}}\)

Full size image
Fig. 17
figure 17

Frequency response for VP = 0V, VAC = 30V, VDC = 50V, a \(\xi = 0.05\) b \(\xi = 0.04\)

Full size image

The illustration indicates that, when VAC increases or \(\xi \) decreases in value, the amplitude of the captured limit cycles also increases. The nonlinear terms become more significant in the response as the amplitude of the oscillations increases. When the VDC is set to 50 V, the system experiences both softening and hardening effects, which are the result of the quadratic and cubic electrostatic stiffness terms that are superimposed on the linear and nonlinear geometric stiffness terms; the result is a bending of the frequency–response curve toward the left in the resonance region, followed by a return toward the right for higher amplitude solutions, resulting in a backward loop at the peak of the resonance zone. This loop gets larger as VAC increases. The frequency–response curves display the bifurcation points, which include cyclic fold and period-doubling bifurcations.

Figure 18 shows the effect of the initial curvature on the frequency–response curves for two different initial curvatures including b0 = 3 μm and b0=5 μm. It is illustrated that as the initial curvature increases the resonance region shifts toward right and primary resonance increases.

Fig. 18
figure 18

Frequency response for VP = 0V, VDC = 50V, VAC = 30V, \(\xi = 0.06\). a \(b_{0} = 3\) μm, (b): \(b_{0} = 5\) μm

Full size image

The effect of the polarity of the piezoelectric voltage on the quality of the frequency–response curves is depicted in Fig. 19.

Fig. 19
figure 19

Frequency response for VDC = 50 V, VAC = 30 V, \(\xi = 0.06\) a \(V_{{\text{p}}} = + 0.3\;{\text{V}}\), (b): \(V_{{\text{p}}} = - 0.3\;{\text{V}}\)

Full size image

It is indicated that applying \({V}_{\mathrm{p}}\) with positive polarity shifts the frequency–response curve rightward along the frequency axis. Conversely piezoelectric excitation with negative polarity shifts the frequency–response curve toward left; this is because positive and negative polarities generate tensile and compressive forces, respectively, which accordingly increases and reduces the linear stiffness. When a positive polarity is applied, not only does the frequency–response curve shift towards the right, but the amplitude of the limit cycles in the resonance region also decreases. This results in a weakening of the non-linearity of the response.

The force–response curves corresponding to three different excitation frequencies including \({\Omega } = 34\) , \({\Omega } = 37\) and \({\Omega } = 40\) and for \(V_{{{\text{AC}}}} = 30\;{\text{V}},\; V_{{{\text{DC}}}} = 50\;{\text{V}},\; \xi = 0.06\) are illustrated in Fig. 20. For \({\Omega } = 34\), the force–response curve is a single-valued curve (Fig. 20a), and the amplitude of the limit cycles monotonically increases as the amplitude of the VAC increases. For \({\Omega } = 37\) the force response curve is depicted in Fig. 20b which exhibit a nonlinear multi-response behavior and the system exhibits two cyclic fold and period doubling bifurcations. Points B, C and D are associated with the corresponding ones in Fig. 11c. When \({\Omega }\) is set to 40, the system exhibits the similar force response curve as of \({\Omega } = 37\) but with lower amplitudes for the periodic solutions corresponding to each individual excitation frequency.

Fig. 20
figure 20

Force–response curves corresponding to (a): \(\Omega = 34\) b \(\Omega = 37\) c \(\Omega = 40 \)with \(V_{{{\text{AC}}}} = 30\;{\text{V}}, \;V_{{{\text{DC}}}} = 50\;{\text{V}},\; \xi = 0.06\)

Full size image

6 Conclusion

This paper explores the nonlinear dynamics of an initially curved microbeam subjected to an out-of-plane fringing field effect. The microbeam is also simultaneously excited by piezoelectric layers attached to both the top and bottom layers along its entire length. The equation of the motion was derived by minimizing the Hamiltonian over the time and reduced to a finite degree of freedom system using the Galerkin technique. The convergency of the reduced-order model was studied, and the reduced order model was justified for the applied excitation parameters. Both static and dynamic analyses were performed, leading to the conclusion that the system exhibits bi-stability and consequently snap-through bifurcation. This finding holds great promise, especially in the context of bifurcation-based MEMS switches. The fringing field electrostatic force was numerically evaluated, and the implicit quadratic and cubic nonlinearities were determined by means of expanding the electrostatic force in Taylor series about the static equilibrium position. It was shown that for the values of the electrostatic force below a certain level, the softening and hardening effects exist simultaneously, whereas beyond that certain level the electrostatic force becomes purely softening. It was concluded that for the VDC below the mentioned threshold, the system exhibits both softening and hardening behaviors; however, for the voltages beyond the threshold voltage the softening nonlinearity dominates the response and the frequency–response curves bent leftward on the resonance region. The frequency–response curves in the vicinity of the primary resonance were computed based on the shooting technique and verified with the continuation method. It was shown that when the nonlinear terms become significant, the system bifurcates and having identified the bifurcation points, they were classified based on the loci of the associated Floquet exponents within the unit circle on the complex plane. The branches of the frequency–response curve emanating from the period–doubling bifurcation points were computed, and the transition from period-1 limit cycle to a period-2 one as the excitation frequency passes over the associated bifurcation point was investigated. The findings from the study are encouraging for the development of high-amplitude MEMS resonators in the future.