An analytical framework for understanding infection progression under social mitigation measures

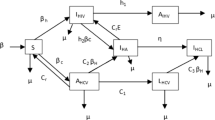
Abstract

While there has been much computational work on the effect of intervention measures, such as vaccination or quarantine, the influence of social distancing on the epidemics’ outbursts is not well understood. We present a realistic, analytically solvable, framework for COVID-19 dynamics in the presence of social distancing measures. The model is a generalization of the compartmental SEIR model that accounts for the effects of these measures. We derive a closed-form mathematical expressions for the time dependence of epidemiological observables, in particular, the detected cases and fatalities. These analytical solutions indicate simple quantitative relations between the model variables and epidemiological observables, which give insights into cause-effect connections that underlie the outburst dynamics but are obscured in more standard (numerical) approaches. While the obtained results and conclusions are based on the study of the COVID-19 pandemic, the presented analysis has general applicability to infection outbursts. Our findings are particularly important in the emergence of new pandemics when effective pharmaceutical treatments are unavailable, and one must rely on well-timed and appropriately chosen social mitigation measures.

A Appendix

1.1 A.1 Analytical derivation of the number of fatalities

To assess the dynamics of COVID-19 infection, we employed the mechanistic model, defined by equations (1)-(8). In Ref. [58], we have already obtained the number of infectious individuals as a function of time (9).

Throughout the derivations, we will distinguish two-time regions: I) $t\le t_0$ and II) $t> t_0$, and will denote the variables in these two regions accordingly.

First, we concentrate on deriving the expression for the time evolution of the number of fatalities. To this end, we start from Eqs. (7)-(8), which lead to a single equation (10). In region I, this second-order inhomogeneous differential equation, after taking into account the first term of Eq. (9) (i.e., $I_I(t)=I_0 \textrm{e}^{\lambda _+ t}$), reduces to:

$$\begin{aligned} \frac{\textrm{d}^2F_I(t)}{\textrm{d}t^2}+(h+m) \frac{\textrm{d}F_I(t)}{\textrm{d}t}-m \epsilon \delta I_0 \textrm{e}^{\lambda _+ t}=0. \end{aligned}$$

(28)

If we assume $F_I(t=0)=0$ and $F'_I(t=0)=0$, the time-dependent fatalities for $t\le t_0$ are given by:

$$\begin{aligned} F_I(t)&= \frac{I_0 \epsilon \delta }{\lambda _+} \frac{m}{m+h}\Big \{-1+\frac{\lambda _+}{h+m+\lambda _+}\textrm{e}^{-(h+m) t} \nonumber \\&\quad +\frac{h+m}{h+m+\lambda _+} \textrm{e}^{\lambda _+ t}\Big \}. \end{aligned}$$

(29)

In region II, for simplicity we shift $t-t_0 \rightarrow t$, and take into account that the expression for infectious now reads $I_{II}(t) =I_0\textrm{e}^{\lambda _+ t_0} \textrm{e}^{-\frac{\gamma +\epsilon \delta + \sigma }{2}t} \textrm{K}\big (\frac{\gamma +\epsilon \delta - \sigma }{\alpha }, \frac{2\sqrt{\textrm{e}^{-\alpha t} \beta \sigma }}{\alpha } \big )/$ $\textrm{K}\big (\frac{\gamma +\epsilon \delta - \sigma }{\alpha }, \frac{2\sqrt{\beta \sigma }}{\alpha }\big )$ (the second term of Eq. (9)). Since $I_{II}(t)$ has this complex form, the further derivations are quite demanding. By substituting $t\rightarrow y=\frac{2 \sqrt{\textrm{e}^{-\alpha t} \beta \sigma }}{\alpha }$, it can easily be verified that Eq. (10) is in region II reduced to the well-known second-order inhomogeneous Cauchy–Euler equation [76, 77] $a x^2 y'' +b x y'+cy =g(x)$. After dividing thus obtained differential equation by $y^2$, we obtain

$$\begin{aligned}&\frac{\textrm{d}^2F_{II}}{\textrm{d}y^2}+\Big [1-\frac{2(h+m)}{\alpha }\Big ] \frac{1}{y} \frac{\textrm{d}F_{II}}{\textrm{d}y} \nonumber \\&\quad = C y^{\frac{\gamma +\epsilon \delta +\sigma }{\alpha }-2} \textrm{K} \Big (\frac{\gamma +\epsilon \delta -\sigma }{\alpha },y \Big ), \end{aligned}$$

(30)

where $C=\frac{4 I_0 \epsilon \delta m}{\alpha ^2} \big (2\sqrt{\beta \sigma }/{\alpha } \big )^{-\frac{\gamma +\epsilon \delta +\sigma }{\alpha }} \textrm{e}^{\lambda _+ t_0}/\textrm{K} \big (\frac{\gamma +\epsilon \delta -\sigma }{\alpha }, \frac{2\sqrt{\beta \sigma }}{\alpha } \big )$.

Next, we apply the standard procedure for solving inhomogeneous differential equation given by Eq. (30): the full solution equals homogeneous plus particular solution $F_{II}(y)=F_{II,h}(y) + F_{II,p}(y)$. It is straightforward to show that auxiliary/characteristic equation yields the following simple form of homogeneous solution $F_{II,h}(y)=C_1 + C_2 y^{\frac{2 (h+m)}{\alpha }}$ (where linearly independent solutions are $F_{II,1}(y)=1$ and $F_{II,2}(y)= y^{\frac{2 (h+m)}{\alpha }}$), while for obtaining particular solution $F_{II,p}(y)$ we used the Lagrange’s method of variation of parameters  [76]. More precisely, we assume that $F_{II,p}(y)= C_1(y)+ C_2(y) y^{\frac{2 (h+m)}{\alpha }}$, where again linearly independent solutions of the homogeneous equation are employed. The unknown functions $C_i$ ($i=1,2$) of variable y are sought for via the standard procedure

$$\begin{aligned} C_1(y)&=-\int {\frac{F_{II,2}(y) f(y)}{W} \textrm{d}y}, \nonumber \\ C_2(y)&=\int {\frac{F_{II,1}(y) f(y)}{W} \textrm{d}y}, \end{aligned}$$

(31)

where f(y) denotes the right-hand side of Eq. (30), while Wronskian [76, 77] is given by $W=F_{II,1} F'_{II,2} -F_{II,2} F'_{II,1}=\frac{2 (h+m)}{\alpha } y^{\frac{2 (h+m)}{\alpha }-1}$. This leads to:

$$\begin{aligned} C_1(t)&=-\frac{C \alpha }{2(h+m)} \int _0^{\frac{2 \sqrt{\textrm{e}^{-\alpha t} \beta \sigma }}{\alpha }}y^{^{\frac{\gamma +\epsilon \delta +\sigma }{\alpha }}-1} \nonumber \\&\quad \textrm{K} \Big (\frac{\gamma +\epsilon \delta -\sigma }{\alpha }, y \Big ) \textrm{d}y, \nonumber \\ C_2(t)&=\frac{C \alpha }{2(h+m)} \int _0^{\frac{2 \sqrt{\textrm{e}^{-\alpha t} \beta \sigma }}{\alpha }}y^{^{\frac{\gamma +\epsilon \delta +\sigma -2 (h+m)}{\alpha }}-1} \nonumber \\&\quad \textrm{K}\Big (\frac{\gamma +\epsilon \delta -\sigma }{\alpha }, y \Big ) \textrm{d}y. \end{aligned}$$

(32)

In spite that the above form of the result will be more useful in what follows, we nevertheless provide also its full-fledged form:

$$\begin{aligned}&C_1(t) =C_0 \Bigg [\left( {{\frac{\sqrt{\beta \sigma }}{\alpha } }}\right) ^{\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \textrm{e}^{-(\gamma +\epsilon \delta )t} \Gamma \left( {{\frac{\gamma +\epsilon \delta }{\alpha } }} \right) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \Bigg (\frac{\gamma +\epsilon \delta }{\alpha }; 1+\frac{\gamma +\epsilon \delta }{\alpha },1 +\frac{\gamma +\epsilon \delta -\sigma }{\alpha }; \frac{\textrm{e}^{-\alpha t} \beta \sigma }{\alpha ^2}\Bigg ) \nonumber \\&\qquad -\left( {{\frac{\sqrt{\beta \sigma }}{\alpha }}}\right) ^{-\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \textrm{e}^{-\sigma t} \Gamma \left( {{\frac{\sigma }{\alpha } }}\right) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \left( {{\frac{\sigma }{\alpha }; 1+\frac{\sigma }{\alpha },1+\frac{\sigma -\gamma -\epsilon \delta }{\alpha }; \frac{\textrm{e}^{-\alpha t} \beta \sigma }{\alpha ^2} }} \right) \Bigg ] \nonumber \\&\quad \frac{\pi }{2}\csc \left[ {{ \frac{\pi (\gamma +\epsilon \delta -\sigma )}{\alpha } }}\right] \nonumber \\&C_2(t) =-C_0 \Bigg [\left( {{ \frac{\sqrt{\beta \sigma }}{\alpha } }}\right) ^{\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \textrm{e}^{-(\gamma +\epsilon \delta )t} \Gamma \left( {{\frac{\gamma +\epsilon \delta -h-m}{\alpha } }}\right) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \left( \frac{\gamma +\epsilon \delta -h-m}{\alpha }; 1+\frac{\gamma +\epsilon \delta -h-m}{\alpha },1 \right. \nonumber \\&\quad \qquad \left. +\frac{\gamma +\epsilon \delta -\sigma }{\alpha }; \frac{\textrm{e}^{-\alpha t} \beta \sigma }{\alpha ^2}\right) \nonumber \\&\quad - \Bigg ({{\frac{\sqrt{\beta \sigma }}{\alpha }}}\Bigg )^{-\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \textrm{e}^{-\sigma t} \Gamma \Bigg ({{\frac{\sigma -h-m}{\alpha } }}\Bigg ) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \Bigg (\frac{\sigma -h-m}{\alpha }; 1+\frac{\sigma -h-m}{\alpha },1\nonumber \\&\quad \qquad +\frac{\sigma -\gamma -\epsilon \delta }{\alpha }; \frac{\textrm{e}^{-\alpha t} \beta \sigma }{\alpha ^2} \Bigg ) \Bigg ] \nonumber \\&\quad \times \frac{\pi }{2} \csc \left[ {{ \frac{\pi (\gamma +\epsilon \delta -\sigma )}{\alpha } }}\right] , \end{aligned}$$

(33)

where $C_0=\frac{ I_0 \epsilon \delta }{\alpha } \frac{m}{h+m} \textrm{e}^{\lambda _+ t_0}/{\textrm{K}\big (\frac{\gamma +\epsilon \delta -\sigma }{\alpha }, \frac{2\sqrt{\beta \sigma }}{\alpha } \big )}$, while

$_p\tilde{\textrm{F}}_q(a_1,a_2,...a_p;b_1,b_2,...b_q;z)$ denotes regularized generalized hypergeometric function [65]. The general solution of Eq. (30), when returned to variable t, has a form:

$$\begin{aligned} F_{II}(t)&=C_1 + C_2 \textrm{e}^{-(h+m)t} + C_1(t)\nonumber \\&\quad +C_2(t)\Big (\frac{2\sqrt{\beta \sigma }}{\alpha } \Big )^{\frac{2 (h+m)}{\alpha }} \textrm{e}^{-(h+m)t}, \end{aligned}$$

(34)

where the only unknown parameters are $C_1$ and $C_2$. In order to determine these constants we use the following boundary conditions: $F_{II}(0)=F_I(t_0)$ and $F'_{II}(0)=F'_I(t_0)$. After some cumbersome calculation steps we obtain the following expressions:

$$\begin{aligned} C_1&= I_0 \epsilon \delta \frac{ m}{(h+m)}\frac{\textrm{e}^{\lambda _+ t_0} -1}{\lambda _+} \nonumber \\&\quad - C_0 \Bigg [\left( {{\frac{\sqrt{\beta \sigma }}{\alpha }}}\right) ^{\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \Gamma \left( {{\frac{\gamma +\epsilon \delta }{\alpha } }}\right) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \left( \frac{\gamma +\epsilon \delta }{\alpha }; 1+\frac{\gamma +\epsilon \delta }{\alpha },1 \right. \nonumber \\&\quad \left. +\frac{\gamma +\epsilon \delta -\sigma }{\alpha }; \frac{ \beta \sigma }{\alpha ^2}\right) \nonumber \\&\quad -\left( {{\frac{\sqrt{\beta \sigma }}{\alpha }}}\right) ^{-\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \Gamma \left( {{\frac{\sigma }{\alpha } }}\right) \nonumber \\&\quad {}_1\tilde{\textrm{F}}_2\Bigg ({{\frac{\sigma }{\alpha }; 1+\frac{\sigma }{\alpha },1+\frac{\sigma -\gamma -\epsilon \delta }{\alpha }; \frac{ \beta \sigma }{\alpha ^2} }} \Bigg ) \Bigg ] \frac{\pi }{2} \nonumber \\&\quad \times \csc \left[ {{ \frac{\pi (\gamma +\epsilon \delta -\sigma )}{\alpha } }}\right] \end{aligned}$$

(35)

$$\begin{aligned} C_2&= I_0 \epsilon \delta \frac{ m}{(h+m)} \frac{\textrm{e}^{-(h+m)t_0} - \textrm{e}^{\lambda _+ t_0}}{h +m +\lambda _+} \nonumber \\&\quad +C_0 \Bigg [\Big ({{\frac{\sqrt{\beta \sigma }}{\alpha }}}\Big )^{\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \Gamma \left( {{\frac{\gamma +\epsilon \delta -h-m}{\alpha } }} \right) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \bigg (\frac{\gamma +\epsilon \delta -h-m}{\alpha }; 1+\frac{\gamma +\epsilon \delta -h-m}{\alpha },1\nonumber \\&\quad \qquad +\frac{\gamma +\epsilon \delta -\sigma }{\alpha }; \frac{\beta \sigma }{\alpha ^2}\Bigg ) \nonumber \\&\quad - \Bigg ({{\frac{\sqrt{\beta \sigma }}{\alpha }}}\Bigg )^{-\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \Gamma \Bigg ({{\frac{\sigma -h-m}{\alpha } }} \Bigg ) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \left( \frac{\sigma -h-m}{\alpha }; 1+\frac{\sigma -h-m}{\alpha },1 \right. \nonumber \\&\quad \qquad \left. +\frac{\sigma -\gamma -\epsilon \delta }{\alpha }; \frac{ \beta \sigma }{\alpha ^2}\right) \Bigg ] \frac{\pi }{2} \nonumber \\&\quad \times \csc \Bigg [{{ \frac{\pi (\gamma +\epsilon \delta -\sigma )}{\alpha } }}\Bigg ] \end{aligned}$$

(36)

Now, if we use the definition of regularized generalized hypergeometric functions, the above expressions can be significantly simplified and reduced to the form similar to Eq. (32). Namely [65]

$$\begin{aligned} _1\tilde{\textrm{F}}_2(a_1;b_1,b_2;z)=\sum _{k=0}^{\infty } \frac{(a_1)_k z^k}{k! \Gamma (k+b_1) \Gamma (k+b_2)}, \end{aligned}$$

(37)

where $(a_1)_0=1$, while for $k\geqslant 1$

$$\begin{aligned} (a_1)_k=a (a+1)...(a+k-1). \end{aligned}$$

(38)

Let us first concentrate on $C_1$, where from Eq. (35) it follows that $z= \beta \sigma /{\alpha ^2}$. By denoting $a_1=(\gamma +\epsilon \delta )/ \alpha$ and $a_2=\sigma / \alpha$, it is straightforward to infer that the expression in the square brackets of Eq. (35) can be rewritten in a form:

$$\begin{aligned} {\mathcal {I}}_1&=z^{\frac{a_1 -a_2}{2}} \Gamma (a_1)\ _1\tilde{\textrm{F}}_2(a_1; 1+a_1,1+a_1-a_2;z) \nonumber \\&\quad - z^{\frac{a_2 -a_1}{2}} \Gamma (a_2)\ _1\tilde{\textrm{F}}_2(a_2; 1+a_2,1+a_2-a_1;z). \end{aligned}$$

(39)

After multiplying the right-hand side by $z^{\frac{a_1 + a_2}{2}}/z^{\frac{a_1 +a_2}{2}}$ we obtain:

$$\begin{aligned} {\mathcal {I}}_1&=\frac{1}{z^{\frac{a_1 +a_2}{2}}} \sum _{k=0}^{\infty } \Big [\frac{z^{k+a_1}}{k! (k+a_1) \Gamma (k+1+a_1-a_2)} \nonumber \\&\qquad \quad -\frac{z^{k+a_2}}{k! (k+a_2) \Gamma (k+1+a_2-a_1)} \Big ], \end{aligned}$$

(40)

where we made use of the fact that $\Gamma (n+1)=n \Gamma (n)$ and $\Gamma (a) (a)_k =\Gamma (a+k)$ (see Eq. (38)). To further simplify Eq. (40), we adopt the following notation ${\mathcal {J}}_1=\sum _{k=0}^{\infty } \frac{z^{k+a_1}}{k! (k+a_1) \Gamma (k+1+a_1-a_2)}$ and differentiate it with respect to z:

$$\begin{aligned} \frac{\textrm{d} {\mathcal {J}}_1}{\textrm{d}z} =\sum _{k=0}^{\infty }\frac{(\sqrt{z})^{2k+2a_1-2}}{k! \Gamma (k+1+a_1-a_2)}. \end{aligned}$$

(41)

As already mentioned, the main idea is to try to reduce Eq. (35) to a form similar to Eq. (32), i.e., to relate the above expression to modified Bessel functions, and the modified Bessel function of the first kind [64] is defined as:

$$\begin{aligned} \textrm{I}_n(x)=\sum _{k=0}^{\infty }\frac{\left( \frac{x}{2}\right) ^{2k+n}}{k! \Gamma (k+n+1)}. \end{aligned}$$

(42)

By comparing Eqs. (41) and (42), we observe that their right-hand sides are of a similar form, if $x/2 \rightarrow \sqrt{z}$, $n \rightarrow a_1-a_2$, that is:

$$\begin{aligned} \frac{\textrm{d} {\mathcal {J}}_1}{\textrm{d}z}= (\sqrt{z})^{a_1+a_2-2} \textrm{I}_{a_1-a_2}(2 \sqrt{z}). \end{aligned}$$

(43)

Proceeding in a similar manner in the case of the remaining term in Eq. (40) ${\mathcal {J}}_2=\sum _{k=0}^{\infty } \frac{z^{k+a_2}}{k! (k+a_2) \Gamma (k+1+a_2-a_1)}$ we arrive at:

$$\begin{aligned} \frac{\textrm{d} {\mathcal {J}}_2}{\textrm{d}z}= (\sqrt{z})^{a_1+a_2-2} \textrm{I}_{a_2-a_1}(2 \sqrt{z}). \end{aligned}$$

(44)

Note, from Eq. (40), that ${\mathcal {I}}_1=z^{-\frac{a_1 +a_2}{2}} ({\mathcal {J}}_1 -{\mathcal {J}}_2)$.

By substituting integrated Eqs. (43) and (44) in Eq. (40), and thus obtained expression in Eq. (35), for $C_1$ we finally obtain:

$$\begin{aligned} C_1&= I_0 \epsilon \delta \frac{m}{(h+m)}\frac{\textrm{e}^{\lambda _+ t_0}-1}{\lambda _+} + 2 C_0 \big ({{\frac{2 \sqrt{\beta \sigma }}{{\alpha }} }}\big )^{-\frac{\gamma +\epsilon \delta +\sigma }{\alpha }} \nonumber \\&\quad \times \int _0^{\frac{2\sqrt{\beta \sigma }}{\alpha }} y^{\frac{\gamma +\epsilon \delta +\sigma }{\alpha }-1} \textrm{K} \big ({{\frac{\gamma +\epsilon \delta -\sigma }{\alpha },y }} \big ) \textrm{d}y. \end{aligned}$$

(45)

Note that, in obtaining the above expression the identity [66, 68] relating modified Bessel function of the first and the second kind $\textrm{I}_{-n}(x) -\textrm{I}_n(x)=\frac{2}{\pi } \sin (n \pi ) \textrm{K}_n(x)$ was used.

The remaining constant $C_2$ (see Eq. (36)) from fatality counts expression is simplified by applying the same procedure as in the case of $C_1$. To avoid redundant derivations (i.e., the repetition of the above calculations), we simply outline the final expression:

$$\begin{aligned} C_2&= I_0 \epsilon \delta \frac{m}{(h+m)}\frac{\textrm{e}^{-(h+m)t_0}- \textrm{e}^{\lambda _+ t_0}}{h+m+\lambda _+} \nonumber \\&\quad - 2 C_0\big ({{\frac{2 \sqrt{\beta \sigma }}{{\alpha }} }}\big )^{-\frac{\gamma +\epsilon \delta +\sigma -2(h +m)}{\alpha }} \nonumber \\&\quad \times \int _0^{\frac{2\sqrt{\beta \sigma }}{\alpha }} y^{\frac{\gamma +\epsilon \delta +\sigma -2(h+m)}{\alpha }-1} \textrm{K} \big ({{\frac{\gamma +\epsilon \delta -\sigma }{\alpha },y }} \big ) \textrm{d}y, \end{aligned}$$

(46)

with the only distinction that, in the process of simplification, parameters $a_1$ and $a_2$ now read $(\gamma +\epsilon \delta -h-m)/ \alpha$ and $(\sigma -h-m)/ \alpha$, respectively.

Now that all terms of fatalities count (given by Eq. (34)) are determined, we note that all constants ($C_1, C_2, C_1(t)$ and $C_2(t)$) are still in their integral form. Since, for all countries that we consider it holds $2 \sqrt{\beta \sigma }/ \alpha \gg 1$, we may further simplify these integrals by utilizing Hankel’s asymptotic expression [66]:

$$\begin{aligned} \textrm{K}_n(x)\sim \sqrt{\frac{\pi }{2 x}} e^{-x} \Big (1+ {\mathcal {O}} \Big (\frac{1}{x} \Big ) \Big ), \end{aligned}$$

(47)

which holds for large $x=2 \sqrt{\beta \sigma }/ \alpha$.

Along these lines, we rewrite Eqs. (32, 45, 46):

$$\begin{aligned} C_1&\approx I_0 \epsilon \delta \frac{m}{(h+m)}\nonumber \\&\quad \Big [\frac{\textrm{e}^{\lambda _+ t_0} -1}{\lambda _+} +\frac{2 }{\alpha } \Big (\frac{2 \sqrt{\beta \sigma }}{{\alpha }} \Big )^{-\frac{\gamma +\epsilon \delta +\sigma }{\alpha }+\frac{1}{2}} \textrm{e}^{\lambda _+ t_0 +\frac{2 \sqrt{\beta \sigma }}{{\alpha }}} \nonumber \\&\quad \times \int _0^{\frac{2\sqrt{\beta \sigma }}{\alpha }} y^{\frac{\gamma +\epsilon \delta +\sigma }{\alpha }-\frac{3}{2}} e^{-y} \textrm{d}y \Big ] \nonumber \\ C_2&\approx I_0 \epsilon \delta \frac{m}{(h+m)}\Big [ \frac{\textrm{e}^{-(h+m)t_0}- \textrm{e}^{\lambda _+ t_0}}{h+m+\lambda _+}\nonumber \\&\quad - \frac{2}{\alpha } \Big (\frac{2 \sqrt{\beta \sigma }}{{\alpha }} \Big )^{-\frac{\gamma +\epsilon \delta +\sigma -2(h +m)}{\alpha } +\frac{1}{2}} \nonumber \\&\quad \times \textrm{e}^{\lambda _+ t_0 +\frac{2 \sqrt{\beta \sigma }}{{\alpha }}} \int _0^{\frac{2\sqrt{\beta \sigma }}{\alpha }} y^{\frac{\gamma +\epsilon \delta +\sigma -2(h+m)}{\alpha }-\frac{3}{2}} \textrm{e}^{-y} \textrm{d}y \Big ] \nonumber \\ C_1(t)&\approx -\frac{2 I_0 \epsilon \delta }{\alpha } \frac{m}{h+m} \Big (\frac{2 \sqrt{\beta \sigma }}{{\alpha }} \Big )^{-\frac{\gamma +\epsilon \delta +\sigma }{\alpha }+\frac{1}{2}} \textrm{e}^{\lambda _+ t_0 +\frac{2 \sqrt{\beta \sigma }}{{\alpha }}} \nonumber \\&\quad \times \int _0^{\frac{2\sqrt{\textrm{e}^{-\alpha t}\beta \sigma }}{\alpha }} y^{\frac{\gamma +\epsilon \delta +\sigma }{\alpha }-\frac{3}{2}} \textrm{e}^{-y} \textrm{d}y \nonumber \\ C_2(t)&\approx \frac{2I_0 \epsilon \delta }{\alpha } \frac{m}{h+m}\Big (\frac{2 \sqrt{\beta \sigma }}{{\alpha }} \Big )^{-\frac{\gamma +\epsilon \delta +\sigma }{\alpha } +\frac{1}{2}} \textrm{e}^{\lambda _+ t_0 +\frac{2 \sqrt{\beta \sigma }}{{\alpha }}}\nonumber \\&\quad \times \int _0^{\frac{2\sqrt{\textrm{e}^{-\alpha t}\beta \sigma }}{\alpha }} y^{\frac{\gamma +\epsilon \delta +\sigma -2(h+m)}{\alpha }-\frac{3}{2}} \textrm{e}^{-y} \textrm{d}y, \end{aligned}$$

(48)

where we also used the same approximation given by Eq. (47) for modified Bessel function of the second kind contained in C and $C_0$. Note that the second terms of $C_1$ and $C_1(t)$ on one side, and the second terms of $C_2$ and $C_2(t)$ on the other have the same exponents (keep in mind that, according to Eq. (34), there is still a remaining factor $\big (2 \sqrt{\beta \sigma }/{{\alpha }} \big )^{\frac{2(h+m)}{\alpha }}$ multiplying $C_2(t)$).

In Eq. (48), we encounter the lower incomplete gamma function [66] $\gamma (s,x)=\int _0^x t^{s-1} \textrm{e}^{-t} \textrm{d}t$, which we go about by utilizing [66]:

$$\begin{aligned} \gamma (s,x)=\Gamma (s)-\Gamma (s,x), \end{aligned}$$

(49)

where $\Gamma (s,x)=\int _x^{\infty } t^{s-1} \textrm{e}^{-t} \textrm{d}t$ represents the upper incomplete gamma function [66].

Finally, upon implementing thus calculated constants of Eq. (48) in Eq. (34), and by taking into account Eq. (29), we obtain the expression (16) for the general solution of Eq. (10) at the entire t region.

1.2 A.2 Analytical derivation of detected cases

Next, we concentrate on the time evolution of detected counts. To this end, we make use of Eqs. (6) and (9), i.e.

$$\begin{aligned} D(t)= \epsilon \delta \int {I(t) \textrm{d}t} + C_i, \end{aligned}$$

(50)

where $C_i$ ($i=3,4$) stands for the constant of integration. In region I the integration of $I_I(t)$ (the first term in Eq. (9)) is straightforward and yields $D_I(t)= \frac{I_0 \epsilon \delta }{\lambda _+} \textrm{e}^{\lambda _+ t} + C_3$, while $C_3$ is obtained from the initial conditions $D_I(t=0)=D_0\equiv \frac{I_0 \epsilon \delta }{\lambda _+}$, leading to:

$$\begin{aligned} D_I(t)= \frac{I_0 \epsilon \delta }{\lambda _+} \textrm{e}^{\lambda _+ t}. \end{aligned}$$

(51)

In region II, the integration is more demanding, due to the form of $I_{II}(t)$ (the second term of Eq. (9)). To address this, we employ the following substitution of variable $t-t_0 \rightarrow x=\frac{2\sqrt{\beta \sigma }}{\alpha } \textrm{e}^{-\frac{\alpha (t-t_0)}{2}}$. Thus:

$$\begin{aligned} D_{II}(t)&=-2 C_0 \frac{h+m}{m} \Big (\frac{2 \sqrt{ \beta \sigma }}{\alpha } \Big )^{-{\frac{\gamma +\epsilon \delta +\sigma }{\alpha }}} \nonumber \\&\quad \times \int _{\frac{2 \sqrt{ \beta \sigma }}{\alpha }}^{\frac{2 \sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma }}{\alpha }}x^{^{\frac{\gamma +\epsilon \delta +\sigma }{\alpha }}-1}\nonumber \\&\quad \textrm{K}\Big (\frac{\gamma +\epsilon \delta -\sigma }{\alpha }, x \Big ) \textrm{d}x + C_4. \end{aligned}$$

(52)

Note that, as opposed to our previous notation during the derivation of $F_{II}(t)$, now we do not make use of the substitution $t-t_0 \rightarrow t$. Because of this, the boundary condition reads: $D_{II}(t_0)=D_I(t_0)$, which is used for determining the integration constant $C_4=\frac{I_0 \epsilon \delta }{\lambda _+} \textrm{e}^{\lambda _+ t_0}$. So, the expression for detected cases reads:

$$\begin{aligned}&D(t)=\theta (t_0-t) \frac{I_0 \epsilon \delta }{\lambda _+} \textrm{e}^{\lambda _+ t} +\theta (t-t_0) \nonumber \\&\quad \Bigg \{\frac{I_0 \epsilon \delta }{\lambda _+} \textrm{e}^{\lambda _+ t_0} + C_0 \frac{ h+m}{m} \nonumber \\&\quad \times \Bigg [ \left( {{\frac{ \sqrt{\beta \sigma }}{{\alpha }} }}\right) ^{-\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \Gamma \left( {{\frac{\sigma }{\alpha }}}\right) \nonumber \\&\quad \qquad {}_1\tilde{\textrm{F}}_2\left( {{\frac{\sigma }{\alpha }; 1+\frac{\sigma }{\alpha },1+\frac{\sigma -\gamma -\epsilon \delta }{\alpha }; \frac{ \beta \sigma }{\alpha ^2} }} \right) \nonumber \\&\quad - \left( {{\frac{\sqrt{\beta \sigma }}{\alpha }}}\right) ^{\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \Gamma \left( {{\frac{\gamma +\epsilon \delta }{\alpha } }}\right) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \left( {{\frac{\gamma +\epsilon \delta }{\alpha }; 1+\frac{\gamma +\epsilon \delta }{\alpha },1+\frac{\gamma +\epsilon \delta -\sigma }{\alpha }; \frac{ \beta \sigma }{\alpha ^2} }} \right) \nonumber \\&\quad + \left( {{\frac{\sqrt{\beta \sigma }}{\alpha }}}\right) ^{\frac{\gamma +\epsilon \delta -\sigma }{\alpha }} \textrm{e}^{-(\gamma +\epsilon \delta )(t-t_0)} \Gamma \left( {{\frac{\gamma +\epsilon \delta }{\alpha } }}\right) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \left( \frac{\gamma +\epsilon \delta }{\alpha }; 1+\frac{\gamma +\epsilon \delta }{\alpha },1 \right. \nonumber \\&\quad \qquad \left. +\frac{\gamma +\epsilon \delta -\sigma }{\alpha }; \frac{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma }{\alpha ^2}\right) \nonumber \\&\quad -\left( {{\frac{ \sqrt{\beta \sigma }}{{\alpha }} }}\right) ^{-\frac{\gamma +\epsilon \delta - \sigma }{\alpha }} \textrm{e}^{-\sigma (t-t_0)} \Gamma \left( {{\frac{\sigma }{\alpha }}}\right) \nonumber \\&\quad \times {}_1\tilde{\textrm{F}}_2 \left( \frac{\sigma }{\alpha }; 1+\frac{\sigma }{\alpha },1 \right. \nonumber \\&\quad \qquad \left. +\frac{\sigma -\gamma -\epsilon \delta }{\alpha }; \frac{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma }{\alpha ^2}\right) \Bigg ] \nonumber \\&\quad \frac{\pi }{2} \times \csc \Bigg [{{ \frac{\pi (\gamma +\epsilon \delta -\sigma )}{\alpha } }}\Bigg ] \Bigg \}. \end{aligned}$$

(53)

After performing the same algebraic manipulations of regularized generalized hypergeometric functions as in the previous Subsect. A.1, as well as applying Hankel’s approximation (47), we obtain the expression  (19) for the general solution of Eq. (11) at the entire t region.

Alternatively, the same expression  (19) could be obtained more straightforwardly. Namely, the expression for the number of infectious individuals (Eq. (9)) can be simplified by utilizing Eq. (47):

$$\begin{aligned} I(t)&= \theta (t_0-t) I_0 \textrm{e}^{\lambda _+ t} + \theta (t-t_0) \nonumber \\&\quad I_0 \textrm{e}^{\lambda _+ t_0 +\frac{2\sqrt{\beta \sigma }}{\alpha }} \textrm{e}^{-\frac{\alpha (t-t_0)}{2}\left( \frac{\gamma +\epsilon \delta +\sigma }{\alpha }-\frac{1}{2}\right) } \nonumber \\&\quad \times \textrm{e}^{-\frac{2 \sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma }}{\alpha }}. \end{aligned}$$

(54)

Now that I(t) has been determined in the desired form, the detected counts can be calculated from Eq. (11). In region I, the derivation is straightforward (and therefore omitted) and leads to Eq. (51). In region II, the integration is more demanding, due to the form of $I_{II}(t)=I_0 \textrm{e}^{\lambda _+ t_0 +\frac{2\sqrt{\beta \sigma }}{\alpha }} \textrm{e}^{-\frac{\alpha (t-t_0)}{2}(\frac{\gamma +\epsilon \delta +\sigma }{\alpha }-\frac{1}{2})} \textrm{e}^{-\frac{2 \sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma }}{\alpha }}$. To address this, again we employ the following substitution of variable $t-t_0 \rightarrow x= \frac{2\sqrt{\beta \sigma }}{\alpha }$ $\textrm{e}^{-\frac{\alpha (t-t_0)}{2}}$, resulting in the boundary condition $D_{II}(t_0)=D_I(t_0)$ (which is used for determining the integration constant $C_4$). In a similar manner as before, we again encounter the incomplete gamma functions [66]:

$$\begin{aligned} D_{II}(t)&=-\frac{2 I_0 \epsilon \delta }{\alpha } \Big ( \frac{2 \sqrt{\beta \sigma }}{\alpha } \Big )^{-\frac{\gamma +\epsilon \delta +\sigma }{\alpha } +\frac{1}{2}} \textrm{e}^{\frac{2 \sqrt{\beta \sigma }}{\alpha } + \lambda _+ t_0} \nonumber \\&\quad \times \int _{\frac{2 \sqrt{\beta \sigma }}{\alpha }}^{\frac{2 \sqrt{\textrm{e}^{-\alpha (t-t_0)}\beta \sigma }}{\alpha }}x^{\frac{\gamma +\epsilon \delta +\sigma }{\alpha } -\frac{3}{2}}\textrm{e}^{-x} \textrm{d}x + C_4. \end{aligned}$$

(55)

The only difference compared to Eq. (48) is that now the lower boundary of integration is not zero but some positive real number. This integral is solved by applying the identity $\int _a^b x^{s-1} \textrm{e}^{-x}\textrm{d}x =\int _0^b x^{s-1} \textrm{e}^{-x}\textrm{d}x -\int _0^a x^{s-1} e^{-x}\textrm{d}x=\Gamma (s,a)-\Gamma (s,b)$. By combining this result with Eq. (51), we finally arrive at the expression (19) for the number of detected cases.

1.3 A.3 Simplified expressions for fatalities and detected cases

In this section, we show that certain terms in the expressions for fatalities and detected cases can be neglected (when epidemiological parameters are in realistic ranges), without significant loss of predictive precision. First, we start with Eq. (16) for fatality counts. We notice that for $t>t_0$ first two terms are much smaller than the remaining terms, due to $2\sqrt{\beta \sigma }/ \alpha \gg 1$, and therefore can be neglected. Additionally, for the same reason all $\Gamma (s,2\sqrt{\beta \sigma }/ \alpha )\rightarrow \Gamma (s,\infty )$ are approximately equal to zero (i.e., the gamma integral is effectively $\int _{\infty }^{\infty }$). Therefore, instead of Eq. (16), the following formula can be safely used in practice:

$$\begin{aligned} F_{simp}(t)&\approx I_0 \epsilon \delta \frac{m}{h+m} \nonumber \\&\quad \bigg \{\theta (t_0-t)\Big (\frac{\textrm{e}^{\lambda _+ t}-1}{\lambda _+} + \frac{\textrm{e}^{-(h+m)t} -\textrm{e}^{\lambda _+ t}}{h+m+\lambda _+} \Big )\nonumber \\&\quad + \theta (t-t_0) \frac{2}{\alpha } \Big (\frac{2 \sqrt{\beta \sigma }}{{\alpha }} \Big )^{-\frac{\gamma +\epsilon \delta +\sigma }{\alpha }+\frac{1}{2}} \textrm{e}^{\lambda _+ t_0 +\frac{2 \sqrt{\beta \sigma }}{{\alpha }}} \nonumber \\&\quad \times \Big [ \Gamma \big ({{\frac{\gamma +\epsilon \delta + \sigma }{\alpha }-\frac{1}{2}, \frac{2\sqrt{\textrm{e}^{-\alpha (t-t_0)}\beta \sigma }}{\alpha } }}\big ) \nonumber \\&\quad - \Big (\frac{2 \sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma }}{{\alpha }} \Big )^{\frac{2(h+m)}{\alpha }} \nonumber \\&\quad \times \Gamma \big (\frac{\gamma +\epsilon \delta + \sigma -2(h+m)}{\alpha }\nonumber \\&\quad -\frac{1}{2}, \frac{2\sqrt{\textrm{e}^{-\alpha (t-t_0)}\beta \sigma }}{\alpha } \big ) \Big ] \bigg \}. \end{aligned}$$

(56)

Continuing in the same manner, the simplified form of the number of detected cases is easily obtained:

$$\begin{aligned} D_{simp}(t)&\approx I_0 \epsilon \delta \nonumber \\&\quad \bigg [\theta (t_0-t)\frac{\textrm{e}^{\lambda _+ t}}{\lambda _+} +\theta (t-t_0)\frac{2}{\alpha } \nonumber \\&\qquad \Big (\frac{2 \sqrt{\beta \sigma }}{\alpha } \Big )^{-\frac{\gamma +\epsilon \delta +\sigma }{\alpha } +\frac{1}{2}} \nonumber \\&\qquad \times \textrm{e}^{\lambda _+ t_0 +\frac{2 \sqrt{\beta \sigma }}{\alpha }} \nonumber \\&\qquad \Gamma \big ({{\frac{\gamma +\epsilon \delta + \sigma }{\alpha }-\frac{1}{2}, \frac{2\sqrt{\textrm{e}^{-\alpha (t-t_0)}\beta \sigma }}{\alpha } }} \big ) \bigg ]. \end{aligned}$$

(57)

We have numerically tested and confirmed that the full-fledged (given by Eq. (16)) and simplified (given by Eq. (56)) fatality curves are practically overlapping (and the same for the detected cases).

1.4 A.4 Expressions for fatalities and detected cases at saturation

We will evaluate the saturation values of fatalities and detected counts, that is, their expressions in the limit of very large t. This means that we can concentrate only on $t>t_0$, i.e., region II, where we set $t\rightarrow \infty$. Building on the results of the previous section, from Eq. (56) we observe that, in this limit, the second term in the square brackets can be neglected, due to $\textrm{e}^{-(h+m)(t-t_0)}\rightarrow 0$. Likewise,

$$\begin{aligned}{} & {} \Gamma \big ({{\frac{\gamma +\epsilon \delta + \sigma }{\alpha }-\frac{1}{2}, \frac{2\sqrt{\textrm{e}^{-\alpha (t-t_0)}\beta \sigma }}{\alpha } }} \big ) \nonumber \\{} & {} \quad \rightarrow \Gamma \big ({{\frac{\gamma +\epsilon \delta + \sigma }{\alpha }-\frac{1}{2}, 0 }} \big )\\{} & {} \quad \equiv \Gamma \big ({{\frac{\gamma +\epsilon \delta + \sigma }{\alpha }-\frac{1}{2} }} \big ). \end{aligned}$$

Therefore, we obtain the expressions (17) and (20) for the saturation values.

1.5 A.5 Expressions for the epidemics peak and tipping points

Other important quantities characterizing infection dynamics during the first wave are epidemics peak time and inflection (tipping and turning) points, for which we here provide analytic expressions. Namely, the epidemics peak time is the moment when infected curve reaches its maximal value (i.e., $\textrm{d}I / \textrm{d}t =0$), or equivalently $\textrm{d}^2D / \textrm{d}t^2 =0$. The second derivative of Eq. (19) in region II (or equivalently Eq. (57) in the same region) yields:

$$\begin{aligned} \frac{\textrm{d}^2 D_{II}}{\textrm{d} t^2}&= I_0 \epsilon \delta \textrm{e}^{\lambda _+ t_0+\frac{2 \sqrt{\beta \sigma }}{\alpha }}\nonumber \\&\quad \textrm{e}^{-\frac{\alpha (t-t_0)}{2}\left( \frac{\gamma +\epsilon \delta +\sigma }{\alpha }-\frac{1}{2}\right) } \textrm{e}^{-\frac{2 \sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma }}{\alpha }} \nonumber \\&\quad \times \Big (-\frac{\gamma +\epsilon \delta +\sigma }{2}+\frac{\alpha }{4} +\sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma } \Big ). \end{aligned}$$

(58)

In deriving the above expression, we made use of equality $\textrm{d}\Gamma (\textrm{s},\textrm{x}) / \textrm{d}x =-x^{s-1} \textrm{e}^{-x}$, following from the definition of incomplete gamma functions [66]. Note that, in this subsection, we are interested in region II, where all relevant points lay. After equating the second derivative of $D_{II}$ with zero, for the epidemics peak time, we obtain:

$$\begin{aligned} t_{max}=t_0 +\frac{1}{\alpha }\ln {\Big [ \frac{16 \beta \sigma }{(2(\gamma +\epsilon \delta +\sigma )-\alpha )^2}\Big ]}. \end{aligned}$$

(59)

By evaluating $\frac{\textrm{d}D}{\textrm{d}t}$ at $t=t_{max}$, we can straightforwardly obtain the maximum of detected cases per day, given by

$$\begin{aligned} \left( \frac{\textrm{d}D}{\textrm{d}t}\right) _{max}&= D_0 \lambda _+ \textrm{e}^{\lambda _+ \left( t_0 + \frac{2}{\alpha }\right) + \frac{1}{2}}\nonumber \\&\quad \left( \frac{ 4 \sqrt{\beta \sigma }}{ 2 (\gamma +\epsilon \delta +\sigma ) - \alpha } \right) ^{\frac{1}{2} - \frac{\gamma +\epsilon \delta +\sigma }{\alpha }} . \end{aligned}$$

(60)

Along the same lines, the epidemics inflection points are defined as $\textrm{d}^2 I / \textrm{d}t^2 =0$, or equivalently $\textrm{d}^3D / \textrm{d}t^3 =0$:

$$\begin{aligned} \frac{\textrm{d}^3 D_{II}}{\textrm{d} t^3}&= I_0 \epsilon \delta \textrm{e}^{\lambda _+ t_0+\frac{2 \sqrt{\beta \sigma }}{\alpha }} \textrm{e}^{-\frac{\alpha (t-t_0)}{2}(\frac{\gamma +\epsilon \delta +\sigma }{\alpha }-\frac{1}{2})}\nonumber \\&\qquad \textrm{e}^{-\frac{2 \sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma }}{\alpha }} \nonumber \\&\quad \times \Big [ \Big (\frac{\gamma +\epsilon \delta +\sigma }{2}-\frac{\alpha }{4} -\sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma } \Big )^2 \nonumber \\&\quad \qquad -\frac{\alpha }{2} \sqrt{\textrm{e}^{-\alpha (t-t_0)} \beta \sigma } \Big ] \nonumber \\&=0. \end{aligned}$$

(61)

Eq. (61) has two solutions, which correspond to the infection tipping points

$$\begin{aligned} t_{1,2}=t_0+\frac{2}{\alpha }\ln \Big (\frac{2 \sqrt{\beta \sigma }}{\gamma +\delta \epsilon +\sigma \mp \sqrt{\alpha \left( \gamma + \epsilon \delta +\sigma -\frac{\alpha }{4}\right) }}\Big ). \end{aligned}$$

(62)

The duration of the epidemic peak can then be defined as a difference between these two tipping points and is equal to:

$$\begin{aligned} \varDelta t_{peak}= \frac{4}{\alpha } \ln {\Big (\frac{\gamma +\epsilon \delta +\sigma +\sqrt{\alpha (\gamma +\epsilon \delta +\sigma -\frac{\alpha }{4})}}{\gamma +\epsilon \delta +\sigma -\alpha /2} \Big )}. \end{aligned}$$

(63)