Stability behavior of a two-susceptibility SHIR epidemic model with time delay in complex networks

Abstract

Taking two susceptible groups into account, we formulate a modified subhealthy-healthy-infected-recovered (SHIR) model with time delay and nonlinear incidence rate in networks with different topologies. Concretely, two dynamical systems are designed in homogeneous and heterogeneous networks by utilizing mean field equations. Based on the next-generation matrix and the existence of a positive equilibrium point, we derive the basic reproduction numbers $R_{0}^{1}$ and $R_{0}^{2}$ which depend on the model parameters and network structure. In virtue of linearized systems and Lyapunov functions, the local and global stabilities of the disease-free equilibrium points are, respectively, analyzed when $R_{0}^{1}<1$ in homogeneous networks and $R_{0}^{2}<1$ in heterogeneous networks. Besides, we demonstrate that the endemic equilibrium point is locally asymptotically stable in homogeneous networks in the condition of $R_{0}^{1}>1$. Finally, numerical simulations are performed to conduct sensitivity analysis and confirm theoretical results. Moreover, some conjectures are proposed to complement dynamical behavior of two systems.

1 Introduction

From historical events, infectious diseases, such as cholera [1], malaria [2], influenza [3] and COVID-19 [4], pose a huge threat to the public health all over the world. Fortunately, mathematical modeling is regarded as a powerful method to characterize the spreading mechanism of the epidemic, which makes it convenient for us to study the dynamics of disease propagation in epidemiology significantly [5,6,7,8,9].

According to the classical theory of epidemic dynamics, many scholars progressively apply and extend compartmental epidemic models to research transmission dynamics in a diverse range of fields [10,11,12,13,14,15]. In recent years, due to the nonuniformity of spread in a population, the thought of classification for susceptible, infected or other state groups is embedded in the modeling of propagation phenomena in Refs. [16,17,18,19,20,21,22,23,24,25,26,27,28]. Dating back to 1976, a multiple groups model proposed by Lajmanovich and Yorke [29] characterizes the epidemiological features of gonorrhea appropriately. In a general way, the specific group is further divided into several disjoint subgroups in the multi-group model, which enriches epidemiological states of individuals. As a result, the application of classifying thought in defining compartmental states can promote the established propagation model more practical. Throughout previous papers, the classification for a certain group is mostly attributed to genetic variation (e.g., gender). For instance, Hyman and Li [17], respectively, formulate thresholds for the spread of infectious disease in the differential susceptibility model, staged progression model, differential infectivity model and so on. Besides, they [18] also study SIR epidemic models with differential susceptibility by classifying the susceptible into various subgroups. Additionally, Wang et al. [20, 21] divide the infected compartment into two sub-compartments and discuss the spreading dynamics of a sexually transmitted disease model when low-risk and high-risk infected individuals coexist. Considering the heterogeneity of host population, Jin et al. [23] investigate the disease transmission dynamics by establishing a general multi-group epidemic model. In view of the coinfection of two strains, Ruan et al. [25] calculate the basic reproduction number and study the threshold dynamics of a diffusive SIS epidemic model where infected individuals are split into the infected with strain one and strain two based on Ref. [26].

In Ref. [30], an SIR epidemic model with consideration of birth, death and two susceptibility is proposed and studied in heterogeneous networks as follows:

$$\begin{aligned} \dfrac{\mathrm {d} S_{1k}(t)}{\mathrm {d} t}= & {} b_{1}\Big (\!1\!-\!S_{1k}(t)\!-\!S_{2k}(t)\!-\!I_{k}(t)\!-\!R_{k}(t)\!\Big )\nonumber \\&-\beta _{1} kS_{1k}(t)\varTheta (t)-\mu S_{1k}(t),\nonumber \\ \dfrac{\mathrm {d} S_{2k}(t)}{\mathrm {d} t}= & {} b_{2}\Big (\!1\!-\!S_{1k}(t)\!-\!S_{2k}(t)\!-\!I_{k}(t)\!-\!R_{k}(t)\!\Big )\nonumber \\&-\beta _{2} kS_{2k}(t)\varTheta (t)-\mu S_{2k}(t),\nonumber \\ \dfrac{\mathrm {d} I_{k}(t)}{\mathrm {d} t}= & {} \beta _{1} kS_{1k}(t)\varTheta (t)+\beta _{2} kS_{2k}(t)\varTheta (t)\nonumber \\&-\gamma I_{k}(t)-\mu I_{k}(t),\nonumber \\ \dfrac{\mathrm {d} R_{k}(t)}{\mathrm {d} t}= & {} \gamma I_{k}(t)-\mu R_{k}(t). \end{aligned}$$

(1.1)

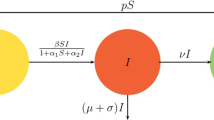
The total population is divided into four disjoint compartments including the 1st susceptible group, the 2nd susceptible group, infected individuals and recovered individuals. Their densities are, respectively, denoted by $S_{1k}(t)$, $S_{2k}(t)$, $I_{k}(t)$ and $R_{k}(t)$ with degree k $(k=1,2,\ldots ,n)$ at time t. Besides, let $T_{k}(t)=S_{1k}(t)+S_{2k}(t)+I_{k}(t)+R_{k}(t)$ be the overall density of individuals with degree k at time t. Here, $(1-T_{k}(t))$ represents the density of empty nodes which can generate newborns belonging to the 1st or 2nd susceptible group at the certain rate $b_{i}$ $(i=1,2)$. $\mu$ is a natural death probability which is identical for all individuals. $\beta _{1}$ or $\beta _{2}$ is the transmission coefficient at which a 1st or 2nd susceptible individual is infected with this disease by getting in contact with infected individuals. Meanwhile, infected individuals can turn into the recovered state at a recovery rate $\gamma$. Besides, $\varTheta$ is known as the probability with which any chosen edge is linked to an infected individual. To be specific, in the uncorrelated networks, $\varTheta$ can be written as

$$\begin{aligned} \varTheta (t)=\sum _{k^{'}=1}^n\frac{k^{'}p(k^{'})I_{k^{'}}(t)}{\overline{k}}, \end{aligned}$$

where $p(k^{'})$ is the degree distribution and $\overline{k}=\sum \limits _{k}kp(k)$ is the average degree of the network.

For system (1.1), Yuan et al. [30] obtain the basic reproduction number, analyze the stability of two equilibria and give the effectiveness of control strategies. Nevertheless, the epidemiologically meaningful time delay is ignored in the spreading process of contagious disease in their modeling, which deviates the realistic situation. Strictly speaking, hysteresis involved in virus production indeed exists because some time is needed for the maturity of the virion after the cells of individuals have catched the virus [31]. That is to say, the infected individuals become infectious and further transmit the infection after a certain period of time. Based on this situation, it’s of biological significance to bring in the time delay in the transition process due to the existence of latent infection. Recently, lots of researchers are passionate about adding the time delay into the epidemic model which consists of a coupled system of delay differential equations in Refs. [32,33,34,35,36,37,38]. Actually, the introduction of time delay may lead to the change in stability of equilibrium points of a dynamical system, which puts forward a challenge to the dynamical analysis of the delayed model. For example, the existence of Hopf bifurcations at various equilibria in a delayed predator–prey model is explored by Xu in Ref. [32]. Moreover, Zhu et al. [34] study the local and global asymptotic stabilities of equilibrium points of a rumor spreading model with and without time delay, respectively. Considering both avian population and human population, Kang et al. [36] employ two discrete time delays $\tau _1$ and $\tau _2$ to delineate the delayed process in state transitions. In consequence, it is highly meaningful for us to incorporate the time delay into the epidemic model (1.1) additionally.

Similar to Ref. [30], most of the existing results focusing on epidemic models usually suppose that the interaction term between the susceptible and infected individuals satisfies the bilinear form according to the law of mass action [39]. Once the bilinear incidence rate is used in the modeling, the number of patients linearly increases in the infection process, which isn’t appropriate in the situation of huge numbers of infected individuals [40]. In fact, if the epidemic is severe enough, the information about the prevalence of disease will impel individuals to take prevention measures to avoid the infection [41]. In consequence, it’s a pity that some researchers don’t think over the behavioral changes of individuals due to the psychological effect in disease transmission process. In 1978, to characterize saturation phenomena for mass infected individuals, Capasso and Serio [42] generalize the Kermack–McKendrick deterministic model by employing a saturated incidence rate Sg(I) where $g(I)=\frac{\beta I}{1+aI}$ is a nonlinear bounded function. As explained in Refs. [43, 44], the incidence function g(I) gradually reaches a saturation level with the scale of infected individuals I increasing. Noticing the insightful effect of nonlinear incidence on epidemic dynamics, lots of authors [40, 45,46,47,48] are devoted to studying the nonlinear dynamics of various epidemic models incorporated with saturated incidence rate. For instance, Zhu et al. [48] perfectly explore the stability of equilibrium points and the effectiveness of control schemes in a delayed SIS epidemic model along with nonlinear incidence rate. Furthermore, Li and Yousef [49] analytically and numerically research the bifurcation behavior of a network-based SIR epidemic model with saturated treatment function which is analogous to the nonlinear type of incidence rate [50] in some sense. To address the mentioned deficit in Ref. [30], we intend to adopt the nonlinear incidence rate by introducing a psychological factor a, which avoids the unbounded contact rate in the epidemic model.

What’s more, the application of complex networks to epidemic modeling gives rise to a wave of research in academia for decades. With respect to the consideration of network topology, more and more scholars are in favor of investigating the dynamics of propagation model in both homogeneous and heterogeneous networks [51,52,53,54,55]. In Ref. [51], Xia et al. present an improved SEIR model with hesitating mechanism and analyze the spreading threshold in homogeneous and heterogeneous networks, respectively. As Zhu and Guan [53] present, the complexity of the network structure can result in the difference of spreading threshold of the disease in magnitude. In addition, the basic reproduction number and the rumor-free equilibrium point of I2S2R rumor propagating model with two rumors are explored in homogeneous networks by Zhang and Zhu [55]. And they are also devoted to proving the stability of the trivial equilibrium point, discussing the global attractivity of the positive equilibrium point and investigating the permanence of system in heterogeneous networks. As the society developing greatly, the connections among people are increasingly convenient and frequent. This situation drives us to take advantage of complex networks to capture the features of social network in reality. According to insights from studying complex networks, homogeneous and heterogeneous networks can be selected, respectively, as the underlying network to investigate the influence of network structure on disease transmission.

As far as we know, however, there are few research results on dynamical analysis of the delayed multi-group epidemic model with nonlinear incidence rate and different topological structures of social network. Motivated by foregoing literature, such as [19, 30], in which Yuan et al. study the stability of the SIR epidemic model with differential susceptibility or infectivity, and [48, 53], in which Zhu et al. incorporate the saturated incidence rate with time delay into propagation model, we establish a delayed epidemic model along with two susceptible groups and nonlinear incidence rate in complex networks. Emphasizing the influence of network structure on disease propagation, we make efforts to investigate threshold dynamics of a two-susceptibility epidemic model with time delay and nonlinear incidence rate in both homogeneous and heterogeneous networks. What’s more, to make recommendations for control measures, we pay attention to the impacts of time delay, nonlinear incidence rate and network structure on the transmission of infectious disease.

To make this epidemic model with two susceptible groups more sensible, assume that personal fitness level results in differences between susceptible individuals. In other words, the susceptibility of individuals to infectious disease depends on the personal fitness level. Taking the health level as the classification criterion of susceptible population, we introduce the subhealthy and healthy compartments to characterize the nonhomogeneous structure for susceptible individuals. Hence, states of individuals cover the subhealthy (S), the healthy (H), the infected (I) and the recovered (R). Based on the practical situation, it’s further supposed that the subhealthy are more likely to catch the infection than the healthy herein. As for the modeling of disease propagation, the network topology and state-transition rules of nodes need to be considered primarily. Since the choice of the network topological structure is discussed above, the expression of interaction rules in the spreading process is briefly presented below.

(1) In virtue of empty nodes, newborns with two levels of health enter the network and all individuals naturally emigrate the network owing to the death.

(2) Upon contacting infectious vectors that carry the pathogen, a subhealthy or healthy individual will turn into an infected individual with a certain probability. Importantly, a nonlinear incidence rate can reflect the crowding effect of infected individuals and inhibitory measures taken by susceptible individuals when the diffusion of disease is especially serious [56].

(3) As a matter of fact, the time delay plays a major role in the epidemic model because the incubation period of disease indeed exists on account of the latency in a vector. Namely, some time is needed for infectious agents developing in the vector, after which infected vectors become infectious and can transmit the infection to humans.

(4) With the aid of modern treatment, infected individuals can be cured and become the recovered state with a certain rate.

Based on the above analysis, we, respectively, establish the delayed two-susceptibility epidemic model with nonlinear incidence rate in homogeneous networks in Sect. 2 and heterogeneous networks in Sect. 3. Basic properties of solutions and the threshold of disease diffusion are analytically derived. Furthermore, we prove the stability of equilibrium points of two dynamical systems in detail. In Sect. 4, quantities of numerical experiments are carried out to verify the correctness of obtained theoretical results. Finally, the paper ends with conclusions and discussions in Sect. 5.

2 Disease transmission in homogeneous networks

2.1 Model description

At first, the delayed system about disease diffusion is considered on the topological structure of homogeneous networks where all nodes are regarded as equivalent statistically. Let S(t), H(t), I(t) and R(t) represent the average densities of subhealthy, healthy, infected and recovered nodes at time t, respectively. The mean field equations of the SHIR epidemic model in homogeneous networks are composed of a set of delay differential equations as follows:

$$\begin{aligned} \dfrac{{\text {d}} S(t)}{{\text {d}} t}= & {} b_{1}\Big (\!1\!-\!S(t)-\!H(t)-\!I(t)-\!R(t)\!\Big )\nonumber \\&-\beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\mu S(t),\nonumber \\ \dfrac{{\text {d}} H(t)}{{\text {d}} t}= & {} b_{2}\Big (\!1\!-\!S(t)-\!H(t)-\!I(t)-\!R(t)\!\Big )\nonumber \\&-\beta _{2}\overline{k} H(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\mu H(t),\nonumber \\ \dfrac{{\text {d}} I(t)}{{\text {d}} t}= & {} \beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}\nonumber \\&+\beta _{2} \overline{k} H(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\gamma I(t)-\mu I(t),\nonumber \\ \dfrac{{\text {d}} R(t)}{{\text {d}} t}= & {} \gamma I(t)-\mu R(t), \end{aligned}$$

(2.1)

where $b_{i}\big (1-S(t)-H(t)-I(t)-R(t)\big )$ denotes the density of newborn susceptible nodes generated by empty nodes with the certain constant rate $b_{i}$ $(i=1,2)$. The psychological factor a characterizes the behavioral changes resulted from the crowding effect of infected individuals during a peak period of epidemic situation. Latent period is shown by the average time delay $\tau$ of disease propagation in the process of infection from the subhealthy and healthy to infected individuals. All parameters in our epidemic model are assumed to be positive. The initial conditions for system (2.1) are given by $\big (S(\vartheta ), H(\vartheta ), I(\vartheta ), R(\vartheta )\big )=\big (\varphi _{1}(\vartheta ), \varphi _{2}(\vartheta ), \varphi _{3}(\vartheta ), \varphi _{4}(\vartheta )\big )$ which satisfy

$$\begin{aligned} \begin{aligned}&\varphi _{i}(\vartheta )\ge 0, \,0<\sum _{i=1}^4\varphi _{i}(\vartheta )\le 1,\; \vartheta \in [-\tau ,0],\\&\varphi _{i}(0)>0\,(i=1,2,3,4). \end{aligned} \end{aligned}$$

(2.2)

Besides, $(\varphi _{1}, \varphi _{2}, \varphi _{3}, \varphi _{4})\in C([-\tau ,0],R_{+}^{4})$ which denotes the Banach space of continuous functions mapping the interval $[-\tau ,0]$ into $R_{+}^{4}=\big \{(x_1, x_2, x_3, x_4)\in R^{4}: x_i\ge 0, i=1,2,3,4 \big \}$.

As the sum of S(t), H(t), I(t) and R(t), the total population size at time t can be expressed by T(t). Add up all equations of system (2.1) and obtain the following differential equation:

$$\begin{aligned} \dfrac{\mathrm {d} T(t)}{\mathrm {d} t}=b_{1}+b_{2}-(b_{1}+b_{2}+\mu )T(t). \end{aligned}$$

Making allowances for the above equation, we transform system (2.1) into the limit system:

$$\begin{aligned} \dfrac{{\text {d}} S(t)}{{\text {d}} t}= & {} b_{1}\Big (1-T^{*}\Big )\nonumber \\&-\beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\mu S(t),\nonumber \\ \dfrac{{\text {d}} H(t)}{{\text {d}} t}= & {} b_{2}\Big (1-T^{*}\Big )\nonumber \\&-\beta _{2}\overline{k} H(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\mu H(t),\nonumber \\ \dfrac{{\text {d}} I(t)}{{\text {d}} t}= & {} \beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}\nonumber \\&+\beta _{2} \overline{k} H(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\gamma I(t)-\mu I(t),\nonumber \\ \dfrac{{\text {d}} R(t)}{{\text {d}} t}= & {} \gamma I(t)-\mu R(t), \end{aligned}$$

(2.3)

where $T^{*}=\frac{b_{1}+b_{2}}{b_{1}+b_{2}+\mu }$. Now, it suffices to study system (2.3) detailedly instead of system (2.1) when exploring the long-time behavior for the solutions of our model. Moreover, the fourth equation of system (2.3) is decoupled from the equations for S(t), H(t) and I(t). Hence, it’s natural to make the limit system (2.3) be reduced as the following system:

$$\begin{aligned} \dfrac{{\text{ d }} S(t)}{{\text{ d }} t}=&{} b_{1}\Big (1-T^{*}\Big ) -\beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\mu S(t),\nonumber \\ \dfrac{{\text{ d }} H(t)}{{\text{ d }} t}=&{} b_{2}\Big (1-T^{*}\Big ) -\beta _{2}\overline{k} H(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\mu H(t),\nonumber \\ \dfrac{{\text{ d }} I(t)}{{\text{ d }} t}=&{} \beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}\nonumber \\&+\beta _{2} \overline{k} H(t)\dfrac{I(t-\tau )}{a+I(t-\tau )}-\gamma I(t)-\mu I(t).\nonumber \\ \end{aligned}$$

(2.4)

For the sake of simplicity, it’s high time to study system (2.4) in place of original system (2.1) sufficiently for subsequent discussion.

2.2 Basic properties of solutions

Lemma 1

For system (2.3) with the initial conditions (2.2), there exists a unique solution $(S(t), H(t), I(t), R(t))$ globally for $t\in [0,\infty )$.

Proof

Under the initial conditions (2.2), the existence and uniqueness of solutions of system (2.3) are to be proved step by step.

For $0<t\le \tau$, it can be seen that $I(t-\tau )\ge 0$ from the given initial condition. Then, we have that the right-hand side of system (2.3) is locally Lipschitz continuous. Therefore, by the existence, uniqueness and continuation theorems of differential equation, there is a unique solution of system (2.3) with the initial conditions (2.2) in the interval $(0, \tau ]$.

In what follows, we prove the nonnegativity of this solution in $(0, \tau ]$. Taking notice of

$$\begin{aligned}&\dfrac{{\text {d}} S(t)}{{\text {d}} t}\Bigg |_{S(t)=0} =\left[ b_{1}\Big (1-T^{*}\Big )\right. \\&\quad \left. -\beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{ a+I(t-\tau )}-\mu S(t)\right] \Bigg |_{S(t)=0}>0, \end{aligned}$$

and the initial condition $S(\vartheta )\ge 0$, we can obtain $S(t)\ge 0$ for $0<t\le \tau$. In the same way, $H(t)\ge 0$ for $0<t\le \tau$. Besides, it’s available that $I(t)\ge 0$ for $0<t\le \tau$. If not, we can find the smallest $t_0\in (0,\tau ]$ which makes $I(t_0)=0$ and $I(t)<0$ for $t\in (t_0, t_0+\delta _1)$ where $\delta _1>0$. In this case, together with the initial value $I(\vartheta )\ge 0$, we know $I(t_0-\tau )\ge 0$. Thus, there exists

$$\begin{aligned} \begin{aligned} \dfrac{{\text {d}} I(t)}{d t}\Bigg |_{I(t_0)=0}&=\left[ \Big (\beta _{1}S(t)+\beta _{2}H(t)\Big )\overline{k} \dfrac{I(t-\tau )}{ a+I(t-\tau )}\right. \\&\qquad \left. -(\gamma +\mu )I(t)\right] \Bigg |_{I(t_0)=0}\ge 0, \end{aligned} \end{aligned}$$

which implies that $I(t)\ge 0$ for $t\in (t_0, t_0+\delta _2)$ where $\delta _2>0$. Apparently, there is a contradiction in the interval $(t_0, t_0+\min \{\delta _1, \delta _2\})$. Therefore, we draw a conclusion $I(t)\ge 0$ for $0<t\le \tau$. Utilizing the nonnegativity of I(t), the initial condition $R(\vartheta )\ge 0$ and

$$\begin{aligned} \dfrac{{\text {d}} R(t)}{{\text {d}} t}\Bigg |_{R(t)=0}=\left[ \gamma I(t)-\mu R(t)\right] \Big |_{R(t)=0}\ge 0, \end{aligned}$$

we derive $R(t)\ge 0$ for $0<t\le \tau$.

For $\tau <t\le 2\tau$, it can be known that $I(t-\tau )\ge 0$ from the above discussion. Then, the existence and uniqueness of solutions can also be guaranteed in the interval $(\tau , 2\tau ]$. Utilizing the similar method of proof, we are able to obtain the nonnegativity of S(t), H(t), I(t) and R(t) for $\tau <t\le 2\tau$.

This process can proceed if we adopt the same way in $(2\tau , 3\tau ], (3\tau , 4\tau ]$ and so on. To sum up, it’s proved that a unique solution (S(t), H(t), I(t), R(t)) of system (2.3) can continuously exist in the maximal interval $[0,\infty )$. $\square$

Lemma 2

For system (2.3) with the initial conditions (2.2), a invariant set contained in the nonnegative cone $R_{+}^{4}$ is as follows

$$\begin{aligned} \varOmega _1= & {} \left\{ \!\big (S, H, I, R\big )\in R_{+}^{4} \Big | 0\le \! S\!\le S^{0}, 0\le \! H\!\le H^{0},\right. \\&\left. 0\le \!S+H+I+R \! \le T^{*} \!\right\} . \end{aligned}$$

Proof

Based on the proof of Lemma 1, it’s obtained that S(t), H(t), I(t) and R(t) are nonnegative. As a result, $S(t)+H(t)+I(t)+R(t)\ge 0$ holds for $t\ge 0$. Observe that the sum of all equations of system (2.3) yields

$$\begin{aligned}&\frac{d \Big (\!S(t)\!+\!H(t)\!+\!I(t)\!+\!R(t)\!\Big )}{d t}\nonumber \\&\quad =(b_{1}+\!b_{2})(1-\!T^{*})\nonumber \\&\qquad -\mu \Big (\!S(t)\!+\!H(t)\!+\!I(t)\!+\!R(t)\!\Big ). \end{aligned}$$

(2.5)

Thus, we can obtain

$$\begin{aligned}&\limsup _{t\rightarrow \infty }\Big (S(t)+H(t)+I(t)+R(t)\Big )\\&\quad =\limsup _{t\rightarrow \infty }T(t)=T^{*}=\frac{b_{1}+b_{2}}{b_{1}+b_{2}+\mu }. \end{aligned}$$

Moreover, from the first equation of system (2.3), we gain

$$\begin{aligned} \begin{aligned} \dfrac{{\text {d}} S(t)}{{\text {d}} t}&=b_{1}\Big (1-T^{*}\Big )-\beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{ a+I(t-\tau )}-\mu S(t)\\&\le b_{1}\Big (1-T^{*}\Big )-\mu S(t). \end{aligned} \end{aligned}$$

By the comparison principle, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty }S(t)\le S^{0}=\dfrac{b_{1}}{b_{1}+b_{2}+\mu }. \end{aligned}$$

In this manner, it’s also acquired that

$$\begin{aligned} \limsup _{t\rightarrow \infty }H(t)\le H^{0}=\dfrac{b_{2}}{b_{1}+b_{2}+\mu }. \end{aligned}$$

$\square$

2.3 The basic reproduction number and equilibrium points

By equating the right sides of $\frac{{\text {d}} S(t)}{{\text {d}}t}, \frac{{\text {d}} H(t)}{{\text {d}}t}$ and $\frac{dI(t)}{{\text {d}}t}$ to zero, we can easily verify that system (2.4) has a disease-free equilibrium point of the form $E_{0}=(\frac{b_{1}}{b_{1}+b_{2}+\mu }, \frac{b_{2}}{b_{1}+b_{2}+\mu },0)$. This is regarded as an idealization where the disease completely disappear in the network. To find the threshold of disease propagation, we are to figure out the basic reproduction number which indicates the scale of the new infected resulted from an infected individual by contact. Based on the method of next-generation matrix [57], define the new infection matrix F and the transition matrix V, namely

$$\begin{aligned} F= & {} \left[ \dfrac{\partial \left[ \big (\beta _{1}S(t)+\beta _{2}H(t)\big )\overline{k}\frac{I(t-\tau )}{a+I(t-\tau )}\right] }{\partial I(t-\tau )}\Bigg |_{E_{0}}\right] \\= & {} \left[ \frac{b_{1}\beta _{1}+b_{2}\beta _{2}}{a(b_{1}+b_{2}+\mu )}\overline{k}\right] , \end{aligned}$$

and

$$\begin{aligned} V=\left[ \frac{\partial \left[ (\gamma +\mu ) I(t)\right] }{\partial I(t)}\Bigg |_{E_{0}}\right] =\left[ \gamma +\mu \right] . \end{aligned}$$

Hence, we can calculate the spectral radius of $FV^{-1}$ and define the basic reproduction number of the infection as

$$\begin{aligned} R_{0}^{1}=p(FV^{-1})=\dfrac{(b_{1}\beta _{1}+b_{2}\beta _{2})\overline{k}}{a(b_{1}+b_{2}+\mu )(\gamma +\mu )}. \end{aligned}$$

(2.6)

Next, the condition for the existence of endemic equilibrium point $E_{*}$ of system (2.4) is determined in the following conclusion.

Theorem 1

For any feasible parameters, system (2.4) always has a disease-free equilibrium point $E_{0}=(S^{0},H^{0},I^{0})=\left( \frac{b_{1}}{b_{1}+b_{2}+\mu }, \frac{b_{2}}{b_{1}+b_{2}+\mu },0\right)$. If the basic reproduction number $R_{0}^{1}>1$, there exists a unique endemic equilibrium point $E_{*}=(S^{*}, H^{*}, I^{*})$ in system (2.4).

Proof

Let $\frac{{\text {d}} S(t)}{{\text {d}} t}=0, \frac{{\text {d}} H(t)}{{\text {d}} t}=0, \frac{{\text {d}} I(t)}{d t}=0$ and suppose $E_{*}=(S^{*}, H^{*}, I^{*})$ as the endemic equilibrium point of system (2.4). Hence, we obtain a quadratic equation about $I^{*}$ which satisfies the form $q_0I^{*2}+q_1I^{*}+q_2=0$ where

$$\begin{aligned} \begin{aligned} q_0&=(b_1+b_2+\mu )(\gamma +\mu )\\&\quad \left[ \beta _{1}\beta _{2}\overline{k}^2+(\beta _{1}+\beta _{2})\overline{k}\mu +\mu ^2\right] >0,\\ q_1&=(b_1+b_2+\mu )(\gamma +\mu )\\&\quad \left[ (\beta _{1}+\beta _{2})\overline{k}\mu a+2\mu ^2a\right] -(b_1+b_2)\mu \beta _{1}\beta _{2}\overline{k}^2\\&\quad -(b_1\beta _{1}+b_2\beta _{2})\mu ^2\overline{k},\\ q_2&=(b_1+b_2+\mu )(\gamma +\mu )\mu ^2a^2\\&\quad -(b_1\beta _{1}+b_2\beta _{2})\mu ^2\overline{k}a. \end{aligned} \end{aligned}$$

Define $g(I^{*})=q_0I^{*2}+q_1I^{*}+q_2$ and note $g(0)=(b_1+b_2+\mu )(\gamma +\mu )\mu ^2 a^2(1-R_{0}^{1})<0$ in the condition of $R_{0}^{1}>1$. Furthermore, we figure out

$$\begin{aligned} \begin{aligned} g(1)&=q_0+q_1+q_2\\&>(b_1+b_2+\mu )(\gamma +\mu )\beta _{1}\beta _{2}\overline{k}^2\\&\quad +(b_1+b_2+\mu )(\gamma +\mu )(\beta _{1}+\beta _{2})\overline{k}\mu (1+ a)\\&\quad -(b_1+b_2)\mu \beta _{1}\beta _{2}\overline{k}^2\\&\quad -(b_1\beta _{1}+b_2\beta _{2})\mu ^2\overline{k}(1+ a)\\&>0. \end{aligned} \end{aligned}$$

From the above discussion about $g(I^{*})$, we conclude that the equation $g(I^{*})=0$ has a unique positive root $I^{*}=\frac{-q_1+\sqrt{q_1^2-4q_0q_2}}{2q_0}$ in the interval (0, 1). Correspondingly, the unique endemic equilibrium point of system (2.4) is

$$\begin{aligned} E_{*}= & {} \left( \!\!\dfrac{b_1\mu ( a+I^{*})}{(b_1+b_2+\mu )[\beta _{1}\overline{k} I^{*}+\mu ( a+I^{*})]}, \right. \\&\left. \dfrac{b_2\mu ( a+I^{*})}{(b_1+b_2+\mu )[\beta _{2}\overline{k} I^{*}+\mu ( a+I^{*})]},I^{*}\!\!\right) . \end{aligned}$$

$\square$

2.4 Stability analysis

As a matter of fact, stability behavior is an important feature of the epidemic model as it reveals the stable characteristic of dynamical system in the long term. In this section, an earnest attempt is made to study the local and global stabilities of two equilibrium points of our delayed system.

Theorem 2

For any $\tau \ge 0$, the disease-free equilibrium point $E_{0}$ of system (2.4) is locally asymptotically stable if $R_{0}^{1}<1$ and unstable if $R_{0}^{1}>1$.

Proof

To investigate the local stability of the disease-free equilibrium point, system (2.4) needs to be linearized at $E_{0}$ and the linear system has the following form

$$\begin{aligned} \left\{ \begin{array}{lcr} \dfrac{{\text {d}} S(t)}{{\text {d}} t}=-\dfrac{\beta _{1}\overline{k} S^0}{ a}I(t-\tau )-\mu S(t),\\ \dfrac{{\text {d}} H(t)}{{\text {d}} t}=-\dfrac{\beta _{2}\overline{k} H^0}{ a}I(t-\tau )-\mu H(t),\\ \dfrac{{\text {d}} I(t)}{{\text {d}} t}=\dfrac{(\beta _{1}S^0+\beta _{2}H^0)\overline{k}}{ a}I(t-\tau )-(\gamma +\mu )I(t). \end{array} \right. \end{aligned}$$

(2.7)

The Jacobian matrix $J(E_{0})$ of system (2.4) at $E_{0}$ can be written as

$$\begin{aligned} J(E_{0})=\left[ \begin{array}{ccc} -\mu &{} 0 &{} -\dfrac{\beta _{1}\overline{k} S^0}{ a}e^{-\lambda \tau }\\ 0 &{} -\mu &{} -\dfrac{\beta _{2}\overline{k} H^0}{ a}e^{-\lambda \tau } \\ 0 &{} 0 &{} \dfrac{(\beta _{1}S^0+\beta _{2}H^0)\overline{k}}{ a}e^{-\lambda \tau }-(\gamma +\mu ) \end{array} \right] . \end{aligned}$$

The characteristic equation of $J(E_{0})$ is given by $|\lambda E-J(E_{0})|=0$ as follows

$$\begin{aligned} (\lambda +\mu )^2\Bigg (\lambda -\dfrac{(\beta _{1}S^0+\beta _{2}H^0)\overline{k}}{ a}e^{-\lambda \tau }+\gamma +\mu \Bigg )=0.\nonumber \!\!\!\!\!\!\\ \end{aligned}$$

(2.8)

The equation (2.8) has two negative real roots equal to $-\mu$. Besides, the remaining eigenvalue of matrix $J(E_{0})$ is the solution of $H(\lambda )=0$, where

$$\begin{aligned} H(\lambda )= & {} \lambda -(\gamma +\mu )\Bigg (\!\!\dfrac{(\beta _{1}S^0+\beta _{2}H^0)\overline{k} }{ a(\gamma +\mu )}e^{-\lambda \tau }-1\!\!\Bigg )\nonumber \\= & {} \lambda -(\gamma +\mu )\big (R_{0}^{1}e^{-\lambda \tau }-1\big ). \end{aligned}$$

(2.9)

In what follows, we discuss the characteristic roots of equation (2.8) for $\tau =0$ and $\tau >0$ separately.

(I) When $\tau =0$, all solutions of the characteristic equation (2.8) have negative real part if $R_{0}^{1}<1$. In this case, the disease-free equilibrium point $E_{0}$ of system (2.4) is locally asymptotically stable. On the contrary, there exists one eigenvalue with positive real part, which implies that $E_{0}$ is unstable in the case of $R_{0}^{1}>1$.

(II) For $\forall \tau >0$, assume that $R_{0}^{1}<1$ first. When instability at $E_{0}$ happens, one eigenvalue of the characteristic equation (2.8) is bound to cross the imaginary axis. Next, we wonder whether there is a pair of complex conjugate roots that passing through the imaginary axis with the increase of $\tau$. Thus, suppose that there is a pair of purely imaginary roots. Substitute $\lambda =i\xi \,(\xi >0)$ into the equation $H(\lambda )=0$. By separating the real and imaginary parts, we obtain

$$\begin{aligned} \left\{ \begin{array}{lcr} \xi =-(\gamma +\mu )R_{0}^{1}\sin (\xi \tau ),\\ \gamma +\mu =(\gamma +\mu )R_{0}^{1}\cos (\xi \tau ). \end{array}\right. \end{aligned}$$

(2.10)

Squaring and adding both sides of the two equations (2.10), we gain the following equation

$$\begin{aligned} \xi ^2=(\gamma +\mu )^2({R_{0}^{1}}^2-1). \end{aligned}$$

(2.11)

In fact, there are no positive real roots $\xi$ satisfying the above equation (2.11) when $R_{0}^{1}<1$.

Then, under the assumption of $R_{0}^{1}>1$, we note $H(0)<0$ and figure out

$$\begin{aligned} \dfrac{{\text {d}} H(\lambda )}{d \lambda }=1+(\gamma +\mu )R_{0}^{1}\tau e^{-\lambda \tau }>0. \end{aligned}$$

Accordingly, find $\lim \limits _{\lambda \rightarrow +\infty } H(\lambda )=+\infty$. As a result, the equation $H(\lambda )=0$ has at least one positive real root if $R_{0}^{1}>1$, which suggests the instability at $E_{0}$ of system (2.4).

To summarize, combining the above two situations $\tau =0$ and $\tau >0$, we prove that the disease-free equilibrium point $E_{0}$ is locally asymptotically stable if $R_{0}^{1}<1$ and unstable if $R_{0}^{1}>1$ for $\forall \tau \ge 0$. $\square$

Theorem 3

For any $\tau \ge 0$, the disease-free equilibrium point $E_{0}$ of system (2.1) is globally asymptotically stable when $R_{0}^{1}\le 1$.

Proof

According to Lemma 2, we find that all solutions of system (2.1) will remain or tend to the invariant region $\varOmega _1$. In consequence, construct the following Lyapunov function $L_1(t)$ in the closed set $\varOmega _1$

$$\begin{aligned} \begin{array}{lcr} L_1(t)=L_{11}(t)+L_{12}(t), \end{array} \end{aligned}$$

(2.12)

where

$$\begin{aligned} L_{11}(t)= & {} S(t)-S^0-S^0 \ln \dfrac{S(t)}{S^0}+H(t)\nonumber \\&-H^0-H^0 \ln \dfrac{H(t)}{H^0}+I(t),\nonumber \\ L_{12}(t)= & {} \int \limits _{t-\tau }^{t}\dfrac{(\beta _{1}b_{1}+\beta _{2}b_{2})\overline{k}}{b_{1}+b_{2}+\mu }\dfrac{I(x)}{ a + I(x)}dx. \end{aligned}$$

(2.13)

In fact, we are to show that the derivative of $L_{1}(t)$ along the solutions of system (2.1) isn’t positive for all $t\ge 0$. Now, calculate the derivative of $L_{11}(t)$ with respect to t as follows:

$$\begin{aligned}&\dfrac{{\text {d}} L_{11}(t)}{{\text {d}}t}\Bigg |_{(2.1)} =\left( 1-\dfrac{S^0}{S(t)}\right) \\&\qquad \Bigg [ b_{1}\Big (1-S(t)-H(t)-I(t)-R(t)\Big )\\&\qquad -\beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{ a+I(t-\tau )}-\mu S(t)\Bigg ]\\&\qquad +\left( 1-\dfrac{H^0}{H(t)}\right) \Bigg [b_{2}\Big (1-S(t)-H(t)-I(t)-R(t)\Big )\\&\qquad -\beta _{2}\overline{k} H(t)\dfrac{I(t-\tau )}{ a+I(t-\tau )}-\mu H(t) \Bigg ]\\&\qquad +\!\beta _{1}\overline{k} S(t)\dfrac{I(t-\tau )}{ a+I(t-\tau )}\!+\!\beta _{2} \overline{k} H(t)\dfrac{I(t-\tau )}{ a+I(t-\tau )}\\&\qquad -(\gamma +\mu )I(t)\\&\quad =-\mu \frac{\Big (S(t)-S^0\Big )^2}{S(t)}+b_{1}\left( 1-\dfrac{S^0}{S(t)}\right) \Big (S^0-T(t)\Big )\\&\qquad +b_{2}S^0\left( 1-\dfrac{S^0}{S(t)}\right) -\mu \frac{\Big (H(t)-H^0\Big )^2}{H(t)}\\&\qquad +b_{2}\left( 1-\dfrac{H^0}{H(t)}\right) \Big (H^0-T(t)\Big )+b_{1}H^0\left( 1-\dfrac{H^0}{H(t)}\right) \\&\qquad +\beta _{1}\overline{k} \left[ -S(t)\left( 1-\dfrac{S^0}{S(t)}\right) +S(t)\right] \dfrac{I(t-\tau )}{ a+I(t-\tau )}\\&\qquad +\beta _{2} \overline{k} \left[ -H(t)\left( 1-\dfrac{H^0}{H(t)}\right) +H(t)\right] \dfrac{I(t-\tau )}{ a+I(t-\tau )}\\&\qquad -(\gamma +\mu )I(t)\\&\quad =-\mu \frac{\Big (S(t)-S^0\Big )^2}{S(t)}-\mu \frac{\Big (H(t)-H^0\Big )^2}{H(t)}\\&\qquad +b_{1}\left( 1-\dfrac{S^0}{S(t)}\right) \Big (S^0+H^0-T(t)\Big )\\&\qquad +b_{2}\left( 1-\dfrac{H^0}{H(t)}\right) \Big (H^0 +S^0-T(t)\Big )-(\gamma +\mu )I(t)\\&\qquad +\beta _{1}\overline{k} S^0\dfrac{I(t-\tau )}{ a+I(t-\tau )}+\beta _{2}\overline{k} H^0\dfrac{I(t-\tau )}{ a+I(t-\tau )}. \end{aligned}$$

Then, calculate the derivative of $L_{12}(t)$ with respect to t as follows:

$$\begin{aligned} \begin{aligned}&\dfrac{d L_{12}(t)}{{\text {d}}t}\Bigg |_{(2.1)}\\&\quad =\Big (\beta _{1}S^0+\beta _{2}H^0\Big )\overline{k}\left( \dfrac{I(t)}{ a+I(t)}-\dfrac{I(t-\tau )}{ a+I(t-\tau )}\right) . \end{aligned} \end{aligned}$$

Thus, the derivative of $L_{1}(t)$ along the solutions of system (2.1) is given by

$$\begin{aligned}&\dfrac{{\text{ d }} L_1(t)}{{\text{ d }}t}\Bigg |_{(2.1)} =\dfrac{{\text{ d }} L_{11}(t)}{{\text{ d }}t}\Bigg |_{(2.1)} +\dfrac{{\text{ d }} L_{12}(t)}{{\text{ d }}t}\Bigg |_{(2.1)}\\&\quad =-\mu \frac{\Big (S(t)-S^0\Big )^2}{S(t)}-\mu \frac{\Big (H(t)-H^0\Big )^2}{H(t)}\\&\qquad +b_{1}\left( 1-\dfrac{S^0}{S(t)}\right) \Big (T^{*}-T(t)\Big )\\&\qquad +b_{2}\left( 1-\dfrac{H^0}{H(t)}\right) \Big (T^{*}-T(t)\Big )\\&\qquad +\Big (\beta _{1}S^0+\beta _{2}H^0\Big )\overline{k} \dfrac{I(t)}{ a+I(t)}-(\gamma +\mu )I(t)\\&\quad \le -\mu \left[ \frac{\Big (S(t)-S^0\Big )^2}{S(t)}+\frac{\Big (H(t)-H^0\Big )^2}{H(t)}\right] \\&\qquad +\left[ b_{1}\left( 1-\dfrac{S^0}{S(t)}\right) +b_{2}\left( 1-\dfrac{H^0}{H(t)}\right) \right] \\&\qquad \Big (T^{*}-T(t)\Big ) +(\gamma +\mu )\Big (R_{0}^{1}-1\Big )I(t). \end{aligned}$$

When the basic reproduction number satisfies $R_{0}^{1}\le 1$, we can obtain $\frac{{\text {d}} L_1(t)}{{\text {d}}t}\le 0$ for all $I(t)\ge 0$ in $\varOmega _1$. Furthermore, the equation $\frac{{\text {d}} L_1(t)}{{\text {d}}t}=0$ holds if and only if $S(t)=S^{0}, H(t)=H^{0}$ and $I(t)=I^{0}$. Namely, singleton $\{E_{0}\}$ is the largest compact invariant set which is contained in the set $\{(S(t),H(t),I(t))\in R_{+}^{3}\big |\frac{{\text {d}} L_1(t)}{{\text {d}} t}=0\}$. Based on the LaSalle Invariance Principle, the disease-free equilibrium point $E_{0}$ of system (2.1) is globally asymptotically stable if $R_{0}^{1}\le 1.$ $\square$

Theorem 4

For any $\tau \ge 0$, the endemic equilibrium point $E_{*}$ of system (2.4) is locally asymptotically stable if $R_{0}^{1}>1$.

Proof

The Jacobian matrix $J(E_{*})$ of system (2.4) at the endemic equilibrium point $E_{*}$ is

$$\begin{aligned} \left[ \begin{array}{ccc} \!-\beta _{1}\overline{k}\dfrac{I^*}{ a+I^*}-\mu &{} 0 &{} -\beta _{1}\overline{k} S^*\dfrac{ a}{( a+I^*)^2}e^{-\lambda \tau }\\ 0 &{} -\beta _{2}\overline{k}\dfrac{I^*}{ a+I^*}-\mu &{} -\beta _{2}\overline{k} H^*\dfrac{ a}{( a+I^*)^2}e^{-\lambda \tau } \\ \beta _{1}\overline{k}\dfrac{I^*}{ a+I^*} &{} \beta _{2}\overline{k}\dfrac{I^*}{ a+I^*} &{} (\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}e^{-\lambda \tau }\!-\!(\gamma +\mu )\! \end{array} \!\right] \!. \end{aligned}$$

By calculation, the characteristic equation of $J(E_{*})$ is equivalent to

$$\begin{aligned}&\lambda ^3+n_1\lambda ^2+n_2\lambda +n_3\nonumber \\&\quad +e^{-\lambda \tau }(n_4\lambda ^2+n_5\lambda +n_6)=0, \end{aligned}$$

(2.14)

where

$$\begin{aligned} n_1=&\,(\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+3\mu +\gamma>0,\\ n_2=&\,\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\ {}&+\Big ((\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu \Big )(\gamma +\mu )\!>\!0,\\ n_3=&\,\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\ {}&\cdot (\gamma +\mu )>0,\\ n_4=&\,-(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}<0,\\ n_5=&\,(\beta _{1}^2S^*+\beta _{2}^2H^*)\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\\ {}&-(\beta _{1}S^*+\beta _{2}H^*)\overline{k}\\ {}&\dfrac{ a}{( a+I^*)^2}\Big ((\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu \Big )\\ =&-\beta _{1}\beta _{2}(S^*+H^*)\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\\ {}&-2\mu (\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}<0,\\ n_6=&\,\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\Bigg [\beta _{1}^2S^*\Big (\beta _{2} \overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\ {}&+\beta _{2}^2H^*\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Bigg ]\\ {}&-(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}\\ {}&\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\ =&-\mu \overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\beta _{1}\beta _{2}(S^*+H^*)\\ {}&-\mu ^2(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2} <0.\\ \end{aligned}$$

(I) When $\tau =0$, the characteristic equation (2.14) at $E_{*}$ can be degenerated into the form

$$\begin{aligned} \lambda ^3+c_1\lambda ^2+c_2\lambda +c_3=0, \end{aligned}$$

(2.15)

where

$$\begin{aligned} \begin{aligned} c_1&=(\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+3\mu +\gamma \\&\quad -(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2},\\ c_2&=\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big ) \Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad +(\beta _{1}^2S^*+\beta _{2}^2H^*)\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\\&\quad +\Big (-(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}+\gamma +\mu \Big )\\&\quad \Big ((\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu \Big ),\\ c_3&=\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big ) \Big (\!\!\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \!\!\Big )\\&\quad \Big (\!\!-\!(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}+\gamma +\!\mu \!\Big )\\&\quad +\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3} \Bigg [\beta _{1}^2S^*\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad +\beta _{2}^2H^*\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Bigg ].\\ \end{aligned} \end{aligned}$$

Pay attention to the identical equation

$$\begin{aligned} \gamma +\mu =(\beta _{1}S^*+\beta _{2}H^*)\overline{k}\dfrac{1}{ a+I^*}. \end{aligned}$$

(2.16)

Therefore, we can find that coefficients $c_1, c_2$ and $c_3$ of the equation (2.15) are all positive. Then, make some calculations in the following

$$\begin{aligned} \varDelta _1&=c_1>0,\\ \varDelta _2&=\begin{vmatrix} c_1&1 \\ c_3&c_2 \end{vmatrix}=c_1c_2-c_3\\&>\Big (\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu \Big )\\&\quad (\beta _{1}^2S^*+\beta _{2}^2H^*)\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\\&\quad +\Big (\mu +\gamma -(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}\Big )\\&\quad \cdot \Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad -\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad \cdot \Big (-(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}+\gamma +\mu \Big )\\&\quad -\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\Bigg [\beta _{1}^2S^*\Big (\beta _{2} \overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad +\beta _{2}^2H^*\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Bigg ]\\&=\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\Big [\beta _{1}^2S^* \Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad +\beta _{2}^2H^*\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big ]>0,\\ \varDelta _3&=c_3\varDelta _2>0. \end{aligned}$$

According to the Hurwitz criterion, it can be proved that the endemic equilibrium point $E_{*}$ of system (2.4) is locally asymptotically stable in the case of $\tau =0$ when $R_{0}^{1}>1$.

(II) When $\tau >0$, we make efforts to study the influence of time delay on the stability of system (2.4) at $E_{*}$. Once system (2.4) generates instability for a specific delay $\tau$, there exists a characteristic root of equation (2.14) which must cross the imaginary axis. Assume that $\lambda =i\xi \,(\xi >0)$ is a solution of the equation (2.14), which meets the following form

$$\begin{aligned}&-i\xi ^3-n_1\xi ^2+in_2\xi +n_3+\Big (\cos (\xi \tau )-i\sin (\xi \tau )\Big )\nonumber \\&(-n_4\xi ^2+in_5\xi +n_6)=0. \end{aligned}$$

(2.17)

By separating the real and imaginary parts of the equation (2.17), we derive

$$\begin{aligned} \left\{ \begin{array}{lcr} n_5\xi \cos (\xi \tau )+(n_4\xi ^2-n_6)\sin (\xi \tau )=\xi ^3-n_2\xi ,\\ (n_6-n_4\xi ^2)\cos (\xi \tau )+n_5\xi \sin (\xi \tau )=n_1\xi ^2-n_3. \end{array}\right. \nonumber \\ \end{aligned}$$

(2.18)

After eliminating $\tau$ in (2.18), it follows that

$$\begin{aligned}&\xi ^6+(n_1^2-2n_2-n_4^2)\xi ^4 +(n_2^2-2n_1n_3-n_5^2\nonumber \\&\quad +2n_4n_6)\xi ^2+n_3^2-n_6^2=0. \end{aligned}$$

(2.19)

Letting $z=\xi ^2$, we can rewrite (2.19) as an equation about z in the following

$$\begin{aligned} z^3+n_{21}z^2+n_{22}z+n_{23}=0, \end{aligned}$$

(2.20)

where $n_{21}=n_1^2-2n_2-n_4^2, n_{22}=n_2^2-2n_1n_3-n_5^2+2n_4n_6$ and $n_{23}=n_3^2-n_6^2$.

Further, we are devoted to analyzing the property of coefficients $n_{21}, n_{22}$ and $n_{23}$. It’s easy to find $n_{23}=(n_3+n_6)(n_3-n_6)>0$ because

$$\begin{aligned} \begin{aligned} n_3+n_6&=\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )(\gamma +\mu )\\&\quad +\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\Bigg [\beta _{1}^2S^*\Big (\beta _{2} \overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad +\beta _{2}^2H^*\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Bigg ]\\&\quad -(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}\\&\quad \Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&=\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad \cdot \Bigg [\gamma +\mu -(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}\Bigg ]\\&\quad +\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\Bigg [\beta _{1}^2S^* \Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad +\beta _{2}^2H^*\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Bigg ]\\&>0. \end{aligned} \end{aligned}$$

Together with the identical equation (2.16), it’s available that

$$\begin{aligned} \begin{aligned} n_{21}&=n_1^2-2n_2-n_4^2=(n_1+n_4)(n_1-n_4)-2n_2\\&=\Bigg ((\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu +\mu +\gamma \\&\quad -(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2} \Bigg )\\&\quad \cdot \Bigg ((\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu +\mu +\gamma \\&\quad +(\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2} \Bigg )\\&\quad -2\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\quad -2\Big ((\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu \Big )(\gamma +\mu )\\&=\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )^2+\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )^2\\&\quad +\Big ((\beta _{1}S^*+\beta _{2}H^*)\overline{k}\Big )^2\\&\quad \Bigg [\Big (\frac{1}{ a+I^*}\Big )^2-\Big (\frac{ a}{( a+I^*)^2}\Big )^2\Bigg ]\\&>0. \end{aligned} \end{aligned}$$

And

$$\begin{aligned} n_{22}=\,&\,n_2^2-2n_1n_3-n_5^2+2n_4n_6\\ =\,&\,\Bigg [\!\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big ) \Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}\\&+\mu \Big )+\Big ((\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu \Big )(\gamma +\mu )\!\Bigg ]^2\\&-2\Big ((\beta _{1}+\beta _{2})\overline{k} \dfrac{I^*}{ a+I^*}+2\mu +\mu +\gamma \Big )\\&\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\\&\cdot \Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )(\gamma +\mu )\\&-\Bigg [\beta _{1}\beta _{2}(S^*+H^*)\overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\\&+2\mu (\beta _{1}S^*+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}\Bigg ]^2\\&+2(\beta _{1}S^*\!+\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}\\&\Bigg [\mu \overline{k}^2 \dfrac{ a I^*}{( a+I^*)^3}\beta _{1}\beta _{2}(S^*\!+\!H^*)\\&+\mu ^2(\beta _{1}S^*\!+\!\beta _{2}H^*)\overline{k} \dfrac{ a}{( a+I^*)^2}\Bigg ]\\ =\,&\,\Bigg [\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Bigg ]^2\\&+\Bigg [\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )^2\\&+\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )^2\Bigg ](\gamma +\mu )^2\\&-\beta _{1}^2\beta _{2}^2(S^*+H^*)^2\overline{k}^4 \dfrac{ a^2 I^{*2}}{( a+I^*)^6}\\&-2\mu ^2(\beta _{1}S^*+\beta _{2}H^*)^2\overline{k}^2 \dfrac{ a^2}{( a+I^*)^4}\\&-2\mu \beta _{1}\beta _{2}(S^*+H^*)(\beta _{1}S^*+\beta _{2}H^*)\overline{k}^3 \dfrac{ a^2 I^*}{( a+I^*)^5}\\ =\,&\,\Bigg [\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Bigg ]^2\\&+\Bigg [\beta _{1}^2\overline{k}^2 \dfrac{I^{*2}}{( a+I^*)^2} +2\mu (\beta _{1}+\beta _{2})\overline{k}\dfrac{I^*}{ a+I^*}\\&+\beta _{2}^2\overline{k}^2 \dfrac{I^{*2}}{( a+I^*)^2}+2\mu ^2\Bigg ]\\&\cdot (\beta _{1}S^*+\beta _{2}H^*)^2\overline{k}^2\frac{1}{( a+I^*)^2}\\&-\beta _{1}^2\beta _{2}^2(S^*+H^*)^2\overline{k}^4 \dfrac{ a^2 I^{*2}}{( a+I^*)^6}\\&-2\mu ^2(\beta _{1}S^*+\beta _{2}H^*)^2\overline{k}^2 \dfrac{ a^2}{( a+I^*)^4}\\&-2\mu \beta _{1}\beta _{2}(S^*+H^*)(\beta _{1}S^*+\beta _{2}H^*)\overline{k}^3 \dfrac{ a^2 I^*}{( a+I^*)^5}\\>&\Bigg [\Big (\beta _{1}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Big (\beta _{2}\overline{k} \dfrac{I^*}{ a+I^*}+\mu \Big )\Bigg ]^2\\&+2\mu ^2(\beta _{1}S^*+\beta _{2}H^*)^2\overline{k}^2 \frac{1}{( a+I^*)^2}\\&\times \Bigg (1-\dfrac{ a^2}{( a+I^*)^2}\Bigg )\\&+2\mu (\beta _{1}S^*+\beta _{2}H^*)\overline{k}^3\dfrac{I^*}{( a+I^*)^3}(\beta _{1}^2S^*+\beta _{2}^2H^*)\\&+\Big (2\beta _{1}^3\beta _{2}S^*H^*+2\beta _{1}\beta _{2}^3 S^*H^*\Big )\overline{k}^4\dfrac{I^{*2}}{( a+I^*)^4}\\ >&0. \end{aligned}$$

Therefore, we prove that $n_{21}, n_{22}$ and $n_{23}$ are all positive. Define $h(z)=z^3+n_{21}z^2+n_{22}z+n_{23}$ and note $h(z)>0$ for $\forall z>0$. The equation (2.20) has no positive roots z, which implies that there are no real roots $\xi$ satisfying the equation (2.17). As a result, it can be concluded that the endemic equilibrium point $E_{*}$ of system (2.4) is locally asymptotically stable for $\forall \tau >0$ in the condition of $R_{0}^{1}>1$. $\square$

3 Disease transmission in heterogeneous networks

In this section, when the network is from homogeneous to heterogeneous, we propose and analyze the corresponding epidemic model which possesses the same modeling mechanism as that in the above section.

3.1 Model description

Compared with homogeneous networks, the network with a heterogeneous topology is closer to social network in the real world accurately, which motivates us to take the heterogeneity of contact between individuals into account. As a result, we make efforts to study disease transmission in heterogeneous networks in which nodes with the same degree are regarded as equivalents. Suppose that the network which we consider is uncorrelated. Denote the densities of the subhealthy, healthy, infected and recovered nodes with degree k $(k=1,2,\ldots ,n)$ at time t as $S_{k}(t)$, $H_{k}(t)$, $I_{k}(t)$ and $R_{k}(t)$, respectively. The SHIR epidemic model in heterogeneous networks is under the framework of the following coupled system:

$$\begin{aligned} \dfrac{{\text{ d }} S_{k}(t)}{{\text{ d }} t}=&\,\,b_{1}\Big (1-S_{k}(t)-H_{k}(t)-I_{k}(t)-R_{k}(t)\Big )\nonumber \\&-\beta _{1} k S_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}-\mu S_{k}(t), \nonumber \\ \dfrac{{\text{ d }} H_{k}(t)}{{\text{ d }} t}=&b_{2}\Big (1-S_{k}(t)-H_{k}(t)-I_{k}(t)-R_{k}(t)\Big )\nonumber \\&-\beta _{2} k H_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}-\mu H_{k}(t),\nonumber \\ \dfrac{{\text{ d }} I_{k}(t)}{{\text{ d }} t}=&\,\beta _{1} k S_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\nonumber \\&+\beta _{2} k H_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\!-\!\gamma I_{k}(t)\!-\!\mu I_{k}(t),\nonumber \\ \dfrac{{\text{ d }} R_{k}(t)}{{\text{ d }} t}=&\gamma I_{k}(t)-\mu R_{k}(t). \end{aligned}$$

(3.1)

Here $b_{i}(1-S_{k}(t)-H_{k}(t)-I_{k}(t)-R_{k}(t))$ $(i=1,2)$ represents the density of newborn susceptible individuals coming from empty nodes. The definitions of all parameters in system (3.1) are same with that in systems (1.1) and (2.1). Most important of all, by introducing the psychological factor a, we significantly adopt a nonlinear incidence rate $\beta _{1} kS_{k}(t)\frac{\varTheta (t)}{ a+\varTheta (t)}$ or $\beta _{2} kH_{k}(t)\frac{\varTheta (t)}{ a+\varTheta (t)}$ to characterize the validity of protective measures taken by the subhealthy or healthy individuals. Furthermore, two susceptible groups need some time to be infected in the spreading process of disease. The consideration of delayed nonlinear incidence rate makes this epidemic model more reasonable and practical. The initial conditions $\big \{(S_{k}(\vartheta ), H_{k}(\vartheta ), I_{k}(\vartheta ), R_{k}(\vartheta ))\big \}_{k}=\big \{(\varphi _{k1}(\vartheta ), \varphi _{k2}(\vartheta ), \varphi _{k3}(\vartheta ), \varphi _{k4}(\vartheta ))\big \}_{k}$ for system (3.1) satisfy

$$\begin{aligned} \begin{aligned}&\varphi _{ki}(\vartheta )\ge 0, \; 0<\sum _{i=1}^4\varphi _{ki}(\vartheta )\le 1, \; \vartheta \in [-\tau ,0],\;\\&\quad \varphi _{ki}(0)>0\,(i=1,2,3,4), \end{aligned} \end{aligned}$$

(3.2)

where $\big \{(\varphi _{k1}, \varphi _{k2}, \varphi _{k3}, \varphi _{k4})\big \}_{k}\in C([-\tau ,0],R_{+}^{4n})$ which is the Banach space of continuous functions mapping the interval $[-\tau ,0]$ into $R_{+}^{4n}=\Big \{\big \{(x_{k1}, x_{k2}, x_{k3}, x_{k4})\big \}_{k}\in R^{4n}: x_{ki}\ge 0, i=1,2,3,4\Big \}$.

The density of total population with degree k at time t is expressed by $T_{k}(t)=S_{k}(t)+H_{k}(t)+I_{k}(t)+R_{k}(t)$. Taking the sum of all 4n equations in system (3.1), we get

$$\begin{aligned} \dfrac{{\text {d}} T_{k}(t)}{{\text {d}} t}= & {} b_{1}+b_{2}-(b_{1}+b_{2}+\mu )T_{k}(t),\\&\,k=1,2,\ldots ,n. \end{aligned}$$

Further, define $T_{k}^{*}=\lim \limits _{t \rightarrow \infty }T_{k}(t)=\frac{b_{1}+b_{2}}{b_{1}+b_{2}+\mu }$. Then, system (3.1) can be transformed into the limit system as follows:

$$\begin{aligned} \dfrac{{\text {d}} S_{k}(t)}{{\text {d}} t}= & {} b_{1}\Big (1-T_{k}^{*}\Big )\nonumber \\&-\beta _{1} k S_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}-\mu S_{k}(t),\nonumber \\ \dfrac{{\text {d}} H_{k}(t)}{{\text {d}} t}= & {} b_{2}\Big (1-T_{k}^{*}\Big )\nonumber \\&-\beta _{2} k H_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}-\mu H_{k}(t),\nonumber \\ \dfrac{{\text {d}} I_{k}(t)}{{\text {d}} t}= & {} \beta _{1} k S_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\nonumber \\&+\beta _{2} k H_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\nonumber \\&-\gamma I_{k}(t)-\mu I_{k}(t),\nonumber \\ \dfrac{{\text {d}} R_{k}(t)}{{\text {d}} t}= & {} \gamma I_{k}(t)-\mu R_{k}(t). \end{aligned}$$

(3.3)

It can be noticed that the variable $R_{k}(t)$ doesn’t affect values of $S_{k}(t), H_{k}(t)$ and $I_{k}(t)$ in the above system. Moreover, the limit system (3.3) is further reduced to the following form:

$$\begin{aligned} \dfrac{{\text {d}} S_{k}(t)}{{\text {d}} t}= & {} b_{1}\Big (1-T_{k}^{*}\Big )\nonumber \\&-\beta _{1} k S_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}-\mu S_{k}(t),\nonumber \\ \dfrac{{\text {d}} H_{k}(t)}{{\text {d}} t}= & {} b_{2}\Big (1-T_{k}^{*}\Big )\nonumber \\&-\beta _{2} k H_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}-\mu H_{k}(t),\nonumber \\ \dfrac{{\text {d}} I_{k}(t)}{{\text {d}} t}= & {} \beta _{1} k S_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\nonumber \\&+\beta _{2} k H_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\nonumber \\&-\gamma I_{k}(t)-\mu I_{k}(t). \end{aligned}$$

(3.4)

In consequence, the subsystem (3.4) of the limit system (3.3) facilitates us to investigate dynamical behavior of system (3.1) sufficiently.

3.2 Basic properties of solutions

Lemma 3

For system (3.3) with the initial conditions (3.2), there exists a unique solution $\big \{(S_{k}(t), H_{k}(t), I_{k}(t), R_{k}(t))\big \}_{k}$ globally for $t\in [0,\infty )$.

Proof

Here, we intend to omit the specific proof which is similar to that of Lemma 1. $\square$

Lemma 4

For system (3.3) with the initial conditions (3.2), a invariant set contained in the nonnegative cone $R_{+}^{4n}$ is as follows

$$\begin{aligned} \begin{aligned} \varOmega _2=&\Bigg \{\Big \{\big (S_{k},H_{k},I_{k},R_{k}\big )\Big \}_k\in R_{+}^{4n} \Big | 0\le S_{k}\le S_{k}^{0}, 0\le H_{k}\le H_{k}^{0},\\&0\le S_{k}+H_{k}+I_{k}+R_{k}\le T_{k}^{*}, k=1,2,\ldots ,n \Bigg \}. \end{aligned} \end{aligned}$$

Proof

The detailed proof is omitted since it has a certain similarity to that of Lemma 2. $\square$

3.3 The basic reproduction number and equilibrium points

Theorem 5

For any feasible parameters, the basic reproduction number of the infection is $R_{0}^{2}=\dfrac{(b_{1}\beta _{1}+b_{2}\beta _{2})\overline{k^2}}{ a(b_{1}+b_{2}+\mu )(\gamma +\mu )\overline{k}}$. System (3.4) always admits a disease-free equilibrium point $E^{0}=\big \{(S_{k}^0,H_{k}^0,I_{k}^0)\big \}_{k}$. There is a unique endemic equilibrium point $E^{*}=\big \{(S_{k}^{*},H_{k}^{*},I_{k}^{*})\big \}_{k}$ of system (3.4) when the basic reproduction number $R_{0}^{2}>1$.

Proof

It’s easily observed that system (3.4) always has a disease-free equilibrium point

$$\begin{aligned} \begin{aligned} E^{0}=\,&\,(S_{1}^0,H_{1}^0,I_{1}^0,\ldots ,S_{k}^0,H_{k}^0,I_{k}^0,\ldots ,S_{n}^0,H_{n}^0,I_{n}^0)\\ =\,&\,\Bigg (\frac{b_{1}}{b_{1}+b_{2}+\mu }, \frac{b_{2}}{b_{1}+b_{2}+\mu }, 0, \ldots ,\\&\frac{b_{1}}{b_{1}+b_{2}+\mu }, \frac{b_{2}}{b_{1}+b_{2}+\mu }, 0, \ldots ,\\&\frac{b_{1}}{b_{1}+b_{2}+\mu }, \frac{b_{2}}{b_{1}+b_{2}+\mu }, 0\Bigg ), \end{aligned} \end{aligned}$$

which implies all of infected and recovered individuals finally degenerate into the susceptible state including the subhealthy and healthy. In addition, the endemic equilibrium point $E^{*}$ satisfies the following equations

$$\begin{aligned} \left\{ \begin{array}{lcr} b_{1}\Big (1-T_{k}^{*}\Big )-\beta _{1} k S_{k}^{*}\dfrac{\varTheta ^{*}}{ a+\varTheta ^{*}}-\mu S_{k}^{*}=0,\\ b_{2}\Big (1-T_{k}^{*}\Big )-\beta _{2} k H_{k}^{*}\dfrac{\varTheta ^{*}}{ a+\varTheta ^{*}}-\mu H_{k}^{*}=0,\\ \beta _{1} k S_{k}^{*}\dfrac{\varTheta ^{*}}{ a+\varTheta ^{*}}+\beta _{2} k H_{k}^{*}\dfrac{\varTheta ^{*}}{ a+\varTheta ^{*}}-\gamma I_{k}^{*}-\mu I_{k}^{*}=0, \end{array}\right. \end{aligned}$$

where $\varTheta ^{*}=\sum \limits _{k=1}^n \dfrac{kp(k)I_{k}^{*}}{\overline{k}}$. Further, the positive solution of the above equations is calculated as

$$\begin{aligned} \left\{ \begin{array}{lcr} S_{k}^{*}=\dfrac{b_{1}\mu ( a+\varTheta ^{*})}{(b_{1}+b_{2}+\mu )\Big (\beta _{1}k\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )},\\ H_{k}^{*}=\dfrac{b_{2}\mu ( a+\varTheta ^{*})}{(b_{1}+b_{2}+\mu )\Big (\beta _{2}k\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )},\\ I_{k}^{*}=\dfrac{k\varTheta ^{*}\mu \left[ \beta _{1}b_{1}\Big (\beta _{2}k\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )+\beta _{2}b_{2}\Big (\beta _{1}k\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )\right] }{(b_{1}+b_{2}+\mu )(\gamma +\mu )\Big (\beta _{1}k\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )\Big (\beta _{2}k\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )}. \end{array}\right. \end{aligned}$$

(3.5)

Inserting the expression of $I_{k}^{*}(t)$ into $\varTheta ^{*}$, we derive a self-consistent equation about $\varTheta ^{*}$, namely

$$\begin{aligned} \begin{aligned} \varTheta ^{*}&=\sum _{k^{'}}\frac{k^{'}p(k^{'})}{\overline{k}}\dfrac{k^{'}\varTheta ^{*}\mu \left[ \beta _{1}b_{1}\Big (\beta _{2}k^{'}\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )+\beta _{2}b_{2}\Big (\beta _{1}k^{'}\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )\right] }{(b_{1}+b_{2}+\mu )(\gamma +\mu )\Big (\beta _{1}k^{'}\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )\Big (\beta _{2}k^{'}\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )}\\&=\sum _{k^{'}}\dfrac{\mu k^{'2}p(k^{'})\varTheta ^{*}\left[ \beta _{1}b_{1}\Big (\beta _{2}k^{'}\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )+\beta _{2}b_{2}\Big (\beta _{1}k^{'}\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )\right] }{(b_{1}+b_{2}+\mu )(\gamma +\mu )\overline{k}\Big (\beta _{1}k^{'}\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )\Big (\beta _{2}k^{'}\varTheta ^{*}+\mu ( a+\varTheta ^{*})\Big )}. \end{aligned} \end{aligned}$$

(3.6)

The above equation (3.6) can be transformed into $\varTheta ^* f(\varTheta ^*)=0$ by defining

$$\begin{aligned} f(\varTheta ^{*})= & {} \sum _{k^{'}}\frac{\mu k^{'2}p(k^{'})}{(b_{1}+b_{2}+\mu ) (\gamma +\mu )\overline{k}}\\&\frac{v_1\varTheta ^*+v_2}{v_3\varTheta ^{*2}+v_4\varTheta ^*+v_5}-1, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} v_1&=(b_1+b_2)\beta _1\beta _2 k^{'}+(\beta _1 b_1+\beta _2 b_2)\mu ,\\ v_2&=(\beta _1b_1+\beta _2b_2)a\mu ,\\ v_3&=\beta _1\beta _2 k^{'2}+(\beta _1+\beta _2)\mu k^{'}+\mu ^2,\\ v_4&=(\beta _1+\beta _2)a\mu k^{'}+2a\mu ^2,\\ v_5&=a^2\mu ^2. \end{aligned} \end{aligned}$$

By calculation, we have $f(0)\!=\!\dfrac{(b_{1}\beta _{1}+b_{2}\beta _{2}) \overline{k^2}}{ a(b_{1}\!+\!b_{2}\!+\!\mu )(\gamma \!+\!\mu )\overline{k}}-1$ where $\overline{k^2}$ is defined by $\sum \nolimits _{k=1}^{n}k^2p(k)$. Besides, there exists the following inequality

$$\begin{aligned} \begin{aligned} &f(1)=\sum _{k^{'}}\dfrac{k^{'}p(k^{'})}{\overline{k}}\dfrac{ \mu k^{'}\left[ \beta _{1}\frac{b_{1}}{b_{1}+b_{2}+\mu }\Big (\beta _{2}k^{'}+\mu ( a+1)\Big )+\beta _{2}\frac{b_{2}}{b_{1}+b_{2}+\mu }\Big (\beta _{1}k^{'}+\mu ( a+1)\Big )\right] }{(\gamma +\mu )\Big (\beta _{1}k^{'}+\mu ( a+1)\Big )\Big (\beta _{2}k^{'}+\mu ( a+1)\Big )}-1\\ &\qquad \ =\sum _{k^{'}}\dfrac{k^{'}p(k^{'})}{\overline{k}}\dfrac{\mu }{\gamma +\mu }\dfrac{\frac{b_{1}+b_{2}}{b_{1}+b_{2}+\mu }\beta _{1}\beta _{2}k^{'2}+ \left( \frac{b_{1}}{b_{1}+b_{2}+\mu }\beta _{1}+\frac{b_{2}}{b_{1}+b_{2}+\mu }\beta _{2}\right) k^{'}\mu ( a+1) }{\beta _{1}\beta _{2} k^{'2}+(\beta _{1}+\beta _{2})k^{'}\mu ( a+1)+\mu ^2( a+1)^2}-1<0. \end{aligned} \end{aligned}$$

(3.7)

In addition, we figure out

$$\begin{aligned} \dfrac{{\text {d}} f(\varTheta ^{*})}{d \varTheta ^{*}}= & {} \sum _{k^{'}}\frac{\mu k^{'2}p(k^{'})}{(b_{1}+b_{2}+\mu )(\gamma +\mu )\overline{k}}\\&\frac{-v_1v_3\varTheta ^{*2}-2v_2v_3\varTheta ^{*}+v_1v_5-v_2v_4}{(v_3\varTheta ^{*2}+v_4\varTheta ^*+v_5)^2}. \end{aligned}$$

Since system parameters are positive, it’s verified that $v_1v_5-v_2v_4<0$. As a result, we derive $\frac{d f(\varTheta ^{*})}{d \varTheta ^{*}}<0$ for $\varTheta ^{*}>0$. To ensure that $f(\varTheta ^{*})=0$ has a non-trivial solution $\varTheta ^{*}\in (0, 1)$ , $f(\varTheta ^{*})$ needs to satisfy the inequation $f(0)>0$. Therefore, the basic reproduction number of the infection is expressed by

$$\begin{aligned} \begin{array}{lcr} R_{0}^{2}=\dfrac{(b_{1}\beta _{1}+b_{2}\beta _{2}) \overline{k^2}}{ a(b_{1}+b_{2}+\mu )(\gamma +\mu )\overline{k}}. \end{array} \end{aligned}$$

(3.8)

In conclusion, only if the condition $R_{0}^{2}>1$ is satisfied, system (3.4) admits a unique endemic equilibrium point $E^{*}=\big \{(S_{k}^{*},H_{k}^{*},I_{k}^{*})\big \}_{k}$ in heterogeneous networks. $\square$

3.4 Stability analysis

Theorem 6

For any $\tau \ge 0$, the disease-free equilibrium point $E^{0}$ of system (3.4) is locally asymptotically stable if $R_{0}^{2}<1$ and unstable if $R_{0}^{2}>1$.

Proof

To study the local stability of system (3.4) at $E^{0}$, we are aimed at deriving the linear system which is a good approximation to the nonlinear system (3.4). The linear dynamical system is expressed as

$$\begin{aligned} \left\{ \begin{array}{lcr} \dfrac{{\text{ d }} S_{k}(t)}{{\text{ d }} t}=-\dfrac{\beta _{1}kS_{k}^0}{ a}\varTheta (t-\tau )-\mu S_{k}(t),\\ \dfrac{{\text{ d }} H_{k}(t)}{{\text{ d }} t}=-\dfrac{\beta _{2}kH_{k}^0}{ a}\varTheta (t-\tau )-\mu H_{k}(t),\\ \dfrac{{\text{ d }} I_{k}(t)}{{\text{ d }} t}=\dfrac{(\beta _{1}S_{k}^0+\beta _{2}H_{k}^0)}{ a}k\varTheta (t-\tau )\\ \qquad \qquad \,\, -(\gamma +\mu )I_{k}(t). \end{array}\right. \end{aligned}$$

(3.9)

Correspondingly, the Jacobian matrix $J(E^{0})$ is a $3n \times 3n$ matrix with the form of

$$\begin{aligned} J(E^{0})=\left[ \begin{array}{ccc} J_{11} &{} 0 &{} J_{13}\\ 0 &{} J_{22} &{} J_{23} \\ 0 &{} 0 &{} J_{33} \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} J_{11}=J_{22}=\left[ \begin{array}{cccc} -\mu &{} 0 &{} \ldots &{} 0\\ 0 &{} -\mu &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} -\mu \end{array} \right] , \end{aligned}$$

and $J_{33}$ has the following form

$$\begin{aligned} \left[ \begin{array}{cccc} \frac{(\beta _{1}S_{1}^0+\beta _{2}H_{1}^0)1\cdot 1 p(1)}{ a\overline{k}}\!e^{-\lambda \tau }\!-\!(\gamma \!+\!\mu )\! &{} \frac{(\beta _{1}S_{1}^0+\beta _{2}H_{1}^0)1\cdot 2 p(2)}{ a\overline{k}}\!e^{-\lambda \tau } &{} \ldots &{} \frac{(\beta _{1}S_{1}^0+\beta _{2}H_{1}^0)1\cdot n p(n)}{ a\overline{k}}\!e^{-\lambda \tau }\\ \frac{(\beta _{1}S_{2}^0+\beta _{2}H_{2}^0)2\cdot 1 p(1)}{ a\overline{k}}\!e^{-\lambda \tau } &{} \frac{(\beta _{1}S_{2}^0+\beta _{2}H_{2}^0)2\cdot 2 p(2)}{ a\overline{k}}\!e^{-\lambda \tau }\!-\!(\gamma \!+\!\mu )\! &{} \ldots &{} \frac{(\beta _{1}S_{2}^0+\beta _{2}H_{2}^0)2\cdot n p(n)}{ a\overline{k}}\!e^{-\lambda \tau }\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \frac{(\beta _{1}S_{n}^0+\beta _{2}H_{n}^0)n\cdot 1 p(1)}{ a\overline{k}}\!e^{-\lambda \tau } &{} \frac{(\beta _{1}S_{n}^0+\beta _{2}H_{n}^0)n\cdot 2 p(2)}{ a\overline{k}}\!e^{-\lambda \tau } &{} \ldots &{} \frac{(\beta _{1}S_{n}^0+\beta _{2}H_{n}^0)n\cdot n p(n)}{ a\overline{k}}\!e^{-\lambda \tau }\!-\!(\gamma \!+\!\mu )\! \end{array} \right] . \end{aligned}$$

Then, we can obtain the characteristic equation of the above Jacobian matrix $J(E^{0})$

$$\begin{aligned}&(\lambda +\mu )^{2n}(\lambda +\gamma +\mu )^{n-1}\nonumber \\&\quad \left( \!\!\lambda +\gamma +\mu -\sum \limits _{k=1}^n \dfrac{\Big (\beta _{1}S_{k}^{0}+\beta _{2}H_{k}^{0}\Big )k^2p(k)}{ a\overline{k}}e^{-\lambda \tau }\!\!\right) =0.\nonumber \\ \end{aligned}$$

(3.10)

As mentioned above, the characteristic equation (3.10) has 2n eigenvalues equal to $-\mu$. In addition, $n-1$ negative roots of the equation (3.10) are calculated as $-(\gamma +\mu )$. The remaining eigenvalue of matrix $J(E^{0})$ satisfies the following equation

$$\begin{aligned} G(\lambda )=&{} \lambda +\gamma +\mu \nonumber \\&-\sum \limits _{k=1}^n \dfrac{\Big (\beta _{1}S_{k}^{0}+\beta _{2}H_{k}^{0}\Big )k^2p(k)}{ a\overline{k}}e^{-\lambda \tau }\nonumber \\ =&{} \lambda -(\gamma +\mu )(R_{0}^{2}e^{-\lambda \tau }-1)=0. \end{aligned}$$

(3.11)

(I) In the case of $R_{0}^{2}<1$, we wonder whether the eigenvalue $\lambda$ can get to the imaginary axis in the plane or not. Suppose first that $Re\lambda \ge 0$. From the equation (3.11), we take advantage of Euler’s formula and derive the following result

$$\begin{aligned} Re\lambda= & {} (\gamma +\mu )\Big (R_{0}^{2}e^{-Re\lambda \tau }cos(Im\lambda \tau )-1\Big )\\< & {} (\gamma +\mu )(R_{0}^{2}-1)<0, \end{aligned}$$

which contradicts the assumption apparently. Now, it’s evidenced that all roots of the characteristic equation (3.10) have negative real part. For any $\tau \ge 0$, we demonstrate that the disease-free equilibrium point $E^{0}$ of system (3.4) is locally asymptotically stable if $R_{0}^{2}<1$.

(II) In the case of $R_{0}^{2}>1$, it’s easy to make a calculation

$$\begin{aligned} \dfrac{{\text {d}} G(\lambda )}{d \lambda }=1+(\gamma +\mu )R_{0}^{2}\tau e^{-\lambda \tau }>0. \end{aligned}$$

Taking notice of $G(0)=-(\gamma +\mu )(R_{0}^{2}-1)<0$ and $\lim \limits _{\lambda \rightarrow +\infty } G(\lambda )=+\infty$, we can infer that there is at least one positive real root of the equation $G(\lambda )=0$.

From the above discussion, it can be concluded that the disease-free equilibrium point $E^{0}$ is locally asymptotically stable for $\forall \tau \ge 0$ if $R_{0}^{2}<1$ and unstable if $R_{0}^{2}>1$. $\square$

Theorem 7

For any $\tau \ge 0$, the disease-free equilibrium point $E^{0}$ of system (3.1) is globally asymptotically stable when $R_{0}^{2}\le 1$.

Proof

In the invariant set $\varOmega _2$, the Lyapunov function $L_2(t)$ is constructed as

$$\begin{aligned} \begin{array}{lcr} L_2(t)=L_{21}(t)+L_{22}(t), \end{array} \end{aligned}$$

(3.12)

where

$$\begin{aligned} \begin{aligned} L_{21}(t)=&\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}}\Bigg [\Bigg (S_{k}(t)-S_{k}^0-S_{k}^0 \ln \dfrac{S_{k}(t)}{S_{k}^0}\Bigg )\\&+\Bigg (H_{k}(t)-H_{k}^0-H_{k}^0 \ln \dfrac{H_{k}(t)}{H_{k}^0}\Bigg )+I_{k}(t)\Bigg ],\\ L_{22}(t)=&\int \limits _{t-\tau }^{t}(\gamma +\mu )\dfrac{\varTheta (x)}{ a+\varTheta (x)}dx. \end{aligned}\nonumber \\ \end{aligned}$$

(3.13)

Figure out the derivative of $L_{21}(t)$ along the trajectories of system (3.1)

$$\begin{aligned}&\dfrac{{\text {d}} L_{21}(t)}{{\text {d}}t}\Bigg |_{(3.1)}\\&\quad =\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} \Bigg [\left( 1-\dfrac{S^0}{S_{k}(t)}\right) \dfrac{{\text {d}} S_{k}(t)}{{\text {d}}t}\\&\qquad +\left( 1-\dfrac{H^0}{H_{k}(t)}\right) \dfrac{{\text {d}} H_{k}(t)}{{\text {d}}t} +\frac{{\text {d}} I_{k}(t)}{{\text {d}}t}\Bigg ]\\&\quad =\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} \left( 1-\dfrac{S^0}{S_{k}(t)}\right) \left[ b_{1}\Big (1-T_{k}(t)\Big )\right. \\&\qquad \left. -\beta _{1} k S_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}-\mu S_{k}(t)\right] \\&\qquad +\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} \left( \!1-\dfrac{H^0}{H_{k}(t)}\!\right) \left[ \!b_{2}\Big (1-T_{k}(t)\Big )\right. \\&\qquad \left. -\beta _{2} k H_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\!-\!\mu H_{k}(t)\!\right] \\&\qquad +\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} \left[ \!\beta _{1} k S_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\right. \\&\qquad \left. +\beta _{2} k H_{k}(t)\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\!-\!(\gamma +\mu ) I_{k}(t)\!\right] \\&\quad =-\mu \sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}} \frac{\Big (S_{k}(t)-S_{k}^0\Big )^2}{S_{k}(t)}\\&\qquad +b_{1}\sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}}\left( 1-\dfrac{S_{k}^0}{S_{k}(t)}\right) \Big (S_{k}^0-T_{k}(t)\Big )\\&\qquad -\mu \sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}} \frac{\Big (H_{k}(t)-H_{k}^0\Big )^2}{H_{k}(t)}\\&\qquad +b_{2}\sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}}\left( 1-\dfrac{H_{k}^0}{H_{k}(t)}\right) \Big (H_{k}^0-T_{k}(t)\Big )\\&\qquad +b_{2}\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} S_{k}^0 \left( 1-\dfrac{S_{k}^0}{S_{k}(t)}\right) \\&\qquad +b_{1}\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} H_{k}^0\left( 1-\dfrac{H_{k}^0}{H_{k}(t)}\right) \\&\qquad +\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} \left[ -S_{k}(t)\left( 1-\dfrac{S_{k}^0}{S_{k}(t)}\right) +S_{k}(t)\right] \\&\qquad \beta _{1}k\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\\&\qquad +\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} \left[ -H_{k}(t)\left( 1-\dfrac{H_{k}^0}{H_{k}(t)}\right) +H_{k}(t)\right] \\&\qquad \beta _{2} k\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )} -\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}}(\gamma +\mu ) I_{k}(t)\\&\quad =-\mu \sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}} \frac{\Big (S_{k}(t)-S_{k}^0\Big )^2}{S_{k}(t)}\\&\qquad -\mu \sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}}\frac{\Big (H_{k}(t)-H_{k}^0\Big )^2}{H_{k}(t)}\\&\qquad +b_{1}\sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}}\left( 1-\dfrac{S_{k}^0}{S_{k}(t)}\right) \Big (S_{k}^0+H_{k}^0-T_{k}(t)\Big )\\ \end{aligned}$$

$$\begin{aligned} \begin{aligned}&\qquad +b_{2}\sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}}\left( 1-\dfrac{H_{k}^0}{H_{k}(t)}\right) \Big (H_{k}^0+S_{k}^0-T_{k}(t)\Big )\\&\qquad +\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}}\left( \beta _{1}S_{k}^0+\beta _{2}H_{k}^0\right) k\\&\qquad \dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}-(\gamma +\mu )\dfrac{\varTheta (t)}{ a}. \end{aligned} \end{aligned}$$

Similarly, we have

$$\begin{aligned}&\dfrac{d L_{22}(t)}{{\text {d}}t}\Bigg |_{(3.1)}\\&\quad =(\gamma +\mu )\dfrac{\varTheta (t)}{ a+\varTheta (t)}-(\gamma +\mu )\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}. \end{aligned}$$

Hence, the derivative of $L_2(t)$ along the trajectories of system (3.1) is as follows

$$\begin{aligned}&\dfrac{{\text {d}} L_2(t)}{{\text {d}}t}\Bigg |_{(3.1)}\\&\quad =\dfrac{{\text {d}} L_{21}(t)}{{\text {d}}t}\Bigg |_{(3.1)}+\dfrac{{\text {d}} L_{22}(t)}{{\text {d}}t}\Bigg |_{(3.1)}\\&\quad \le -\mu \sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}} \frac{\Big (S_{k}(t)-S_{k}^0\Big )^2}{S_{k}(t)}\\&\qquad -\mu \sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}}\frac{\Big (H_{k}(t)-H_{k}^0\Big )^2}{H_{k}(t)}\\&\qquad +b_{1}\sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}}\left( 1-\dfrac{S_{k}^0}{S_{k}(t)}\right) \Big (T_{k}^{*}-T_{k}(t)\Big )\\&\qquad +b_{2}\sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}}\left( 1-\dfrac{H_{k}^0}{H_{k}(t)}\right) \Big (T_{k}^{*}-T_{k}(t)\Big )\\&\qquad +\sum \limits _{k=1}^n \dfrac{kp(k)}{ a\overline{k}} \left( \beta _{1}S_{k}^0+\!\beta _{2}H_{k}^0\right) \\&\qquad \!k\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\!\!-\!\!(\!\gamma +\!\mu )\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}\\&\quad =-\mu \sum \limits _{k=1}^n\dfrac{kp(k)}{ a\overline{k}} \left[ \frac{\Big (S_{k}(t)-S_{k}^0\Big )^2}{S_{k}(t)}\right. \\&\qquad \left. +\frac{\Big (H_{k}(t)-H_{k}^0\Big )^2}{H_{k}(t)}\right] \\&\qquad +\sum \limits _{k=1}^n\dfrac{kp(k)}{a\overline{k}} \left[ b_{1}\left( 1-\dfrac{S_{k}^0}{S_{k}(t)}\right) \right. \\&\left. \qquad \!+\!b_{2}\left( 1-\dfrac{H_{k}^0}{H_{k}(t)}\right) \right] \!\!\Big (\!T_{k}^{*}-\!T_{k}(t)\!\Big )\\&\qquad +(\gamma +\mu ) \Big (R_{0}^{2}-1\Big )\dfrac{\varTheta (t-\tau )}{ a+\varTheta (t-\tau )}. \end{aligned}$$

Obviously, it’s available that $\frac{{\text {d}} L_2(t)}{{\text {d}}t}\le 0$ in $\varOmega _2$ in the condition of $R_{0}^{2}\le 1$ . And the equation $\frac{{\text {d}} L_2(t)}{{\text {d}}t}=0$ holds if and only if $S_{k}= S_{k}^0$, $H_{k}= H_{k}^0$ and $I_{k}= I_{k}^0$. In other words, the largest compact invariant set contained in the set $\Big \{\big \{\big (S_{k}(t),H_{k}(t),I_{k}(t)\big )\big \}\in R_{+}^{3n}\big |\frac{{\text {d}} L_2(t)}{{\text {d}} t}=0\Big \}$ is the singleton $\{E^{0}\}$. When $R_{0}^{2}\le 1$, the global asymptotic stability of disease-free equilibrium point $E^0$ of system (3.1) is proved according to the LaSalle Invariance Principle. That is to say, all solution trajectories initiating from different initial conditions arrive at the disease-free equilibrium point $E^0$ in the end, which implies that the infectious disease ultimately dies out regardless of the initial density of infected individuals in heterogeneous networks. $\square$

Remark 1

From (2.6) and (3.8), it’s observed that the basic reproduction numbers $R_0^1$ and $R_0^2$ depend on the birth (death) rates, transmission coefficients, recovery rate, psychological factor and network structure. Comparing the conditions for the global stability of disease-free equilibrium points $E_0$ and $E^0$, we find that $R_0^2\le 1$ is harder to be satisfied than $R_0^1\le 1$ under the same parameters.

4 Numerical simulations

In this section, numerical simulations are carried out to illustrate analytical results obtained above. Besides, we also attempt to complement dynamics of the SHIR epidemic model with time delay. More precisely, system (2.4) is used as the object for simulations in homogeneous networks. For system (3.4), the scale-free network with $p(k)\propto 2m^2k^{-3}$ is considered as the underlying network. Here, the minimum and maximum degrees of nodes are, respectively, assumed to be $m=1$ and $n=200$. Moreover, the average degree of all nodes is computed as $\overline{k}=1.9802$ in the network.

4.1 The effect of model parameters on the basic reproduction number

As a crucial threshold, the basic reproduction number can determine the existence and stability of equilibrium points of dynamical systems. Hence, we are to observe the influence of model parameters on the basic reproduction number. Firstly, we focus on presenting the influence of average degree $\overline{k}$ and psychological factor a on $R_{0}^{1}$ in homogeneous networks together. Model parameters are chosen as $b_1=0.06, b_2=0.09, \beta _1=0.35, \beta _2=0.28, \gamma =0.8, \mu =0.5, a\in [0.1,1]$ and $\overline{k}\in [0.1,60]$. As Fig. 1 displays, different color codings characterize different values of basic reproduction number $R_{0}^{1}$ vividly. It can be observed that $R_{0}^{1}$ increases as $\overline{k}$ increases or a decreases. This result suggests that the epidemic situation becomes more severe when an individual has the greater average number of neighbors in the social network. Nevertheless, good psychological quality of the public facing the epidemic can be beneficial to reduce the transmission of infectious disease. In addition, when the transmission rate $\beta _{1}$ or $\beta _{2}$ gets larger, the basic reproduction number $R_{0}^{2}$ becomes larger, which implies reducing the transmission rate from the subhealthy or healthy to infected individuals can weaken the spread of disease. With the increase of psychological factor, recovery or death rate, the basic reproduction number $R_{0}^{2}$ decreases gradually. Besides, the heterogeneity of underlying network expressed by $\overline{k^2}/\overline{k}$ contributes to $R_{0}^{2}$, which reveals the decline of heterogeneity is conductive to eradicating the disease propagation. The influence of network heterogeneity on $R_{0}^{2}$ can also be observed by replacing $\overline{k}$ with $\overline{k^2}/\overline{k}$ in the abscissa of Fig. 1. In Fig. 2a, set the following parameters $\beta _{1}=0.5, \beta _{2}=0.05, a=0.86,\gamma =0.77, \mu =0.55, b_{1}\in [0,1]$ and $b_{2}\in [0,1]$. Under the given parameters, the larger $b_{2}$ is, the smaller $R_{0}^{2}$ is. Similarly, the larger $\beta _{1}$ or $b_{1}$ can result in the growth of $R_{0}^{2}$, as shown in Fig. 2b, which implies a higher birth rate of subhealthy individuals makes the disease easier to spread.

Fig. 1

The value of $R_{0}^{1}$ as a function of $\overline{k}$ and a in homogeneous networks

Fig. 2

The relationship of $R_{0}^{2}$ among $b_{1}$, $b_{2}$ and $\beta _{1}$ in heterogeneous networks

4.2 Dynamical behavior of system (2.4) in homogeneous networks

Consider system (2.4) with parameters $b_{1}=0.5, b_{2}=0.53, \beta _{1}=0.6, \beta _{2}=0.3, a=0.9, \gamma =0.72, \mu =0.8, \tau =2$ and the initial conditions $S(0)=0.1, H(0)=0.22, I(0)=0.08$. By calculation, the basic reproduction number is $R_{0}^{1}=0.3631<1$. Figure 3 depicts the changing trend of mean densities of subhealthy and infected nodes with the elapse of time. Likewise, take parameters $b_{1}=0.5, b_{2}=0.53, \beta _{1}=0.6, \beta _{2}=0.3, a=0.9, \gamma =0.32, \mu =0.42, \tau =2$ and same initial conditions. The basic reproduction number is given by $R_{0}^{1}=0.9412<1$. Figure 3 shows that the mean density of subhealthy nodes stabilizes to a constant state and that of infected nodes reduces to zero gradually when $R_{0}^{1}<1$, which implies the disease wipes out at last. From Theorem 2, the disease-free equilibrium point $E_{0}$ is locally asymptotically stable, which is in line with the observed result in Fig. 3 to some extent.

Fig. 3

Densities of S(t) and I(t) over time with $R_{0}^{1}<1$ in homogeneous networks

To verify the global asymptotic stability of the disease-free equilibrium point $E_{0}$, we would like to observe the influence of initial conditions on the spread of disease by choosing 13 sets of different initial densities of subhealthy, healthy and infected individuals. Besides, model parameters are taken as $b_{1}=0.4, b_{2}=0.5, \beta _{1}=0.82, \beta _{2}=0.5, a=0.6, \gamma =0.92, \mu =0.55, \tau =3.5$. Under this condition, the basic reproduction number is $R_{0}^{1}=0.8950<1$ and the disease-free equilibrium point of system (2.4) is $E_{0}=(0.276, 0.345, 0)$. What’s more, it can be seen in Fig. 4 that all trajectories of system (2.4) in homogeneous networks ultimately converge toward $E_{0}$, which is consistent with Theorem 3.

Fig. 4

Trajectories of system (2.4) with $R_{0}^{1}=0.8950$ in homogeneous networks

For system (2.4), choose tested parameters $b_{1}=0.3, b_{2}=0.43, \beta _{1}=0.5, \beta _{2}=0.35, a=0.32, \gamma =0.8, \mu =0.2, \tau =3.3$ and the initial conditions $S(0)=0.12, H(0)=0.16, I(0)=0.08$, for which $R_{0}^{1}=1.9995>1$. Then, take the following parameters $b_{1}=0.13, b_{2}=0.22, \beta _{1}=0.45, \beta _{2}=0.38, a=0.28, \gamma =0.5, \mu =0.2, \tau =3.3$ and figure out $R_{0}^{1}=2.2332>1$. Furthermore, parameters $b_{1}=0.3, b_{2}=0.42, \beta _{1}=0.65, \beta _{2}=0.4, a=0.12, \gamma =0.8, \mu =0.2, \tau =3.3$ and the same initial conditions are again selected. Correspondingly, $R_{0}^{1}=6.5110>1$. According to Theorem 4, the endemic equilibrium point $E_{*}$ of system (2.4) is locally asymptotically stable. As Fig. 5 displays, mean densities of subhealthy and infected nodes are to keep on the respective positive levels when $R_{0}^{1}>1$, which illustrates the disease is persistent in homogeneous networks. In addition, we discover the mean density of S(t) becomes smaller while that of I(t) gets bigger with $R_{0}^{1}$ increasing. In other words, the larger $R_{0}^{1}$ gives rise to the higher level of disease propagation, which suggests we can control the spread of disease effectively by decreasing the basic reproduction number.

Fig. 5

Densities of S(t) and I(t) over time with $R_{0}^{1}>1$ in homogeneous networks

Next, numerical method is resorted to explore dynamical behavior at the endemic equilibrium point $E_{*}$. Set parameters as $b_{1}=0.32, b_{2}=0.36, \beta _{1}=0.48, \beta _{2}=0.36, a=0.2, \gamma =0.44, \mu =0.3, \tau =1.8$ in our delayed model (2.4). Accordingly, the basic reproduction number is calculated as $R_{0}^{1}=3.8665>1$. By choosing quantities of different initial conditions for system (2.4), we plot curves of solutions of system (2.4) which consist of the triplet (S(t), H(t), I(t)) over time in Fig. 6. Importantly, it can be observed that trajectories of system (2.4) converge at the endemic equilibrium point $E_{0}=(0.1379, 0.1814, 0.1519)$ in the end. Based on the simulation result shown in Fig. 6, we can make a conjecture with respect to the global asymptotic stability of the endemic equilibrium point $E_{*}$ in homogeneous networks.

Fig. 6

Trajectories of system (2.4) with $R_{0}^{1}=3.8665$ in homogeneous networks

Fig. 7

Densities of H(t) and I(t) over time with $R_{0}^{2}<1$ in heterogeneous networks

4.3 Dynamical behavior of system (3.4) in heterogeneous networks

Parameters $b_{1}=0.24, b_{2}=0.36, \beta _{1}=0.3, \beta _{2}=0.2, a=0.98, \gamma =0.6, \mu =0.72, \tau =3$ are chosen in system (3.4) to guarantee the basic reproduction number $R_{0}^{2}=0.6632<1$. Besides, consider system (3.4) with the following parameters $b_{1}=0.24, b_{2}=0.36, \beta _{1}=0.3, \beta _{2}=0.2, a=0.93, \gamma =0.6, \mu =0.52, \tau =3$, for which $R_{0}^{2}=0.9707<1$. Together with the initial conditions $S_{k}(0)=0.12, H_{k}(0)=0.25, I_{k}(0)=0.18$, Fig. 7 describes the time series of densities of healthy and infected nodes with degree $k=80$ as an example. It can be exemplified that densities of healthy and infected nodes get to the respective steady states, specifically $H_{80}=0.273, I_{80}=0$ and $H_{80}=0.321, I_{80}=0$. Namely, infected individuals are no longer in existence and the disease will fade out the social network in the end, which reflects the observed result from Fig. 7 and agrees with Theorem 6 to some extent.

With the aim of confirming the global asymptotic stability of $E^{0}$, take parameters $b_{1}=0.24, b_{2}=0.36, \beta _{1}=0.3, \beta _{2}=0.2, a=0.7, \gamma =0.8, \mu =0.6, \tau =1.5$ and 11 sets of different initial conditions in system (3.4). By calculation, the basic reproduction number is $R_{0}^{2}=0.9629<1$ and the disease-free equilibrium point is $E^{0}=(S_{k}^{0}, H_{k}^{0}, I_{k}^{0})=(0.2, 0.3, 0)$. From Fig. 8, regardless of various initial conditions, all solution curves composed of the triplet $(S_{80}(t), H_{80}(t), I_{80}(t))$ finally gather at $(S_{80}^{0}, H_{80}^{0}, I_{80}^{0})$ over time in heterogeneous networks. It’s worth noting that we only take nodes with degree $k=80$ as an example in the network. From Fig. 8, the disease will gradually disappear no matter how many initial infected individuals there are in the social network if $R_{0}^{2}<1$, which confirms the validity of Theorem 7.

Fig. 8

Trajectories of system (3.4) with $R_{0}^{2}=0.9629$ in heterogeneous networks

Fig. 9

Evolutions of $S_{80}(t), H_{80}(t)$ and $I_{80}(t)$ with $R_{0}^{2}>1$ in heterogeneous networks

For system (3.4), consider model parameters $b_{1}=0.24, b_{2}=0.36, \beta _{1}=0.3, \beta _{2}=0.1, a=0.43, \gamma =0.66, \mu =0.64, \tau =1.5$ and the initial conditions $S_{k}(0)=0.1, H_{k}(0)=0.25, I_{k}(0)=0.18$ in Fig. 9a. Correspondingly, we derive the basic reproduction number $R_{0}^{2}=1.2252>1$. Moreover, Fig. 9b displays how densities of subhealthy, healthy and infected nodes with $k=80$ vary over time in the case of $b_{1}=0.24, b_{2}=0.36, \beta _{1}=0.3, \beta _{2}=0.2, a=0.36, \gamma =0.65, \mu =0.5, \tau =1.3$, for which $R_{0}^{2}=2.4865>1$. And the initial conditions are given by $S_{k}(0)=0.2, H_{k}(0)=0.1, I_{k}(0)=0.12$. As shown in Fig. 9, the density of infected individuals originally increases at a rapid speed, then approaches the peak, ultimately descends to a positive constant and achieve stability. Meanwhile, densities of subhealthy and healthy individuals have the opposite variation trend roughly. Therefore, it’s evidential that densities of subhealthy, healthy and infected nodes of system (3.4) will not oscillate and keep stable when $R_{0}^{2}>1$ in heterogeneous networks.

To further replenish dynamicity of system (3.4) at the endemic equilibrium point $E^{*}$, choose the following set of parameters $b_{1}=0.2, b_{2}=0.3, \beta _{1}=0.42, \beta _{2}=0.33, a=0.26, \gamma =0.48, \mu =0.52, \tau =2.5$ and calculate the basic reproduction number $R_{0}^{2}=5.4263>1$. In addition, diverse initial conditions for system (3.4) are chosen at random. Through multiple simulation experiments, taking nodes with degree $k=80$ for example, we see that Fig. 10 presents all trajectories of solutions finally set down to $(S_{80}(t), H_{80}(t), I_{80}(t))$. This visual result inspires us to conjecture that the endemic equilibrium point $E^{*}$ of system (3.4) is of local or global asymptotic stability if $R_{0}^{2}>1$ in heterogeneous networks.

Fig. 10

Trajectories of system (3.4) with $R_{0}^{2}=5.4263$ in heterogeneous networks

Fig. 11

Evolutions of $H_{k}(t)$ and $I_{k}(t)$ with different k in heterogeneous networks

4.4 The effect of node degree k on disease propagation

By changing the value of k, we try to analyze the effect of degree k on disease propagation with fixed parameters $b_{1}=0.24, b_{2}=0.36, \beta _{1}=0.31, \beta _{2}=0.25, a=0.36, \gamma =0.43, \mu =0.5, \tau =3.8$ and the initial conditions $S_{k}(0)=0.2, H_{k}(0)=0.1, I_{k}(0)=0.2$ in system (3.4). The basic reproduction number is calculated as $R_{0}^{2}=3.5103>1$. Figure 11 portrays evolutions of healthy and infected nodes with different $k=20, 60, 100, 140$ and 180, respectively. With the rise of k, the density of healthy individuals decreases whereas the density of infected individuals increases. In reality, this phenomenon shown in Fig. 11 is actually understandable since nodes with more neighbors have easier accesses to be infected with the disease by contacting with the infected. In heterogeneous networks, regarded as hot spots, nodes connected with quantities of edges have major roles in propagating the disease. This result provides us with the idea to focus on this kind of nodes for the purpose of controlling the spread of disease quickly and effectively.

4.5 The effect of time delay $\tau$ on disease propagation

To study the impact of time delay $\tau$ on disease propagation, take the following parameters $b_{1}=0.13, b_{2}=0.2, \beta _{1}=0.8, \beta _{2}=0.5, a=0.15, \gamma =0.7, \mu =0.15$ and the initial conditions $S(0)=0.15, H(0)=0.2, I(0)=0.08$ in system (2.4). Then, the basic reproduction number is $R_{0}^{1}=6.6007>1$ correspondingly. By choosing $\tau =0$ and 10, Fig. 12 presents the difference between the evolutions of individuals without and with time delay. It can be observed that time delay $\tau$ has a remarkable influence on the convergence rates of S(t), H(t) and I(t). To be specific, once hysteresis exists in the infection process, more time is needed for system (2.4) to approach the endemic steady state. As also shown in Fig. 12, the peak of the density of infected individuals I(t) with delay is lower than that without delay, which implies that infection delay weakens the maximum prevalence of disease. Besides, set $b_{1}=0.24, b_{2}=0.36, \beta _{1}=0.31, \beta _{2}=0.25, a=0.9, \gamma =0.86, \mu =0.5$ and $S_{k}(0)=0.15, H_{k}(0)=0.1, I_{k}(0)=0.2$ in system (3.4). Under this condition, the basic reproduction number is $R_{0}^{2}=0.9602<1$. For different $\tau =0.5, 1.5, 2.5, 3.5$ and 4.5, densities of healthy and infected individuals, respectively, converge to the steady state $H_{k}^{0}=0.327$ and $I_{k}^{0}=0$ at last in Fig. 13. Nevertheless, system needs more time to gather to the disease-free equilibrium point $E^{0}$ with the increase of $\tau$. As a result, diminishing the time delay in the process of disease propagation can make the epidemic enter a stable situation at a faster speed. Through the simulation, it’s shown that systems (2.4) and (3.4) produce only stable steady-state dynamics, which implies that the time delay incorporated in nonlinear incidence rate is harmless in our model essentially.

Fig. 12

Trajectories of system (2.4) without and with time delay in homogeneous networks

Fig. 13

Evolutions of $H_{80}(t)$ and $I_{80}(t)$ with different $\tau$ in heterogeneous networks

4.6 The effect of psychological factor a on disease propagation

As one of features of our epidemic model, psychological factor a is introduced to constitute a nonlinear incidence rate. Consider system (2.4) with parameters $b_{1}=0.15, b_{2}=0.18, \beta _{1}=0.52, \beta _{2}=0.48, \gamma =0.2, \mu =0.1, \tau =1.3$. When the nonlinear incidence rate is considered, we take the psychological factor $a=1.3$. The initial conditions are given by $S(0)=0.15, H(0)=0.12, I(0)=0.1$. For system (2.4) with bilinear and nonlinear incidence rates, Fig. 14 shows the evolutions of subhealthy, healthy and infected individuals. From Fig. 14, the nonlinear incidence rate makes a difference to both convergence rates and steady-state values of S(t), H(t) and I(t). Moreover, the density of infected individuals in system (2.4) with bilinear incidence rate is always higher than that in system (2.4) with nonlinear incidence rate. In addition,parameters $b_{1}=0.24, b_{2}=0.36, \beta _{1}=0.31, \beta _{2}=0.25, \gamma =0.83, \mu =0.5, \tau =5$ and the initial conditions $S_{k}(0)=0.25, H_{k}(0)=0.2, I_{k}(0)=0.18$ are taken in system (3.4). Let a be 0.3, 0.5, 0.7, respectively, and compute $R_{0}^{2}=2.8805, 1.7283, 1.2345>1$. Note that the basic reproduction number $R_{0}^{2}$ decreases with the increase of psychological factor a. From Fig. 15, it takes longer for healthy and infected nodes with the larger a to converge toward the respective steady states. Furthermore, the positive steady level of infected individuals becomes lower when increasing a. This result indicates that strengthening the psychological quality of individuals in the face of serious epidemic can suppress the disease propagation.

Fig. 14

Trajectories of system (2.4) with bilinear and nonlinear incidence rates in homogeneous networks

Fig. 15

Evolutions of $H_{80}(t)$ and $I_{80}(t)$ with different a in heterogeneous networks

4.7 The effect of network structure on disease propagation

From the standpoint of modeling, the epidemic model in heterogeneous networks can be regarded as the more complex version of that in homogeneous networks. In other words, we are able to derive system (3.1) by applying system (2.1) to heterogeneous networks. To investigate the effect of network structure on disease propagation, we make a comparison between homogeneous and heterogeneous networks by selecting the same system parameters. Specifically, $b_{1}=0.13, b_{2}=0.11, \beta _{1}=0.45, \beta _{2}=0.36, a=3, \gamma =0.2, \mu =0.1, \tau =1.1$. Besides, the initial conditions are given, respectively, by $S(0)=0.15, H(0)=0.1, I(0)=0.2$ in homogeneous networks and $S_{k}(0)=0.15, H_{k}(0)=0.1, I_{k}(0)=0.2$ in heterogeneous networks. By calculation, obtain the basic reproduction numbers $R_{0}^{1}=0.6348<1$ and $R_{0}^{2}=2.5210>1$. With the same parameters, there exists an obvious difference in the value of basic reproduction number, which can be attributed to the complexity of network structure. In heterogeneous networks, the total density of subhealthy nodes at time t is defined as $S(t)=\sum _{k=1}^{n}p(k)S_{k}(t)$. Similarly, $H(t)=\sum _{k=1}^{n}p(k)H_{k}(t)$ and $I(t)=\sum _{k=1}^{n}p(k)I_{k}(t)$ denote the total densities of healthy and infected nodes at time t. As displayed in Fig. 16, S(t), H(t) and I(t) converge more slowly in homogeneous networks than that in heterogeneous networks due to $R_{0}^{1}<R_{0}^{2}$. Furthermore, the density of infected nodes tends to zero in homogeneous networks while that approaches the endemic steady state in heterogeneous networks. Namely, even if system parameters and initial conditions are same, the disease disappears eventually in homogeneous networks, whereas it still prevails in heterogeneous networks. This reveals that the heterogeneity of network is capable to exacerbate the propagation of disease. If the heterogeneous network is divided into several homogeneous networks, the prevalence of disease will be reduced to some extent.

Fig. 16

Evolutions of subhealthy, healthy and infected nodes in both homogeneous and heterogeneous networks

5 Conclusions and discussions

Based on an SIR model with two susceptible groups in Ref. [30], in this paper we come up with a modified SHIR epidemic model with time delay and nonlinear incidence rate in complex networks. In virtue of the compartment approach, two susceptible groups are interpreted as subhealthy and healthy individuals in view of the difference in fitness levels which indirectly affects the susceptibility of individuals to infectious disease. By introducing the psychological factor a, we adopt the nonlinear incidence rate to reflect the behavioral changes of susceptible individuals due to the psychological effect during the progression of disease diffusion. Besides, time delay $\tau$ is taken into account in the transformation process from the susceptible to the infected, which poses a challenge to the stability analysis of our network-based epidemic model. Specifically, it’s logical for us to think about two scenarios incorporating $\tau =0$ and $\tau >0$ in studying the local asymptotic stability of equilibrium points. Meanwhile, the construction of Lyapunov function is also closely related to the time delay when analyzing the global asymptotic stability of equilibrium points. In addition, the topological structure of network is considered in homogeneous and heterogeneous networks, respectively. Some main results of the delayed SHIR epidemic model in complex networks are presented as follows.

(1) In homogeneous networks, we obtain equilibrium points and a positive invariant set of system based on the mean field equations. The basic reproduction number $R_{0}^{1}$ of the infection is defined according to the method of next-generation matrix. In the condition of $R_{0}^{1}<1$, we prove that the disease-free equilibrium point $E_{0}$ is both locally and globally asymptotically stable. Furthermore, the proof of the local asymptotic stability of $E_{*}$ is given in detail when $R_{0}^{1}>1$.

(2) In heterogeneous networks, for the subsystem of the limit system, we investigate the disease-free equilibrium point $E^{0}=\Big \{\Big (\frac{b_{1}}{b_{1}+b_{2}+\mu }, \frac{b_{2}}{b_{1}+b_{2}+\mu },0\Big )\Big \}_{k}$ and the endemic equilibrium point $E^{*}=\Big \{\big (S_{k}^{*}, H_{k}^{*}, I_{k}^{*}\big )\Big \}_{k}$. The basic reproduction number $R_{0}^{2}$ is derived on the basis of the existence of a positive equilibrium point. By means of linearization, we demonstrate the local asymptotic stability of $E^{0}$ if $R_{0}^{2}<1$ and instability of $E^{0}$ if $R_{0}^{2}>1$. Additionally, by constructing suitable Lyapunov function, the global asymptotic stability of $E^{0}$ is also studied when $R_{0}^{2}\le 1$.

(3) To examine and complement analytical results, quantities of numerical simulations are executed orderly. We conduct the sensitivity analysis of model parameters on the basic reproduction number. In particular, the heterogeneity of network structure makes significant difference in disease propagation. Then, stability of equilibrium points in complex networks is verified intuitively. Further, we devise several numerical experiments to explore the potential dynamical behavior at the endemic equilibrium points in both homogeneous and heterogeneous networks. Moreover, the influence of key parameters on disease diffusion mainly reflects in the speed of propagation and steady-state densities of individuals.

In fact, the study of our two-susceptibility epidemic model with time delay and nonlinear incidence rate lays the foundation for studying the more complicated dynamical system with multiple groups later. Driven by the practical significance of epidemic models, we hope to access actual data to carry out statistical research in the future.