Numerical simulation and stability analysis of a novel reaction–diffusion COVID-19 model

Abstract

In this study, a novel reaction–diffusion model for the spread of the new coronavirus (COVID-19) is investigated. The model is a spatial extension of the recent COVID-19 SEIR model with nonlinear incidence rates by taking into account the effects of random movements of individuals from different compartments in their environments. The equilibrium points of the new system are found for both diffusive and non-diffusive models, where a detailed stability analysis is conducted for them. Moreover, the stability regions in the space of parameters are attained for each equilibrium point for both cases of the model and the effects of parameters are explored. A numerical verification for the proposed model using a finite difference-based method is illustrated along with their consistency, stability and proving the positivity of the acquired solutions. The obtained results reveal that the random motion of individuals has significant impact on the observed dynamics and steady-state stability of the spread of the virus which helps in presenting some strategies for the better control of it.

1 Introduction

In the late December 2019, the new coronavirus (COVID-19) spreads first from the Wuhan province in China to all parts of the world causing a devastating effect. This virus infects people through the tiny droplets emerging when infected person coughs or sneezes from a short distance to susceptible individual making him infected with the virus. This is considered as the primary source of infection according to WHO [1]. Infection can be also caused when an uninfected person touches an infected surface and then touches his nose, eye or mouth which may cause him to catch the virus. It is reported that almost every country in the world has been affected by this virus and the reported total cases until now is more than 155 million and more than three million deaths are recorded so far. Poor countries as well as developed countries are continuously reporting new cases every day, and all the countries in the world are facing increasing case of infection. China was the first country to act against the deadly virus by performing lock down and mandatory face masks in public areas and practicing social distancing to slow the spread of the virus to some extent until newly developed vaccines become available to everybody.

The major symptoms of COVID-19 are high fever over $38^{\circ }$, dry cough and tenderness. Some patients may have different symptoms such as aches, runny nose, nasal congestion, diarrhea and sore throat. These common symptoms occur almost to each infected person and are considered normally mild and gradually the symptoms become severe. More than 80 percent of infected people have mild symptoms, and they recover without receiving any special treatment for the virus. They need only some domestic or minor medication to reduce the symptoms. One patient out of six gets seriously ill and is required to be admitted in the hospital with shortness of breathing. The people most affected by the virus are old people with underlying health conditions such as diabetes, cardiovascular disease, cancer and chronic respiratory disease.

In general, the basic model of the COVID-19 pandemic can be simulated by an SIR model which divides the population into three categories, namely S(t) which represents the susceptible to infection individuals, I(t) which represents the infected individuals and R(t) which refers to the eliminated or recovered individuals [2]. The division of these categories was investigated through an integer-order model by several researchers for the better simulation of the virus dynamics. For example, a mathematical model for the spread of COVID-19 in India is presented in [3] by Biswas et al. Also, in [4], an SEIR model for the dynamics at Hubei province in China with some control strategies is studied. A mathematical model is studied in [5] to simulate the spread in Spain along with study of the effects of different parameters in the model. A generalized logistic function model has been studied by Xianbo et al. [6] to forecast the spreading of the infections of this disease. An estimation for the outbreak of the virus in Harbin, China, is investigated different categories and parameters in [7] . The effect of the awareness programs and different hospitalization schemes to study the transmission dynamics of the virus through an epidemic model is presented in [8]. A new proposed model is given in [9] to simulate the new cases and deaths of the virus outbreak in India. The study of the virus impact in Brazil through a multiple-delay mathematical model and the optimal control strategies is illustrated in [10]. Other relative studies of integer-order models can be found in [11, 12].

Moreover, iterative methods in the Gompertz model are employed to estimate the total number of infections and deaths caused by COVID-19 in Brazil and also in Rio de Janeiro and Sao Paulo Brazilian states [13]. Qualitative and quantitative study is presented to investigate the key factors affecting the development of COVID-19 epidemic in two different regions in China and determine the effects of varying strengths of intervention measures on secondary outbreaks of COVID-19 [14]. A deterministic compartmental SEAIQHR model to study the spreading of COVID-19 disease in India is introduced in [15] where the model parameters are found by fitting the model with reported data of the epidemic in India and also sensitivity analysis is carried out to identify the influential and critical parameters in the model. Prediction of bifurcations is conducted by varying critical parameters of SEIR COVID-19 model in [16]. The transcritical bifurcation in SEIR and SEQIR COVID-19 models, in [17] and [18], respectively, is explored by applying bifurcation theory and varying the basic reproduction number and the other critical parameters on which it depends on. The occurrence of backward bifurcation in COVID-19 model under the imperfect lockdown effect is examined in [19] where it is depicted that that stable disease-free equilibrium point can coexist with a stable endemic equilibrium point. This implicates that making basic reproduction number less than unity is a necessary but not a sufficient requirement for efficient and perfect controlling of the spread of COVID-19. While dealing with the simulations of such models, fractional calculus becomes an important tool which may help building more accurate and realistic models and better understanding of their spread. Fractional calculus has attracted a wide audience in the last few years due to its ability to provide realistic models for epidemic models. For example, a fractional-order model for simulating the HIV with the Caputo definition is introduced by Günerhan et al. [20] is helpful. Also, in [21] Nauman et al. proposed a fractional model for simulating the HIV–AIDS transmission with numerical verification by using a finite difference method. In other models, COVID-19 model [22], fractional-order Schnakenberg model [23], fractional-order model with time delay [24], model of childhood disease [25], model for granular SEIR epidemic with uncertainty [26], epidemic models of cholera [27], model of influenza dynamics [28], immune system simulation [29], fractional dengue model [30] Leslie–Gower predator–prey model [31] and many other related models may be studied in the existing literature.

The other approaches for improving COVID-19 model are to consider latency period of the infection and the more realistic nonlinear incidence rate which accurately determines the transmission mechanism of the infection. The latent period is the time duration in which the exposed person attains the infectious state where he can infect others. These approaches have been applied to understand deeply about the dynamics of the spread of the disease [32,33,34]. Further, development of the model is presented by proposing a new stage called quarantined and its effect on the transmission dynamics of the virus is studied [35, 36]. Also, in [37] a delayed version of the same model is proposed to incorporate the incubation period of the virus.

In spite of recent extensive interest of COVID-19 mathematical modeling, the influences of individuals’ daily movements and activities are ignored in most of the works, with a few exceptions such as the model in [38, 39] which consider diffusive COVID-19 model with conventional linear incident rate. This motivates the authors to extend the more realistic COVID-19 model having nonlinear incident rate to the spatiotemporal case.

Temporal-only model:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\frac{\mathrm{d}S}{\mathrm{d}t}= \mu - \frac{\beta SI}{1+\alpha I^{2}}- \mu S ,\\ &{}\frac{\mathrm{d}A}{\mathrm{d}t} = \frac{\beta SI}{1+\alpha I^{2}}-(\sigma +\delta +\epsilon +\mu )A,\\ &{}\frac{\mathrm{d}I}{\mathrm{d}t} =\sigma A -(\gamma +d+\mu ) I, \\ &{} \frac{\mathrm{d}R}{\mathrm{d}t} = \gamma I+\epsilon A -\mu R. \end{array}\right. } \end{aligned}$$

(1)

Spatiotemporal model:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\frac{\partial S}{\partial t}= d_1 \frac{\partial ^2 S}{\partial x^2} + \mu - \frac{\beta SI}{1+\alpha I^{2}}- \mu S ,\\ &{}\frac{\partial A}{\partial t}= d_2 \frac{\partial ^2 A}{\partial x^2} + \frac{\beta SI}{1+\alpha I^{2}}-(\sigma +\delta +\epsilon +\mu )A,\\ &{}\frac{\partial I}{\partial t}=d_3 \frac{\partial ^2 I}{\partial x^2} + \sigma A -(\gamma +d+\mu ) I , \\ &{}\frac{\partial R}{\partial t}=d_4 \frac{\partial ^2 R}{\partial x^2} + \gamma I+\epsilon A -\mu R. \end{array}\right. } \end{aligned}$$

(2)

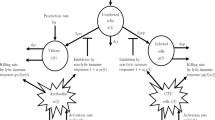
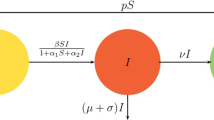
Here, for any time t, S(t) represents susceptible humans, A(t) represents the asymptomatic humans, I(t) represents the infected humans and R(t) represents the recovered or quarantine humans. The description of the parameters of the model is given as follows: $\mu$ denotes the natural birth or death rate, $\beta$ the rate by which susceptible humans move to asymptomatic humans, $\alpha$ the bilinear incidence rate, $\sigma$ the rate by which asymptomatic humans move to infected humans, $\delta$ the mortality rate of asymptomatic humans due to virus, $\epsilon$ the immunity rate of asymptomatic humans, $\gamma$ the rate of vaccination, quarantine or treatment and finally d the death rate of infected humans due to virus. The dynamics of the proposed model are presented in Fig. 1. It is worth mentioning that the model presented in this paper is a modification to the model presented in [11] by taking into account the effects of random movements of individuals from different compartments in their environments.

The current COVID-19 pandemic has become a symbol of horror for the mankind. Most existing models of this murderous virus do not take into account the diffusion process of the humans. However, this is an important factor that influences the disease dynamics and stability of equilibrium states. Therefore, the spatiotemporal version of COVID-19 model should be considered for accurate modeling for COVID-19 dynamics of spread. The present novel reaction–diffusion COVID-19 model is the first model which considers the random movements of individuals along with the more realistic nonlinear incidence rates. Moreover, the numerical technique adopted in this work provides the adequate structure preserving analysis like positive solution and stability of steady states for the proposed model.

Fig. 1

Flowchart of the proposed COVID-19 model

The organization of the paper is as follows. In Sect. 2, we study the equilibrium points and stability analysis of the two versions of the model, i.e., the diffusive and non-diffusive cases. In Sect. 2, we propose a numerical verification using a structure preserving finite difference method and illustrate the main steps of solution in Eq. (1). Section 4 is devoted for studying the consistency of this method and proving the order of accuracy of $(\tau +h^{2})$. The stability of the proposed technique is provided in Sect. 5 proving the method to be stable. The positivity of the acquired numerical solutions is proved in Sect. 6. Section 7 gives the numerical results for the finite difference method, while Sect. 8 concludes the study.

2 Equilibrium points and stability analysis

In this section, the key results associated with stability of equilibrium points for both non-diffusive model (1) and diffusive model (2) are presented.

The equilibrium points of model (1) are the disease-free equilibrium point $S_{f}=(1,0,0,0)$ and the endemic equilibrium point $S_{e}$ which is defined as follows:

$$\begin{aligned} S_{e}=(S^{*},A^{*},I^{*},R^{*}), \end{aligned}$$

where

$$\begin{aligned}&S^{*}=\frac{1+\alpha I^{*}}{R_{0}}, \ A^{*}=\frac{(\gamma +d+\mu )I^{*}}{\sigma },\\&I^{*}=\frac{-\beta +\sqrt{\beta ^{2}-4\alpha \mu ^{2}(1-R_{0})}}{2\alpha \mu },\\&R^{*}=\frac{\gamma I^{*}+\epsilon A^{*}}{\mu }, \end{aligned}$$

and $R_{0}$ is the reproduction number that is found to be

$$\begin{aligned} R_{0}=\frac{\beta \sigma }{(\sigma +\delta +\epsilon +\mu )(\gamma +d+\mu )}. \end{aligned}$$

Note that the equilibrium point $S_{e}$ can exist only if the following condition is achieved

$$\begin{aligned} -4\alpha \mu ^{2}(1-R_{0})>0, \end{aligned}$$

i.e.,

$$\begin{aligned} R_{0}>1, \ or \ \frac{\beta \sigma }{(\sigma +\delta +\epsilon +\mu )(\gamma +d+\mu )}>1. \end{aligned}$$

The uniform constant steady-state solutions of diffusive system (2) are the disease-free equilibrium point $S_{f}^{d}=S_{f}$ and endemic equilibrium point $S_{e}^{d}=S_{e}$ where $S_{f}$ and $S_{e}$ are given above.

2.1 Non-diffusive model

The diffusion coefficients vanish in this case, and the Jacobian matrix computed at $S_{f}$ steady state takes the following form

$$\begin{aligned} J_{f}=\left( \begin{array} [c]{cccc} -\mu &{} 0 &{} -\beta &{} 0\\ 0 &{} -\sigma -\delta -\epsilon -\mu &{} \beta &{} 0\\ 0 &{} \sigma &{} -\gamma -d-\mu &{} 0\\ 0 &{} \epsilon &{} \gamma &{} -\mu \end{array} \right) . \end{aligned}$$

The eigenvalues of matrix $J_{f}$ are computed from the associated characteristic equation, and they are given as

$$\begin{aligned} \lambda _{1,2}=-\mu ,\lambda _{3,4}=\frac{1}{2}(-C_{1}\pm \sqrt{C_{1} ^{2}-C_{2}}), \end{aligned}$$

where

$$\begin{aligned} C_{1}&=\sigma +\delta +\epsilon +2\mu +d+\gamma ,\\ C_{2}&=-\beta \sigma +\gamma \delta +\gamma \mu +\gamma \sigma +\gamma \epsilon +d\delta +d\mu +\delta \mu \\&\quad +d\sigma +d\epsilon +\mu ^{2}+\mu \sigma +\mu \epsilon . \end{aligned}$$

Hence, the equilibrium point $S_{f}$ is locally asymptotically stable if the following conditions are satisfied

$$\begin{aligned} \mu&>0, \sigma +\delta +\epsilon +2\mu +d+\gamma>0,\\ C_{2}&>0. \end{aligned}$$

Notice that the last conditions for asymptotic stability of $S_{f}$ are equivalent to saying that $R_{0}<1.$

Theorem 1

The equilibrium point $S_{f}$ of model (1) is locally asymptotically stable if

$$\begin{aligned} \mu>0,\sigma +\delta +\epsilon +2\mu +d+\gamma >0,R_{0}<1, \end{aligned}$$

where

$$\begin{aligned} R_{0}=\frac{\beta \sigma }{(\sigma +\delta +\epsilon +\mu )(\gamma +d+\mu )}. \end{aligned}$$

Similarly, the Jacobian matrix at endemic equilibrium point $S_{e}$ is found as

$$\begin{aligned} J_{e}=\left( \begin{array} [c]{cccc} -\mu -\frac{I^{*}\beta }{1+\alpha I^{*2}} &{} 0 &{} \frac{2S^{*}I^{*^{2}}\alpha \beta }{(1+\alpha I^{*2})^{2}}-\frac{S^{*}\beta }{1+\alpha I^{*2}} &{} 0\\ \frac{I^{*}\beta }{1+\alpha I^{*2}} &{} -\sigma -\delta -\epsilon -\mu &{} -\frac{2S^{*}I^{*^{2}}\alpha \beta }{(1+\alpha I^{*2})^{2}} +\frac{S^{*}\beta }{1+\alpha I^{*2}} &{} 0\\ 0 &{} \sigma &{} -\gamma -d-\mu &{} 0\\ 0 &{} \epsilon &{} \gamma &{} -\mu \end{array} \right) . \end{aligned}$$

The characteristic equation of matrix $J_{e}$ can be expressed in the following form

$$\begin{aligned} \lambda ^{4}+b_{3}\lambda ^{3}+b_{2}\lambda ^{2}+b_{1}\lambda +b_{0}=0, \end{aligned}$$

where the coefficients of the equation are obtained by

$$\begin{aligned} b_{0}= & {} \mu \left( \frac{\beta \left( \text {I}^* \left( \alpha \left( \text {I}^*\right) ^2+1\right) (\gamma +d+\mu ) (\delta +\mu +\epsilon )+\text {I}^* \sigma (\gamma +d) \left( \alpha \left( \text {I}^*\right) ^2+1\right) +\mu \sigma \left( \alpha \left( \text {I}^*\right) ^2 \left( \text {I}^*+S^*\right) +\text {I}^*-S^*\right) \right) }{\left( \alpha \left( \text {I}^*\right) ^2+1\right) ^2}\right) \\&+\,\mu ^{2} (\gamma +d+\mu ) (\delta +\mu +\sigma +\epsilon ),\\ b_{1}= & {} \mu (\gamma (2 \delta +3 \mu +2 \sigma +2 \epsilon )+d (2 \delta +3 \mu +2 \sigma +2 \epsilon )+\mu (3 \delta +4 \mu +3 \sigma +3 \epsilon ))\\&+\,\frac{\beta \left( \text {I}^* \left( \alpha \left( \text {I}^*\right) ^2+1\right) \left( 2 \mu (\gamma +d+\delta +\epsilon )+(\gamma +d) (\delta +\epsilon )+3 \mu ^2\right) +\sigma \left( \text {I}^* (\gamma +d) \left( \alpha \left( \text{ I}^*\right) ^2+1\right) +2 \mu \left( \alpha \left( \text {I}^*\right) ^2 \left( \text {I}^*+S^*\right) +\text {I}^*-S^*\right) \right) \right) }{\left( \alpha \left( \text {I}^*\right) ^2+1\right) ^2} ,\\ b_{2}= & {} \,\gamma (\delta +3 \mu +\sigma +\epsilon )+d (\delta +3 \mu +\sigma +\epsilon )\\&+\,\frac{\beta \left( \text {I}^* \left( \alpha \left( \text {I}^*\right) ^2+1\right) (\gamma +d+\delta +3 \mu +\epsilon )+\sigma \left( \alpha \left( \text{ I}^*\right) ^2 \left( \text {I}^*+S^*\right) +\text {I}^*-S^*\right) \right) }{\left( \alpha \left( \text {I}^*\right) ^2+1\right) ^2} +3 \mu (\delta +2 \mu +\sigma +\epsilon ) , \end{aligned}$$

and finally,

$$\begin{aligned} b_{3}= \gamma +d+\delta +\frac{\beta \text {I}^*}{\alpha \left( \text {I}^*\right) ^2+1}+4 \mu +\sigma +\epsilon . \end{aligned}$$

The equilibrium point $S_{e}$ is locally asymptotically stable if the following Routh–Hurwitz conditions are satisfied

$$\begin{aligned} b_{i}>0, i=0,1,2,3,\quad b_{2}b_{3}-b_{1}>0,\\ b_{1}b_{2}b_{3}-b_{1}^{2}-b_{3}^{2}b_{0}>0. \end{aligned}$$

However, simple analytical expressions for stability conditions of Routh−Hurwitz criterion cannot be attained due to the very complicated forms of these coefficients and conditions. Therefore, it is essential to employ numerical investigation of $S_{e}$ regions of stability in parameters’ space of model (1).

2.2 Diffusive model

The spatiotemporal model (2) has nonzero diffusion coefficients $d_{i},$ $i=1,2,3,4$. Assuming that the uniform equilibrium point of the model takes the form $({\bar{S}},{\bar{A}},{\bar{I}},{\bar{R}})$ and hence by applying small perturbations ${\hat{S}}=S-{\bar{S}},$ ${\hat{A}}=A-{\bar{A}},$ ${\hat{I}}=I-{\bar{I}},{\hat{R}}=R-{\bar{R}}$ around it to linearize the system, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\frac{\partial {\hat{S}}}{\partial t} =d_{1}\frac{\partial ^{2}{\hat{S}} }{\partial x^{2}}+c_{11}{\hat{S}}+c_{12}{\hat{A}}+c_{13}{\hat{I}}+c_{14}\hat{R},\\ &{}\frac{\partial {\hat{A}}}{\partial t} =d_{1}\frac{\partial ^{2}{\hat{A}} }{\partial x^{2}}+c_{21}{\hat{S}}+c_{22}{\hat{A}}+c_{23}{\hat{I}}+c_{24}{\hat{R}},\\ &{}\frac{\partial {\hat{I}}}{\partial t} =d_{1}\frac{\partial ^{2}{\hat{I}} }{\partial x^{2}}+c_{31}{\hat{S}}+c_{32}{\hat{A}}+c_{33}{\hat{I}}+c_{34}{\hat{R}},\\ &{}\frac{\partial {\hat{R}}}{\partial t} =d_{1}\frac{\partial ^{2}{\hat{R}} }{\partial x^{2}}+c_{41}{\hat{S}}+c_{42}{\hat{A}}+c_{43}{\hat{I}}+c_{44}{\hat{R}}. \end{array}\right. } \end{aligned}$$

(3)

The coefficients $c_{ij}$ are determined according to whether equilibrium point $S_{f}^{d}$ or $S_{e}^{d}$ is considered. Now, suppose that the solution of linearized system (3) is given as

$$\begin{aligned} \left( \begin{array} [c]{c} {\hat{S}}\\ {\hat{A}}\\ {\hat{I}}\\ {\hat{R}} \end{array} \right) =\left( \begin{array} [c]{c} S_{0}\\ A_{0}\\ I_{0}\\ R_{0} \end{array} \right) e^{-i\kappa x+\omega t}, \end{aligned}$$

(4)

where $S_{0},A_{0},I_{0}$ and $R_{0}$ have sufficiently small values. Substituting (4) into system (3), we get

$$\begin{aligned}&\omega \left( \begin{array} [c]{c} {\hat{S}}\\ {\hat{A}}\\ {\hat{I}}\\ {\hat{R}} \end{array} \right) \nonumber \\&\quad =\left( \begin{array} [c]{cccc} c_{11}-\kappa ^{2}d_{1} &{} c_{12} &{} c_{13} &{} c_{14}\\ c_{21} &{} c_{22}-\kappa ^{2}d_{2} &{} c_{23} &{} c_{24}\\ c_{31} &{} c_{32} &{} c_{33}-\kappa ^{2}d_{3} &{} c_{34}\\ c_{41} &{} c_{42} &{} c_{43} &{} c_{44}-\kappa ^{2}d_{4} \end{array} \right) \nonumber \\&\qquad \quad \times \left( \begin{array} [c]{c} {\hat{S}}\\ {\hat{A}}\\ {\hat{I}}\\ {\hat{R}} \end{array} \right) , \end{aligned}$$

(5)

where the specific forms of elements $c_{ij}$ are identical to the elements in matrices $J_{f}$ and $J_{e}\$of steady states $S_{f}$ and $S_{e},$ respectively.

Parameters $\kappa$ and $\omega$ represent the wave number and growth rate of the perturbations around the selected equilibrium point, respectively. Indeed, the linear stability of the equilibrium point is determined according to the sign of real part of $\omega$. In particular, the local asymptotic stability of certain uniform equilibrium point in spatiotemporal model requires that all real parts of $\omega$ have negative signs. Stability of equilibrium point is lost if at least one of real parts of $\omega$ crosses the imaginary axis and changes its sign from negative to positive. In this case, one of the next two bifurcation scenarios may be observed according to the critical value of $\omega$. In first scenario, the value of critical $\omega$ is zero (pure real), while the associated equilibrium point in model (1) is still stable and therefore model (2) exhibits Turing instability bifurcation. In the second scenario, the critical $\omega$ is pure imaginary and hence model (2) undergoes wave instability bifurcation, provided that the corresponding equilibrium point in model (1) remains stable.

Fig. 2

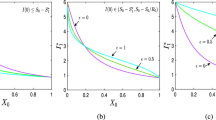
The region of stability of $S_{f}$ is shown in (a, c) for $\alpha -\beta -\gamma$ space and $\beta -\gamma$ plane ($\alpha =0.05)$, respectively. The region of stability of $S_{f}^{d}$ is shown in (b, d) for $\alpha -\beta -\gamma$ space and $\beta -\gamma$ plane ($\alpha =0.05)$, respectively. The values of other parameters are $\mu =0.1$; $\delta =0.001$; $\epsilon =0.03$; $\sigma =0.05$; $d= 0.02$; $\kappa =1$; $d_{i}=0.05$, $i=1,2,3,4$

Fig. 3

Similar to Fig. 2 yet the value of $\sigma$ is increased to $\sigma =0.1$

Fig. 4

Similar to Fig. 2 but the value of $\epsilon$ is increased to $\epsilon =0.07$

Fig. 5

Similar to Fig. 2 but the colored stability regions are associated with $S_{e}$ in (a, c) and with $S_{e}^{d}$ in (b, d)

Fig. 6

Similar to Fig. 3 but the colored stability regions are associated with $S_{e}$ in (a, c) and with $S_{e}^{d}$ in (b, d)

Fig. 7

Similar to Fig. 4 but the colored stability regions are associated with $S_{e}$ in (a, c) and with $S_{e}^{d}$ in (b, d)

Fig. 8

Stability regions for disease-free equilibrium point in parameters’ space for a $d_1=0$, b $d_1=0.07$, c $d_2=0$ and d $d_2=0.07$. The values of other $d_i$s equal zero and the values of other parameters are the same as those in Fig. 2

Fig. 9

Similar to Fig. 8 but for diffusion coefficients $d_3$ in (a, b) and $d_4$ in (c, d)

2.3 Numerical investigation

Now, we proceed to explore stability regions of equilibrium points in the space of parameters of models (1) and (2) and examine the influences of different parameters. First, the effects of $\alpha ,$ $\beta$ and $\gamma$ are considered, whereas the values of other parameters are fixed as $\mu =0.1$; $\delta =0.001$; $\epsilon =0.03$; $\sigma =0.05$; $d=0.02$. Figure 2a, b illustrates the red-colored region of stability for $S_{f}$ and green-colored region of stability of $S_{f}^{d}$ in $\alpha -\beta -\gamma$ space. Figure 2c, d shows projections of stability regions $S_{f}$ and $S_{f}^{d},$ respectively, in $\beta -\gamma$ plane when $\alpha$ is fixed at $\alpha =0.05$. The values of diffusion coefficients are taken as $d_{i}=0.05,$ $i=1,2,3,4$, in simulations. Two interesting points can be observed as follows: The first point is that equilibrium points $S_{f}$ and $S_{f}^{d}$ maintain their stabilities at small values of infection rate $\beta .$ When the value of $\beta$ increases, the treatment rate $\gamma$ should be increased to still keep the stability of equilibria. The second point of interest is that the regions of stability for steady state $S_{f}^{d}$ of spatiotemporal model (2) are larger than the corresponding $S_{f}$ point of temporal model (1). Second, we increase the value of $\sigma$ to $\sigma =0.1$ which corresponds to the assumption that the rate in which asymptomatic individuals move to infected ones is high. From Fig. 3, it is obvious that the regions of stability for $S_{f}$ and $S_{f}^{d}$ considerably shrink in this case. Third, the value of $\epsilon$ is increased to $\epsilon =0.07$   which results in boosting the immunity level of asymptomatic individuals. Figure 4 demonstrates that the regions of stability for both the equilibrium points are enlarged, which indicates that local stability is preserved for greater values of $\beta$ and lower values of $\gamma .$

Now, we turn into investigate the stabilities of $S_{e}$ and $S_{e}^{d}$ in the same way as carried out above. Figures 5, 6 and 7 are similar to Figs. 1, 2 and 3 but depict the stability regions of steady states $S_{e}$ and $S_{e}^{d}$ instead of $S_{f}$ and $S_{f}^{d}.$ A crucial observation is found when spatiotemporal dynamics are considered. More specifically, the two uniform equilibrium points of spatiotemporal model (2) can be simultaneously stable at certain values of parameters. As an example, from Figs. 2d and 5d it is clear that at $\beta =0.7$ and $\gamma =0.02$ both $S_{f}^{d}$ and $S_{e}^{d}$ are stable in the way that the simultaneous occurrence of two stable uniform equilibrium points is permitted in state space. When diffusion influences are neglected, which is the case in model (1), only one stable equilibrium point can exist in state space. The values of initial sizes of different compartments in model (2) determine the equilibrium point to which the solution trajectory will attract. Therefore, the diffusion process can result in significant dynamic qualitative change on temporal models when it is taken into account. The effects of each diffusion coefficient $d_i$, i=1,2,3,4, are investigated separately. Starting with the diffusive term of susceptible individuals, i.e., the term involves $d_1$. It is observed that when other coefficients are fixed at zero and $d_1$ is increased above zero, $d_1$ has negligible influence on the dynamics and stability of spatially homogeneous equilibrium states of the model. On the other side, the diffusion term of asymptomatic individuals has significant effect on the stability of spatially homogeneous equilibrium points of the model when $d_2$ is increased above zero and the other coefficients are kept at zero. Similarly, the diffusion term of infected people has also significant effect on stability of spatially homogeneous equilibrium points of the model when $d_3$ is increased above zero and the other coefficients are kept at zero. More specifically, the two diffusion coefficients $d_2$ and $d_3$ enlarge the regions of stability of disease-free equilibrium point and induce the interesting case of coexistence stable equilibrium points (disease-free and endemic). Finally, the diffusion coefficient $d_4$ of recovered individuals has negligible influence on the dynamics of the model as like as $d_1$ does. For example, Figs. 8 and 9 show the effects of each diffusion coefficient when it is assigned a chosen positive value while the remaining coefficients have zero values. In particular, the left columns illustrate stability regions for disease-free equilibrium point in parameters’ space for temporal-only model and the right columns show stability regions for the case of a nonzero diffusion coefficient. These figures demonstrate that the most influential diffusion coefficients are $d_2$ and $d_3$. For different values of spatial mobility of the population $d_i$s in their environments, i.e., for other values of each diffusion coefficient in numerical simulations, the obtained results confirm the aforementioned conclusions regarding the changes in qualitative dynamics of the model. It is worth mentioning that many values of $d_i\in (0,1)$ are employed in numerical simulations to determine the most important diffusive terms and the figures presented here are selected sample for brevity.

3 Numerical modeling

In this section, we will verify the numerical simulation of model (2) . We begin with dividing the domain of $x\in [0,L]$ and $t\in [0,T]$ into $M^2\times N$ cubes with step size $h=\frac{L}{M}$ and $\tau = \frac{T}{N}$ where

$$\begin{aligned}&x_i=\frac{i}{h},\, i=0,1,\ldots ,M, \\&t_n=\tau n,\, n=0,1,2,\ldots ,N. \end{aligned}$$

For this use

$$\begin{aligned}&\frac{\partial u}{\partial t}=\frac{u^{n+1}_{i} -u^{n}_{i}}{\tau } \nonumber \\&\frac{\partial ^2 u}{\partial x^2}=\frac{u^{n+1}_{i-1} -2u^{n+1}_{i}+{u^{n+1}_{i+1}}}{h^{2}} \end{aligned}$$

(6)

and then discretizing Eq. (2) will result in

$$\begin{aligned}&\frac{S^{n+1}_{i} -S^{n}_{i}}{\tau }=d_1 \frac{S^{n+1}_{i-1} -2S^{n+1}_{i}+{S^{n+1}_{i+1}}}{h^{2}}\nonumber \\&\quad + \mu - \frac{\beta S^{n+1}_{i}I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}- \mu S^{n+1}_{i}\nonumber \\&S^{n+1}_{i}=S^{n}_{i}+\frac{\tau d_1}{h^{2}}\left( S^{n+1}_{i-1} -2S^{n+1}_{i}+{S^{n+1}_{i+1}}\right) \nonumber \\&\quad + \mu \tau - \tau \frac{\beta S^{n+1}_{i}I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}- \tau \mu S^{n+1}_{i}\nonumber \\&S^{n+1}_{i}(1+2\lambda _1+\tau \frac{\beta I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}\nonumber \\&\quad +\tau \mu )-\lambda _1\left( S^{n+1}_{i-1}+{S^{n+1}_{i+1}}\right) =S^{n}_{i}+\mu \tau . \end{aligned}$$

(7)

$$\begin{aligned}&\frac{A^{n+1}_{i}-A^{n}_{i}}{\tau }=d_2 \frac{A^{n+1}_{i-1} -2A^{n+1}_{i}+{A^{n+1}_{i+1}}}{h^{2}}\nonumber \\&\quad + \frac{\beta S^{n}_{i}I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}- (\sigma +\delta +\epsilon +\mu )A^{n+1}_{i}\nonumber \\&A^{n+1}_{i}=A^{n}_{i}+\frac{\tau d_2}{h^{2}}\left( A^{n+1}_{i-1}-2A^{n+1}_{i}+{A^{n+1}_{i+1}}\right) \nonumber \\&\quad + \tau \frac{\beta S^{n+1}_{i}I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}- \tau (\sigma +\delta +\epsilon +\mu )A^{n+1}_{i}\nonumber \\&A^{n+1}_{i}(1+2\lambda _2 +\tau (\sigma +\delta +\epsilon +\mu ))-\lambda _2\left( A^{n+1}_{i-1}\right. \nonumber \\&\quad \left. + A^{n+1}_{i+1}\right) =A^{n}_{i}+\tau \frac{\beta S^{n}_{i}I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}} . \end{aligned}$$

(8)

$$\begin{aligned}&\frac{I^{n+1}_{i}-I^{n}_{i}}{\tau }=d_3 \frac{I^{n+1}_{i-1} -2I^{n+1}_{i}+I^{n+1}_{i+1}}{h^{2}}\nonumber \\&\quad +\sigma A^{n}_{i}-(\gamma +d+\mu ) I^{n+1}_{i}\nonumber \\&I^{n+1}_{i}=I^{n}_{i}+d_3 \tau \frac{I^{n+1}_{i-1} -2I^{n+1}_{i}+I^{n+1}_{i+1}}{h^{2}}\nonumber \\&\quad +\tau \sigma A^{n}_{i}-(\gamma +d+\mu )\tau I^{n+1}_{i}\nonumber \\&I^{n+1}_{i}(1+2\lambda _3+(\gamma +d+\mu )\tau )-\lambda _3(I^{n+1}_{i-1}+I^{n+1}_{i+1})\nonumber \\&\quad =I^{n}_{i}+\tau \sigma A^{n}_{i}. \end{aligned}$$

(9)

$$\begin{aligned}&\frac{R^{n+1}_{i}-R^{n}_{i}}{\tau }=d_4 \frac{R^{n+1}_{i-1} -2R^{n+1}_{i}+R^{n+1}_{i+1}}{h^{2}}\nonumber \\&\quad +\gamma I^{n+1}_{i}+\epsilon A^{n}_{i} -\mu R^{n+1}_{i}\nonumber \\&R^{n+1}_{i}=R^{n}_{i}+d_4 \tau \frac{R^{n+1}_{i-1} -2R^{n+1}_{i}+R^{n+1}_{i+1}}{h^{2}}\nonumber \\&\quad +\tau \gamma I^{n+1}_{i}+\tau \epsilon A^{n}_{i} -\mu \tau R^{n+1}_{i}\nonumber \\&R^{n+1}_{i}(1+2\lambda _4+\mu \tau )-\lambda _4(I^{n+1}_{i-1}+I^{n+1}_{i+1})=R^{n}_{i}+\tau \epsilon A^{n}_{i}. \end{aligned}$$

(10)

Then, by solving the above-mentioned system, the values of the parameters will be found and the solution is acquired. Next, we shall provide the consistency of this method.

4 Consistency of the proposed method

Here, we examine the consistency of the proposed scheme. Consistency is one of the major properties of the numerical scheme. We prove that our proposed implicit scheme is second order consistent in space and first order consistent in time . By using Taylor-series expansion, it follows that

$$\begin{aligned} {\pounds _{S}}= & {} \frac{S^{n+1}_{i} -S^{n}_{i}}{\tau }-d_1 \frac{S^{n+1}_{i-1} -2S^{n+1}_{i}+{S^{n+1}_{i+1}}}{h^{2}}\\&-\mu + \frac{\beta S^{n+1}_{i}I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}+ \mu S^{n+1}_{i}\\= & {} \left( {\frac{\partial S}{\partial t}+\frac{\tau }{2!}\frac{\partial ^2 S}{\partial t^2}+\frac{\tau ^2}{3!}\frac{\partial ^3 S}{\partial t^3}}+\ldots \right) \\&-\frac{d_1}{h^2} \left( h^2\left( \frac{\partial ^2 S}{\partial x^2}+2\frac{h^2}{4!} \frac{\partial ^4 S}{\partial x^4}+\cdots \right) \right) \\&+ \left( \frac{\beta I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}+\mu \right) \\&\times \left( S^{n}_{i}+\tau \frac{\partial S}{\partial t}+\frac{\tau ^2}{2!}\frac{\partial ^2 S}{\partial t^2}+\frac{\tau ^3}{3!}\frac{\partial ^3 S}{\partial t^3}+\cdots \right) -\mu \\= & {} \frac{\partial S}{\partial t}-\frac{d_1}{h^2}\left( h^2\frac{\partial ^2 S}{\partial x^2}\right) + \left( \frac{\beta I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}+\mu \right) S^{n}_{i}-\mu \\&-\frac{d_1 h^2}{12}\left( \frac{\partial ^4S}{\partial x^4}\right) +\tau \left( \left( \frac{\beta I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}+\mu \right) \frac{\partial S}{\partial t}+\cdots \right) \\= & {} -\frac{d_1 h^2}{12}\left( \frac{\partial ^4S}{\partial x^4}\right) +\tau \left( \left( \frac{\beta I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}+\mu \right) \frac{\partial S}{\partial t}+\cdots \right) \end{aligned}$$

$\rightarrow 0$ as $h^2,\tau \rightarrow 0$.

Similarly, the relations for A, I and R are obtained, i.e.,

$$\begin{aligned}&{\pounds _{A}}=-\frac{d_1 h^2}{12}\left( \frac{\partial ^4A}{\partial x^4}\right) +\tau \left( (\sigma +\delta +\epsilon +\mu )\frac{\partial A}{\partial t}+\cdots \right) \\&{\pounds _{I}}=-\frac{d_1 h^2}{12}\left( \frac{\partial ^4I}{\partial x^4}\right) +\tau \left( (\gamma +d+\mu )\frac{\partial I}{\partial t}+\cdots \right) \\&{\pounds _{R}}=-\frac{d_1 h^2}{12}\left( \frac{\partial ^4R}{\partial x^4}\right) +\tau \left( (\mu )\frac{\partial R}{\partial t}+\cdots \right) . \end{aligned}$$

The last three equations $\rightarrow 0$ as $h^2,\tau \rightarrow 0$. Hence, the proposed implicit scheme is first order accurate in time and second order in space. Its order of accuracy is $(\tau + h^2)$. The stability of the method is tested in the next section.

5 Stability of the proposed method

In this segment, stability, which is another important property of any numerical scheme, is tested. First, let $S^{n}_{i}=\eta _{S}^{n} e^{j\theta _S (ih)}$ , $S^{n+1}_{i}=\eta _{S}^{n+1} e^{j\theta _S (ih)}$ , $S^{n+1}_{i-1}=\eta _{S}^{n+1} e^{j\theta _S (i-1)h}$, $S^{n+1}_{i+1}=\eta _{S}^{n+1} e^{j\theta _S (i+1)h}$ in Eq. (7) and nonlinear terms as,

$$\begin{aligned}&\eta _{S}^{n+1} e^{j\theta _S (ih)}(1+2\lambda _1+\tau (\upsilon ^I+ \mu ))\nonumber \\&\quad -\lambda _1\left( \eta _{S}^{n+1} e^{j\theta _S (i+1)h}+\eta _{S}^{n+1} e^{j\theta _S (i-1)h}\right) =\eta _{S}^{n} e^{j\theta _S (ih)} \nonumber \\&\eta _{S}\left( (1+2\lambda _1+\tau (\upsilon ^I+ \mu ))-\lambda _1(e^{j\theta _S h}+ e^{-j\theta _S h})\right) =1\nonumber \\&\eta _{S}=\frac{1}{\left( 1+4\lambda _1\sin ^{2}\frac{\theta h}{2}+\tau (\upsilon ^I+\mu )\right) }\nonumber \\&|\eta _{S}|=\left| \frac{1}{\left( 1+4\lambda _1\sin ^{2}\frac{\theta _S h}{2}+\tau (\upsilon ^I+\mu )\right) }\right| \le 1 \end{aligned}$$

(11)

Similarly, by following the same process we can obtain for Eqs. (8–10)

$$\begin{aligned}&|\eta _{A}|=\left| \frac{1}{\left( 1+4\lambda _2\sin ^{2}\frac{\theta _A h}{2}+\tau (\sigma +\delta +\epsilon +\mu )\right) }\right| \le 1\nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned}&|\eta _{I}|=\left| \frac{1}{\left( 1+4\lambda _3\sin ^{2}\frac{\theta _I h}{2}+\tau (\gamma +d+\mu )\right) }\right| \le 1\nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned}&|\eta _{R}|=\left| \frac{1}{\left( 1+4\lambda _4\sin ^{2}\frac{\theta _R h}{2}+\tau \mu \right) }\right| \le 1 \end{aligned}$$

(14)

with $j=\sqrt{-1},\upsilon ^I=\frac{\beta I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}.$

Inequalities (11)to(14) reveal that our proposed scheme is satisfying von Neumann stability criteria. Hence, the proposed scheme is von Neumann stable.

6 Positivity of the proposed method

We employ M-matrix and mathematical induction method to prove the positivity of the solutions of discretized system. The proposed implicit scheme guarantees that the real matrices involved are M-matrices. So, they are invertible and their inverses are positive. Let us write our discretized systems (7)–(10) into the following vector form

$$\begin{aligned}&BS^{n+1}=S^n+\mu \tau \end{aligned}$$

(15)

$$\begin{aligned}&CA^{n+1}=A^n+\tau \frac{\beta S^{n}I^{n}}{1+\alpha (I^{n})^{2}} \end{aligned}$$

(16)

$$\begin{aligned}&DI^{n+1}=I^n+\tau \sigma A^{n} \end{aligned}$$

(17)

$$\begin{aligned}&ER^{n+1}=R^n+\tau \epsilon A^{n} \end{aligned}$$

(18)

where B, C, D and E are real matrices. If F represents any of B, C, D or E, then

$$\begin{aligned} F=\begin{pmatrix} f^n_{3} &{} f_{1} &{} 0 &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} 0 \\ f_{2} &{} f^n_{3} &{} f_{4} &{} \ddots &{} &{}&{} &{} \vdots \\ 0 &{} f_{2} &{} f^n_{3} &{} f_{4} &{} \ddots &{} &{} &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} &{} \ddots &{} f_{2} &{} f^n_{3} &{} f_{4} &{} 0\\ \vdots &{} &{}&{} &{} \ddots &{} f_{2} &{} f^n_{3} &{} f_{4}\\ 0 &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} 0 &{} f_{1} &{} f^n_{3} \\ \end{pmatrix}. \end{aligned}$$

(19)

The non-diagonal entries of B, C, D and E are 0 or $b_1=-\lambda _1, b_2=-\lambda _1$, $b_4=-\lambda _1, c_1=-\lambda _2$, $c_2=-\lambda _2$, $c_4=-\lambda _2, d_1=-\lambda _3$, $d_2=-\lambda _3$, $d_4=-\lambda _3$, $e_1=-\lambda _4$, $e_2=-\lambda _4, e_4=-\lambda _4$, respectively. The diagonal entries of B, C, D and E are $b_3^n=(1+2\lambda _1+\tau \frac{\beta I^{n}_{i}}{1+\alpha (I^{n}_{i})^{2}}+\tau \mu ), c_3^n =1+2\lambda _2 +\tau (\sigma +\delta +\epsilon +\mu ), d_3^n=1+2\lambda _3+(\gamma +d+\mu )\tau , e_3^n=1+2\lambda _4+\mu \tau$, respectively.

Theorem 2

If initial conditions of a system are positive, then any solution of Eqs. (7)–(10) is positive.

Proof

We will use mathematical induction to prove this claim. It is true for $n=0$ that $S^0, A^0, I^0$ and $R^0 >0$ due to initial condition of the system. Assume it is true for $n>0$, i.e., $S^{n}>0, A^{n}>0, I^{n}>0$ and $R^{n}>0$. Since B, C, D, E are M-matrices, this implies that they are invertible and their inverses are positive. Now,

$$\begin{aligned} S^{n+1}=B^{-1}(S^n+\mu \tau \ge 0), \end{aligned}$$

(20)

where $B^{-1}>0$ and $S^n+\mu \tau >0$. Similarly, we can check for the rest of equations

$$\begin{aligned}&A^{n+1}=C^{-1}(A^n+\tau \frac{\beta S^{n}I^{n}}{1+\alpha (I^{n})^{2}})\ge 0, \end{aligned}$$

(21)

$$\begin{aligned}&I^{n+1}=D^{-1}(I^n+\tau \sigma A^{n})\ge 0, \end{aligned}$$

(22)

$$\begin{aligned}&R^{n+1}=E^{-1}(R^n+\tau \epsilon A^{n})\ge 0. \end{aligned}$$

(23)

So by the induction, the theorem is true for all n. $\square$

Table 1 Values of parameters

Fig. 10

Simulations of a S(x, t), b A(x, t), c I(x, t) and d R(x, t) using positivity preserving implicit method for $h=0.1$, $R_j=0.3$, $j=1,2,3,4$ and $d_i=0.01, i=1,2,3,4$

Fig. 11

Simulations of a S(x, t), b A(x, t), c I(x, t) and d R(x, t) using positivity preserving implicit method for $h=0.1$, $R_j=0.3$, $j=1,2,3,4$ and $d_i=0.01, i=1,2,3,4$

7 Numerical and graphical simulations

In this section, a numerical application of system (2) is given . For numerical solutions of the proposed reaction–diffusion COVID-19 infectious disease model, the initial conditions have non-negative values due to the fact that the number of individuals in each compartment cannot be negative. The initial conditions are set in the way that the fraction of infected individuals attains its maximum value at specific region of space x and it then gradually decreases when moving away from this region. Also, the no-flux boundary conditions (homogeneous Neumann boundary conditions) are employed in numerical simulations. The reason for this choice is that when certain contagious disease outbreaks in a specific region, the condition is imposed that nobody can enter or leave the area. So, the cases of complete lockdown are better described by no-flux boundary conditions. These conditions proved their efficacy among the most effective measures against COVID-19 outbreak. Then, the model can be utilized to track the changes in infections and their spatial distribution in the course of time. Consider system (2) with the following initial conditions and no flux boundary conditions,

$$\begin{aligned}&S(x,0) = \left\{ \begin{array}{ll} 0.5x &{} \quad 0\le x\le 1/2, \\ 0.5(1-x) &{} \quad 1/2\le x\le 1, \\ \end{array} \right. \\&A(x,0) = \left\{ \begin{array}{ll} 0.3x &{} \quad 0\le x\le 1/2, \\ 0.3(1-x) &{} \quad 1/2\le x\le 1, \\ \end{array} \right. \\&I(x,0) = \left\{ \begin{array}{ll} 0.1x &{} 0\le x\le 1/2, \\ 0.1(1-x) &{} \quad 1/2\le x\le 1, \\ \end{array} \right. \\&R(x,0) = \left\{ \begin{array}{ll} 0.1x &{} \quad 0\le x\le 1/2, \\ 0.1(1-x) &{} \quad 1/2\le x\le 1. \\ \end{array} \right. \end{aligned}$$

Figure 10 shows that the numerical solution converges to the uniform disease-free steady state at the selected values of parameters, whereas the other values of parameters for Fig. 11 render that the solution approaches the uniform endemic steady state. As it can be seen from these figures, the results of numerical simulations are in agreement with stability analysis results which are presented in Sect. 2.

All the sketches in Fig. 10 reflect that at disease-free state point, the susceptible populace S(x, t) becomes equal to the whole population, which is one in this case. As at this point infected populace becomes zero, so are the values of A(x, t) and R(x, t). These values are in line with the disease phenomenon. Graphically pattern (a) unlocks the important fact that the susceptible population attains the disease-free steady state within the due course of time. Also, the graph (a) shows that the rate of convergence is appropriate. Similarly, the template (b) depicts that asymptomatic individuals become zero within a due course of time and within a required space. Also, the graph (b) shows that initially at $t=0$, the asymptomatic populace has some nonzero value. But, with the passage of time, the value of the state variables A(x, t) becomes zero. In addition, the other state variables I(x, t), infected individuals at certain time t, and fixed space x and R(x, t), the removed or recovered individuals at some time t and certain place x converge toward infection-free stable state, which is in accordance with the natural phenomenon of disease. All the facts reflected by the graphs represented in Fig. 11 illustrate that the projected numerical scheme converges toward the exact steady state as computed analytically. Moreover, the projected scheme retains the positivity property as pre-assumed for the scheme.

All the numerical patterns in Fig 11 exhibit that numerical solutions converge toward the correct homogeneous endemic stable state of the system. The endemic stable state is calculated in Sect. 2. The numerical template (a) shows the trajectory of convergence for the susceptible portion. The numerical value and the analytical value coincide at the point of convergence, which implicates the worth of the proposed implicit method. Also, the numerical solution for S(x, t) shows that it remains positive over the whole domain of the model and further the solution presented by the implicit scheme does not show any abrupt behavior or non-physical oscillation. Pacing on the same track, the graph (b) also targets the endemic equilibrium within the feasible time duration and in certain region of space domain. Moreover, the graphical pattern shows no anomalous behavior and provides with the positive solutions throughout the domain of space and time. Since the diffusion is considered in the model along with the space, the infected individuals are represented by I(x, t). The graph (c) reflects the behavior of the numerical solutions in the domain of time and space along with the suitably chosen values of parameters. These values of parameters help to understand the dynamics of the COVID-19 reaction–diffusion system. It is evident from the graph that the state variable I(x, t) reaches toward the true value of the endemic steady state. By adopting the different values of space and time coordinates. Likewise, the recovered individuals R(x, t) also provide the correct numerical solutions against the selected set of parametric values. The parametric values are selected in such a way that they obey some specific criteria. Hence, the proposed implicit scheme is a strong numerical tool that provides reliable set of solutions for this type of models.

8 Conclusion

A novel reaction–diffusion COVID-19 model is considered in this work. The system is first investigated in view of its equilibrium points and their stability analysis. Stability regions and influences of key parameters are explored and discussed. The importance of results obtained arises because the movement activities of people are found to cause significant dynamic qualitative changes relative to those of classical temporal-only model. In particular, the simultaneous occurrence of two stable uniform equilibrium points is permitted in state space of spatiotemporal model in contrast to ODEs-based model in which only one stable equilibrium point can exist in its state space. Furthermore, we develop a structure preserving finite difference method for simulating the new COVID-19 model. A consistency and stability analysis for the proposed system are provided along with positivity of the its solutions. The results prove that the proposed new system better simulates the spread of the virus and can stimulate study of some actions to control it in near future work.