A mathematical interpretation for outbreaks of bacterial meningitis under the effect of time-dependent transmission parameters

Abstract

We consider a SIR-type compartmental model divided into two age classes to explain the seasonal exacerbations of bacterial meningitis, especially among children outside of the meningitis belt. We describe the seasonal forcing through time-dependent transmission parameters that may represent the outbreak of the meningitis cases after the annual pilgrimage period (Hajj) or uncontrolled inflows of irregular immigrants. We present and analyse a mathematical model with time-dependent transmission. We consider not only periodic functions in the analysis but also general non-periodic transmission processes. We show that the long-time average values of transmission functions can be used as a stability marker of the equilibrium. Furthermore, we interpret the basic reproduction number in case of time-dependent transmission functions. Numerical simulations support and help visualize the theoretical results.

1 Introduction

Bacterial meningitis is a severe infection that occurs as an explosive epidemic every 5–10 years in the sub-Saharan African meningitis belt, as well as seasonal outbreaks in different parts of the world [1]. The bacterium Neisseria meningitidis is known to be the main cause of bacterial meningitis. It has been reported that the infection has high rates of fatality and may leave serious sequelae in survivors [2]. Six (A, B, C, W, X, and Y) of the twelve serogroups are responsible for nearly all cases of invasive meningococcal disease (IMD), with a large variation of serogroups in different age groups and geographic regions [3]. IMD is transmitted through respiratory droplets by a close contact, and the asymptomatic carriers play a major role in the spread of the disease, although only less than $1\%$ of them develop meningococcal disease [4]. The seasonal as well as irregular outbreak patterns of IMD have been discussed by various researchers in the concept of dry season (from December to May) along the meningitis belt [5,6,7]. IMD displays seasonal exacerbations outside of the meningitis belt, too. In 1987, an outbreak was caused by a strain of N. meningitidis serogroup A associated with the Hajj pilgrimage [8], which is one of the religious duties of Islam that consists of visiting the Kaaba in Mecca at least for a week and participating in communal worship processions. According to the data of the General Authority for Statistics (GASTAT) of the Kingdom of Saudi Arabia, 2.4 million Muslims from different parts of the world joined to pilgrimage in 2019, of which 634 thousand were domestic pilgrims [9]. The geographic and ethnic diversity of the people promote the transmission of respiratory infections during the Hajj [10]. Furthermore, pilgrims from hyper-endemic areas, including the African meningitis belt, carry different N. meningitidis strains to this community that will soon transfer the disease to their home country, and thus, seasonal outbreaks all over the world come forward [4, 8, 11,12,13,14].

The Saudi authorities have required all Hajj pilgrims to receive the quadrivalent (serogroups A, C, W, and Y) meningococcal (MenACWY) polysaccharide vaccine prior to their arrival in Saudi Arabia since 2002 [15]. However, there is no vaccine available to protect people against all serogroups today [16]. In addition, meningococcal polysaccharide vaccination does not prevent the acquisition of carriage, whereas a quadrivalent conjugate vaccine may prevent acquisition of new carriage. Nevertheless, no vaccine can remove an existing carriage that may take two months or more [13]. In some studies, researchers have noticed the seasonal spikes of IMD among the household contacts of returning pilgrims [4, 17,18,19].

Pilgrimage and Umrah (a voluntary pilgrimage to Mecca) were temporarily suspended in 2020 because of the COVID-19 pandemic, and Hajj pilgrimage was limited to just 60,000 citizens and residents in 2021 by the Saudi Arabian authorities. However, as of August 2021 it was announced that the requests of two million Muslim pilgrims who want to perform Umrah from abroad will be accepted every month. As one can predict heuristically, the number of pilgrims may increase in the coming years with the decrease in the effect of the COVID-19 pandemic. Taking into account the spread dynamics of infectious diseases, preventive measures may also be increased and new regulations may be put into effect during the worship process [20, 21].

Since Daniel Bernoulli’s publication on an early mathematical model for smallpox [22], mathematical epidemiology has largely been devoted to explaining the dynamics of the spread of contagious diseases and suggesting control strategies. There are various modelling approaches for the spread of bacterial meningitis, but only a few of them deal with the seasonal transmission dynamics of the disease [23,24,25,26,27]. On the other hand, there exist modelling studies on the seasonality of several other infectious diseases (influenza, measles, chickenpox, pertussis, malaria, etc.) or epidemiological models with a generic aspect [28,29,30,31,32,33,34].

In this paper, we consider a mathematical model motivated by explaining possible seasonal outbreaks of IMD that are caused by the returning pilgrims from Hajj, who transmit the disease to their close contacts, or other mass movements such as uncontrolled migration. We draw attention to the fact that the time-dependent transmission rates do not have to be periodic functions. Consequently, we present a mathematical analysis of the model under time-dependent transmission parameters in the most general sense. We include various examples for seasonal exacerbation of IMD in the simulations.

This paper is organized as follows. The main modelling ideas are given in Sect. 2. Basic properties of the nonlinear model are derived in Sect. 3, and a linear stability analysis of the disease-free equilibrium is presented in Sect. 4. The concept of the basic reproduction number is discussed in Sect. 5. The analytical results are numerically verified in Sect. 6. A brief conclusion in Sect. 7 ends the paper.

2 Modelling ideas

Our starting point is the autonomous model given in [35], which describes the transmission dynamics of a contagious disease between children and adults. While presenting a general approach that could be applied to different childhood diseases, the authors also mention there the specific example of IMD carried by Hajj pilgrims. Since IMD displays temporary outbreaks rather than stable epidemics all over the world except the meningitis belt, a non-autonomous system may better explain the seasonal exacerbation of the disease. Inspired by this idea, an age-structured model driven by a seasonal forcing function was introduced in [34] that takes into account the variability of the climate describing the transmission dynamics between children and adults, where the authors obtained sufficient conditions that assure the existence and global attractivity of a positive periodic solution. In the present paper, we concentrate on the stability of the disease-free state in the time-dependent transmission case and show that the mean values of transmission functions enable to define the exacerbation of IMD as an outbreak.

Fig. 1

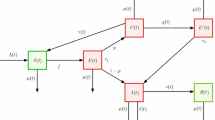
Flowchart of model (1)

The basic structure of the model and the transmission routes are shown in Fig. 1. Our aim is to investigate the seasonal spikes of IMD among the household contacts of returning pilgrims. Although people of any age can develop IMD, children are at increased risk of the disease [36]. The incidence of IMD in infants and young children (aged less than 5 years) occupies $75 \%$ of all cases of meningococcal meningitis and meningococcemia in children. Further, the second peak of incidence according to age scale appears in adolescents and young adults [14]. In this sense, the population is divided into two age groups: adults and children, indicated by the subscripts A and C in this paper. The key assumption here is that these close contacts are households and that children largely constitute the target group. However, in the absence of a large dataset on the prevalence of the IMD in sub-age groups of childhood, the childhood is limited to a single age group. As a result of this assumption, the interpretation of the transmission parameters of the disease is limited to two age groups. As usual, S, I, and R represent the susceptible, infectious, and recovered individuals, respectively.

We assume that all adults are vaccinated and they may carry IMD to the children with a time-dependent transmission rate. While the vaccines for IMD offer protection against some most common serogroups of the disease, the rarer serogroups of disease may cause novel outbreaks. The available literature claims that the majority of pilgrims receive the polysaccharide MenACWY vaccine and that this does not affect carriage and onward transmission. A more complete compliance and transition to a conjugate MenACWY vaccine could provide more robust and broader protection for pilgrims, and additional immunization options could be considered [37]. Because of not displaying any symptoms of the disease, the recovery process for adults is neglected. Although the prevalence of the disease varies in age subgroups of children, we do not define an age threshold between adult and child classes clearly, as we do not analyse any other age subgroup of children. We assume that all surviving children are recovered, although some of them are effected by neurologic sequelae [38]. Certainly, children continuing their lives with severe sequelae cannot be considered as a complete recovery, but since our study focuses on the spread of the disease rather than recovery, leaving sequelae is not considered as a distinct class.

The time-dependent parameters $\beta _{AA}(t), \beta _{CC}(t)$ and $\beta _{AC}(t)$ represent the transmission rate among adults, among children, and between adults and children, respectively. We ignore the transmission from children to adults since biological literature indicates that children ($< 18$ years) are drastically more likely to contract IMD than adults. The parameter $B_C$ is the number of daily births in the households of pilgrims, and $B_A$ represents the daily entrance of adult people to the system. Further, $\mu$ represents the natural death rate and r denotes the recovery rate from the disease. The parameters $B_A, B_C, \mu$, and r are positive and the time-dependent transmission rates. $\beta _{AA}(t)$, $\beta _{AC}(t)$ and $\beta _{CC}(t)$ are taken to be non-negative bounded functions.

Based on the foregoing considerations, we arrive at the following non-autonomous model, which is an extension of the autonomous model studied in [35].

$$\begin{aligned} \begin{aligned}&\dfrac{dS_{A}}{dt} = B_{A} - \beta _{AA}(t) I_{A} S_{A} - \mu S_{A} \\&\dfrac{dS_{C}}{dt} = B_{C} - \big ( \beta _{CC}(t) I_{C} + \beta _{AC}(t) I_{A} \big ) S_{C} - \mu S_{C} \\&\dfrac{dI_{A}}{dt} = \beta _{AA}(t) I_{A} S_{A} - \mu I_{A} \\&\dfrac{dI_{C}}{dt} = \big ( \beta _{CC}(t) I_{C} + \beta _{AC}(t) I_{A} \big ) S_{C} - \mu I_{C} - r I_{C}\\&\dfrac{dR_{C}}{dt} = r I_{C} - \mu R_{C}. \end{aligned} \end{aligned}$$

(1)

3 Basic properties of the nonlinear system

We first show the positivity and boundedness of the solutions of the model (1).

Theorem 3.1

Solutions of the system (1) are non-negative and bounded for all $t>0$ whenever the initial values are non-negative.

Proof

Treating the right-hand side of each equation in the system (1) as a linear equation of the variable on the left, the solutions can be written as

$$\begin{aligned} S_{A}(t)= & {} \phi _{AA}(t) \Big ( S_{A}(0) + B_{A} \int _{0}^{t} \phi _{AA}^{-1}(\tau ) \, d\tau \Big ) \nonumber \\ S_{C}(t)= & {} \phi _{AC}(t) \Big ( S_{C}(0) + B_{C} \int _{0}^{t} \phi _{AC}^{-1}(\tau ) \, d\tau \Big ) \nonumber \\ I_{A}(t)= & {} I_{A}(0) \cdot \exp \Big \{\int _{0}^{t} (\beta _{AA}(\tau ) S_{A}(\tau ) - \mu ) \, d\tau \Big \} \nonumber \\ I_{C}(t)= & {} \phi _{CC}(t) \Big ( I_{C}(0) \nonumber \\{} & {} \quad + \! \int _{0}^{t} \beta _{AC}(\tau ) I_{A}(\tau ) S_{C}(\tau ) \phi _{CC}^{-1}(\tau ) \, d\tau \Big ) \nonumber \\ R_{C}(t)= & {} e^{-\mu t} \Big (R_{C}(0) + r \int _{0}^{t} I_{C}(\tau ) e^{\mu \tau } \, d\tau \Big ). \end{aligned}$$

(2)

where

$$\begin{aligned} \phi _{AA}(t)&\!=\! \exp \Big \{ \!-\!\!\int _{0}^{t}[\beta _{AA}(\tau ) I_{A}(\tau ) + \mu ] \, d\tau \Big \}\\ \phi _{AC}(t)&\!=\! \exp \Big \{\!\!-\!\!\! \int _{0}^{t} [\beta _{CC}(\tau ) I_{C}(\tau ) \nonumber \\&\quad +\! \beta _{AC}(\tau ) I_{A}(\tau ) \!+\! \mu ] d\tau \Big \} \\ \phi _{CC}(t)&\!= \! \exp \Big \{\int _{0}^{t} [\beta _{CC}(\tau ) S_{C}(\tau ) - \mu - r] \, d\tau \Big \} \end{aligned}$$

The non-negativity of $S_{A}$, $S_{C}$, and $I_{A}$ are immediate from the first three equations in (2) since the $\phi$ are positive functions, and the non-negativity of $I_{C}$ and $R_{C}$ follows from the last two equations due to integration of non-negative functions. To show boundedness, consider the equations for the adult and children population sizes, $N_{A} = S_{A} + I_{A}$ and $N_{C} = S_{C} + I_{C} + R_{C}$, as well as the total population size $N = N_{A} + N_{C}$, obtained by adding appropriate equations from the model (1):

$$\begin{aligned} \frac{d N_{A}}{dt}&= B_{A} - \mu N_{A} \nonumber \\ \frac{d N_{C}}{dt}&= B_{C} - \mu N_{C} \nonumber \\ \frac{d N}{dt}&= B_{A} + B_{C} - \mu N. \end{aligned}$$

(3)

The system (3) has solutions

$$\begin{aligned} N_A (t)&= S_{A}(t) + I_{A}(t) \nonumber \\&= \frac{B_{A}}{\mu } + \Big ( N_{A}(0) - \frac{B_{A}}{\mu }\Big ) e^{-\mu t} \end{aligned}$$

(4a)

$$\begin{aligned} N_{C}(t)&= S_{C}(t) + I_{C}(t) + R_{C}(t) \nonumber \\&= \frac{B_{C}}{\mu } + \Big ( N_{C}(0) - \frac{B_{C}}{\mu } \Big ) e^{-\mu t} \end{aligned}$$

(4b)

$$\begin{aligned} N(t)&= \frac{B_{A} + B_{C}}{\mu } + \Big ( N(0) - \frac{B_{A} + B_{C}}{\mu } \Big ) e^{-\mu t}, \end{aligned}$$

(4c)

which show that the non-negative solutions of (1) are bounded for $t>0$. $\square$

Remark 3.2

Note that only the non-negativity of $\beta _{AC}(t)$ is needed to show the non-negativity and hence the boundedness of the solutions.

On the basis of (4), a reduction is possible in the equation (1), which yields an exact solution for the adult subpopulations. Solving for $S_A$ from (4a) as

$$\begin{aligned} S_A(t)= \frac{B_{A}}{\mu }+(S_{A}(0)+I_{A}(0)-\frac{B_{A}}{\mu })e^{-\mu t} -I_A (t)\nonumber \\ \end{aligned}$$

(5)

and substituting into the equation for $I_A$ in (1), we obtain

$$\begin{aligned} \frac{dI_{A}}{dt} = \Big (\lambda _{3}(t)+k_{1}\beta _{AA}(t)e^{-\mu t}\Big )I_{A}-\beta _{AA}(t)I_{A}^{2}, \end{aligned}$$

(6)

where $k_1 = (S_{A}(0)+I_{A}(0)-\frac{B_{A}}{\mu })$ is a constant that depends on the initial conditions and

$$\begin{aligned} \lambda _{3}(t) = \beta _{AA}(t) \frac{B_{A}}{\mu } - \mu . \end{aligned}$$

(7)

(The reason for the choice of notation will become clear in the next section, where we will see that $\lambda _3(t)$ appears as one of the time-dependent eigenvalues of the system’s Jacobian.) Equation (6) is a Bernoulli differential equation and can be solved after reduction to a linear equation via the well-known substitution $u=I_A^{-1}$. This gives an exact solution for $I_A (t)$ as

$$\begin{aligned} I_{A}(t) = \frac{I_{A}(0) \, \eta (t)}{\displaystyle 1 + I_{A}(0) \int _{0}^{t} \beta _{AA}(\tau ) \, \eta (\tau ) \, d\tau }, \end{aligned}$$

(8)

where

$$\begin{aligned} \eta (t) = \exp \left\{ \int _{0}^{t} [\lambda _{3}(\tau ) + k_{1} \beta _{AA}(\tau ) e^{-\mu \tau } ] \, d\tau \right\} . \end{aligned}$$

Furthermore, substituting (8) into (5) gives the exact solution for $S_A(t)$. Therefore, the dynamics of the adult subgroups are explicitly determined.

One can follow a similar procedure for the young age groups. Although in this case it is not possible to obtain explicit formulas for the solutions, one can reduce the problem essentially to a knowledge of $I_C$. Indeed, if $I_C$ is known, then $R_C$ can be found from the last equation in (1) as

$$\begin{aligned} R_{C}(t) = e^{-\mu t} \Big (R_{C}(0) + r \int _{0}^{t} I_{C}(\tau ) e^{\mu \tau } \, d\tau \Big ), \end{aligned}$$

(9)

following which, $S_C$ can be determined from (4b) as

$$\begin{aligned} S_{C}(t) = \frac{B_{C}}{\mu }+k_{2}e^{-\mu t}-I_{C}(t)-R_{C}(t), \end{aligned}$$

(10)

where $k_2 = (S_{C}(0)+I_{C}(0)+R_{C}(0)-\frac{B_{C}}{\mu })$. Substituting (10) into the equation for $I_C$ in (1), we obtain

$$\begin{aligned} \frac{dI_{C}}{dt}&= \beta _{AC}(t)I_{A}(t)\Big (\frac{B_{C}}{\mu }+k_{2}e^{-\mu t}-R_{C}(t)\Big )\nonumber \\&\quad +\Big (\lambda _{4}(t)+\beta _{CC}(t)(k_{2}e^{-\mu t}\nonumber \\&\quad -R_{C}(t))-\beta _{AC}(t)I_{A}(t)\Big )I_{C} \nonumber \\&-\beta _{CC}(t)I_{C}^{2} \end{aligned}$$

(11)

where

$$\begin{aligned} \lambda _{4}(t) = \beta _{CC}(t) \frac{B_{C}}{\mu } - \mu -r. \end{aligned}$$

(12)

Thus, the solution of the system (1) is in principle reduced to solving (11). With $I_A (t)$ being a known function given by (8), equation (11) is a Riccati-like differential equation for $I_C$, except that the expression for $R_C$ that must be substituted from (9) further contains an integral of $I_C$.

Although finding the exact solution of (11) is difficult, the foregoing derivation already identifies the key quantities that will prove to be important for the dynamical behaviour of the model (1), namely $\lambda _3$ and $\lambda _4$, as defined in (7) and (12). In the next section, we will see that these are the two time-dependent eigenvalues of the system’s Jacobian matrix and thus play a decisive role in the stability of the equilibrium (as the remaining eigenvalues are constant and negative).

4 Disease-free equilibrium and linear stability analysis

With time-dependent transmission rates, the system (1) turns out to have a single equilibrium point, which is the disease-free state.

Theorem 4.1

If $\beta _{AA}(t)$ and $\beta _{CC}(t)$ are non-constant functions, then the system (1) has a unique equilibrium $(S_{A}^{*}, S_{C}^{*}, I_{A}^{*}, I_{C}^{*}, R_{C}^{*}) = \big ( \frac{B_{A}}{\mu }, \frac{B_{C}}{\mu }, 0, 0, 0 \Big )$, which corresponds to the disease-free state.

Proof

Let $(S_{A}^{*}, S_{C}^{*}, I_{A}^{*}, I_{C}^{*}, R_{C}^{*})$ denote an equilibrium point of the system (1). Thus, we have

$$\begin{aligned} 0&= B_{A} - \beta _{AA}(t) I_{A}^{*} S_{A}^{*} - \mu S_{A}^{*} \\ 0&= B_{C} - \big ( \beta _{CC}(t) I_{C}^{*} + \beta _{AC}(t) I_{A}^{*} \big ) S_{C}^{*} - \mu S_{C}^{*} \\ 0&= I_{A}^{*} \big (\beta _{AA}(t) S_{A}^{*} - \mu \big ) \\ 0&= \big ( \beta _{CC}(t) I_{C}^{*} + \beta _{AC}(t) I_{A}^{*} \big ) S_{C}^{*} - \mu I_{C}^{*} - r I_{C}^{*} \\ 0&= r I_{C}^{*} - \mu R_{C}^{*}. \end{aligned}$$

By the third equation, either $I_{A}^{*} = 0$ or $\beta _{AA}(t) S_{A}^{*} = \mu > 0$. The latter cannot hold since it implies $S_{A}^{*} \ne 0$ and thus $\beta _{AA}(t) = {\mu }/{S_{A}^{*}}$, which is not possible if $\beta _{AA}(t)$ is non-constant. Therefore, $I_{A}^{*} = 0$. Substituting this value in the fourth equation and following a similar reasoning, we find $I_{C}^{*} = 0$. Substituting these in the remaining equations, we obtain $(S_{A}^{*}, S_{C}^{*}, I_{A}^{*}, I_{C}^{*}, R_{C}^{*}) = ( B_{A} / \mu , B_{C} / \mu , 0, 0, 0)$. $\square$

We associate the outbreaks of the disease as deviations from the disease-free state, and to analyse them we consider the linear variational equation for (1) around the unique equilibrium point $(S_{A}^{*}, S_{C}^{*}, I_{A}^{*}, I_{C}^{*}, R_{C}^{*}) = \left( {B_{A}}/{\mu }, {B_{C}}/{\mu }, 0, 0, 0 \right)$. To this end, we denote deviations from the equilibrium values by $\Delta S_{A} = S_{A} - S_{A}^{*}$, $\Delta S_{C} = S_{C} - S_{C}^{*}$, $\Delta I_{A} = I_{A} - I_{A}^{*}$, $\Delta I_{C} = I_{C} - I_{C}^{*}$, and $\Delta R_{C} = R_{C} - R_{C}^{*}$. Then the linear variational equations are

$$\begin{aligned} \frac{d \, \Delta S_{A}}{dt}= & {} -\mu \, \Delta S_{A} - \beta _{AA}(t) \frac{B_{A}}{\mu } \Delta I_{A} \nonumber \\ \frac{d \, \Delta S_{C}}{dt}= & {} {-}\mu \, \Delta S_{C} {-} \beta _{AC}(t) \dfrac{B_{C}}{\mu } \Delta I_{A} {-} \beta _{CC}(t) \dfrac{B_{C}}{\mu } \Delta I_{C} \nonumber \\ \frac{d \, \Delta I_{A}}{dt}= & {} \Big ( \beta _{AA}(t) \frac{B_{A}}{\mu } - \mu \Big ) \Delta I_{A} \nonumber \\ \frac{d \, \Delta I_{C}}{dt}= & {} \beta _{AC}(t) \frac{B_{C}}{\mu } \, \Delta I_{A} {+} \Big ( \beta _{CC}(t) \frac{B_{C}}{\mu } {-} \mu {-} r \Big ) \Delta I_{C} \nonumber \\ \frac{d \, \Delta R_{C}}{dt}= & {} r \, \Delta I_{C} - \mu \, \Delta R_{C}, \end{aligned}$$

(13)

or, equivalently, in matrix form

$$\begin{aligned} \frac{d}{dt} \Delta = J^{*}(t) \Delta , \end{aligned}$$

where $\Delta = \begin{bmatrix} \Delta S_{A}&\Delta S_{C}&\Delta I_{A}&\Delta I_{C}&\Delta R_{C} \end{bmatrix}^{\top }$ and

$$\begin{aligned} J^{*}(t) = \begin{bmatrix} -\mu &{} 0 &{} -\beta _{AA}(t) \frac{B_{A}}{\mu } &{} 0 &{} 0 \\ 0 &{} - \mu &{} -\beta _{AC}(t) \frac{B_{C}}{\mu } &{} -\beta _{CC}(t) \frac{B_{C}}{\mu } &{} 0 \\ 0 &{} 0 &{} \quad \beta _{AA}(t) \frac{B_{A}}{\mu } - \mu &{} 0 &{} 0 \\ 0 &{} 0 &{} \beta _{AC}(t) \frac{B_{C}}{\mu } &{} \;\beta _{CC}(t) \frac{B_{C}}{\mu } - \mu - r &{} 0 \\ 0 &{} 0 &{} 0 &{} r &{} \; -\mu \end{bmatrix}. \end{aligned}$$

We note that the eigenvalues of $J^*$ are $\lambda _{1,2,5} = -\mu$, $\lambda _{3}(t) = \beta _{AA}(t) \frac{B_{A}}{\mu } - \mu$, and $\lambda _{4}(t) = \beta _{CC}(t) \frac{B_{C}}{\mu } - \mu - r$. The time-dependent eigenvalues $\lambda _3(t)$ and $\lambda _4(t)$ are precisely the quantities defined in (7) and (12), and they play an important role in the stability of the equilibrium, as we will see below.

The solution to the linear variational system (13) can be written as

$$\begin{aligned}{} & {} \Delta S_{A}(t) = \Delta S_{A}(0) \, e^{-\mu t} \nonumber \\{} & {} ~~~~~~~~~~~\quad - \frac{B_{A}}{\mu } \int _{0}^{t} e^{-\mu (t-\tau )} \beta _{AA}(\tau ) \Delta I_{A}(\tau ) \, d\tau \nonumber \\ \end{aligned}$$

(14a)

$$\begin{aligned}{} & {} \Delta S_{C}(t) = \Delta S_{C}(0) \, e^{-\mu t} \nonumber \\{} & {} \quad ~~~~~~~~~~~- \dfrac{B_{C}}{\mu } \int _{0}^{t} e^{-\mu (t-\tau )} \Big ( \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \nonumber \\{} & {} \quad ~~~~~~~~~~~+ \beta _{CC}(\tau ) \Delta I_{C}(\tau ) \Big ) \, d\tau \end{aligned}$$

(14b)

$$\begin{aligned}{} & {} \Delta I_{A}(t) = \Delta I_{A}(0) \cdot \eta _3 (t) \end{aligned}$$

(14c)

$$\begin{aligned}{} & {} \Delta I_{C}(t) = \Delta I_{C}(0) \cdot \eta _4 (t) \nonumber \\{} & {} \quad ~~~~~~~~~~~+ \frac{B_{C}}{\mu } \int _{0}^{t} \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \, \frac{\eta _4 (t)}{\eta _4 (\tau )} \, d\tau \end{aligned}$$

(14d)

$$\begin{aligned}{} & {} \Delta R_{C}(t) = \Delta R_{C}(0) \, e^{-\mu t}\nonumber \\{} & {} \quad ~~~~~~~~~~~~+ r \int _{0}^{t} e^{-\mu (t-\tau )} \, \Delta I_{A}(\tau ) \, d\tau . \end{aligned}$$

(14e)

where the positive functions $\eta _3$ and $\eta _4$ are defined by

$$\begin{aligned} \eta _3 (t)&= \exp \left\{ \int _ {0}^{t} \lambda _{3} (\tau ) \, d\tau \right\} \\ \eta _4 (t)&=\exp \left\{ \int _{0}^{t} \lambda _{4}(\omega ) \, d\omega \right\} . \end{aligned}$$

We investigate the conditions under which the perturbations $\Delta$ around the equilibrium go to zero. The next lemma shows that the question can be reduced to a consideration of only the pair $(\Delta I_{A},\Delta I_{C})$.

Lemma 4.2

$\displaystyle \lim _{t\rightarrow \infty }\Delta (t) = {\varvec{0}}$ if and only if $\displaystyle \lim _{t\rightarrow \infty }\Delta I_{A}(t)$$= \lim _{t\rightarrow \infty }\Delta I_{C}(t) = 0$.

Proof

If $\Delta \rightarrow {\varvec{0}}$, then $\Delta I_{A}$ and $\Delta I_{C}$ clearly go to zero, being components of $\Delta$. To prove the other direction, let $\Delta N_{A}(t) = \Delta S_{A}(t) + \Delta I_{A}(t)$, $\Delta N_{C}(t) = \Delta S_{C}(t) + \Delta I_{C}(t) + \Delta R_{C}(t)$, and $\Delta N(t) = \Delta N_{A}(t) + \Delta N_{C}(t)$. Then from (13),

$$\begin{aligned} \frac{d \, \Delta N_{A}}{dt}&= - \mu \, \Delta N_{A},\quad \frac{d \, \Delta N_{C}}{dt} = - \mu \, \Delta N_{C},\\ \frac{d \, \Delta N}{dt}&= - \mu \, \Delta N, \end{aligned}$$

yielding

$$\begin{aligned} \Delta N_{A}(t)&= \Delta N_{A}(0) e^{-\mu t}, \quad \Delta N_{C}(t) = \Delta N_{C}(0) e^{-\mu t},\\ \Delta N(t)&= \Delta N(0) e^{-\mu t}. \end{aligned}$$

Thus, $\Delta N_{A}(t)$, $\Delta N_{C}(t)$, and $\Delta N(t)$ go to zero as $t \rightarrow \infty$.

Now assume that both $\Delta I_{A}$ and $\Delta I_{C}$ go to 0 as $t \rightarrow \infty$. Then $\Delta S_{A} \rightarrow 0$ since $\Delta S_{A} = \Delta N_{A} - \Delta I_{A}$ and both terms on the right go to zero. Similarly, $\Delta S_{C} \rightarrow 0$ since $\Delta S_{C} = \Delta N_{C} - \Delta I_{C} - \Delta R_{C}$ and each term on the right goes to zero. To show that $\Delta R_{C} \rightarrow 0$ as $t \rightarrow \infty$, we compute the limit from (14e) using L’Hospital’s rule:

$$\begin{aligned} \lim _{t \rightarrow \infty } \Delta R_{C}(t)&= \lim _{t \rightarrow \infty } \left[ \Delta R_{C}(0) \, e^{-\mu t}\right. \\&\quad \left. + e^{-\mu t} \int _{0}^{t} r e^{\mu \tau } \Delta I_{A}(\tau ) \, d\tau \right] \\ {}&= \lim _{t \rightarrow \infty } \frac{\int _{0}^{t} r e^{\mu \tau } \Delta I_{A}(\tau ) \, d\tau }{e^{\mu t}} \\&= \lim _{t \rightarrow \infty } \frac{r e^{\mu t} \Delta I_{A}(t)}{\mu e^{\mu t}} \\&= \lim _{t \rightarrow \infty } \frac{r}{\mu } \Delta I_{A}(t) = 0. \end{aligned}$$

Hence, $\Delta \rightarrow {\varvec{0}}$ since all of its components go to zero. $\square$

On the basis of the above lemma, we focus on the conditions that yield $\displaystyle \lim _{t\rightarrow \infty }\Delta I_{A}(t) =0$ and $\displaystyle \lim _{t\rightarrow \infty }\Delta I_{C}(t) = 0$. The first limit is straightforward, as (14c) implies that a necessary and sufficient condition for $\Delta I_{A}(t) \rightarrow 0$ is that $\int _{0}^{\infty } \lambda _{3}(t) \, dt = -\infty$. The case for $\Delta I_{C}(t) \rightarrow 0$ is more involved: by (14d) it can be seen that a similar condition $\int _{0}^{\infty } \lambda _{4}(t) \, dt = -\infty$ is only a necessary condition for $\Delta I_{C}(t) \rightarrow 0$ but not a sufficient one. A full characterization of stability therefore requires consideration of additional conditions. Below we list several relevant conditions and investigate their implications for stability.

• (C1) $\int _{0}^{\infty } \lambda _{3}(t) \, dt = \int _{0}^{\infty } ( \beta _{AA}(t) \frac{B_{A}}{\mu } - \mu ) dt = -\infty$.

• (C2) $\int _{0}^{\infty } \lambda _{4}(t) \, dt = \int _{0}^{\infty } ( \beta _{CC}(t) \frac{B_{C}}{\mu } - \mu - r ) dt = -\infty$.

• (C3) There exists $M > 0$ such that $\lambda _{4}(t) = \beta _{CC}(t) \frac{B_{C}}{\mu } - \mu - r \le -M$ for $t \ge 0$.

• (C4) There exists $a > 0$ such that $a \beta _{AC}(t) \le \beta _{AA}(t) \frac{B_{A}}{\mu } - \beta _{CC}(t) \frac{B_{C}}{\mu } + r$ for $t \ge 0$, or equivalently $a \beta _{AC}(t) \le \lambda _{3}(t) - \lambda _{4}(t)$ for $t \ge 0$.

As noted above, the first two conditions (C1)–(C2) are necessary for the stability of equilibrium solution, which we state as a theorem.

Theorem 4.3

The disease-free equilibrium of the non-autonomous system (1) is unstable if either (C1) or (C2) fails to hold.

Proof

If either (C1) or (C2) does not hold, then the variations $\Delta I_{A}(t) \not \rightarrow 0$ or $\Delta I_{C}(t) \not \rightarrow 0$ since the exponential terms in (14c) or (14d) do not tend to zero, and the result follows from Lemma 4.2. $\square$

For the remainder of this section, we focus on the local stability of the unique equilibrium solution of (1), in the sense of stability of the zero solution of the linear variational equation (13).

Theorem 4.4

Suppose the condition (C1) holds. Then all solutions of the variational equation (13) decay to zero if either of the conditions (C3) or (C4) holds.

Proof

Condition (C1) guarantees that $\Delta I_{A}(t) \rightarrow 0$ by (14c). By Lemma 4.2, it suffices to show $\Delta I_{C}(t) \rightarrow 0$. We consider the limit under each of the conditions (C3) and (C4) separately.

i) If (C3) holds, then $\int _{0}^{\infty } \lambda _{4}(t) \, dt \le \int _{0}^{\infty } -M \,dt = -\infty$, so the first term on the right-hand side of (14d) goes to zero. For the remaining term, the limit is calculated using L’Hospital’s rule as

$$\begin{aligned}&\lim _{t \rightarrow \infty } \frac{\displaystyle \int _{0}^{t} \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \frac{B_{C}}{\mu } \, e^{ -\int _{0}^{\tau } \lambda _{4}(w) \, dw } \, d\tau }{\exp \left\{ \displaystyle -\int _{0}^{t} \lambda _{4}(\tau ) \, d\tau \right\} }\\&= \lim _{t \rightarrow \infty } \frac{\beta _{AC}(t) \Delta I_{A}(t) \frac{B_{C}}{\mu } \, e^{ -\int _{0}^{t} \lambda _{4}(w) \, dw }}{-\lambda _{4}(t) \cdot \exp \left\{ \displaystyle -\int _{0}^{t} \lambda _{4}(\tau ) \, d\tau \right\} } \\&= \lim _{t \rightarrow \infty } \frac{\beta _{AC}(t) \Delta I_{A}(t) \frac{B_{C}}{\mu }}{-\lambda _{4}(t)} = 0, \end{aligned}$$

showing that $\Delta I_{C}(t) \rightarrow 0$.

ii) If (C4) holds, then $\lambda _{3}(t) - \lambda _{4}(t) \ge 0$ since a is positive and $\beta _{AC}$ is non-negative. Therefore, $\int _{0}^{\infty } \lambda _{4}(t) \, dt \le \int _{0}^{\infty } \lambda _{3}(t) \, dt = -\infty$ by (C1). This yields $\int _{0}^{\infty } \lambda _{4}(t) \, dt = - \infty$, i.e. the condition (C2). Thus, the first term on the right-hand side of (14d) goes to zero. Now, using (14c) and (C4), we write the integral in the second term of (14d) as

$$\begin{aligned}&\int _{0}^{t} \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \frac{B_{C}}{\mu } \, e^{ -\int _{0}^{\tau } \lambda _{4}(w) \, dw }\\&= \Delta I_{A}(0) \frac{B_{C}}{\mu }\! \int _{0}^{t}\! \beta _{AC}(\tau ) e^{ \int _{0}^{\tau } [\lambda _{3}(w) {-} \lambda _{4}(w)] \, dw} d\tau \\&{\le } \frac{\Delta I_{A}(0) B_{C}}{a \mu } \!\int _{0}^{t}\! \left( \lambda _{3}(\tau )0 {-} \lambda _{4}(\tau ) \right) e^{ \int _{0}^{\tau } [\lambda _{3}(w) - \lambda _{4}(w)] dw} d\tau \\&= \frac{\Delta I_{A}(0) B_{C}}{a \mu } \Big ( e^{ \int _{0}^{\tau } [\lambda _{3}(w) - \lambda _{4}(w)] dw} - 1 \Big ). \end{aligned}$$

Hence, the second term on the right-hand side of (14d) is bounded above by

$$\begin{aligned} \frac{\Delta I_{A}(0) B_{C}}{a \mu } \Big ( \exp \Big \{ \!\int _{0}^{t}\! \lambda _{3}(\tau ) \, d\tau \Big \} {-} \exp \Big \{ \int _{0}^{t} \lambda _{4}(\tau ) \, d\tau \Big \} \Big ), \end{aligned}$$

which goes to zero as $t \rightarrow \infty$ since (C1) and (C2) hold. Hence, $\Delta I_{C}(t) \rightarrow 0$. $\square$

We now establish stability criteria in terms of average quantities. Recall that if $f:[0, \infty ) \rightarrow {\mathbb {R}}$ is integrable on [0, t] for all $t > 0$, then the average of f is the (extended) real number defined by

$$\begin{aligned} {\bar{f}}:= \lim _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} f(\tau ) \, d\tau . \end{aligned}$$

(15)

If f is a T-periodic function, then its average (15) can be calculated over one period:

$$\begin{aligned} {\bar{f}} = \frac{1}{T} \int _{0}^{T} f(t) \, dt. \end{aligned}$$

(16)

Useful results about averages are summarized in Appendix.

We list further conditions in terms of averages that play a role in stability.

• (C5) ${\bar{\beta }}_{AA} < \frac{\mu ^2}{B_{A}}$ and ${\bar{\beta }}_{CC} < \frac{\mu (\mu + r)}{B_{C}}$, or equivalently, ${\bar{\lambda }}_{3} < 0$ and ${\bar{\lambda }}_{4} < 0$.

• (C6) $\int _{0}^{t} (\beta _{CC}(\tau ) - {\bar{\beta }}_{CC}) \, d\tau$, or equivalently $\int _{0}^{t} (\lambda _{4}(\tau ) - {\bar{\lambda }}_4) \, d\tau$, is bounded for $t \ge 0$.

• (C7) ${\bar{\beta }}_{AA} \frac{B_{A}}{\mu }< {\bar{\beta }}_{CC} \frac{B_{C}}{\mu } - r < \mu$, or equivalently, ${\bar{\lambda }}_{3}< {\bar{\lambda }}_{4} < 0$.

Theorem 4.5

All solutions of the variational equation (13) decay to zero if either (C7) holds, or else both (C5) and (C6) hold together.

Proof

In both cases $\Delta I_{A}(t) \rightarrow 0$, so by Lemma 4.2 it suffices to show that $\Delta I_{C}(t) \rightarrow 0$. Now the first term on the right-hand side of (14d) goes to zero by Lemma A.3. It remains to show that the second term

$$\begin{aligned}{} & {} \exp \left\{ \int _{0}^{t} \lambda _{4}(\tau ) \, d\tau \right\} \nonumber \\{} & {} \quad \cdot \int _{0}^{t} \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \frac{B_{C}}{\mu } \, e^{ -\int _{0}^{\tau } \lambda _{4}(w) \, dw } \, d\tau \end{aligned}$$

(17)

goes to zero as well, which we will establish under each of the given assumptions.

i) Suppose both (C5) and (C6) hold. Multiplying and dividing the expression (17) by $e^{ -{\bar{\lambda }}_{4} t}$ gives

$$\begin{aligned}{} & {} \underbrace{\exp \left\{ \int _{0}^{t} (\lambda _{4}(\tau ) - {\bar{\lambda }}_{4}) \, d\tau \right\} }_\text {bounded by (C6)}\nonumber \\{} & {} \quad \cdot \frac{\int _{0}^{t} \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \frac{B_{C}}{\mu } \, e^{ -\int _{0}^{\tau } \lambda _{4}(w) \, dw } \, d\tau }{ e^{ -{\bar{\lambda }}_{4} t } }. \end{aligned}$$

Taking the limit for the fraction using L’Hospital’s rule yields

$$\begin{aligned} \lim _{t \rightarrow \infty }&\frac{\int _{0}^{t} \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \frac{B_{C}}{\mu } \, e^{ -\int _{0}^{\tau } \lambda _{4}(w) \, dw } \, d\tau }{e^{ -{\bar{\lambda }}_{4} t}}\\&= \lim _{t \rightarrow \infty } \frac{\beta _{AC}(t) \Delta I_{A}(t) \frac{B_{C}}{\mu } \, e^{ -\int _{0}^{t} \lambda _{4}(w) \, dw }}{-{\bar{\lambda }}_{4} \cdot e^{ -{\bar{\lambda }}_{4} t}} \\&= \lim _{t \rightarrow \infty } \underbrace{e^{\int _{0}^{t} {\bar{\lambda }}_{4} - \lambda _{4}(\tau ) \, d\tau }}_\text { bounded by (C6)} \frac{1}{-{\bar{\lambda }}_{4}} \frac{B_{C}}{\mu } \beta _{AC}(t) \Delta I_{A}(t)\\&= 0, \end{aligned}$$

which shows the expression (17) goes to zero. Therefore, $\Delta I_{C}(t) \rightarrow 0$.

ii) Suppose (C7) holds. Note that $\beta _{AC}(t)$ is bounded. Using (14c) in expression (17) gives

$$\begin{aligned}&\int _{0}^{t} \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \frac{B_{C}}{\mu } \, e^{ -\int _{0}^{\tau } \lambda _{4}(w) \, dw } \, d\tau \\&= \Delta I_{A}(0) \frac{B_{C}}{\mu } \int _{0}^{t} \beta _{AC}(\tau ) e^{ \int _{0}^{\tau } \lambda _{3}(w) - \lambda _{4}(w) \, dw} d\tau \\&\le K \int _{0}^{t} e^{ \int _{0}^{\tau } \lambda _{3}(w) - \lambda _{4}(w) dw} d\tau \end{aligned}$$

for some $K>0$. If we let $f(t) = \lambda _{3}(t) - \lambda _{4}(t)$, then ${\bar{f}} = {\bar{\lambda }}_3 - {\bar{\lambda }}_4 < 0$ by (C7), and using Lemma A.4 we observe boundedness of the left-hand side of the above inequality. Thus, expression (17) has the bound

$$\begin{aligned}&e^{ \int _{0}^{t} \lambda _{4}(\tau ) \, d\tau } \int _{0}^{t} \beta _{AC}(\tau ) \Delta I_{A}(\tau ) \tfrac{B_{C}}{\mu } \, e^{ -\int _{0}^{\tau } \lambda _{4}(w) \, dw } \, d\tau \\&\le K N e^{ \int _{0}^{t} \lambda _{4}(\tau ) \, d\tau } \end{aligned}$$

for some $K,N > 0$, which goes to zero by Lemma A.3. Therefore, $\Delta I_{C}(t) \rightarrow 0$. $\square$

Finally, in case of periodic transmission functions, we can give a simple and sharp criterion for stability in terms of averages.

Theorem 4.6

Suppose $\beta _{AA}(t)$ and $\beta _{CC}(t)$ are periodic functions. Then the origin of the variational equation (13) is asymptotically stable if and only if (C5) holds.

Proof

If $\beta _{CC}(t)$ is periodic, then (C6) is satisfied by Lemma A.5. Therefore, if (C5) holds then stability follows by Theorem 4.5. On the other hand, if (C5) does not hold, then either (C1) or (C2) does not hold by Lemmas A.3 and A.7, and instability follows by Theorem 4.3. $\square$

To summarize, considering outbreaks as small deviations from the disease-free equilibrium state of the system, we have constructed the linear variational Eq. (13) around the disease-free equilibrium for the model (1) and analysed the non-autonomous system. This approach is not only specific to epidemiological models but can also be used for compartmental models representing various dynamical processes in various disciplines like sociology, chemistry, finance etc.

5 Note on the basic reproduction number under time-dependent transmission

In autonomous epidemic models, the basic reproduction number ${\mathscr {R}}_0$ is commonly defined as the number of secondary infections that result from the introduction of a single infectious individual into an entirely susceptible population [39], and is typically associated with the local stability of the equilibria via the method of next-generation matrix [40]. However, this standard definition of ${\mathscr {R}}_0$ is no longer applicable in periodic environments [41]. One of the earliest works for the case of time-dependent systems is [42], where the authors approximate the basic reproduction number for a periodically transmitted disease model. This work and its followers revealed that a general explicit formula for ${\mathscr {R}}_0$ does not exist under seasonal dynamics [43,44,45]. Moreover, in numerical simulations large outbreaks have been observed even when ${\mathscr {R}}_0$ was below the threshold value 1 [46, 47]. Since then, the computation and interpretation of an appropriate formula for ${\mathscr {R}}_0$ for non-autonomous systems have attracted much attention [34, 48, 49].

The derivation of the basic reproduction number is based on the linearization of the ODE model about a disease-free equilibrium, and is therefore directly related to the analysis of Sect. 4. Hence, considering only the infected compartments, let the matrices F and V denote, as usual, the rate at which secondary infections increase the compartment size and the net outflow from the compartment, respectively. Hence, for the model (1),

$$\begin{aligned} F(t) = \begin{bmatrix} \beta _{AA}(t) \dfrac{B_{A}}{\mu } &{} 0\\ \beta _{AC}(t) \dfrac{B_{C}}{\mu } &{} \quad \beta _{CC}(t) \dfrac{B_{C}}{\mu } \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} V(t) = \begin{bmatrix} \mu &{} 0\\ 0 &{} \; \mu + r \end{bmatrix} \end{aligned}$$

and the next-generation matrix $M= FV^{-1}$ is given by

$$\begin{aligned} M(t) = \begin{bmatrix} \beta _{AA}(t) \dfrac{B_{A}}{\mu ^{2}} &{} 0\\ \beta _{AC}(t) \dfrac{B_{C}}{\mu ^{2}} &{} \quad \beta _{CC}(t) \dfrac{B_{C}}{\mu (\mu + r)} \end{bmatrix}. \end{aligned}$$

In autonomous systems, the basic reproduction number is defined as the dominant eigenvalue of the next-generation matrix M. In our case, M(t) and its eigenvalues are time dependent. We denote the eigenvalues as

$$\begin{aligned} \Lambda _{3}(t) = \beta _{AA}(t) \dfrac{B_{A}}{\mu ^{2}} \quad \text {and} \quad \Lambda _{4}(t) = \beta _{CC}(t) \dfrac{B_{C}}{\mu (\mu + r)}. \end{aligned}$$

The reason for the notation is that these eigenvalues are directly related to the two eigenvalues (7) and (12) that are responsible for the stability of the disease-free equilibrium, namely

$$\begin{aligned} \lambda _3 (t)= \mu (\Lambda _3 (t) -1) \; \text {and} \; \lambda _4 (t)= (\mu + r)(\Lambda _4 (t) -1). \end{aligned}$$

Therefore, $\lambda _3 <0$ (resp., $\lambda _4 <0$) if and only if $\Lambda _3 <1$ (resp., $\Lambda _4 < 1$), and conditions (C1)–(C4) can be readily expressed in terms of the eigenvalues $\Lambda _3,\Lambda _4$ of the next-generation matrix.

To obtain a single quantity that can play the role of the basic reproduction number, it is thus natural to consider time averages, in the sense of (15). Hence, the mean next-generation matrix is $\displaystyle {\bar{M}}=\lim _{t\rightarrow \infty }\frac{1}{t}\int _0^t M(\tau )\,d\tau$ and has eigenvalues

$$\begin{aligned} {\bar{\Lambda }}_{3} = {\bar{\beta }}_{AA} \frac{B_{A}}{\mu ^{2}} \quad \text {and} \quad {\bar{\Lambda }}_{4} = {\bar{\beta }}_{CC} \frac{B_{C}}{\mu (\mu + r)}, \end{aligned}$$

which are related to the time averages of the Jacobian eigenvalues by

$$\begin{aligned} {\bar{\lambda }}_3 = \mu ({\bar{\Lambda }}_3 -1) \quad \text {and} \quad {\bar{\lambda }}_4 = (\mu + r)({\bar{\Lambda }}_4 -1). \end{aligned}$$

(18)

The conditions (C5)–(C7) for the stability of the disease-free equilibrium are then immediately available in terms of ${\bar{\Lambda }}_{3,4}$. A mean basic reproduction number $\bar{{\mathscr {R}}}_0$ can be defined as the spectral radius of ${\bar{M}}$, that is,

$$\begin{aligned} \bar{{\mathscr {R}}}_0&= \max \{ |{\bar{\Lambda }}_3|, |{\bar{\Lambda }}_4| \} \nonumber \\&= \max \left\{ {\bar{\beta }}_{AA} \frac{B_{A}}{\mu ^{2}}, \ {\bar{\beta }}_{CC} \frac{B_{C}}{\mu (\mu + r)} \right\} . \end{aligned}$$

(19)

For periodic transmission functions, the relation of $\bar{{\mathscr {R}}}_0$ to stability is sharp by Theorem 4.6, which we state as a corollary.

Corollary 5.1

Suppose $\beta _{AA}(t)$ and $\beta _{CC}(t)$ are periodic functions. Then the disease-free equilibrium is locally asymptotically stable if and only if $\bar{{\mathscr {R}}}_0 < 1$.

The situation is less clear-cut for non-periodic transmission functions. As Theorem 4.5 indicates, condition (C5), i.e. $\bar{{\mathscr {R}}_0}$ being less than 1, may not be enough for the stability of the disease-free state, unless condition (C6) holds as well. Indeed, the sufficient condition (C7) shows that both eigenvalues, and not just the dominant eigenvalue, may have a role in stability. More precisely, using (18), condition (C7) can be expressed as

$$\begin{aligned} \frac{{\bar{\Lambda }}_4-{\bar{\Lambda }}_3}{1-{\bar{\Lambda }}_4} > \frac{r}{\mu } \end{aligned}$$

when $\bar{{\mathscr {R}}_0}<1$, which is the condition that ${\bar{\Lambda }}_4$ be larger than ${\bar{\Lambda }}_3$ by an amount that depends on the ratio $r/\mu$. Hence, there may be subtler cases when the condition $\bar{{\mathscr {R}}_0}<1$ by itself does not suffice to guarantee the stability of the disease-free equilibrium. On the other hand, $\bar{{\mathscr {R}}_0}>1$ is always a marker of instability.

Corollary 5.2

If $\bar{{\mathscr {R}}_0}>1$, then the disease-free equilibrium is unstable.

Proof

If $\bar{{\mathscr {R}}_0}>1$, then either ${\bar{\lambda }}_3$ or ${\bar{\lambda }}_4$ is positive by (18), in which case Lemma A.3 implies that either $\int _{0}^{\infty } \lambda _3(t) \, dt = \infty$ or $\int _{0}^{\infty } \lambda _4(t) \, dt = \infty$. The result then follows by Theorem 4.3. $\square$

6 Numerical simulations

To visualize the dynamical behaviour of the mathematical model (1) in the light of the theoretical results obtained from mathematical analysis, we perform numerical simulations using the standard Matlab routines for solving systems of differential equations [50]. Although local and international outbreaks of IMD have been strictly associated with Umrah/Hajj travel in different studies, data on IMD are still sparse or lacking in the Eastern Mediterranean and North Africa regions [14, 51, 52]. For this reason, we cannot fit the model (1) to a particular data set, but we use the findings from different studies when choosing the model parameters. While there are gaps in the available statistical data, the reality is that Hajj, one of the world’s largest mass movements and gatherings of people, is directly related to a variety of health problems, including the seasonal outbreaks of infectious diseases. The World Bank classifies the countries in the African meningitis belt as low-middle income countries. Since we have noted seasonal outbreaks of IMD outside the meningitis belt, we perform our simulations for a hypothetical upper-middle income country.

Dogu et al. [14] presented a recent review of available IMD data by scanning the literature between January 2000–February 2021. Based on 11 different studies, they report that the rates of asymptomatic carriage in the pilgrim risk group range from $0.0 \%$ [53, 54] to $27.4 \%$ [18]. The IMD incidence in the general population ranges from 0 to 20.5/100, 000 in children aged under 5 years [14]. The most recent study among them refers to a data set from Turkey and indicates an incidence of 0.9/100, 000 [55]. Another recent study from Morocco points out an incidence of 3.75/100, 000 for children aged under 18 years [56]. From the perspective of mathematical models, the transmission rate $\beta$ of IMD among the whole population is estimated between 0.137–0.548 per day [24, 57]. As a matter of fact, it is statistically difficult to assign a transmission rate specific to age groups. We assume that the average values of transmission parameters ($\beta _{AA}, \beta _{AC}, \beta _{CC}$) remain in the interval [0.00005,0.05]. To estimate the natural death rate $\mu$, we use the World Bank data, according to which the average life expectancy at birth varies from 64 years in low-income countries to 81 years in high-income countries. Therefore, in the numerical simulations, we take the life expectancy for an upper-middle income country [58] as $\mu =\frac{1}{76} \frac{1}{\text {year}}$. For the recovery rate r, we use the value $26.06 \, \frac{1}{\text {year}}$, based on the fact that recovery from bacterial meningitis in infants and children takes approximately 14 days [59].

Table 1 Parameters of the model (1)

The Saudi government has established a Hajj visa quota of 1 pilgrim per 1000 people for each Muslim country since 1987 [61]. Let us assume a hypothetical upper-middle income country with a total population number of 1000. Only 1 person per year from this country would go to Hajj and come back home; therefore, we take $B_A=1$. For the remaining parameters, we use the available data set of a specific upper-middle income country (Turkey) in order to have more precise values. Thus, the number of yearly births is chosen to be 13.1 in a population of 1000 people and the initial population $S_{A }(0)=734$ and $S_{C}(0) =265$ according to the percentage of young people aged under 18 in Turkey [60].

To visualize the results of Sect. 4, we create three different scenarios for various choice of the transmission functions where we mainly focus on their average values. We study the short-and long-term behaviour of outbreaks by taking the average values of transmission functions ${\bar{\beta }}_{AA} (t)$, ${\bar{\beta }}_{CC}(t)$ and ${\bar{\beta }}_{AC}(t)$ equal and in the range [0.00005,0.05] for different types of transmission functions.

The choices of transmission functions represent the model in three possible scenarios, see Fig. 2. In scenario 1, we employ periodic transmission functions $\beta _{AA} (t)$, $\beta _{CC}(t)$, and $\beta _{AC}(t)$ with a sinusoidal shape (Fig. 2a) that may represent a yearly outbreak caused by the seasonal transmission after the annual Hajj pilgrimage. In scenario 2, we choose a discontinuous periodic transmission function in the form of $\beta (t) = 2 {\bar{\beta }} H( 1/2 - t + \lfloor t \rfloor )$, where H(t) is the Heaviside function with $H(0) = 1$ and $\lfloor t \rfloor$ is the floor function (Fig. 2b), that may correspond to the behaviour of an outbreak after an Umrah-like intermittent movement of people. In scenario 3, we consider more general non-periodic transmission functions (Fig. 2c) that may describe irregular mass movements such as migration.

Fig. 2

The three categories of transmission functions used in the simulations

In the following simulations, we manipulate the average values of ${\bar{\beta }}_{AA}$, ${\bar{\beta }}_{CC}$, and ${\bar{\beta }}_{AC}$ in the interval [0.00005,0.05] to get different signs of ${\bar{\lambda }}_3$ and ${\bar{\lambda }}_4$, which are markers of stability according to theorems 4.4–4.3. Table 2 summarizes the organization of the simulations.

Table 2 Summary of the presentation of simulation results

Fig. 3

${\bar{\beta }}_{AA}= {\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.005$ (${\bar{\lambda }}_3 = 0.3668$, ${\bar{\lambda }}_4 = -21.1066$)

Fig. 4

${\bar{\beta }}_{AA}=0.00005$, ${\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.005 \$ (${\bar{\lambda }}_3 = -0.0094$, ${\bar{\lambda }}_4 = -21.1066$)

Fig. 5

${\bar{\beta }}_{AA}=0.0005$, ${\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.05$ (${\bar{\lambda }}_3 = 0.0248$, ${\bar{\lambda }}_4 = 23.6954$)

Fig. 6

${\bar{\beta }}_{AA}= {\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.005$ (${\bar{\lambda }}_3 = 0.3668$, ${\bar{\lambda }}_4 = -21.1066$)

Fig. 7

${\bar{\beta }}_{AA}=0.00005$, ${\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.005$ (${\bar{\lambda }}_3 = -0.0094$, ${\bar{\lambda }}_4 = -21.1066$)

Fig. 8

${\bar{\beta }}_{AA}=0.0005$, ${\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.05$ (${\bar{\lambda }}_3 = 0.0248$, ${\bar{\lambda }}_4 = 23.6954$)

Fig. 9

${\bar{\beta }}_{AA}= {\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.005$ (${\bar{\lambda }}_3 = 0.3668$, ${\bar{\lambda }}_4 = -21.1066$)

Fig. 10

${\bar{\beta }}_{AA}=0.00005$, ${\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.005$ (${\bar{\lambda }}_3 = -0.0094$, ${\bar{\lambda }}_4 = -21.1066$)

Fig. 11

${\bar{\beta }}_{AA}=0.0005$, ${\bar{\beta }}_{CC}={\bar{\beta }}_{AC}=0.05$ (${\bar{\lambda }}_3 = 0.0248$, ${\bar{\lambda }}_4 = 23.6954$)

7 Conclusion

Bacterial meningitis shows various seasonal patterns outside of the African meningitis belt, which consists of a group of countries in sub-Saharan Africa where major epidemics occur every few years [62, 63]. Increased incidences in Europe, Middle East, Australia, and America are often associated with Hajj, Umrah, or other mass gatherings [64]. Indeed, over two million Muslims visit Mecca every year in the Hajj season where all pilgrims stay in close contact for a long time period [13]. Furthermore, the role of migrants and refugees in the spread of bacterial meningitis has been highlighted under current global conditions [65]. Based on the seriousness of the issue, the World Health Organization (WHO) has put forward a roadmap to defeat meningitis by 2030.

In this paper, we have presented and analysed a mathematical model (1) to understand the seasonal outbreaks of meningitis among adults and children by taking account the time-dependent transmission processes of IMD. Outbreaks are identified with deviations from the disease-free equilibrium state. Mathematical analysis of the model (1) shows that the long-time average values ${\bar{\lambda }}_3$ and ${\bar{\lambda }}_4$ of the time-dependent eigenvalues of the Jacobian matrix (4) determine the stability of the disease-free equilibrium. Thus, we are able to establish the average values ${\bar{\lambda }}_3$ and ${\bar{\lambda }}_4$ as “markers of stability.” Furthermore, stability is connected to a time-averaged basic reproduction number. In this study, the time-dependent transmission rates $\beta _{AA}(t)$, $\beta _{AC}(t)$ and $\beta _{CC}(t)$ are taken as non-negative bounded functions in the most general sense. Thus, an advantageous model setup is presented which can also address the case where the transmission rates are non-periodic. However, in real-life problems, it may not be possible to determine the functions $\beta _{AA}(t)$, $\beta _{AC}(t)$ and $\beta _{CC}(t)$ in some cases. Being aware of this limitation, we have extracted the parameter values used in the numerical simulations from real statistical data. Since the irregular migration process has a very complicated structure, and the data are not available, we have used some hypothetical functions to describe them. We hope that our results motivate more detailed research in this area to determine more realistic functional forms.

We have carried out numerical simulations to support our analysis via three different scenarios of time-varying transmission: periodic sinusoidal functions, periodic discontinuous step functions, and arbitrary non-periodic functions. Periodic sinusoidal functions represent a seasonal transmission of the disease once a year as in the Hajj season, periodic step function represents the transmission rate during Umrah mass movement, and non-periodic functions represent irregular migration. Our methodology can also be applied to similar epidemiological and social processes that involve adult/children age groups and time-dependent transmission between them.

Appendix A: The average of a function

Let $f:[0, \infty ) \rightarrow {\mathbb {R}}$ be integrable on [0, t] for all $t > 0$. The average of f is the number defined by $\displaystyle {\bar{f}}:= \lim _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} f(\tau ) \, d\tau$, whenever the limit exists as an extended real number. We provide some properties about the average of a function.

Lemma A.1

If $\int _{0}^{t} (f(\tau ) - \alpha ) \, d\tau$ is bounded for $t > 0$, then $\lim _{t \rightarrow \infty } \frac{1}{t} \int _{0}^{t} f(\tau ) \, d\tau = \alpha$.

Proof

Suppose $| \int _{0}^{t} f(\tau ) - \alpha \, d\tau | \le M$ for $t > 0$. Then $\left| \frac{1}{t} \int _{0}^{t} f(\tau ) \, d\tau - \alpha \right| \le M/t$ and letting $t \rightarrow \infty$ proves the result. $\square$

The converse of Lemma A.1 is not always true, that is, the existence of ${\bar{f}}$ does not imply the boundedness of $\int _{0}^{t} (f(\tau ) - {\bar{f}}) \, d\tau$. An example is provided by the function $\displaystyle f(x) = (x+2)/(x+1)$.

Lemma A.2

If $\lim _{t \rightarrow \infty } f(t) = \alpha$ and $\int _{0}^{t} f(\tau ) \, d\tau$ exists for $t > 0$, then ${\bar{f}} = \alpha$.

Proof

For a given $\epsilon > 0$, there is a $t_{0} > 0$ such that $|f(x) - \alpha | < {\epsilon }/{2}$ for $t \ge t_{0}$. Let $I_{\epsilon } = \int _{0}^{t_{0}} \left| f(\tau ) - \alpha \right| d\tau$ and $t_{1} = {2 I_{\epsilon }}/{\epsilon }$. Then for all $t > \max \{t_{0}, t_{1}\}$,

which completes the proof. $\square$

The converse of Lemma A.2 is not true, as the existence of ${\bar{f}}$ does not necessarily imply that f(t) has a limit as $t \rightarrow \infty$. (As an example, consider $f(t) = \sin t$.)

Lemma A.3

If ${\bar{f}} > 0$ (resp., $<0$), then $\int _{0}^{\infty } f(t) \, dt = \infty$ (resp., $-\infty$).

Proof

$\int _{0}^{\infty } f(t) \, dt = \lim _{t \rightarrow \infty } \int _{0}^{t} f(\tau ) \, d\tau$$= \lim _{t \rightarrow \infty } \ t \left( \frac{1}{t}\int _{0}^{t} f(\tau ) \, d\tau \right)$. $\square$

Here ${\bar{f}} = \pm \infty$ are also included, as the proof suggests.

Lemma A.4

If ${\bar{f}} > 0$, then $\int _{0}^{\infty } \exp \{\int _{0}^{t} f(\tau ) \, d\tau \} dt = \infty$. If ${\bar{f}} < 0$, then $\int _{0}^{\infty } \exp \{\int _{0}^{t} f(\tau ) \, d\tau \} dt$ exists as a positive real number.

Proof

Limit comparison with the integral of $\displaystyle \exp ({\bar{f}} t / 2)$ gives the result. $\square$

Here ${\bar{f}} = \pm \infty$ are also included, because in this case there exists $t_{0} > 0$ such that for $t \ge t_{0}$, $\int _{0}^{t} f(\tau ) \, d\tau > t$ or $\int _{0}^{t} f(\tau ) \, d\tau < -t$, and the result follows from comparison with $e^{t}$ or $e^{-t}$, respectively.

Lemma A.5

If there is a $T>0$ such that $f(t+T) = f(t)$ for $t \ge 0$ and $\frac{1}{T}\int _{0}^{T} f(t) \, dt = \alpha$, then the function defined by $g(t):= \int _{0}^{t} f(\tau ) \, d\tau - \alpha t$ is continuous, T-periodic, and hence bounded on $[0, \infty )$.

Proof

Since f is integrable, $\int _{0}^{t} f(\tau ) \, d\tau$ is continuous, and so is $\alpha t$. Thus, g is continuous and

$$\begin{aligned} g(t+T)&= \int _{0}^{t+T} f(\tau ) \, d\tau - \alpha (t+T)\\ {}&= \underbrace{\int _{0}^{t} f(\tau ) \, d\tau - \alpha t}_{g(t)} + \underbrace{\int _{t}^{t+T} f(\tau ) \, d\tau - \alpha T}_{0}\\ {}&= g(t) \end{aligned}$$

so g is T-periodic. Hence, g is bounded on $[0, \infty )$, being continuous on [0, T]. $\square$

Corollary A.6

If f is T-periodic and $\frac{1}{T}\int _{0}^{T} f(t) \, dt = \alpha$ then ${\bar{f}} = \alpha$.

Proof

$\int _{0}^{t} (f(\tau ) - \alpha ) \, d\tau$ is bounded by Lemma A.5 and the result follows by Lemma A.1. $\square$

In case f is a periodic function, we can be more precise when ${\bar{f}} = 0$ in Lemmas A.3 and A.4.

Lemma A.7

Let f be T-periodic and $\int _{0}^{T} f(t) \, dt = 0$. Then $\int _{0}^{\infty } f(t) \, dt$ does not exist unless f is the zero function. Furthermore, $\int _{0}^{\infty } \exp \left\{ \int _{0}^{t} f(\tau ) \, d\tau \right\} dt = \infty$.

Proof

$g(t):= \int _{0}^{t} f(\tau ) \, d\tau$ and $h(t):= \exp (g(t))$ are periodic by Lemma A.5 thus g(t) cannot have a limit as $t \rightarrow \infty$ unless it is constant. Also, $\int _{0}^{\infty } h(t) \, dt = \lim _{n \rightarrow \infty } n \int _{0}^{T} h(t) \, dt = \infty$ since $h(t) > 0$ and T-periodic. $\square$