1 Introduction

Energy transfer is part of many natural systems. Developing means to deal with undesirable vibrations in engineering systems is of primary importance. These vibrations are either completely unwanted or their energy must be transferred to another part of the system. Hence, there is a growing interest toward the study of energy cascades and targeted energy transfer (TET). Many studies demonstrate the superior dissipative property of nonlinear energy sinks (NES), that are essentially nonlinear dissipative attachments, over linear tuned mass dampers [1,2,3,4] (although there are exceptions, see, for example, [5]). Vakakis et al. [6] discuss energy transfer through the example of simple mechanical oscillators. They argue that strong, essential nonlinearities must be present in the system to realize efficient irreversible transfer of energy toward the dissipative elements of the system. Systems having multiple NESs attached are even capable of exhibiting chaotic dynamics. In recent works of Chen et al. [7, 8], a chain of NESs were attached to a primary linear oscillator and the system was subjected to the harmonic forcing of the linear oscillator. They showed that for sufficiently high excitation amplitude the response of the system can be chaotic for specific frequency bands that depend on the excitation amplitude.

Recently, some special types of NESs were also investigated. Al-Shudeifat et al. [9] studied a bistable NES with two nontrivial stable and a trivial unstable equilibria, attached to a primary linear oscillator. They constructed the frequency energy plot of the system and analyzed the behavior of the system with the help of wavelet transforms to depict the dynamics and identify the underlying mechanism of the occurring TET. The advantage of such a bistable NES is that it can significantly reduce the excitation amplitude threshold that is required to activate the NES [10, 11]. In another work, Zhang et al. [12] studied 1-DoF and 2-DoF NESs that incorporated nonlinear dampings besides the nonlinear springs. They found that the 1-DoF variant had a failure frequency where the NES vibration reduction becomes ineffective, while the 2-DoF variant had none and was found to perform better anyways. An interesting mechanical engineering application is the work of Yang et al. [13], who proposed a fluid-conveying pipe with an enhanced NES to achieve adaptive vibration suppression. A recent review on NES is provided by Ding et al. [14], while an overview on the state of the art of nonlinear TET is given by Vakakis et al. [15].

The frequency energy plot (FEP) [16, 17] and wavelet transforms [18, 19] of the vibration are often computed to analyze the driving mechanism of the energy transfer in such vibrational systems. The FEP essentially shows the nonlinear normal modes (NNM) of the system as the function of their energy content for the conservative (no damping) case. Although the FEP corresponds to the undamped case, it qualitatively shows how the weakly damped system will behave. The wavelet transform shows the frequency of the vibration as function of the energy content of the system. It is extracted from the displacement and energy time history of the vibration and can be superimposed onto the FEP to highlight which NNMs are excited.

Turbulent fluid flow [20] is a natural process that is strongly nonlinear in nature and dissipates kinetic energy rapidly through an energy cascade, a primarily one-way energy transfer from large to small scales. In turbulent flow, large unstable vortices form that eventually break up into smaller vortices. Thus, the kinetic energy of the flow is transferred to smaller and smaller scales. This energy is dissipated at the smallest scales due to viscous friction [21]. The above description of turbulent flows is called Richardson’s eddy hypothesis [22, 23]. The turbulent energy cascade was extensively studied in the literature [24,25,26,27]. Kolmogorov [28] was the first who described the energy spectrum of homogeneous isotropic turbulence that shows the energy content of the fluid flow as the function of the eddy scales.

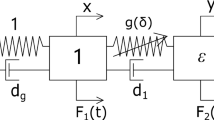
Inspired by the eddy hypothesis of turbulent flows, we proposed a mechanistic model whose structure resembles the hierarchical connection among the vortices of turbulent flow [29]. The model is a binary tree of masses connected by springs and dampers (Fig. 1). The idea to propose and investigate a mechanistic model based on the vortex breakdown in turbulent flows has motivated research in this field previously [30].

In previous works [29, 31, 32], we studied a purely linear version of this mechanistic model. The discrete energy spectrum of the model was defined as the fraction of the total energy stored in the different mass scales. Similarly, the discrete energy flux function of the system was defined as the set of energy fluxes between levels scaled by the dissipation rate.

In this study, we add essential nonlinearity to the mechanistic model by adding cubic stiffnesses to the bottom level of the tree. We analyze the response of the system for different types of excitations. Our goal is to examine the energy cascade developing in the mechanistic model to identify the driving mechanism of the occurring irreversible energy transfer. Thus, this study provides some insight to energy transfer processes of systems involving multiple scales. We believe that this will stimulate further research and provide a new aspect to study phenomena involving energy cascade such as turbulent flows.

This paper is structured as follows. In Sect. 2, we introduce the nonlinear mechanistic model and recall how the energy spectrum and the energy flux function of the model are defined. In Sect. 3, we explain the choice of parameters, introduce the simplified FEP of the mechanistic model as a means of analyzing the response of multi-degree-of-freedom systems for impulsive excitations, and show the response of the mechanistic model for different impulsive excitations and identify the main energy transfer mechanism for each case. We also investigate the response of the system for continuous harmonic excitation and identify the nonlinear bands in which the NES blocks are active. In Sect. 4, conclusions are drawn.

2 The nonlinear mechanistic model

2.1 Model description

The subject of this study is an n-level binary tree of blocks connected by linear and nonlinear springs and dampers shown in Fig. 1. In this model, the blocks are connected with linear springs across all levels, except the last two levels where the connection is provided by dampers and cubic nonlinear springs.

Fig. 1
figure 1

Nonlinear mechanistic model with \(n=3\) levels

Full size image

The mechanistic model has n levels; level \(l\in \left\{ 1,\ldots ,n\right\} \) consists of \(2^{l-1}\) blocks; the total number of blocks is \(N=2^{n}-1\). The leftmost (top) block (mass \(m_{1}\)) is connected to a fixed wall via a spring having a stiffness of \(k_{1}\). Every block has an index i; each has a parent (except the top block \(m_{1}\)) and two children (except the blocks in the rightmost or in other words bottom level) whose indices are \({\mathcal {P}} (i)=\lfloor i/2\rfloor ,\ {\mathcal {L}}(i)=2i,\ {\mathcal {R}}(i)=2i+1\), respectively (\(i=1,\ldots ,N\)). Here \(\lfloor .\rfloor \) denotes the floor operation, e.g., \({\mathcal {P}}(1)=\lfloor 1/2\rfloor =0\).

The equation of motion together with the initial conditions can be written in a general form as

$$\begin{aligned} \begin{aligned} m_{i}{\ddot{x}}_{i}&=k_{i} (x_{{\mathcal {P}}(i)}-x_{i})^{\gamma _{i} }+k_{{\mathcal {L}}(i)}(x_{{\mathcal {L}}(i)}-x_{i})^{\gamma _{{\mathcal {L}}(i)}}\\&\quad +k_{{\mathcal {R}}(i)}(x_{{\mathcal {R}}(i)}-x_{i})^{\gamma _{{\mathcal {R}}(i)}}\\&\quad +c_{i}({\dot{x}}_{{\mathcal {P}}(i)}-{\dot{x}} _{i})+c_{{\mathcal {L}}(i)}({\dot{x}}_{{\mathcal {L}}(i)}-{\dot{x}}_{i})\\&\quad +c_{{\mathcal {R}} (i)}({\dot{x}}_{{\mathcal {R}}(i)}-{\dot{x}}_{i}),\\ x_{i}(0)&=x_{i,0},\ {\dot{x}}_{i}(0)=v_{i,0},\quad i=1,\ldots ,N, \end{aligned} \end{aligned}$$
(1)

with \(x_{0}(t)=0\) (the wall is motionless).

Since the bottom level is the “loose end” of the tree, \(k_{i}=0\) for \(i>N\). The dampers are only incorporated between the last two levels, so \(c_{i}\) is only nonzero for \(i=2^{n-1},\ldots ,N\). Likewise, the exponents \(\gamma _{i}=3\) for \(i=2^{n-1},\ldots ,N\), because only the springs that connect the last two levels are nonlinear (cubic). Otherwise, \(\gamma _{i}=1\) for the linear springs connecting the rest of the blocks. To summarize, the following conditions apply for the parameters \(k_{i},c_{i},\gamma _{i}\):

$$\begin{aligned} \begin{aligned}&k_{i}=0,\quad i>N,\\&c_{i}=0,\quad 1\le i<2^{n-1},\\&\gamma _{i}=1,\quad 1\le i<2^{n-1},\\&\gamma _{i}=3,\quad i\ge 2^{n-1}. \end{aligned} \end{aligned}$$
(2)

For a typical block in the lth level of the tree for \(l\in \left\{ 2,n-2\right\} \), the terms corresponding to the dampers vanish and the exponents \(\gamma _{i}\) are ones, i.e.,

$$\begin{aligned} \begin{aligned}&m_{i}{\ddot{x}}_{i}=k_{i}(x_{{\mathcal {P}}(i)}-x_{i})+ k_{{\mathcal {L}} (i)}(x_{{\mathcal {L}}(i)}-x_{i})\\&\quad +k_{{\mathcal {R}}(i)}(x_{{\mathcal {R}}(i)}-x_{i}),\\&x_{i}(0)=x_{i,0},\ {\dot{x}}_{i}(0)=v_{i,0},\quad i=2,\ldots ,2^{n-2}-1. \end{aligned} \end{aligned}$$
(3)

For the blocks in the \(n-1\)th level, we have

$$\begin{aligned} \begin{aligned}&m_{i}{\ddot{x}}_{i}=k_{i}(x_{{\mathcal {P}}(i)}-x_{i})+k_{{\mathcal {L}} (i)}(x_{{\mathcal {L}}(i)}-x_{i})^{3}\\&\quad +k_{{\mathcal {R}}(i)}(x_{{\mathcal {R}}(i)} {-}x_{i})^{3}{+}c_{{\mathcal {L}}(i)}({\dot{x}}_{{\mathcal {L}} (i)}{-}{\dot{x}}_{i}) \\&\quad {+}c_{{\mathcal {R}}(i)}({\dot{x}}_{{\mathcal {R}}(i)} {-}{\dot{x}}_{i}),\\&\quad x_{i}(0)\!=\!x_{i,0},\ {\dot{x}}_{i}(0)\!=\!v_{i,0}, i\!=\!2^{n-2},\ldots ,2^{n-1}-1, \end{aligned} \end{aligned}$$
(4)

since these blocks are connected to the nth last level with nonlinear springs and dampers.

The blocks in the last (nth) level do not have any children blocks; for these blocks we have

$$\begin{aligned} \begin{aligned}&m_{i}{\ddot{x}}_{i}=k_{i}(x_{{\mathcal {P}}(i)}-x_{i})^{3}+c_{i}(\dot{x}_{{\mathcal {P}}(i)}-{\dot{x}}_{i}),\\&\quad x_{i}(0)=x_{i,0}, {\dot{x}} _{i}(0)=v_{i,0}, i=2^{n-1},\ldots ,N. \end{aligned} \end{aligned}$$
(5)

The equations of motion (1) of the binary tree can be formulated in matrix form as

$$\begin{aligned}{} & {} {\mathcal {M}}\ddot{{\textbf{x}}}(t)+{\mathcal {C}}\dot{{\textbf{x}}}(t)+{\mathcal {K}} {\textbf{x}}(t)+{\textbf{N}}({\textbf{x}}(t))=0,\nonumber \\{} & {} \quad {\textbf{x}}(0)={\textbf{x}} _{0},\quad \dot{{\textbf{x}}}(0)={\textbf{v}}_{0}, \end{aligned}$$
(6)

where \({\textbf{x}}(t)\) is the vector of displacements; \({\mathcal {M}}\), \({\mathcal {C}}\), \({\mathcal {K}}\) are the mass, damping, and stiffness matrices, respectively. The nonlinear terms are collected in the vector \({\textbf{N}} ({\textbf{x}}(t))\). Without formally performing the nondimensionalization of Eq. (6), we will treat this equation as nondimensional and fix the values \(m_{1}=k_{1}=1\).

2.2 Temporal energy spectrum and energy flux function

We recall the definitions for the temporal energy spectrum and energy flux function of the mechanistic model that are discussed in detail in [29].

We set every mass, stiffness, and damping coefficient equal within a level l. Let \(M_{l}\) denote the constant “mass scale” representing the mass of each block in level \(l\in \{1,\ldots ,n\}\). Similarly, \(K_{l}\) and \(C_{l}\) refer to the springs and dampers connecting the blocks of the \(l-1\)th and lth levels, e.g., for the second level the mass scale is \(M_{2}=m_{2}=m_{3}\), and \(K_{2}=k_{2}=k_{3}\). The total mechanical energy E(t) of the system is

$$\begin{aligned} E(t)= & {} \frac{1}{2}\dot{{\textbf{x}}}^{T}(t){\mathcal {M}}\dot{{\textbf{x}}}(t)+\frac{1}{2}{\textbf{x}}^{T}(t){\mathcal {K}}{\textbf{x}}(t)\nonumber \\{} & {} +\int ||{\textbf{N}} ({\textbf{x}}(t))||_{1}\textrm{d}x, \end{aligned}$$
(7)

where \(||.||_{1}=\sum _{i=1}^{N}|.|\) denotes the 1-norm of \({\textbf{N}} ({\textbf{x}}(t))\). The total energy is the sum of level energies, i.e.,

$$\begin{aligned} E(t)=\sum _{l=1}^{n}E_{l}(t), \end{aligned}$$
(8)

where \(E_{l}(t)\) is defined so that the potential energy of the springs connecting two masses is distributed equally between the two levels and the potential energy of the top spring is added to \(E_{1}(t)\):

$$\begin{aligned} \begin{aligned}&E_{l}(t)=\frac{1}{2}M_{l}\sum \limits _{i\in I(l)}{\dot{x}}_{i}^{2}\\&\quad +\frac{(1+\delta _{l,1})K_{l}}{4+4\delta _{l,n}}\sum \limits _{i\in I(l)} {(x_{i}-x_{{\mathcal {P}}(i)})^{2+2\delta _{l,n}}}\\&\quad +\frac{K_{l+1}}{4+4\delta _{l,n-1}} \sum \limits _{i\in I(l+1)}{(x_{i}-x_{{\mathcal {P}}(i)})^{2+2\delta _{l,n-1}} },\\&l=1,\ldots ,n. \end{aligned} \end{aligned}$$
(9)

Here \(I(l)=\{2^{l-1},\ldots ,2^{l}-1\}\) are the indices on level l and \(\delta \) is the Kronecker delta (\(\delta _{i,j}=1\) for \(i=j\), 0 otherwise). Due to the “loose end” of the tree, \(K_{n+1}=0\).

We define the mean energy \({\bar{E}}\) for a time window \([\tau ,\tau +{\varDelta }\tau ]\) as

$$\begin{aligned} {\bar{E}}=\frac{1}{{\varDelta }\tau }\int _{\tau }^{\tau +{\varDelta }\tau }E(t)\textrm{d}t, \end{aligned}$$
(10)

and we similarly define the mean level energy \({\bar{E}}_{l}\) for \(l=1,\ldots ,n\). The mean energy is the sum of the mean level energies, i.e., \({\bar{E}}=\sum _{l=1}^{n}{\bar{E}}_{l}\).

The energy fraction stored in level l (and hence corresponding to the scale \(M_{l}\)) is defined as

$$\begin{aligned} {\hat{E}}_{l}={\bar{E}}_{l}/{\bar{E}},\quad l=1,\ldots ,n. \end{aligned}$$
(11)

The \({\hat{E}}_{l}\) values constitute the discrete temporal energy spectrum \({\hat{E}}\) of the mechanistic model.

We define the dissipation rate of the system as

$$\begin{aligned} \epsilon (t)=-{\dot{E}}(t). \end{aligned}$$
(12)

Similar to the energy spectrum, a set of fluxes can be calculated. The energy flux \({\varPi }_{l}(t)\) of level l is defined as the rate of energy transfer between levels l and \(l+1\), i.e.,

$$\begin{aligned}{} & {} {\varPi }_{l}(t)={\varPi }_{l-1}(t)-{\dot{E}}_{l}(t),\nonumber \\{} & {} {\varPi }_{n}(t)=-{\dot{E}}_{n}\left( t\right) ,\quad l=1,\ldots ,n-1. \end{aligned}$$
(13)

Here \({\varPi }_{0}(t)=0\), since no energy is passed from the top block toward the motionless wall. For \(l<n\), we have \({\varPi }_{l}(t)>0\) when energy is transferred from level l to level \(l+1\). It can be shown that the recursive formula (13) leads to \({\varPi }_{l}(t)=-\sum _{l=1}^{l} {\dot{E}}_{l}(t)\) for \(l\!\in \!\{1,...,n\!-\!1\}\). Since there is no level below the nth level, the flux of this level is simply \({\varPi }_{n}\left( t\right) =-{\dot{E}}_{n}\left( t\right) \). This means that for \({\varPi }_{n}>0\) the last level “loses” energy, it is either dissipated or passed back to the \(n-1\)th level. When \({\varPi }_{n}<0\), the energy content of the last level increases.

Similar to the mean energy, the mean dissipation rate of the system is also defined for a time window \([\tau ,\tau +{\varDelta }\tau ]\):

$$\begin{aligned} {\bar{\epsilon }}=-\frac{1}{{\varDelta }\tau }\int _{\tau }^{\tau +{\varDelta }\tau }{\dot{E}}(t)\textrm{d}t. \end{aligned}$$
(14)

The mean fluxes \({\bar{{\varPi }}}_{l}\) are defined similarly for \(l=1,\ldots ,n-1\).

Analogously to the scaling of the mean level energies with \({\bar{E}}\), we scale the mean level fluxes with \({\bar{\epsilon }}\) to yield the scaled energy flux for level l, i.e.

$$\begin{aligned} {\hat{{\varPi }}}_{l}={\bar{{\varPi }}}_{l}/{\bar{\epsilon }},\quad l=1,..,n. \end{aligned}$$
(15)

The \({\hat{{\varPi }}}_{l}\) values constitute the discrete temporal energy flux function \({\hat{{\varPi }}}\) of the mechanistic model.

3 Results

3.1 Model parameters

Let \(M_{l}\) denote the constant “mass scale” representing the mass of each block in level \(l\in \{1,\ldots ,n\}\). Similarly, \(K_{l}\) and \(C_{l}\) refer to the springs and dampers connecting the blocks of the \(l-1\)th and lth levels.

We define two systems having slightly different set of parameters: a baseline system and a modified system. For both systems, the masses of the blocks are gradually decreased according to a power law as

$$\begin{aligned} M_{l}=(1/2)^{l-1},\quad l=1,\ldots ,n-1, \end{aligned}$$
(16)

For the baseline system, this power law decrease holds for the last level as well

$$\begin{aligned} M_{n}=(1/2)^{n-1}, \end{aligned}$$
(17)

whereas in the modified system the masses of the blocks in the bottom level are further reduced as

$$\begin{aligned} M_{n}=\frac{1}{4}(1/2)^{n-1}. \end{aligned}$$
(18)

Thus, the bottom level will comprise efficient NESs with lightweight masses compared to the large linear part of the system. The stiffnesses \(K_{l}\) are scaled by the same power law distribution for both cases:

$$\begin{aligned} K_{l}=(1/2)^{l-1},\quad l=1,\ldots ,n. \end{aligned}$$
(19)

In [29], other power law stiffness distributions were used as well and the dependence of the behavior of the system on this type of stiffness distribution was extensively analyzed.

By design only \(C_{n}=c\) is nonzero and the small value of \(c=0.001\) is chosen to enhance the effect of the NES. This means that each damper has \(c=0.001\) and that dampers are only incorporated between the \(n-1\)th and nth level blocks, connected parallel with the nonlinear springs as Fig. 1 suggests. The systems discussed in this paper have \(n=6\) levels.

3.2 The simplified frequency energy plot of the mechanistic model

The frequency energy plot depicts the vibration frequency \(\omega \) of the undamped system as the function of the energy content for different nonlinear normal modes. The harmonic balance method [33] is suitable to construct the FEP of the system described by Eq. (1). However, this task becomes cumbersome as the number of degrees of freedom of the system increases. In our case, an extra level added to the system roughly doubles the number of blocks! Hence, instead of computing the FEP of the binary tree-structured mechanistic model, we compute the FEP of a reduced chain oscillator variant of the model that is described in [29]. This chain oscillator is obtained by simply replacing a level of blocks/springs/dampers with a single block/spring/damper whose mass/stiffness/damping coefficient is the sum of those of the replaced elements. The FEP of this reduced chain oscillator is shown in Fig. 2 for the modified version of the system and it is called the simplified FEP of the mechanistic model.

Fig. 2
figure 2

Simplified frequency energy plot of the mechanistic model for the modified system

Full size image

Such a nonlinear system can have several nonlinear normal modes. These can be distinguished based on the oscillation frequency of the individual blocks and their phases relative to each other. In Fig. 2, only the backbone curves are depicted that correspond to the NNMs in which all blocks oscillate with the same frequency. We also note that only those NNMs of the mechanistic model can be computed using the reduced chain oscillator model in which every block in the same level oscillates in-phase. The thin pairs of horizontal lines in Fig. 2 correspond to the “pairs” of eigenfrequencies of the underlying linear systems. One of these underlying linear systems is constructed by removing the nonlinear springs; the higher eigenfrequency of the pair comes from this one. The other one is constructed by replacing the nonlinear springs with rigid rods that yields the lower eigenfrequency of the pair.

Even though this simplified FEP corresponds to the reduced chain oscillator, the computed backbone branches agree well with those of the binary tree-structured system. For the two model versions (baseline and modified) discussed in this paper, we also computed the full FEP corresponding to the binary tree-structured mechanistic model. The full FEPs and the simplified FEPs of the baseline and the modified systems are compared in Fig. 3. The good agreement between the full and simplified FEPs shows that even the latter gives us insight into the complex dynamics of the binary tree-structured mechanistic model.

Fig. 3
figure 3

Full and simplified frequency energy plots of the mechanistic model for a the baseline system and b the modified system

Full size image

3.3 Impulsive excitation

First, both the baseline system and the modified system were investigated for impulsive excitations applied to the top levels. We chose to excite the first two levels as these represent the largest scales, and we can prescribe a variety of different excitation combinations. The nonzero initial conditions were

$$\begin{aligned} {\dot{x}}_{1}(0)={\dot{x}}_{2}(0)={\dot{x}}_{3}(0)=1; \end{aligned}$$
(20)

thus, the initial energy is expressed using the mass scales \(M_{1}\) and \(M_{2}\) as

$$\begin{aligned} E(0)= & {} \frac{1}{2}M_{1}{\dot{x}}_{1}^{2}(0)+\frac{1}{2}M_{2}({\dot{x}}_{2} ^{2}(0)+{\dot{x}}_{3}^{2}(0))\nonumber \\ {}= & {} \frac{1}{2}M_{1}+M_{2}=1. \end{aligned}$$
(21)

We will see that this amount of initial energy is enough to trigger the efficient irreversible energy transfer mechanisms provided by the energy sinks.

Figure 4 shows the total energy decay over time t for both cases. For comparison, the purely linear version of the baseline system is also included with dampers having the same weak damping \(c=0.001\) as well as with dampers having the optimal damping \(c=0.125\) given by the spectral abscissa criterion [34]. The optimal damping case shows the highest dissipation rate that can be achieved with the linear model. It is evident from the figures that the dissipation of the nonlinear energy sinks is superior compared to that of the linear springs and dampers in case of weak dampings. The total energy decay suggests strongly nonlinear behavior, especially in case of the modified system.

Fig. 4
figure 4

Total energy of different mechanistic models as the function of time for initial conditions \({\dot{x}}_{1}(0)={\dot{x}}_{2}(0)={\dot{x}}_{3}(0)=1\)

Full size image
Fig. 5
figure 5

Energy percentage stored in the bottom level of the a baseline and b modified mechanistic models for initial conditions \({\dot{x}}_{1}(0)={\dot{x}}_{2}(0)={\dot{x}}_{3}(0)=1\). The long and small dashings mark the end of nonlinear beats and the escape from TRC, respectively

Full size image
Fig. 6
figure 6

Wavelet transform of the vibration superimposed onto the FEP of the a baseline and b modified mechanistic models for initial conditions \({\dot{x}}_{1}(0)={\dot{x}}_{2}(0)={\dot{x}}_{3} (0)=1\).

Full size image

In Figs. 5 and 6, we show the energy percentage stored in the bottom level as function of the time as well as the wavelet plot of the system superimposed onto the simplified FEP. We see two fundamentally different behavior in the two cases. In the baseline case, initially a very efficient irreversible transfer of energy is realized through nonlinear beats that is sustained until \(t\approx 180\). After that point, the in-phase NNM—that is characterized by every block oscillating in-phase—dominates the vibration and a less efficient in-phase targeted energy transfer is realized through 1:1 transient resonance capture (TRC) of the blocks in the last two levels. The system escapes from TRC around \(t\approx 180\). In the modified system, the initial nonlinear beats are weaker, but the in-phase targeted energy transfer kicks in around \(t\approx 200\) and it is much more efficient for this system. The rapid dissipation of energy via the in-phase TET is sustained until \(t\approx 1500\). The referred time instances are determined based on the qualitative changes that are visible in the \(E_{6}(t)/E(t)\) graphs as well as in the x(t) displacement time histories. One can also see the changes in the slope of E(t) in Fig. 4 around these time instances, e.g., the escape of the modified system from TRC around \(t\approx 1500\) is particularly spectacular in this figure.

In Fig. 7, the displacements \(x_{16}\) and \(x_{32}\) of two directly connected blocks located in the 5th and 6th levels are shown. Based on the numbering shown in Fig. 1, the 16th and 32nd blocks are located at the “edge of the tree” similar to the 1st, 2nd, 4th, and 8th blocks. In the first part of the motion, the highly modulated displacement signals indicate that indeed nonlinear beats are the mechanism of the irreversible energy transfer toward the NESs. However, a difference can be noticed between the baseline and the modified cases when TET triggers. In the baseline case, the vibration of the larger block is somewhat modulated, meaning that a subharmonic NNM tongue is also excited here, not just the main branch. This is why the system escapes the 1:1 TRC much sooner, whereas in the modified case a clear 1:1 transient resonance capture is realized that induces strong in-phase TET on the in-phase NNM backbone branch.

Fig. 7
figure 7

Displacement of two connected blocks in the last two levels of the a baseline and b modified mechanistic models for initial conditions \({\dot{x}}_{1}(0)={\dot{x}}_{2}(0)={\dot{x}}_{3}(0)=1\). The long dashing marks the end of nonlinear beats

Full size image
Fig. 8
figure 8

Energy spectra of the a baseline and b modified mechanistic models for initial conditions \({\dot{x}}_{1}(0)={\dot{x}} _{2}(0)={\dot{x}}_{3}(0)=1\)

Full size image
Fig. 9
figure 9

Flux functions of the a baseline and b modified mechanistic models for initial conditions \({\dot{x}}_{1}(0)=\dot{x}_{2}(0)={\dot{x}}_{3}(0)=1\)

Full size image

In Figs. 8 and 9, the energy spectra and flux functions are depicted for three different stages of the vibration. The time window of the first stage roughly corresponds to the initial nonlinear beats, while the in-phase TET occurs in the second stage. In the third stage, the baseline system already escaped the 1:1 TRC, while in the modified case we are still experiencing in-phase TET.

Fig. 10
figure 10

Total energy of different mechanistic models as the function of time for initial conditions \({\dot{x}}_{1}(0)={\dot{x}}_{3}(0)=1,{\dot{x}}_{2}(0)=-1\)

Full size image

One can notice that the spectrum is very stable for the modified system, indicating that the in-phase NNM already becomes dominant in the first stage. For the baseline system, we see fundamentally different energy spectra in the three stages. Again, the evidence of the escape from the 1:1 TRC can be seen in this figure, since the energy spectrum of the third time window is very similar to those observed by linear systems in previous research [29]. This implies that in the third stage no more dissipation is induced by the nonlinearity. In Fig. 9, we can also see that in this third stage the scaled flux \({\bar{{\varPi }}}_{6}/{\bar{\varepsilon }}\) is highly negative for the baseline system. This means that a large portion of the energy is not dissipated, but rather passed toward the energy storing elements of the sixth level.

The richness of the dynamics of this binary tree-structured oscillator can be demonstrated by another simple example. Let us change the sign of the initial condition \({\dot{x}}_{2}(0)\), i.e., let \({\dot{x}}_{2}(0)=-1\). Figure 10 shows the total energy decay over time t for both the baseline and the modified cases. For comparison, the purely linear version of the baseline system is again included with dampers having the same damping \(c=0.001\) as well as with dampers having the optimal damping \(c=0.125\). The modified case is again much more efficient; hence, we only analyze the modified version of the system from hereon.

In Fig. 11, we show the energy percentage stored in the bottom level as function of the time as well as the wavelet plot of the modified system superimposed onto the simplified FEP. The wavelet transform shows the excitation of multiple NNMs with a very interesting “swiss cheese-like” pattern that is caused by the initial nonlinear beats that last until \(t\approx 120\).

Fig. 11
figure 11

a Energy percentage stored in the bottom level. The long and small dashings mark the end of nonlinear beats and the escape from TRC, respectively. b Wavelet transform of the vibration superimposed onto the FEP of the modified mechanistic model with initial conditions \(\dot{x}_{1}(0)=\dot{x}_{3}(0)=1,\,\dot{x}_{2}(0)=-1\)

Full size image
Fig. 12
figure 12

a Displacement of two connected blocks in the last two levels of the modified mechanistic model. The long dashing marks the end of nonlinear beats. b The energy spectral density of \(x_{32}(t)\) with initial conditions. The long dashing marks the end of the initial nonlinear beats. \({\dot{x}}_{1}(0)={\dot{x}}_{3}(0)=1,\,\dot{x}_{2}(0)=-1\)

Full size image
Fig. 13
figure 13

a Energy spectrum and b flux function of the modified mechanistic model for initial conditions \(\dot{x}_{1}(0)=\dot{x}_{3}(0)=1,\, \dot{x}_{2}(0)=-1\)

Full size image

Even though in Fig. 11a the energy stored in the NESs over time looks similar to what is observed in Fig. 5a, we do not have TET on the in-phase NNM with 1:1 TRC this time. In fact, the nonlinear beats persist, as Fig. 12a shows modulated displacement signals for the investigated two connected blocks in the last two levels. Inspecting the energy spectral density of \(x_{32}(t)\) shown in Fig. 12b reveals that besides the frequency corresponding to the in-phase NNM, there is another close, but slightly higher frequency peak with similar magnitude (the dashed vertical lines mark the eigenfrequencies of the underlying linear systems). The superposition of the corresponding modes causes the typical beating pattern on the displacement plot. The NNM corresponding to the higher frequency vibration component is not included in the FEP, since this one is exclusive to the binary tree structure and is not present in the reduced chain oscillator version of the model.

In Fig. 13, the energy spectrum and the scaled fluxes of the system are depicted for the modified initial conditions. The energy spectra are different for the three different stages of the vibration. The first stage is the initial nonlinear beats, the second is the beating of two NNMs, and the third stage is the steadily decaying phase where the nonlinearity is no longer significant.

Fig. 14
figure 14

Mean energies of the modified mechanistic model with harmonic forcing \(A\text {cos}({\varOmega } t)\), \({\varOmega } \in [0.2,0.35]\) applied to the top block, a \(A=0.001\), b \(A=0.01\)

Full size image
Fig. 15
figure 15

Displacement \(x_{1}\) and \(x_{32}\) of the modified mechanistic model with harmonic forcing \(A\text {cos}({\varOmega } t)\), \(A=0.01\) applied to the top block, a \({\varOmega }=0.25\), b \({\varOmega }=0.29\)

Full size image

3.4 Continuous excitation

In this case, every initial condition is set to zero and a harmonic forcing of the form Acos\(({\varOmega } t)\) is applied to the top (leftmost) block. The response of the modified system is investigated for different amplitudes A and excitation frequencies \({\varOmega }\). In each case, the investigated excitation frequency range contains a “forbidden zone” that is between a pair of eigenfrequencies of the underlying linear systems that are marked by the horizontal lines in Fig. 2. We call them forbidden zones, because no NNM crosses these in the FEP.

In Fig. 14, we show the mean energies \({\bar{E}},{\bar{E}}_{5},{\bar{E}}_{6}\) for \(A=0.001\) and \(A=0.01\), \({\varOmega }\in [0.2,0.35]\). Figure 14a shows that the forcing having the lower excitation amplitude \(A=0.001\) does not trigger the nonlinear dynamics provided by the NESs; the response is similar to that of a linear system. However, in the response depicted in Fig. 14b for the higher excitation amplitude \(A=0.01\) we see a much more interesting frequency response. This excitation amplitude is already high enough to sustain efficient energy transfer toward the NESs for a narrow frequency band that includes the forbidden zone. This “nonlinear band” is approximately \({\varOmega }\in [0.26,0.31]\) while the forbidden zone is the vibrational frequency range \(\omega \in [0.27,0.285]\). A similar behavior was observed by Chen et al. [7] where this was attributed to a chaotic synchronization among the blocks of the system.

In Fig. 15, we depicted the displacements of the top block and a NES block in the bottom level to show the difference between the responses inside and outside of the nonlinear band for the higher excitation amplitude \(A=0.01\). For \({\varOmega }=0.25\), there is no sign of nonlinear behavior, whereas for \({\varOmega }=0.29\) we see the evidence of efficient irreversible energy transfer. The vibration amplitude of the NES block is far higher than that of the forced top block. We also note that the displacement \(x_{32}(t)\) of the observed NES block is strongly modulated and the peak magnitudes are irregular relative to each other.

Investigating the associated energy spectra depicted in Fig. 16 for the four cases \(A\in \left\{ 0.001,0.01\right\} \) and \({\varOmega }\in \left\{ 0.25,0.29\right\} \) shows that in three of the four cases the energy spectra are very similar. We have a decreasing energy spectrum when the excitation amplitude is low or when the excitation frequency is outside of the nonlinear band, since there is no efficient nonlinear energy transfer in these cases. For the high amplitude case in the nonlinear band (\(A=0.01\) and \({\varOmega }=0.29\)), the energy spectrum is fundamentally different. The energy fraction concentrated in the NESs is much higher compared to the other cases.

Fig. 16
figure 16

Energy spectra of the modified mechanistic model with harmonic forcing \(A\text {cos}({\varOmega } t)\) applied to the top block

Full size image
Fig. 17
figure 17

a Mean energies for \(A = 0.5, \varOmega \in [0.7, 1]\) and b energy spectra of the modified mechanistic model with harmonic forcing \(A\text {cos} ({\varOmega } t)\), applied to the top block

Full size image
Fig. 18
figure 18

Displacement \(x_{1}\) and \(x_{32}\) of the modified mechanistic model with harmonic forcing \(A\text {cos}({\varOmega } t)\), \(A=0.05\), \({\varOmega }=0.85\) applied to the top block

Full size image

For the next forbidden zone between \(\omega \in [0.8,0.83]\), a similar behavior is observed; the frequency response is shown in Fig. 17a. The lower and upper thresholds of the nonlinear band are much clearer in this case; the nonlinear band is approximately \({\varOmega }\in [0.78,0.89]\) for the investigated excitation amplitude \(A=0.05\). The trends of the energy spectra depicted in Fig. 17b also show similarities with the previously investigated frequency band. The energy fraction stored in the NESs is only significant when the excitation frequency \({\varOmega }\) is within the nonlinear band and the excitation amplitude A is sufficiently high (\(A=0.05\) and \({\varOmega }=0.89\)). In the other three cases, significant energy transfer toward the NESs is not realized; hence, the energy fraction stored in the NESs is much lower and the shapes of the energy spectra share similarities.

The displacement solutions shown in Fig. 18 are strongly modulated indicating the realization of nonlinear energy transfer by means of nonlinear beats.

4 Conclusions

The motivation of this paper stems from the study of processes involving different scales and exhibiting an energy cascade, a primarily one-way energy transfer from the larger scales to the smaller ones. A notable example of such a process is turbulent flow where the kinetic energy of the flow is passed from larger vortices to smaller ones and dissipation only prevails at the smallest scale. The structure of the mechanistic model studied here resembles the hierarchical relation among the vortices of different scales and also features nonlinear energy sinks as dissipative elements by the smallest scales.

The response of a binary tree-structured multi-DoF mechanical oscillator with light damping was investigated for impulsive and continuous excitations. The analysis covered two model variants: in the baseline model the mass of the NES blocks obeyed Eq. (16), while in the modified model the mass of these blocks were decreased by 75\(\%\). A methodology involving the simplified FEP of the underlying reduced chain oscillator was presented to analyze the dynamic response for the impulsive excitations. It was shown that decreasing the mass of the NES blocks leads to a fundamentally different energy transfer mechanism that is far more efficient and outperforms also the linear version of the system, even if the damping coefficient is significantly increased for the linear model to reach the optimal damping value. The response of the system also heavily depends on the initial conditions. In the first case for nonzero initial conditions \({\dot{x}}_{1}={\dot{x}}_{2}={\dot{x}} _{3}\), only the in-phase NNM was excited once the initial nonlinear beats expired. A simple example showed that by changing the sign of \({\dot{x}}_{2}\) we can excite a NNM that is only present in the binary tree-structured model and are missing from the underlying reduced chain oscillator. For continuous harmonic excitation, we found that there are well-bounded nonlinear bands that overlap the forbidden zones of the FEP. The NESs are activated only in these nonlinear bands; no significant energy transfer toward the NES blocks is observed outside of these bands. The displacement solutions show heavily modulated signals indicating that the primary mechanism of the energy transfer is nonlinear beating. Though these modulated displacement signals show some regularity, the peak values vary. In future work, we plan to extend nonlinearities toward the higher levels of the tree to investigate whether this triggers chaotic dynamics in the nonlinear bands.

In future research, we plan to connect the findings of this study with the characteristics of turbulent flows. We plan to relate the parameters of the mechanistic model with measured parameters of turbulent flows. A long term goal of this research is to realize an energy cascade within the mechanistic model that is similar to the turbulent energy cascade, e.g., the energy spectrum follows a similar trend. We believe that this will lead us to a better understanding of energy cascades in general and how these energy cascades efficiently transfer energy through different scales.