Revisit of rogue wave solutions in the Yajima–Oikawa system

Abstract

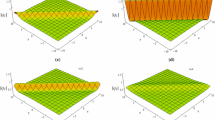
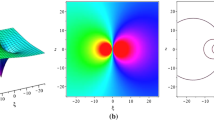
The general rogue wave solutions for the one-dimensional (1D) Yajima–Oikawa (YO) system are derived through Hirota’s bilinear method and the Kadomtsev–Petviashvili hierarchy reduction method. Different from the previous work, we improve the construction of the differential operators to save the complicated recursiveness and obtain the rogue wave solutions in a purely algebraic expression. Based on this simple expression, the new shape of the third-order rogue waves’ arrangement is found. Moreover, three types of fundamental rogue waves and the rogue wave patterns from second to fifth order are graphically illustrated. In particular, there exist $N-1$ ($2\le N$) polygonal configurations of Nth-order rogue waves for the 1D YO system, which is proven to be related to the Yablonskii–Vorob’ev polynomial hierarchy.

Appendix: the proof of Lemma 2

In this appendix, we give the proof of Lemma 2.

• 1. Recalling (53), we can rewrite $\sigma _n$ as

  $$\begin{aligned} \begin{aligned} \sigma _{n} =&\left| \begin{array}{cc} {\textbf{O}}_{N \times N} &{} \Phi _{N \times 2 N} \\ -\Psi _{2 N \times N} &{} {\textbf{I}}_{2 N \times 2 N} \end{array}\right| , \end{aligned} \end{aligned}$$

  (63)

  where

  $$\begin{aligned} \Phi _{i,j}=\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{j-1} S_{2i-j}\left( \hat{{\varvec{x}}}^{+}(n)+(j-1) {\varvec{s}}\right) , \end{aligned}$$

  and

  $$\begin{aligned} \Psi _{i,j}=\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{i-1} S_{2j-i}\left( \hat{{\varvec{x}}}^{-}(n)+(i-1) \varvec{s^*}\right) . \end{aligned}$$

  By using the similar technique in [58], we find

  $$\begin{aligned} \sigma _n=\lambda _3\left| \begin{array}{cc} {\textbf{O}}_{N_{0} \times N_{0}} &{} {\hat{\Phi }}_{N_{0} \times 2 N_{0}} \\ -\Psi _{2 N_{0} \times N_{0}} &{} {\textbf{I}}_{2 N_{0} \times 2 N_{0}} \end{array}\right| \left[ 1+O\left( \epsilon _{2 m+1}^{-1}\right) \right] ,\nonumber \\ \end{aligned}$$

  (64)

  where $\lambda _3$ is a multiplication of a constant dependent of (m, N), ${\hat{\Phi }}_{i,j}=\left( \vert p_1\vert /(p_0 + p^*_0)\right) ^{j-1} S_{2i-j}\left( \hat{{\varvec{y}}}^{+}(n)+(j-1) {\varvec{s}}\right)$, ${\hat{\Psi }}_{i,j}=\left( \vert p_1\vert /(p_0 + p^*_0)\right) ^{i-1} S_{2j-i}\left( \hat{{\varvec{y}}}^{-}(n)+(i-1) \varvec{s^*}\right)$, $\hat{{\varvec{y}}}^{+}(n) = \hat{{\varvec{x}}}^{+}(n)-(0, 0, \ldots ,\epsilon _{2\,m+1}, \ldots ,0)$, $\hat{{\varvec{y}}}^{-}(n) = \hat{{\varvec{x}}}^{-}(n)-\left( 0, 0, \ldots ,\epsilon _{2\,m+1}^*, \ldots ,0\right)$ and $\nu _0=N-N_0$. After rewriting ${\varvec{s}}$ as $\varvec{s_{\text{ odd } }} + \varvec{s_{\text{ even } }}$, the matrix elements of $\sigma _n$ can be reduced to

  $$\begin{aligned} {\hat{\Phi }}_{i, j}= & {} \left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{j-1} \nonumber \\{} & {} S_{2 i-j}\left[ \varvec{{\hat{y}}}^{+}+(j-1) {\varvec{s}}+v_{0} {\varvec{s}}_{o d d}\right] \end{aligned}$$

  (65)

  and

  $$\begin{aligned} {\hat{\Psi }}_{i, j}= & {} \left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{i-1} \nonumber \\{} & {} S_{2 j-i}\left[ \varvec{{\hat{y}}}^{-}+(i-1) {\varvec{s}}+v_{0} {\varvec{s}}_{o d d}\right] \end{aligned}$$

  (66)

  where ${\varvec{s}}_{\text{ odd } }=\left( s_{1}, 0, s_{3},0, \ldots \right)$. Furthermore, by taking the variable replacements ${\hat{\epsilon }}_{2 r-1}=\epsilon _{2 r-1}+\left( N-N_{0}\right) s_{2 r-1}$ and ${\hat{\epsilon }}^*_{2 r-1}=\epsilon ^*_{2 r-1}+\left( N-N_{0}\right) s^*_{2 r-1}$, $\sigma _n$ yield an expression for a $N_0$th-order rouge wave with internal parameters $({\hat{\epsilon }}_1,{\hat{\epsilon }}_2,{\hat{\epsilon }}_3,\dots ,{\hat{\epsilon }}_{2 N_0 -1})$. Here, the approximation error is $O\left( \epsilon _{2\,m+1}^{-1}\right)$.

• 2. Far away from the origin and $\sqrt{x^{2}+t^{2}}=O\left( \left| \epsilon _{2\,m+1}\right| ^{1 /(2\,m+1)}\right)$, we get

  $$\begin{aligned} S_{k}\left( {\varvec{x}}^{+}(n)+v {\varvec{s}}\right)= & {} S_{k}({\textbf{v}})\left[ 1+O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) \right] , \nonumber \\{} & {} \left| \epsilon _{2 m+1}\right| \gg 1, \end{aligned}$$

  (67)

  where ${\textbf{v}}=\left( \nu _1 x - \gamma _1 \textrm{i} t, 0, \ldots , 0, \epsilon _{2\,m+1}, 0, \ldots \right)$. After recalling the definition of Schur polynomial (43) and $p_{k}^{[m]}(z)$ (56), the relationship between them can be revealed as

  $$\begin{aligned} S_{k}({\textbf{v}})=\Omega ^{k}p_{k}^{[m]}(z), \end{aligned}$$

  (68)

  where $\Omega =(-(2 m+1)/(2^{2 m}) \epsilon _{2 m+1})^{ 1 /(2 m+1)}$ and $z=\Omega ^{-1}( \nu _1 x - \gamma _1 \textrm{i} t)$.Let $z_{0}=\Omega ^{-1}\left( \nu _1{\tilde{x}}_{0}-\gamma _1 \textrm{i} {\tilde{t}}_{0}\right)$ to be a root of the polynomial $Q_{N}^{[m]}(z)$. When z is not at or near $z_0$, we have

  $$\begin{aligned} \begin{aligned}&\det _{1 \le i, j \le N}\left[ S_{2 i-j}\left( \hat{{\varvec{x}}}^{+}(n)+j {\textbf{s}}\right) \right] \\&\sim c_{N}^{-1} \Omega ^{\frac{N(N+1)}{2}} Q_{N}^{[m]}(z),\quad \left| \epsilon _{2 m+1}\right| \gg 1. \end{aligned} \end{aligned}$$

  (69)

  Likewise,

  $$\begin{aligned} \begin{aligned}&\det _{1 \le i, j \le N}\left[ S_{2 i-j}\left( \hat{{\varvec{x}}}^{-}(n)+j \mathbf {s^*}\right) \right] \\&\sim c_{N}^{-1} (\Omega ^*)^{\frac{N(N+1)}{2}} Q_{N}^{[m]}(z^*),\quad \left| \epsilon _{2 m+1}\right| \gg 1. \end{aligned} \end{aligned}$$

  (70)

  Since the highest order term of $\epsilon _{2m+1}$ comes from the index choices $v=(0,1, \ldots , N-1)$, i.e., $v_j = j-1$, it can be derived that when (x, t) is not at or near (x, t) locations $({\tilde{x}}_0, {\tilde{t}}_0)$,

  $$\begin{aligned} \sigma _n \sim \vert \chi \vert ^2 \left| \epsilon _{2m+1} \right| ^{\frac{N(N+1)}{2m+1}}\left| Q_{N}^{[m]}(z)\right| ^{2},\quad \left| \epsilon _{2 m+1}\right| \gg 1, \end{aligned}$$

  (71)

  where

  $$\begin{aligned} \chi =c_{N}^{-1}\left( \frac{\vert p_1\vert }{p_0 + p^*_0} \right) ^{\frac{N(N-1)}{2}} \left( -\frac{2m+1}{2^{2m}}\right) ^{\frac{N(N+1)}{2(2m+1)}}. \end{aligned}$$

  (72)

  Due to the independence between $\chi$ and n, we found $\sigma _{1}/\sigma _{0}\sim 1$, i.e., the solution $S_N(x,t)$ is approximated as the constant background $e^{\textrm{i}\left[ \alpha x+\left( h+\alpha ^{2}\right) t\right] }$. Moreover, from the asymptotic analysis above, it can be concluded that the highest order term of $\epsilon _{2m+1}$ vanishes when (x, t) is near $({\tilde{x}}_0, {\tilde{t}}_0)$. To derive the leading-order term of $\epsilon _{2m+1}$ which determines the approximation of $\sigma _n$, we let

  $$\begin{aligned} S_{k}\left( \hat{{\varvec{x}}}^{+}(n)+\nu {\varvec{s}}\right) =S_{k}(\hat{{\textbf{v}}})\left[ 1+O\left( \epsilon _{2 m+1}^{-2 /(2 m+1)}\right) \right] ,\nonumber \\ \end{aligned}$$

  (73)

  where

  $$\begin{aligned}{} & {} \hat{{\textbf{v}}}=\left( {\hat{x}}^{+}_1 + v s_1, 0, \ldots , 0, \epsilon _{2 m+1}, 0, \ldots \right) \nonumber \\{} & {} =\left( \nu _1 x - \gamma _1 \textrm{i} t+n u_1 + \epsilon _1 + v s_1,\right. \nonumber \\{} & {} \left. 0, \ldots , 0, \epsilon _{2 m+1}, 0, \ldots \right) . \end{aligned}$$

  (74)

  By denoting ${\hat{z}}=\Omega ^{-1} {\hat{x}}_{1}^{+}$, the above relations indicate that

  $$\begin{aligned}{} & {} S_{k}\left( \hat{{\varvec{x}}}^{+}+v {\varvec{s}}\right) =\Omega ^{k} p_{k}^{[m]}\left( {\hat{z}}+v s_{1} \Omega ^{-1}\right) \nonumber \\{} & {} \left[ 1+O\left( \epsilon _{2 m+1}^{-2 /(2 m+1)}\right) \right] \end{aligned}$$

  (75)

  and

  $$\begin{aligned}{} & {} S_{k}\left( \hat{{\varvec{x}}}^{-}+v \varvec{s^*}\right) =(\Omega ^*)^{k} p_{k}^{[m]}\left( {\hat{z}}^* +v s_{1}^* (\Omega ^*)^{-1}\right) \nonumber \\{} & {} \left[ 1+O\left( \epsilon _{2 m+1}^{-2 /(2 m+1)}\right) \right] . \end{aligned}$$

  (76)

  Then, the leading-order terms of $\epsilon _{2m+1}$ in $\sigma _n (x, t)$ come from two index choices which are $v=(0,1, \ldots , N-1)$ and $v=(0,1, \ldots , N-2, N)$. For the first index choice $v=(0,1, \ldots , N-1)$, i.e., $v_j = j-1$, we get

  $$\begin{aligned} \begin{aligned}&\det _{1 \le i, j \le N}\left[ \left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{v_{j}} S_{2 i-1-v_{j}}\left( \hat{{\varvec{x}}}^{+}(n)+v_{j} {\varvec{s}}\right) \right] \\&= \Omega ^{\frac{N(N+1)}{2}}\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{\frac{N(N-1)}{2}} \det _{1 \le i, j \le N}\\&\quad \left[ p_{2 i-j}^{[m]}\left( {\hat{z}}+(j-1) s_{1} \Omega ^{-1}\right) \right] \\&\quad \times \left[ 1+O\left( \epsilon _{2 m+1}^{-2 /(2 m+1)}\right) \right] . \end{aligned} \end{aligned}$$

  (77)

  Inspired by Yang and Yang, we rewrite ${\hat{z}}+(j-1) s_{1} \Omega ^{-1}$ as

  $$\begin{aligned}{} & {} {\hat{z}}+(j-1) s_{1} \Omega ^{-1}=z_{0}+\Omega ^{-1}\nonumber \\{} & {} \quad \left[ {\hat{x}}_{1}^{+}\left( x-{\tilde{x}}_{0}, t-{\tilde{t}}_{0}\right) +(j-1) s_{1}\right] . \end{aligned}$$

  (78)

  After expanding $p_{2 i-j}^{[m]}\left( {\hat{z}}+(j-1) s_{1} \Omega ^{-1}\right)$ around $z_0$ and substituting the expansion into (77), we have

  $$\begin{aligned} \begin{aligned}&\det _{1 \le i, j \le N}\left[ p_{2 i-j}^{[m]}\left( {\hat{z}}+(j-1) s_{1} \Omega ^{-1}\right) \right] \\&=\Omega ^{-1}c_{N}^{-1}\left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}\right) \\&\quad \left[ {\hat{x}}_{1}^{+}\left( x-{\tilde{x}}_{0}, t-{\tilde{t}}_{0}\right) +(N-1) s_{1}\right] +O\left( \Omega ^{-2}\right) . \end{aligned} \end{aligned}$$

  (79)

  By taking a phase shift, the above determinant can be simplified as

  $$\begin{aligned} \begin{aligned}&\det _{1 \le i, j \le N}\left[ p_{2 i-j}^{[m]}\left( {\hat{z}}+(j-1) s_{1} \Omega ^{-1}\right) \right] \\&=\Omega ^{-1}c_{N}^{-1}\left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}\right) {\hat{x}}_{1}^{+}\\&\quad \left( x-{\hat{x}}_{0}, t-{\hat{t}}_{0} \right) +O\left( \Omega ^{-2}\right) . \end{aligned} \end{aligned}$$

  (80)

  Similarly,

  $$\begin{aligned} \begin{aligned}&\det _{1 \le i, j \le N}\left[ p_{2 i-j}^{[m]}\left( {\hat{z}}^{*}+(j-1) s_{1}^{*} (\Omega ^{*})^{-1}\right) \right] \\&=(\Omega ^{*})^{-1}c_{N}^{-1}\left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}^{*}\right) {\hat{x}}_{1}^{-}\\&\quad \left( x-{\hat{x}}_{0}, t-{\hat{t}}_{0} \right) +O\left( \Omega ^{-2}\right) . \end{aligned} \end{aligned}$$

  (81)

  In this way, we obtain the dominant contribution of the first index choice:

  $$\begin{aligned} \begin{aligned}&\vert \chi _{2}\vert ^2\left| \left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}\right) \right| ^{2}\left| \epsilon _{2 m+1}\right| ^{\frac{N(N+1)-2}{2 m+1}} \\&\quad {\hat{x}}_{1}^{+}\left( \tilde{x}, \tilde{t}\right) {\hat{x}}_{1}^{-}\left( \tilde{x}, \tilde{t}\right) \left[ 1+O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) \right] \\&=\vert \chi _{2}\vert ^2\left| \epsilon _{2 m+1}\right| ^{\frac{N(N+1)-2}{2 m+1}} \\&\quad (\nu _1 (\tilde{x}) - \gamma _1 \textrm{i} (\tilde{t})+n u_1 )(\nu ^{*}_1 (\tilde{x}) + \gamma _1^{*} \textrm{i} (\tilde{t})-n u_1^{*} )\\&\quad \times \left| \left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}\right) \right| ^{2}\left[ 1+O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) \right] , \end{aligned} \end{aligned}$$

  where

  $$\begin{aligned} \chi _{2}=c_{N}^{-1}\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{\frac{N(N-1)}{2}}\left( -\frac{2 m+1}{2^{2 m}}\right) ^{\frac{N(N+1)-2}{2(2 m+1)}}, \end{aligned}$$

  $\tilde{x}=x-{\hat{x}}_0$ and $\tilde{t}=t-{\hat{t}}_0$. For the second choice of index $v=(0,1, \ldots , N-2,N)$, we can calculate its dominant contribution by dropping the $v s_1 \Omega ^{-1}$ terms and replacing z with $z_0$ directly. Following the similar calculation steps of (77), we get

  $$\begin{aligned}{} & {} \det _{1 \le i, j \le N}\left[ \left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{v_{j}} S_{2 i-1-v_{j}}\left( \hat{{\varvec{x}}}^{+}(n)+v_{j} {\varvec{s}}\right) \right] \nonumber \\{} & {} =\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{\frac{N(N-1)+2}{2}} \Omega ^{\frac{N(N+1)-2}{2}}\nonumber \\{} & {} \times \det _{1 \le i, j \le N}\left[ p_{2 i-1-v_{j}}^{[m]}\left( z_{0}\right) \right] \left[ 1+O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) \right] \nonumber \\{} & {} =\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{\frac{N(N-1)+2}{2}} \Omega ^{\frac{N(N+1)-2}{2}}\left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}\right) \nonumber \\{} & {} \times \left[ 1+O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) \right] , \end{aligned}$$

  (82)

  and

  $$\begin{aligned}{} & {} \det _{1 \le i, j \le N}\left[ \left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{v_{j}} S_{2 i-1-v_{j}}\left( \hat{{\varvec{x}}}^{-}(n)+v_{j} \varvec{s^*}\right) \right] \nonumber \\{} & {} =\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{\frac{N(N-1)+2}{2}} (\Omega ^*)^{\frac{N(N+1)-2}{2}}\nonumber \\{} & {} \times \det _{1 \le i, j \le N}\left[ p_{2 i-1-v_{j}}^{[m]}\left( z_{0}^*\right) \right] \left[ 1+O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) \right] \nonumber \\{} & {} =\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^{\frac{N(N-1)+2}{2}} (\Omega ^*)^{\frac{N(N+1)-2}{2}}\left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}^*\right) \nonumber \\{} & {} \times \left[ 1+O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) \right] . \end{aligned}$$

  (83)

  Then, the dominant contribution of the second index choice is

  $$\begin{aligned}{} & {} \vert \chi _{2}\vert ^2\left( \vert p_1\vert /(p_0 + p^*_0)\right) ^2\left| \left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}\right) \right| ^{2}\\{} & {} \left| \epsilon _{2 m+1}\right| ^{\frac{N(N+1)-2}{2 m+1}} \left[ 1+O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) \right] . \end{aligned}$$

  Therefore, by combining the results of the above two index choices, we can obtain

  $$\begin{aligned} \begin{aligned}&\sigma _n \sim \left( \left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^2+\left( \nu _1 \tilde{x} - \gamma _1 \textrm{i} \tilde{t}+n u_1 \right) \right. \\&\quad \left. \left( \nu ^{*}_1 \tilde{x} + \gamma _1^{*} \textrm{i} \tilde{t}-n u_1^{*} \right) \right) \\&\quad \times \vert \chi _2\vert ^2 \bigg \vert \epsilon _{2 m+1}\bigg \vert ^{\frac{N(N+1)-2}{2 m+1}} \bigg \vert \left[ Q_{N}^{[m]}\right] ^{\prime }\left( z_{0}\right) \bigg \vert ^{2},\\&\quad \bigg \vert \epsilon _{2 m+1}\bigg \vert \gg 1, \end{aligned} \end{aligned}$$

  (84)

  where $\tilde{x}=x-{\hat{x}}_0$ and $\tilde{t}=t-{\hat{t}}_0$. Finally, assuming that all nonzero roots are simple, the above leading asymptotic term of $\sigma _n$ will not be eliminated. It has been proven that when $\sqrt{x^{2}+t^{2}}=O\left( \left|\epsilon _{2\,m+1} \right|^{1 /(2\,m+1)}\right)$,

  $$\begin{aligned} \begin{aligned} S_N(x,t)=&\,e^{\textrm{i}\left[ \alpha x+\left( h+\alpha ^{2}\right) t\right] }\\&\times \frac{\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^2+\left( \nu _1 \tilde{x} - \gamma _1 \textrm{i} \tilde{t}+ u_1 + \epsilon _1\right) \left( \nu ^{*}_1 \tilde{x} + \gamma _1^{*} \textrm{i} \tilde{t}+ u_1^{*} + \epsilon _1^{*}\right) }{\left( \frac{\vert p_1\vert }{p_0 + p^*_0}\right) ^2+\left( \nu _1 \tilde{x} - \gamma _1 \textrm{i} \tilde{t}+ \epsilon _1\right) \left( \nu ^{*}_1 \tilde{x} + \gamma _1^{*} \textrm{i} \tilde{t}+ \epsilon _1^{*}\right) } +O\left( \epsilon _{2 m+1}^{-1 /(2 m+1)}\right) , \end{aligned} \end{aligned}$$

  (85)

  where $\tilde{x}=x-{\hat{x}}_0$ and $\tilde{t}=t-{\hat{t}}_0$, is the first-order rouge wave of 1D YO system.