Skip to main content
SpringerLink
Log in

The Davey–Stewartson I equation: doubly localized two-dimensional rogue lumps on the background of homoclinic orbits or constant

  • Published:
Letters in Mathematical Physics Aims and scope Submit manuscript

Abstract

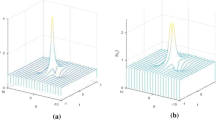
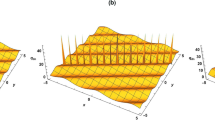
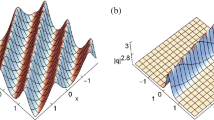
General doubly localized two-dimensional lumps on a background of homoclinic orbits or constant in the Davey–Stewartson I equation are studied. These special lumps first emerge from the background and then rapidly merge into the background again after existing for a very short period. Since these lumps are localized in time as well as in two-dimensional space, and possess the features of rogue wave phenomenon in two-dimensional physics; thus, they are termed “rogue lumps”. Technically, our derivation of the rogue lumps is achieved by a generalization of tau functions into multi-component forms in the Kadomtsev–Petviashvili (KP) hierarchy reduction method, and this generalized procedure allows us to construct the solutions containing rational solitary waves, periodic solitons, dark solitons and their mixed solitons in the DSI equation. Our results are extensions of doubly localized waves in two-dimensional integrable systems and are valuable in understanding rogue wave phenomena.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Davey, A., Stewartson, K.: On three-dimensional packets of surface waves. In: Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 338(1613), 101–110 (1974)

  2. Djordjevic, V.D., Redekopp, L.G.: On two-dimensional packets of capillary-gravity waves. J. Fluid Mech. 79(4), 703–714 (1977)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. Ablowitz, M.J., Segur, H.: On the evolution of packets of water waves. J. Fluid Mech. 92(4), 691–715 (1979)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Ablowitz, M.J., Biondini, G., Blair, S.: Nonlinear Schrödinger equations with mean terms in nonresonant multidimensional quadratic materials. Phys. Rev. E 63(4), 046605 (2001)

    Article  ADS  Google Scholar 

  5. Ioannou-Sougleridis, I., Frantzeskakis, D.J., Horikis, T.P.: A Davey-Stewartson description of two-dimensional solitons in nonlocal media. Stud. Appl. Math. 144(1), 3–17 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  6. Khismatullin, D., Akhatov, I.S.: Sound-ultrasound interaction in bubbly fluids: theory and possible applications. Phys. Fluids 13(12), 3582–3598 (2001)

    Article  ADS  MATH  Google Scholar 

  7. Huang, G., Konotop, V.V., Tam, H.-W., Hu, B.: Nonlinear modulation of multidimensional lattice waves. Phys. Rev. E 64(5), 056619 (2001)

    Article  ADS  MathSciNet  Google Scholar 

  8. Benney, D., Roskes, G.: Wave instabilities. Stud. Appl. Math. 47(5), 377–385 (1969)

    Article  MATH  Google Scholar 

  9. Chakravarty, S., Kent, S., Newman, E.: Some reductions of the self-dual Yang-Mills equations to integrable systems in 2+ 1 dimensions. J. Math. Phys. 36(2), 763–772 (1995)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Dysthe, K., Krogstad, H.E., Müller, P.: Oceanic rogue waves. Annu. Rev. Fluid Mech. 40, 287–310 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. Kharif, C., Pelinovsky, E., Slunyaev, A.: Rogue Waves in the Ocean, vol. 1. Springer, Cham (2008)

    MATH  Google Scholar 

  12. Kibler, B., Fatome, J., Finot, C., Millot, G., Dias, F., Genty, G., Akhmediev, N., Dudley, J.M.: The peregrine soliton in nonlinear fibre optics. Nat. Phys. 6(10), 790–795 (2010)

    Article  Google Scholar 

  13. Solli, D.R., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature 450(7172), 1054–1057 (2007)

    Article  ADS  Google Scholar 

  14. Akhmediev, N., Ankiewicz, A., Taki, M.: Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 373(6), 675–678 (2009)

    Article  ADS  MATH  Google Scholar 

  15. Chabchoub, A., Hoffmann, N., Onorato, M., Akhmediev, N.: Super rogue waves: observation of a higher-order breather in water waves. Phys. Rev. X 2(1), 011015 (2012)

    Google Scholar 

  16. Chabchoub, A., Hoffmann, N., Akhmediev, N.: Rogue wave observation in a water wave tank. Phys. Rev. Lett. 106(20), 204502 (2011)

    Article  ADS  Google Scholar 

  17. Baronio, F., Frisquet, B., Chen, S., Millot, G., Wabnitz, S., Kibler, B.: Observation of a group of dark rogue waves in a telecommunication optical fiber. Phys. Rev. A 97(1), 013852 (2018)

    Article  ADS  Google Scholar 

  18. Peregrine, D.H.: Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 25(1), 16–43 (1983)

    MATH  Google Scholar 

  19. Guo, B., Ling, L., Liu, Q.: Nonlinear Schrödinger equation: generalized darboux transformation and rogue wave solutions. Phys. Rev. E 85(2), 026607 (2012)

    Article  ADS  Google Scholar 

  20. Ohta, Y., Yang, J.: General high-order rogue waves and their dynamics in the nonlinear Schrödinger equation. In: Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 468(2142), 1716–1740 (2012)

  21. He, J., Zhang, H., Wang, L., Porsezian, K., Fokas, A.: Generating mechanism for higher-order rogue waves. Phys. Rev. E 87(5), 052914 (2013)

    Article  ADS  Google Scholar 

  22. Akhmediev, N., Ankiewicz, A., Soto-Crespo, J.M.: Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 80(2), 026601 (2009)

    Article  ADS  Google Scholar 

  23. Ling, L., Guo, B., Zhao, L.-C.: High-order rogue waves in vector nonlinear Schrödinger equations. Phys. Rev. E 89(4), 041201 (2014)

    Article  ADS  Google Scholar 

  24. Baronio, F., Degasperis, A., Conforti, M., Wabnitz, S.: Solutions of the vector nonlinear Schrödinger equations: evidence for deterministic rogue waves. Phys. Rev. Lett. 109(4), 044102 (2012)

    Article  ADS  Google Scholar 

  25. Chen, S., Mihalache, D.: Vector rogue waves in the Manakov system: diversity and compossibility. J. Phys. A Math. Theor. 48(21), 215202 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. Bilman, D., Miller, P.D.: A robust inverse scattering transform for the focusing nonlinear Schrödinger equation. Commun. Pure Appl. Math. 72(8), 1722–1805 (2019)

    Article  MATH  Google Scholar 

  27. Bilman, D., Ling, L., Miller, P.D.: Extreme superposition: rogue waves of infinite order and the Painlevé-III hierarchy. Duke Math. J. 169(4), 671–760 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  28. Yang, B., Yang, J.: Universal rogue wave patterns associated with the Yablonskii-Vorobév polynomial hierarchy. Phys. D Nonlinear Phenom. 425, 132958 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  29. Mu, G., Qin, Z., Grimshaw, R.: Dynamics of rogue waves on a multisoliton background in a vector nonlinear Schrödinger equation. SIAM J. Appl. Math. 75(1), 1–20 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  30. Chen, J., Pelinovsky, D.E., White, R.E.: Rogue waves on the double-periodic background in the focusing nonlinear Schrödinger equation. Phys. Rev. E 100(5), 052219 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  31. Chen, J., Pelinovsky, D.E., White, R.E.: Periodic standing waves in the focusing nonlinear Schrödinger equation: Rogue waves and modulation instability. Phys. D 405, 132378 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  32. Zhang, G., Ling, L., Yan, Z., Konotop, V.V.: Parity-time-symmetric vector rational rogue wave solutions in any n-component nonlinear Schrödinger models. arXiv preprint arXiv:2012.15538 (2020)

  33. Zhao, L.-C., Guo, B., Ling, L.: High-order rogue wave solutions for the coupled nonlinear Schrödinger equations-ii. J. Math. Phys. 57(4), 043508 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. Feng, B.-F., Ling, L., Takahashi, D.A.: Multi-breather and high-order rogue waves for the nonlinear Schrödinger equation on the elliptic function background. Stud. Appl. Math. 144(1), 46–101 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  35. Yang, B., Yang, J.: Rogue wave patterns in the nonlinear Schrödinger equation. Phys. D 419, 132850 (2021)

    Article  MATH  Google Scholar 

  36. Zhang, G., Yan, Z., Wen, X.-Y., Chen, Y.: Interactions of localized wave structures and dynamics in the defocusing coupled nonlinear Schrödinger equations. Phys. Rev. E 95(4), 042201 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  37. Ohta, Y., Yang, J.: Rogue waves in the Davey-Stewartson I equation. Phys. Rev. E 86(3), 036604 (2012)

    Article  ADS  Google Scholar 

  38. Ohta, Y., Yang, J.: Dynamics of rogue waves in the Davey-Stewartson II equation. J. Phys. A Math. Theor. 46(10), 105202–105202 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Rao, J., Fokas, A.S., He, J.: Doubly localized two-dimensional rogue waves in the Davey-Stewartson I equation. J. Nonlinear Sci. 31(4), 1–44 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  40. Yuan, Y.-Q., Tian, B., Qu, Q.-X., Zhao, X.-H., Du, X.-X.: Periodic-wave and semirational solutions for the (\(2+1\))-dimensional Davey-Stewartson equations on the surface water waves of finite depth. Z. Angew. Math. Phys. 71(2), 1–14 (2020)

    MathSciNet  MATH  Google Scholar 

  41. Fokas, A.S.: The Davey-Stewartson equation on the half-plane. Commun. Math. Phys. 289(3), 957–993 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  42. Fokas, A.S.: Inverse scattering of first-order systems in the plane related to nonlinear multidimensional equations. Phys. Rev. Lett. 51(1), 3 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  43. Fokas, A.S., Ablowitz, M.J.: Method of solution for a class of multidimensional nonlinear evolution equations. Phys. Rev. Lett. 51(1), 7 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  44. Tajiri, M., Arai, T.: Quasi-line soliton interactions of the Davey-Stewartson I equation: on the existence of long-range interaction between two quasi-line solitons through a periodic soliton. J. Phys. A Math. Theor. 44(23), 235204 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  45. Ablowitz, M.J., Herbst, B.: On homoclinic structure and numerically induced chaos for the nonlinear Schrödinger equation. SIAM J. Appl. Math. 50(2), 339–351 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  46. Balmforth, N.: Solitary waves and homoclinic orbits. Annu. Rev. Fluid Mech. 27(1), 335–373 (1995)

    Article  ADS  MathSciNet  Google Scholar 

  47. Jimbo, M., Miwa, T.: Solitons and infinite dimensional lie algebras. Publ. Res. Inst. Math. Sci. 19(3), 943–1001 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  48. Sato, M.: Soliton equations as dynamical systems on infinite dimensional grassmann manifold. In: North-Holland Mathematics Studies, vol. 81, pp. 259–271. Elsevier, Amsterdam (1983)

    Google Scholar 

  49. Hirota, R.: The Direct Method in Soliton Theory, vol. 155. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  50. Matveev, V., Salle, M.: Darboux Transformations and Solitons, vol. 1. Springer, Cham (1991)

    Book  MATH  Google Scholar 

  51. Lester, C., Gelash, A., Zakharov, D., Zakharov, V.: Lump chains in the KP-I equation. Stud. Appl. Math. 147, 1425–1442 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  52. Rao, J., Chow, K.W., Mihalache, D., He, J.: Completely resonant collision of lumps and line solitons in the Kadomtsev-Petviashvili I equation. Stud. Appl. Math. 147(3), 1007–1035 (2021)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The work was supported by the National Natural Science Foundation of China (Grant Nos. 12071304 and 11871446), the Guangdong Basic and Applied Basic Research Foundation (Grant 2022A1515012554), and the Research and Development Funds of Hubei University of Science and Technology (Grant BK202302).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Hubei University of Science and Technology, Xianning, 437100, Hubei, People’s Republic of China

    Jiguang Rao

  2. Institute for Advanced Study, Shenzhen University, Shenzhen, 518060, Guangdong, People’s Republic of China

    Jingsong He

  3. School of Mathematical Sciences, USTC, Hefei, 230026, Anhui, People’s Republic of China

    Yi Cheng

Authors
  1. Jiguang Rao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jingsong He
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yi Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jingsong He.

Ethics declarations

Conflict of interest

We declare we have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file 1 (mp4 2738 KB)

Supplementary file 2 (mp4 2517 KB)

Supplementary file 3 (mp4 4220 KB)

Supplementary file 4 (mp4 992 KB)

Supplementary file 5 (mp4 3631 KB)

Supplementary file 6 (mp4 969 KB)

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rao, J., He, J. & Cheng, Y. The Davey–Stewartson I equation: doubly localized two-dimensional rogue lumps on the background of homoclinic orbits or constant. Lett Math Phys 112, 75 (2022). https://doi.org/10.1007/s11005-022-01571-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11005-022-01571-w

Keywords

Search

Navigation