Travelling wave solution for the Landau-Ginburg-Higgs model via the inverse scattering transformation method

Abstract

The Landau-Ginzburg-Higgs (LGH) equation explains the ocean engineering models, superconductivity and drift cyclotron waves in radially inhomogeneous plasma for coherent ion-cyclotron waves. In this paper, with a simple modification of the Ablowitz-Kaup-Newell-Segur (AKNS) formalism, the integrability of LGH equation is proved by deriving the Lax pair. Hence for that, the inverse scattering transformation (IST) is applied, and the travelling wave solutions are obtained and graphically represented in 2d and 3d profiles.

1 Introduction

Nonlinear evolution equations (NLEE’s) are one of the most important fields of ocean engineering models, modern physics, through which physical phenomena and other fields of modern physics are modeled. Accordingly, many effective methods have been established to obtain exact and explicit solutions of this type of equation, such as: the improved Bernoulli sub-equation function method [1, 2], the modified simple equation method [3], solitary wave ansatz [4], the extended tanh-function method [5, 6], the sine–Gordon expansion method [7], the extended mapping method [8], the first integral method [9], the improved Kudryashov method [10, 11], the hyperbola function method [12], the improved tanh-method [13], Hirota's bilinear method [14], Lie symmetry analysis [15, 16], Bäcklund transformation method [17], Darboux transformation method [18], inverse scattering transformation (IST) method [19,20,21,22], the $\left( {G^{\prime } /G} \right)$-expansion method [23,24,25], the $\left( {G^{\prime } /G,\;1/G} \right)$-expansion method [26, 27], and reference therein.

One of the more general classes of NLEE’s with a nonlinear term of any order is [28]:

$$ u_{{{\text{TT}}}} + a_{1} u_{{{\text{XX}}}} + a_{2} u + a_{3} u^{p} + a_{4} u^{2p - 1} = 0 $$

(1)

where ${a}_{1},{a}_{2},{a}_{3},{a}_{4},$ and $p\ne 1$ are arbitrary constants. When $p=3$ and ${a}_{4}=0$, the following special case is stated

$${u}_{\mathrm{TT}}+a{u}_{\mathrm{XX}}+bu+c{u}^{3}=0$$

(2)

Depending on the arbitrary constants $a,b$ and $c$, typical forms of Eq. (2) are specified, one of them is the Landau-Ginzburg-Higgs (LGH) equation. When $a=-1, b={-m}^{2}$ and $c={n}^{2}$, the LGH equation is stated as

$${u}_{\mathrm{TT}}-{u}_{\mathrm{XX}}-{m}^{2}u+{n}^{2}{u}^{3}=0$$

(3)

where $u(X,T)$ symbolizes the electrostatic potential of the ion-cyclotron wave, $X$ and $T$ stand for the nonlinearized spatial and temporal coordinates and $m$ and $n$ are real parameters. The LGH Eq. (3) was formulated by Lev Devidovich Landau and Vitaly Lazarevich Ginzburg with broad applications for the internal processes of complex physical phenomena which occur to explain superconductivity and drift cyclotron waves in radially inhomogeneous plasma for coherent ion-cyclotron waves [11]. Another typical form of Eq. (2) can be stated, such as ${\phi }^{4}$ equation($a=-1, b=1, c=-1$), Klein–Gordon equation ($a=-1,b={m}^{2},c=n$), Duffing equation ($a=0$ with $b$ and $c$ arbitrary), Sine–Gordon equation ($a=-1,b=1,c=-1/6$) [8].

It is worth mentioning that there are many attempts in the literature to obtain the exact solutions of Eq. (2), as well as the special case of it, LGH Eq. (3), using different analytical methods. Considering the more general model in Eq. (2), there are different schemes to obtain the exact and explicit solutions, such as the extended mapping method, the hyperbola function method, the Improved tanh-method, the modified extended tanh-function method, a direct and unified algebraic method [8, 12, 13, 16, 29], while for the particular case, LGH Eq. (3), the travelling wave solutions have been investigated in different contexts using different approaches such as solitary wave ansatz method in [4], the first integral method in [9], the $\left( {G^{\prime } /G,\;1/G} \right)$-expansion method in [26], the improved Bernoulli sub-equation function (IBSEFM) method in [1], the sine–Gordon expansion (SGE) method in [7], the extended tanh scheme in [6], the generalized Kudryashov technique in [11].

In this paper, under some conditions, the integrability of LGH Eq. (3) is proved by deriving the Lax pair using AKNS scheme. It is worth noting that, there are many different methods for deducing the Lax pair for integrable NLEE's, such as the prolongation method [30], the extended homogeneous balance method [31], the singular manifold method [32,33,34], and the AKNS approach [21, 22, 35]. Accordingly, and using the inverse scattering transformation (IST) method, we obtain a closed form solution to Eq. (3) of type Kink soliton solution.

The residue of the paper is organized as follows: in Sect. 2, we investigate the Lax pair for Eq. (3) using AKNS approach. The inverse scattering transformation is applied to Eq. (3) in Sect. 3. In Sect. 4, the kink type soliton solution is obtained and graphically represented in 2d and 3d plots and a comparison between our solution and different solutions in the literature is represented in tabularized form.

2 The derivation of Lax pair

In this section, we derive the Lax pair in matrix form for Eq. (3) by applying a simple modification of the standard AKNS formalism.

Make the following transformation to Eq. (3):

$$x=\frac{X+T}{2}, t=\frac{X-T}{2}$$

(4)

Then by chain rule, we have

$$ \begin{gathered} \frac{\partial }{\partial X} = \frac{\partial x}{{\partial X}}\frac{\partial }{\partial x} + \frac{\partial t}{{\partial X}}\frac{\partial }{\partial t} = \frac{1}{2}\left( {\frac{\partial }{\partial x} + \frac{\partial }{\partial t}} \right) \hfill \\ \frac{\partial }{\partial T} = \frac{\partial x}{{\partial T}}\frac{\partial }{\partial x} + \frac{\partial t}{{\partial T}}\frac{\partial }{\partial t} = \frac{1}{2}\left( {\frac{\partial }{\partial x} - \frac{\partial }{\partial t}} \right) \hfill \\ \end{gathered} $$

(5)

From which we have

$$ \begin{gathered} \frac{{\partial^{2} u}}{{\partial X^{2} }} = \frac{1}{4}\left( {\frac{\partial }{\partial x} + \frac{\partial }{\partial t}} \right)\left( {\frac{\partial u}{{\partial x}} + \frac{\partial u}{{\partial t}}} \right) = \frac{1}{4}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + 2\frac{{\partial^{2} u}}{\partial x\partial t} + \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right) \hfill \\ \frac{{\partial^{2} u}}{{\partial T^{2} }} = \frac{1}{4}\left( {\frac{\partial }{\partial x} - \frac{\partial }{\partial t}} \right)\left( {\frac{\partial u}{{\partial x}} - \frac{\partial u}{{\partial t}}} \right) = \frac{1}{4}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} - 2\frac{{\partial^{2} u}}{\partial x\partial t} + \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right) \hfill \\ \end{gathered} $$

(6)

According to the above, the differential terms can be written in the form

$${u}_{\mathrm{TT}}-{u}_{\mathrm{XX}}=-{u}_{\mathrm{xt}}$$

(7)

Then Eq. (3) become

$${u}_{xt}=-{m}^{2}u+{n}^{2}{u}^{3}$$

(8)

Consider the following linear spectral problems

$${\psi }_{x}=\left[\begin{array}{cc}-i\alpha \lambda & q(x,t)\\ r(x,t)& i\alpha \lambda \end{array}\right]\psi $$

(9)

$${\psi }_{t}=\left[\begin{array}{cc}A& B\\ C& -A\end{array}\right]\psi $$

(10)

where $\psi \left(x,t\right)={\left({\psi }_{1}\left(x,t\right),{\psi }_{2}\left(x,t\right)\right)}^{T}$ and $\lambda$ is the spectral parameter with ${\lambda }_{t}=0$.

From Eq. (9) we have

$${\psi }_{1x}=-i\alpha \lambda {\psi }_{1}+q{\psi }_{2}$$

(11)

$${\psi }_{2x}=r{\psi }_{1}+i\alpha \lambda {\psi }_{2}$$

(12)

and from Eq. (10) we have

$${\psi }_{1t}=A{\psi }_{1}+B{\psi }_{2}$$

(13)

$${\psi }_{2t}=C{\psi }_{1}-A{\psi }_{2}$$

(14)

From Eqs. (11) and (13) we have

$${\psi }_{1xt}=-i\alpha \lambda A{\psi }_{1}-i\alpha \lambda B{\psi }_{2}+Cq{\psi }_{1}-Aq{\psi }_{2}+{q}_{t}{\psi }_{2}$$

(15)

$${\psi }_{1tx}=-i\alpha \lambda A{\psi }_{1}+Aq{\psi }_{2}+{A}_{x}{\psi }_{1}+Br{\psi }_{1}+i\alpha \lambda B{\psi }_{2}+{B}_{x}{\psi }_{2}$$

(16)

From Eqs. (12) and (14) we have

$${\psi }_{2xt}=Ar{\psi }_{1}+Br{\psi }_{2}+{r}_{t}{\psi }_{1}+i\alpha \lambda C{\psi }_{1}-i\alpha \lambda A{\psi }_{2}$$

(17)

$${\psi }_{2tx}=-i\alpha \lambda C{\psi }_{1}+Cq{\psi }_{2}+{C}_{x}{\psi }_{1}-Ar{\psi }_{1}-i\alpha \lambda A{\psi }_{2}-{A}_{x}{\psi }_{2}$$

(18)

The compatibility condition ${\psi }_{1xt}={\psi }_{1tx}$ yields

$$\left({A}_{x}+Br-Cq\right){\psi }_{1}+\left(2i\alpha \lambda B+2Aq+{B}_{x}-{q}_{t}\right){\psi }_{2}=0$$

(19)

While the compatibility condition ${\psi }_{2xt}={\psi }_{2tx}$ yields

$$\left(2i\alpha \lambda C+2Ar-{C}_{x}+{r}_{t}\right){\psi }_{1}+\left(Cq-Br-{A}_{x}\right){\psi }_{2}=0$$

(20)

Equating the coefficients of ${\psi }_{1}$ and ${\psi }_{2}$ to zero, we obtain the following system of equations

$$ \begin{gathered} A_{x} = qC - rB \hfill \\ B_{x} + 2i\alpha \lambda B = q_{t} - 2qA \hfill \\ C_{x} - 2i\alpha \lambda C = r_{t} + 2rA \hfill \\ \end{gathered} $$

(21)

Now, expand $A, B$ and $C$ as follows

$$A=\frac{a(x,t)}{\lambda }, B=\frac{b(x,t)}{\lambda }, C=\frac{c(x,t)}{\lambda }$$

(22)

Then

$${A}_{x}=\frac{{a}_{x}}{\lambda }, {B}_{x}=\frac{{b}_{x}}{\lambda }, {C}_{x}=\frac{{c}_{x}}{\lambda }$$

(23)

Substituting from Eq. (23) into Eq. (21), we obtain the following system of equations

$$ \begin{gathered} a_{x} = qc - rb \hfill \\ 2i\alpha b - q_{t} + \frac{{b_{x} + 2aq}}{\lambda } = 0 \hfill \\ - 2i\alpha c - r_{t} + \frac{{c_{x} - 2ar}}{\lambda } = 0 \hfill \\ \end{gathered} $$

(24)

Equating the coefficients of ${\lambda }^{0}$ to zero gives

$${a}_{x}=qc-rb$$

(25)

$${q}_{t}=2i\alpha b$$

(26)

$${r}_{t}=-2i\alpha c$$

(27)

While equating the coefficients of ${\lambda }^{-1}$ to zero gives

$${b}_{x}+2aq=0$$

(28)

$${c}_{x}-2ar=0$$

(29)

Multiply Eq. (30) by $2i$, and use Eqs. (26, 27), we have

$$2i{a}_{x}=-\frac{1}{\alpha }{\left(qr\right)}_{t}$$

(30)

Suppose the following quantities for $\alpha , a\left(x,t\right), b\left(x,t\right), c\left(x,t\right),q(x,t)$ and $r(x,t)$

$$\alpha ={m}^{2}$$

(31)

$$a\left(x,t\right)=-\frac{i}{4}\left(1-\frac{3{n}^{2}}{{m}^{2}}{\left(u\left(x,t\right)\right)}^{2}+\frac{3{n}^{4}}{2{m}^{4}}{\left(u\left(x,t\right)\right)}^{4}\right)$$

(32)

$$b\left(x,t\right)=c\left(x,t\right)=-\frac{i}{4}\left(\frac{\sqrt{6}n}{m}u\left(x,t\right)-\frac{\sqrt{6}{n}^{3}}{{m}^{3}}{\left(u\left(x,t\right)\right)}^{3}+\frac{3\sqrt{6}{n}^{5}}{10{m}^{5}}{\left(u\left(x,t\right)\right)}^{5}\right)$$

(33)

$$q\left(x,t\right)=-r\left(x,t\right)=\frac{-\sqrt{6}n}{2m}{\left(u\left(x,t\right)\right)}_{x}$$

(34)

Under these considerations, Eq. (30) become

$$\frac{1}{2}\left(\frac{-6{n}^{2}}{{m}^{2}}u+\frac{6{n}^{4}}{{m}^{4}}{u}^{3}\right){u}_{x}=\frac{3{n}^{2}}{{m}^{4}}{u}_{xt}{u}_{x}$$

(35)

i.e.,

$${u}_{xt}=\frac{{m}^{4}}{6{n}^{2}}\left(\frac{-6{n}^{2}}{{m}^{2}}u+\frac{6{n}^{4}}{{m}^{4}}{u}^{3}\right)=-{m}^{2}u+{n}^{2}{u}^{3}$$

(36)

which is the LGH equation given in Eq. (3). We also noted that under the considerations given in Eqs. (31–34), Eqs. (29) and (30) are satisfied. Therefore, The Lax pair for LGH Eq. (3) can be written as

$${\psi }_{x}=\left[\begin{array}{cc}-i{m}^{2}\lambda & \frac{-\sqrt{6}n}{2m}{u}_{x}\\ \frac{\sqrt{6}n}{2m}{u}_{x}& i{m}^{2}\lambda \end{array}\right]\psi ,$$

(37)

$${\psi }_{t}=\frac{-i}{4\lambda }\left[\begin{array}{cc}1-\frac{3{n}^{2}}{{m}^{2}}{u}^{2}+\frac{3{n}^{4}}{2{m}^{4}}{u}^{4}& \frac{\sqrt{6}n}{m}u-\frac{\sqrt{6}{n}^{3}}{{m}^{3}}{u}^{3}+\frac{3\sqrt{6}{n}^{5}}{10{m}^{5}}{u}^{5}\\ \frac{\sqrt{6}n}{m}u-\frac{\sqrt{6}{n}^{3}}{{m}^{3}}{u}^{3}+\frac{3\sqrt{6}{n}^{5}}{10{m}^{5}}{u}^{5}& -\left(1-\frac{3{n}^{2}}{{m}^{2}}{u}^{2}+\frac{3{n}^{4}}{2{m}^{4}}{u}^{4}\right)\end{array}\right]\psi $$

(38)

Remark (1)

Under the assumptions given in Eqs. (31–34), at $\left|x\right|\to \infty$ with the initial condition $u\to 0$, the limits of $A, B$ and $C$ defined in Eq. (22) are evaluated as.

$$\underset{x\to \pm \infty }{\mathrm{lim}}A=\underset{x\to \pm \infty }{\mathrm{lim}}-\frac{i}{4\lambda }\left(1-\frac{3{n}^{2}}{{m}^{2}}{u}^{2}+\frac{3{n}^{4}}{2{m}^{4}}{u}^{4}\right)=-\frac{i}{4\lambda }=\delta (\lambda )$$

(39)

$$\underset{x\to \pm \infty }{\mathrm{lim}}B=\underset{x\to \pm \infty }{\mathrm{lim}}C=\underset{x\to \pm \infty }{\mathrm{lim}}-\frac{i}{4\lambda }\left(\frac{\sqrt{6}n}{m}u-\frac{\sqrt{6}{n}^{3}}{{m}^{3}}{u}^{3}+\frac{3\sqrt{6}{n}^{5}}{10{m}^{5}}{u}^{5}\right)=0$$

(40)

3 The inverse scattering transformation for LGH Eq. (3)

In this section, the inverse scattering transform (IST) procedures will be followed for Eq. (3). Starting from Eq. (9), which may be written in the form

$$\left[\begin{array}{cc}\frac{\partial }{\partial x}& -q\\ r& -\frac{\partial }{\partial x}\end{array}\right]\psi =-i\alpha \lambda \psi $$

(41)

Assume that $q\left(x,t\right), r(x,t)$ and it's derivative with respect to $x$ are decay sufficiently rapidly as.

$\left|x\right|\to \infty$, then we can introduce the following four solutions to Eq. (9), which are defined by their asymptotic behaviors at infinity as

$${\psi }_{+}\left(x;\lambda \right)\sim \left(\begin{array}{c}1\\ 0\end{array}\right){e}^{-i\alpha \lambda x}, {\overline{\psi }}_{+}\left(x;\lambda \right)\sim \left(\begin{array}{c}0\\ 1\end{array}\right){e}^{i\alpha \lambda x}, as x\to \infty $$

(42)

$${\psi }_{-}\left(x;\lambda \right)\sim \left(\begin{array}{c}1\\ 0\end{array}\right){e}^{-i\alpha \lambda x}, {\overline{\psi }}_{-}\left(x;\lambda \right)\sim \left(\begin{array}{c}0\\ -1\end{array}\right){e}^{i\alpha \lambda x}, as x\to -\infty $$

(43)

These solutions may be written in matrix form as

$${{\varvec{\Psi}}}_{+}=\left[\begin{array}{cc}{\psi }_{1+}& {\overline{\psi }}_{1+}\\ {\psi }_{2+}& {\overline{\psi }}_{2+}\end{array}\right], {{\varvec{\Psi}}}_{-}=\left[\begin{array}{cc}{\psi }_{1-}& {\overline{\psi }}_{1-}\\ {\psi }_{2-}& {\overline{\psi }}_{2-}\end{array}\right]$$

(44)

Since solutions given in Eq. (42) and Eq. (43) are linearly dependent, where there Wronskian denoted $W\left({\psi }_{+},{\psi }_{-}\right)$ and $W\left({\overline{\psi }}_{+},{\overline{\psi }}_{-}\right)$ is equal to zero

$$W\left({\psi }_{+},{\psi }_{-}\right)={\psi }_{1+}{\psi }_{2-}-{\psi }_{2+}{\psi }_{1-}=\left({e}^{-i\alpha \lambda x}\right)\left(0\right)-\left(0\right)\left({e}^{-i\alpha \lambda x}\right)=0$$

(45)

$$W\left({\overline{\psi }}_{+},{\overline{\psi }}_{-}\right)={\overline{\psi }}_{1+}{\overline{\psi }}_{2-}-{\overline{\psi }}_{2+}{\overline{\psi }}_{1-}=\left(0\right)\left(-{e}^{-i\alpha \lambda x}\right)-\left({e}^{i\alpha \lambda x}\right)\left(0\right)=0$$

(46)

Then solutions ${\Psi }_{+}$ and ${\Psi }_{-}$ may be connected via the scattering matrix denoted $S(\lambda )$ as follows

$${{\varvec{\Psi}}}_{-}\left(x;\lambda \right)={{\varvec{\Psi}}}_{+}\left(x;\lambda \right)S(\lambda )$$

(47)

i.e.,

$$ \begin{gathered} \psi_{ - } = a\psi_{ + } + b\overline{\psi }_{ + } \hfill \\ \overline{\psi }_{ - } = \overline{b}\psi_{ + } - \overline{a}\overline{\psi }_{ + } \hfill \\ \end{gathered} $$

(48)

where

$$S\left(\lambda \right)=\left[\begin{array}{cc}a(\lambda )& \overline{b }(\lambda )\\ b(\lambda )& -\overline{a }(\lambda )\end{array}\right]$$

(49)

The solution ${{\varvec{\Psi}}}_{+}\left(x;\lambda \right)$ may always be represented by an integral over an appropriate Kernel, while ${{\varvec{\Psi}}}_{-}$ can be obtained using the relation (47)

$${{\varvec{\Psi}}}_{+}\left(x;\lambda \right)={{\varvec{\Psi}}}_{0}\left(x;\lambda \right)+\underset{x}{\overset{\infty }{\int }}K(x;\lambda ){{\varvec{\Psi}}}_{0}\left(x;\lambda \right)\mathrm{d}y$$

(50)

i.e.,

$$\left[\begin{array}{cc}{\psi }_{1+}& {\overline{\psi }}_{1+}\\ {\psi }_{2+}& {\overline{\psi }}_{2+}\end{array}\right]=\left[\begin{array}{cc}{e}^{-i\alpha \lambda x}& 0\\ 0& {e}^{i\alpha \lambda x}\end{array}\right]+\underset{x}{\overset{\infty }{\int }}\left[\begin{array}{cc}{k}_{11}& {k}_{21}\\ {k}_{12}& {k}_{22}\end{array}\right]\left[\begin{array}{cc}{e}^{-i\alpha \lambda y}& 0\\ 0& {e}^{i\alpha \lambda y}\end{array}\right]\mathrm{d}y$$

(51)

where at $\left|x\right|\to \infty$ and $\underset{x}{\overset{\infty }{\int }}K(x,\lambda ){\Psi }_{0}\left(x;\lambda \right)dy=0$ we have ${{\varvec{\Psi}}}_{+}\left(x;\lambda \right)={{\varvec{\Psi}}}_{0}\left(x;\lambda \right)$ which describe the behavior given in Eqs. (42,43). To find the equations satisfied by the elements of $K(x;\lambda )$, it is necessary to ensure that ${{\varvec{\Psi}}}_{+}\left(x;\lambda \right)$ is indeed a solution of (41).

From Eqs. (41,50) we have

$$-i\alpha \lambda {{\varvec{\Psi}}}_{+}=-i\alpha \lambda \left[{{\varvec{\Psi}}}_{0}(x;\lambda )+\underset{x}{\overset{\infty }{\int }}K{{\varvec{\Psi}}}_{0}\left(y;\lambda \right)\mathrm{d}y\right]$$

(52)

and

$$\left[\begin{array}{cc}\frac{\partial }{\partial x}& -q\\ r& -\frac{\partial }{\partial x}\end{array}\right]{{\varvec{\Psi}}}_{+}=\left[\begin{array}{cc}\frac{\partial }{\partial x}& -q\\ r& -\frac{\partial }{\partial x}\end{array}\right]\left[{{\varvec{\Psi}}}_{0}(x;\lambda )+\underset{x}{\overset{\infty }{\int }}K{{\varvec{\Psi}}}_{0}\left(y;\lambda \right)\mathrm{d}y\right]$$

(53)

using the Leibniz integral rule for differentiation under the integral sign which is defined as

$$\frac{d}{dx}\underset{{a}_{1}(x)}{\overset{{a}_{2}(x)}{\int }}f\left(x,y\right)dy=f\left(x,{a}_{2}\right)\frac{d{a}_{2}}{dx}-f\left(x,{a}_{1}\right)\frac{d{a}_{1}}{dx}+\underset{{a}_{1}(x)}{\overset{{a}_{2}(x)}{\int }}\frac{\partial }{\partial x}f\left(x,y\right)\mathrm{d}y$$

(54)

Equations (52, 53) gives

$$-i\alpha \lambda \left[{{\varvec{\Psi}}}_{0}+\underset{x}{\overset{\infty }{\int }}K{{\varvec{\Psi}}}_{0}dy\right]=-i\alpha \lambda {{\varvec{\Psi}}}_{0}+Q{{\varvec{\Psi}}}_{0}+\widehat{I}K\left(x,x\right){{\varvec{\Psi}}}_{0}-\widehat{I}\underset{x}{\overset{\infty }{\int }}{K}_{x}{{\varvec{\Psi}}}_{0}dy+Q\underset{x}{\overset{\infty }{\int }}K{{\varvec{\Psi}}}_{0}\mathrm{d}y$$

(55)

where

$$Q=\left[\begin{array}{cc}0& -q\\ r& 0\end{array}\right], \widehat{I}=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$$

(56)

Using integration by parts for $\underset{x}{\overset{\infty }{\int }}K{{\varvec{\Psi}}}_{0}dy$ we have

$$-i\alpha \lambda \underset{x}{\overset{\infty }{\int }}K{{\varvec{\Psi}}}_{0}dy=K\left(x,x\right){{\varvec{\Psi}}}_{0}\widehat{I}+\underset{x}{\overset{\infty }{\int }}{K}_{y}{{\varvec{\Psi}}}_{0}\widehat{I}\mathrm{d}y$$

(57)

Then Eq. (55) become

$$\widehat{I}K{{\varvec{\Psi}}}_{0}-K{{\varvec{\Psi}}}_{0}\widehat{I}+Q{{\varvec{\Psi}}}_{0}-\underset{x}{\overset{\infty }{\int }}\widehat{I}{K}_{x}{{\varvec{\Psi}}}_{0}+{K}_{y}{{\varvec{\Psi}}}_{0}\widehat{I}-QK{{\varvec{\Psi}}}_{0}\mathrm{d}y=0$$

(58)

Equation (58) is satisfied if $K(x,y)$ is a solution of the following system of equations

$$\widehat{I}K(x,x)-K(x,x)\widehat{I}+Q(x)=0$$

(59)

$$\widehat{I}{K}_{x}+{K}_{y}\widehat{I}-Q(x)K=0$$

(60)

From Eq. (59) we obtain the equations for $q(x)$ and $r(x)$ as

$$q\left(x\right)=-2{k}_{12}(x,x)$$

(61)

$$r\left(x\right)=-2{k}_{21}(x,x)$$

(62)

From Eq. (47) we have

$$ \left[ {\begin{array}{*{20}c} {\psi_{1 - } } & {\overline{\psi }_{1 - } } \\ {\psi_{2 - } } & {\overline{\psi }_{2 - } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\psi_{1 + } } & {\overline{\psi }_{1 + } } \\ {\psi_{2 + } } & {\overline{\psi }_{2 + } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} a & {\overline{b}} \\ b & { - \overline{a}} \\ \end{array} } \right] $$

(63)

Then

$$ \left[ {\begin{array}{*{20}c} {\psi_{1 - } /a} & {\overline{\psi }_{1 - } /\overline{a}} \\ {\psi_{2 - } /a} & {\overline{\psi }_{2 - } /\overline{a}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\psi_{1 + } } & {\overline{\psi }_{1 + } } \\ {\psi_{2 + } } & {\overline{\psi }_{2 + } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & {\overline{b}/\overline{a}} \\ {b/a} & { - 1} \\ \end{array} } \right] $$

(64)

Assume that

$$ \overline{\Psi }_{ - } = \left[ {\begin{array}{*{20}c} {\psi_{1 - } /a} & {\overline{\psi }_{1 - } /\overline{a}} \\ {\psi_{2 - } /a} & {\overline{\psi }_{2 - } /\overline{a}} \\ \end{array} } \right], \;{\rm T}\left( \lambda \right) = \left[ {\begin{array}{*{20}c} 1 & {\overline{b}/\overline{a}} \\ {b/a} & { - 1} \\ \end{array} } \right] $$

(65)

Then Eq. (47) may be rewritten as

$${\overline{{\varvec{\Psi}}} }_{-}={{\varvec{\Psi}}}_{+}\mathrm{\rm T}\left(\lambda \right)$$

(66)

Substituting from Eq. (50) into Eq. (66) gives

$${\overline{{\varvec{\Psi}}} }_{-}=\left({{\varvec{\Psi}}}_{0}+\underset{x}{\overset{\infty }{\int }}K{{\varvec{\Psi}}}_{0}\mathrm{d}y\right)\mathrm{\rm T}$$

(67)

To get an integral equation for $K$, we multiply Eq. (67) by $\frac{1}{2\pi }{{\varvec{\Psi}}}_{0}\left(z;\lambda \right)$ for $z>x$, then we have

$$\frac{1}{2\pi }{\overline{{\varvec{\Psi}}} }_{-}\left(x;\lambda \right){{\varvec{\Psi}}}_{0}\left(z;\lambda \right)=\frac{1}{2\pi }{{\varvec{\Psi}}}_{0}\left(x;\lambda \right)\mathrm{\rm T}\left(\lambda \right){{\varvec{\Psi}}}_{0}\left(z;\lambda \right)+\frac{1}{2\pi }\left[\underset{x}{\overset{\infty }{\int }}K\left(x,y\right){{\varvec{\Psi}}}_{0}\left(y;\lambda \right)dy\right]\mathrm{\rm T}(\lambda ){{\varvec{\Psi}}}_{0}\left(z;\lambda \right)$$

(68)

Integrate with respect to $\lambda$ a long appropriate contour in the complex $\lambda$-plane from $-\infty$ to $+\infty$. This contour is indented into the upper half-plane for terms involving ${e}^{i\alpha \lambda z}$ and into the lower half-plane for ${e}^{-i\alpha \lambda z}$, we call these contours ${C}_{+}$ and ${C}_{-}$, respectively. One can arrive to the matrix Marchenko equation

$$K\left(x,z\right)+F\left(x+z\right)+\underset{x}{\overset{\infty }{\int }}K\left(x,y\right)F\left(y+z\right)\mathrm{d}y=0$$

(69)

where

$$F\left(X\right)=\left[\begin{array}{cc}0& -\overline{f }(X)\\ f(X)& 0\end{array}\right]$$

(70)

$$f\left(X\right)=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}\rho (\lambda ){e}^{i\alpha \kappa X}\mathrm{d}\kappa -i\sum_{n=1}^{N}{c}_{n}\left(t\right){e}^{i\alpha {\lambda }_{n}X}$$

(71)

$$\overline{f }\left(X\right)=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}\overline{\rho }(\lambda ){e}^{-i\alpha \kappa X}\mathrm{d}\kappa +i\sum_{n=1}^{N}{\overline{c} }_{m}\left(t\right){e}^{-i\alpha {\overline{\lambda }}_{m}X}$$

(72)

$$\rho \left(\lambda \right)=\frac{b(\lambda )}{a(\lambda )}, \overline{\rho }\left(\lambda \right)=\frac{\overline{b }(\lambda )}{\overline{a }(\lambda )}$$

(73)

where $\rho \left(\lambda \right)$ and $\overline{\rho }\left(\lambda \right)$ are defined as reflection coefficients, while ${c}_{n}\left(t\right)$ and ${\overline{c} }_{m}\left(t\right)$ are defined as the normalizing coefficients given by

$${c}_{n}\left(t\right)=\frac{b}{\mathrm{d}a/\mathrm{d}\lambda }, {\overline{c} }_{m}\left(t\right)=\frac{\overline{b}}{\mathrm{d }\overline{a }/\mathrm{d}\lambda }$$

(74)

The solution of the matrix Marchenko Eq. (69) gives $K(x,z)$ from which and by using Eqs. (61, 62) we can recover the potentials $q(x)$ and $r(x)$.when $A\sim \delta (\lambda )$, $B\sim 0$ and $C\sim 0$ as $\left|x\right|\to \infty$ and $u\to 0$, the time evolution of scattering data can be evaluated as follow (see e.g. [20, 21])

$$ \begin{gathered} a\left( {\lambda ,t} \right) = a\left( {\lambda ,0} \right), \overline{a}\left( {\lambda ,t} \right) = \overline{a}\left( {\lambda ,0} \right) \hfill \\ b\left( {\lambda ,t} \right) = b\left( {\lambda ,0} \right)e^{ - 2\delta \left( \lambda \right)t} , \overline{b}\left( {\lambda ,t} \right) = \overline{b}\left( {\lambda ,0} \right)e^{2\delta \left( \lambda \right)t} \hfill \\ c_{n} \left( t \right) = c_{n} \left( 0 \right)e^{ - 2\delta \left( \lambda \right)t} , \overline{c}_{m} \left( t \right) = \overline{c}_{m} \left( 0 \right)e^{2\delta \left( \lambda \right)t} \hfill \\ \end{gathered} $$

(75)

Then from Remark (1), one can obtain the time evolution of the scattering data for Eq. (3) as follows

$$ \begin{gathered} a\left( {\lambda ,t} \right) = a\left( {\lambda ,0} \right), \overline{a}\left( {\lambda ,t} \right) = \overline{a}\left( {\lambda ,0} \right) \hfill \\ b\left( {\lambda ,t} \right) = b\left( {\lambda ,0} \right)e^{{\frac{i}{2\lambda }t}} , \overline{b}\left( {\lambda ,t} \right) = \overline{b}\left( {\lambda ,0} \right)e^{{\frac{ - i}{{2\lambda }}t}} \hfill \\ \end{gathered} $$

(76)

$${c}_{n}\left(t\right)={c}_{n}\left(0\right){e}^{\frac{i}{2{\lambda }_{n}}t}, n=\mathrm{1,2},\dots ,N$$

(77)

$${\overline{c} }_{m}\left(t\right)={\overline{c} }_{m}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{m}}t}, m=\mathrm{1,2},\dots ,\overline{N }$$

(78)

4 Travelling wave solutions for LGH Eq. (3)

In this section, we consider the reflectionless potential $\rho \left(\lambda \right)=\overline{\rho }\left(\lambda \right)=0$ and $N=\overline{N }=1$. Substitute by these considerations in Eqs. (70–78) we have

$$f\left(X\right)=-i{c}_{1}\left(0\right){e}^{\frac{i}{2{\lambda }_{1}}t+i\alpha {\lambda }_{1}X}$$

(79)

$$\overline{f }\left(X\right)=i{\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{1}}t-i\alpha {\overline{\lambda }}_{1}X}$$

(80)

Substituting Eqs. (79, 80) with the help of Eq. (70) into Eq. (69), we obtain the following system of equations

$${k}_{11}\left(x,z\right)-i{c}_{1}\left(0\right){e}^{\frac{i}{2{\lambda }_{1}}t+i\alpha {\lambda }_{1}z}\underset{x}{\overset{\infty }{\int }}{k}_{12}\left(x,y\right){e}^{i\alpha {\lambda }_{1}y}\mathrm{d}y=0$$

(81)

$${k}_{12}\left(x,\mathrm{z}\right)-i{\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{1}}t-i\alpha {\overline{\lambda }}_{1}x-i\alpha {\overline{\lambda }}_{1}z}-i{\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{1}}t-i\alpha {\overline{\lambda }}_{1}z}\underset{x}{\overset{\infty }{\int }}{k}_{11}\left(x,y\right){e}^{-i\alpha {\overline{\lambda }}_{1}y}\mathrm{d}y=0$$

(82)

$${k}_{21}\left(x,\mathrm{z}\right)-i{c}_{1}\left(0\right){e}^{\frac{i}{2{\lambda }_{1}}t+i\alpha {\lambda }_{1}x+i\alpha {\lambda }_{1}z}-i{c}_{1}\left(0\right){e}^{\frac{i}{2{\lambda }_{1}}t+i\alpha {\lambda }_{1}z}\underset{x}{\overset{\infty }{\int }}{k}_{22}\left(x,\mathrm{y}\right){e}^{i\alpha {\lambda }_{1}y}\mathrm{d}y=0$$

(83)

$${k}_{22}\left(x,\mathrm{z}\right)-i{\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{1}}t-i\alpha {\overline{\lambda }}_{1}z}\underset{x}{\overset{\infty }{\int }}{k}_{21}\left(x,y\right){e}^{-i\alpha {\overline{\lambda }}_{1}y}\mathrm{d}y=0$$

(84)

Starting from Eqs. (81) and (82), assume that

$$L\left(x,t\right)=i{c}_{1}\left(0\right){e}^{\frac{i}{2{\lambda }_{1}}t}\underset{x}{\overset{\infty }{\int }}{k}_{12}\left(x,y\right){e}^{i\alpha {\lambda }_{1}y}\mathrm{d}y$$

(85)

Then Eq. (81) become

$${k}_{11}\left(x,z\right)=L\left(x,t\right){e}^{i\alpha {\lambda }_{1}z}$$

(86)

Inserting Eq. (86) in Eq. (82), we have

$${k}_{12}\left(x,z\right)=i{\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{1}}t-i\alpha {\overline{\lambda }}_{1}x-i\alpha {\overline{\lambda }}_{1}z}+i{\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{1}}t-i\alpha {\overline{\lambda }}_{1}z}L\left(x,t\right)\underset{x}{\overset{\infty }{\int }}{e}^{i\alpha ({\lambda }_{1}-{\overline{\lambda }}_{1})y}\mathrm{d}y=0$$

(87)

Assume that ${\lambda }_{1}-{\overline{\lambda }}_{1}$ is pure imaginary, then Eq. (87) become

$${k}_{12}\left(x,z\right)=i{\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{1}}t-i\alpha {\overline{\lambda }}_{1}x-i\alpha {\overline{\lambda }}_{1}z}-\frac{{\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2{\overline{\lambda }}_{1}}t-i\alpha {\overline{\lambda }}_{1}z+i\alpha ({\lambda }_{1}-{\overline{\lambda }}_{1})x}L\left(x,t\right)}{\alpha \left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)}$$

(88)

Inserting Eq. (88) into Eq. (85), we obtain

$$L\left(x,t\right)=\frac{-i\alpha {c}_{1}\left(0\right){\overline{c} }_{1}\left(0\right)\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right){e}^{\left(\frac{-i\left({\lambda }_{1}-\overline{{\lambda }_{1}}\right)}{2{\uplambda }_{1}\overline{{\uplambda }_{1}}}\right)t+i\alpha ({\lambda }_{1}-2{\overline{\lambda }}_{1})x}}{{\alpha }^{2}{\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)}^{2}-{c}_{1}\left(0\right){\overline{c} }_{1}\left(0\right){e}^{\left(\frac{-i\left({\lambda }_{1}-\overline{{\lambda }_{1}}\right)}{2{\uplambda }_{1}\overline{{\uplambda }_{1}}}\right)t+2\alpha i\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)x}}$$

(89)

Inserting Eq. (89) into Eq. (88), we obtain

$${k}_{12}\left(x,x\right)=\frac{{i{\alpha }^{2}\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)}^{2}{\overline{c} }_{1}\left(0\right)}{{\alpha }^{2}{\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)}^{2}{e}^{\frac{i}{2\overline{{\lambda }_{1}}}t+2\alpha i{\overline{\lambda }}_{1}x}-{c}_{1}\left(0\right){\overline{c} }_{1}\left(0\right){e}^{\frac{i}{2{\lambda }_{1}}t+2\alpha i{\lambda }_{1}x}}$$

(90)

Then from Eq. (61)

$$q\left(x,t\right)=\frac{-2{i{\alpha }^{2}\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)}^{2}{\overline{c} }_{1}\left(0\right)}{{\alpha }^{2}{\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)}^{2}{e}^{\frac{i}{2\overline{{\lambda }_{1}}}t+2\alpha i{\overline{\lambda }}_{1}x}-{c}_{1}\left(0\right){\overline{c} }_{1}\left(0\right){e}^{\frac{i}{2{\lambda }_{1}}t+2\alpha i{\lambda }_{1}x}}$$

(91)

In similar way, by solving Eqs. (83, 84) and using Eq. (62) we obtain the potential $r(x,t)$ as

$$r\left(x,t\right)=\frac{-2{i{\alpha }^{2}\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)}^{2}{c}_{1}\left(0\right)}{{\alpha }^{2}{\left({\lambda }_{1}-{\overline{\lambda }}_{1}\right)}^{2}{e}^{\frac{-i}{2{\lambda }_{1}}t-2\alpha i{\lambda }_{1}x}-{c}_{1}\left(0\right){\overline{c} }_{1}\left(0\right){e}^{\frac{-i}{2\overline{{\lambda }_{1}}}t-2\alpha i{\overline{\lambda }}_{1}x}}$$

(92)

Case (1)

Let ${\lambda }_{1}=i\beta , \overline{{\lambda }_{1}}=-i\beta$, then according to the symmetry $q=-r$ we have from Eq. (91) and Eq. (92) that $\overline{{c }_{1}}\left(0\right)=-{c}_{1}\left(0\right)$, let ${c}_{1}\left(0\right)=2i\beta$, then at these symmetries, and since $\alpha ={m}^{2}$, the potentials $q(x,t)$ in Eq. (91) and $r(x,t)$ in Eq. (92) can be written as

$$q\left(x,t\right)=\frac{-4{m}^{4}\beta }{{m}^{4}{e}^{\frac{-1}{2\beta }t+2{m}^{2}\beta x}+{e}^{\frac{1}{2\beta }t-2{m}^{2}\beta x}}$$

(93)

And

$$r\left(x,t\right)=\frac{4{m}^{4}\beta }{{m}^{4}{e}^{\frac{-1}{2\beta }t+2{m}^{2}\beta x}+{e}^{\frac{1}{2\beta }t-2{m}^{2}\beta x}}$$

(94)

Since $q(x,t)=\frac{-\sqrt{6}n}{2m}{u}_{x}$ then

$$u\left(x,t\right)=\frac{8{m}^{5}\beta }{\sqrt{6}n}\int \frac{1}{{m}^{4}{e}^{\frac{-1}{2\beta }t+2{m}^{2}\beta x}+{e}^{\frac{1}{2\beta }t-2{m}^{2}\beta x}}\mathrm{d}x=\frac{2\sqrt{6}m}{3n}{\mathrm{tan}}^{-1}\left({m}^{2}{e}^{\frac{4{m}^{2}{\beta }^{2}x-t}{2\beta }}\right)$$

(95)

Use the transformation (4) we obtain the solution ${u}_{1}\left(X,T\right)$ for the LGH Eq. (3) as

$${u}_{1}\left(X,T\right)=\frac{2\sqrt{6}m}{3n}{\mathrm{tan}}^{-1}\left({m}^{2}{e}^{\frac{\left(4{m}^{2}{\beta }^{2}-1\right)X+\left(4{m}^{2}{\beta }^{2}+1\right)T}{4\beta }}\right)$$

(96)

where $m$ and $n$ are real parameters.

Case (2)

Let ${\lambda }_{1}$ and ${\overline{\lambda }}_{1}$ as defined in case (1) and assume that ${c}_{1}\left(0\right)=-{\overline{c} }_{1}\left(0\right)=2\beta$, then the potentials $q(x,t)$ in Eq. (91) and $r(x,t)$ in Eq. (92) can be written as

$$q\left(x,t\right)=\frac{4i{m}^{4}\beta }{{m}^{4}{e}^{\frac{-1}{2\beta }t+2{m}^{2}\beta x}-{e}^{\frac{1}{2\beta }t-2{m}^{2}\beta x}}$$

(97)

and

$$r\left(x,t\right)=\frac{-4i{m}^{4}\beta }{{m}^{4}{e}^{\frac{-1}{2\beta }t+2{m}^{2}\beta x}-{e}^{\frac{1}{2\beta }t-2{m}^{2}\beta x}}$$

(98)

Since $q(x,t)=\frac{-\sqrt{6}n}{2m}{u}_{x}$ then after integration with respect to $x$

$$u\left(x,t\right)=\frac{-8i{m}^{5}\beta }{\sqrt{6}n}\int \frac{1}{{m}^{4}{e}^{\frac{-1}{2\beta }t+2{m}^{2}\beta x}-{e}^{\frac{1}{2\beta }t-2{m}^{2}\beta x}}\mathrm{d}x=\frac{2\sqrt{6}im}{3n}{\mathrm{tanh}}^{-1}\left({m}^{2}{e}^{\frac{4{m}^{2}{\beta }^{2}x-t}{2\beta }}\right)$$

(99)

Use the transformation (4) we obtain another solution, ${u}_{2}\left(X,T\right)$, for the LGH Eq. (3) as

$${u}_{2}\left(X,T\right)=\frac{2\sqrt{6}im}{3n}{\mathrm{tanh}}^{-1}\left({m}^{2}{e}^{\frac{\left(4{m}^{2}{\beta }^{2}-1\right)X+\left(4{m}^{2}{\beta }^{2}+1\right)T}{4\beta }}\right)$$

(100)

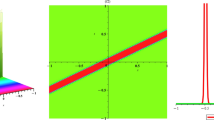
In Figs. 1 and 2 different solutions extracted from Eq. (96) are graphically represented with different values of $\beta ,m$ and $n$

Fig. 1

Soliton structure of the solution (96) for the values $\beta =0.4, m=1, n=1$

Fig. 2

Soliton structure of the solution (96) for the values $\beta =0.7, m=0.5, n=0.5$

In Figs. 3 and 4 different solutions extracted from Eq. (100) are graphically represented with different values of $\beta ,m$ and $n$

Fig. 3

Soliton structure of the solution (100) for the values $\beta =0.4, m=1, n=1$

Fig. 4

Soliton structure of the solution (100) for the values $\beta = 0.27, \;m = \sqrt 2 ,\; n = 1$

As we mentioned earlier that there exist some attempts for obtaining travelling wave solutions for LGH Eq. (3) in the literature.

5 Conclusion

In this article, we have investigated the Landau-Ginzburg-Higgs (LGH) equation which explain the superconductivity and drift cyclotron waves in radially inhomogeneous plasma for coherent ion-cyclotron waves by the aid of the inverse scattering transformation (IST) method. The integrability has been proved by deriving the Lax pair under a simple modification of Ablowitz-Kaup-Newell-Segur (AKNS) formalism. Different types of travelling wave solutions have been established and graphically represented in 2d and 3d profiles.