Abstract
In this paper, we study transverse and longitudinal oscillations and resonances in a hoisting system induced by boundary disturbances. The dynamics can be described by an initial-boundary value problem for a coupled system of nonlinear wave equations on a slowly time-varying spatial domain. It will be shown how the boundary excitations and the nonlinear terms influence transverse and longitudinal vibrations of the system. Firstly, due to the slow variation of the cable length, a singular perturbation problem arises. By using an interior layer analysis, many resonance manifolds are detected. Secondly, it will be shown that resonances in the system are caused not only by boundary disturbances but also by nonlinear interactions. Based on these observations, a three-timescales perturbation method is used to approximate the solution of the initial-boundary value problem analytically. It turns out that for special frequencies in the boundary excitations and for certain parameter values of the longitudinal stiffness and the conveyance mass, many oscillation modes jump up from small to large amplitudes in the transverse and longitudinal directions. Finally, numerical simulations are presented to verify the obtained analytical results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Within the last decades, hoisting systems are widely used for transportation of objects to a large height or depth. Such systems consist of a drum, a head sheave, a driving motor, a flexible hoisting cable with time-varying length, and a hoisting conveyance moving along two guiding ropes. When the flexible hoisting cable’s bending stiffness is not considered, the mathematical model for this system can be described as an axially moving string with a time variable length [1]. Compared with rigid structures, the flexible cable has many advantages, such as low costs, high speeds, and high load carrying capacities, which are applied in various engineering fields, for instance, elevators [2], marine risers [3, 4], suspension bridges [5, 6], medical rescue systems [7], etc. In hoisting processes [8, 9], vibration-induced structural failure for hoisting cables may occur due to external disturbances such as airflows or earthquakes, or due to other internal or external excitations. These failures are usually related to internal or external resonances. Resonance refers to the phenomenon that a small periodic excitation can produce large vibrations when the frequency of the external or internal excitation is close to one of the natural frequencies of the system. In most cases resonance is harmful, it will not only lead to significant deformations and dynamic stress, but also leads to accidents. Therefore, it is important to develop advanced analytical models to figure out the nature of these large vibrations in moving media.
There is an abundance of papers on the analysis of moving flexible string models. Some researchers focus on traveling strings defined on a fixed domain, and other researchers focus on traveling strings subject to moving boundaries. For the analysis on the fixed domain: Zhu et al. in [10] considered a constrained translating cable with a spring-mass-dashpot located at any position along the cable. They determined asymptotic approximations of the eigenvalues of the system. Nguyen and Hong in [11] investigated an active control scheme for an axially moving cable system by employing the Lyapunov method. The controller suppresses the vibrations and regulates the transport velocity of the cable to track a desired moving velocity profile. Gaiko and van Horssen in [12] considered transverse vibrations of a traveling string with a spring-mass-dashpot boundary. They constructed approximations of the solutions and eigenvalues on a long timescale. For the analysis on the moving boundaries: Zhu in [13] considered the transverse vibration stability of a class of translating media with an arbitrarily varying length from energy standpoint. Sandilo and van Horssen in [14] studied the vertically translating string with a time varying length and a space–time-varying tension by an interior layer analysis. Gaiko and van Horssen in [15] discussed resonances and vibrations in an elevator cable system due to boundary sway by using a multiple timescales perturbation method. Wang et al. in [16] studied resonances of transversally vibrating cables for a fixed domain, in which resonances are induced by an external force and a time-dependent coefficient in a Robin boundary condition. This problem may serve as a simplified model describing longitudinal vibrations (see also [17]) as well as resonances in axially moving strings for which the length changes in time.
In recent years, researchers found that, due to external excitation and loading conditions, the nonlinear interactions between transverse and longitudinal string motions may influence the vibration behaviour in two directions when the hoisting conveyance is moving up or down. Some research has been conducted on similar types of problems by using numerical simulations. Crespo et al. in [18] introduced a stationary high-rise elevator cable system model and presented its numerical simulations. Wang et al. in [19] investigated a coupled dynamic model for a flexible guiding hoisting system and presented the response of the system by numerical simulations. In this paper, we will construct analytical approximate solutions for the nonlinear coupled transverse and longitudinal vibration string problem with time-varying length.
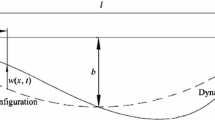
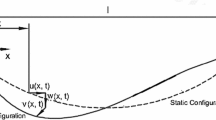
The hoisting system considered in this paper is described by a vertically translating string with a time-varying length and a mass attached at one of the ends of the string. The time-varying length of the string is given by \(l(t) = l_0 + vt\), where \(l_0\) is the cable initial length, and v is the longitudinal velocity of the hoisting cable, and where \(l_0\), v are constants. It is assumed that the axial velocity of the string is small compared to nominal wave velocity, and that the string mass is small compared to cage mass. The system is excited at the upper end by small displacements in the horizontal and vertical directions from its equilibrium position caused by, for instance, wind forces (see Fig. 1). By Hamilton’s principle, the model can be written as a coupled system of nonlinear wave equations (in transverse and longitudinal directions) on a slowly time-varying spatial domain. The string is excited at a boundary by two harmonic functions in the horizontal and in the vertical directions. The main objective of this paper is to study how the boundary excitations and nonlinear interactions between the two motion directions influence the vibration behaviour in the transverse and in the longitudinal directions for the moving string. In contrast to previous research, where only the transverse or the longitudinal vibration behaviour was studied, the coupled model is more accurate. However, the appearance of nonlinear and coupled terms increases the complexity of the system analysis. For the problem with nonlinearly coupled terms, and with moving boundary conditions, the traditional (analytical) methods, such as the method of separation of variables (SOV), and the (equivalent) Laplace transform method, can usually not be applied. In order to deal with these difficulties, perturbation methods and an internal layer analysis are used in this paper to approximate the vibrations and the resonances, including determining the resonance amplitudes and the size of the resonance zones. Based on this analysis, solutions of the coupled initial-boundary value problem for the transverse and the longitudinal motions can be predicted analytically. To the best of our knowledge, the results about analytical approximations of the solutions have not been proposed for the coupled transverse and longitudinal vibrations of the moving cable system until now.
The remaining part of this paper is organized as follows. In Sect. 2, the problem is formulated. In Sect. 3, the problem is reformulated from a partial differential equations formulation to an ordinary differential equations formulation by using the method of separation of variables. Many resonance manifolds for the transverse and longitudinal motions are detected by an inner layer analysis. In Sect. 4, approximate solutions are constructed analytically for the transverse and longitudinal motions by using a three-timescales perturbation method. In Sect. 5, some numerical approximations are presented by using a central finite difference scheme to validate the theoretical results from Sect. 4. Finally, in the last section we draw some conclusions.
2 Formulation of the physical system
2.1 Modelling of the problem
In this section, the mathematical model of the hoisting system is described and the equations for the transverse and the longitudinal motions of the system are derived and explained.
Nomenclature | |
|---|---|
w(x, t) | the transverse displacement |
u(x, t) | the longitudinal displacement |
l(t) | the length of the hoisting cable |
\(v={\dot{l}}(t)\) | the longitudinal velocity of the hoisting cable |
\({{\hat{a}}}=\ddot{l}(t)\) | the longitudinal acceleration of the hoisting cable |
\(\rho \) | the linear density of the hoisting cable |
m | the mass of the hoisting conveyance |
EA | the longitudinal stiffness, |
E Young’s elasticity modulus, A the cross-sectional area | |
T(x, t) | the spatiotemporally varying tension in hoisting cable |
\(c_{1}\), \(c_{2}\) | transverse and longitudinal viscous damping coefficients |
in hoisting cable | |
g | the standard gravity |
\(E_{gs}\) | initial gravitational potential energy |
\(c_{u}\) | longitudinal viscous damping coefficient |
in hoisting conveyance | |
\(e_{w}(t)\), \(e_{u}(t)\) | the transverse and longitudinal fundamental excitations |
at the top of the hoisting cable | |
\(e_{w}(t)=\beta _{1} cos(\omega _{1} t+\alpha )\), \(e_{u}(t)=\beta _{2} cos(\omega _{2} t)\) | |
\(\beta _{1}\), \(\beta _{2}\) | the amplitudes of the transverse and longitudinal |
fundamental excitations | |
\(\alpha \) | primary phase of the transverse fundamental excitation |
By using Hamilton’s principle [20], the mathematical problem for the vibrating cable (Fig. 1) can be written as an initial boundary value problem for the transverse vibration (see also Appendix A):
and as an initial boundary value problem for the longitudinal vibration:
where \(z=u_{x}+\frac{1}{2}w_{x}^{2}\) and
In this paper, we use the following assumptions for the parameters and functions:
-
The longitudinal velocity v is small compared to the wave velocities \(\sqrt{\frac{EA}{\rho }}\) and \(\sqrt{\frac{mg}{\rho }}\), that is, \(v=\varepsilon v_{0}\);
-
The nominal wave velocities \(\sqrt{\frac{EA}{\rho }}\) and \(\sqrt{\frac{mg}{\rho }}\) are of the same order of magnitude, that is, \(\frac{EA}{mg}=O(1)\), \(\sqrt{\frac{EA}{mg}}> 1\), and \(\frac{EA}{mg}\) is not near 1, i.e. \(\sqrt{\frac{EA}{mg}}-1>>O(\varepsilon )\);
-
The cable mass \(\rho L\) is small compared to the car mass m (L is the maximum length of the cable), that is, \(\mu =\frac{\rho L}{m}=\varepsilon \mu _{0}\);
-
The viscous damping parameters \(c_{1}\), \(c_{2}\), and \(c_{u}\) are small, that is, \(c_{1}=\varepsilon c_{1,0}, c_{2}=\varepsilon c_{2,0}, c_{u}=\varepsilon c_{u,0}\);
-
The fundamental excitations at the top of the hoisting rope are small, and the longitudinal excitation is smaller than the transverse excitation, that is, \(\beta _{1}=\varepsilon \beta _{1,0}, \beta _{2}=\varepsilon ^{2}\beta _{2,0}\);
-
The initial conditions \(w_{0}(x)=O(\varepsilon ), w_{1}(x)=O(\varepsilon ), u_{0}(x)=O(\varepsilon ^{2})\) and \(u_{1}(x)=O(\varepsilon ^{2})\);
-
For convenience, we only consider a non-accelerating cable, that is, the cable length \(l(t)=l_{0}+vt\) and \({{\hat{a}}}=0\), where \(l_{0}\) is the initial string length.
In the above assumptions, \(v_{0}\), \(\mu _{0}\), \(c_{1,0}\), \(c_{2,0}\), \(c_{u,0}\), \(\beta _{1,0}\), \(\beta _{2,0}\), \(\alpha \) m, \(\rho \), \(\omega _{1}\), \(\omega _{2}\), L, and \(l_{0}\) are positive constants and are of order 1, and \(\varepsilon \) is a small parameter with \(0<\varepsilon<<1\).
To put Eq. (1) and (2) into non-dimensional forms, the following dimensionless variables and parameters are used:
The initial boundary value problem for the transverse motion in non-dimensional form becomes:
and the initial boundary value problem for the longitudinal motion in non-dimensional form becomes:
where the asterisks (indicating the dimensionless variables and parameters) are omitted in the problems (4) and (5) for convenience.
2.2 Transformations of the problem
In order to convert the time-varying spatial domain \([\beta _{2} cos(\omega _{2} t), l(t)]\) for x to a fixed domain [0,1] for \(\xi \), a new independent spatial coordinate \( \xi =\frac{x-\beta _{2} cos(\omega _{2} t)}{h(t)}\), where \(h(t)=l(t)-\beta _{2} cos(\omega _{2} t)\), is introduced. After this spatial transformation, new dependent variables \({\bar{w}}(\xi , t) = w(x,t)\), \({\bar{u}}(\xi , t) = u(x,t)\), and all the partial derivatives have to be rewritten as follows:
Then, the equation for the transverse motion becomes:
where \({\bar{w}}_{0}(\xi )=w_{0}(\xi l_{0}+\beta _{2}(1-\xi ))\) and \({\bar{w}}_{1}(\xi )=w_{1}(\xi l_{0}+\beta _{2}(1-\xi ))\). It should be observed that the order of the term \(-\frac{EA}{mgh^{3}(t)}({\bar{u}}_{\xi }{\bar{w}}_{\xi })_{\xi }\) in (6) is unknown a priori due to possibly occurring resonances. So, we keep this term explicitly in the equation, and analyse it later. The equation for the longitudinal motion then becomes:
where \({\bar{u}}_{0}(\xi )=u_{0}(\xi l_{0}+\beta _{2}(1-\xi ))\) and \({\bar{u}}_{1}(\xi )=u_{1}(\xi l_{0}+\beta _{2}(1-\xi ))\). The orders of the term \( -\frac{EA}{mgh^{3}(t)} {\bar{w}}_{\xi }{\bar{w}}_{\xi \xi }\) and the term \(\frac{\mu EA}{2mgh^{2}(t)} {\bar{w}}^{2}_{\xi }(1,t)\) in (7) are unknown a priori due to possible resonances. So, we keep these terms in the equation, and analyse them later.
In order to eliminate the time-variable coefficients in \(\frac{1}{h^{2}(t)}{\bar{w}}_{\xi \xi }\) and in \(\frac{EA}{mgh^{2}(t)} {\bar{u}}_{\xi \xi }\) in the initial boundary problems (6) and (7), the Liouville–Green transformation (see also the WKBJ method [25] [26]) is introduced with \(\frac{ds}{dt}=\frac{1}{l(t)}\). In accordance with a new time variable s, all the partial derivatives have to be rewritten as follows:
Substituting these derivatives into the problem (6), the initial boundary value problem for the transverse motion becomes:
The initial boundary value problem for the longitudinal motion becomes:
The initial boundary value problem (9) can further be rewritten as
In order to eliminate the non-homogenous terms in the boundary conditions in (8) and in (10), the following transformations are used:
Then, the initial boundary value problem in the transverse direction becomes:
where according to the initial condition assumptions, the terms in “h.o.t.”, consisting of \(O(\varepsilon {\hat{u}})\), \(O(\varepsilon ^{2}{\hat{w}})\), \(O(\varepsilon {\hat{w}}^{2})\), \(O(\varepsilon {\hat{u}}{\hat{w}})\) and \(O(\varepsilon {\hat{w}}^{3})\), cannot influence the lowest order of the solution of problem (13) on timescales of \(O(\frac{1}{\varepsilon })\).
The initial boundary value problem in the longitudinal direction then becomes:
where according to the initial condition assumptions, the terms in \(O(\varepsilon {\hat{w}}^{2})\), \(O(\varepsilon ^{2}{\hat{u}})\), \(O(\varepsilon ^{2}{\hat{w}})\), and \(O(\varepsilon ^{3})\) cannot influence the lowest order of the solution \({\hat{u}}(\xi ,s)\) in problem (14) on timescales of \(O(\frac{1}{\varepsilon })\), so they can be neglected in the further analysis. In the following sections, the solutions of \({\hat{w}}(\xi ,s), {\hat{u}}(\xi ,s)\) in problem (13) and (14) will be approximated by using an interior layer analysis and a three-timescales perturbation method.
3 Inner layer analysis
It will be shown that an interior layer analysis (including a rescaling and balancing procedure) leads to a description of an (un-)expected resonance manifold and leads to timescales which describe the solutions of the partial differential equations (13) and (14) sufficiently accurately. To derive the solutions \({\hat{w}}(\xi ,s)\) and \({\hat{u}}(\xi ,s)\) in problem (13) and (14), firstly the method of separation of variables is employed. In accordance with the method of separation of variables, the general solution of the transverse problem (13) can be expanded in the following form:
and the general solution of the longitudinal problem (14) can be expanded in the following form:
Substituting (15) into the initial boundary value problem (13), and substituting (16) into problem (14), further by multiplying the obtained equations with \(\sin (k\pi \xi )\), and by integrating with respect to \(\xi \) from \(\xi =0\) to \(\xi =1\), and by using the orthogonality properties of the sin-functions on \(0<\xi <1\), we obtain the following ordinary differential equations for \( T_{k}(s)\) (with \(k=1,2,3,...\)) in the transverse direction:
where
where \(F_{k}=O(\varepsilon )\) and \(G_{k}=O(\varepsilon )\). \(c^{1}_{n,k}\), \(c^{2}_{n,k}\), \(c^{3}_{n,k}\) and \(d_{k}\) are given by:
Further, the differential Eq. (17) can be written as:
where \(T_{k}(0)\) and \(T_{k,s}(0)\) are given by (18), \(c^{1}_{n,k}\), \(c^{2}_{n,k}\), \(c^{3}_{n,k}\) and \(d_{k}\) are given by (19). Note that the term “h.o.t.”(including \(T_{n}T_{p}T_{j}\) in (17)) cannot influence the lowest order of the solution of the differential Eq. (20) on timescales of \(O(\frac{1}{\varepsilon })\). This can be seen as follows. When the addition or subtraction of the three subscripts in \(T_{n}T_{p}T_{j}\) equals to k or \(-k\), then for the given initial conditions of \(O(\varepsilon )\), \(T_{n}T_{p}T_{j}\) leads to \(O(\varepsilon ^{2})\) contributions in the solution of the differential Eq. (20) on timescales of \(O(\frac{1}{\varepsilon })\); otherwise, \(T_{n}T_{p}T_{j}\) will lead to contributions of \(O(\varepsilon ^{3})\) in the solution of the differential Eq. (20) on timescales of \(O(\frac{1}{\varepsilon })\).
Similarly, we obtain the following differential equations for \(Y_{k}\) ( with \(k=1,2,3,...\)) in the longitudinal direction:
where \(f_{k}=O(\varepsilon ^{2})\) and \(g_{k}=O(\varepsilon ^{2})\). \(d^{1}_{n,k}\), \(d^{3}_{n,k}\), \(d_{n,j}^{4}\), \(d_{1,k}\), \({\tilde{d}}_{k,k}^{4}\) are given by:
Before approximately solving the ordinary differential Eqs. (20) and (21), according to an inner layer analysis process (see also [16]), we can make the following remarks beforehand. For the given initial conditions for \(Y_{k}\) (which are of \(O(\varepsilon ^{2})\)), the terms in the right-hand side of Eq. (21) can lead to different contributions in the solution \(Y_{k}\) on timescales of \(O(\frac{1}{\varepsilon })\). The first three terms in the right-hand side of Eq. (21) only lead to contributions of \(O(\varepsilon ^{2})\). The coupled, nonlinear terms including \(T_{p}T_{j}\) can lead to contributions up to \(O(\frac{1}{\varepsilon }T_{p}T_{j})\), and the term with frequency \(\omega _{1}\) lead to contributions up to \(O(\sqrt{\varepsilon }T_{k})\). The term with frequency \(\omega _{2}\) can lead to contributions up to \(O(\varepsilon \sqrt{\varepsilon })\). Since \(T_{k}\) may increase from the initial state order of \(O(\varepsilon )\) to lower orders, the orders of the terms including \(T_{p}T_{j}\) determine that of the solution \(Y_{k}\). Therefore, the solution of Eq. (21) can be approximated as \(Y_{k}=O(\frac{1}{\varepsilon }T_{p}T_{j})\). Similarly, we obtain that for the given initial conditions for \(T_{k}\) ( which are of \(O(\varepsilon )\)), terms in the right-hand side of Eq. (20) can also have different contributions to the solution \(T_{k}\) on timescales of \(O(\frac{1}{\varepsilon })\). The first five terms in the right-hand side of Eq. (20) only can lead to contributions of \(O(\varepsilon )\). Based on the fact that \(Y_{k}=O(\frac{1}{\varepsilon }T_{p}T_{j})\), terms including \(Y_{p}T_{j}\) can lead to contributions up to \(O(\varepsilon )\), and the last term with frequency \(\omega _{1}\) can lead to contributions up to \(O(\sqrt{\varepsilon })\). This implies that in Eq. (20) only the external forcing with frequency \(\omega _{1}\) produces resonance, and leads to a jump in the solution \(T_{k}\) from \(O(\varepsilon )\) to \(O(\sqrt{\varepsilon })\). Further, it follows from Eq. (21) that the coupled terms including \(T_{p}T_{j}\) produce maximum amplitude responses, and the amplitude responses depend on the solution \(T_{k}\) of Eq. 20).
After the above made observations, to obtain the (un-)expected resonance manifolds which describe the solutions of ordinary differential Eqs. (20) and (21) sufficiently accurately, the following standard transformations are introduced:
where \(\lambda _{k}=\sqrt{\frac{EA}{mg}}k\pi \). The transverse problem (20) can now be rewritten in the following form (where the dot \(\cdot \) represents differentiation with respect to s):
Large transverse amplitude responses in (23) and (24), due to the external forcing with frequency \(\omega _{1}\), can be expected when \(k\pi -\omega _{1}{\dot{\chi }}(s)\approx 0\), or \(k\pi +\omega _{1}{\dot{\chi }}(s)\approx 0\). But since \(k\pi >0\) and \(\omega _{1}{\dot{\chi }}(s)>0\), resonance only will occur when
So, transverse resonances are expected for times s around \(s^{(k)}\) with
To study the situation in the transverse resonance zone, we introduce time-like variables
and rescale \(\tau -\tau ^{(k)}=\delta (\varepsilon ){\hat{\tau }}\) with \({\hat{\tau }}=O(1)\) and \(\tau ^{(k)}=\varepsilon s^{(k)}=\frac{1}{ v_{0}}\ln (\frac{k\pi }{\omega _{1}l_{0}})\). Then
and \({\dot{A}}_{1,k}(s)\), \({\dot{B}}_{1,k}(s)\) are given by (23). It now follows that a balance in system (27) occurs when \(\frac{\varepsilon }{\delta (\varepsilon )}=\delta (\varepsilon )\), and this implies that in the transverse resonance zone that \(\delta (\varepsilon )=\sqrt{\varepsilon }\), i.e. the size of transverse resonance zone is \(O(\frac{1}{\sqrt{\varepsilon }})\) for times s. So, together with \(\tau -\tau ^{(k)}=\delta (\varepsilon ){\hat{\tau }}\), it follows from (27) that
Further, from (27), we obtain \(\psi _{k}(s)=\psi _{k}(s^{(k)})+\frac{1}{2}\omega _{1} l_{0}v_{0} \textrm{e}^{ v_{0}\tau ^{(k)}}\varepsilon (s-s^{(k)})^{2}\). Hence, in the transverse resonance zone, we can write
where \(\psi _{k}(s^{(k)})=k\pi s^{(k)}-\frac{k\pi -\omega _{1} l_{0}}{\varepsilon v_{0}}-\alpha \).
So far it can be concluded that the resonance responses for \(Y_{k}\) in (21) depend on the terms including \(T_{p}T_{j}\), and the resonance responses for \(T_{k}\) in (20) depend on the terms with frequency \(\omega _{1}\). So, based on the inner layer analysis, the size of the resonance zones has been obtained, and this size will also be used as a new asymptotic scale to be introduced in the three-timescale perturbation method in the next section of this paper to study problems (20) and (21) in detail, and to construct asymptotic approximations of the solutions of the initial-boundary value problems (13) and (14).
4 Three-timescales perturbation method
In the previous section, it was shown that (under certain condition on the external frequency \(\omega _{1}\)) resonances in the transverse direction can occur around time \(s=\frac{1}{\varepsilon v_{0}}\ln (\frac{k\pi }{\omega _{1}l_{0}})\), and that resonances in the longitudinal direction depend on the solutions \(T_{k}\) of Eq. (20). For this reason, we rescale s by defining \(s={\tilde{s}}+\frac{1}{\varepsilon v_{0}}\ln (\frac{k\pi }{\omega _{1}l_{0}})\). Thus, problem (20) can be rewritten in \({\tilde{s}}\) as follows:
and problem (21) can be rewritten in \({\tilde{s}}\) as follows:
Next, we study problems (30) and (31) in detail under the assumption that \(\omega _{1}\) is such that a resonance zone exits for the \(k^{th}\) oscillation mode. The application of the straightforward expansion method to solve (30) and (31) will result in the occurrence of so-called secular terms which cause the approximations of the solutions to become unbounded on long timescales. For this reason, to remove secular terms, and to obtain approximations which are valid on long timescales, we introduce three timescales \(s_{0}={\tilde{s}}\), \(s_{1}=\sqrt{\varepsilon }{\tilde{s}}\), \(s_{2}=\varepsilon {\tilde{s}}\). The timescale \(s_{1}=\sqrt{\varepsilon }{\tilde{s}}\) is introduced because of the size of the resonance zone which has been found in the previous section, and the other two timescales are the natural scalings for nonlinear equations such as (30) and (31). By using the three-timescales perturbation method, the functions \(T_{k}({\tilde{s}};\sqrt{\varepsilon })\) and \(Y_{k}({\tilde{s}};\sqrt{\varepsilon })\) are supposed to be functions of \(s_{0}\), \(s_{1}\) and \(s_{2}\),
By substituting \({\widetilde{T}}_{k}(s_{0}, s_{1}, s_{2})\) and \({\widetilde{Y}}_{k}(s_{0}, s_{1}, s_{2})\) into the differential Eq. (20), we obtain the following equations up to \(O(\varepsilon \sqrt{\varepsilon })\):
where \({\tilde{F}}_{k}=O(1)\) and \({\tilde{G}}_{k}=O(1)\). Similarly, by substituting \({\widetilde{T}}_{k}(s_{0}, s_{1}, s_{2})\), \({\widetilde{Y}}_{k}(s_{0}, s_{1}, s_{2})\) into the differential Eq. (21), we obtain the following equations up to \(O(\varepsilon \sqrt{\varepsilon })\):
where \(\lambda _{k}=\sqrt{\frac{EA}{mg}}k\pi \), \({\tilde{f}}_{k}=O(1)\), \({\tilde{g}}_{k}=O(1)\), and
Since the functions \({\tilde{T}}_{k}\) and \({\tilde{Y}}_{k}\) can increase in s from the initial state orders to \(O(\sqrt{\varepsilon })\) as has been shown in the previous section, a three-timescales perturbation method will be used, and \({\tilde{T}}_{k}(s_{0}, s_{1}, s_{2})\) and \({\tilde{Y}}_{k}(s_{0}, s_{1}, s_{2})\) will be approximated by the following formal asymptotic expansions:
where \({\tilde{T}}_{k,0}, {\tilde{T}}_{k,1}, {\tilde{T}}_{k,2}, {\tilde{Y}}_{k,0}, {\tilde{Y}}_{k,1}, {\tilde{Y}}_{k,2}\) are all functions of O(1). In the transverse direction, by substituting (35) and (36) into problem (32), and after equating the coefficients of like powers in \(\sqrt{\varepsilon }\), we obtain: the \(O(\sqrt{\varepsilon })\)-problem:
the \(O(\varepsilon )\)-problem:
and the \(O(\varepsilon \sqrt{\varepsilon })\)-problem:
The solution of the \(O(\sqrt{\varepsilon })\)-problem (37) can be written as:
where \(A_{k}(b,c)=0\), \(B_{k}(b,c)=0\), and where \(A_{k}(s_{1}, s_{2})\), \(B_{k}(s_{1}, s_{2})\) can be obtained explicitly by solving the \(O(\varepsilon )\)-problem (38) and the \(O(\varepsilon \sqrt{\varepsilon })\)-problem (39). We will study these problems later in this section.
In the longitudinal direction, by substituting (35) and (36) into problem (33), and after equating the coefficients of like powers in \(\varepsilon \), we obtain: the \(O(\sqrt{\varepsilon })\)-problem:
the \(O(\varepsilon )\)-problem:
and the \(O(\varepsilon \sqrt{\varepsilon })\)-problem:
where \(\lambda _{k}=\sqrt{\frac{EA}{mg}}k\pi \).
The solution of the \(O(\sqrt{\varepsilon })\)-problem (41) can be written as:
where \(C_{k}(s_{1}, s_{2})\), and \(D_{k}(s_{1}, s_{2})\) are still unknown functions in the slow variables \(s_{1}\) and \(s_{2}\), and these functions can be determined by avoiding secular terms in the \(O(\varepsilon )-\) problem (42) and in the \(O(\varepsilon \sqrt{\varepsilon })-\) problem (43). By using the initial conditions in (41), it follows that \(C_{k}(b,c)=D_{k}(b,c)=0\). Now, we shall solve the \(O(\varepsilon )-\) problem (42). By using (40) for \({\tilde{T}}_{k,0}\), and by using \(d^{1}_{k,k}=-\frac{1}{2k\pi }\), which is given in (22), problem (42) can be written as:
It is obvious that the right-hand side of (45) contains resonant terms, such as \(\sin (\lambda _{k}s_{0})\) and \(\cos (\lambda _{k}s_{0})\). But the term in the right-hand side of (45) involving \(\sin ((2j-k)\pi s_{0}), \cos ((2j-k)\pi s_{0}), \sin ((k+2j)\pi s_{0})\) or \(\cos ((k+2j)\pi s_{0})\) is also a resonant term when there exist \(k, j_{1}, j_{2}\), s.t., \(\frac{2 j_{1}}{k}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{k}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\). Actually, for any fixed parameter value of \(\sqrt{\frac{EA}{mg}}\) with assumptions \(\sqrt{\frac{EA}{mg}}=O(1)\) and \(\sqrt{\frac{EA}{mg}}-1>O(\varepsilon )\), there always exist k s.t. \(\frac{2 j_{1}}{k}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{k}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\) with \(j_{1}=\frac{(1+\sqrt{\frac{EA}{mg}})k}{2}\) and \(j_{2}=\frac{(\sqrt{\frac{EA}{mg}}-1)k}{2}\). Therefore, to avoid secular terms in (45) the functions \(C_{k}(s_{1}, s_{2})\) and \(D_{k}(s_{1}, s_{2})\) have to satisfy the following:
-
When k does not satisfy the conditions that there always exist \(j_{1}, j_{2}\) s.t. \(\frac{2 j_{1}}{k}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{k}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\), then:
and \(C_{k}(s_{1}, s_{2})\) and \(D_{k}(s_{1}, s_{2})\) are given by:
-
When k satisfies the conditions that there always exist \(j_{1}, j_{2}\) s.t. \(\frac{2 j_{1}}{k}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{k}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\), then:
and \(C_{k}(s_{1}, s_{2})\) and \(D_{k}(s_{1}, s_{2})\) can be obtained as:
where the functions \({\tilde{P}}_2\) and \({\tilde{Q}}_2\) are given by (48), and where \({\overline{C}}_{k}(s_{2})\) and \({\overline{D}}_{k}(s_{2})\) in (47) and (49) are still unknown functions in the slow variable \(s_{2}\). By \(C_{k}(b, c)=0\) and \(D_{k}(b, c)=0\), we obtain that \({\overline{C}}_{k}(c)=0\) and \({\overline{D}}_{k}(c)=0\). The undetermined behaviour with respect to \(s_{2}\) can be used to avoid secular terms in the solution of the \(O(\varepsilon \sqrt{\varepsilon })-\) problem (43).
According to (45), taking into account the secularity conditions, the general solution of the \(O(\varepsilon )-\) problem (42) is given by
where
Then, the \(O(\varepsilon \sqrt{\varepsilon })-\) problem (43) can be written as:
Note that in the analysis of Sect. 3, the last term including \(\cos (\omega _{1} \chi (s_{0}-a)+\alpha )\) in (52) can not affect the function \({\tilde{Y}}_{k,0}\). So, to avoid secular terms in the solution \({\tilde{Y}}_{k,2}\) in Eq. (52), the following different cases have to be considered:
-
When k does not satisfy the conditions that there always exist \(j_{1}, j_{2}\) s.t. \(\frac{2 j_{1}}{k}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{k}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\), then:
$$\begin{aligned}{} & {} -2\frac{\partial ^{2}E_{k}}{\partial s_{0}\partial s_{1}}-2\lambda _{k}\frac{\partial H_{k}}{\partial s_{1}}\nonumber \\{} & {} \quad =2\lambda _{k}\frac{\partial {\overline{D}}_{k}}{\partial s_{2}}-(v_{0}-c_{2,0}{\hat{l}})\lambda _{k}{\overline{D}}_{k}\nonumber \\{} & {} \qquad -2v_{0}k\pi d_{k,k}^{1}\lambda _{k}{\overline{D}}_{k} +\frac{EA}{mg}\mu _{0}{\hat{l}}k\pi d_{k,k}^{3}{\overline{C}}_{k},\quad \nonumber \\{} & {} \qquad -2\frac{\partial ^{2}H_{k}}{\partial s_{0}\partial s_{1}}+2\lambda _{k}\frac{\partial E_{k}}{\partial s_{1}}\nonumber \\{} & {} \quad =-2\lambda _{k}\frac{\partial {\overline{C}}_{k}}{\partial s_{2}}+(v_{0}-c_{2,0}{\hat{l}})\lambda _{k}{\overline{C}}_{k}\nonumber \\{} & {} \qquad +2v_{0}k\pi d_{k,k}^{1}\lambda _{k}{\overline{C}}_{k} +\frac{EA}{mg}\mu _{0}{\hat{l}}k\pi d_{k,k}^{3}{\overline{D}}_{k}.\quad \end{aligned}$$(53) -
When k satisfies the conditions that there always exist \(j_{1}, j_{2}\) s.t. \(\frac{2 j_{1}}{k}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{k}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\), then:
Solving (53) and (54) for \(E_{k}\) and \(H_{k}\), we observe that the solution will be unbounded in \(s_{0}\) and \(s_{1}\), due to terms which are only depending on \(s_{2}\). Therefore, to have secular-free solutions for \(E_{k}\) and \(H_{k}\), the following conditions have to be imposed independently:
Due to \(d^{2}_{k,k}=-\frac{1}{2k\pi }\), we then obtain from (55):
Since \({\overline{C}}_{k}(c)=0\) and \({\overline{D}}_{k}(c)=0\), this implies that
Now, all unknown functions in (44) can be determined, and the solution of the \(O(\sqrt{\varepsilon })\)-problem (41) can be written as:
where \(C_{k}(s_{1}, s_{2})\) and \(D_{k}(s_{1}, s_{2})\) are given by (47), (49) and (56).
Now, substituting (40) and (57) into the \(O(\varepsilon )\)-problem (38) for \({\tilde{T}}_{k,1}\), together with \(c^{1}_{k,k}=\frac{1}{2}\), \(c^{2}_{k,k}=0\) and \(c^{3}_{k,k}=-\frac{1}{2k\pi }\) in (19), problem (38) becomes a nonlinear ordinary differential equation without coupling term:
where \(C_{p}\) and \(D_{p}\) are given by (47) and (49). The right-hand side of Eq. (58) contains resonant terms: for instance, at least one of the I terms is a resonant term when there exist \(k, p_{1}, p_{2}\) s.t. \(\frac{2 k}{p_{1}}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 k}{p_{2}}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\). The II term with \(\omega _{1}\) can be resonant when \(k\pi -\omega _{1} {\dot{\chi }}(s)\approx 0\) or \(k\pi +\omega _{1} {\dot{\chi }}(s)\approx 0\). Obviously, the terms in (58) involving \(\sin (k\pi s_{0})\) or \(\cos (k\pi s_{0})\) are resonant.
Outside the resonance zone (or equivalently the resonance manifold), the corresponding timescales are \(s_{0}={\tilde{s}}\) and \(s_{2}=\varepsilon {\tilde{s}}\) (without \(s_{1}=\sqrt{\varepsilon }{\tilde{s}}\)). So to avoid secular terms in (58), \(A_{k}\) and \(B_{k}\) have to satisfy the following equations depending on the parameter values:
which implies that:
where \({\overline{A}}_{k}(s_{2})\) and \({\overline{B}}_{k}(s_{2})\) are still unknown functions in the slow variable \(s_{2}\). Since \(A_{k}(b, c)=0\) and \(B_{k}(b, c)=0\), we obtain that \({\overline{A}}_{k}(c)=0\) and \({\overline{B}}_{k}(c)=0\). The undetermined behaviour with respect to \(s_{2}\) can be used to avoid secular terms in the \(O(\varepsilon \sqrt{\varepsilon })-\) problem (39). According to (58), taking into account the secularity conditions, the general solution of the \(O(\varepsilon )-\) problem (38) can be written as
where
Then, together with \(c^{1}_{k,k}=\frac{1}{2}\), \(c^{2}_{k,k}=0\) and \(c^{3}_{k,k}=-\frac{1}{2k\pi }\) in (19), the \(O(\varepsilon \sqrt{\varepsilon })-\) problem (39) can be written as
To avoid secular terms in \({\tilde{T}}_{k,2}\) in Eq. (63), the following conditions have to be imposed
By solving (64) for \(L_{k}\) and \(M_{k}\), we observe that the solution will be unbounded in \(s_{0}\) and \(s_{1}\), due to terms which are only depending on \(s_{2}\). Therefore, to have secular-free solutions for \(L_{k}\) and \(M_{k}\), the following conditions have to be imposed independently
we then obtain
Since \({\overline{A}}_{k}(c)=0\) and \({\overline{B}}_{k}(c)=0\), together with (66), this implies that
Now, outside the resonance zone, all these unknown functions in (40) have been determined in (60). So the solution of the \(O(\sqrt{\varepsilon })\)-problem (37) is \({\tilde{T}}_{k,0}(s_{0}, s_{1}, s_{2}) \equiv 0\).
Inside the resonance zone around \(s=s^{(k)}\) (or equivalently, in the resonance manifold), according to the inner analysis as presented in Sect. 3, and to avoid secular terms in (58), \(A_{k}\), \(B_{k}\) have to satisfy the following equations:
-
When k does not satisfy the conditions that there always exist \(p_{1}, p_{2}\) s.t. \(\frac{2 k}{p_{1}}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 k}{p_{2}}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\), then:
$$\begin{aligned} \frac{\partial A_{k}}{\partial s_{1}}= & {} \frac{\beta _{1,0} d_{k}\omega _{1}^{2}{\hat{l}}^{2}}{2}\nonumber \\{} & {} \sin \left( \frac{1}{2}\omega _{1} l_{0}v_{0} \textrm{e}^{ v_{0}\tau ^{(k)}}s_{1}^{2}+\psi _{k}(s^{(k)})\right) ,\nonumber \\ \frac{\partial B_{k}}{\partial s_{1}}= & {} -\frac{\beta _{1,0} d_{k}\omega _{1}^{2}{\hat{l}}^{2}}{2}\nonumber \\{} & {} \cos \left( \frac{1}{2}\omega _{1} l_{0}v_{0} \textrm{e}^{ v_{0}\tau ^{(k)}}s_{1}^{2}+\psi _{k}(s^{(k)})\right) , \end{aligned}$$(68)
which implies that
where \({\tilde{\alpha }}=\omega _{1} l_{0}v_{0} \textrm{e}^{ v_{0}\tau ^{(k)}}\), and
which are the well-known Fresnel integrals. The presence of Fresnel functions \(C_{Fr}(s_{1})\) and \(S_{Fr}(s_{1})\) causes resonance jumps in the system. In (69), \({\overline{A}}_{k}(s_{2})\) and \({\overline{B}}_{k}(s_{2})\) are still unknown functions in the slow variable \(s_{2}\). Since \(A_{k}(b, c)=0\) and \(B_{k}(b, c)=0\), we obtain that \({\overline{A}}_{k}(c)=0\) and \({\overline{B}}_{k}(c)=0\). The undetermined behaviour with respect to \(s_{2}\) can be used to avoid secular terms in the solutions of the \(O(\varepsilon \sqrt{\varepsilon })-\) problem (39). Following the derivation of (61)–(67) together with (69), we obtain
-
When k satisfies the conditions that there always exist \(p_{1}, p_{2}\) s.t. \(\frac{2 k}{p_{1}}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 k}{p_{2}}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\), then there exist \(j_{1}=k, j_{2}=\frac{k p_{1}}{p_{2}}=\theta k\) s.t. \(\frac{2 j_{1}}{p_{1}}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{p_{1}}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\); and there exist \(j_{1}=\frac{k p_{2}}{p_{1}}=\vartheta k, j_{2}=k\) s.t. \(\frac{2 j_{1}}{p_{2}}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{p_{2}}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\). Then, the functions of \(A_{k}(s_{1}, s_{2})\) and \(B_{k}(s_{1}, s_{2})\) have to satisfy:
where
and \(p_{1}(k)=\frac{2k}{1+\sqrt{\frac{EA}{mg}}}\), \(p_{2}(k)=\frac{2k}{\sqrt{\frac{EA}{mg}}-1}\), \(\theta =\frac{\sqrt{\frac{EA}{mg}}-1}{1+\sqrt{\frac{EA}{mg}}}\), \(\vartheta =\frac{\sqrt{\frac{EA}{mg}}+1}{\sqrt{\frac{EA}{mg}}-1}\).
By noting that \(A_{\vartheta k}=0\) and \(B_{\vartheta k}=0\) inside the resonance zone around \(s^{(k)}\), it follows that system (72) can be written as
where \(C_{p_{1}(k)}(s_{1},s_{2})\) and \(D_{p_{1}(k)}(s_{1},s_{2})\) are given by (73). For any mode k satisfying the conditions that there exist \(p_{1}, p_{2}\) s.t. \(\frac{2 k}{p_{1}}=\sqrt{\frac{EA}{mg}}+1\) or \(\frac{2 k}{p_{2}}=\sqrt{\frac{EA}{mg}}-1\), we can always find \(k_{1}\) (\(k_{1}\) is an integer), s.t. \(\theta ^{n-1} k=k_{1}\), and \(\theta ^{n} k\) is not an integer, \(n=1,2,..\). From that, we get a mode sequence \((k_{1}, \vartheta k_{1}, \vartheta ^{2} k_{1},\ldots ,k, \vartheta ^{n} k_{1},...)\). We firstly solve the ordinary differential equations (74) for mode \(k_{1}\), which can be rewritten as (68) (here the mode \(k_{1}\) is denoted by k), and it can be solved as in (69). For the mode \(k_{2}\) in (74), \(k=k_{2}\), \(A_{\theta k}=A_{k_{1}}\) and \(B_{\theta k}=B_{k_{1}}\), thereby inside the resonance zone around \(s^{(k_{2})}\), we can obtain the solutions \(A_{k_{2}}\) and \(B_{k_{2}}\) from (74). Next, by using an iterative method we can predict and obtain the functions \(A_{k}\) and \(B_{k}\). Note that (74) is a nonlinear perturbation problem. It is hard to obtain the analytical, explicit solution, but we can find properties of \(A_{k}\) and \(B_{k}\) by the above analysis, which can be used to describe the behaviour of the solution \({\tilde{T}}_{k,0}(s_{0}, s_{1}, s_{2})\) of the \(O(\sqrt{\varepsilon })\)-problem (37). Moreover, the solution of (74) can be obtained by numerical calculations. Now, inside the resonance zone around \(s^{(k)}\) in (26), the solution of the \(O(\sqrt{\varepsilon })\)-problem (37) is given by (69) and (74).
To summarize, the solution \({\hat{w}}(\xi ,s)\) of Eq. (13) readily follows:
where \(s^{(n)}\) is given by (26), and \(A_{n}\) and \(B_{n}\) are given by (60), (67), (69), and (74).
In the longitudinal direction, according to the analysis of (44)–(57), \({\tilde{Y}}_{k,0} \) in Eq. (44) can be approximated as:
-
When k does not satisfy the conditions that there always exist \(j_{1}, j_{2}\) s.t. \(\frac{2 j_{1}}{k}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{k}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\), then:
which follows from (47) and (56).
-
When k satisfies the conditions that there always exist \(j_{1}, j_{2}\) s.t. \(\frac{2 j_{1}}{k}=\sqrt{\frac{EA}{mg}}+1+O(\varepsilon )\) or \(\frac{2 j_{2}}{k}=\sqrt{\frac{EA}{mg}}-1+O(\varepsilon )\), then:
which follows from (49) and (56). And inside the resonance zone around \(s^{(k)}\), \(A_{k}\) and \(B_{k}\) are given by (69) and (74); outside the resonance zone, \(A_{k}\) and \(B_{k}\) are given by (60) and (67).
The solution \({\hat{u}}(\xi ,s)\) of Eq. (14) readily follows:
where \(s^{(n)}\) is given by (26), \(C_{n}\) and \(D_{n}\) are given by (77) and (78).
By the three-timescales perturbation method, we obtained that for special frequencies in the boundary excitations and for certain parameter values of the longitudinal stiffness and the conveyance mass, the transverse solution \({\hat{w}}(\xi ,s)\) of Eq. (13) jumps up from \(O(\varepsilon )\) to \(O(\sqrt{\varepsilon })\), and the longitudinal solution \({\hat{u}}(\xi ,s)\) of Eq. (14) jumps up from \(O(\varepsilon ^{2})\) to \(O(\sqrt{\varepsilon })\). We cannot (always) construct formal approximations of the solutions, but we can get properties and predictions of solution behaviours analytically on timescales of \(O(\frac{1}{\varepsilon })\). Based on the properties and equations in the analysis, the approximated solutions for transverse and longitudinal motions will be computed by using an iterative method as well as by using a numerical method in the next section. Also the approximations will be computed by using a central finite difference scheme in the next section to verify the analytical results in this section.
5 Numerical results
Since the initial boundary value problem (1) for the transverse vibration and the initial boundary value problem (2) for the longitudinal vibration are complicated with nonlinear and coupled terms and a lot of parameters, we cannot construct formal explicit approximations of the solutions. To make the problems easier to analyse and simulate, we transform the problems (1)–(2) to the problems (13)–(14) by putting the problems dimensionless, by converting the problems to a fixed spatial domain, and by Liouville–Green transformation. So, on the one hand, we can compute the transverse and the longitudinal motions of the cable for (13) and (14) by computing numerically the solutions of the ordinary differential Eq. (75) and (79). On the other hand, we can compute numerically the solutions of the problem (13) and the problem (14) straight-forwardly by applying a finite difference method. By comparing the results (the displacements and the energy) in the above two different methods, the obtained analytical results in the last section can be verified.
5.1 Analytical approximations
The numerical results simulating the transverse and the longitudinal vibration responses are computed based on the analytical expression (75) for \({\hat{w}}(\xi ,s)\) and the expression (79) for \({\hat{u}}(\xi ,s)\). The computations are performed by using the following parameters:
and the initial conditions are taken to be:
By using the Liouville–Green transformation with \(\frac{ds}{dt}=\frac{1}{l(t)}=\frac{1}{l_{0}+vt}\), we have
It follows from (82) and the resonance times given by (26) that the resonance zones (in the transverse direction) are located around the times
where the resonance time depends on the mode number k. For the first three oscillation modes of transverse motions, resonance emerges at times \(t_{1}\approx 100, t_{2}\approx 300, t_{3}\approx 500\). The displacements of the first and third mode are given by (69) and (75), the displacements of the second mode are given by (74) and (75). Around the first resonance time \(t_{1}\), the displacement amplitudes jump up from initial states \(O(\varepsilon )\) to \(O(\sqrt{\varepsilon })\). Around the second resonance time \(t_{2}\) and the third resonance time \(t_{3}\), the amplitudes jump up again from the \(O(\varepsilon )\) level to the \(O(\sqrt{\varepsilon })\) level. They are all illustrated in Fig. 2a.
The displacements of the longitudinal motion are given by (79), which are illustrated in Fig. 2b.
Also, to observe the displacement amplitudes of transverse motion clearly, Fig. 3 shows the close-up of the fragments of Fig. 2a. Figure 3a, b, and c shows the first mode displacement, the second mode displacement, and the third mode displacement of the transverse motions, respectively.
5.2 Numerical approximations
In this subsection, the finite difference method is applied in both the time and the space domain for both PDEs and boundary conditions in (6) and (7) with space grid size \(d\xi =5\times 10^{-2}\), and time step \(dt=5\times 10^{-3}\). We rewrite the so-obtained discretized Eq. (6) and (7) in matrix forms and use as numerical time integration method, the Crank–Nicolson method (see Appendix B). Note that the same parameter values as for the analytic approximations in Sect. 5.1 are used here for the computations.
In Fig. 4, the transverse displacements and the vibratory energy of the cable on timescales up to t = 600 are presented. In Fig. 4, one can see that the transverse resonances emerge around times \(t_{1}=100\), \(t_{2}=300\) and \(t_{3}=500\). In the resonance zones, the displacements and the energy increase, and in between these zones, stay constant (approximately). Around the first resonance time \(t_{1}\), the displacement amplitudes jump up from \(O(\varepsilon )\) to \(O(\sqrt{\varepsilon })\). Around the second resonance time \(t_{2}\) and the third resonance time \(t_{3}\), the amplitudes change again at the \(O(\sqrt{\varepsilon })\) level, where \(\varepsilon \) is a small parameter with \(\varepsilon = 0.01\).
In Fig. 5, the longitudinal displacements and the vibratory energy of the cable on timescales up to t = 600 are given. In Fig. 5, one can see that the longitudinal displacements increase from \(O(\varepsilon ^{2})\) to \(O(\sqrt{\varepsilon })\), and that the vibratory energy increases from \(O(\varepsilon ^{4})\) to \(O(\varepsilon )\). In Fig. 6, the total mechanical energy (see also Appendix C for definitions) based on the analytical results and the total energy based on the numerical results can be compared. Based on the Figs. 2, 4, 5, and 6, we can draw the conclusion that the general dynamic behaviour of the solution as approximated by direct numerical integration of the problem is in agreement with the analytic approximations as obtained by applying perturbation methods.
Moreover, in Fig. 7, we make different choices for \(\varepsilon \) in the numerical approximations to see the influence of the values of \(\varepsilon \) on the system dynamics. For \(\varepsilon =0.02\), the first three resonance times become \(t_{1}=50\), \(t_{2}=150\), and \(t_{3}=250\), and the displacement amplitudes also change. In Fig. 8, we make different choices for the frequencies of boundary excitations in the numerical approximations. For \(\omega _{1}=0.75\pi \), the first three resonance times become \(t_{1}=33\), \(t_{2}=167\), and \(t_{3}=300\), and the displacement amplitudes also change.
6 Conclusion
In this paper, we studied the coupled transverse and longitudinal vibrations and associated resonances induced by boundary excitations in a hoisting system. The problem is described by nonlinear coupled partial differential equations on a time-varying spatial interval with small harmonic disturbances at one end and a moving nonclassical boundary condition at the other end. Assuming that the transverse harmonic boundary disturbances and the corresponding initial values are of order \(\varepsilon \), and the longitudinal harmonic boundary disturbances and the corresponding initial values are of order \(\varepsilon ^{2}\), it is shown in this paper that for special frequencies in the boundary excitations and that for certain parameter values of the longitudinal stiffness and the conveyance mass, many large oscillations arise in transverse and longitudinal directions. The oscillation modes for transverse motion jump up from \(O(\varepsilon )\) to \(O(\sqrt{\varepsilon })\), and the oscillation modes for longitudinal motion jump up from \(O(\varepsilon ^{2})\) to \(O(\sqrt{\varepsilon })\). To obtain these results, the method of separation of variables is presented, and perturbation methods (such as averaging methods, and singular perturbation techniques) are used. Furthermore, since the initial-boundary value problems for the transverse motion and the longitudinal motion are nonlinearly coupled, we cannot (always) construct formal approximations of the solutions but we can get properties and predictions of solution behaviour analytically on timescales of order \(\varepsilon ^{-1}\). Furthermore, approximations of the solutions are computed by using an iterative method as well as by using a numerical method. Also approximations of the solutions of the initial-boundary value problems are computed by using a central finite difference scheme. The numerical approximations are in agreement with the analytically obtained approximations. The analytical scheme in this problem can be extended to study other, and more complicated types of moving cable systems and also to other types of gyroscopic systems, where transverse and longitudinal motions are both involved and are governed by coupled differential equations with in time slowly varying coefficients.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Dareing, D.W., Livesay, B.J.: Longitudinal and angular drill-string vibrations with damping. J. Eng. Ind. 90(4), 671–679 (1968). https://doi.org/10.1115/1.3604707
Arakawa, A., Miyata, K.: Method of suppressing elevator vibration to improve ride quality : Vibration-proof structure of machine-room-less elevator. Trans. Jpn. Soc. Mech. Eng. 66(651), 3547–3553 (2000). https://doi.org/10.1299/kikaic.66.3547
Do, K.D., Pan, J.: Boundary control of three-dimensional inextensible marine risers. J. Sound Vib. 327(3), 299–321 (2009). https://doi.org/10.1016/j.jsv.2009.07.009
Do, K.D., Pan, J.: Boundary control of transverse motion of marine risers with actuator dynamics. J. Sound Vib. 318(4–5), 768–791 (2008). https://doi.org/10.1016/j.jsv.2008.05.009
Siringoringo, D.M., Fujino, Y.: System identification of suspension bridge from ambient vibration response. Eng. Struct. 30(2), 462–477 (2008). https://doi.org/10.1016/j.engstruct.2007.03.004
Chen, J., Xu, Y.L., Zhang, R.C.: Modal parameter identification of tsing ma suspension bridge under typhoon victor: Emd-ht method. J. Wind Eng. Ind. Aerodyn. 92(10), 805–827 (2004). https://doi.org/10.1016/j.jweia.2004.04.003
Ottaviano, E., Ceccarelli, M., Ciantis, M.: A 4–4 cable-based parallel manipulator for an application in hospital environment. Conf. Control Autom. (2007). https://doi.org/10.1109/MED.2007.4433839
Kaczmarczyk, S., Ostachowicz, W.: Transient vibration phenomena in deep mine hoisting cables. part 1: Mathematical model. J. Sound Vib. 262(2), 219–244 (2003). https://doi.org/10.1016/S0022-460X(02)01137-9
Kaczmarczyk, S., Ostachowicz, W.: Transient vibration phenomena in deep mine hoisting cables. part 2: Numerical simulation of the dynamic response. J. Sound Vib. 262(2), 245–289 (2003). https://doi.org/10.1016/S0022-460X(02)01148-3
Zhu, W.D., Mote, C.D., Guo, B.Z.: Asymptotic distribution of eigenvalues of a constrained translating string. J. Appl. Mech. 64(3), 613–619 (1997). https://doi.org/10.1115/1.2788937
Nguyen, Q.C., Hong, K.S.: Simultaneous control of longitudinal and transverse vibrations of an axially moving string with velocity tracking. J. Sound Vib. 331(13), 3006–3019 (2012). https://doi.org/10.1016/j.jsv.2012.02.020
Gaiko, N.V., van Horssen, W.T.: On the transverse, low frequency vibrations of a traveling string with boundary damping. J. Vib. Acoust. 137(4), 041004 (2015). https://doi.org/10.1115/1.4029690
Zhu, W., Ni, J.: Energetics and stability of translating media with an arbitrarily varying length. J. Vib. Acoust. 122(3), 295–304 (2000). https://doi.org/10.1115/1.1303003
Sandilo, S.H., van Horssen, W.T.: On a cascade of autoresonances in an elevator cable system. Nonlinear Dyn. 80(3), 1613–1630 (2015). https://doi.org/10.1007/s11071-015-1966-8
Gaiko, N.V., van Horssen, W.T.: Resonances and vibrations in an elevator cable system due to boundary sway. J. Sound Vib. 424, 272–292 (2018). https://doi.org/10.1016/j.jsv.2017.11.054
Wang, J., van Horssen, W.T., Wang, J.M.: On resonances in transversally vibrating strings induced by an external force and a time-dependent coefficient in a robin boundary condition. J. Sound Vib. 512, 116356 (2021). https://doi.org/10.1016/j.jsv.2021.116356
Wang, J., van Horssen, W.T.: Analysis of longitudinal oscillations in a vertically moving cable subject to nonclassical boundary conditions. Appl. Math. Model. (2022). https://doi.org/10.1016/j.apm.2022.04.021
Crespo, R.S., Kaczmarczyk, S., Picton, P., Su, H.: Modelling and simulation of a stationary high-rise elevator system to predict the dynamic interactions between its components. Int. J. Mech. Sci. 137, 24–45 (2018). https://doi.org/10.1016/j.ijmecsci.2018.01.011
Wang, N., Cao, G., Yan, L., Wang, L.: Modelling and passive control of flexible guiding hoisting system with time-varying length. Math. Comput. Model. Dyn. Syst. 26(1), 31–54 (2020). https://doi.org/10.1080/13873954.2019.1699121
Meirovitch, L.: Principles and techniques of vibrations, Vol. 1, Prentice Hall Upper Saddle River, NJ (1997). https://zh.usa1lib.org/book/16349580/928e9e
Pham, P.T., Hong, K.S.: Dynamic models of axially moving systems: A review. Nonlinear Dyn. 100(4), 315–349 (2020). https://doi.org/10.1007/S11071-020-05491-Z
Hong, K.S., Pham, P.T.: Control of axially moving systems: a review. Int. J. Control Autom. Syst. 17(12), 2983–3008 (2019). https://doi.org/10.1007/s12555-019-0592-5
Pham, P.T., Nguyen, Q.C., Yoon, M., Hong, K.S.: Vibration control of a nonlinear cantilever beam operating in the 3D space. Sci. Rep. 12(1), 13811 (2022). https://doi.org/10.1038/s41598-022-16973-y
Nguyen, Q.C., Hong, K.S.: Transverse vibration control of axially moving membranes by regulation of axial velocity. IEEE Trans. Control Syst. Technol. 20(4), 1124–1131 (2012). https://doi.org/10.1109/TCST.2011.2159384
Cole, J. D., Kevorkian, J.: Multiple scale and singular perturbation methods, Appl. Math. Sci. 114 (1996). https://zh.usa1lib.org/book/441459/f142e7
Nayfeh, A. H., Pai, P. F.: Linear and Nonlinear Structural Mechanics, Wiley, (2004). https://zh.usa1lib.org/book/2345551/dd30b2
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: The derivation of Eqs. (1) and (2)
According to Fig. 1, the partial differential equation (PDE) can be derived by the extended Hamilton’s principle:
The kinetic energy \(E_{k}(t)\) can be represented as
where the operator \(\frac{Du}{Dt}\) is defined as \(\frac{Du}{Dt}=\frac{\partial u}{\partial t}+v\frac{\partial u}{\partial x}=u_{t}+vu_{x}\), and the operator \(\frac{Dw}{Dt}\) is defined as \(\frac{Dw}{Dt}=\frac{\partial w}{\partial t}+v\frac{\partial w}{\partial x}=w_{t}+vw_{x}\). The potential energy \(E_{p}(t)\) can be expressed as
where \(z=u_{x}+\frac{1}{2}w_{x}^{2}\), and
The virtual work \(\delta W_{c}\) done by the distributed and the lumped damping force is given as
By substituting equation (A2)–(A5) into (A1), we obtain
By integrating by parts, it follows from (A6) that
So, the governing equations of motion are given by
The corresponding boundary conditions on the upper end at \(x=e_{u}(t)\) are given by:
and the boundary conditions at \(x=l(t)\) are given by:
Note that (A9) and (A10) are the natural boundary conditions. But (A9) is not appropriate for our problem, since the string is excited at the top boundary with the fundamental excitations \(e_{u}(t)\) and \(e_{w}(t)\). Thus, the correct boundary condition at the upper end are:
where \(e_{u}(t)\) and \(e_{w}(t)\) are given in Nomenclature in section 2.1, and at the bottom boundary, the string is assumed to be fixed in horizontal direction. Thus, the corresponding transverse boundary condition at \(x=l(t)\) is:
Considering
together with the governing equations given in (A7) and in (A8), the boundary excitations conditions given in (A10), (A11), and (A12), we obtain the initial boundary value problem (1) for the transverse vibration and (2) for the longitudinal vibration. The reader is also referred to the papers [21,22,23,24] for detailed derivations of the dynamic models for strings, beams, plates, and membranes.
Appendix B: Discretization and time integration
To solve (13) numerically, it is convenient to rewrite the second order partial differential equation as a system of two coupled, first-order partial differential equations:
Next, let us use the mesh grids \(\xi _{j}=(j-1)\Delta \xi \) for \(j = 1, 2,ldots, n, n+1\) with \(n\Delta \xi =1\). By introducing the differences, \({\check{w}}_{\xi \xi }(\xi _{j}, t)=\frac{{\check{w}}_{j+1}-2{\check{w}}_{j}+{\check{w}}_{j-1}}{(\Delta \xi )^{2}}+O((\Delta \xi )^{2}),\; \check{\zeta }_{\xi }(\xi _{j}, t)=\frac{\check{\zeta }_{j+1}-\check{\zeta }_{j-1}}{2\Delta \xi }+O((\Delta \xi )^{2}),\) it follows how system (B14) can be discretized, yielding:
where \(r_{j}=\frac{1+\mu l(1-\xi _{j})}{l^{2}(\Delta \xi )^{2}}\), \(q_{j}=\frac{v(\xi _{j}-1)}{l\Delta \xi }\), \(p=\frac{\mu }{2\,l\Delta \xi }\) for j=1,2,..,n. Further,
The four matrices \(\emptyset \), I, R, and P compose the system matrix M:
where \(\emptyset \) is the zero matrix, and I is the identity matrix. In addition, let us introduce the following
vectors: \(w=(w_{1}(\xi _{1},t), w_{2}(\xi _{2},t),\ldots , w_{n}(\xi _{n},t), \zeta _{1}(\xi _{1},t), \zeta _{2}(\xi _{2},t),...\), \(\zeta _{n}(\xi _{n},t))^{T}\), \(s=(\underbrace{0, 0,\ldots , 0}_{\text {n times}}, \underbrace{{\bar{s}}_{1}, {\bar{s}}_{2},\ldots , {\bar{s}}_{n}}_{\text {n times}})^{T},\) where \({\bar{s}}_{i}=(1-\xi _{i})\omega _{2}^{2}\beta _{2}\cos (\omega _{2}t+\alpha )\). So, system (B14) can be written in the following matrix form: \(\frac{dw}{dt}=Mw+s\). In order to perform a time integration, we apply the Crank–Nicolson method. Introducing the mesh grid in time, \(t_{k}=k\Delta t\) for k=1,2,...,n, we obtain
where \(w^{k}=(w_{1}(\xi _{1},t_{k}), w_{2}(\xi _{2},t_{k}),\ldots , w_{n}(\xi _{n},t_{k}), \zeta _{1}(\xi _{1},t_{k}), \zeta _{2}(\xi _{2},t_{k}),...\),
\(\zeta _{n}(\xi _{n},t_{k}))^{T}\), \(s^{k}=(\underbrace{0, 0,\ldots , 0}_{\text {n times}}, \underbrace{{\bar{s}}^{k}_{1}, {\bar{s}}^{k}_{2},\ldots , {\bar{s}}^{k}_{n}}_{\text {n times}})^{T}\) with \({\bar{s}}^{k}_{i}=(1-\xi _{i})\omega _{2}^{2}\beta _{2}\cos (\omega _{2}t_{k}+\alpha )\), I is the identity matrix and \(I\in {\mathbb {R}}^{2n\times 2n}\), and \(D=(I-\frac{\Delta t}{2}M^{k+1})^{-1}(I+\frac{\Delta t}{2}M^{k})\). Similarly, we can also directly integrate problem (7) with the above numerical scheme.
Appendix C: Energy
The mechanical energy of the initial-boundary value problem (2) related to the transverse motion is given by
where T is given by (3). Using the dimensionless quantities, we rewrite the energy in a dimensionless form:
In order to define the energy on the interval (0,1), we change the variables by using the following transformation \(\xi =\frac{x}{l(t)}\):
The mechanical energy of the initial-boundary value problem (1) related to the longitudinal motion is given by
Using the dimensionless quantities, we rewrite the energy in a dimensionless form:
In order to define the energy on the interval (0,1), we change the variables by using the following transformation \(\xi =\frac{x}{l(t)}\):
The total mechanical energy is now given by
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, J., van Horssen, W.T. On resonances and transverse and longitudinal oscillations in a hoisting system due to boundary excitations. Nonlinear Dyn 111, 5079–5106 (2023). https://doi.org/10.1007/s11071-022-08052-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-022-08052-8