Nonlinear interaction of parametric excitation and self-excited vibration in a 4 DoF discontinuous system

Abstract

Interaction between parametric excitation and self-excited vibration has been subjected to numerous investigations in continuous systems. The ability of parametric excitation to quench self-excited vibrations in such systems has also been well documented. But such effects in discontinuous systems do not seem to have received comparable attention. In this article, we investigate the interaction between parametric excitation and self-excited vibration in a four degree of freedom discontinuous mechanical system. Unlike majority of studies in which oscillatory nature of stiffness accounts for parametric excitation, we consider a much more practical case in which parametric excitation is provided by a massless rotor of rectangular cross section with a cylinder-like mass concentrated at the center. The rotor arrangement is placed on a friction-induced self-excited support in the form of a frame placed on a belt moving with constant velocity. This frame is connected to a supplementary mass. A Stribeck friction model is considered for the mass in contact with the belt. The frictional force between the mass and the belt is oscillatory in nature because of the variation of normal force due to parametric excitation from the rotor. Our investigations reveal mutual synchronization of parametric excitation and self-excited vibration in the system for specific parameter values. The existence of a stable limit cycle with constant synchronized fundamental frequency, for a range of parametric excitation frequencies, is established numerically. Investigation based on frequency spectra and Lissajous curves reveals complex synchronization patterns owing to the presence of higher harmonics. The system is also shown to exhibit Neimark–Sacker bifurcations under the variation of belt velocity. Furthermore, variation in belt velocity and coupling stiffness is seen to cause a breakup of quasi-periodic torus with small-amplitude oscillations to form large amplitude chaotic orbits. This points toward the possibility of vibration suppression in the system by tuning the parameters for stabilizing the small-amplitude quasi-periodic response. An example of co-existence of different attractors in the system is also presented.

1 Introduction

Interaction between different excitation mechanisms can lead to interesting dynamic phenomena in various engineering systems. One such significant interaction is one between self-excited vibration and parametric excitation. Such interactions and their practical effects have been subject to many studies in the past. Initial studies focused mainly on the synchronization of self-excited vibration and parametric excitation [1, 2]. Ales Tondl [3], while investigating such synchronization behavior, discovered the phenomenon of quenching self-excited vibrations by means of parametric excitation in single degree of freedom systems. Subsequently, Tondl and his coworkers demonstrated the possibility of full suppression of self-excited vibration under some conditions and in the appropriate frequency interval of parametric excitation [4,5,6]. Such quenching has been called parametric anti-resonance [7]. Tondl and Nabergoj [8] have also studied parametric anti-resonance in multi-degree of freedom systems. Since then, experimental studies have been successful in demonstrating the quenching of self-excited vibrations using parametric excitations [9, 10].

Mode interactions between self-excitation and parametric excitation in one degree of freedom systems were initially studied by Yano [11, 12]. Amplitude-dependent self- and parametric excitations and their reciprocal interactions were also investigated by Yano [12]. Interaction of parametric and self-excited vibrations in the presence of external inertial excitation was studied by Szabelski and Warminski [13]. An inertial excitation with half the frequency of parametric excitation was considered, and synchronization and stability were studied analytically. The same authors have studied the occurrence of these three types of excitations in two degree of freedom systems [14]. Warminski et al. [15] have further examined the case of two van der Pol oscillators coupled by a periodically varying Mathieu type stiffness using multiple scales. Synchronization regions and possibility of occurrence of hyper-chaos were analyzed. Warminski et al. [16] have also studied synchronization and parametric resonance due to the interaction between non-ideal parametric excitation and self-excited vibration. More recently, Warminski [17] has reported the dynamics of a single degree of freedom system acted upon by self-, parametric and external excitations along with a time-delayed input. The possibility of controlling the system response using the time delay was investigated in this work.

Recent investigations have focused on the effect of such interactions in practical engineering systems. The effect of wind-induced parametric, external, and self-excitations on a two-tower system was investigated in [18], with steady part of the wind responsible for self-excitation and the turbulent part causing parametric and external excitations. Use of parametric anti-resonance in tuning the transient dynamics of mechatronic systems was demonstrated in [19]. This was accomplished by tuned energy transfer between vibration modes. Nino and Luongo [20] have investigated the interaction between wind-induced parametric and self-excited vibrations in a continuous model of a base-isolated tower and in a planar prismatic visco-elastic structure [21].

Parametric excitation has emerged as an efficient semi-active control strategy, especially in self-excited systems, because of its quenching properties, well documented in works cited above. Dohnal [22] has reported damping properties of anti-parametric resonance in systems with an arbitrary number of degrees of freedom subjected to parametric and self-excitations. Dohnal and Tondl [23] studied the suppression of flow-induced vibration of a slender structure using open-loop parametric inertia excitation. Suppression of machining chatter, another important type of self-excited vibration, using parametric excitation was experimentally demonstrated by Yao et al. [24]. Self-excited vibration suppression in drive trains by the use of parametric excitation induced via speed control of the electrical drive was shown by Ecker and Pumhössel [25]. Much more recently, reduction in self-excited drill string vibrations using parametric excitation [26] and design of a novel aero-elastic energy harvester using parametric variations [27] have been proposed.

The interaction between parametric and self-excitations in discontinuous systems, unfortunately, does not seem to have received the same amount of interest. Initial studies were conducted by Yano [28] on the self-excited vibrations of a system with dry friction under parametric excitation. But in this study, the self-induced vibrations were not due to friction. Awrejcewicz [29, 30] was the first to study the effect of parametric excitation on friction-induced self-excited vibrations. Analytical investigation on zones of instability in such systems was carried out by Awrejcewicz et al. [31]. A parametric absorber to suppress friction-induced self-excited vibrations was proposed by Ecker [32]. Promising cues in these works do not seem to have been taken up by subsequent research.

The present work attempts to study the interaction of parametric excitation and self-excited vibration in discontinuous systems. Friction-induced self-excitation is considered here, while parametric excitation comes from a rotor with rectangular cross section and a cylinder-like mass concentrated at the center. The model considered is a generalization of the model studied by Awrejcewicz et al. [31]. The novel aspects of the present work are summarized as follows.

• 1. We investigate the interaction effects between parametric excitation arising due to the rotation of a rectangular rotor and friction-induced self-excited vibration in a 4 DoF mechanical system.

• 2. Thus, the self-parametric interaction in the system is bi-directional and is shown to cause mutual synchronization.

• 3. Complex synchronization patterns between parametric and self-excitations and the possibility of vibration suppression in the system are demonstrated. Power flow analysis is used to quantify this suppression.

• 4. Different bifurcation scenarios including Neimark–Sacker (secondary Hopf) bifurcations and quasi-periodic transition to chaos are illustrated in the system.

2 Model description

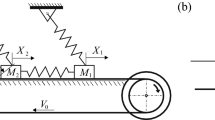
Consider the 4 DoF system shown in Fig. 1, which consists of a frame of ${M}_{1}$ placed on a belt moving with a constant velocity ${v}_{0}$. This frame houses a weightless shaft with rectangular cross section, with a cylinder-like mass ${m}_{1}$ concentrated at the center. Thus, this part of the model consists of a rotor placed on a self-excited support. The frame $M_{1}$ is connected to another mass $m_{4}$, placed on a frictionless surface, using a linear spring of stiffness $k_{{\text{c}}}$. The stiffness and damping of the frame $M_{1}$ and mass $m_{4}$ are, respectively, given by $k_{0} , \;c_{0}$ and $k_{4} , \;c_{4}$. Horizontal displacements of $M_{1}$ and $m_{4}$ are denoted by $x_{1}$ and $x_{4}$. The concentrated mass $m_{1}$ at the center of the rotor is assumed to have two DoF, with $x_{2}$ and $x_{3}$ denoting the horizontal and vertical displacements, respectively. The rotor has a constant angular velocity of ω.

Fig. 1

Model of rotor with parametric excitation placed on friction-induced self-excited support, connected to a supplementary degree of freedom

The friction ${b}_{\mathrm{r}}$ between the frame and the belt makes the model discontinuous. The frame ${M}_{1}$ placed on the belt undergoes friction-induced self-excited oscillation. The variable cross section of the rotor leads to parametric vibrations, which change the normal force holding the frame to the belt in the vertical direction. This makes the frictional force in the model time-dependent. It is assumed that the frame maintains contact with the belt always. Majority of studies consider parametric excitation of the stiffness type in which an oscillation in stiffness is externally imposed. This restricts the interaction between parametric and self-excitations unidirectional; self-excited vibrations do not act back on parametric excitations in such models. In the present system considered, the self-excited motion of the support can interact with the horizontal motion of the rotor mass, thus making the interaction mutual.

This model is the generalization of the one considered in [31], in which the stability regions of the sub-system involving the rotor placed on the self-excited support were analyzed analytically. But, in most of the practically occurring mechanical systems, such systems are connected to a rigid support using a mass-stiffness element. The present model includes mass ${m}_{4}$ to include such effects. This generalization equips the model to represent mechanical systems like disc brakes with the belt modeling the disk and the frame ${M}_{1}$ modeling the brake pad. The sub-system with mass ${m}_{4}$ models the caliper mass and stiffness, with parametric excitation provided by unbalanced rotating parts of the vehicle. In such contexts, the main objective is to quantify the effects of parametric excitation on the self-excited system consisting of the frame and the supplementary mass ${m}_{4}$.

3 The governing equations of the model

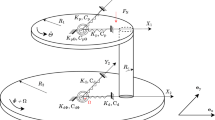
The different coordinate systems used and the free-body diagram are presented in Figs. 2 and 3, respectively. The coordinate of the center of mass of ${m}_{1}$ is denoted ${(x}_{\mathrm{c}},{y}_{\mathrm{c})}$ and the mass moment of inertial of mass ${m}_{1}$ in connection to the axis $z^{\prime\prime}$ of the defined coordinate $(O^{\prime\prime} ,x^{\prime\prime} ,z^{\prime\prime} )$ moving with translatory motion in relation to $(O,x,y,z)$ is given by $I_{{z^{\prime \prime } }}$ . The coordinates of the point of puncture by the shaft in the coordinate system $({O}^{^{\prime}},\epsilon ,\sigma )$ is $({\epsilon }_{\mathrm{w}},{\sigma }_{\mathrm{w}})$. $({O}^{^{\prime}},\epsilon ,\sigma )$ is the coordinate system whose axes are parallel to the main central inertial axes of the cross section of the shaft. ${k}_{\epsilon }$ and ${k}_{\sigma }$ are the rotor shaft rigidities in the direction of the axes $\epsilon$ and $\sigma$, respectively. The driving torque ${M}_{\mathrm{q}}$ is reduced by resistance torques. The eccentricity $a$ and the parameter $\phi_{0}$ show the center of mass of $m_{1}$ in relation to the point of puncture by the shaft. Hence the governing equations for mass $m_{1}$ are given by

$$ \begin{aligned} m_{1} \ddot{x}_{{\text{c}}} & = - \epsilon_{{\text{w}}} k_{\epsilon } \cos \phi - \sigma_{{\text{w}}} k_{\sigma } \sin \phi \\ m_1 \ddot{y}_{\text{c}}= - \sigma_{\text{w}} k_{\sigma} \cos{\phi} + \epsilon_{\text{w}} k_{\epsilon} \sin{\phi}+ m_{1} g \\ I_{{z^{\prime\prime}}} \ddot{\phi } & = - M_{{\text{q}}} + a\left( { - \epsilon_{{\text{w}}} k_{\epsilon } \cos \phi_{0} + \sigma_{{\text{w}}} k_{\sigma } \sin \phi_{0} } \right) \\ \end{aligned} $$

(1a-c)

Fig. 2

Coordinate space representation of the mass ${m}_{1}$

Fig. 3

Free body diagram of the coupled oscillators

In addition, the following geometric relations can be obtained from Fig. 2

$$ \begin{aligned} \epsilon_{{\text{w}}} & = \left( {x_{{\text{w}}} - x_{{\text{m}}} } \right)\cos \phi - y_{{\text{w}}} \sin \phi \\ \sigma_{{\text{w}}} & = \left( {x_{{\text{w}}} - x_{{\text{m}}} } \right)\sin \phi + y_{{\text{w}}} \cos \phi \\ y_{{\text{c}}} & = y_{{\text{w}}} + a\cos \left( {\phi + \phi_{0} } \right) \\ x_{{\text{c}}} & = x_{{\text{w}}} + a\sin \left( {\phi + \phi_{0} } \right) \\ \end{aligned} $$

(2a-d)

Assuming that the torque is negligibly small near steady state and introducing inertial radius $r_{{\text{i}}}$ such that

$$ I_{{z^{\prime\prime}}} = m_{1} r_{{\text{i}}}^{2} $$

(3a)

Equation (1c) thus takes the form:

$$ \ddot{\phi } = \frac{a}{{m_{1} r_{{\text{i}}}^{2} }}\left( { - \epsilon_{{\text{w}}} k_{\epsilon } \cos \phi_{0} + \sigma_{{\text{w}}} k_{\sigma } \sin \phi_{0} } \right) $$

(3b)

The eccentricity $a$ and the shaft deflections $\epsilon_{{\text{w}}}$ and $\sigma_{{\text{w}}}$ are small compared to $r_{{\text{i}}}$, and hence

$$ \ddot{\phi } = 0, \dot{\phi } = \omega , \quad \phi = \omega t $$

(3c)

For the motion of the frame of mass $M_{1}$, the dynamic reactions at the points of support obey the relations

$$ X_{1} + X_{2} + \epsilon_{{\text{w}}} k_{\epsilon } \cos \omega t + \sigma_{{\text{w}}} k_{\sigma } \sin \omega t = 0 $$

(4a)

$$ Y_{1} + Y_{2} - \epsilon_{{\text{w}}} k_{\epsilon } \sin \omega t + \sigma_{{\text{w}}} k_{\sigma } \cos \omega t = 0 $$

(4b)

The rotor reactions on the support are thus

$$ R_{sx} = - X_{1} - X_{2} $$

(5a)

$$ R_{sy} = - Y_{1} - Y_{2} $$

(5b)

Now, the governing equations for the frame $M_{1}$ and the mass $m_{4}$ connected (Fig. 3) to it are given by

$${M}_{1}{\ddot{x}}_{\mathrm{m}}=-{c}_{0}{\dot{x}}_{\mathrm{m}}-\left({k}_{0}+{k}_{\mathrm{c}}\right){x}_{\mathrm{m}}+{k}_{\mathrm{c}}{x}_{4}+{R}_{sx}+\left({R}_{sy}+{M}_{1}g\right)\cdot {b}_{\mathrm{r}}({v}_{\mathrm{r}})$$

(6a)

$$ m_{4} \ddot{x}_{4} = k_{{\text{c}}} x_{{\text{m}}} - \left( {k_{{\text{c}}} + k_{4} } \right)x_{4} - c_{4} \dot{x}_{4} $$

(6b)

where the frictional interaction is modeled using Stribeck model given by

$${b}_{\mathrm{r}}\left({v}_{\mathrm{r}}\right)={\rho }_{0}\cdot \mathrm{sgn}\left({v}_{\mathrm{r}}\right)-{\rho }_{1}{v}_{\mathrm{r}}+{\rho }_{2}{v}_{\mathrm{r}}^{3}$$

(7)

Here, ${v}_{\mathrm{r}}={v}_{0}-{\dot{x}}_{\mathrm{m}}$ is the relative velocity between the frame and the belt, and

$$\mathrm{sgn}\left({v}_{\mathrm{r}}\right)=\left\{\begin{array}{ll} 1 &\quad {\text{for}}\quad {v}_{0}>{\dot{x}}_{\mathrm{m}}\\ -1 &\quad {\text{for}} \quad{v}_{0}<{\dot{x}}_{\mathrm{m}}\end{array}\right.$$

(8)

${\rho }_{0}, {\rho }_{1}, {\rho }_{2}$ are coefficients of the Stribeck friction curve. We first use the conditions (3c) to reduce Eq. (2). The rotor reactions in (5) are then calculated using (4). These reactions are substituted in (6a). If we define new variables as follows:

$${x}_{\mathrm{m}}={x}_{1}, {x}_{\mathrm{w}}={x}_{2},\; \mathrm{and} \;{y}_{\mathrm{w}}={x}_{3}$$

Then, the governing equations in these variables become:

$${\ddot{x}}_{1}=-{x}_{1}\left({\varOmega }^{2}+{\varOmega }_{c}^{2}+\left({\varOmega }_{\epsilon }^{2}+{\varOmega }_{\sigma }^{2}\right)+\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}\right)\mathrm{cos}\left(2\varOmega t\right)\right)+{x}_{2}\left(\left({\varOmega }_{\epsilon }^{2}+{\varOmega }_{\sigma }^{2}\right)+\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}\right)\mathrm{cos}\left(2\omega t\right)\right)-{x}_{3}\left(\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}\right)\mathrm{sin}\left(2\omega t\right)\right)+{x}_{4}{\varOmega }_{c}^{2}-{\dot{x}}_{1}{H}_{1}+\left[{x}_{1}\left(\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\upsigma }^{2}\right)\mathrm{sin}\left(2\omega t\right)\right)-{x}_{2}\left(\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}\right)\mathrm{sin}\left(2\omega t\right)\right)+{x}_{3}\left(\left({\varOmega }_{\epsilon }^{2}+{\varOmega }_{\sigma }^{2}\right)-\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}\right)\mathrm{cos}\left(2\omega t\right)\right)+g\right]{b}_{r}$$

(9)

$${\ddot{x}}_{2}={x}_{1}({\omega }_{\epsilon }^{2}+{\omega }_{\sigma }^{2}+\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right)\mathrm{cos}\left(2\omega t\right))-{x}_{2}({\omega }_{\epsilon }^{2}+{\omega }_{\sigma }^{2}+\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right)\mathrm{cos}\left(2\omega t\right))+{x}_{3}\left(\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right)\mathrm{sin}\left(2\omega t\right)\right)+a{\omega }^{2}\mathrm{sin}(\omega t+{\phi }_{0})$$

(10)

$${\ddot{x}}_{3}=-{x}_{1}\left(\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right)\mathrm{sin}\left(2\omega t\right)\right)+{x}_{2}\left(\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right)\mathrm{sin}\left(2\omega t\right)\right)-{x}_{3}\left(\left({\omega }_{\epsilon }^{2}+{\omega }_{\sigma }^{2}\right)-\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right)\mathrm{cos}\left(2\omega t\right)\right)+a{\omega }^{2}\mathrm{cos}\left(\omega t+{\phi }_{0}\right)+g$$

(11)

$${\ddot{x}}_{4}={x}_{1}{\omega }_{c}^{2}-{x}_{4}\left({\omega }_{c}^{2}+{\omega }_{4}^{2}\right)-{\dot{x}}_{4}{H}_{4}$$

(12)

where the parameters are defined as follows:

$${\varOmega }^{2}=\frac{{k}_{0}}{{M}_{1}}, {\varOmega }_{\upepsilon }^{2}=\frac{{k}_{\epsilon }}{2{M}_{1}}, {\varOmega }_{\upsigma }^{2}=\frac{{k}_{\sigma }}{2{M}_{1}}, {\varOmega }_{\mathrm{c}}^{2}=\frac{{k}_{c}}{{M}_{1}}, {H}_{1}=\frac{{c}_{0}}{{M}_{1}},{b}_{\mathrm{r}}={\varepsilon }_{0}\cdot \mathrm{sgn}\left({v}_{0}-{\dot{x}}_{1}\right)-{\alpha }_{0}\left({v}_{0}-{\dot{x}}_{1}\right)+{\beta }_{0}{\left({v}_{0}-{\dot{x}}_{1}\right)}^{3}, {\omega }_{\epsilon }^{2}=\frac{{k}_{\epsilon }}{2{m}_{1}} , {\omega }_{\sigma }^{2}=\frac{{k}_{\sigma }}{2{m}_{1}},{\omega }_{c}^{2}=\frac{{k}_{c}}{m4}, {\omega }_{4}^{2}=\frac{{k}_{4}}{m4}, {H}_{4}=\frac{{c}_{4}}{{m}_{4}}.$$

We now put $t={t}_{\mathrm{s}}\tau$ and ${x}_{\mathrm{i}}={X}_{\mathrm{s}}{X}_{\mathrm{i}}$, where ${t}_{\mathrm{s}}$ and ${X}_{\mathrm{s}}$ are given by

$${t}_{\mathrm{s}}=\frac{1}{\sqrt{{\omega }_{\mathrm{c}}^{2}+{\omega }_{4}^{2}}}\;\mathrm{and}\;{X}_{\mathrm{s}}=\frac{g{\gamma }^{2}}{{\omega }^{2}}$$

Then, $\frac{{{\mathrm{d}}^{n}x}_{\mathrm{i}}}{\mathrm{d}{t}^{n}}=\frac{{X}_{\mathrm{s}}}{{t}_{\mathrm{s}}^{n}}\frac{{\mathrm{d}}^{n}{X}_{\mathrm{i}}}{\mathrm{d}{\tau }^{n}}$ and the governing Eqs. (9–12) can be written in terms of the nondimensional time $\tau$ and displacements ${X}_{\mathrm{i}}$ as

$${\ddot{X}}_{1}=-{X}_{1}\left(A{\gamma }^{2}+{A}_{1}{\gamma }^{2}+{A}_{2}{\gamma }^{2}\mathrm{cos}\left(2\gamma \tau \right)\right)+{X}_{2}\left({A}_{1}{\gamma }^{2}+{A}_{2}{\gamma }^{2}\mathrm{cos}\left(2\gamma \tau \right)\right)-{X}_{3}\left({A}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+{X}_{4}D{\gamma }^{2}-{\dot{X}}_{1}{h}_{1}\gamma +\left[{X}_{1}\left({A}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)-{X}_{2}\left({A}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+{X}_{3}\left({A}_{1}{\gamma }^{2}-{A}_{2}{\gamma }^{2}\mathrm{cos}\left(2\gamma \tau \right)\right)+1\right]{b}_{\mathrm{r}}$$

(13)

$${\ddot{X}}_{2}={X}_{1}({b}_{1}{\gamma }^{2}+{b}_{2}{\gamma }^{2}\mathrm{cos}\left(2\gamma \tau \right))-{X}_{2}({b}_{1}{\gamma }^{2}+{b}_{2}{\gamma }^{2}\mathrm{cos}\left(2\gamma \tau \right))+{X}_{3}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+\kappa {\gamma }^{2}\mathrm{sin}(\gamma \tau +{\phi }_{0})$$

(14)

$${\ddot{X}}_{3}=-{X}_{1}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+{X}_{2}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)-{X}_{3}\left({b}_{1}{\gamma }^{2}-{b}_{2}{\gamma }^{2}\mathrm{cos}\left(2\gamma \tau \right)\right)+\kappa {\gamma }^{2}\mathrm{cos}\left(\gamma \tau +{\phi }_{0}\right)+1$$

(15)

$${\ddot{X}}_{4}={X}_{1}\mathrm{d}{\gamma }^{2}-{X}_{4}-{\dot{X}}_{4}{h}_{4}\gamma $$

(16)

where

$\frac{g{t}_{s}^{2}}{{X}_{s}}=1, \gamma =\frac{\omega }{\sqrt{{\omega }_{c}^{2}+{\omega }_{4}^{2}}}$, $A=\frac{{\varOmega }^{2}+{\varOmega }_{c}^{2}}{{\omega }^{2}}$, ${A}_{1} =\frac{{\varOmega }_{\epsilon }^{2}+{\varOmega }_{\sigma }^{2}}{{\omega }^{2}}$, ${A}_{2}=\frac{{\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}}{{\omega }^{2}}$, $D=\frac{{\varOmega }_{c}^{2}}{{\omega }^{2}}$, ${h}_{1}=\frac{{H}_{1}}{\omega }$, $G=\frac{g}{{\omega }^{2}{X}_{s}}$ , ${b}_{1}=\frac{{\upomega }_{\epsilon }^{2}+{\upomega }_{\sigma }^{2}}{{\omega }^{2}}$, ${b}_{2}=\frac{{\upomega }_{\epsilon }^{2}-{\upomega }_{\sigma }^{2}}{{\omega }^{2}}$, $\kappa =\frac{a}{{X}_{s}}$, $d=\frac{{\upomega }_{c}^{2}}{{\omega }^{2}}$, ${h}_{4}=\frac{{H}_{4}}{\omega }$, $v=\frac{{v}_{0}{t}_{s}}{{X}_{s}}$, $\varepsilon =\frac{{\varepsilon }_{0}{X}_{s}}{{t}_{s}}$, $\alpha =\frac{{\alpha }_{0}{X}_{s}}{{t}_{s}}, \beta ={\beta }_{0}{\left(\frac{{X}_{s}}{{t}_{s}}\right)}^{3}$.

To simplify the equations, let ${\eta }_{1}=\frac{{m}_{1}}{{M}_{1}}$ and ${\eta }_{2}=\frac{{m}_{4}}{{M}_{1}}$. It follows that

$$ \frac{{\Omega_{c}^{2} }}{{\omega_{c}^{2} }} = \frac{{m_{4} }}{{M_{1} }} = \eta_{2} ,\quad \Rightarrow \Omega_{c}^{2} = \eta_{2} \omega_{c}^{2} . $$

(17)

$$ \frac{{\Omega_{\epsilon}^2 + \Omega_{\sigma }^{2} }}{{\Omega_{\epsilon}^2 + \omega_{\sigma }^{2} }} = \frac{{m_{1} }}{{M_{1} }} = \eta_{1} ,\quad \Rightarrow \Omega_{\epsilon}^2 + \Omega_{\sigma }^{2} = \eta_{1} \left( {\Omega_{\epsilon}^2 + \omega_{\sigma }^{2} } \right) $$

(18)

$$ \frac{{\Omega_{\epsilon}^2 - \Omega_{\sigma }^{2} }}{{\Omega_{\epsilon}^2 - \omega_{\sigma }^{2} }} = \frac{{m_{1} }}{{M_{1} }} = \eta_{1} ,\quad \Rightarrow \Omega_{\epsilon}^2 - \Omega_{\sigma }^{2} = \eta_{1} \left( {\Omega_{\epsilon}^2 - \omega_{\sigma }^{2} } \right) $$

(19)

$$ \frac{D}{d} = \frac{{\Omega_{c}^{2} }}{{\omega_{c}^{2} }} = \eta_{2} ,\quad \Rightarrow D = \eta_{2} d $$

(20)

With

$$ A = \frac{{{\varOmega }^{2} }}{{\omega^{2} }} + \frac{{{\varOmega }_{c}^{2} }}{{\omega^{2} }} = A_{0} + D,\quad {\text{where}}\quad A_{0} = \frac{{{\varOmega }^{2} }}{{\omega^{2} }}\quad {\text{then}}\quad A = A_{0} + \eta_{2} d $$

(21)

$$ \frac{{A_{1} }}{{b_{1} }} = \frac{{\Omega_{\epsilon}^{2} + \Omega_{\sigma }^{2} }}{{\Omega_{\epsilon}^{2} + \omega_{\sigma }^{2} }} = \eta_{1} ,\quad \Rightarrow A_{1} = \eta_{1} b_{1} $$

(22)

$$ \frac{{A_{2} }}{{b_{2} }} = \frac{{\Omega_{\epsilon}^{2} - \Omega_{\sigma }^{2} }}{{\Omega_{\epsilon}^{2} - \omega_{\sigma }^{2} }} = \eta_{1} ,\quad \Rightarrow A_{2} = \eta_{1} b_{2} $$

(23)

Now, expressing $A, {A}_{1}, {A}_{2},\; \mathrm{and}\; D$ in terms of ${\eta }_{1}, {\eta }_{2}, {A}_{0}, d, {b}_{1}\;\mathrm{and}\; {b}_{2}$ i.e., substituting Eqs. (17)–(23) where applicable in Eqs. (13)–(16), we have

$${\ddot{X}}_{1}=-{X}_{1}\left({A}_{0}+{\eta }_{2}d+{\eta }_{1}{b}_{1}+{\eta }_{1}{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)\right){\gamma }^{2}+{X}_{2}\left({\eta }_{1}{b}_{1}+{\eta }_{1}{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)\right){\gamma }^{2}-{X}_{3}\left({\eta }_{1}{b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+{X}_{4}{\upeta }_{2}d{\gamma }^{2}-{\dot{X}}_{1}{h}_{1}\gamma +\left[{X}_{1}\left({\eta }_{1}{b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)-{X}_{2}\left({\eta }_{1}{b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+{X}_{3}\left({\eta }_{1}{b}_{1}-{\eta }_{1}{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)\right){\gamma }^{2}+1\right]{b}_{r}$$

(24a)

$${\ddot{X}}_{2}={X}_{1}({b}_{1}+{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)){\gamma }^{2}-{X}_{2}({b}_{1}+{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)){\gamma }^{2}+{X}_{3}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+\kappa {\gamma }^{2}\mathrm{sin}(\gamma \tau +{\phi }_{0})$$

(25a)

$${\ddot{X}}_{3}=-{X}_{1}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+{X}_{2}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)-{X}_{3}\left({b}_{1}{\gamma }^{2}-{b}_{2}{\gamma }^{2}\mathrm{cos}\left(2\gamma \tau \right)\right)+\kappa {\gamma }^{2}\mathrm{cos}\left(\gamma \tau +{\phi }_{0}\right)+1$$

(26a)

$${\ddot{X}}_{4}={X}_{1}\mathrm{d}{\gamma }^{2}-{X}_{4}-{\dot{X}}_{4}{h}_{4}\gamma $$

(27a)

Finally, ${b}_{\mathrm{r}}$ is now defined as:

$${b}_{\mathrm{r}}=\left\{\begin{array}{l}\varepsilon \cdot sgn\left(v-{\dot{X}}_{1}\right)-\alpha \left(v-{\dot{X}}_{1}\right)+\beta {\left(v-{\dot{X}}_{1}\right)}^{3}, \quad v\ne {\dot{X}}_{1}\\ \\ 0, \quad v={\dot{X}}_{1},\end{array}\right.$$

The value of the constants is given by

$$ \alpha = \frac{3}{2}\frac{{\mu_{{\text{s}}} - \mu_{{\text{m}}} }}{{v_{{\text{m}}} }}\quad {\text{and}}\quad \beta = \frac{1}{2}\frac{{\mu_{{\text{s}}} - \mu_{{\text{m}}} }}{{v_{{\text{m}}}^{3} }} $$

where ${\mu }_{\mathrm{s}}$ is the coefficient of static friction, and ${v}_{\mathrm{m}}$ is the velocity corresponding to the minimum coefficient of dynamic friction ${\mu }_{\mathrm{m}}$. Figure 4 gives the characteristic of the Stribeck curve when $v\ne {\dot{X}}_{1}$.

Fig. 4

Stribeck dry friction characteristic for a ${\dot{X}}_{1}= -0.9$ b ${\dot{X}}_{1} = 0.9$

Equations (24a)–(27a) are only valid during the slip phase of the system, when $v\ne {\dot{X}}_{1}$. When the mass ${M}_{1}$ sticks to the belt ($v={\dot{X}}_{1}$), its acceleration becomes zero, and the system of equations become:

$${\ddot{X}}_{1}=0$$

(24b)

$${\ddot{X}}_{2}={X}_{1}({b}_{1}+{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)){\gamma }^{2}-{X}_{2}({b}_{1}+{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)){\gamma }^{2}+{X}_{3}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+\kappa {\gamma }^{2}\mathrm{sin}(\gamma \tau +{\phi }_{0})$$

(25b)

$${\ddot{X}}_{3}=-{X}_{1}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+{X}_{2}\left({b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)-{X}_{3}\left({b}_{1}{\gamma }^{2}-{b}_{2}{\gamma }^{2}\mathrm{cos}\left(2\gamma \tau \right)\right)+\kappa {\gamma }^{2}\mathrm{cos}\left(\gamma \tau +{\phi }_{0}\right)+1$$

(26b)

$${\ddot{X}}_{4}={X}_{1}\mathrm{d}{\gamma }^{2}-{X}_{4}-{\dot{X}}_{4}{h}_{4}\gamma $$

(27b)

The switching conditions between the slip and stick phase can be formulated in terms of the horizontal force acting on the frame ${M}_{1}$ (${f}_{\mathrm{h}}$) and the normal force exerted on the belt (${f}_{\mathrm{N}}$). These forces are given by

$${f}_{\mathrm{h}}={X}_{1}\left({A}_{0}+{\eta }_{2}d+{\eta }_{1}{b}_{1}+{\eta }_{1}{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)\right){\gamma }^{2}-{X}_{2}\left({\eta }_{1}{b}_{1}+{\eta }_{1}{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)\right){\gamma }^{2}+{X}_{3}\left({\eta }_{1}{b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)-{X}_{4}{\upeta }_{2}\mathrm{d}{\gamma }^{2}+{\dot{X}}_{1}{h}_{1}\gamma $$

$${f}_{\mathrm{N}}={X}_{1}\left({\eta }_{1}{b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)-{X}_{2}\left({\eta }_{1}{b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)+{X}_{3}\left({\eta }_{1}{b}_{1}-{\eta }_{1}{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)\right){\gamma }^{2}+1$$

Equations (24a)–(27a), governing the slipping motion of mass ${M}_{1}$ on the belt, have to be solved when

$$ v \ne \dot{X}_{1} \quad {\text{and}}\quad \left| {f_{{\text{h}}} } \right| > \mu_{{\text{s}}} f_{{\text{N}}} . $$

(28)

Equations governing the sticking motion of ${M}_{1}$, (24b)–(27b), become active when

$$ v = \dot{X}_{1} \quad {\text{and}}\quad \left| {f_{{\text{h}}} } \right| \le \mu_{{\text{s}}} f_{{\text{N}}} . $$

(29)

4 System parameters and solution methodology

The model under consideration was analyzed for four different parameter sets, taken from the literature [31]. The values of these parameter sets are given in Table 1. Analysis for each of the Data Sets (DS) was done for two different belt velocities, $v=0.1$ (low belt velocity) and $v=0.5$ (high belt velocity).

Table 1 Simulation parameters [31]

The ode45 routine in MATLAB was used to solve the governing equations after incorporating the appropriate switching conditions specified in Sect. 3. As the system is self-excited, zero initial conditions were imposed on all oscillators. To ensure the complete die out of transience and convergence to steady state, a simulation time of 50,000 s was used. As there is no characteristic forcing frequency with respect to which Poincare points can be determined, the hyperplane ${v}_{4}=0$ for state ${y}_{1}$ and ${v}_{1}=0$ was taken as the Poincare section. The frequency content of the responses were computed using the FFT routine in MATLAB, applied to the steady-state part of the response alone.

5 Self-excited dynamics in the absence of parametric excitation

The dynamics of the system in the absence of parametric excitation are obtained by putting the rotation of the rotor to be zero ($\omega =0$). In this case, the governing equations (in the dimensional form) reduce to the form

$${\ddot{x}}_{1}=-{x}_{1}\left({\varOmega }^{2}+{\varOmega }_{c}^{2}+\left({\varOmega }_{\epsilon }^{2}+{\varOmega }_{\sigma }^{2}\right)+\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}\right)\right)+{x}_{2}\left(\left({\varOmega }_{\epsilon }^{2}+{\varOmega }_{\sigma }^{2}\right)+\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}\right)\right)+{x}_{4}{\varOmega }_{c}^{2}-{\dot{x}}_{1}{H}_{1}+\left[{x}_{3}\left(\left({\varOmega }_{\epsilon }^{2}+{\varOmega }_{\sigma }^{2}\right)-\left({\varOmega }_{\epsilon }^{2}-{\varOmega }_{\sigma }^{2}\right)\right)+g\right]{b}_{r}$$

(30)

$${\ddot{x}}_{2}={x}_{1}({\omega }_{\epsilon }^{2}+{\omega }_{\sigma }^{2}+\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right))-{x}_{2}({\omega }_{\epsilon }^{2}+{\omega }_{\sigma }^{2}+\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right))$$

(31)

$${\ddot{x}}_{3}=-{x}_{3}\left(\left({\omega }_{\epsilon }^{2}+{\omega }_{\sigma }^{2}\right)-\left({\omega }_{\epsilon }^{2}-{\omega }_{\sigma }^{2}\right)\right)+g$$

(32)

$${\ddot{x}}_{4}={x}_{1}{\omega }_{c}^{2}-{x}_{4}\left({\omega }_{c}^{2}+{\omega }_{4}^{2}\right)-{\dot{x}}_{4}{H}_{4}$$

(33)

For the parameter values specified as Data Set 1 (DS1) in Table 1 and for low belt velocity ($v=0.1$), Eqs. (30)–(33) are solved in dimensional form considering appropriate switching conditions specified in Sect. 3 and using the scaling factor ${X}_{\mathrm{s}}$ to convert the solutions to the nondimensional equivalence. The state-space variables become ${x}_{1}={y}_{1},\dot{{x}_{1}}={v}_{1},{x}_{1}={y}_{2},\dot{{x}_{2}}={v}_{2},{x}_{3}={y}_{3},\dot{{x}_{4}}={v}_{4}$. Figure 5a–c shows the phase portraits and their respective frequency responses.

Fig. 5

Phase portraits and frequency responses of the self-excited system for $\omega =0$ using DS1

Since the internal mass is not rotating, the vertical component of the displacement ${y}_{3}$ of the mass ${m}_{1}$ is negligible and is not shown. Figure 5 shows that the system, in the absence of parametric excitation, undergoes self-excited vibrations with a fundamental frequency of ${\varOmega }_{s1}=19.774$ rad/s. The frame ${M}_{1}$ undergoes friction-induced self-excited vibration with a discontinuity surface at the belt velocity value, $v=0.1$. It is this self-excited motion that drives the horizontal vibrations of masses ${m}_{1}$ and ${m}_{4}$. ${M}_{1}$ exhibits the fundamental harmonic ${\varOmega }_{s1}$ along with its second multiple ${\varOmega }_{s2}=39.5379\mathrm{ rad}/\mathrm{s}\approx 2{\varOmega }_{s1}$. Horizontal displacement of mass ${m}_{1}$ exhibits ${\varOmega }_{s1}, {\varOmega }_{s2}$ and a further multiple ${\varOmega }_{s3}=59.3219 \mathrm{rad}/\mathrm{s}\approx 3{\varOmega }_{s1}$, while ${m}_{4}$ exhibits ${\varOmega }_{s1}, {\varOmega }_{s2}$ and ${\varOmega }_{s4}=79.0959 \mathrm{rad}/\mathrm{s}\approx 4{\varOmega }_{s1}$.

6 Synchronization of self-excited vibration and parametric excitation

To understand the effect of parametric excitation, due to the rotation of the rotor, on the self-excited vibration of the system documented in Sect. 5, the bifurcation diagram of the system with rotor speed $\upomega$ as the bifurcation parameter is constructed. Nondimensional Eqs. (24a)–(27a) and (24b)–(27b) are used, along with switching conditions given by Eqs. (28) and (29), to develop the bifurcation diagram. The specification of the Poincare section and other specifications are given in Sect. 4. The bifurcation diagram for the frame ${M}_{1}$ is shown in Fig. 6a. Parameter set DS1 was used here. It is seen that we have quasi-periodic and chaotic regimes interspersed by periodic windows. Figure 6b, c shows the orbits, along with Poincare points, at two typical values $\omega =11.22$ rad/s and $\omega =12.47$ rad/s, respectively. The orbit shows chaotic behavior at the former frequency and then becomes periodic at the latter one.

Fig. 6

a Bifurcation diagram with $\omega$ as the bifurcation parameter, with phase portrait and corresponding Poincare section taken at b $\omega =11.22 \mathrm{rad}/\mathrm{s}$, c $\omega =12.47 \mathrm{rad}/\mathrm{s}$

To understand the qualitative transitions in the nature of the response as the rotor frequency $\upomega$ is increased, Fig. 7 shows the response characteristics for four $\upomega$ values between 32 rad/s and 49 rad/s. The response is periodic at $\omega =32\mathrm{ rad}/\mathrm{s}$ (Fig. 7a) and changes to two-periodic at $\omega =36\mathrm{ rad}/\mathrm{s}$ Fig. 7b. At $\omega = 43 \mathrm{rad}/\mathrm{s}$, Fig. 7c shows a strange nonchaotic attractor with a non-correlated number of frequencies, similar to the result of intermittency effects demonstrated in [33, 34]. The dynamics again becomes periodic at $\omega =48.25 \mathrm{rad}/\mathrm{s}$ as shown in Fig. 7d.

Fig. 7

phase portrait and FFT plots for DS1, with varying parameter $\omega$ taken at a $\omega =32 \mathrm{rad}/\mathrm{s}$ b $\omega =36 \mathrm{rad}/\mathrm{s}$ c $\omega =43 \mathrm{rad}/\mathrm{s}$ d $\omega =48.25 \mathrm{rad}/\mathrm{s}$

In Sect. 5, it was shown that the self-excited fundamental frequency of the system, in the absence of parametric excitation ($\omega =0$), was given by ${\varOmega }_{s1}=19.774$ rad/s. Hence, to understand the bifurcation mechanism, the bifurcation diagram for state variable ${y}_{1}$, in a neighborhood of $\omega ={\varOmega }_{s1}$ is given in Fig. 8. It can be seen that parametric excitation in the neighborhood of the fundamental limit cycle frequency produces interspersed periodic windows. These periodic orbits are produced by the synchronization phenomenon happening between the parametric excitation and the friction-induced self-excited vibrations.

Fig. 8

Bifurcation diagram with rotor frequency $\omega$ in the neighborhood of fundamental self-excited frequency ${\varOmega }_{s1}$ for DS1

To study the mechanism of this synchronization, the response of the system at two values of $\upomega$ which fall in periodic windows in Fig. 8 is analyzed. The phase portraits along with Poincare points and the frequency content of all the four degrees of freedom at rotor frequency value $\omega =12.97$ rad/s are shown in Fig. 9. Phase portraits show periodic orbits. Furthermore, it can be observed that all the masses have the same fundamental harmonic ${\varOmega }_{r1}=13.0694$. This fundamental harmonic is different from both the parametric frequency $\omega$ and self-excited frequency ${\varOmega }_{s1}$. Thus, we have the mutual adjustments of rhythms, a phenomenon characteristic of synchronization, between the parametrically excited sub-system and the self-excited one, so that the system response converge to a common fundamental harmonic. Figure 9 also shows that all the higher harmonics of self-excited mass ${M}_{1}$ (Fig. 9a) are present in the vertical and horizontal components of the rotor mass ${m}_{1}$ (Fig. 9b, c). Mass ${m}_{4}$ undergoes more complicated oscillations with more harmonics, but its fundamental frequency is the same as that of the other masses.

Fig. 9

Phase portraits and frequency spectra for $\omega = 12.97$ rad/s showing synchronization between self-excited vibration and parametric excitation

Figure 10 shows the phase portraits and frequency of the oscillators at $\omega =21$ rad/s, which belongs to another periodic window, as is clear from Fig. 8. This case also shows a similar synchronization pattern as in the case studied in Fig. 9. All oscillators exhibit the same fundamental frequency of ${\varOmega }_{r1}=13.0694$ rad/s. The self-excited oscillator (Fig. 10a) exhibits one higher harmonic at $2{\varOmega }_{r1}$, whereas the parametric system (Fig. 10b, c) contains two more higher harmonics, $3{\varOmega }_{r1}$ and $4{\varOmega }_{r1}$. Furthermore, the frequency content of the connected oscillator ${m}_{4}$ (Fig. 10d) is exactly similar to that of the parametric vibration. An interesting feature that emerges from the comparison of Figs. 9 and 10 is that the fundamental synchronization frequency ${\varOmega }_{r1}$ remains the same in both cases. This points toward the existence of a common fundamental synchronizing frequency in the system for varying values of rotor frequency $\omega$. This is a consequence of the two-way interactions between parametric and self-excitations in the system, discussed in Sects. 1 and 2.

Fig. 10

Synchronization of self-excited vibration with parametric excitation at $\omega =21$ rad/s

To study the synchronization phenomenon further, we plot the Lissajous curves for both the rotor frequency values studied above. Figure 11 shows the Lissajous plots of the system for $\omega =12.97$rad/s, and Fig. 12 shows the same for $\omega =21$ rad/s. Figure 11 shows the configuration space of all three other degrees of freedom with respect to the self-excited mass ${M}_{1}$. Closed curves in all the configuration spaces show that the self-excited vibration is synchronized with parametric vibration in both directions and with the supplementary mass. The complicated nature of closed curves is due to the presence of higher harmonics of fundamental synchronization frequency ${\varOmega }_{r1}$ in other degrees of freedom, as noted in the discussion in Fig. 9. Furthermore, the pattern of Poincare points obtained in Fig. 9 shows that the Poincare map exhibits a 6-period behavior for ${M}_{1}$, while it is 2-periodic in other degrees of freedom. This makes the curves in configuration space complicated.

Fig. 11

Lissajous curves of mass ${M}_{1}$ with other oscillators at $\omega =12.97$ rad/s. Closed curves in all plots show synchronization in the system

Fig. 12

Lissajous curves of mass ${M}_{1}$ with other oscillators at $\omega =21$ rad/s

The Lissajous plots for $\omega =21$ rad/s (Fig. 12) also show synchronization between the self-excited and parametric vibrations. As evident from Fig. 10, the Poincare map is 6-periodic in mass ${M}_{1}$ while it is only 1-periodic in other oscillators. Hence the complicated structure of the configuration curves, especially in Fig. 12c.

7 Effect of belt velocity on the interaction

Another important parameter affecting the dynamics of the system is the velocity of the belt, $v$. It is responsible for the self-excited vibration in the system. As mentioned in Sect. 2, in the case when model in Fig. 1 is representative of a mechanical system like disk brake, the velocity of the belt models important system parameter like rotational speed of the brake disk. As this is directly related to vehicle speed, study of the influence of $v$ on system dynamics, especially on the interaction effects between self-excited and parametric vibration, is important. The effect of $v$ on system dynamics is studied here by generating the bifurcation diagram of the system with $v$ as the bifurcation parameter. Figure 13 shows the bifurcation diagram for parameter values in DS3 in Table 1. It is generated at a rotor speed $\omega =5.2$ rad/s. The hyperplane ${v}_{1}=0$ is selected as the Poincare section. For the mass ${M}_{1}$, ${v}_{4}=0$ is taken as the Poincare section to make the Poincare points in its state space more intuitive.

Fig. 13

Bifurcation figures of all degrees of freedom for belt velocity $v$. Parameter values are taken from DS3 in Table 1 and rotor speed $\omega =5.2$ rad/s

Figure 13 shows that the system exhibits non-periodic motion for smaller values of $v$. At $v=0.242$, these non-periodic orbits undergo bifurcation to produce one-period orbits. To understand the mechanism of this bifurcation, state space orbits of all degrees of freedom are plotted in Fig. 14 for different values of $v$. Figure 14a shows the chaotic behavior exhibited by the system at $v=0.1$. As the belt velocity is increased to $v=0.235$, the orbit changes to quasi-periodic one, as shown by the closed nature of Poincare points in Fig. 14b. We get a one -period orbit at the bifurcation point $v=0.242$ (Fig. 14c) and these limit cycles are sustained for higher belt velocities like $v=0.5$ as well (Fig. 14d). This shows that the bifurcation seen at $v=0.242$ is the Neimark–Sacker bifurcation (secondary Hopf bifurcation). On the Poincare plane, closed orbits as shown in Fig. 14b bifurcate into fixed points in Fig. 14c, d. This is a clear instance of Neimark–Sacker bifurcation in the Poincare map of the system. The presence of Neimark–Sacker bifurcations has been reported recently in continuous systems with self- and parametric excitations in the presence of time delay [17]. An instance of the same in discontinuous systems due to interaction between self- and parametric vibration is seen here.

Fig. 14

State space orbits and Poincare points corresponding to four different values of $v$ in Fig. 13a $v=0.1,$ b $v=0.235,$ c $v=0.242,$ d $v=0.5$

Instances of Neimark–Sacker bifurcations are not limited to the parameter values in DS3 alone. Bifurcation diagram with respect to $v$ for DS1 in Table 1 for the same rotor speed as before ($\omega =5.2$ rad/s) is given in Fig. 15. The orbits exhibit non-periodic characteristics till $v=0.175$ after which they become two-periodic.

Fig. 15

Bifurcation figures of all degrees of freedom for belt velocity $v$. Parameter values are taken from DS1 in Table 1 and rotor speed $\omega =5.2$ rad/s

This transition is studied in state space in Fig. 16. Unlike the case with DS3, DS1 exhibits quasi-periodic orbits for small belt velocities as well (Fig. 16a). These quasi-periodic orbits get transformed to two-periodic ones at the bifurcation point $v=0.176$ (Fig. 16b, c) and these two-period limit cycles are sustained for high belt velocity as well (Fig. 16d). On the Poincare section, the cycle associated with quasi-periodicity gets transformed to alternating 2-period points in this case.

Fig. 16

State space orbits and Poincare points corresponding to four different values of $v$ in Fig. 15. a $v=0.1,$ b $v=0.175,$ c $v=0.176,$ d $v=0.5$

8 Quenching of oscillations

Quenching of oscillations due to the interaction between parametric and self-excited vibrations has been well studied in continuous systems, as outlined in Sect. 1. An instance of such quenching in the discontinuous system under consideration is demonstrated in this section. The bifurcation diagram, with belt velocity $v$ as the parameter, for system parameters taken from DS2 and for rotor speed $\upomega =5.2$ rad/s is shown in Fig. 17. It is clear that for the given rotor speed, oscillations in all degrees of freedom are quenched till a critical belt velocity, $v=0.124$, is attained. After this belt velocity, large amplitude oscillations set in.

Fig. 17

Bifurcation figures of all degrees of freedom for belt velocity $v$. Parameter values are taken from DS2 in Table 1 and rotor speed $\omega =5.2$ rad/s

The quenching effect for smaller belt velocities and the bifurcation associated with the value of belt velocity $v=0.124$, observed in Fig. 17, are investigated further in Fig. 18 using state space representations and Poincare points. Figure 18a shows the case of belt velocity $v=0.1$ at which quasi-periodic orbits with small amplitudes are observed. These small-amplitude quasi-periodic oscillations persist for values of $v$ lesser than the bifurcation point (Fig. 18b). At the bifurcation point $v=0.124$, we observe a transition from quasi-periodic to chaotic orbits with large amplitudes (Fig. 18c). This transition points toward the breakup of the toroidal surface on which the quasi-periodic orbits are confined, and is usually associated with the quasi-periodic route to chaos. These high-amplitude chaotic orbits persist for larger values of belt velocities too, as shown in Fig. 18d.

Fig. 18

State space orbits and Poincare points corresponding to four different values of $v$ in Fig. 17. a $v=0.1$, b $v=0.118,$ c $v=0.124,$ d $v=0.5$

Bifurcation diagram in Fig. 17 showed the small-amplitude quasi-periodic solutions getting destabilized to yield high-amplitude chaotic ones at higher values of belt velocity. But, other parameter values may also be adjusted to quench these high-amplitude vibrations. Figure 19 shows the bifurcation diagram with nondimensional coupling stiffness $d$ between masses ${M}_{1}$ and ${m}_{4}$. The diagram is plotted for parameter values given in DS4, at a high value of belt velocity $v=0.5$. It can be seen that small-amplitude oscillations are stabilized for this high belt velocity till a critical value of stiffness, ${d}_{\mathrm{c}}=46.9$. Large-amplitude vibrations appear after this critical value of $d$. Hence, the results presented in this section show that the interaction between self and parametric excitations can lead to quenching of oscillations in some range of system parameters.

Fig. 19

Bifurcation figures of all degrees of freedom for non-dimensional coupling stiffness $d$ for belt velocity $v=0.5$. Parameter values are taken from DS4 in Table 1

To quantify this quenching effect, a power flow analysis is carried out in the model. From Eqs. (24a)–(27a), it is clear that the excitation force on masses ${M}_{1}$ and ${m}_{4}$ comes from the parametric excitation and excitation due to belt friction. Hence, Eqs. (24a) and (27a) can be rewritten as

$$\left\{\begin{array}{l}{\ddot{X}}_{1}+{X}_{1}{A}_{0}{\gamma }^{2}+{\eta }_{2}d{\gamma }^{2}({X}_{1}-{X}_{4})+{\dot{X}}_{1}{h}_{1}\gamma ={F}_{\mathrm{pe}}+{F}_{\mathrm{br}}\\ {\ddot{X}}_{4}-{X}_{1}d{\gamma }^{2}+{X}_{4}+{\dot{X}}_{4}{h}_{4}\gamma =0\end{array}\right.$$

(34)

${F}_{\mathrm{pe}}$ and ${F}_{\mathrm{br}}$ are excitations imparted by parametric and friction terms and are given by

$${F}_{\mathrm{pe}}=-{X}_{1}\left({\eta }_{1}{b}_{1}+{\eta }_{1}{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)\right){\gamma }^{2}+{X}_{2}\left({\eta }_{1}{b}_{1}+{\eta }_{1}{b}_{2}\mathrm{cos}\left(2\gamma \tau \right)\right){\gamma }^{2}-{X}_{3}\left({\eta }_{1}{b}_{2}{\gamma }^{2}\mathrm{sin}\left(2\gamma \tau \right)\right)$$

(35a)

$$ F_{{{\text{br}}}} = \left( {X_{1} \left( {\eta _{1} b_{2} \gamma ^{2} \sin \left( {2\gamma \tau } \right)} \right) - X_{2} \left( {\eta _{1} b_{2} \gamma ^{2} \sin \left( {2\gamma \tau } \right)} \right) + X_{3} \left( {\eta _{1} b_{1} - \eta _{1} b_{2} \cos \left( {2\gamma \tau } \right)} \right)\gamma ^{2} + 1} \right)b_{{\text{r}}} $$

(35b)

For studying the power balance, Eqs. (35a) and (35b) are multiplied by their respective velocities [35], which gives

$$\left\{\begin{array}{l}{\dot{X}}_{1}{\ddot{X}}_{1}+{\dot{X}}_{1}{X}_{1}{A}_{0}{\gamma }^{2}+{\dot{X}}_{1}{\eta }_{2}d{\gamma }^{2}({X}_{1}-{X}_{4})+{\dot{X}}_{1}{\dot{X}}_{1}{h}_{1}\gamma ={\dot{X}}_{1}{F}_{\mathrm{pe}}+{\dot{X}}_{1}{F}_{\mathrm{br}}\\ {{\dot{X}}_{4}\ddot{X}}_{4}-{\dot{X}}_{4}{X}_{1}d{\gamma }^{2}+{\dot{X}}_{4}{X}_{4}+{\dot{X}}_{4}{\dot{X}}_{4}{h}_{4}\gamma =0\end{array}\right.$$

(36)

Summing these two equations, we have

$${\dot{X}}_{1}{\ddot{X}}_{1}+{{\dot{X}}_{4}\ddot{X}}_{4}+{\dot{X}}_{1}{X}_{1}{A}_{0}{\gamma }^{2}+{\dot{X}}_{1}{\eta }_{2}\mathrm{d}{\gamma }^{2}({X}_{1}-{X}_{4})-{\dot{X}}_{4}{X}_{1}\mathrm{d}{\gamma }^{2}+{\dot{X}}_{4}{X}_{4}+{\dot{X}}_{1}{\dot{X}}_{1}{h}_{1}\gamma +{\dot{X}}_{4}{\dot{X}}_{4}{h}_{4}\gamma ={\dot{X}}_{1}({F}_{\mathrm{pe}}+{F}_{\mathrm{br}})$$

(37)

It can be seen that Eq. (37) is of the form

$$\dot{K}+\dot{U}+{P}_{\mathrm{d}}={P}_{\mathrm{in}}$$

(38)

where $\dot{K}$ and $\dot{U}$ represent the rate of change of kinetic and potential energies respectively and are given by

$$\dot{K}={\dot{X}}_{1}{\ddot{X}}_{1}+{{\dot{X}}_{4}\ddot{X}}_{4}$$

(39)

$$\dot{U}={\dot{X}}_{1}{X}_{1}{A}_{0}{\gamma }^{2}+{\dot{X}}_{1}{\eta }_{2}\mathrm{d}{\gamma }^{2}({X}_{1}-{X}_{4})-{\dot{X}}_{4}{X}_{1}d{\gamma }^{2}+{\dot{X}}_{4}{X}_{4}$$

(40)

${P}_{\mathrm{d}}$ and ${P}_{\mathrm{in}}$ define the total power dissipation and input power in the system:

$${P}_{\mathrm{d}}={\dot{X}}_{1}{\dot{X}}_{1}{h}_{1}\gamma +{\dot{X}}_{4}{\dot{X}}_{4}{h}_{4}\gamma $$

(41)

$${P}_{\mathrm{in}}={\dot{X}}_{1}{F}_{\mathrm{pe}}+{\dot{X}}_{1}{F}_{\mathrm{br}}$$

(42)

Now, integrating Eq. (38) from $t={t}_{0}$ over a time span $t={t}_{0}+{t}_{\mathrm{f}}$ leads to energy balance equation for the system

$$\Delta K+\Delta U+{E}_{\mathrm{d}}={E}_{\mathrm{in}}$$

(43)

Here, $\Delta K$ and $\Delta U$ are the net changes in kinetic and potential energies and, ${E}_{\mathrm{d}}={\int }_{{t}_{0}}^{{t}_{0}+{t}_{f}}{P}_{\mathrm{d}}\mathrm{d}\tau$ and ${E}_{\mathrm{in}}={\int }_{{t}_{0}}^{{t}_{0}+{t}_{f}}{P}_{\mathrm{in}}\mathrm{d}\tau$ are the total dissipated energy and total work done respectively.

The time-average instantaneous input power is given by

$${\overline{P} }_{\mathrm{in}}=\frac{1}{T}{\int }_{0}^{T}{P}_{\mathrm{in}}\mathrm{d}\tau =\frac{1}{T}{\int }_{0}^{T}{\dot{X}}_{2}{F}_{\mathrm{pe}}+{\dot{X}}_{1}{F}_{\mathrm{br}}\mathrm{d}\tau $$

(44)

The time-average total instantaneous dissipated power is

$${\overline{P} }_{\mathrm{d}}=\frac{1}{T}{\int }_{0}^{T}{P}_{d}\mathrm{d}\tau =\frac{1}{T}{\int }_{0}^{T}{\dot{X}}_{1}{\dot{X}}_{1}{h}_{1}\gamma +{\dot{X}}_{4}{\dot{X}}_{4}{h}_{4}\gamma \mathrm{ d}\tau $$

(45)

From this, we can obtain the normalized power absorbed as

$${\overline{P} }_{\mathrm{a}}=\frac{1}{T {P}_{pp}}{\int }_{0}^{T}{\dot{X}}_{1}{\dot{X}}_{1}{h}_{1}\gamma +{\dot{X}}_{4}{\dot{X}}_{4}{h}_{4}\gamma \mathrm{ d}\tau $$

(46)

where the peak power ${P}_{pp}$ is given by

$${P}_{pp}=\frac{\gamma }{T}{\int }_{0}^{T}\left({\dot{{X}^{2}}}_{1\mathrm{max}}{h}_{1}+{{\dot{X}}^{2}}_{4\mathrm{max}}{h}_{4} \right)\mathrm{d}\tau $$

(47)

The input power can also be normalized similarly. Now, power absorption ratio is given as

$${R}_{\mathrm{a}}=\frac{{\overline{P} }_{\mathrm{a}}}{{\overline{P} }_{\mathrm{in}}}$$

(48)

It has to be noted that one cycle ${T}_{\mathrm{i}}$ is typically made up of sticking-time interval ${t}_{\mathrm{ki}}$ and slipping-time interval ${t}_{\mathrm{li}}$ as shown in Fig. 20. Hence, ${T}_{\mathrm{i}}={t}_{\mathrm{ki}}+{t}_{\mathrm{li}}$.

Fig. 20

Time measurement over one period of excitation

Figure 21 shows the variation of normalized input and output power and the absorption ratio with the belt velocity $v$ for DS2 with rotor speed $\omega =5.2$rad/s. The bifurcation diagram for these parameter values was given in Fig. 17. It was noted that the system exhibited quenching for belt velocity values less than $v=0.124$. This quenching effect can be also inferred from Fig. 21, where the absorbed power and the absorption ratio start decreasing after $v=0.124$. Variations in input power are due to the bi-directional nature of interaction between rotor and friction oscillator.

Fig. 21

Normalized power and absorption ratio as function of belt velocity $v$ for parameter values in DS2 and rotor speed $\omega =5.2$ rad/s

9 Presence of co-existing attractors

The presence of co-existing quasi-periodic attractors in the model is demonstrated with the help of an example in this section. Using the system parameter values DS1 given in Table 1, the Poincare points for ${y}_{4}$ for different initial conditions are given in Fig. 22. In generating the plot, only the initial conditions pertaining to ${y}_{4}$ were varied in the interval ${y}_{4}\left(0\right)\in [1,-1]$. Three different quasi-periodic attractors ${A}_{1}$, ${A}_{2}$ and ${A}_{3}$ observed are labeled in the figure. As evident from the plot, ${A}_{1}$ occurs in three different intervals of initial condition given by ${y}_{4}\left(0\right)\in \left[-1.00, -0.92\right]\cup \left[-0.56, -0.08\right]\cup \left[0.44, 1.00\right]$. ${A}_{2}$ is observed in two different intervals specified by ${y}_{4}\left(0\right)\in \left[-0.90, -0.58\right]\cup \left[-0.06, 0.00\right]$. The attractor ${A}_{3}$ is observed to occur in the interval ${y}_{4}\left(0\right)\in [0.02, 0.42]$.

Fig. 22

Co-existing attractors for parameter values given in DS1 for different initial conditions of ${y}_{4}$

Basins of attraction of these three quasi-periodic attractors in a subset of ${y}_{2},{y}_{4}$ configuration space are given in Fig. 23. The closed curves on the Poincare sections for these three solutions are given in the insets. Difference in the vibratory characteristics of the system for these three different attractors is evident from the time histories corresponding to these different solutions presented in Fig. 24.

Fig. 23

Basins of attraction in ${y}_{2},{y}_{4}$ configuration space for the three co-existing solutions observed in Fig. 22; Gray (${A}_{1}$), Blue (${A}_{2}$) and Red (${A}_{3}$)

Fig. 24

Time histories corresponding to the three co-exiting solutions in Fig. 20. a ${A}_{1}$, b ${A}_{2}$ and c ${A}_{3}$

10 Conclusion

This work investigated the bi-directional interactions between parametric excitation and self-excited vibration in a 4 DoF discontinuous mechanical system. Bifurcation analysis with respect to the parametric excitation variable $\omega$ showed the presence of synchronized periodic orbits. These periodic orbits shared the same fundamental synchronized frequency for different values of $\omega$, which shows the existence of adjustment of rhythms between the sub-systems, which is a characteristic of mutual synchronization. The Lissajous plots of the self-excited mass reveal complex synchronization patterns owing to the presence of higher harmonics in other degrees of freedom of the system. Variation in belt velocity $v$ revealed the presence of Neimark–Sacker bifurcations in the system. Similar qualitative changes from quasi-periodic cycles to 2-period orbits on the Poincare section were also observed. The quasi-periodic transition to chaos observed under the variation of belt velocity was associated with small-amplitude vibrations in the quasi-periodic phase which transformed into high-amplitude chaotic orbits after bifurcation. The same phenomenon was observed in the bifurcation diagram for coupling stiffness $d$. This points toward the possibility of vibration suppression in the system by proper tuning of the parameters to generate small-amplitude quasi-periodicity. The complexity of the system is also revealed by the presence of co-existing quasi-periodic attractors. Future work is aimed toward the realization of the mechanical discontinuous systems which would be studied using the model considered. A disk brake under the effect of unbalanced vehicle vibrations is one such system to which the study can be extended.