Nonlinear dynamics of self-, parametric, and externally excited oscillator with time delay: van der Pol versus Rayleigh models

Abstract

The regular and chaotic vibrations of a nonlinear structure subjected to self-, parametric, and external excitations acting simultaneously are analysed in this study. Moreover, a time delay input is added to the model to control the system response. The frequency-locking phenomenon and transition to quasi-periodic oscillations via Hopf bifurcation of the second kind (Neimark–Sacker bifurcation) are determined analytically by the multiple time scales method up to the second-order perturbation. Approximate solutions of the quasi-periodic motion are determined by a second application of the multiple time scales method for the slow flow, and then, slow–slow motion is obtained. The similarities and differences between the van der Pol and Rayleigh models are demonstrated for regular, periodic, and quasi-periodic oscillations, as well as for chaotic oscillations. The control of the structural response, and modifications of the resonance curves and bifurcation points by the time delay signal are presented for selected cases.

1 Introduction

Interactions among different vibration types can occur in various engineering systems. Classical examples are vortex-induced vibrations occurring owing to fluid flow [1], which may interact with other vibrations generated by different mechanisms, such as parametric excitation or external loading. Under specific conditions, different vibration interactions may lead to dangerous resonant states. Interacting self- and parametric vibrations have led to large riser motion being observed in the offshore industry [2, 3]. The huge riser vibration was caused by the so-called frequency-locking phenomenon. Self-, parametric, and external oscillations have also been studied for a tower under turbulent flow [4, 5]. An interesting example of fluid structure interactions is rotating composite helicopter blades [6], which performed complex bending–twisting oscillations owing to structural couplings. By adding aerodynamic forces and considering the rotation of blades as well as possible flight manoeuvres, interactions may occur between self-excitation and other possible vibrations, such as parametric or external excitations.

An in-depth theoretical study of self- and parametric systems has been presented by Tondl and co-authors. The effect of cancelling self-excitation by parametric vibrations was presented in [7, 8]. Detailed bifurcation analysis through Hopf or Neimark–Sacker bifurcations leading to the quenching of self-excited systems was presented by Verhulst [9] and for self-excited auto-parametric models by Abadi in a Ph.D. thesis [10].

In the papers of [11, 12], new phenomena were detected for nonlinear systems with an external force added to a vibrating self-parametric oscillator. If the frequency of the added force was in the ratio of 1:2 with respect to the frequency of the parametric excitation, the resonance curve changed shape from classical to new, with an internal loop. It has been demonstrated that, in the selected frequency domain, up to five steady states may exist, but stability analysis has indicated that only two of these are stable. This fact has also been confirmed for a two-degree-of-freedom (2-DOF) model for the principal parametric resonances around the first and second natural frequencies [13].

To control the structural response, a model with a time delay was considered with application to the MEMS oscillator [14]. The delay signals (the time delay displacement and velocity) were considered in the study to control the system dynamics. It has been demonstrated that the existence of the internal loop inside the resonance curve of the MEMS device can be controlled by a time delay. Appropriate selection of the gain and time delay may completely reduce or create the loop.

The above-mentioned studies have mainly dealt with the analytical determination of the periodic solutions, bifurcation points, and scenarios of transition from periodic to quasi-periodic oscillations through Hopf (or Neimark–Sacker) bifurcation. However, in recent years, the interactions among various vibration types have been of interest in terms of energy harvesting [15, 16]. Authors have considered van der Pol systems with a time-varying delay amplitude coupled with an electromagnetic harvester induced by self-excitations and oscillating near the main parametric resonance. A delayed Mathieu–van der Pol–Duffing oscillator coupled with a piezoelectric mechanism was presented in [17]. To optimise the harvested energy, it was necessary to determine not only the periodic solutions, but also the quasi-periodic oscillations of the harvester. Quasi-periodic solutions have been determined by applying the multiple time scales method twice, firstly to obtain modulation equations representing the slow flow and secondly to obtain periodic solutions of the slow flow. The periodic solutions of the slow flow represent the quasi-periodic motion of the original system. This method has been applied to an externally excited Mathieu oscillator with quadratic and cubic nonlinearities [18] and subsequently to systems with time delay [19], which has previously been studied for periodic response in the paper of [20].

In the above-mentioned literature, self-excited oscillations were studied based on a phenomenological model represented by van der Pol or equivalent Rayleigh nonlinear damping. In both self-excitation models, for the appropriate selection of parameters, the equilibrium position of the system becomes unstable and the solution tends towards a limit cycle (LC), which is stable in such a case. This type of self-excitation is known as soft, in contrast to the so-called hard self-excitation with an unstable LC. In the latter case, the solution tends towards a stable equilibrium or, under certain initial conditions, approaches infinity. Thus, hard self-excitation is often referred to as catastrophic. Another method of self-excitation modelling is to apply the time delay signal, which may also generate an LC. Therefore, self-excited vibrations are also modelled by differential equations with a time delay, for example in the studies of [21,22,23].

In this study, we investigate a 1-DOF Duffing-type oscillator, which includes all possible excitation types, self-excitation, parametric terms, external forcing, and a time delay signal, which can be treated as a control input. Furthermore, we compare two different self-excitation types given by van der Pol or Rayleigh terms and demonstrate their differences. The solution of such a general model is determined analytically by the multiple time scales method, taking into account the periodic motion (slow flow) and quasi-periodic oscillations (slow–slow flow). The studied general model can be simplified by equalling certain parameters to zero, and then, the simpler cases can easily be compared with results already published in the literature. This study is a continuation of the paper [14]; however, in this case, the model considers van der Pol or Rayleigh damping and nonlinear parametric excitation producing higher-order terms. The analytical solutions are determined for periodic as well as quasi-periodic oscillations.

2 Model

Let us consider a model of a structure reduced to an oscillator with 1-DOF. Despite its structural simplicity, we assume that vibrations can be induced by three different mechanisms: self-excitation arising from nonlinear damping, parametric excitation caused by periodically varying stiffness, and external periodic force imposed on the oscillator. All three of these vibration types may interact, in which case various important phenomena may occur. Furthermore, we assume that there exists an additional time delay signal, which is considered as an input of the closed-loop control (Fig. 1). If the gain $g_1$ of the input signal is equal to zero, the dynamics of the 1-DOF system (the plant) is not controlled. However, by changing the gain $g_1$ and time delay $\tau$ we may influence the plant dynamics, reduce the oscillations, or induce complex vibrations.

Fig. 1

Nonlinear model of system with self-, parametric, and external excitations as well as time delay

The dynamics of the nonlinear oscillator is governed by a nonlinear ordinary differential equation given in the dimensionless form

$$\begin{aligned}&\ddot{x} + f_d(x,\dot{x}) + \left( \omega _0^2 - \mu \cos 2 \Omega t \right) \left( x + \gamma x^3 \right) \nonumber \\&\quad = f \cos \omega t + g_1 x\left( t - \tau \right) \,. \end{aligned}$$

(1)

We assume nonlinear, periodically varied stiffness of the structure, defined by the parameter $\mu$ and frequency $2\Omega$, which, owing to the coupling with linear and nonlinear components of the stiffness characteristic, generates linear and nonlinear parametric excitation terms. The natural linear frequency of the oscillator is defined by $\omega _0$ and normalised to the dimensionless value $\omega _0=1$. However, in the further analytical computations, we maintain the notation $\omega _0$ to observe its influence in the analytical solutions. Cubic nonlinearity is represented by the dimensionless parameter $\gamma$. As mentioned previously, the oscillator is also driven by an external periodic force with amplitude f and frequency $\omega$ and additionally controlled by a time delay input with gain $g_1$ and delay $\tau$.

The damping of the system is considered as the nonlinear function $f_d(x, \dot{x})$, producing self-excited vibrations. In the literature, there are two commonly used phenomenological models of self-excited oscillations, namely van der Pol or Rayleigh models, which are defined by the nonlinear functions $f_v=(-\alpha _v + \beta _v x^2 ) \dot{x}$ and $f_R=(-\alpha _R + \beta _R \dot{x}^2 ) \dot{x}$, with subscripts v and R, respectively. In the literature, both models are often treated as equivalent. In fact, starting with the Rayleigh model

$$\begin{aligned} \ddot{x} + \left( -\alpha _R \dot{x} + \beta _R \dot{x}^3 \right) + \omega _0^2 x = 0 \end{aligned}$$

and differentiating it with respect to time, we obtain

$$\begin{aligned} \dddot{x} + \left( -\alpha _R \ddot{x} + 3 \beta _R \dot{x}^2 \ddot{x} \right) + \omega _0^2 \dot{x} = 0 . \end{aligned}$$

Substituting $\dot{x} =z$, we have

$$\begin{aligned} \ddot{z} + \left( -\alpha _v + \beta _v z^2 \right) \dot{z} + \omega _0^2 z = 0 \,. \end{aligned}$$

It is observed that van der Pol damping can be treated as an equivalent Rayleigh model if $\alpha _v=\alpha _R$ and $\beta _v=3 \beta _R$. However, the transformation has been performed for linear stiffness. If we consider a nonlinear system, such as that in the study, expressed by Eq. (1), the equivalent replacement of the damping $f_d(x,\dot{x})$ from Rayleigh to van der Pol, without any transformation of other terms, does not guarantee the equivalence of both models. Thus, we study the solution to Eq. (1) in two variants, for Rayleigh $f_d=f_R$ or van der Pol $f_d=f_v$ nonlinear damping, with no changes in the remaining nonlinear terms.

3 Analytical approach: multiple time scales method

We assume that the differential equation of motion is not strongly nonlinear. Therefore, the nonlinear terms, damping, external, and parametric excitations, as well as time delay, can be expressed by the formal small parameter $\varepsilon$:

$$\begin{aligned} \ddot{x} + \omega _0^2 x= & {} \varepsilon \left[ {{\tilde{f}}}_d(x,\dot{x}) + {{\tilde{\mu }}} x \cos 2 \Omega t - {{\tilde{\gamma }}} x^3 \right. \nonumber \\&\left. + {{\tilde{f}}} \cos \omega t + {{\tilde{g}}}_1 x \left( t - \tau \right) \right] \nonumber \\&+\, \varepsilon ^2 {{\tilde{\gamma }}} {{\tilde{\mu }}} x^3 \cos \Omega t \,, \end{aligned}$$

(2)

where

$$\begin{aligned} {{\tilde{f}}}_d(x, \dot{x})= & {} {{\tilde{f}}}_v(x, \dot{x})\\= & {} (-{{\tilde{\alpha }}}_v + {{\tilde{\beta }}}_v x^2 ) \dot{x} \quad \\&\text {for the van der Pol model} \end{aligned}$$

and

$$\begin{aligned} {{\tilde{f}}}_d(x, \dot{x})= & {} {{\tilde{f}}}_R(x, \dot{x})\\= & {} (-{{\tilde{\alpha }}}_R + {{\tilde{\beta }}}_R \dot{x}^2 ) \dot{x} \quad \text {for the Rayleigh model.} \end{aligned}$$

The coefficients in Eq. (2) are expressed by the formal small parameter $\alpha = \varepsilon {{\tilde{\alpha }}}$, $\beta = \varepsilon {{\tilde{\beta }}}$, $\gamma = \varepsilon \tilde{\gamma }$, $\mu = \varepsilon {{\tilde{\mu }}}$, $f = \varepsilon {{\tilde{f}}}$, and $g_1 = \varepsilon {{\tilde{g}}}_1$. To simplify the notation, we omit the ‘tilde’ in further analytical computations.

Owing to nonlinear parametric excitation, the system is excited parametrically in both the first and second perturbation orders; therefore, an analytical solution should be sought, at least up to the second approximation order.

The system response depends on the excitation frequency, and in the case of parametric and external excitations acting simultaneously, we may have an infinite number of combinations of parametric and external excitations leading to parametric and/or external resonances [24]. The parametric resonances occur for $m \Omega \approx n \omega _0$, where n and m are natural numbers.

In this study, we concentrate on the principal parametric resonance, which is the most essential from a practical point of view. Therefore, we assume that $\Omega \approx \omega _0$. Furthermore, we assume excitation of the external force $\omega = \Omega$. This means that parametric and external terms excite the system in the ratio of 2:1 around its linear natural frequency $\omega _0$. Thus, for the accepted assumptions, we can write

$$\begin{aligned} \Omega ^2 = \omega _0^2 + \varepsilon \sigma _1, \end{aligned}$$

(3)

where $\sigma _1$ is the frequency detuning parameter.

To determine the analytical solution, we apply the multiple time scales method. According to Nayfeh [25, 26], the solution is expressed in a series of the small parameter

$$\begin{aligned} x(t,\varepsilon )= & {} {x_0}({T_0},{T_1},{T_2}) + \varepsilon {x_1}({T_0},{T_1},{T_2}) \nonumber \\&+\,{\varepsilon ^2}{x_2}({T_0},{T_1},{T_2}) \nonumber \\ {x_\tau }(t,\varepsilon )= & {} {x_{0\tau }}({T_0},{T_1},{T_2}) + \varepsilon {x_{1\tau }}({T_0},{T_1},{T_2}) \nonumber \\&+\,{\varepsilon ^2}{x_{2\tau }}({T_0},{T_1},{T_2}), \end{aligned}$$

(4)

where $x_j(T_0, T_1, T_2)$ and $x_{j\tau }(T_0, T_1, T_2)$ denote the solution and delayed solution, respectively, in the zeroth, first, and second perturbation orders ($j = 0, 1, 2$). According to this method, the time is also expressed by scales of the small parameter

$$\begin{aligned} t = T_0, \quad T_1 = \varepsilon t, \quad T_2 = \varepsilon ^2 t, \end{aligned}$$

(5)

where $T_0$ is the fast time scale (fast flow) and $T_1$ and $T_2$ are the slow time scales (slow flow).

The time definition (5) yields new definitions of the first- and second-order time derivatives

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d} t} = \frac{\partial }{{\partial {T_0}}} + \varepsilon \frac{\partial }{\partial T_1} + {\varepsilon ^2}\frac{\partial }{\partial T_2} = D_0 + \varepsilon D_1 + \varepsilon ^2 D_2 \nonumber \\&\frac{\hbox {d}^2}{\hbox {d} t^2} = D_0^2 + 2\varepsilon D_0 D_1 + \varepsilon ^2 \left( 2 D_0 D_2 + D_1^2 \right) , \end{aligned}$$

(6)

where $D_j^k = \frac{\partial ^k}{\partial {T_j}^k}$ denotes the kth-order partial derivative with respect to the $T_j$ time scale.

Solutions are sought near the principal parametric resonance (3). Thus, substituting (4) into (2) and considering the definitions of the time scales (5) and time derivatives (6), we obtain a set of successive ordinary differential equations in the zeroth, first, and second perturbation orders:

$$\begin{aligned}&D_0^2{x_0} + \Omega ^2 x_0 = 0 \end{aligned}$$

(7)

$$\begin{aligned}&D_0^2{x_1} + \Omega ^2 x_1 = \sigma _1 x_0 - 2 D_0 D_1 x_0 + F_{d0} \nonumber \\&\qquad \qquad \qquad \qquad \quad + \mu x_0 \cos 2\Omega T_0 - \gamma x_0^3 \nonumber \\&\qquad \qquad \qquad \qquad \quad + f \cos \Omega T_0 + g_1 x_{0 \tau } \end{aligned}$$

(8)

$$\begin{aligned}&D_0^2{x_2} + \Omega ^2 x_2 = \sigma _1 x_1 - 2 D_0 D_1 x_1 - 2 D_0 D_2 x_0 \nonumber \\&\quad -\, D_1^2 x_0 + F_{d1} - 3 \gamma x_0^2 x_1 + \mu x_1 \cos 2 \Omega T_0 \nonumber \\&\quad +\, \mu \gamma x_0^3 \cos 2 \Omega T_0 + g x_{1 \tau }. \end{aligned}$$

(9)

The functions $F_{d0}$ and $F_{d1}$ are defined in “Appendices A and B” for the van der Pol (40) and Rayleigh (48) models, respectively.

The solution to Eq. (7) takes the form

$$\begin{aligned} {x_0}({T_0},{T_1},{T_2})= & {} A({T_1},{T_2})\exp (i \Omega {T_0}) \nonumber \\&+ {{\bar{A}}}({T_1},{T_2})\exp ( - i \Omega {T_0}) \nonumber \\ {x_0}_\tau ({T_0},{T_1},{T_2})= & {} A({T_1},{T_2})\exp \left[ i( \Omega {T_0} - \tau ) \right] \nonumber \\&+ {{\bar{A}}}({T_1},{T_2})\exp \left[ -i (\Omega {T_0} - \tau ) \right] ,\nonumber \\ \end{aligned}$$

(10)

where i is the imaginary unit, A is the complex amplitude, and ${{\bar{A}}}$ is its complex conjugate.

Following substitution of (10) into (8) and grouping the exponential terms, we obtain

$$\begin{aligned}&D_0^2 x_1 + \Omega ^2 x_1\nonumber \\&\quad = ST_1 e^{i \Omega T_0} + \left( \frac{1}{2} \mu A - \gamma A^3 + Q_3 \right) e^{3i \Omega T_0} \, + cc,\nonumber \\ \end{aligned}$$

(11)

where cc denotes the complex conjugate functions for the right-side terms and $ST_1$ represents the secular generating terms of the first order, which must vanish to eliminate the secular terms in the solution. Thus, substituting $ST_1=0$ yields

$$\begin{aligned}&2 i \Omega D_1 A - \sigma _1 A - Q_1 + 3\gamma A^2 {{\bar{A}}} \nonumber \\&\quad - \frac{1}{2} \mu {{\bar{A}}} - g_1 \Omega A e^{- i \tau } - \frac{1}{2} f = 0. \end{aligned}$$

(12)

The functions $Q_1$ and $Q_3$ are defined by (41) and (49) for the van der Pol and Rayleigh models, respectively.

Next, for $ST_1=0$, we determine the particular solutions to Eq. (11):

$$\begin{aligned} x_1 = \frac{1}{16 \Omega ^2} \left( 2\gamma A^3 - \mu A - 2 Q_3 \right) e^{ 3 i \Omega T_0} + cc. \end{aligned}$$

(13)

Substituting solutions (13) into (9), we obtain

$$\begin{aligned} D_0^2{x_2} + {\Omega ^2}{x_2} = NS{T_2} + S{T_2}{e^{i\Omega \,{T_0}\,}} + cc, \end{aligned}$$

(14)

where $NST_2$ are nonsecular generating terms of the second order and, for the sake of brevity, are not reported in this paper, while $ST_2$ are secular generating terms which we consider as equal to zero:

$$\begin{aligned}&D_1^2A + 2 i \Omega D_2 A +P_1 + \frac{1}{32 \Omega ^2} \mu ^2 A + \frac{3}{8 \Omega ^2} \gamma ^2 A^3 {{\bar{A}}}^2 \nonumber \\&\quad - \frac{1}{2}\gamma \mu A \left( A^2 + 3 {{\bar{A}}}^2 \right) \left( 1 + \frac{1}{8 \Omega ^2} \right) = 0, \end{aligned}$$

(15)

with $P_1$ defined by (42) and (50) for both damping models.

Applying the so-called reconstitution method [25, 27, 28], based on Eqs. (12) and (15), we reconstruct the ordinary differential equation describing the complex amplitudes A:

$$\begin{aligned}&2 i \Omega \dot{A}\, =\, \varepsilon \left( G_1 {+} \frac{1}{2} \mu {{\bar{A}}} {-} 3 \gamma A^2 {{\bar{A}}} {+} \sigma _1 A_1{+} \frac{1}{2} f {+} g_1 e^{-i\tau } \right) \nonumber \\&\qquad \qquad \quad +\, \varepsilon ^2 \left\{ G_2 + \frac{1}{2 \Omega ^2} A \left( \frac{1}{2} \sigma _1^2 - \frac{3}{16} {\mu }^2 \right. \right. \nonumber \\&\qquad \qquad \quad \left. +\, \frac{15}{4} {\gamma }^2 A^2 {\bar{A}}^2 - 3 \gamma \sigma _1 A {{\bar{A}}} \right) \nonumber \\&\qquad \qquad \quad +\left. \, \frac{1}{2} \gamma \mu A \left[ \frac{1}{8 \Omega ^2} \left( 7 A^2 {-} 3 {{\bar{A}}}^2 \right) {+} A^2 {+} 3 {{\bar{A}}}^2 \right] \right. \nonumber \\&\qquad \qquad \quad + \left. \, \frac{1}{4 \Omega ^2} f \left[ \frac{1}{2} \sigma _1 {-}\frac{1}{4} \mu {+} 3 \gamma A \left( \frac{1}{2} A {+} 3 {{\bar{A}}} \right) \right] \right. \nonumber \\&\qquad \qquad \quad +\left. \, \frac{1}{2 \Omega ^2} g_1 \left[ \left( \frac{1}{4} f {+} \sigma _1 A {+} \frac{1}{4} \mu {{\bar{A}}} {-} \frac{9}{2} \gamma A^2 {{\bar{A}}} \right) e^{-i\tau } \right. \right. \nonumber \\&\qquad \qquad \quad \left. +\, {{\bar{A}}} \left( -\frac{1}{4} \mu + \frac{3}{2} \gamma A^2 \right) e^{i\tau } \right] \nonumber \\&\qquad \qquad \quad + \,\left. \frac{1}{4 \Omega ^2} g_1^2 A e^{-2 i\tau } \right\} , \end{aligned}$$

(16)

where $G_1$ and $G_2$ are defined by (43) and (51).

The complex amplitude A is expressed in the polar form:

$$\begin{aligned} A = \frac{1}{2}a{e^{i\phi }}, \end{aligned}$$

(17)

with a and $\phi$ as the amplitude and phase, respectively. Substituting (17) into (16) and separating the real and imaginary parts, we obtain the modulation equations for the amplitude a and phase $\phi$, the so-called slow flow, in the form

$$\begin{aligned}&2 \Omega \frac{\hbox {d}a}{\hbox {d}t}= \varepsilon \left( { W_1 - \frac{1}{2} a \mu \sin 2\phi } - g_1 a \sin \tau - f\sin \phi \right) \nonumber \\&\qquad \qquad \quad + \varepsilon ^2 \left\{ W_2 + \frac{1}{4} \mu \gamma a^3 \left( \frac{5}{8 \Omega ^2} - 1 \right) \sin 2 \phi \right. \nonumber \\&\qquad \qquad \quad +\, \frac{1}{4 \Omega ^2} f \left( \frac{1}{2} \mu - \sigma _1 + \frac{9}{4} \gamma a^2 \right) \sin \phi \nonumber \\&\qquad \qquad \quad +\, \frac{1}{2 \Omega ^2} g_1 \left[ a \left( - \sigma _1 +\frac{3}{2} \gamma a^2 \right. \right. \nonumber \\&\qquad \qquad \quad \left. \left. -\, \frac{1}{2} \mu \cos 2 \phi \right) \sin \tau - \frac{1}{2} f \sin \phi \cos \tau \right] \nonumber \\&\qquad \qquad \quad - \left. \frac{1}{4 \Omega ^2} g_1^2 a \sin 2\tau \right\} \end{aligned}$$

(18)

$$\begin{aligned}&2\Omega a \frac{\hbox {d}\phi }{\hbox {d}t}= \varepsilon \left( \frac{3}{4}{a^3}\gamma - a \sigma _1 - \frac{1}{2} a \mu \cos 2\phi \right. \nonumber \\&\qquad \qquad \quad \left. -\, g_1 a \cos \tau - f\cos \phi \right) \nonumber \\&\qquad \qquad \quad +\, \varepsilon ^2 \left\{ W_3 + \frac{3}{32\Omega ^2} a \mu ^2 + \frac{3}{8\Omega ^2}a^3\gamma \sigma _1 \right. \nonumber \\&\qquad \qquad \quad -\, \frac{1}{4\Omega ^2}a \sigma _1^2 - \frac{15}{128} \gamma ^2 a^5 \nonumber \\&\qquad \qquad \quad -\, \frac{1}{2}\mu \gamma a^3 \left( \frac{1}{8 \Omega ^2} + 1 \right) \cos 2 \phi \nonumber \\&\qquad \qquad \quad +\, \frac{1}{4 \Omega ^2} f \left( \frac{1}{2} \mu - \sigma _1 + \frac{3}{4} \gamma a^2 \right) \cos \phi \nonumber \\&\qquad \qquad \quad +\, g_1 \left[ \frac{1}{2 \Omega ^2} a \left( \frac{3}{4} \gamma a^2 - \sigma _1 - \frac{1}{2} f \cos \phi \right) \cos \tau \right. \nonumber \\&\qquad \qquad \quad \left. +\, \frac{1}{2} \left( a \mu \sin 2 \phi + f \sin \phi \right) \sin \tau \nonumber \right] \nonumber \\&\qquad \qquad \quad -\, \left. \frac{1}{4\Omega ^2} g_1^2 a \cos 2 \tau \right\} , \end{aligned}$$

(19)

where $W_1$, $W_2$, and $W_3$ are defined by (44) and (52).

The approximate solution is constructed based on Eq. (4). Applying (17) and thereafter transforming the exponential into trigonometric functions, the final form of the solution is obtained:

$$\begin{aligned} x\left( t \right)= & {} a \cos \left( {\Omega t + \phi } \right) \nonumber \\&-\, \frac{1}{16 \Omega ^2} a \varepsilon \left[ \mu \cos \left( {3 \Omega t + \phi } \right) \right. \nonumber \\&-\,\frac{1}{2}\gamma a^2 \cos 3 \left( \Omega t + \phi \right) \nonumber \\&\left. +\, C_1 \sin 3\left( \Omega t + \phi \right) \right] , \end{aligned}$$

(20)

with $C_1$ provided in (45) and (53). The amplitude a and phase $\phi$ in the above solution are defined by the modulation equations (18) and (19). In the steady state, $\frac{\hbox {d}a}{\hbox {d}t}=0$ and $\frac{\hbox {d} \phi }{\hbox {d}t}=0$, and thus, by equalling the right-hand sides of Eqs. (18) and (19) to zero, we obtain the amplitude and phase for the steady-state solution, which correspond to the periodic oscillations of the original system.

4 Steady-state periodic oscillations

The system dynamics can be analysed based on the modulation equations (18) and (19). However, we begin from the modulation equations, taking into account the first-order perturbation, and then, we move to the second-order approximation. Therefore, in the first step, we neglect terms of the $\varepsilon ^2$ order in the modulation equations (18) and (19). For a steady state, we obtain

$$\begin{aligned}&W_1 - \frac{1}{2} a \mu \sin 2\phi - g_1 a \sin \tau = f\sin \phi \nonumber \\&\frac{3}{4} a^3 \gamma - a \sigma _1 - \frac{1}{2} a \mu \cos 2\phi \nonumber \\&\quad -\, g_1 a \cos \tau = f \cos \phi . \end{aligned}$$

(21)

The above equations allow for preliminary analysis of the system and understanding the meaning of the terms responsible for the self-excitation (parameters $\alpha$ and $\beta$ included in the variable $W_1$), parametric excitation (coefficient $\mu$), external force (coefficient f), and time delay (gain $g_1$ and delay $\tau$). The above set of equations can be solved analytically for the case without external force, namely $f=0$. By eliminating the functions $\sin 2 \phi$ and $\cos 2 \phi$, we can obtain the resonance curve equation

$$\begin{aligned}&a^4 \left( \frac{9}{16} \gamma ^2 + U_1 \right) + a^2 \left[ U_2 -\frac{3}{2} \gamma \left( \sigma _1 + g_1 \cos \tau \right) \right] \nonumber \\&\quad +\, g_1^2 + \sigma _1^2 - \frac{1}{4} {\mu }^2 + U_3= 0, \end{aligned}$$

(22)

with the coefficients $U_1$, $U_2$, and $U_3$ defined in (46) for the van der Pol model and in (54) for the Rayleigh model. From Eq. (22), we can determine the amplitude of oscillations in a steady state for a self-parametric system with time delay. Setting $a=0$ in Eq. (22), we can also determine the bifurcation points of the trivial ($a=0$) into nontrivial ($a>0$) solutions, defined as

$$\begin{aligned} \Omega _{1,2} = \sqrt{ \frac{2 \omega _0^2 - \alpha ^2 - 2 g_1 \cos \tau \mp \sqrt{ \Delta }}{2}}, \end{aligned}$$

(23)

where

$$\begin{aligned} \Delta = \sqrt{ \alpha ^4 {+} \mu ^2 {-} 4 \alpha ^2 \omega _0^2 {+} 4 g_1 \alpha ( \alpha \cos \tau {+} 2 \Omega \sin \tau ) {-} 2 g_1^2 (1 {-} \cos 2 \tau ) }.\!\!\!\!\!\!\!\nonumber \\ \end{aligned}$$

(24)

The bifurcation points of the trivial into nontrivial solutions exist if $\Delta >0$; thus, we obtain

$$\begin{aligned} \mu \ge \sqrt{ \alpha ^2 ( 4 \omega _0^2 {-} \alpha ^2) {-} 4 g_1 \alpha (\cos \tau {+} 2 \Omega \sin \tau ) {+} 2 g_1^2 (1 {-} \cos 2 \tau ) }.\nonumber \\ \end{aligned}$$

(25)

We note that condition (25) does not depend on the $\beta$ parameters, which means that it does not depend on a model of self-excitation, and the conditions of existence are the same for the van der Pol and Rayleigh models.

In the case without time delay, namely $g_1=0$, we obtain

$$\begin{aligned} \Omega _{1,2} = \sqrt{ \frac{2 \omega _0^2 - \alpha ^2 \mp \sqrt{ \alpha ^4 + \mu ^2 - 4 \alpha ^2 \omega _0^2}}{2} }, \end{aligned}$$

(26)

and assuming that $\alpha$ is small, which results in $\alpha ^4 \approx 0$, we obtain the approximate condition for the existence of the bifurcation points

$$\begin{aligned} \frac{\mu }{\alpha } \ge 2. \end{aligned}$$

(27)

For the complete model with self-, parametric, and external force, we must solve the set of Eq. (21). Then, the solution depends on all parameters of the system and has been determined numerically.

5 Slow–slow motion of self-excited oscillator with time delay, and parametric and external excitations

Modulation equations allow for determining oscillations in a steady state by equalling them to zero. The obtained fixed points correspond to the periodic solutions of the original system (1). Nevertheless, the modulation equations (18) and (19) also provide information on the transient behaviour or periodic motion of the slow motion, which corresponds to the quasi-periodic oscillations of the original system. Therefore, using Eqs. (18) and (19), we may attempt to determine the slow motion of the slow flow, the so-called slow–slow motion. Thus, we expect to obtain analytical solutions for the quasi-periodic oscillations, which play an important role in the studied problem. For this purpose, we apply an extension of the multiple time scales method proposed by Belhaq and Houssni in [18] for parametric and externally excited systems and later also applied to the oscillator with time delay [19] or a more advanced model of a self-excited MEMS device [16, 17].

Returning to the original definitions of the parameters involving $\varepsilon$, the modulation equations (18) and (19) are rewritten in the following forms:

$$\begin{aligned} {\dot{a}}= & {} S_1 a + S_8 a \cos 2 \phi + S_9 a \sin 2\phi + 3 S_3 a^2 \sin \phi \nonumber \\&+\, S_{16} a^2 \cos \phi + S_4 a^3 + S_{10} a^3 \cos 2\phi \nonumber \\&+\, S_{11} a^3 \sin 2\phi + S_{14} \sin \phi + S_{15} \cos \phi + S_7 a^5 \nonumber \\ a {{\dot{\phi }}}= & {} S_2 a - S_8 a \sin 2 \phi + S_9 a \cos 2 \phi + S_3 a^2 \cos \phi \nonumber \\&-\, 3 S_{16} a^2 \sin \phi + S_5 a^3 + S_{12} a^3 \cos 2 \phi \nonumber \\&+\, S_{13} a^3 \sin 2 \phi + S_{14} \cos \phi \nonumber \\&-\, S_{15} \sin \phi + S_6 a^5. \end{aligned}$$

(28)

The definitions of the coefficients $S_i$ (with $i=1,\ldots ,16$) result from regrouping the modulation equations (18) and (19), and these are provided in (47) and (55).

To determine a periodic solution of the modulation equations, we transform them into the Cartesian form by substituting new coordinates

$$\begin{aligned} u=a \cos \phi \,, \quad v=-a \sin \phi . \end{aligned}$$

(29)

Then, by introducing a new small parameter as a book-keeping device, we obtain

$$\begin{aligned} \frac{\hbox {d} u}{\hbox {d} t}= & {} \, \left( S_2-S_9 \right) v + S_{15} \nonumber \\&+\, \varepsilon \left[ S_7 u^5 + 3 S_{16} v^2 + u^3 \left( S_{10} + S_4 + 2 S_7 v^2 \right) \right. \nonumber \\&+\, u \left( S_1 + S_8 - 2 S_3 v + (S_4 - S_{10} - 2 S_{13} ) v^2\right. \nonumber \\&\left. +\, s_7 v^4 \right) + S_6 v( u^4 + v^4) + v^3 (S_5 - S_{12} ) \nonumber \\&\left. + \,u^2 \left( S_{16} + 2 S_6 v^3 + v (S_{12} - 2 S_{11} + S_5) \right) \right] \nonumber \\ \frac{\hbox {d} v}{\hbox {d} t}= & {} - \left( S_2 + S_9 \right) u - S_{14} \nonumber \\&+\, \varepsilon \left[ (S_1 - S_8) v - S_6 u^5 + S_7 u^4 v \right. \nonumber \\&-\,3 S_3 v^2 + (S_4-S_{10})v^3 \nonumber \\&+\, S_7 v^5 - u^3 (S_{12} + S_5 + 2 S_6 v^2 ) \nonumber \\&+\, u^2 \left( v (S_{10} + 2 S_{13} + S_4 ) + 2 S_7 v^3 - S_3 \right) \nonumber \\&+\, u (-2 S_{16} v + (S_{12} \nonumber \\&\left. -\,2 S_{11} - S_5)v^2 - S_6 v^4 ) \right] . \end{aligned}$$

(30)

Solutions to the equation in (30) are sought in the form of

$$\begin{aligned} u(t) = u_0(T_1,T_2) + \varepsilon u_1(T_1,T_2) + O(\varepsilon ^2) \nonumber \\ v(t) = v_0(T_1,T_2) + \varepsilon v_1(T_1,T_2) + O(\varepsilon ^2). \end{aligned}$$

(31)

Substituting (31) into (30), taking into account the derivative definitions (6), and collecting the $\varepsilon ^0$ and $\varepsilon ^1$ terms, we obtain

$$\begin{aligned} D_1^2 u_0 + \lambda ^2 u_0= & {} S_{14} (S_9 - S_2) \nonumber \\ D_1 u_0= & {} (S_2 - S_9) v_0 + S_{15} \end{aligned}$$

(32)

$$\begin{aligned} D_1^2 u_1 + \lambda ^2 u_1= & {} -\,S_6 (S_2-S_9) u_0^5 -(-S_1S_2 \nonumber \\&+\, S_8 (S_2 - S_9) + S_1 S_9 ) v_0 - S_7 (S_9\nonumber \\&-\,S_2) u_0^4 v_0 + 3 S_3 (S_2 - S_9) v_0^2 \nonumber \\&+\, (S_{10} S_2 - S_2 S_4 - S_{10} S_9 + S_4 S_9 ) v_0^3 \nonumber \\&+\, S_7 (S_2-S_9) v_0^5 - (S_{12} S_2 + S_2 S_5 \nonumber \\&-\, S_{12} S_9 {-} S_5 S_9 {+} 2 S_6 (S_2 {-} S_9) v_0^2 ) u_0^3 \nonumber \\&+\, (S_3 (S_2-S_9) + (-S_2( S_{10} \nonumber \\&+\, 2 S_{13} S_4 ) + (S_{10} + 2 S_{13} + S_4 )S_9)v_0 \nonumber \\&+\, 2 S_7(-S_2 + S_9)v_03 + u_0 (2 S_{16}(S_2 \nonumber \\&-\,S_9)v_0 + (S_2 (2 S_{11} - S_{12} + S_5) \nonumber \\&+\,(- 2S_{11} + S_{12} - S_5) S_9 )v_0^2 \nonumber \\&+\,S_6(S_2{-}S_9)v_0^4)) {+} D_1 u_0({-}S_1-S_8 \nonumber \\&-\, 5 S_7 u_0^4 + 2 S_3 v_0- 4 S_6 u_0^3 v_0 \nonumber \\&+\,(S_{10} + 2S_{13} - S_4) v_0^2 - S_7 v_0^4 \nonumber \\&+\, 3 u_0^2 (-S_{10} - S_4 - 2S_7 v_0^2) + 2 u_0\nonumber \\&\,( -S_{16} + ( 2S_{11} - S_{12} - S_5 )v_0 \nonumber \\&-\,2S_6 v_0^3)) + D_1 v_0 (-S_6 u_0^4 - 6 S_{16} v_0 \nonumber \\&-\, 4 S_7 u_0^3 v_0 + 3( S_{12} -S_5) V_0^2 \nonumber \\&-\, 5 S_6 v_0^4 + u_0^2 (2S_{11} - S_{12} -S_5 \nonumber \\&-\, 6 S_6 v_0^2) + 2 u_0(S_3 \nonumber \\&+\,(S_{10} + 2 S_{13} - S_4)v_0 - 4 S_7 v_0^3)) \nonumber \\&+\, D_2v_0(S_2-S_9) + D_1D_2u_0 \nonumber \\ D_1 u_1= & {} (S_2-S_9) v_1 - D_2 u_0 + (S_1+S_8)u_0 \nonumber \\&+\, S_{16} u_0^2 + (S_{10}+S_4) u_0^3 + S_7 u_0^5 \nonumber \\&-\, ( S_3 u_0 + (2 S_{11} - S_{12} - S_5) u_0^2 \nonumber \\&-\,S_6u_0^4)v_0 + (3 S_{16} + (S_{10}+2S_{13} \nonumber \\&-\,S_4)u_0 -2S_7u_0^3) v_0^2 - (S_{12} -S_5 \nonumber \\&-\,2 S_6 u_0^2) v_0^3 - S_7 u_0 v_0^4 \nonumber \\&-\, S_6 v_0^5 (S_2-S_9)v_1, \end{aligned}$$

(33)

where $\lambda = \sqrt{S_2^2 - S_9^2}$ represents the LC frequency and depends on the parameters $S_2$ and $S_9$.

The solution of Eq. (32) takes the form

$$\begin{aligned} u_0= & {} R(T_2) \cos \left[ \lambda T_1 + \theta (T_2) \right] + \frac{S_{14}(S_9 - S_2)}{\lambda ^2} \nonumber \\ v_0= & {} R(T_2) \frac{\lambda }{S_9-S_2} \sin \left[ \lambda T_1 + \theta (T_2) \right] \nonumber \\&+ \frac{S_{15}}{(S_9 - S_2)}. \end{aligned}$$

(34)

Substituting the solutions in (34) into the first-order perturbation, expanding the nonlinear terms into the sine and cosine functions of multiple angles, and then grouping the harmonics, we can determine the secular generating terms, which must be equal to zero. Thus, we obtain modulation equations of the second kind, which represent the amplitude and phase of the quasi-periodic motion

$$\begin{aligned}&\frac{\hbox {d} R}{\hbox {d} t} = c_1 R^5 + c_2 R^3 + c_3 R \nonumber \\&R \frac{\hbox {d} \theta }{\hbox {d} t} = d_1 R^5 + d_2 R^3 + d_3 R, \end{aligned}$$

(35)

where the coefficients c and d depend on the parameters $S_1 \ldots S_{15}$. By setting Eq. (35) equal to zero, we determine the steady state, which is defined by the amplitude

$$\begin{aligned} R = \sqrt{ - \frac{ c_2 \pm \sqrt{c_2^2 - 4 c_1 c_3} }{2 c_1}}. \end{aligned}$$

(36)

The amplitude of the quasi-periodic vibrations $a=\sqrt{u^2+v^2}$ can be computed from (34) in the first approximation order and takes the following form:

$$\begin{aligned} a = \sqrt{ R^2 {\cos }^2\phi + \frac{2 R S_{14} (S_9-S_2)}{\lambda ^2} \cos \phi + \frac{S_{15}^2 \lambda ^2 + S_{14}^2 (S_9-S_2)^4 + 2 R_{15} \lambda ^5 \sin \phi + R^2 \lambda ^6 \sin ^2 \phi }{\lambda ^4 (S_9-S_2)}}. \end{aligned}$$

(37)

The envelope of the modulated amplitude is defined by the maximal $a_\mathrm{max}$ and minimal $a_\mathrm{min}$ values of Eq. (37).

The frequency of a LC corresponding to the quasi-periodic oscillations of the original system is defined by the parameter $\lambda$. Considering the definitions of $S_2$ and $S_9$, we obtain

$$\begin{aligned} \lambda = \frac{1}{64\Omega ^3} \sqrt{\left[ 8 \sigma _1^2 + 32 \sigma _1 \Omega ^2 - 3 \mu ^2 + 8 \alpha ^2 \Omega ^2 + 16 g_1 \left( \sigma _1 + 2 \Omega ^2 \right) \cos \tau + 8 g_1^2 \cos 2\tau \right] ^2 -256 \mu ^2 \Omega ^4}. \end{aligned}$$

(38)

The derived equations facilitate determining the amplitude of slow–slow motion and its frequency $\lambda$, which correspond to a quasi-periodic limit cycle of the original system. When analysing Eq. (38), we note that the period of the modulated amplitude $T_{\lambda } = 2 \pi /\lambda$ depends on the detuning parameter $\sigma _1$, damping coefficient $\alpha$, and parametric excitation $\mu$, as well as the delay parameters $g_1$ and $\tau$. It is interesting to note that it is independent of the nonlinear component of the nonlinear damping $\beta$ and external force f, taking into account the first-order approximation of the slow–slow motion. This result is in agreement with the results presented in the paper of [15].

Fig. 2

Resonance curve for nonlinear system with self- and parametric excitations for van der Pol model (black curve) or Rayleigh model (magenta curve): a full resonance curve; b zoom near Hopf bifurcation point; data (39), $g_1=0$, $f=0$. (Color figure online)

Fig. 3

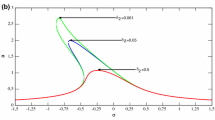
Resonance curves for nonlinear system with self- and parametric excitations for a van der Pol and b Rayleigh models for selected values of the parametric excitation amplitude: $\mu =0.2$: black, $\mu =0.1$: red, $\mu =0.05$: green, and $\mu =0.02$: blue; data (39), $g_1=0$, $f=0$. (Color figure online)

6 Analysis of self- and parametrically excited system with time delay

The analytical solutions obtained in the previous sections enable the analysis of a very general Duffing-type oscillator, which consists of self-excitation, a parametric term, external loading, and time delay input. The approximate solutions are also determined for periodic and quasi-periodic oscillations. By equalling the selected parameters to zero, we can study several interesting dynamic cases.

Let us consider the self- and parametric excitation acting on the model. Therefore, we set the external force equal to zero, namely $f=0$. For numerical examples, we take the following parameters:

$$\begin{aligned}&\alpha =0.01\,, \quad \beta _v=0.05 \,, \quad \beta _R=\frac{1}{3}\beta _v \,, \quad \nonumber \\&\quad \gamma =0.1 \,, \quad \mu =0.2 \,, \quad \omega _0=1. \end{aligned}$$

(39)

Fig. 4

Influence of amplitude of parametric excitation $\mu$ on bifurcation scenario for a van der Pol and b Rayleigh models of self-excitation and fixed parametric excitation frequency: $\Omega =0.95$: black, $\Omega =1.0$: blue, and $\Omega =1.2$: green; data (39), $g_1=0$, $f=0$. (Color figure online)

The values of the parameters provided in (39) are treated as basic, but several can be varied in specific analyses. The parameter of nonlinear damping $\beta$ is maintained in an appropriate ratio to compare the van der Pol and Rayleigh models.

The resonance curves for the principal parametric resonance are obtained based on the second-order approximation by equalling Eqs. (18) and (19) to zero and then determining the amplitude a as a function of the frequency $\Omega$. The comparison of the resonance curves for the van der Pol (black) and Rayleigh (magenta) models is presented in Fig. 2. The two considered models exhibit similar qualitative behaviour. The curves represent periodic oscillations, which occur following Hopf bifurcation of the second kind (Neimark–Sacker bifurcation), as indicated by $HB_v$ or $HB_R$ for the van der Pol or Rayleigh models, respectively. The Hopf bifurcation point occurs earlier, and the resonance zone is wider for the van der Pol model (see Fig. 2b). This fact is also confirmed in Fig. 3 for various parametric excitation parameters $\mu$. For smaller values of parametric excitation, the resonance zone decreases and the amplitude is smaller. The decreasing tendency of the resonance zones is stronger for the Rayleigh function of self-excitation.

The bifurcation points of the trivial into nontrivial solutions (points at which the resonance curves arise) can be determined from Eq. (26) and depend on the parameters $\mu$ and $\alpha$, but not on $\beta$. Thus, considering the first-order approximation, they are located in the same place for the van der Pol and Rayleigh models. Furthermore, they may exist if the condition (27) is satisfied. In fact, for $\mu =0.02$, the resonance curve arises almost from a single point, as illustrated in Fig. 3a, b by the blue resonance curves. For values of $\mu$ smaller than the determined critical $\mu =0.02$, the resonance curves do not bifurcate from the trivial solutions, but form the shape of a separate island located above the axis (not presented here).

To determine the influence of the parametric excitation amplitude on the system dynamics, we fix the excitation frequency $\Omega$, while maintaining the remaining parameters as provided in (39), and then compute the amplitude versus bifurcation parameter $\mu$. In Fig. 4a, b, we present the bifurcation diagrams for the van der Pol and Rayleigh functions, respectively. The bifurcation curves computed for $\Omega =0.95$, $\Omega =1.0$, and $\Omega =1.2$ begin from unstable periodic solutions, which, while increasing $\mu$, become stable periodic oscillation. Two possible scenarios exist: (1) after supercritical bifurcation of the trivial solution, the curve becomes stable above the Hopf bifurcation point, which corresponds to bifurcation of quasi-periodic to periodic motion, and (2) the curve starts from subcritical bifurcation of the trivial solution and then becomes stable after the limit point (turning point). The first scenario is presented in Fig. 4a for $\Omega =0.95$ and $\Omega =1.0$ (black and blue curves, respectively) and Fig. 4b for $\Omega =0.95$ (black curve). The second scenario is observed in Fig. 4a for $\Omega =1.2$ (green line) and Fig. 4b for $\Omega =1.0$ (blue curve) and $\Omega =1.2$ (green curve). The behaviour of the two models is completely different in the studied cases. The periodic solutions in the Rayleigh model are stable for large values of the parameter $\mu$, while for the van der Pol model, the second turning point occurs and the solutions become unstable.

Fig. 5

a Comparison of amplitude of quasi-periodic and periodic oscillations around principal parametric resonance for van der Pol (black) and Rayleigh (magenta) self-excitation models; b comparison of analytical (AR) and direct numerical simulation (NS) results; data (39), $g_1=0$, $f=0$. (Color figure online)

The periodic solutions presented above exist near the principal parametric resonance zone. When moving beyond this zone, the system response is no longer periodic, but becomes quasi-periodic. To obtain the analytical solutions of quasi-periodic motion, the second type of multiple time scales is applied, as presented in Chapter 5.

The maximal and minimal values of the modulated amplitude, as well as the periodic resonance curves, are presented in Fig. 5a. The black lines represent the analytical solutions the for van der Pol model, while the solutions for the Rayleigh model are plotted in magenta. The dynamics of both models is qualitatively similar. However, for the Rayleigh model, the modulations are smaller either before or after the resonance zone, and the transition from quasi-periodic to periodic oscillations begins slightly earlier and ends later for the van der Pol model. This is in agreement with the result presented earlier in Fig. 2b, where a shift in the Hopf bifurcation point for both self-excitation models is illustrated. The numerical verification of the analytical results by means of direct numerical simulation of the original model for the van der Pol self-excitation is presented in Fig. 5b. The blue vertical lines indicate the maximal and minimal values of the modulated amplitude, while the blue dots represent the amplitudes of the periodic motion. The analytical prediction of the periodic solutions exhibits very strong agreement with the numerical simulations, while the analytical results of the quasi-periodic motion exhibit larger differences. This can be explained by the fact that the slow–slow flow is solved in the first-order approximation, while the periodic motion is determined up to the second-order perturbation terms.

The period of slow–slow motion $T_\lambda$ computed from (38) is independent of the self-excitation type, at least up to the first-order approximation, but depends on the parametric excitation amplitude $\mu$. When approaching the resonance zone, the modulated amplitude period tends towards infinity (Fig. 6). For higher values of parametric excitation $\mu$, the increasing tendency of the period $T_{\lambda }$ is higher, as indicated by the blue curve in Fig. 6. The period of slow–slow motion for $\mu =0.2$ obtained from the analytical formula is presented in Fig. 6 by a black solid line, while the results of the corresponding direct numerical simulation are marked by black dots. The gain of the input signal is equal to zero in the mentioned solutions, namely $g_1=0$. The solution is in strong agreement with a slight shift of the analytical curves into the lower frequency direction. The solutions for the period $T_\lambda$ do not exist in the zone near $\Omega =1$, as in this domain, only periodic motion may exist. The analytical prediction of the amplitude and period of the quasi-periodic motion enables identification of the most important features of the system dynamics.

Fig. 6

Period of quasi-periodic oscillations around principal parametric resonance: $\mu =0.2$: black, $\mu =0.1$: red, $\mu =0.5$: blue; data (39), $g_1=0$, $f=0$

The analytical results are further verified by a bifurcation diagram (Fig. 7) plotted based on the direct numerical simulation of Eq. (1). The solution is computed starting from various basins of attraction, and the transient response is neglected by the rejection of 200 periods. The stroboscopic effect based on the excitation frequency $\Omega$ is used to create the diagram. The periodic response versus excitation frequency $\Omega$ is represented by the double solid line, which indicates the subharmonic solution in the principal parametric resonance zone. The quasi-periodic solutions with modulated amplitudes are represented by the dark areas. The transition from quasi-periodic motion to the so-called frequency-locking zone with periodic oscillations for the van der Pol oscillator is demonstrated by Poincaré sections in Fig. 8. Starting from low frequencies and moving forward in the bifurcation diagrams in Figs. 5b and 7, we approach the resonance zone. The Poincaré portraits in Fig. 8a–d demonstrate the changes in the system response. For $\Omega =0.95$, we observe a quasi-periodic LC with an unstable focus (UF) point in the centre. For $\Omega =0.962$, two unstable focuses arise inside the LC, with a saddle point in the centre, while for $\Omega =0.967$, the UFs bifurcate into two stable focuses (SFs) inside the LC. A small increase in $\Omega$ up to $\Omega =0.968$ leads to destruction of the LC, and only periodic oscillations represented by double SF may exist. Moving backwards, starting from $\Omega =1.11$ in Fig. 8e, depending on the initial conditions, the response may be quasi-periodic, represented by a LC with UF in the centre, or periodic, with two SF points located outside of the LC. A small variation in the bifurcation parameter up to $\Omega =1.105$ destroys the LC, and in Fig. 8f, only the periodic solution exists.

Fig. 7

Bifurcation diagram of van der Pol–Mathieu–Duffing oscillator against excitation frequency $\Omega$ around principal parametric resonance; direct numerical simulation; data (39), $g_1=0$, $f=0$

Fig. 8

Poincaré maps corresponding to bifurcation diagram in Figs. 5b and 7 for van der Pol model of self-excitation around principal parametric resonance: direct numerical simulation results for $\Omega =0.95$, $\Omega =0.962$, $\Omega =0.967$, $\Omega =0.968$, $\Omega =1.11$, and $\Omega =1.105$; data (39), $g_1=0$, $f=0$

Analysing Eq. (38), we notice that the control parameters $g_1$ and $\tau$ influence the period of slow–slow motion. Thus, we consider the quasi-periodic system response before and after the resonance zone. We fix the excitation frequency as $\Omega =0.8$ and $\Omega =1.2$ and vary the control parameters $g_1$ and $\tau$. The three-dimensional (3D) plots of the period $T_{\lambda }$ computed based on the analytical solution (38) are presented in Fig. 9. We may effectively change the period and amplitude of the modulated oscillations; however, the tendency when selecting the control parameters for the slow–slow motion before and after the resonance zone is the opposite. As observed in Fig. 9a ($\Omega =0.8$), when varying the time delay $\tau$ from zero we decrease the period $T_{\lambda }$, while in Fig. 9b ($\Omega =1.2$), the period is increased.

Fig. 9

Effect of time delay parameters $g_1$ and $\tau$ on period of slow–slow motion for a$\Omega =0.8$ and b$\Omega =1.2$; data (39)

Fig. 10

Amplitude of quasi-periodic and periodic oscillations around principal parametric resonance for van der Pol model without control: $g_1=0$ and $\tau =0$ (black colour) and with delay control signal: $g_1=0.05$ and $\tau =0.1$ (magenta); data (39). (Color figure online)

Fig. 11

Time histories of quasi-periodic motion for van der Pol model without time delay for a$\Omega =0.9$ and c$\Omega =1.15$, and influence of time delay b$\Omega =0.9$, $g_1=0.05$, $\tau =0.1$, and d$\Omega =1.15$, $g_1=0.05$, $\tau =0.1$; data (39)

The time delay signal enables control of the periodic and quasi-periodic response in terms of the frequency and amplitudes, as well as a shift in the resonance zone. This means we can design the system response according to the required criteria, based on the analytical solution, which may differ, for example for energy harvesting or vibration absorption. In this study, we do not present a detailed analysis of any specific dedicated control strategy, but in Fig. 10 we provide an example of the possible influence of delay parameters for the van der Pol model. By introducing a small gain $g_1=0.05$ and delay $\tau =0.1$, we can reduce the periodic oscillations slightly and move the resonance curve towards the lower frequencies, in addition to reducing the amplitudes of the quasi-periodic response. This is demonstrated by the magenta curves in Fig. 10.

The change in the response for the quasi-periodic oscillations is confirmed by the time histories computed for selected excitation frequencies $\Omega =0.9$ and $\Omega =1.15$ by direct numerical integration of Eq. (1). The time histories in black in Fig. 11a–c correspond to a system without control, while those in magenta, (b) and (d), correspond to a system with control. The results demonstrate very strong agreement with the analytical solution presented in Fig. 10.

Fig. 12

Bifurcation diagrams versus parametric excitation $\mu$ for nonlinear oscillator with a van der Pol and b Rayleigh self-excitation models; data (39), $\Omega =1.0$, $g_1=0$, $f=0$

Fig. 13

Basins of attraction of van der Pol model for parametric excitation: a$\mu =1.55$ and b$\mu =1.60$; data (39), $\Omega =1.0$, $g_1=0$, $f=0$. (Color figure online)

The obtained analytical solutions provide very deep insight into the system dynamics and its possible control; however, they are limited to mainly weakly nonlinear systems. To determine the difference between the van der Pol and Rayleigh self-excitation for a strongly nonlinear model and large oscillations, we perform numerical analysis of Eq. (1). The two bifurcation diagrams in Fig. 12 illustrate the difference in response of the self- and periodically excited oscillator when the parametric excitation amplitude is increased with a frequency $\Omega =1$ and the remaining parameters are fixed, as given in (39).

Fig. 14

Resonance curves around principal parametric resonance for model with van der Pol and parametric terms as well as external force: a$f=0.01$; b$f=0.1$; c$f=0.1875$; d$f=0.1875$: zoom of zone A; data (39), $g_1=0$

Fig. 15

Resonance curves around principal parametric resonance for a van der Pol and b Rayleigh models of self-excitation; data (39), $f=0.05$, $g_1=0$

Fig. 16

Effect of external force on resonance curves around principal parametric resonance: a$f=0.1$ and b$f=0.3$. Comparison of van der Pol (black) and Rayleigh (magenta) models; data (39), $g_1=0$. (Color figure online)

Fig. 17

Bifurcation diagrams versus excitation frequency $\Omega$ for nonlinear oscillator with a van der Pol and b Rayleigh models, and parametric and external excitations for $\alpha =0.01$, $\beta =0.05$, $\gamma =0.1$, $\mu =0.2$, $f=0.2$, and $g_1=0$

For very small values of $\mu$, we obtain the quasi-periodic oscillations represented by a black zone on the left-hand side of the bifurcation diagrams in Fig. 12a, b, which, by means of the second type of Hopf bifurcation, bifurcates into periodic, subharmonic motion, represented by the double line. For large values of the bifurcation parameter $\mu \approx 1.4$, period-doubling bifurcation occurs. However, above this point, the bifurcation scenarios differ for varying self-excitation models. For the van der Pol model, after period doubling, a cascade of period doubling takes place and the system enters chaotic motion (Fig. 12a). Then, after the boundary crisis bifurcation, the system returns to regular subharmonic oscillations. The transition from chaos to regular motion is illustrated in Fig. 13. For $\mu =1.55$ (Fig. 13a), a regular attractor, represented by the double point, coexists with a strange chaotic attractor located in the middle of the phase plane, which almost touches the boundaries of its attraction basins. A small change in the bifurcation parameter $\mu =1.60$ destroys the chaotic attractor (owing to the boundary crisis), and the periodic oscillation is maintained, with a fractal basin of attractions in the middle (Fig. 13b).

The analysed 1-DOF nonlinear oscillator with Rayleigh self-excitation does not demonstrate a chaotic response for the range of studied parameters. In contrast, chaotic motion is detected for the van der Pol oscillator with equivalent parameters.

7 Influence of external force on self- and parametrically excited system

We now consider the self-, parametric, and externally excited system. We assume that the system is excited by three different mechanisms simultaneously. Therefore, an external force occurs on the right-hand side of Eq. (1). We assume that the parametric term and external force excite the system in a ratio of 2:1. This means that we analyse the oscillations near the principal resonance zone, with the additional external force having a frequency corresponding to the subharmonic system response. Such a situation is common in numerous mechanical systems [14].

The influence of the external force is illustrated in Fig. 14 for the van der Pol model. By imposing a very small force $f=0.01$ on the system, we obtain a resonance curve with an internal loop and two Hopf bifurcation points, located very close to one another (Fig. 14a). This is a qualitatively new response with five periodic solutions; however, only the two upper branches are stable, while the three lower ones are unstable (dashed line). The periodic solutions beyond the resonance zone are unstable. The phenomenon of the resonance curve with the loop and double Hopf bifurcation point is observed for very small values of the external force f. If the force f is increased, the loop becomes smaller and the Hopf bifurcation point located on the left side of the loop disappears (Fig. 14b). A further increase in the parameter f eliminates the loop and stabilises part of the lower branch of the resonance curve, with a new Hopf bifurcation point occurring on the right side of the resonance curve. This situation of the loop almost disappearing is illustrated in Fig. 14c and a zoom presenting the very small loop in Fig. 14d.

The external force influences both self-excited oscillators in a similar manner. The resonance curves for $f=0.05$ are presented in Fig. 15 for the (a) van der Pol and (b) Rayleigh models. In both cases, we can observe the existence of five solutions, with $\Omega \sim (1.05,1.32)$ for the van der Pol and $\Omega \sim (1.07,1.23)$ for the Rayleigh models. The stability analysis based on the modulation equations (18), (19) and then confirmed numerically demonstrates that only the two upper branches of the curve are stable (solid line), while the three lower ones are unstable (dashed line). A direct comparison of the resonance curves for $f=0.1$ for both models is presented in Fig. 16a. We note that, for the van der Pol model, the Hopf bifurcation point is located further beyond the resonance zone, and the loop is larger compared to that of the Rayleigh model (see black and magenta curves in Fig. 16a). The loop in the resonance zone for the Rayleigh model is smaller and disappears earlier if the amplitude of excitation f is increased, as illustrated in Fig. 16b.

The accuracy of the analytical solutions is verified by means of direct numerical simulation of Eq. (1). Bifurcation diagrams of the solution x versus frequency $\Omega$ for $f=0.2$ are presented in Fig. 17 for the (a) van der Pol and (b) Rayleigh models. The dark zones correspond to quasi-periodic oscillations, while the solid lines indicate stable periodic solutions. The unstable solutions are not presented in the figures. The solutions corresponding to the internal loop are located in the negative parts of the diagrams, which means that they are shifted in phase compared to the excitation phase. The dynamics of the response can be changed by adding a time delay signal. We can modify the solution stability, shift the resonance zone, move the Hopf bifurcation points, and eliminate the additional resonance loop. The influence of the delay parameters on the periodic and quasi-periodic dynamics of the overall system will be elaborated in detail in a separate paper.

8 Conclusions

The interactions among self-, parametric, and external oscillations have been studied for two different self-excitation models, represented by the van der Pol or Rayleigh functions. For a weakly nonlinear system and relatively small oscillations, both considered models exhibit quantitatively similar behaviours. The frequency- locking phenomenon is observed for the system with self- and parametric excitations near the principal resonance zone. The system transits from quasi-periodic to periodic oscillations via Hopf bifurcation of the second kind. The periodic and quasi-periodic solutions are obtained by applying the multiple time scales method twice to determine the amplitudes of the periodic motion (slow flow) and next amplitude of the quasi-periodic motion (slow–slow flow). The solutions are in strong agreement with the direct numerical simulations.

In general, the vibration amplitudes and resonance zones are smaller for the Rayleigh model compared to its van der Pol counterpart. Moreover, the Hopf bifurcation points are slightly shifted. The amplitude of the modulated quasi-periodic response demonstrates similar tendencies. The time delay signal enables control of the dynamics of self-parametric systems, with either periodic or quasi-periodic motions. The analytical solutions obtained provide deep insight into the system dynamics and may aid in the design of a dedicated control strategy.

For strongly nonlinear vibrations, the system response differs quantitatively and qualitatively for varying self-excitation functions. The increase in the parametric excitation transits the van der Pol model to chaotic motion by means of period-doubling bifurcation and then escapes from chaotic motion to a periodic response by means of boundary crisis bifurcation. For the Rayleigh model and equivalent parameters, only period doubling is observed. The van der Pol model demonstrates a higher tendency of moving to chaotic oscillations. For the Rayleigh 1-DOF model, chaotic motion is not observed in the studied parameters domain.

The added small external force changes the dynamics essentially. Near the principal parametric resonance zone, additional solutions occur with an internal loop shape. The stability analysis demonstrates that only the upper parts of the resonance curve are stable. If the amplitude of the external force increases, the loop decreases or totally disappears. The effect of the loop exists for both studied models and is quantitatively similar; however, it exhibits a tendency of decreasing amplitudes for the Rayleigh model.

Appendices

Appendix A: Multiple time scales method—van der Pol model

Analytical expressions for van der Pol model

$$\begin{aligned} F_{d0}= & {} \alpha D_0 x_0 - \beta D_0 x_0 x_0^2 \nonumber \\ F_{d1}= & {} \alpha \left( D_0 x_1 + D_1 x_0 \right) \nonumber \\&-\, \beta \left[ x_0^2 \left( D_0 x_1 + D_1 x_0 \right) + 2 x_0 x_1 D_0 x_0 \right] \end{aligned}$$

(40)

$$\begin{aligned} Q_1= & {} i \Omega A \left( \alpha - \beta A \bar{A} \right) \nonumber \\ Q_3= & {} - i \beta \Omega A^3 \end{aligned}$$

(41)

$$\begin{aligned} P_1= & {} - \alpha D_1 A + \beta \left[ A^2 \bar{A} + 2 A \bar{A} D_1 A -\frac{1}{8} A^3 \bar{A}^2 \right. \nonumber \\&\left. +\, \frac{1}{2 \Omega } i \gamma A^3 \bar{A}^2 - \frac{1}{16 \Omega } \mu \left( i A^3 - \Omega A \bar{A}^2 \right) \right] \end{aligned}$$

(42)

$$\begin{aligned} G_1= & {} i \Omega A \left( \alpha - \beta A \bar{A} \right) \nonumber \\ G_2= & {} \frac{1}{4} \alpha ^2 A + \frac{7}{8} \beta ^2 A^3 \bar{A}^2 - \frac{3}{2 \Omega } i \alpha \gamma A^2 \bar{A}^2 \nonumber \\&-\, \frac{1}{\Omega } i \beta \gamma A^3 \bar{A}^2 + \frac{3}{16 \Omega } i \beta \mu A \bar{A}^2 - \frac{1}{16} i \beta \mu A^3 \nonumber \\&+\, f \left[ -\frac{1}{8 \Omega } i \alpha + \frac{1}{4 \Omega } i \beta A \left( \frac{1}{2} A + \bar{A} \right) \right] \nonumber \\&+\, \frac{1}{4 \Omega } g_1 i \beta A^2 \bar{A} \left( e^{-i \tau } + e^{i \tau } \right) \end{aligned}$$

(43)

$$\begin{aligned} W_1= & {} \Omega a \left( \alpha - \frac{1}{4} \beta a^2 \right) \nonumber \\ W_2= & {} - \frac{3}{8 \Omega } \alpha \gamma a^3 + \frac{1}{16 \Omega } \beta \gamma a^5 \nonumber \\&+\, \frac{1}{4 \Omega } f \left( - \alpha + \frac{1}{4} \beta a^2 \right) \cos \phi \nonumber \\&+\, \frac{1}{32 \Omega } \beta \mu a^3 \cos 2 \phi \nonumber \\ W_3= & {} -\, \frac{1}{4}a \alpha ^2 + \frac{1}{4} \alpha \beta a^3 - \frac{7}{128} \beta ^2 a^5 \nonumber \\&- \,\frac{1}{16 \Omega } \beta \mu a^3 \sin 2 \phi \nonumber \\&+\, \frac{1}{4 \Omega } f \left( \alpha - \frac{3}{4} \beta a^2 \right) \sin \phi \nonumber \\&-\, \frac{1}{8 \Omega } g_1 \beta a^3 \sin \tau \end{aligned}$$

(44)

$$\begin{aligned} C_1= & {} - \frac{1}{32 \Omega } \beta a^2 \end{aligned}$$

(45)

$$\begin{aligned} U_1= & {} \frac{\beta ^2 \Omega ^2}{16} \nonumber \\ U_2= & {} -\frac{1}{2} \alpha \beta \Omega ^2 + \frac{1}{2} g_1 \beta \Omega \sin \tau \nonumber \\ U_3= & {} \alpha ^2 \Omega ^2 \end{aligned}$$

(46)

Analytical expressions for van der Pol model—modulation equations (28)

$$\begin{aligned} S_1= & {} \frac{1}{2} \alpha - \frac{1}{2 \Omega } g_1 \sin \tau \left( 1 + \frac{\sigma _1}{2 \Omega ^2} \right) \nonumber \\&-\, \frac{1}{4 \Omega ^3} g_1^2 \sin \tau \cos \tau \nonumber \\ S_2= & {} \frac{3}{64 \Omega ^3} \mu ^2 - \frac{1}{8 \Omega } \alpha ^2 - \frac{\sigma _1}{2 \Omega } \left( 1 + \frac{\sigma _1}{4 \Omega ^2} \right) \nonumber \\&-\, \frac{1}{2 \Omega } g_1 \left( 1 + \frac{\sigma _1}{2 \Omega ^2} \right) \cos \tau \nonumber \\&+\, \frac{1}{8 \Omega ^3} g_1^2 \left( \sin ^2 \tau - \cos ^2 \tau \right) \nonumber \\ S_3= & {} \frac{3}{32 \Omega ^3} f \gamma \nonumber \\ S_4= & {} - \frac{3}{16 \Omega ^2} \alpha \gamma -\frac{1}{8} \beta + \frac{3}{8\Omega ^3} g_1 \gamma \sin \tau \nonumber \\ S_5= & {} \frac{1}{8 \Omega } \alpha \beta + \frac{3}{8 \Omega } \gamma \left( 1 + \frac{1}{2 \Omega ^2} \sigma _1 \right) \nonumber \\&+\, \frac{1}{16 \Omega ^2} g_1 \left( \frac{3}{\Omega } \gamma \cos \tau - \beta \sin \tau \right) \nonumber \\ S_6= & {} - \,\frac{1}{256 \Omega } \left( \frac{15}{\Omega ^2} \gamma ^2 + 7 \beta ^2 \right) \nonumber \\ S_7= & {} \frac{1}{32 \Omega ^2} \beta \gamma \nonumber \\ S_8= & {} -\, \frac{1}{8 \Omega ^3} g_1 \mu \sin \tau \nonumber \\ S_9= & {} -\,\frac{1}{4 \Omega } \mu \nonumber \\ S_{10}= & {} \frac{1}{64 \Omega ^2} \beta \mu \nonumber \\ S_{11}= & {} -\frac{1}{64 \Omega ^3} \gamma \mu \left( 8 \Omega ^2 -5 \right) \nonumber \\ S_{12}= & {} - \frac{1}{4 \Omega } \left( 1 + \frac{1}{8 \Omega ^2} \right) \gamma \mu \nonumber \\ S_{13}= & {} -\, \frac{1}{32 \Omega ^2} \beta \mu \nonumber \\ S_{14}= & {} \frac{1}{2 \Omega } f \left[ -1 + \frac{1}{4 \Omega ^2} \left( \frac{1}{2} \mu - \sigma _1 - g_1 \cos \tau \right) \right] \nonumber \\ S_{15}= & {} -\,\frac{1}{8 \Omega ^2} g_1 \left( \alpha + g_1 \frac{1}{\Omega } \sin \tau \right) \nonumber \\ S_{16}= & {} \frac{1}{32 \Omega ^2} f \beta \nonumber \\ S_{17}= & {} -\, \frac{3}{32 \Omega ^2 } f \beta \end{aligned}$$

(47)

Appendix B: Multiple time scales method—Rayleigh model

Analytical expressions for Rayleigh model

$$\begin{aligned} F_{d0}= & {} \alpha D_0 x_0 - \beta D_0 x_0^3 \nonumber \\ F_{d1}= & {} \alpha \left( D_0 x_1 + D_1 x_0 \right) \nonumber \\&-\, 3 \beta (D_0 x_0)^2 \left( D_0 x_1 + D_1 x_0 \right) \end{aligned}$$

(48)

$$\begin{aligned} Q_1= & {} i \Omega A \left( \alpha - 3 \beta \Omega ^2 A \bar{A} \right) \nonumber \\ Q_3= & {} - i \beta \Omega ^3 A^3 \end{aligned}$$

(49)

$$\begin{aligned} P_1= & {} -\, \alpha D_1 A - 3 \beta \Omega ^2 A^2 D_1 \bar{A} + 6 \beta \Omega ^2 A \bar{A} D_1 A \nonumber \\&-\, \frac{3}{2} \Omega i \beta \gamma A^3 \bar{A}^2 + \frac{1}{16} \Omega i \beta \mu A^3 \nonumber \\&+\, \frac{9}{16} \Omega \beta \mu A \bar{A}^2 -\frac{9}{8} \beta ^2 \Omega ^4 A^3 \bar{A}^2 \end{aligned}$$

(50)

$$\begin{aligned} G_1= & {} i \Omega A \left( \alpha - 3 \beta \Omega ^2 A \bar{A} \right) \nonumber \\ G_2= & {} \frac{1}{4} \alpha ^2 A - \frac{9}{8} \beta ^2 \Omega ^4 A^3 \bar{A}^2 - \frac{3}{2 \Omega } i \alpha \gamma A^2 \bar{A} \nonumber \\&+\, 3 i \beta \Omega \sigma _1 A^2 \bar{A} - 3 i \beta \Omega \gamma A^3 \bar{A}^2 \nonumber \\&-\,\frac{3}{16 \Omega } i \beta \mu A \bar{A}^2 + \frac{17}{16} i \beta \Omega \mu A^3 \nonumber \\&+\, f \left[ -\frac{1}{8 \Omega } i \alpha + \frac{3}{4} \Omega i \beta A \left( \frac{3}{2} A + \bar{A} \right) \right] \nonumber \\&+\,\frac{3}{4} \Omega g_1 i \beta A^2 \bar{A} \left( e^{-i \tau } + 3 e^{i \tau } \right) \end{aligned}$$

(51)

$$\begin{aligned} W_1= & {} \Omega a \left( \alpha - \frac{3}{4} \beta \Omega ^3 a^2 \right) \nonumber \\ W_2= & {} - \frac{3}{8 \Omega } \alpha \gamma a^3 - \frac{3}{16} \Omega \beta \gamma a^5 \nonumber \\&+\, \frac{1}{4 \Omega } f \left( - \alpha + \frac{15}{4} \beta \Omega ^2 a^2 \right) \cos \phi \nonumber \\&+\, \frac{7}{32} \Omega \beta \mu a^3 \cos 2 \phi \nonumber \\ W_3= & {} - \frac{1}{4}a \alpha ^2 + \frac{9}{128} \beta ^2 \Omega ^2 a^5 + \frac{5}{16} \Omega \beta \mu a^3 \sin 2 \phi \nonumber \\&+\, \frac{1}{4 \Omega } f \left( \alpha + \frac{3}{4} \beta \Omega a^2 \right) \sin \phi \nonumber \\&-\, \frac{3}{8} \Omega g_1 \beta a^3 \sin \tau \end{aligned}$$

(52)

$$\begin{aligned} C_1= & {} \frac{1}{32} \beta \Omega a^2 \end{aligned}$$

(53)

$$\begin{aligned} U_1= & {} \frac{9 \beta ^2 \Omega ^6}{16} \nonumber \\ U_2= & {} -\frac{3}{2} \alpha \beta \Omega ^4 + \frac{3}{2} g_1 \beta \Omega ^3 \sin \tau \nonumber \\ U_3= & {} \alpha ^2 \Omega ^2 \end{aligned}$$

(54)

Analytical expressions for Rayleigh model—modulation equations (28)

$$\begin{aligned} S_1= & {} \frac{1}{2} \alpha - \frac{1}{2 \Omega } g_1 \sin \tau \left( 1 + \frac{\sigma _1}{2 \Omega ^2} \right) \nonumber \\&-\, \frac{1}{4 \Omega ^3} g_1^2 \sin \tau \cos \tau \nonumber \\ S_2= & {} \frac{3}{64 \Omega ^3} \mu ^2 - \frac{1}{8 \Omega } \alpha ^2 - \frac{\sigma _1}{2 \Omega } \left( 1 + \frac{\sigma _1}{4 \Omega ^2} \right) \nonumber \\&-\, \frac{1}{2 \Omega } g_1 \left( 1 + \frac{\sigma _1}{2 \Omega ^2} \right) \cos \tau \nonumber \\&+\, \frac{1}{8 \Omega ^3} g_1^2 \left( \sin ^2 \tau - \cos ^2 \tau \right) \nonumber \\ S_3= & {} \frac{3}{32 \Omega ^3} f \gamma \nonumber \\ S_4= & {} - \frac{3}{16 \Omega ^2} \alpha \gamma + \frac{3}{8} \beta \left( \sigma _1 - \Omega ^2 \right) \nonumber \\&+\, \frac{3}{8} g_1 \left( \beta \cos \tau + \frac{1}{\Omega ^2} \gamma \sin \tau \right) \nonumber \\ S_5= & {} \frac{3}{8 \Omega } \gamma \left( 1 + \frac{1}{2 \Omega ^2} \sigma _1 \right) \nonumber \\&+\, \frac{3}{16} g_1 \left( \beta \sin \tau + \frac{1}{\Omega ^2} \gamma \cos \tau \right) \nonumber \\ S_6= & {} \frac{3}{256} \left( - \frac{5}{\Omega ^3} \gamma ^2 + 3 \beta ^2 \Omega ^3 \right) \nonumber \\ S_7= & {} - \frac{3}{32} \beta \gamma \nonumber \\ S_8= & {} - \frac{1}{8 \Omega ^3} g_1 \mu \sin \tau \nonumber \\ S_9= & {} -\frac{1}{4 \Omega } \mu \nonumber \\ S_{10}= & {} \frac{7}{64} \beta \mu \nonumber \\ S_{11}= & {} \frac{1}{64 \Omega ^3} \gamma \mu \left( 8 \Omega ^2 -5 \right) \nonumber \\ S_{12}= & {} - \frac{1}{4 \Omega } \left( 1 + \frac{1}{8 \Omega ^2} \right) \gamma \mu \nonumber \\ S_{13}= & {} \frac{5}{32} \beta \mu \nonumber \\ S_{14}= & {} \frac{1}{2 \Omega } f \left[ -1 + \frac{1}{4 \Omega ^2} \left( \frac{1}{2} \mu - \sigma _1 - g_1 \cos \tau \right) \right] \nonumber \\ S_{15}= & {} -\frac{1}{8 \Omega ^2} \left( \alpha + g_1 \frac{1}{\Omega } \sin \tau \right) \nonumber \\ S_{16}= & {} \frac{15}{32} f \beta \nonumber \\ S_{17}= & {} \frac{3}{32} f \beta \end{aligned}$$

(55)