Stochastic response and reliability of electromagnetic energy harvester with mechanical impact and Coulomb friction

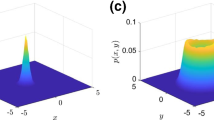
Abstract

Combining the complex factors of mechanical impact, Coulomb friction, harmonic excitation, and Gaussian white noise, an electromagnetic energy harvesting system is analytically studied. Based on stochastic averaging, Fokker–Planck–Kolmogorov equation of the probability density function (pdf) and backward Kolmogorov equation of the conditional reliability function are analytically derived. Solutions are correspondingly calculated by means of finite difference method. Numerical results are shown simultaneously for the purpose of verifying the effectiveness of such a semi-analytical procedure. Effects of the system coefficients on the pdfs, conditional reliability function, mean first passage time, and mean square electric current are discussed. It is found that the relation between energy harvesting performance and reliability should be balanced instead of ignoring the influence on system reliability while pursuing the increase of output electric current by tuning the system coefficients.

Appendices

Appendix A

The implicit finite difference approximation to Eq. 36 is

$$\begin{aligned}&\frac{{\partial \left( {{{\bar{m}}_1}p} \right) }}{{\partial H}} = \frac{{8\left[ {{{\left( {{{\bar{m}}_1}} \right) }_{i,j + 1}}{p_{i,j + 1}} - {{\left( {{{\bar{m}}_1}} \right) }_{i,j - 1}}{p_{i,j - 1}}} \right] - \left[ {{{\left( {{{\bar{m}}_1}} \right) }_{i,j + 2}}{p_{i,j + 2}} - {{\left( {{{\bar{m}}_1}} \right) }_{i,j - 2}}{p_{i,j - 2}}} \right] }}{{12 \cdot \Delta H}},\nonumber \\&\frac{{\partial \left( {{{\bar{m}}_2}p} \right) }}{{\partial \Gamma }} = \frac{{8\left[ {{{\left( {{{\bar{m}}_2}} \right) }_{i + 1,j}}{p_{i + 1,j}} - {{\left( {{{\bar{m}}_2}} \right) }_{i - 1,j}}{p_{i - 1,j}}} \right] - \left[ {{{\left( {{{\bar{m}}_2}} \right) }_{i + 2,j}}{p_{i + 2,j}} - {{\left( {{{\bar{m}}_2}} \right) }_{i - 2,j}}{p_{i - 2,j}}} \right] }}{{12 \cdot \Delta \Gamma }},\nonumber \\&\frac{{{\partial ^2}\left( {{{\bar{b}}_{11}}p} \right) }}{{\partial {H^2}}} = \frac{{16\left[ {{{\left( {{{\bar{b}}_{11}}} \right) }_{i,j + 1}}{p_{i,j + 1}} + {{\left( {{{\bar{b}}_{11}}} \right) }_{i,j - 1}}{p_{i,j - 1}}} \right] - \left[ {{{\left( {{{\bar{b}}_{11}}} \right) }_{i,j + 2}}{p_{i,j + 2}} + {{\left( {{{\bar{b}}_{11}}} \right) }_{i,j - 2}}{p_{i,j - 2}}} \right] - 30{{\left( {{{\bar{b}}_{11}}} \right) }_{i,j}}{p_{i,j}}}}{{12{{\left( {\Delta H} \right) }^2}}},\nonumber \\&\frac{{{\partial ^2}\left( {{{\bar{b}}_{22}}p} \right) }}{{\partial {\Gamma ^2}}} = \frac{{16\left[ {{{\left( {{{\bar{b}}_{22}}} \right) }_{i + 1,j}}{p_{i + 1,j}} + {{\left( {{{\bar{b}}_{22}}} \right) }_{i - 1,j}}{p_{i - 1,j}}} \right] - \left[ {{{\left( {{{\bar{b}}_{22}}} \right) }_{i + 2,j}}{p_{i + 2,j}} + {{\left( {{{\bar{b}}_{22}}} \right) }_{i - 2,j}}{p_{i - 2,j}}} \right] - 30{{\left( {{{\bar{b}}_{22}}} \right) }_{i,j}}{p_{i,j}}}}{{12{{\left( {\Delta \Gamma } \right) }^2}}}, \nonumber \\ \end{aligned}$$

(48)

where

$$\begin{aligned} {\left( {{{\bar{m}}_r}} \right) _{i,j}}= & {} {{\bar{m}}_r}\left( {j\Delta H,i\Delta \Gamma } \right) ,{\left( {{{\bar{b}}_{rs}}} \right) _{i,j}}\\&\quad = {{\bar{b}}_{rs}}\left( {j\Delta H,i\Delta \Gamma } \right) ,{p_{i,j}}\\&\quad = p\left( {j\Delta H,i\Delta \Gamma } \right) ,\quad r.s = 1,2; \\&\quad \quad i = 1,2, \ldots ,M;\quad j = 1,2, \ldots ,N. \end{aligned}$$

And $\Delta H, \Delta \Gamma$ are discrete steps of variables H and $\Gamma$, respectively. Boundary conditions are ${p_{M + 1,j}} = {p_{1,j}},{p_{0,j}} = {p_{M,j}},{p_{i,0}} = {p_{i,1}},{p_{i,N}} = 0$. Substituting Eq. 48 into Eq. 36 and letting $\partial p/\partial t=0$, the stationary joint pdf $p(H,\Gamma )$ can be obtained by means of finite difference method and successive over relaxation method [52, 53].

Appendix B

The implicit finite difference equations to Eqs. 39 and 47 are

$$\begin{aligned}&\frac{{R_{i,j}^{n + 1} - R_{i,j}^n}}{{\Delta t}} = {\left( {{\alpha _1}} \right) _{i,j}}\frac{{R_{i,j + 1}^{n + 1} - R_{i,j - 1}^{n + 1}}}{{2\Delta {H_0}}}\nonumber \\&\quad + {\left( {{\alpha _2}} \right) _{i,j}}\frac{{R_{i + 1,j}^{n + 1} - R_{i - 1,j}^{n + 1}}}{{2\Delta {\Gamma _0}}}\nonumber \\&\quad + \frac{1}{2}{\left( {{\beta _{11}}} \right) _{i,j}}\frac{{R_{i,j + 1}^{n + 1} - 2R_{i,j}^{n + 1} + R_{i,j - 1}^{n + 1}}}{{{{\left( {\Delta {H_0}} \right) }^2}}}\nonumber \\&\quad + \frac{1}{2}{\left( {{\beta _{22}}} \right) _{i,j}}\frac{{R_{i + 1,j}^{n + 1} - 2R_{i,j}^{n + 1} + R_{i - 1,j}^{n + 1}}}{{{{\left( {\Delta {\Gamma _0}} \right) }^2}}}, \end{aligned}$$

(49)

$$\begin{aligned}&- 1 = {\left( {{\alpha _1}} \right) _{i,j}}\frac{{{\mu _{i,j + 1}} - {\mu _{i,j - 1}}}}{{2\Delta {H_0}}} + {\left( {{\alpha _2}} \right) _{i,j}}\frac{{{\mu _{i + 1,j}} - {\mu _{i - 1,j}}}}{{2\Delta {\Gamma _0}}}\nonumber \\&\quad + \frac{1}{2}{\left( {{\beta _{11}}} \right) _{i,j}}\frac{{{\mu _{i,j + 1}} - 2{\mu _{i,j}} + {\mu _{i,j - 1}}}}{{{{\left( {\Delta {H_0}} \right) }^2}}}\nonumber \\&\quad + \frac{1}{2}{\left( {{\beta _{22}}} \right) _{i,j}}\frac{{{\mu _{i + 1,j}} - 2{\mu _{i,j}} + {\mu _{i - 1,j}}}}{{{{\left( {\Delta {\Gamma _0}} \right) }^2}}}, \end{aligned}$$

(50)

respectively, where

$$\begin{aligned} {\left( {{\alpha _r}} \right) _{i,j}}= & {} {\alpha _r}\left( {j\Delta {H_0},i\Delta {\Gamma _0}} \right) ,{\left( {{\beta _{rs}}} \right) _{i,j}} \\&= {\beta _{rs}}\left( {j\Delta {H_0},i\Delta {\Gamma _0}} \right) ,\\&R_{i,j}^n = R\left( {n\Delta t\mid j\Delta {H_0},i\Delta {\Gamma _0}} \right) ,{\mu _{i,j}} \\&= \mu \left( {j\Delta {H_0},i\Delta {\Gamma _0}} \right) ,\\&r.s = 1,2; \quad i = 1,2, \ldots ,M; \\&\quad j = 1,2, \ldots ,N; \quad n = 1,2, \ldots . \end{aligned}$$

$\Delta t$ is the time step, $\Delta H_0, \Delta \Gamma _0$ are discrete steps of variables $H_0$ and $\Gamma _0$, respectively. Boundary conditions for Eq. 49 are $R_{M + 1,j}^{n + 1} = R_{1,j}^{n + 1},R_{0,j}^{n + 1} = R_{M,j}^{n + 1},R_{i,0}^{n + 1} = R_{i,1}^{n + 1},R_{i,N}^{n + 1} = 0$, and for Eq. 50 are ${\mu _{M + 1,j}} = {\mu _{1,j}},{\mu _{0,j}} = {\mu _{M,j}},{\mu _{i,0}} = {\mu _{i,1}},{\mu _{i,N}} = 0$.