1 Introduction

1.1 Mechanical energy harvesting

Among the various energy harvesting categories, harvesting energy from ambient vibration has received much attention over the past few decades. A key factor that has contributed to this is the dramatic increase in the use of sensors [1, 2]. A conventional way of powering sensors is using batteries; however, batteries have to be monitored and replaced when necessary. This monitoring and replacement work can be onerous when the sensors are in remote and/or hazardous places. Energy harvesters that convert the ambient vibration energy into electricity enable the development of self-powered wireless sensors that can address these problems.

According to their basic working mechanisms, there are mainly three types of vibration-based energy harvesters: namely piezoelectric energy harvesters (PEHs), magnetoelectric energy harvesters (MEHs) and triboelectric energy harvesters (TEHs). Compared to PEH and MEH, TEH is relatively new and has been gaining research attention in recent years. The working mechanism of TEH involves a combination of triboelectrification and electrostatic induction through relative motion (e.g. contact-separation and sliding) between materials that have the opposite tribopolarities [1,2,3]. Moreover, TEH can work in four fundamental modes: namely, the vertical contact-separation mode, the in-plane sliding mode, the single-electrode mode, and the free-standing triboelectric-layer mode [1,2,3]. So far, most research on TEHs is limited to experimental studies, especially involving the technology of material surface processing. This has resulted in some self-powered prototype sensors tailored to far-reaching applications including active alcohol breath analysers [4], 3D acceleration sensors [5], dynamic displacement monitoring systems [6], and wind-speed sensors [7]. The triboelectric energy harvester studied in this paper can be modified for use in a number of real applications. A notable example is to power wireless health monitoring sensors on structures such as bridges, wind turbines and undersea gas/oil pipe lines. Similar devices could also be used to harvest energy from human motion, and/or to partially replace conventional batteries so as to reduce pollution and cost [8].

1.2 Vibro-impact systems in energy harvesting

Vibro-impact systems are usually characterized by repeated vibration and impact between the components in the systems. Vibro-impact appears in many engineering applications, such as hand-held percussion machines, pile driving machines, periodic rubbing between the rotor blades and the stators in turbomachinery, braking systems in automobiles and cutting and grinding machines [9,10,11,12]. Vibro-impact systems have been studied extensively in different contexts. For example, Cao et al. [13] studied the bifurcations and penetrating rate of percussive drilling, while others have focused on suppressing the vibration of civil engineering structures by using SMAs (shape memory alloys) [14, 15]. Other studies have focused on the finite codimension bifurcation and coexisting attractors in forming machines [16, 17], the numerical and experimental bifurcation of a forced impacting beam [18, 19], the dynamic analysis of an impact force generator in a heat exchanger [20], and vibro-impact systems under random excitation [21, 22]. Interestingly, some systems purposely exploit the vibro-impact, while others try to avoid it. For example, percussion and pile driving machines employ vibro-impact motion, while turbomachinery and braking system are designed to prevent in vibro-impact conditions. However, examples of vibro-impact systems can be found in almost all types of vibration-based energy harvesters.

Vibro-impact is often used in PEH systems since impact improves harvesting efficiency through frequency up-conversion [23,24,25,26], which helps cope with the frequency incompatibility between the ambient vibration and the harvester [23]. The vibro-impact in PEH systems usually happens between flexible beams and relatively rigid stoppers. In one of the two scenarios, stoppers vibrate and trigger the oscillation of the beams [23], which are mostly cantilevers. Alternatively, the beams oscillate and hit the stoppers [27]. Either way, the low-frequency ambient vibration can be up-converted to the higher frequency vibration of the beams, which then improves harvesting efficiency. Frequency up-conversion can also be achieved without any physical impact or contact in PEH systems, for instance, through magnetic plucking [28,29,30] or using a cantilever shell structure [31]. Both of these configurations can generate an impact-like force or impulsive excitation which then increases the dominant response frequency of the cantilevers. Alternatively, some PEH designs use techniques other than frequency up-conversion to harvest energy across relatively wider frequency ranges. Examples of these techniques include the use of variable-width bistable piezoelectric cantilever beams [32] and the use of self-resonating behaviour to create a passive self-tuning PEH [33].

The most common configuration of MEH uses a tube-structure to house magnets of opposing polarity [34]. In the modelling of such systems, vibro-impact motion between the magnets is generally not considered since impact only occurs at large accelerations. However, some studies [35,36,37,38,39] have employed vibro-impact beam systems to enhance the harvesting efficiency of MEH designs using frequency up-conversion. In these cases, magnets [35, 36] or coils [37,38,39] are mounted on the free end of a cantilever beam as well as on a stopper or another beam. The theoretical modelling of such vibro-impact system is mostly done by simplifying the continuous beam system into a corresponding discrete mass-spring-damper system and modelling a non-smooth impact into a bilinear or non-smooth stiffness and damping, such as in Refs. [36, 37].

Among the four fundamental triboelectric energy harvesting modes, the vertical contact-separation mode and the in-plane contact-sliding mode are the two most commonly used modes. Generally speaking, the vertical contact-separation mode relies on vibro-impact. The TEHs which work on the vertical contact-separation mode take on simple structural forms, such as the most common experimental TEH system [40] which consists of two plates (assumed rigid) connected by springs. Thus far, TEH research is mostly experimental in nature and is mainly focused on the state-of-the-art surface processing technology of triboelectric materials, such as the nanopore-, nanowire- or nanotube-based surface modifications [40, 41]. A more complicated configuration is the triple-cantilever TEH [8, 42] which may have rich dynamic responses, but the corresponding theoretical model has not yet been studied. The contact-mode freestanding TEH [43, 44] seems to have higher working efficiency, and the relevant research shows some applications, such as quantitative measurements of vibration amplitude [43] and the portable power-supplying system [44].

In addition to the experimental research on TEHs, theoretical modelling of the power generation (but not the structural dynamics) of the contact-mode as well as other working modes has been explored as well. The V–Q–x relationships (where V is the voltage between electrodes, Q is the amount of transferred charges between the electrodes, and x is the separation distance in between) for contact-mode TEHs have been developed [2, 45,46,47]. The theoretical simulation for the equivalent circuit model of the TEH in the SPICE software has also been investigated [48], but structural dynamic aspects (such as impact) are not involved in the simulation. In these studies, only the constant and harmonic variations of the separation distance are used as the dynamic input to describe the relative motion between electrodes or plates, and then the equivalent capacitance and voltage are used in SPICE. However, if the dynamic input is more complicated, SPICE may not adequately model the variable capacitor and voltage source. Therefore, there is a need for more robust circuit simulators for vibro-impact systems.

Although vibro-impact systems have been employed and studied extensively both in PEH and MEH devices, a theoretical study of the dynamics of a vibro-impact TEH system has yet to be reported. Looking beyond energy harvesting, there are few reports that study three-degree-of-freedom vibro-impact systems where any two adjacent masses can come into impact. In the study of the impact among rotating shrouded blades [49,50,51], each blade is usually simplified as a cantilever beam with a tip mass (the shroud). Its impact with the adjacent shrouds is modelled using the impact between the tip mass and the two-sided weightless rigid bodies that are supported by springs. Therefore, the impact is modelled as a bilinear or non-smooth contact stiffness. A more sophisticated recent model [52] treats one active blade and two passive blades as cantilever Euler–Bernoulli beams. A tip mass representing the shroud is at each free end and any two adjacent shrouds can impact. In addition to the above, a friction wedge damper in a train suspension system was investigated both experimentally [53] and theoretically [54]. The system was simplified to a three-degree-of-freedom vibro-impact model in the latter work. Both impact (which might cause chatter) and friction (which might induce stick-slip motion) between the wedges and the bolster were considered. The theoretical model developed here is distinct from the aforementioned vibro-impact systems as it considers a three-degree-of-freedom vibro-impact system in the context of TEH.

The rest of this paper is structured as follows: Sect. 2 presents the mechanical model and formulates the dynamical equations. The conservation of momentum and the coefficient of restitution are used to calculate the just-after-impact velocities. The contact forces during sticking motion are derived and applied to prevent interpenetration and keep the equilibrium of forces. Section 3 gives the theoretical electrical model of the oscillator-based triboelectric generator and shows the Simulink simulator. Then, Sect. 4 illustrates the study of the impact characteristics, the effects of initial mass spacing, mass ratio, and the use of chatter, respectively. Section 5 presents the conclusions that can be drawn in this study.

2 Mechanical model and dynamic equations

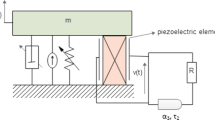
The configuration of the three-degree-of-freedom vibro-impact system representing the dynamic elements of a TEH is shown in Fig. 1. This model could be used to approximate a physical system in which three beams or flat plates are stacked. The three masses are initially separated by two gaps-\(\delta _1\) between \(m_1\) and \(m_2\), and \(\delta _2\) between \(m_2\) and \(m_3\). The masses are connected to the sinusoidally driven base via springs and dampers.

Fig. 1
figure 1

The three-degree-of-freedom vibro-impact system

Full size image

The equations of motion away from any two consecutive impacts of the system are given as

$$\begin{aligned} m_i x_i^{{\prime \prime }}+c_i \left( {x_i^{{\prime }}-{y}^{{\prime }}} \right) +k_{i}\left( x_{i}-y\right) = 0, \left( {i=1, 2, 3} \right) \end{aligned}$$
(1)

where \(y=A\sin \left( {\omega t} \right) \), and the prime denotes a derivative with respect to time, t. The separation distances, between \(m_1\) and \(m_2\), and between \(m_2\) and \(m_3\) are represented by \(d_1\) and \(d_2\), respectively. These distances are given by

$$\begin{aligned} d_1 =\delta _1 -\left( {x_2 -x_1 } \right) , \,\, d_2 =\delta _2 -\left( {x_3 -x_2 } \right) \end{aligned}$$
(2)

Now let \(\tau =\frac{t}{t_c }\), \(X_1 =\frac{x_1 }{x_c}\), \(X_2 =\frac{x_2 }{x_c}\), \(X_3 =\frac{x_3 }{x_c}\), \(t_c =\sqrt{\frac{m_1}{k_1}}\), and \(x_c =\delta _1\). The non-dimensional equations are then

$$\begin{aligned}&{\ddot{X}_1 } +2\zeta _1 \dot{X}_1 +X_1 =2\zeta _1 \frac{A\Omega }{\delta _1 }\cos \left( {\Omega \tau } \right) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \quad +\,\frac{A}{\delta _1 }\sin \left( {\Omega \tau } \right) \end{aligned}$$
(3)
$$\begin{aligned}&{\ddot{X}_2} +2\zeta _2 \frac{\Omega _2 }{\Omega _1 } \dot{X}_2 +\frac{\Omega _2^2 }{\Omega _1^2 }X_2 =2\zeta _2 \frac{\Omega _2 }{\Omega _1 }\frac{A\Omega }{\delta _1 }\cos \left( {\Omega \tau } \right) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad +\,\frac{\Omega _2^2 }{\Omega _1^2 }\frac{A}{\delta _1 }\sin \left( {\Omega \tau } \right) \end{aligned}$$
(4)
$$\begin{aligned}&{\ddot{X}_3} +2\zeta _3 \frac{\Omega _3 }{\Omega _1 }\dot{X}_3 +\frac{\Omega _3^2 }{\Omega _1^2 }X_3 =2\zeta _3 \frac{\Omega _3 }{\Omega _1 }\frac{A\Omega }{\delta _1 }\cos \left( {\Omega \tau } \right) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad +\,\frac{\Omega _3^2 }{\Omega _1^2 }\frac{A}{\delta _1 }\sin \left( {\Omega \tau } \right) \end{aligned}$$
(5)

where \(\zeta _i =\frac{c_i }{2\sqrt{m_i k_i }}\), \(\Omega _i =\sqrt{\frac{k_i }{m_i }} \quad \left( {i=1, 2, 3} \right) \) and \(\Omega =\frac{\omega }{\Omega _1}\). The over-dot denotes a derivative with respect to \(\tau \), and the separation distances become

$$\begin{aligned} D_1 =1-\left( {X_2 -X_1 } \right) , \,\, D_2 =\frac{\delta _2 }{\delta _1 }-\left( {X_3 -X_2 } \right) \end{aligned}$$
(6)

When impact occurs, i.e. \(D_1 =0\) and/or \(D_2 =0\), by employing the principle of conservation of momentum and the coefficient of restitution, one can find the velocities just after the impact as

$$\begin{aligned} \dot{X}_{p+}= & {} \frac{{{m_p} - \mu {m_q}}}{{{m_p} + {m_q}}}\dot{X}_{p-} + \frac{{{m_q}\left( {1 + \mu } \right) }}{{{m_p} + {m_q}}}\dot{X}_{q-} \end{aligned}$$
(7)
$$\begin{aligned} \dot{X}_{q+}= & {} \frac{{{m_p}\left( {1 + \mu } \right) }}{{{m_p} + {m_q}}}\dot{X}_{p-} + \frac{{{m_q} - \mu {m_p}}}{{{m_p} + {m_q}}}\dot{X}_{q-} \end{aligned}$$
(8)

where \(\mu \) is the coefficient of restitution, and the subscript ‘–’ represents the state just before impact, while ‘+’ represents the state just after impact. If impact takes place between \(m_1\) and \(m_2\), then \(m_p =m_1\), \(m_q =m_2\). If it occurs between \(m_2\) and \(m_3\), then \(m_p =m_2\), \(m_q =m_3\). If \(m_1\) and \(m_2\) are stuck together and impact occurs with \(m_3\), then \(m_p =m_1 +m_2\), \(m_q =m_3\). Finally, if \(m_1\) impacts with \(m_2 \) and \(m_3 \) joined together, then \(m_p =m_1\), \(m_q =m_2 +m_3\).

Fig. 2
figure 2

The charge transfer process of the oscillator-based triboelectric generator [2] (please see the descriptions of the subfigures in the context)

Full size image

Sticking motion between any two adjacent masses can happen since the impact is assumed to be partially elastic. During sticking, contact force must maintain the dynamic equilibrium and prevent interpenetration between two sticking masses. Let \(N_{12}\) and \(N_{23}\) represent the contact forces between \(m_1\) and \(m_2\), and between \(m_2\) and \(m_3\), respectively. Then, the sticking conditions between \(m_1\) and \(m_2\) are \(D_1 =0\), \(\dot{X}_{1}=\dot{X}_{2}\) and \(N_{12} >0\), while those between \(m_2\) and \(m_3\) are \(D_2 =0\), \(\dot{X}_{2}=\dot{X}_{3}\) and \(N_{23} >0\), and the expressions of the contact forces are given as

$$\begin{aligned} N_{12}= & {} \frac{1}{2}\left[ \phantom {\frac{\Omega _2^2 }{\Omega _1^2 }X_2}2\left( {\zeta _2 \frac{\Omega _2 }{\Omega _1 }-\zeta _1 } \right) \frac{A\Omega }{\delta _1 }\cos \left( {\Omega \tau } \right) \right. \nonumber \\&+\left( {\frac{\Omega _2^2 }{\Omega _1^2 }-1} \right) \frac{A}{\delta _1 }\sin \left( {\Omega \tau } \right) \nonumber \\&\left. +\,2\zeta _1 \dot{X}_1 -2\zeta _2 \frac{\Omega _2 }{\Omega _1 }\dot{X}_2 +X_1 -\frac{\Omega _2^2 }{\Omega _1^2 }X_2 \right] \end{aligned}$$
(9)
$$\begin{aligned} N_{23}= & {} \frac{1}{2}\left[ \phantom {\frac{\Omega _3^2 }{\Omega _1^2 }X_3}2\left( {\zeta _3 \frac{\Omega _3 }{\Omega _1 }-\zeta _2 \frac{\Omega _2 }{\Omega _1 }} \right) \frac{A\Omega }{\delta _1 }\cos \left( {\Omega \tau } \right) \right. \nonumber \\&+\left( {\frac{\Omega _3^2 }{\Omega _1^2 }-\frac{\Omega _2^2 }{\Omega _1^2 }} \right) \frac{A}{\delta _1 }\sin \left( {\Omega \tau } \right) +2\zeta _2 \frac{\Omega _2 }{\Omega _1 }\dot{X}_2 \nonumber \\&\left. -\, 2\zeta _3 \frac{\Omega _3 }{\Omega _1 }\dot{X}_3 +\frac{\Omega _2^2 }{\Omega _1^2 }X_2 -\frac{\Omega _3^2 }{\Omega _1^2 }X_3 \right] \end{aligned}$$
(10)

3 Theoretical model of triboelectric generator and the Simulink simulator

3.1 Theoretical model of the oscillator-based triboelectric generator

To simulate the harvester’s electrical output and assess its performance, the theoretical model of the triboelectric energy harvester based on the three-degree-of-freedom vibro-impact oscillator is established. The middle metal layer (aluminium layer) is attached to the middle mass \(m_2\) and is assumed to have negligible mass. This layer is regarded as a freestanding layer [2, 47], which works only as a charge inductor. This kind of triboelectric generator is called the contact-mode freestanding triboelectric generator [1, 3, 47].

The working principle of the vertical contact-separation triboelectric generator involves a combination of contact electrification and electrostatic induction [1,2,3]. The charge transfer process is shown in Fig. 2. Initially, there is no charge induced, hence no electric potential difference exists between the two electrodes. As the freestanding metal layer (i.e. the middle mass \(m_2\)) moves upward, it comes into contact with the top dielectric (e.g. PTFE film) which is assumed massless and is attached to the top electrode (which is adhered to \(m_1\)). Here, charge transfer takes place at the contact area as a result of the triboelectric effect [1, 2]. The aluminium tends to lose electrons, while the PTFE gains electrons in accordance with the triboelectric series [2]. This charge transfer process then results in net positive charge on the aluminium layer and equivalent net negative charge on the dielectric film (Fig. 2a). When the middle metal layer separates from the top dielectric and moves downward, an electric potential difference is simultaneously formed. The electrons in the bottom electrode are then driven to flow to the top electrode, which results in an instantaneous current that flows in the opposite direction of the electron flow (Fig. 2b). After the middle metal layer contacts with the bottom PTFE film, all induced charges are neutralized and rebalanced between those two contact surfaces (Fig. 2c). Hereafter, they separate and form the electric potential difference, and the electrons are forced to flow from the top electrode to the bottom electrode, which results in a reversed current flow (Fig. 2d). Finally, the middle metal layer comes into contact with the top PTFE film again and the cycle begins anew.

The model equation of the triboelectric generator [2, 45,46,47,48] can be given as

$$\begin{aligned} V=-\frac{1}{C}Q+V_{\mathrm{oc}} \end{aligned}$$
(11)

where V is the electric potential difference between electrodes, C is the equivalent capacitance, Q is the amount of transferred charges between electrodes, and \(V_{\mathrm{oc}}\) is the open-circuit voltage. The equivalent capacitance and the open-circuit voltage are given as [46, 47]

$$\begin{aligned}&C=\frac{\varepsilon _0 S}{d_0 +D_1 +D_2 } \end{aligned}$$
(12)
$$\begin{aligned}&V_{\mathrm{oc}} =\frac{2\sigma D_2 }{\varepsilon _0} \end{aligned}$$
(13)

where \(\varepsilon _0\) is the electric constant, S is the contact area, \(\sigma \) is the tribo-charge surface density; and \(d_0 =\frac{d_1 }{\varepsilon _{r1} }+\frac{d_2 }{\varepsilon _{r2} }\), where \(d_1\) and \(d_2\) are the thicknesses of the top dielectric and the bottom dielectric, respectively, and \(\varepsilon _{r1}\) and \(\varepsilon _{r2}\) are the dielectric constants of the materials of the top and bottom dielectric layers, respectively (the two dielectric layers are both assumed to be PTFE films with dielectric constants of \(\varepsilon _{r1} =\varepsilon _{r2} =2.0)\). \(D_1\) and \(D_2\) are the separation distances between the top dielectric and the middle metal layer, and between the middle metal layer and the bottom dielectric, respectively. Assumed values for the physical parameters are \(S=0.01 \hbox {m}^{2}\), \(\sigma =15~\upmu \hbox {C}/\hbox {m}^{2}\) and \(d_1 =d_2 =0.1\times 10^{-3}~\hbox {m}\). By combining Eqs. (11)–(13), one can obtain a charge transfer equation similar to the one presented as Eq. (9) in Ref. [55], the latter of which has been validated by experiment [55], providing a degree of confidence in the present modelling approach. Moreover, the results of this study agree with those in Ref. [55] in the sense that both studies conclude that higher impact or contact velocity corresponds to higher electrical output. See Sect. 4.3.2 for more discussion of this.

3.2 The Simulink simulator

The equivalent circuit model [2, 46, 48] for the triboelectric generator can be modelled by using the equivalent capacitance and the open-circuit voltage to represent the electrical properties of the triboelectric generator in the circuit as shown in Fig. 3.

Fig. 3
figure 3

The configuration of the equivalent circuit model

Full size image
Fig. 4
figure 4

The Simulink simulator of the equivalent circuit

Full size image

By using Simulink software package, the output performance of the oscillator-based triboelectric generator can be simulated and analysed conveniently. The Simulink model of the equivalent circuit is shown in Fig. 4, in which the input signals, i.e. the variable capacitor and the controlled voltage source, are defined by Eqs. (12) and (13). These are combined with the dynamic responses, i.e. the separations \(D_1\) and \(D_2\), of the three-degree-of-freedom vibro-impact oscillator to calculate the dynamic current and voltage across the resistor.

To assess the performance of the oscillator-based triboelectric energy harvester, the average output power per forcing cycle is introduced:

$$\begin{aligned} P_a =\frac{R \displaystyle \int _0^{N T} I^{2}\left( t \right) \hbox {d}t}{N T} \end{aligned}$$
(14)

where R is the resistance used in circuit and taken to be \(R=100~\hbox {kOhm}\), T is the dimensional excitation period, N is the number of dimensional excitation periods, and \(I\left( t \right) \) is the current across the resistor.

4 Numerical simulation

4.1 Impact characteristics

The mass distribution of the three-degree-of-freedom vibro-impact system influences the way in which the three masses interact with each other. To determine designs that work best for energy harvesting, four configurations are considered: two symmetric distributions, (1) \(m_1 =m_3 <m_2\) and (2) \(m_1 =m_3 >m_2\), and two asymmetric distributions, (3) \(m_1>m_2 >m_3\) and (4) \(m_1<m_2 <m_3\). The values of the parameters used are \(k=120~\hbox {N}/\hbox {m}\), \(\Omega =0.70\), \(A=0.08~\hbox {m}\), \(\mu =0.60\), \(\delta _1 =\delta _2 =20~\hbox {mm}\) and \(c_i =0.02~\hbox {N s}/\hbox {m}\) (\(i=1, 2, 3\)), if not otherwise specified. The fourth-order Runge-Kutta method is used to solve the differential equations. The tolerances used to detect impact or sticking between two masses are both set to \(10^{-6}\).

4.1.1 Different impact characteristics

It has been found that different mass distributions can lead to different impact positions. In symmetric case (1), impact only occurs over the static equilibrium of \(m_1\) and below that of \(m_3\) while it exists on both sides of the static equilibrium position of \(m_2\), as shown in Fig. 5a. Interestingly, the opposite is true in symmetric case (2), as shown in Fig. 5b. In the third configuration, impact only appears below the static equilibrium of each mass, even for \(m_2\) (see Fig. 5c), and it turns out to be the opposite in case (4), as shown in Fig. 5d. From the energy harvesting perspective, it is preferable for \(m_2\) to encounter impact both above and below its static equilibrium position. Therefore, the two symmetric configurations are of greater interest and will be compared in the following study.

Fig. 5
figure 5

Response examples of the four configurations: a Phase plots of configuration (1), \(m_2 =120\times 10^{-3}\,\hbox { kg}\), \(m_1 =m_3 =0.75~m_2 \); b phase plots of configuration (2), \(m_1 =m_3 =120\times 10^{-3}\hbox { kg}\), \(m_2 =0.50~m_1\); c phase plots of configuration (3), \(m_1 =120\times 10^{-3}\hbox { kg}\), \(m_2 =0.80~m_1\), \(m_3 =0.50~m_1\); d phase plots of configuration (4), \(m_3 =120\times 10^{-3}\hbox { kg}\), \(m_2 =0.80~m_3\), \(m_1 =0.60~m_3\); impacts between \(m_1\) and \(m_2\) are represented by red dotted lines, while impacts between \(m_2\) and \(m_3\) are denoted by green ‘+’ dotted lines

Full size image

4.1.2 Comparison between the two symmetric configurations

It is not easy to make general observations regarding the two symmetric configurations since altering some of the specified parameters (e.g. the mass ratio or excitation frequency) might lead to different conclusions. In an attempt to make a broad comparison, both low and high mass ratios of each configuration are considered, and the average power output of each configuration at each mass ratio is calculated both at lower and higher excitation frequencies.

In the first symmetric configuration, the mass distribution is configured to \(m_2 =120\times 10^{-3}\hbox { kg}\), \(m_1 =m_3\), and \(R_m =\frac{m_2 }{m_1 }\), where \(R_m >1\), and \(R_m \in \left[ {1.5, 2.0, 3.0} \right] \) are taken in the comparison; and that of the second configuration is \(m_1 =120\times 10^{-3}\hbox { kg}\), \(m_1 =m_3 \), and \(R_m =\frac{m_2 }{m_1 }\), where \(0<R_m <1\), and \(R_m \in \left[ {0.3, 0.5, 0.7} \right] \) are taken in the comparison.

The average power \(P_a\) versus the number of excitation periods \(N_p\) is calculated for different excitation frequencies and mass ratios for both configurations. The results are shown in Fig. 6. It can be seen that the first symmetric configuration has overall better electrical output performance than the second. Therefore, the first symmetric configuration will be studied further.

Fig. 6
figure 6

The average power output at different excitation frequencies of the two symmetric configurations in different mass ratios: a the first configuration and b the second configuration

Full size image

4.2 The effect of mass spacing

The initial mass spacing, \(\delta _1\) and \(\delta _2\), could be symmetric or asymmetric, and the choice will influence the dynamics of the system deeply because the spacing determines the impact criteria. Additionally, the mass spacing affect the equivalent capacitance and voltage directly, which then results in the change of electrical output.

4.2.1 Asymmetric mass spacing

Let \(R_\delta =\frac{\delta _2 }{\delta _1 }\) be the mass spacing ratio in the asymmetric spacing case. The bifurcation diagram of \(X_2\) versus \(R_\delta \) and its local enlargement are calculated and shown in Fig. 7a, b, respectively, while Fig. 7c, d show the corresponding “bifurcation diagrams of the velocities just prior to impact”, in which the values of the quantities concerned, for example, relative velocities between \(m_1\) and \(m_2\), (i.e. \(V_{12}\)), and between \(m_2\) and \(m_3\), (i.e. \(V_{23}\)), are only sampled at impact events within each forcing cycle. This is one way of displaying the dynamic behaviour of vibro-impact and the present bifurcation idea is similar to that in Ref. [56], which is quite different from the conventional bifurcation concept. Therefore, the countable dots at each value of \(R_\delta \) represent the number of impacts, rather than the order of periodicity, in one vibration period of periodic motions, while the uncountable dots indicate the impacts of non-periodic vibrations. The parameter values used in simulation are \(\delta _1 =20~\hbox {mm}\), \(\Omega =0.70\), \(m_1 =m_3 =90\times 10^{-3}\hbox { kg}\) and \(m_2 =120\times 10^{-3}\hbox { kg}\).

Fig. 7
figure 7

Bifurcation diagrams of a \(X_2\) versus \(R_\delta \) and b its local enlargement, and the bifurcation diagrams of \(V_{12}\) and \(V_{23}\) versus \(R_\delta \), i.e. (c) and (d), respectively

Full size image

From the bifurcation diagrams of \(X_2\), i.e. Fig. 7a, b, it could be seen that the system undertakes complicated dynamic variation with the change of \(R_\delta \). The corresponding bifurcation diagrams of the just before impact velocities, i.e. Fig. 7c, d, show the relevant impact situations. It is clear that there exists a jump at which the vibration amplitude drops suddenly and the number of impacts that happen in one motion period or one forcing cycle decreases from two to one as \(R_\delta \) passes through the jump point from left to right. The corresponding time history and phase plot of \(D_1\) at the jump point and the point just after the jump are given in Fig. 8 to show the details of the impact and vibration characteristics.

Fig. 8
figure 8

The time history (left) and phase plot (right) of \(D_1\) for a \(R_\delta =1.085\) and b \(R_\delta =1.090\)

Full size image
Fig. 9
figure 9

Time histories (left) and phase plots (right) of a \(D_1\) and b \(D_2\) for grazing impact at \(R_\delta =1.419\)

Full size image

Grazing bifurcation occurs at \(R_\delta =1.419\), and it is obvious in Fig. 7b that the dynamics of the system becomes much more complicated due to grazing bifurcation. The time history and phase plot of both \(D_1\) and \(D_2\) are given in Fig. 9 to verify and show the details, and it is clear that grazing impact appears only between \(m_1\) and \(m_2\). Besides, the vibration responses are asymmetric owing to the asymmetric mass spacing.

Since there occurs period-doubling bifurcation with non-periodic windows in Fig. 7b, and both periodic and non-periodic motions appear with the variation of \(R_\delta \), a comparison of the electrical output among different motion characteristics is convenient. The PSD (power spectral density) and Poincaré section of \(X_2\), the average harvested power versus the number of excitation periods are shown in Fig. 10 for different types of response. The average power output for these different responses is shown in Fig. 11. It is concluded that high-order periodic motion has lower average power output relative to simple periodic motion. It appears that power decreases as the order of the periodicity increases. However, none of them seem to generate more than a few micro-watts of power.

Fig. 10
figure 10

The PSD and Poincaré section of \(X_2\), time history of average power (from left to right) for a \(R_\delta =1.415\) (periodic motion), b \(R_\delta =1.423\) (non-periodic motion), c \(R_\delta =1.430\) (period-8 motion) and d \(R_\delta =1.512\) (period-13 motion)

Full size image

4.2.2 Symmetric mass spacing

In the consideration of symmetric mass spacing, the structural parameters (i.e. mass, stiffness, damping, mass spacing) are also all assumed symmetric. Consequently, the dynamic response of the system is mostly symmetric, though symmetry-breaking [57] of the dynamic response can exist.

In the modelling of the non-dimensional system, the mass spacing, \(\delta _1\), is used as a normalization parameter (i.e. the non-dimensional displacements are \(X_i =\frac{x_i }{\delta _1 } \left( {i=1, 2, 3} \right) )\). Therefore, for a given dimensional displacement, a smaller mass spacing would result in a larger non-dimensional displacement. To circumvent this dependence, the bifurcation diagram in Fig. 12 is shown in terms of \(\delta X_2\) versus \(\delta \) rather than \(X_2\) versus \(\delta \). Here, the excitation frequency is held fixed at \(\Omega =0.75\). The diagram shows that vibration amplitude tends to grow with an increase in mass spacing and that the response can be complicated at smaller mass spacing. It is noted that there exists Hopf bifurcation, which might be of great importance in some dynamic systems, such as in railway vehicle systems, where Hopf bifurcation can lead to unstable motions, such as hunting [58].

4.3 The effect of mass ratio

While the size of the mass spacing mostly affects the location at which the masses come into contact, the mass ratio can influence the way the masses interact with each other. If the mass ratio equals one, i.e. \(R_m =\frac{m_2 }{m_1 }=\frac{m_2 }{m_3 }=1\), all three masses are equal, there is no impact among them after the system reaches its steady state (all other parameters, i.e. the mass spacings, the stiffness and the dampings, are assumed to be symmetric as well). This is due to the absolute symmetry of the structural parameters.

4.3.1 Mass ratio’s effect on the number of impacts

Fig. 11
figure 11

The comparison of \(P_a\) between different types of motions

Full size image
Fig. 12
figure 12

The bifurcation diagram of \(\delta X_2\) versus the symmetric mass spacing \(\delta \)

Full size image

To observe the dynamic response and electric output at mass ratios other than one, the time histories of \(D_1\) and the generated current I and the diagram of the average power \(P_a\) are shown in Fig. 13 for different mass ratios. It is be observed that the number of impacts between \(m_1\) and \(m_2\) in one excitation period increases from one to three as the mass ratio \(R_m\) increases. This results in an increase in electrical output (note that impacts between \(m_2\) and \(m_3\) show the same effect).

Fig. 13
figure 13

Time histories of \(D_1\) and I and the diagram of average power \(P_a\) against the number of excitation periods \(N_p\) (from left to right) of a \(R_m =1.2\), b \(R_m =1.6\) and c \(R_m =2.5\)

Full size image

4.3.2 Optimal mass ratio

The bifurcation diagram of \(X_2\) versus \(R_m\) when \(\Omega =0.72\) is shown in Fig. 14a, while Fig. 14b shows the corresponding “bifurcation diagram of \(V_{12}\) against \(R_m\)”. Here, it can be seen that there is an optimal mass ratio at which the impact velocities reach a maximum at each impact. In Fig. 14b, the number of the countable dots at each \(R_m\) represents the number of impacts that happen in one excitation period for periodic motions; for instance, there are three impacts between \(m_1\) and \(m_2\) in one forcing cycle of the periodic motion at \(R_m =4\), while the number of the ‘line segments’ at each \(R_m\) (of the values approximately between \(R_m =3.06\) and \(R_m =3.64\)) corresponds to the number of impacts that happen in one excitation period for non-periodic motions; for example, three impacts happen between \(m_1\) and \(m_2\) at the non-periodic motion of \(R_m =3.5\). Because higher impact velocity corresponds to higher electrical output, there exists an optimal \(R_m\) at which the system has the best electrical output performance. Figure 15 shows the average power outputs of three different mass ratios for comparison and verification. It is clear that the average power output reaches the maximum around \(R_m =3.5\). The parameters used are the same as before except \(\delta _1 =\delta _2 =20~\hbox {mm}\) and \(m_1 =m_3 =50\times 10^{-3}\hbox { kg}\). It is again noted that a higher impact or contact velocity induces a higher electrical output agrees with the conclusion drawn in Ref. [55].

Fig. 14
figure 14

Bifurcation diagrams of a \(X_2\) and b \(V_{12}\), respectively, versus \(R_m\) of \(\Omega =0.72\)

Full size image

The optimal mass ratios, \(R_{mo}\), of the frequencies between \(\Omega =0.55\) and \(\Omega =0.95\) are obtained and shown in Fig. 16, and it is clear that the optimal mass ratio decreases with the increase of excitation frequency. The fitted polynomial is found to be \(R_{mo} =11.43 \Omega ^{2}-28.46 \Omega +18.03\), \(\Omega \in \left[ {0.55\,0.95} \right] \);

However, there would be no impact owing to the absolute symmetry of structural parameters as \(R_{mo}\) gradually approaches one. The bifurcation diagrams of \(X_2\) and \(V_{12}\) of two higher excitation frequencies, \(\Omega =1.30\) and \(\Omega =2.00\), are calculated and given in Fig. 17 as examples to show the variation of impact velocity at higher excitation frequencies. It can be observed that the magnitude of impact velocity would gradually approach a stable value as the mass ratio grows bigger, which means there is not an obvious optimal mass ratio for higher excitation frequencies.

Fig. 15
figure 15

Average power outputs of three different mass ratios at \(\Omega =0.72\) (blue solid line represents \(R_m =3.5\), black dashed line \(R_m =3.0\), and red dash-dot line \(R_m =2.5\))

Full size image
Fig. 16
figure 16

The variation of \(R_{mo}\) against \(\Omega \)

Full size image
Fig. 17
figure 17

Bifurcation diagrams of a \(X_2\) and b \(V_{12}\) for \(\Omega =1.30\) (in blue) and \(\Omega =2.00\) (in black) (for interpretation of the references to colour in this figure, the reader is referred to the web version of this article)

Full size image

For lower excitation frequencies, the response of the system can become quite complicated with the variation of mass ratio. The bifurcation diagram of \(X_2\) versus \(R_m\) for \(\Omega =0.30\) and its local enlargement are given in Fig. 18 as an example, and there appears a period-doubling cascade with non-periodic windows in Fig. 18b. Figure 19 shows the Poincaré sections of the non-periodic motion of \(\Omega =0.30\) and \(R_m =4.21\) from Fig. 18b.

4.4 Use of chatter

Chatter is a challenge in machining processes including turning, milling and drilling. It can cause problems like poor surface finish, excessive noise, breakage of machine tools, decreased tool life, and low productivity [59, 60]. Chatter is characterized by many consecutive impacts and might therefore be exploited in triboelectric energy harvesting from vibro-impact systems. In the study of a multi-degree-of-freedom vibro-impact system, Wagg [56, 61] discussed the chattering and sticking behaviour which appeared at low forcing frequencies, and showed that a variety of non-smooth events could possibly occur. Here, a numerical simulation is conducted to determine whether chatter can appear in the present system at low forcing frequencies.

The bifurcation diagram of \(X_2\) versus \(\Omega \), which includes a chatter range, is shown in Fig. 20. The parameters used are \(m_1 =50\times 10^{-3}~\hbox {kg}\), \(R_m =3\) and \(\delta =5~\hbox {mm}\). To observe the details of the chatter range as well as the resonant range, local views are shown in Fig. 21(a1), (b1), respectively, while Fig. 21(a2), (b2) gives the relevant “bifurcation diagrams of \(V_{12}\)”, in which the number of the dots at each \(\Omega \) represents the number of impacts that happen in one excitation period, and the y-values of the dots represent the relative impact velocities. It is clear that there are plenty of consecutive impacts when chatter takes place while only three impacts exist at the excitation frequencies around resonance. Besides, chatter does not appear around a resonance but at some lower frequencies. Resonance, as usual, can have the strongest vibration and impact, but its high vibration amplitude would results in large separation distances between plates, which might not be beneficial to triboelectric energy harvesting. Therefore, there is the possibility of using chatter to harvest more energy than can be harvested by operating at resonance.

Fig. 18
figure 18

Bifurcation diagrams of \(X_2\) versus \(R_m\) for a \(\Omega =0.30\) and b its local enlargement

Full size image
Fig. 19
figure 19

Poincaré sections of a \(X_1\), b \(X_2\) and c \(X_3\) of a non-periodic motion at \(\Omega =0.30\), \(R_m =4.21\)

Full size image
Fig. 20
figure 20

Bifurcation diagram of \(X_2\) versus \(\Omega \) with a chatter range

Full size image

To see the details of the vibration and impact both around chatter frequency and resonant frequency, two excitation frequencies, \(\Omega =0.600\) and \(\Omega =0.76\), are chosen as the examples. The corresponding time history and phase plot of \(D_1\) at these two excitation frequencies are shown in Fig. 22.

It can be seen, from Fig. 22a2, that the middle mass \(m_2\) encounters chatter on both sides. Hence, there are many impact events. However, only six impacts in total would occur in the resonant case in Fig. 22b. On the other hand, most of the impacts in chatter are quite small compared with those at resonance. Therefore, to determine which one is superior in terms of harvesting energy, the average power output both around chatter zone and resonant zone are given in Fig. 23 to compare the capability of efficient energy harvesting, in which it is clear that chatter frequencies perform much better than resonant frequencies in producing higher electrical output. Besides, since the chatter zone appears in a relatively lower frequency range compared with the resonant zone under the present parameters, it will be quite beneficial to harvesting energy from low-frequency ambient vibrations.

Fig. 21
figure 21

The local enlargements of Fig.18 for (a1) chatter range and (b1) resonant range, and their corresponding bifurcation diagrams of \(V_{12}\), i.e. (a2) and (b2), respectively

Full size image

To consider the details of both chatter and resonance cases and understand why forcing the system in the chatter regime results in such relatively high power output, some more detailed results of \(\Omega =0.600\) and \(\Omega =0.765\) are shown in Figs. 24 and 25. The non-dimensional time and dimensional time in these figures correspond to each other. It can be seen that the equivalent capacitance gets bigger when \(\left( {D_1 +D_2 } \right) \) becomes smaller, and the peaks of the equivalent capacitance correspond to the peaks of current. Although the non-chatter case has higher equivalent voltage, i.e. at \(\Omega =0.765\), the equivalent capacitance in the chatter case is much bigger, actually two orders of magnitude bigger, than in the non-chatter case. The relationship between the equivalent capacitance and the generated current indicates that the equivalent capacitance’s variation seems to play a bigger role than that of the equivalent voltage. Besides, from Fig. 24a, b, it can be observed that the two chatter events, respectively, between \(m_1\) and \(m_2\), and \(m_2\) and \(m_3\) appear just one after the other, which means that the middle mass \(m_2\) gets into chatter motion with one of the side masses, i.e. \(m_1\) or \(m_3\), firstly and then gets into chatter motion with the other one. More specifically, the relative motion between the middle mass \(m_2\) and one of the side masses firstly undergoes chattering until they split apart from sticking, just after which the other side mass impacts the middle mass (Fig. 24d, e) pushing it into an additional impact with the mass from which it had just separated. After this, the original side mass flies away, while the newcomer (the other side mass) begins chattering with the middle mass. This is similar to the motion of a Newton’s cradle. Interestingly, it seems that the small impact events during chatter are not directly responsible for the spikes of the electric output. Rather, it is the chatter-induced sticking motion that provides a chance for these three masses to come into impact nearly at the same time. When this occurs, the capacitance between the top and bottom electrodes spikes up because of the great decrease in the separation distance between them (the capacitance between two electrodes is inversely proportional to the separation distance in between, see Eq. (12)).

Fig. 22
figure 22

The time history (left) and phase plot (right) of \(D_1\), respectively, for a \(\Omega =0.600\) and b \(\Omega =0.765\)

Full size image
Fig. 23
figure 23

The average power output both at around a chatter zone and b resonant zone

Full size image
Fig. 24
figure 24

Time histories of a \(D_1\), b \(D_2\), (c) \(D_1 +D_2\) and the corresponding local views (d) and (e), and (f) and (g), respectively, the equivalent voltage V and capacitance C, and (h) the generated current in one excitation period when \(\Omega =0.600\) (red dashed lines and green dotted lines in a, b, c, d, and e are reference lines)

Full size image
Fig. 25
figure 25

Time histories of a \(D_1\), b \(D_2\), c \(D_1 +D_2\), and (d) and (e), respectively, the equivalent voltage V and capacitance C, and f the generated current in one excitation period when \(\Omega =0.765\) (red dashed lines and green dotted lines in a, b, and c are reference lines)

Full size image

5 Conclusions

A dynamic model of a three-degree-of-freedom vibro-impact oscillator is developed. In this system, every mass can impact its neighbour(s), which produces very complicated vibro-impact motions. Then the theoretical model of the oscillator-based triboelectric energy harvester is constructed, and the equivalent circuit model is developed in Simulink to simulate the corresponding electrical output. Both the nonlinear dynamics of the vibro-impact system and the electrical output performance of the harvester are investigated, and the conclusions are drawn as follows:

  1. (1)

    Different mass distributions could lead to very distinct impact characteristics. Among those four possible configurations, i.e. two symmetric configurations: \(m_1 =m_3 <m_2\) and \(m_1 =m_3 >m_2\), and two asymmetric configurations: \(m_1>m_2 >m_3\) and \(m_1<m_2 <m_3\), symmetric cases tend to be more beneficial to energy harvesting than asymmetric cases, and the first symmetric configuration has better harvesting performance than the second.

  2. (2)

    The initial mass spacing between the three masses affect the displacement conditions of impact directly, thus grazing bifurcation or impact is likely to appear, which could influence the dynamics of the system and the electrical output deeply. Besides, it has been found that period-doubling motion could somewhat reduce the electrical output, and the higher the order of the periodicity, the more the reduction.

  3. (3)

    The mass ratio determines how the masses impact and interact with each other. The number of impacts in one excitation period increases with the growth of the mass ratio, which then leads to the improvement of electrical output. There may also exist an optimal mass ratio at which the electrical output reaches the maximum, and it decreases with the increase in excitation frequency.

  4. (4)

    The electrical output increases greatly when chatter and sticking occur in motion. Resonance, as usual, can have the highest vibration amplitudes and impact velocities, but this can be detrimental to electrical output and thus the maximal electric output does not appear at around resonance, which is different from other types of vibration-based energy harvesters, such as piezoelectric energy harvesters and magnetoelectric energy harvesters, both of which usually have the highest electrical output at resonance. In addition, the appearance of chatter and sticking in the low excitation frequency range can help harvest energy from low-frequency ambient vibration, which should be leveraged in the design of future systems.