Stochastic analysis of a nonlinear energy harvester with fractional derivative damping

Abstract

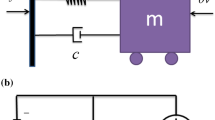
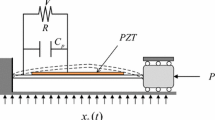
A fractionally damped vibration energy harvester excited by the wide-band random noise is investigated theoretically in this paper. Firstly, by introducing the generalized harmonic transformation, an equivalent uncoupled system only with respect to the mechanical states is established, while the external circuit and the fractional derivative damping are decoupled into damping and stiffness with amplitude-dependent coefficients, respectively. Then, a stochastic averaging operator technique is carried out to derive the stationary distribution of the mechanical states and furtherly obtain the mean square electric voltage (MSEV) and mean output power (MOP) of the energy harvester theoretically. Finally, the relationships between the fractional derivative and the MSEV and MOP are explored in detail to help improve the performance of the energy harvester.

Appendix

1.1 Appendix A: The averaging of the fractional derivative damping

Due to A and ϕ are slow variables, the following approximate relation can be obtained by Eq. (9):

$$ \theta (t - \tau ) \approx \theta (t) - \omega \tau . $$

(36)

Using Eq. (36), the averaging of the term associated with fractional derivative of Eq. (16) can be simplified as follows:

$$ \begin{aligned} C\left( A \right) & = \frac{{c_{0} }}{\pi A\omega \left( A \right)}\int_{0}^{2\pi } {D^{\alpha } \left( {A\cos \Theta } \right)} \sin \Theta {\text{d}}\Theta \\ & = \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)\omega \left( A \right)A}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\frac{{\text{d}}}{{{\text{d}}t}}\int_{0}^{t} {\frac{{X\left( {t - \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } \sin \Theta {\text{d}}t \\ & = \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)\omega \left( A \right)}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\cos \Theta \omega \left( A \right)\int_{0}^{t} {\frac{{\cos \left[ {\Theta \left( {t - \tau } \right)} \right]}}{{\tau^{\alpha } }}{\text{d}}\tau } } {\text{d}}t \\ & \approx \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)\omega \left( A \right)}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\cos \Theta \omega \left( A \right)\left[ {\cos \Theta \int_{0}^{t} {\frac{{\cos \left( {\omega \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } \right.} \\ & \quad \left. { + \sin \Theta \int_{0}^{t} {\frac{{\sin \left( {\omega \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } \right]{\text{d}}t \\ \end{aligned} $$

(37)

$$ \begin{aligned} K\left( A \right) & = \frac{{c_{0} }}{\pi A}\int_{0}^{2\pi } {D^{\alpha } } \left( {A\cos \Theta } \right)\cos \Theta {\text{d}}\Theta = \frac{{c_{0} }}{2}\omega^{\alpha } \left( A \right)\cos \left( {\frac{\alpha \pi }{2}} \right) \\ & = \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)A}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\left[ {\frac{{\text{d}}}{{{\text{d}}t}}\int_{0}^{t} {\frac{{X\left( {t - \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } \right]} \cos \Theta {\text{d}}t \\ & = \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)A}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\left\{ {\left. {\left( {\cos \Theta \int_{0}^{t} {\frac{{A\cos \left[ {\Theta \left( {t - \tau } \right)} \right]}}{{\tau^{\alpha } }}{\text{d}}\tau } } \right)} \right|_{0}^{T} } \right. \\ & \left. {\quad + \int_{0}^{T} {\sin \Theta \omega \left( A \right)\int_{0}^{t} {\frac{{A\cos \left[ {\Theta \left( {t - \tau } \right)} \right]}}{{\tau^{\alpha } }}{\text{d}}\tau } } {\text{d}}t} \right\} \\ & \approx \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\sin \Theta \omega \left( A \right)\left[ {\cos \Theta \int_{0}^{t} {\frac{{\cos \left( {\omega \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau + \sin \Theta \int_{0}^{t} {\frac{{\sin \left( {\omega \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } } \right]} {\text{d}}t \\ \end{aligned} $$

(38)

In Eqs. (37) and (38), A is treated as a constant since it varies slowly. To simplify Eqs. (37) and (38) furtherly, the following asymptotic integrals can be applied:

$$ \int_{0}^{t} {\frac{{\cos \left( {\omega \tau } \right)}}{{\tau^{q} }}{\text{d}}\tau } = \omega^{{\left( {q - 1} \right)}} \left[ {\Gamma \left( {1 - q} \right)\sin \left( {\frac{q\pi }{2}} \right) + \frac{\sin \left( s \right)}{{s^{q} }} + O\left( {s^{( - q - 1)} } \right)} \right] $$

(39)

$$ \int_{0}^{t} {\frac{{\sin \left( {\omega \tau } \right)}}{{\tau^{q} }}{\text{d}}\tau } = \omega^{{\left( {q - 1} \right)}} \left[ {\Gamma \left( {1 - q} \right)\cos \left( {\frac{q\pi }{2}} \right) + \frac{\cos \left( s \right)}{{s^{q} }} + O\left( {s^{( - q - 1)} } \right)} \right] $$

(40)

Substituting Eqs. (39)–(40) into Eqs. (37)–(38), and completing the averaging can lead to

$$ C\left( A \right) = \frac{{c_{0} }}{\pi A\omega (A)}\int_{0}^{2\pi } {D^{\alpha } } \left( {A\cos \Theta } \right)\sin \Theta {\text{d}}\Theta = \frac{{c_{0} }}{2}\omega^{\alpha - 1} \left( A \right)\sin \left( {\frac{\alpha \pi }{2}} \right) $$

(41)

$$ K\left( A \right) = \frac{{c_{0} }}{\pi A}\int_{0}^{2\pi } {D^{\alpha } } \left( {A\cos \Theta } \right)\cos \Theta {\text{d}}\Theta = \frac{{c_{0} }}{2}\omega^{\alpha } \left( A \right)\cos \left( {\frac{\alpha \pi }{2}} \right) $$

(42)

1.2 Appendix B: The simulation of the fractional derivative damping and wide-band noises

(i). The definition of the fractional derivative in Eq. (2) could be reformulated as:

$$ \begin{aligned} D^{\alpha } \overline{X}\left( \tau \right) & = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{{\text{d}}}{{{\text{d}}\tau }}\int_{0}^{\tau } {\frac{{\overline{X}\left( {\tau - \varsigma } \right)}}{{\varsigma^{\alpha } }}{\text{d}}\varsigma = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\left( {\frac{X(0)}{{\tau^{\alpha } }} + \int_{0}^{\tau } {\frac{{\dot{\overline{X}}\left( \varsigma \right)}}{{(\tau - \varsigma )^{\alpha } }}{\text{d}}\varsigma } } \right) \, } \\ & = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\left( {\frac{X(0)}{{\tau^{\alpha } }} + \int_{0}^{\tau } {\frac{{\dot{\overline{X}}\left( {\tau - \varsigma } \right)}}{{\varsigma^{\alpha } }}{\text{d}}\varsigma } } \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{X(0)}{{\tau^{\alpha } }} \\ & \quad + \frac{1}{{\Gamma \left( {2 - \alpha } \right)}}\int_{0}^{{\tau^{1 - \alpha } }} {\dot{\overline{X}}\left( {\tau - s^{{{1 \mathord{\left/ {\vphantom {1 {(1 - \alpha )}}} \right. \kern-\nulldelimiterspace} {(1 - \alpha )}}}} } \right){\text{d}}s} \quad (s = \varsigma^{\alpha } ,0 < \alpha < 1) \\ \end{aligned} $$

(43)

Thus, the following numerical integration can be employed with the initial condition $D^{\alpha } \overline{X}\left( 0 \right) = \dot{\overline{X}}_{0}$ given in Ref. [14],

$$ \begin{aligned} D^{\alpha } \overline{X}\left( {n\Delta \tau } \right) & = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{{\overline{X}_{0} }}{{(n\Delta \tau )^{\alpha } }} + \frac{1}{{\Gamma \left( {2 - \alpha } \right)}}\sum\limits_{j = 1}^{n} {\int_{{((j - 1)\Delta \tau )^{1 - \alpha } }}^{{(j\Delta \tau )^{1 - \alpha } }} {\dot{\overline{X}}\left( {n\Delta \tau - s^{{{1 \mathord{\left/ {\vphantom {1 {(1 - \alpha )}}} \right. \kern-\nulldelimiterspace} {(1 - \alpha )}}}} } \right){\text{d}}s} } \\ & { = }\frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{{\overline{X}(0)}}{{(n\Delta \tau )^{\alpha } }} + \frac{1}{{\Gamma \left( {2 - \alpha } \right)}}\sum\limits_{j = 1}^{n} {\frac{{(j\Delta \tau )^{1 - \alpha } - ((j - 1)\Delta \tau )^{1 - \alpha } }}{2}(\dot{\overline{X}}_{n - j} + \dot{\overline{X}}_{n + 1 - j} )} \, \\ \end{aligned} $$

(44)

(ii). To generate the samples of independent wide-band noises $\xi_{i} (t)$, the following second-order linear filters can be adopted:

$$ \ddot{\xi }_{i} + 2\kappa_{i} \omega_{i} \dot{\xi }_{i} + \omega_{i}^{2} \xi_{i} = W_{i} \left( t \right), \, i = 1,2. $$

(45)

where $W_{i} (t)$ denote the independent Gaussian white noises with intensities $D_{i}$.