Revisiting the averaged problem in the case of mean-motion resonances in the restricted three-body problem

Abstract

A classical approach to the restricted three-body problem is to analyze the dynamics of the massless body in the synodic reference frame. A different approach is represented by the perturbative treatment: in particular the averaged problem of a mean-motion resonance allows to investigate the long-term behavior of the solutions through a suitable approximation that focuses on a particular region of the phase space. In this paper, we intend to bridge a gap between the two approaches in the specific case of mean-motion resonant dynamics, establish the limit of validity of the averaged problem and take advantage of its results in order to compute trajectories in the synodic reference frame. After the description of each approach, we develop a rigorous treatment of the averaging process, estimate the size of the transformation and prove that the averaged problem is a suitable approximation of the restricted three-body problem as long as the solutions are located outside the Hill’s sphere of the secondary. In such a case, a rigorous theorem of stability over finite but large timescales can be proven. We establish that a solution of the averaged problem provides an accurate approximation of the trajectories on the synodic reference frame within a finite time that depend on the minimal distance to the Hill’s sphere of the secondary. The last part of this work is devoted to the co-orbital motion (i.e., the dynamics in 1:1 mean-motion resonance) in the circular-planar case. In this case, an interpretation of the solutions of the averaged problem in the synodic reference frame is detailed and a method that allows to compute co-orbital trajectories is displayed.

1 Introduction

This work focuses on the restricted three-body problem, that is the study of the motion of a massless body affected by the gravitational attraction of two massive bodies. More precisely, we will consider the situation for which the mass of the secondary body is treated as a small quantity. Since the planetary three-body problem will also be mentioned, we recall that it corresponds to the study of the motion of two massive bodies orbiting a more massive one, the three bodies being governed only by their mutual gravitational interactions.

The analysis of the dynamics in the synodic reference frame, that is the frame rotating with the mean longitude of the secondary, is the classical approach adopted for the restricted three-body problem. Usually, periodic orbit families and the dynamics located in their neighborhood are computed by using Poincaré maps and continuation methods (see, e.g., [13, 37]).

Perturbative treatments provide another approach. They allow to investigate specific regions of the phase space through a proper approximation. Among them, averaging methods are common techniques in order to study the long-term dynamics of the solutions. For instance, the secular problem studies the long-term deformation of the ellipse of the massless body as well as the evolution of its orientation in the tridimensional space. It is obtained by the averaging of the Hamiltonian over the mean longitudes of the secondary and of the massless body. More precisely, it corresponds to a symplectic transformation, that is supposed to be close to the identity, and that maps the original Hamiltonian to the secular one.

Lagrange [17] introduced the secular problem in the framework of the stability of the Solar System and the expression of the secular Hamiltonian of the planetary three-body problem was given by Poincaré [26]. Precise estimates on the size of the transformation of averaging were required in order to prove theorems of stability like KAM theory and were provided, especially by Arnol’d [1], Féjoz [10], Chierchia and Pinzari [6].

When the massless body is in mean-motion resonance with the secondary, that is, when their orbital periods are commensurable, the transformation leading to the secular Hamiltonian is no more close to the identity and the solutions of the secular problem do not provide a good representation of the real motion. In such a case, it is still possible to use averaging techniques: the averaging process is performed over one mean longitude, generally the one of the secondary, and after the introduction of a resonant angle, that is a particular linear combination of the two mean longitudes which characterizes the mean-motion resonance. This defines the averaged problem that will be considered in this work.

Many authors investigated mean-motion resonances through an averaged Hamiltonian and the literature on this subject has become so rich that it is impossible to cite all the articles here. Nevertheless, let us mention the important series of works realized by Schubart [31,32,33], which took advantage of the canonical variables and method suggested by Poincaré [27] and applied an averaging process in order to get the interesting part of the Hamiltonian for mean-motion resonances. Likewise, the second fundamental model of resonance, developed by Henrard and Lemaitre [16], follows the strategy of Poincaré [27], and is commonly used in order to study mean-motion resonances. Moons [19] extended the work of Schubart and presented an integrator adapted to the solutions of the averaged problem. Being the latter not valid for the 1:1 mean-motion resonance, Nesvorný et al. [24] adapted the algorithm with a different choice of canonical variables.

The co-orbital motion, or equivalently, the trajectories in 1:1 mean-motion resonance with the secondary, has been intensively studied in the framework of the averaged problem (see, e.g., [18, 20, 34, 35]). In such a case, since the semimajor axis of the massless body is almost the same as the one of the secondary, the issue generated by periodical close encounters arises, even for quasi-circular trajectories. In particular, Robutel and Pousse [30] and Pousse et al. [28] highlighted, with the help of a frequency analysis, that the averaged Hamiltonian reflects poorly the dynamics close to the singularity associated with the collision between the secondary and the massless body. Rigorous estimates on the averaging process have been given by Robutel et al. [29]. More precisely, they allowed the authors to prove in the planetary three-body problem, that the averaged problem is valid for two co-orbital bodies on quasi-circular orbits that stand at a mutual distance larger than their respective Hill’s radius.

The limit of validity of the averaged problem is not specific to the case of the co-orbital motion and can also occur for other resonant trajectories that cross the orbit of the secondary (i.e., trajectories with a non-negligible eccentricity). This weakness was already outlined in the works of Schubart [31] and Moons [19]. Therefore, in the present paper, we intend to generalize the result given by Robutel et al. [29] and provide rigorous estimates on the averaging process in order to define a domain of validity of the averaged problem, in the case of a generic mean-motion resonance, and for any value of inclination and eccentricities (massless body as well as secondary).

According to the Poincaré classification (see, e.g., [5] for more details), some of the periodic families described in the synodic reference frame are related to mean-motion resonances and thus can also be tackled in the averaged problem as defined here. For that reason, we also intend to bridge a gap between the classical approach in the synodic reference frame and the averaged problem with a unified Hamiltonian formalism that allows to represent solutions in both approaches. The underlying idea of this work is to understand the limit of validity of the averaged problem and take advantage of its solutions (e.g., initial conditions, types of motion, frequencies) for the computation of trajectories in the synodic reference frame.

The paper is structured as follows. Section 2 introduces the restricted three-body problem through the classical approach, recalls some remarkable solutions in the synodic reference frame that are connected to the co-orbital motion, and presents the reasoning that led to the averaged problem.

In Sect. 3, the size of the transformation of averaging is estimated. This allows to define a domain of validity of the approximation and to prove a rigorous theorem of stability over finite times.

In Sect. 4, we focus on the co-orbital motion in the circular-planar case and detail the correspondence between a solution of the averaged problem and its corresponding trajectory in the synodic reference frame. In particular, we will recover the remarkable solutions described in Sect. 2. Finally, a method that allows to compute co-orbital trajectories in the synodic reference frame will be described.

Appendix A gives the proof of the theorems and lemma used in our reasonings.

2 Two approaches for the restricted three-body problem

2.1 The restricted three-body problem

2.1.1 Definition in the heliocentric reference frame

Let $(\mathbf{r} , {\dot{\mathbf{r} }})$ be, respectively, the heliocentric position and velocity vector in ${\mathbb {R}}^3$ of a massless body (particle, spacecraft or asteroid), that is affected by the gravitational attraction of a massive primary (the Sun or a planet) of mass $1-{\varepsilon }>1/2$, and a secondary (a planet or a moon) of mass ${\varepsilon }>0$.

The motion of the two massive bodies, respectively, denoted as Sun and planet, follows a solution of the two-body problem. Hence, the trajectory of the planet, denoted $\mathbf{r} '(t)$ in the heliocentric reference frame, lies on an ellipse that can be defined by the orbital elements ${(a', e', I', \varOmega ', \omega ', v')}$, i.e., respectively, semimajor axis, eccentricity, inclination, longitude of the node, argument of the periaster and true anomaly. Without loss of generality, the scale and orientation of the orbit are arbitrarily chosen such that

$$\begin{aligned} (a', I', \varOmega ', \omega ') = (1, 0, 0, 0). \end{aligned}$$

Likewise, the orbital period of the planet is fixed to $2\pi$ (and therefore its mean motion to 1) which imposes the gravitational constant to be equal to 1. The eccentricity $e'$ is a parameter of the problem associated with the shape of the planet’s orbit while the angle $v'$ stands for its position on the ellipse. Instead of using the true anomaly, the mean longitude $\lambda '$ will be adopted in order to take advantage of its proportionality to time since

$$\begin{aligned} t = \lambda '(t) + 2k\pi \quad \text{ where } k\in {{\mathbb {Z}}}. \end{aligned}$$

In the heliocentric reference frame, the equations of motion of the particle read (see [22]):

$$\begin{aligned} \ddot{\mathbf{r} } = - (1-{\varepsilon }) \frac{\mathbf{r} }{\left\| \mathbf{r} \right\| ^3} - {\varepsilon }\frac{\mathbf{r} - \mathbf{r} '(\lambda ')}{\left\| \mathbf{r} - \mathbf{r} '(\lambda ') \right\| ^3} - {\varepsilon }\frac{\mathbf{r} '(\lambda ')}{\left\| \mathbf{r} '(\lambda ') \right\| ^3} \nonumber \\ \end{aligned}$$

(1)

where “$\left\| \,\cdot \, \right\|$” is the Euclidean norm associated with the scalar product denoted “$\,\bullet \,$” in what follows. The two first terms are, respectively, the gravitational force of the Sun and of the planet. The third term is associated with the acceleration of the heliocentric reference frame generated by the Sun–planet gravitational interactions.

2.1.2 Hamiltonian formalism

Since the heliocentric vectors $\mathbf{r}$ and ${\dot{\mathbf{r} }}$ are canonical variables, then the Hamiltonian function

$$\begin{aligned} {{\mathcal {H}} }(\mathbf{r} , {\dot{\mathbf{r} }}, \lambda ')= & {} \frac{\left\| {\dot{\mathbf{r} }} \right\| ^2}{2} - \frac{1-{\varepsilon }}{\left\| \mathbf{r} \right\| } - \frac{{\varepsilon }}{\left\| \mathbf{r} -\mathbf{r} '(\lambda ') \right\| }\nonumber \\&+ {\varepsilon }\frac{\mathbf{r} \bullet \mathbf{r} '(\lambda ')}{\left\| \mathbf{r} '(\lambda ') \right\| ^3} \end{aligned}$$

(2)

provides the equations of motion (1). As ${{\mathcal {H}} }$ depends on the periodicity of the planet, it is non-autonomous. Moreover, the system just written, that describes the dynamics of the particle, has 3 degrees of freedom associated with the position and velocity vectors in the tridimensional space. A classical technique that allows to overcome the non-autonomous character of the system consists in extending the phase space with the addition of a generic variable $\hat{\varXi }$ conjugated with $\lambda '$. In this extended phase space, the Hamiltonian reads ${{\mathcal {H}} }+ \hat{\varXi }$, it has 4 degrees of freedom and describes the coupled motion of the particle and the planet, namely

$$\begin{aligned} \frac{{\mathrm d }}{{\mathrm d }t}(\mathbf{r} ,{\dot{\mathbf{r} }}, \lambda ', \hat{\varXi }) = \left( \frac{\partial {{\mathcal {H}} } }{\partial {\dot{\mathbf{r} }}}, -\frac{\partial {{\mathcal {H}} } }{\partial \mathbf{r} }, 1, -\frac{\partial {{\mathcal {H}} } }{\partial \lambda '}\right) . \end{aligned}$$

As a consequence, investigating the restricted three-body problem consists in studying an autonomous ODE whose solutions belong to a 8-dimensional phase space (position and velocity in the tridimensional space, the mean longitude of the planet and its conjugated variable). A classical approach in order to simplify the analysis is to consider the behavior of the particle in the synodic reference frame, that is the frame that rotates with $\lambda '$ in the orbital plane of the planet.

2.2 A classical approach: the synodic reference frame

2.2.1 The synodic reference frame

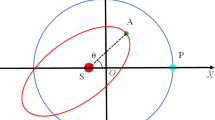
Let us denote ${{\mathfrak {R}} }_k(\alpha )$, the rotation matrix of an angle $\alpha$ about the k-axis ($k\in \{1,2,3\}$), and

$$\begin{aligned} \varvec{{\mathrm L }}(\mathbf{r} , {\dot{\mathbf{r} }}) = \mathbf{r} \times {\dot{\mathbf{r} }}, \end{aligned}$$

the angular momentum of the particle in the heliocentric reference frame. We recall that due to the influence of the planet, $\varvec{{\mathrm L }}(\mathbf{r} , {\dot{\mathbf{r} }})$ is not a conserved quantity of the restricted three-body problem.

With the help of the Hamiltonian formalism, the symplectic transformation associated with the synodic reference frame reads

$$\begin{aligned} \varUpsilon _{{\mathrm S }{\mathrm F }}: (\mathbf{R} , {\tilde{\mathbf{R} }} , \lambda ', \varXi _{{\mathrm S }{\mathrm F }}) \mapsto (\mathbf{r} , {\dot{\mathbf{r} }}, \lambda ', \hat{\varXi }) \end{aligned}$$

with

$$\begin{aligned} \mathbf{R}= & {} {{\mathfrak {R}} }_3(-\lambda ') \mathbf{r} =(X,Y,Z),\\ {\tilde{\mathbf{R} }}= & {} {{\mathfrak {R}} }_3(-\lambda ') {\dot{\mathbf{r} }}=(p_X, p_Y, p_Z),\\ \hat{\varXi }= & {} \varXi _{{\mathrm S }{\mathrm F }} - \varvec{{\mathrm L }}_3(\mathbf{R} ,{\tilde{\mathbf{R} }} ) = \varXi _{{\mathrm S }{\mathrm F }} + Yp_X - Xp_Y. \end{aligned}$$

It provides the Hamiltonian

$$\begin{aligned} {({{\mathcal {H}} }+ \hat{\varXi }) \circ \varUpsilon _{{\mathrm S }{\mathrm F }} = {{\mathcal {H}} }_{{\mathrm S }{\mathrm F }}+ \varXi _{{\mathrm S }{\mathrm F }}} \end{aligned}$$

such that

$$\begin{aligned} {{\mathcal {H}} }_{{\mathrm S }{\mathrm F }}(\mathbf{R} , {\tilde{\mathbf{R} }} , \lambda ')= & {} \frac{1}{2}\left\| {\tilde{\mathbf{R} }} \right\| ^2 - \frac{1-{\varepsilon }}{\left\| \mathbf{R} \right\| } - \frac{{\varepsilon }}{\left\| \mathbf{R} - \mathbf{R} '(\lambda ') \right\| }\\&+ {\varepsilon }\frac{\mathbf{R} \bullet \mathbf{R} '(\lambda ')}{\left\| \mathbf{R} '(\lambda ') \right\| ^3} - \varvec{{\mathrm L }}_3(\mathbf{R} , {\tilde{\mathbf{R} }} ) \end{aligned}$$

with $\mathbf{R} '(\lambda ') = {{\mathfrak {R}} }_3(-\lambda ')\mathbf{r} '(\lambda ')$ that corresponds to the position of the planet. Moreover, the velocity of the particle in the synodic reference frame is deduced as follows:

$$\begin{aligned} {\dot{\mathbf{R} }}= \frac{\partial }{\partial {\tilde{\mathbf{R} }} }{{\mathcal {H}} }_{{\mathrm S }{\mathrm F }}(\mathbf{R} , {\tilde{\mathbf{R} }} , \lambda ') = {\tilde{\mathbf{R} }} + (Y, -X, 0). \end{aligned}$$

This framework gives rise to an important reduction in the context of the circular case ($e' = 0$): since the planet is a fixed point located in $\mathbf{R} ' = (1, 0, 0)$, the Hamiltonian does not depend on $\lambda '$ and $\varXi _{{\mathrm S }{\mathrm F }}$ is an integral of motion that can be dropped. Hence, the dimension of the phase space to explore is reduced by two units. Moreover, ${{\mathcal {H}} }_{{\mathrm S }{\mathrm F }}$ is related to the Jacobi constant that defines the energy of the particle. In the synodic reference frame centered on the Sun, the Jacobi constant can be written as follows:

$$\begin{aligned} {{\mathscr {C}}}(\mathbf{R} , {\dot{\mathbf{R} }})= & {} - 2{{\mathcal {H}} }_{{\mathrm S }{\mathrm F }}(\mathbf{R} , {\tilde{\mathbf{R} }} ) + {\varepsilon }\nonumber \\= & {} (X-{\varepsilon })^2 + Y^2 + {\varepsilon }(1-{\varepsilon })\nonumber \!\!\! \\&\quad + 2\left( \frac{{\varepsilon }}{\left\| \mathbf{R} - (1,0,0) \right\| } +\frac{1-{\varepsilon }}{\left\| \mathbf{R} \right\| }\right) -\left\| {\dot{\mathbf{R} }} \right\| ^2.\nonumber \!\!\! \\ \end{aligned}$$

(3)

Thus, for a given value of ${{\mathscr {C}}}$, the corresponding isoenergetic hypersurface is a manifold of dimension 5. ${{\mathscr {C}}}$ being the only conserved quantity (see [37]), it is not possible to reduce the problem through another global transformation. A further way to simplify the study is to consider the particle’s motion restricted to the orbital plane of the planet. Hence, the phase space to explore can be reduced by two units. Consequently, investigating the restricted three-body problem in the circular-planar case is equivalent to explore a one-parameter family of 3-dimensional manifolds parametrized by the energy. Without too much details, the following part is dedicated to some remarkable solutions of the circular-planar case that are relevant for the scope of this work, i.e., the families that are connected to the co-orbital motion.

2.2.2 Some remarkable solutions in the circular-planar case ($e'=0$)

Fig. 1

Periodic orbits in the synodic reference frame for a Sun–Jupiter-like system (${{\varepsilon }= 1/1000}$) in the circular-planar case. More precisely, the periodic orbits belong to (a) the Lyapunov family ${{\mathscr {L}}}_3$, (b) the short-periodic family ${{\mathscr {L}}}_4^s$, (c) the long-periodic family ${{\mathscr {L}}}_4^l$, and (d) the family f. Their initial conditions are computed with the help of the Poincaré maps defined by the following sections: (a, d) $\varSigma _0 = \{Y = 0, \,\dot{Y}<0 \}$, (b) $\varSigma = \{ Y = \sqrt{3}/2, \,\dot{Y}>0\}$, and (c) ${\varSigma \cap \{X>0\}}$

Fig. 2

Dynamics located in the neighborhood of (a, b) the family f, (c) the long-periodic family ${{\mathscr {L}}}_4^l$, (d) the short-periodic family ${{\mathscr {L}}}_4^s$ and (e, f) the Lyapunov family ${{\mathscr {L}}}_3$. Considering a periodic orbit that belongs to each family (black curve) whose cross section is denoted ${(X_0, Y_0, \dot{X}_0, \dot{Y}_0)}$ a trajectory located in its vicinity, that is, with an initial condition $(X,Y, \dot{X}, \dot{Y}) = (X_0,Y_0, \dot{X}_0, \dot{Y}_0) + {{\mathcal {O}}} ({\varepsilon })$ is propagated after 100 revolutions of Jupiter. The dynamics observed are : (a) the “satellized” retrograde satellite orbits, (b) the quasi-satellite motion, (c, d, e) the tadpole motion, and (f) the horseshoe motion . (Color figure online)

We recall that the configuration space of the circular-planar case coincides with the orbital plane of the planet. In the following, the motion of the particle will be described in terms of polar coordinates with ${\phi = \arg (\mathbf{R} )}$ that illustrates the relative motion between the planet and the particle and ${R =\left\| \mathbf{R} \right\| }$. Most of the results mentioned below can be found with different notations in the book of Szebehely [37].

First of all, the five Lagrange fixed points, denoted $L_j$ for ${j=1,2,3,4,5}$, are the unique equilibria of the restricted three-body problem in the circular case. $L_1$ and $L_2$ belong to the Sun–planet axis, in

$$\begin{aligned} {\phi _{j} = 0\,^{\circ }}, \quad {R_{j} = 1 + (-1)^j \times \left( \frac{{\varepsilon }}{3}\right) ^{1/3} + {{\mathcal {O}}} ({\varepsilon }^{2/3})}, \end{aligned}$$

that is, from either side of the planet. Moreover, they embody the diameter of the Hill’s sphere of the planet, that is the region of the configuration space inside which the gravitational influence of the planet dominates with respect to the one of the Sun. $L_3$ is also located on the Sun–planet axis, in

$$\begin{aligned} \phi _{3}=180\,^{\circ }, \quad R_3 = 1 - \frac{7}{12}{\varepsilon }+ {{\mathcal {O}}} ({\varepsilon }^2). \end{aligned}$$

$L_4$ and $L_5$ are the Lagrange configurations such that the particle lie at the vertex of an equilateral triangle formed with the Sun and the planet, that is, in ${\phi _{j} = (-1)^j \times 60\,^{\circ }}$ and ${R_{j}= 1}$.

For ${j=4,5}$ and ${\varepsilon }$ small enough¹, $L_j$ is an elliptic equilibrium where two one-parameter families of periodic orbits stem from. They are tangential to each center eigenspace of the equilibrium point. Being the two center eigenspaces associated with frequencies, respectively, in ${{\mathcal {O}}} (1)$ and ${{\mathcal {O}}} (\sqrt{{\varepsilon }})$, these families are generally denoted as short-periodic ${{\mathscr {L}}}_j^s$ and long-periodic ${{\mathscr {L}}}_j^l$, in correspondence to their associated timescale in the neighborhood of the equilibrium. $L_1$, $L_2$ and $L_3$ are unstable for all ${\varepsilon }>0$ and each equilibrium possesses one center eigenspace. The same reasoning applies and provides three one-parameter families of periodic orbits generally known as the Lyapunov families ${{\mathscr {L}}}_1$, ${{\mathscr {L}}}_2$ and ${{\mathscr {L}}}_3$. Only ${{\mathscr {L}}}_3$ will be discussed in the following.

The Poincaré map is the classical way to compute periodic orbits. For ${{\mathscr {L}}}_j^s$ and ${{\mathscr {L}}}_j^l$, suitable sections are given by ${\varSigma = \{ Y = R_j \sin \phi _j,\, \dot{Y}>0 \}}$ and ${\varSigma \cap \{ X>0\}}$, which require three free parameters (e.g., the energy, X and $\dot{X}$) in order to locate the crossing. We recall that the Lyapunov trajectories are symmetrical with respect to the Sun–planet axis and cross the X-axis in ${\dot{X} = 0}$. Thus, a natural section, that requires only two parameters (e.g., the energy and X), is given by ${\varSigma _0 = \{ Y = 0, \, \dot{Y}<0, \,\dot{X} = 0 \}}$. Then, a fixed-point method is generally performed from a suitable initial guess that makes the method convergent. For that purpose, a first approximation of a crossing is obtained by the resolution of the linearized system associated with the equilibrium $L_j$ and a continuation method is implemented.

Figure 1 displays some periodic orbits, computed in the case of a Sun–Jupiter-like system (${{\varepsilon }= 1/1000}$) by varying X along the section.

Since ${X> -R_3}$ increases, the size of a trajectory that belongs to ${{\mathscr {L}}}_3$ (Fig. 1a) increases and its shape no longer looks like to an ellipse centered on $L_3$. More precisely, $\phi$ and R oscillate, respectively, about $180\,^{\circ }$ and 1, whose respective amplitude increases with X and reaches large values close to $180\,^{\circ }$ and 1. Moreover, the “guiding center” of each periodic trajectory (the approximate position around which the trajectory oscillates) remains $L_3$. Decreasing ${X< 1/2}$, the shape of the trajectories of ${{\mathscr {L}}}_4^s$ (Fig. 1b) has a quite similar evolution to the one of ${{\mathscr {L}}}_3$. However, two main differences exist: the shape is not symmetric, and the guiding center shifts from $L_4$ toward $L_3$ along the circle ${R = 1}$. The same behavior is observed symmetrically for ${{\mathscr {L}}}_5^s$. We point out that, for a given energy, ${{\mathscr {L}}}_4^s$ and ${{\mathscr {L}}}_5^s$ merge together with ${{\mathscr {L}}}_3$. This result was found by Deprit et al. [9] for an Earth–Moon-like system (${{\varepsilon }=1/81}$) in the circular-planar case. The features of ${{\mathscr {L}}}_4^l$ (Fig. 1c) are different. Indeed, as long as ${X<1/2}$ decreases, the size of a trajectory increases, while its shape changes and looks like a tadpole, with the head centered on $L_4$ and the tail that extends toward $L_3$. In other words, by decreasing X, R oscillates about 1 with an amplitude that increases but remains much smaller than 1, while $\phi$ encompasses $60\,^{\circ }$ with increasing oscillations included in the range $]0\,^{\circ },180\,^{\circ }[$.

Other families of periodic orbits exist, and several classifications have been realized (see [14, 36, 37]). Among them, the family f is especially remarkable: it is a one-parameter family of symmetrical periodic orbits whose motion in the synodic reference frame looks like the one of a retrograde satellite of the planet, and that extends from an infinitesimal neighborhood of the planet (i.e., inside its Hill’s sphere) to the collision with the Sun (i.e., far beyond the Hill’s sphere of the planet). Its computation is similar to the one of the Lyapunov families. However, since it does not originate from a Lagrange fixed point, the initial guess of the method is given by the two following limit cases (see [4]):

• $\dot{Y} = -X + \sqrt{\frac{2-X}{X}}$ for ${\varepsilon }\simeq 0$,

• $\dot{Y} = -(X-1) - \sqrt{\frac{{\varepsilon }}{X-1}}$ for $X\simeq 1$.

Figure 1d depicts some trajectories of the family f. By varying ${X>1}$, their shape has the same evolution to the one of ${{\mathscr {L}}}_3$. More precisely, the family f seems the symmetrical family of ${{\mathscr {L}}}_3$ with respect to the Y-axis, characterized by $\phi$ that oscillates about zero and thus a guiding center located on the planet.

The linear stability character of a periodic orbit can be deduced from the monodromy matrix. For ${\varepsilon }$ small enough², the family f is normally elliptic except in two particular orbits that split the neighborhood of the family in three different domains (see [28] for more details). One belongs to the Hill’s sphere and corresponds to the “satellized” retrograde satellite orbits. The two others stand for the quasi-satellite orbits, also known as distant retrograde orbits (DRO). Examples of “satellized” retrograde satellite and quasi-satellite orbits, computed during 100 revolutions of Jupiter, are depicted in Fig. 2a–b. Both of the families ${{\mathscr {L}}}_j^l$ and ${{\mathscr {L}}}_j^s$ are normally elliptic close to the equilibrium. The tadpole-shaped trajectories depicted in Fig. 2c and d, start in the neighborhood of periodic orbits that belongs to ${{\mathscr {L}}}_4^l$ and ${{\mathscr {L}}}_4^s$, respectively. A part of ${{\mathscr {L}}}_3$ near the equilibrium is normally hyperbolic and two types of dynamics can be observed in its neighborhood: tadpole-shaped orbits with a large amplitude (Fig. 2e), and horseshoe-shaped orbits that encompass the three fixed points $L_3$, $L_4$ and $L_5$ (Fig. 2f). The horseshoe-shaped orbit is characterized by R that oscillates about 1 with an amplitude smaller than 1, and $\phi$ that features very large oscillations centered on $180\,^{\circ }$.

To summarize the situation, we described four types of dynamics— “satellized” retrograde satellite, quasi-satellite, tadpole motion and horseshoe motion—that starts in the vicinity of periodic orbits that belong to the six families mentioned above. These dynamics are related by the same features, that is, R that oscillates about 1 and $\phi$ that does not circulates but oscillates around a given value. A natural issue is to understand how these dynamics are organized in the phase space of the restricted three-body problem, and especially, if some boundaries can be identified. Nevertheless, the four dimensions of the phase space make difficult the achievement of this goal.

A way to overcome this difficulty is given by a suitable perturbative treatment that focuses on the families of periodic orbits. First of all, let us recall that the particle and the planet are considered in mean-motion resonance, and especially in p:q mean-motion resonance, if they complete, respectively, p and q revolutions around the Sun in the same time. According to the Poincaré classification (see [5]), a periodic orbit of the second or the third “sort” (also translated as “kind”) is the continuation, from the limit case ${\varepsilon }=0$, of a heliocentric Kepler orbit in mean-motion resonance with the planet. For instance, the families ${{\mathscr {L}}}_3$, ${{\mathscr {L}}}_j^s$ as well as the part of the family f that stands outside the Hill’s sphere are the continuation of Kepler orbits in 1:1 mean-motion resonance (see the book of Hénon [14] for complete details on the periodic orbit classification). Hence, a perturbative treatment that considers ${\varepsilon }$ as a small parameter, and focuses on a small enough neighborhood of a given mean-motion resonance provides another way to approach some families of periodic orbits and thus to understand the corresponding dynamics. This is the underlying idea associated with the averaged problem that is considered in this work and that we recall in the following section.

2.3 Perturbative treatment of a mean-motion resonance: the averaged problem

From now on, we go back to the general case of the restricted three-body problem. If we consider ${\varepsilon }$ as a small parameter, the Hamiltonian function given in the heliocentric reference frame, Eq. (2), can be split in two terms, namely ${{\mathcal {H}} }= {{\mathcal {H}} }_{\mathrm K }+ {{\mathcal {H}} }_{\mathrm P }$ such that

$$\begin{aligned} \begin{aligned} {{\mathcal {H}} }_{\mathrm K }(\mathbf{r} , {\dot{\mathbf{r} }})&= \frac{1}{2}\left\| {\dot{\mathbf{r} }} \right\| ^2 - \frac{1}{\left\| \mathbf{r} \right\| },\\ {{\mathcal {H}} }_{\mathrm P }(\mathbf{r} , \lambda ')&= -\frac{{\varepsilon }}{\left\| \mathbf{r} - \mathbf{r} '(\lambda ') \right\| } + \frac{{\varepsilon }}{\left\| \mathbf{r} \right\| } + {\varepsilon }\frac{\mathbf{r} \bullet \mathbf{r} '(\lambda ')}{\left\| \mathbf{r} '(\lambda ') \right\| ^3}. \end{aligned} \end{aligned}$$

(4)

${{\mathcal {H}} }_{\mathrm K }$ corresponds to the unperturbed Kepler motion of the particle, more precisely the motion around a fixed center of mass 1, while ${{\mathcal {H}} }_{\mathrm P }$ models the perturbations that depend on ${\varepsilon }$: the gravitational influence of the planet, the acceleration of the heliocentric frame and a term associated with our choice of Kepler problem.

A closed solution of ${{\mathcal {H}} }_{\mathrm K }$ describes an ellipse whose shape, orientation and position at a time t are given by the orbital elements ${(a, e, I, \varOmega , \omega , v(t))}$. We recall that the position at a time t can also be described by the mean anomaly M(t), a fictitious angle, linear with respect to the time and whose rate of variation—generally known as mean motion—reads ${\dot{M}(a) = 1/\sqrt{a}^3}$ in the units adopted here. Instead of using the orbital elements, the Poincaré complex variables are adopted because of their regularity for circular and coplanar orbits and since they preserve the symplectic geometry of the problem. In the following, the angles ${\varpi = \varOmega + \omega }$ and ${\lambda = M + \varpi }$ denote, respectively, the longitude of the periaster and the mean longitude. The symplectic transformation associated with the Poincaré variables reads

$$\begin{aligned} \hat{\varUpsilon }: (\mathbf{r} , {\dot{\mathbf{r} }}, \lambda ', \hat{\varXi }) \mapsto (\lambda , \varLambda , {\tilde{x} }, x, {\tilde{y}{}} , y, \lambda ', \hat{\varXi }) \end{aligned}$$

with

$$\begin{aligned} \varLambda= & {} \sqrt{a}, \\ x= & {} \sqrt{\varLambda (1-\sqrt{1-e^2})}\exp i\varpi ,\\ y= & {} \sqrt{\varLambda \sqrt{1-e^2}(1-\cos I)}\exp i\varOmega , \end{aligned}$$

that are, respectively, conjugated to $\lambda$, ${\tilde{x} }= -i{\overline{x} }$ and ${\tilde{y}{}} = -i {\overline{y}{}}$. We specify that x and y derive from the angular momentum in the heliocentric reference frame as follows:

$$\begin{aligned} \left\| \varvec{{\mathrm L }} \right\| \circ \hat{\varUpsilon }= \varLambda - \left| x \right| ^2, \quad \varvec{{\mathrm L }}_3\circ \hat{\varUpsilon }= \varLambda - \left| x \right| ^2 -\left| y \right| ^2. \end{aligned}$$

Moreover, $x\sqrt{2/\varLambda }$ and $y\sqrt{8/\varLambda }$ are equivalent to $e \exp (i\varpi )$ and $I \exp (i\varOmega )$ for quasi-circular and quasi-planar orbits.

In the extended phase space, the integrable motion is given by the Hamiltonian ${\hat{\varXi }+ \hat{H} _{\mathrm K }}$ with $\hat{H} _{\mathrm K }(\varLambda ) = -1/(2\varLambda ^2)$. Notice that the variable linked to the time is an action variable since the system is periodic. That is the reason why the unperturbed Hamiltonian is integrable. Being the planet and the particle coupled but independent, the solutions describe two ellipses whose respective mean motions are equal to ${\dot{\lambda }(\varLambda ) = 1/\varLambda ^3}$ and ${\dot{\lambda }' = 1}$. In other words, the solutions of the problem correspond to quasi-periodic orbits with two frequencies. Since the frequencies are commensurable, the orbits can be periodic. In such a case, the planet and the particle are considered in mean-motion resonance. Studying the restricted three-body problem in this perturbative framework consists in understanding how the perturbation ${\hat{H} _{\mathrm P }={{\mathcal {H}} }_{\mathrm P }\circ \hat{\varUpsilon }}$ transforms the unperturbed phase space. More precisely, the analysis can be split in two disjoint situations:

• At a suitable distance to mean-motion resonances via a secular model built in order to study the persistence of the quasi-periodic solutions;

• Or, on the contrary, in a neighborhood of a mean-motion resonance with the help of special variables and an adapted averaging process.

2.3.1 The resonant variables

For p and q two coprime positive integers, let us consider a neighborhood of the p:q mean-motion resonance. An unperturbed solution is associated with the p:q mean-motion resonance if the semimajor axis of the particle is equal to ${\tilde{a} = (q/p)^{2/3}}$. In what follows, $\tilde{a}$ will be defined as the semimajor axis of the “exact” mean-motion resonance.

The symplectic transformation

$$\begin{aligned} \check{\varUpsilon }\!: (\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y, \lambda ', \varXi ) \!\mapsto \! (\lambda , \varLambda , {\tilde{x} }, x, {\tilde{y}{}} , y, \lambda ', \hat{\varXi }) \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} \theta = \lambda - \frac{p}{q}\lambda ', \quad u = \varLambda - \sqrt{\tilde{a}}, \quad \hat{\varXi }= \varXi - \frac{p}{q}u, \end{aligned} \end{aligned}$$

(5)

introduces the resonant angle³$\theta$ that characterizes the commensurability, and u, its conjugated action, whose modulus measures the distance to the “exact” mean-motion resonance. We recall that $\theta$ is not a physical angle and thus it is difficult to represent. Nevertheless, for quasi-circular and quasi-planar orbits, the angular separation $\phi$ between the particle and the planet is equivalent to ${\theta + (p-q)q^{-1}\lambda '}$.

In the resonant variables given by Eq. (5), the integrable Hamiltonian reads ${\varXi + H_{\mathrm K }}$ with

$$\begin{aligned} H_{\mathrm K }(u) = -\frac{1}{2(\sqrt{\tilde{a}} + u)^2} - \frac{p}{q}u. \end{aligned}$$

$H_{\mathrm K }$ highlights that $\theta$ is constant for ${u=0}$, while it circulates for ${\left| u \right| > 0}$. More precisely, the angular variables evolve at different rates: $\lambda '$ is a “fast” angle with a frequency 1, $\theta$ undergoes “slow” drift in ${{\mathcal {O}}} (u)$ while $(\varpi , \varOmega )$ are fixed. Consequently, for a small enough $\left| u \right|$, the timescales of the integrable problem are separated. In the full problem that reads ${\varXi + H}$ with

$$\begin{aligned} H = H_{\mathrm K }+ H_{\mathrm P }\quad \text{ and } \quad H_{\mathrm P }= \hat{H} _{\mathrm P }\circ \check{\varUpsilon }, \end{aligned}$$

all the variables might vary and the motion is very tricky to understand. However, for ${\varepsilon }$ and $\left| u \right|$ small enough, the timescales separation between the “fast” and “slow” degrees of freedom still remains. A classical way to exploit this feature is to replace the original problem by another one in which the fast oscillations have been removed. For that purpose, an averaging over the period of revolution of the planet is performed. This process defines the averaged problem.

2.3.2 The averaged problem

The averaged Hamiltonian reads ${\overline{H} = H_{\mathrm K }+ \overline{H} _{\mathrm P }}$ with

$$\begin{aligned} \begin{aligned}&\overline{H} _{\mathrm P }(\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y) \\&\quad = \frac{1}{2\pi }\int _0^{2\pi } H_{\mathrm P }(\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y, \lambda '){\mathrm d }\lambda '. \end{aligned} \end{aligned}$$

(6)

Since $\overline{H}$ does not depend on $\lambda '$, $\varXi$ is a first integral that can be dropped. Hence, only three degrees of freedom are required in order to explore the averaged phase space: the resonant variables $(\theta , u)$, and $({\tilde{x} },x)$, $( {\tilde{y}{}} , y)$, that are, respectively, the Poincaré variables associated with eccentricity and inclination.

There exist at least two classical techniques of computation of the averaged problem. The analytical one is based on the expansion of the Hamiltonian in power series of eccentricity and inclination (see, e.g., [30]). In spite of its efficiency for quasi-circular and quasi-coplanar orbits, reaching higher values of eccentricity or inclination requires high-order expansions which generate very heavy expressions. Also worth mentioning the asymmetric expansion developed by Ferraz-Mello and Sato [11] in order to deal with highly eccentric trajectories in mean-motion resonance. The other technique consists on a numerical evaluation of the integral of Eq. (6) and its derivatives. It is a powerful tool since it deals with the Hamiltonian in its exact form which allows to explore the phase space for all values of eccentricity lower than one and all values of inclination.

Following the idea of Poincaré [27], Schubart [31,32,33] developed a numerical averaging procedure for the Hamiltonian in canonical resonant variables. Moons [19] extended the method of Schubart and provided an algorithm that allows to compute the equations of motion of the averaged problem, and thus to construct an integrator for trajectories in p:q mean-motion resonance, for $p\ne q$. This algorithm has been adapted by Nesvorný et al. [24] in order to deal with the 1:1 mean-motion resonance. In either case, the numerical averaging can be implemented as follows. Let f an auxiliary function that depends on $(\theta , u , {\tilde{x} }, x, {\tilde{y}{}} , y, E, E')$ where E and $E'$ are, respectively, the eccentric anomaly of the particle and the planet. The averaging of f over $\lambda '$ being calculated for fixed $(\theta , u, {\tilde{x} },x, {\tilde{y}{}} ,y)$, the Kepler equation implies that: ${{\mathrm d }\lambda ' = L(u,x,E){\mathrm d }E}$ with ${L(u,x,E)= qp^{-1}(1-e(u,x)\cos E)}$. Moreover, since

$$\begin{aligned} \theta = E - e(u, x)\sin E + \varpi (x) - pq^{-1}(E' - e'\sin E') \end{aligned}$$

then $E'$ can be expressed in terms of $(\theta , u, x, E)$ and $e'$. Finally, the averaging of $2\pi f$, that reads

$$\begin{aligned} \begin{aligned}&2\pi \overline{f}(\theta , u, {\tilde{x} },x, {\tilde{y}{}} ,y)\\&\quad =\int ^{2\pi }_0 f(\theta , u , {\tilde{x} }, x, {\tilde{y}{}} , y, E, E'(\theta , u,x,E))\\&\qquad \times L(u,x,E){\mathrm d }E, \end{aligned} \end{aligned}$$

is computed by discretizing the variable E as $E_k= k2\pi /N$ with ${100 \le N \le 300}$ (see [31] for more details).

In the averaged problem, the phase space to explore is 6-dimensional. However, and similarly to the classical approach, the dimension can be reduced in the framework of the circular case ($e'=0$).

Table 1 Comparison of the features of the restricted three-body problem in the averaged phase space and in the synodic reference frame. ${{\mathscr {C}}}$, $\overline{H}$ and K denote, respectively, the Jacobi constant, the averaged Hamiltonian and the quantity conserved in the averaged problem in the circular case. The notations “(N d.o.f)” and “(Non-aut.)” stand, respectively, for “N degrees of freedom” and “non-autonomous”

2.3.3 Reduction in the circular case ($e'=0$)

First of all, we recall that the perturbation ${{\mathcal {H}} }_P$ is analytical outside the collision manifold and thus can be expanded in power series of eccentricity and inclination. In the Poincaré complex variables, the expansion reads

$$\begin{aligned} \sum _{(l,{{\tilde{l}} },m,{{\tilde{m}} }, k,k')\in {{\mathscr {D}}}} f_{l,{{\tilde{l}} },m,{{\tilde{m}} }}^{k,k'}(u)x^l{\tilde{x} }^{{\tilde{l}} }y^m {\tilde{y}{}} ^{{\tilde{m}} }e^{ i(k\lambda + k'\lambda ') } \end{aligned}$$

where the integers occurring in these summations satisfy the relations

$$\begin{aligned} {{\mathscr {D}}}= \left\{ \quad \begin{aligned}&(l,{{\tilde{l}} }, m, {{\tilde{m}} }, k, k')\in {{\mathbb {N}}}^4\times {{\mathbb {Z}}}^2\\&\text {s.t.}\quad m - {{\tilde{m}} }=2j, \quad j\in {{\mathbb {Z}}},\\&\text {and}\quad l + m -({{\tilde{l}} }+ {{\tilde{m}} }) + k + k' = 0 \end{aligned}\quad \right\} \end{aligned}$$

known as D’Alembert rules. These relations are the result of the invariance of the Hamiltonian ${{\mathcal {H}} }$ under the action of symmetry groups: the orthogonal symmetry with respect to the orbital plane of the planet, and the group of rotations SO(2) around the vertical axis. In the resonant variables, since the expansion of $H_{\mathrm P }$ reads

$$\begin{aligned} \sum _{(l,{{\tilde{l}} },m,{{\tilde{m}} }, k,k')\in {{\mathscr {D}}}} f_{l,{{\tilde{l}} },m,{{\tilde{m}} }}^{k,k'}(u)x^l{\tilde{x} }^{{\tilde{l}} }y^m {\tilde{y}{}} ^{{\tilde{m}} }e^{i\left( k\theta + (pk+qk')q^{-1}\lambda '\right) }, \end{aligned}$$

the integers occurring in the expansion of the integral of Eq. (6) satisfy the relations

$$\begin{aligned} {\overline{ {{\mathscr {D}}}}}= {{\mathscr {D}}}\cap \left\{ \quad \begin{aligned}&(l,{{\tilde{l}} }, m, {{\tilde{m}} }, k, k')\in {{\mathbb {N}}}^4\times {{\mathbb {Z}}}^2 \\&\text {s.t.}\quad kp + k'q = 0 \end{aligned}\quad \right\} . \end{aligned}$$

In other words, the angular part of the averaged Hamiltonian depends on the linear combination of only two angles: a “modified” resonant angle ${\theta - (q-p)q^{-1}\varpi }$ and the argument of periaster ${\omega =\varpi -\varOmega }$. Since the averaged Hamiltonian is invariant under the rotations of a third angle, the symplectic geometry imposes the following quantity

$$\begin{aligned} K= \left| x \right| ^2 + \left| y \right| ^2 + (p-q)q^{-1}u \end{aligned}$$

to be a first integral. We point out that this property can also be derived from the Jacobi constant, Eq. (3). Indeed, for a given c, such that ${{{\mathscr {C}}}(\mathbf{R} , {\dot{\mathbf{R} }}) = c}$, the composition of transformations ${\varUpsilon _{{\mathrm S }{\mathrm F }}\circ \hat{\varUpsilon }\circ \check{\varUpsilon }}$ in resonant variables provides the following expression of the Jacobi constant:

$$\begin{aligned} c = 2\sqrt{\tilde{a}}+ {\varepsilon }-2(H +K). \end{aligned}$$

(7)

Thus, the average of the Jacobi constant over $\lambda '$ introduces the averaged Hamiltonian $\overline{H}$, such as $c = 2\sqrt{\tilde{a}}+ {\varepsilon }-2(\overline{H} +K)$, that is conserved in the averaged problem and implies that K is also a first integral of the averaged problem.

Without revealing details on the symplectic transformation that takes advantage of K, we outline that ${q(p-q)^{-1}K}$, $\left| x \right| ^2$ and $\left| y \right| ^2$, respectively, conjugated with $\theta$, ${-\varpi + q(q-p)^{-1}\theta }$ and ${-\varOmega + q(q-p)^{-1}\theta }$, are action-angle variables that can be used. Since these previous variables are singular for the 1:1 mean-motion resonance, the canonical variables that can be adopted are u, K and $\left| y \right| ^2$, respectively, conjugated to $\theta$, $-\varpi$ and $\omega$.

Being the degree of freedom associated with K separable to the other two, a reduction is possible. By fixing a value K, seen as a parameter, and eliminating its conjugated cyclic angle, one degree of freedom is removed. Consequently, the averaged phase space can be described by a 1-parameter family of reduced Hamiltonians with two degrees of freedom. We point out that in the circular-planar case, the number of degrees can be reduced to one. Hence, for a fixed K, the “reduced” averaged Hamiltonian is integrable and the description of the phase portrait obtained for various values of K allows to understand the global dynamics of the mean-motion resonance.

2.3.4 Some conclusions about the averaged problem

In Table 1, we summarize the respective features of the averaged problem with respect to the classical approach in the synodic reference frame. First of all, the averaged problem has the advantage to describe the solutions in terms of orbital elements (or variables close to these ones), and thus profits of the symplectic geometry of the problem which allows to reduce by one unit the dimension of the phase space to explore in any case. The algorithms of Moons [19] and Nesvorný et al. [24] are easy to implement to this end. Furthermore, it gives a complete understanding of the resonant dynamics in the circular-planar case.

However, the averaged problem possesses also some important drawbacks. First of all, since H has been replaced by $\overline{H}$ in order to remove the fast oscillations, it does not correspond to the original problem but approximates it with an accuracy that depends on the size of ${\varepsilon }$. Besides, according to the remark of Schubart [31], it has been shown by Robutel and Pousse [30] and Pousse et al. [28], that the averaged problem fails to describe trajectories that feature close encounters with the planet. In such a case, the “distance” between the averaged Hamiltonian and the original one is important, and the results given by the averaged problem may not be reliable. The clarification of the accuracy as well as the limit of validity is a serious issue. We devote the next section to that purpose.

3 On the validity of the averaged problem

3.1 Notations

Before going further, let us introduce some useful notations associated with the Hamiltonian formalism.

In the following, since it will be necessary to switch from the resonant variables to the heliocentric coordinates, we denote

$$\begin{aligned} \varUpsilon :(\theta ,u,{\tilde{x} }, x, {\tilde{y}{}} , y, \lambda ', \varXi ) \mapsto (\mathbf{r} , {\dot{\mathbf{r} }}, \lambda ', \hat{\varXi }) \end{aligned}$$

the composition of transformations ${\hat{\varUpsilon }\circ \check{\varUpsilon }}$. These two sets of variables preserve the symplectic form, that is,

$$\begin{aligned} \sum _{i=1}^3 {\mathrm d }\mathbf{r} _i&\wedge&{\mathrm d }{\dot{\mathbf{r} }}_i + {\mathrm d }\lambda '\wedge {\mathrm d }\hat{\varXi }\\= & {} {\mathrm d }\theta \wedge {\mathrm d }u + {\mathrm d }{\tilde{x} }\wedge {\mathrm d }x + {\mathrm d } {\tilde{y}{}} \wedge {\mathrm d }y + {\mathrm d }\lambda '\wedge {\mathrm d }\varXi . \end{aligned}$$

Hence, the Lie derivative of an auxilliary function ${{{\mathcal {G}} }(\mathbf{r} , {\dot{\mathbf{r} }}, \lambda ', \hat{\varXi })}$ along the Hamiltonian flow of a given function ${{{\mathcal {F}} }(\mathbf{r} , {\dot{\mathbf{r} }}, \lambda ', \hat{\varXi })}$ reads:

$$\begin{aligned} \begin{aligned} {{\mathcal {L}} }_{{\mathcal {F}} }{{\mathcal {G}} }&= \frac{\partial {{\mathcal {G}} } }{\partial \mathbf{r} } \bullet \frac{\partial {{\mathcal {F}} } }{\partial {\dot{\mathbf{r} }}} - \frac{\partial {{\mathcal {F}} } }{\partial \mathbf{r} } \bullet \frac{\partial {{\mathcal {G}} } }{\partial {\dot{\mathbf{r} }}} + \frac{\partial {{\mathcal {G}} } }{\partial \lambda '}\frac{\partial {{\mathcal {F}} } }{\partial \hat{\varXi }} -\frac{\partial {{\mathcal {F}} } }{\partial \lambda '}\frac{\partial {{\mathcal {G}} } }{\partial \hat{\varXi }}\\&= \frac{\partial g }{\partial \theta }\frac{\partial f }{\partial u} - \frac{\partial f }{\partial \theta }\frac{\partial g }{\partial u} + \frac{\partial g }{\partial {\tilde{x} }}\frac{\partial f }{\partial x} - \frac{\partial f }{\partial {\tilde{x} }}\frac{\partial g }{\partial x} + \frac{\partial g }{\partial {\tilde{y}{}} }\frac{\partial f }{\partial y} \\&\quad - \frac{\partial f }{\partial {\tilde{y}{}} }\frac{\partial g }{\partial y} + \frac{\partial g }{\partial \lambda '}\frac{\partial f }{\partial \varXi } -\frac{\partial f }{\partial \lambda '}\frac{\partial g }{\partial \varXi }\\&= {{\mathcal {L}} }_f g \end{aligned} \end{aligned}$$

with ${f = {{\mathcal {F}} }\circ \varUpsilon }$ and ${g = {{\mathcal {G}} }\circ \varUpsilon }$. Finally, $\varPhi _t^h(\mathbf{{X} }_0)$ denotes the Hamiltonian flow at a time t, generated by an auxiliary function $h(\mathbf{{X} })$ that crosses $\mathbf{{X} }_0$ at $t=0$. We recall that it is connected to the Lie derivative through the exponential of an operator, denoted $\exp$, such as:

$$\begin{aligned} \varPhi _t^h = \exp {{\mathcal {L}} }_h = {\mathrm I }{\mathrm d }+ \sum _{k>0} \frac{t^k}{k!}\underbrace{{{\mathcal {L}} }_h\ldots {{\mathcal {L}} }_h{{\mathcal {L}} }_h}_{k \,times}. \end{aligned}$$

3.2 The averaging process

According to the perturbation theory, the averaging process coincides with the existence of a symplectic transformation $\overline{\varUpsilon }$, close to the identity, which maps the original Hamiltonian ${\varXi + H}$ to ${\varXi + \overline{H} + H_*}$, where $H_*$ is a remainder that is supposed to be small with respect to $\overline{H} _{\mathrm P }$ and thus neglected in the averaged problem. $\overline{\varUpsilon }$ is computed with the time-one map of the Hamiltonian flow generated by some auxiliary function S, that is, ${\overline{\varUpsilon }= \varPhi _1^S = \exp {{\mathcal {L}} }_{S}}$, which satisfies

$$\begin{aligned} {{\mathcal {L}} }_S\varXi = -\frac{\partial S }{\partial \lambda '} = \overline{H} _{\mathrm P }- H_{\mathrm P }. \end{aligned}$$

In this paper, we choose

$$\begin{aligned} \begin{aligned}&S(\theta , u, {\tilde{x} }, x, {\tilde{y}{}} ,y,\lambda ') \\&\quad = \frac{1}{2\pi } \int _0^{2\pi } s (H_{\mathrm P }- \overline{H} _{\mathrm P })_{(\theta , u, {\tilde{x} },x, {\tilde{y}{}} ,y,\lambda ' + s)} {\mathrm d }s. \end{aligned} \end{aligned}$$

Based on the previous assumptions, the remainder of the averaging process reads

$$\begin{aligned} H_* = (\exp {{\mathcal {L}} }_S - {{\mathrm I }{\mathrm d }})H + (\exp {{\mathcal {L}} }_S - {{\mathcal {L}} }_S - {\mathrm I }{\mathrm d })\varXi . \end{aligned}$$

(8)

$H_*$ can be neglected if and only if it is a perturbation of higher order with respect to $\overline{H} _P$. However, since $H_*$ depends on the derivatives of $H_{\mathrm P }$ and S that increase as long as the planet and the particle are getting closer, then $\left| H_* \right|$ and $\left| \overline{H} _{\mathrm P } \right|$ can increase simultaneously according to the distance to the singularity and can be at least of the same order. In such a case, the hierarchy between the perturbative terms is not ensured and the approximation provided by the averaged Hamiltonian $\overline{H}$ might not reflect properly the dynamics of the restricted three-body problem. In other words, in the neighborhood of the collision manifold can exist an “exclusion zone” inside which the solutions of the restricted three-body problem fall outside the scope of the averaged Hamiltonian.

The following section is devoted to the characterization of this exclusion zone through a quantitative treatment of the averaging process.

3.3 Quantitative treatment of the averaging process

We first introduce a domain and a norm on the extended phase space that will allow us to compute quantitative estimates.

For given $\rho >0$, $\sigma >0$, $\varDelta >0$, $\tilde{\varDelta }>0$, small enough, and a given $\kappa >0$, independent of the previous quantities, we define the following domain of the extended phase space:

$$\begin{aligned}&{{\mathfrak {D}}} _\kappa \\&\quad =\left\{ \, \begin{aligned}&(\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y, \lambda ', \varXi ) \in {{\mathbb {T}}}\times {\mathbb {R}}\times {{\mathbb {C}}}^4 \times {{\mathbb {T}}}\times {\mathbb {R}}\\&\text{ s.t. }\quad \left| u \right| \le \kappa \rho , \quad \max (\left| x \right| , \left| {\tilde{x} } \right| ) \le \tilde{r}_{\sigma /\kappa },\\&\min _{\lambda '\in {{\mathbb {T}}}}\left( \left\| \mathbf{r} \circ \varUpsilon - \mathbf{r} ' \right\| \right) \ge \varDelta /\kappa , \quad \min _{\lambda '\in {{\mathbb {T}}}}\left\| \mathbf{r} \circ \varUpsilon \right\| \ge \tilde{\varDelta }/\kappa \end{aligned}\,\right\} \end{aligned}$$

with ${\tilde{r}_{\sigma /\kappa }= \tilde{a}^{1/4}(1-\sigma /\kappa )}$ and being $\tilde{a}$ the resonant semimajor axis $\tilde{a}= (q/p)^{2/3}$. Hence, we consider a neighborhood of the p:q mean-motion resonance which excludes very high eccentricities (${\left| x \right| \simeq \tilde{a}^{1/4}}$) as well as sets of elements associated with the crossing of the spheres of radius $\varDelta /\kappa$ and $\tilde{\varDelta }/\kappa$, respectively, centered on the planet and the Sun in the heliocentric reference frame.

In this development, we are not interested in the situations of close encounters with the Sun, that occur for a very high eccentricity. They are avoided by considering $\tilde{\varDelta }$ and $\sigma$ as arbitrarily fixed small numbers independent of ${\varepsilon }$, $\rho$ and $\varDelta$.

The estimates will be computed through the supremum norm on ${{\mathfrak {D}}} _\kappa$, denoted $\left\| \,\cdot \, \right\| _{\kappa }$ such that

$$\begin{aligned} \left\| \mathbf{{f} } \right\| _{\kappa }= \max _{i\le n } \sup _{{{\mathfrak {D}}} _\kappa } \left| \mathbf{{f} }_i \right| \end{aligned}$$

where $\mathbf{{f} }=(\mathbf{{f} }_i)_{i\le n}$ is a n-dimensional vector field that depends on the resonant variables $(\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y, \lambda ', \varXi )$. Since we do not attempt to obtain estimates with particularly sharp constants, all constants have been suppressed and replaced by the Pöschel’s notation, that is,

$$\begin{aligned} x {\,\le \! \bullet \,}y, \quad x {\,\bullet \! \le \,}y, \quad \text{ and } \quad x {\, =\!\bullet \,}y \end{aligned}$$

to indicate, respectively, that

$$\begin{aligned} x< Cy, \quad Cx <y, \quad \text{ and } \quad x = Cy \end{aligned}$$

with some constant $C\ge 1$ independent of ${\varepsilon }$, $\rho$ and $\varDelta$.

In this setting, the size of the functions involved in the averaging process can be estimated. Hence, we state the following:

Lemma 1

For ${\rho >0}$, ${\varDelta >0}$ and ${{\varepsilon }>0}$, small enough quantities, that is

$$\begin{aligned} \rho {\,\bullet \! \le \,}1, \quad \varDelta {\,\bullet \! \le \,}1, \quad {\varepsilon }{\,\bullet \! \le \,}1, \end{aligned}$$

the Hamiltonian of the restricted three-body problem ${\varXi +H}$, the averaged Hamiltonian ${\varXi + \overline{H} }$ and the symplectic transformation $\varUpsilon$, are analytic on the collisionless domain ${{\mathfrak {D}}} _2$.

Consequently, $H_{\mathrm K }$, $H_{\mathrm P }$, $\overline{H} _{\mathrm P }$ and $\varUpsilon$ are bounded together with their partial derivatives with respect to $\theta$, u, ${\tilde{x} }$, x, ${\tilde{y}{}}$ and y. More precisely, for each order k lower or equal to an arbitrarily fixed ${n\ge 1}$ and ${(W_i)_{i\le k}\in \{\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y\}}$, the following thresholds are satisfied on ${{\mathfrak {D}}} _{2}$:

$$\begin{aligned} \begin{aligned}&\begin{array}{lll} \left\| H_{\mathrm K } \right\| _{2} {\, =\!\bullet \,}1,&{}\quad \left\| H_{\mathrm P } \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta },&{}\quad \left\| \overline{H} _{\mathrm P } \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta },\\ \left\| H_{\mathrm K }' \right\| _{2} {\,\le \! \bullet \,}\rho ,&{}\quad \left\| H_{\mathrm K }'' \right\| _{2} {\,\le \! \bullet \,}1,\\ \end{array}\\&\left\| \frac{\partial ^k H_{\mathrm P }}{\partial W_1 \ldots \partial W_k} \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^{k+1}},\quad \! \left\| \frac{\partial ^k(\mathbf{r} \circ \varUpsilon )}{\partial {W_1}\ldots \partial {W_k}} \right\| _{2} {\,\le \! \bullet \,}1. \end{aligned} \end{aligned}$$

The previous lemma allows to state an averaging theorem where quantitative estimates on the averaging process are computed.

Theorem 1

Assuming ${\varepsilon }$, $\rho$ and $\varDelta$ small enough such that

$$\begin{aligned} {\varepsilon }{\,\bullet \! \le \,}\rho \varDelta ^2 \quad \text{ and } \quad {\varepsilon }{\,\bullet \! \le \,}\varDelta ^3, \end{aligned}$$

(9)

there exists a symplectic transformation close to the identity, denoted as

$$\begin{aligned} \overline{\varUpsilon }: \left\{ \begin{array}{ccc} {{{\mathfrak {D}}} _{3/2}} &{}\rightarrow &{}{{\mathfrak {D}}} _{2}\\ ({\mathop {\theta }\limits _{\dot{}}}, {\mathop {u}\limits _{\dot{}}}, {\mathop {{\tilde{x} }}\limits _{\dot{}}}, {\mathop {x}\limits _{\dot{}}}, {\mathop { {\tilde{y}{}} }\limits _{\dot{}}}, {\mathop {y}\limits _{\dot{}}}, \lambda ',{\mathop {\varXi }\limits _{\dot{}}}) &{}\mapsto &{} (\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y, \lambda ', \varXi ) , \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} \left\| {\mathop {\varXi }\limits _{\dot{}}} - \varXi \right\| _{{3/2}} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta },\quad \left\| {\mathop {W}\limits _{\dot{}}} - W \right\| _{{3/2}} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^2}\\ \end{aligned} \end{aligned}$$

for $W \in \{\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y\}$, such that, in the “averaged” resonant variables ${({\mathop {\theta }\limits _{\dot{}}}, {\mathop {u}\limits _{\dot{}}}, {\mathop {{\tilde{x} }}\limits _{\dot{}}}, {\mathop {x}\limits _{\dot{}}}, {\mathop { {\tilde{y}{}} }\limits _{\dot{}}}, {\mathop {y}\limits _{\dot{}}}, \lambda ',{\mathop {\varXi }\limits _{\dot{}}})}$, the Hamiltonian reads:

$$\begin{aligned} (\varXi + H)\circ \overline{\varUpsilon }= {\mathop {\varXi }\limits _{\dot{}}} + \overline{H} + H_* \end{aligned}$$

where $H_*$ is the remainder of the averaging process.

Furthermore, on the domain ${{\mathfrak {D}}} _{3/2}$, $H_*$ together with its partial derivatives with respect to $\theta$, u, ${\tilde{x} }$, x, ${\tilde{y}{}}$ and y are bounded and satisfy the following thresholds:

Lemma 1 and Theorem 1 provide the estimates that allow to compare how $\left| \overline{H} _{\mathrm P } \right|$ and $\left| H_* \right|$ increase as long as the planet and the particle are getting closer. In order to understand the role of the distance to the planet in the size of the remainder, we first relate the upper bound of the distance to the resonance to ${\varepsilon }$ and $\varDelta$ by choosing

$$\begin{aligned} \rho {\, =\!\bullet \,}\sqrt{\frac{{\varepsilon }}{\varDelta }} \end{aligned}$$

(10)

which satisfies Eq. (9) and such that the two terms in $\eta$ depend on the same quantity: the ratio $\frac{{\varepsilon }}{\varDelta ^3}$. Hence, we have

$$\begin{aligned} \eta {\, =\!\bullet \,}\sqrt{\frac{{\varepsilon }}{\varDelta ^3}}\left( 1 + \sqrt{\frac{{\varepsilon }}{\varDelta ^3}}\right) \end{aligned}$$

(11)

which imposes the lower bound ${\varDelta {\,\ge \! \bullet \,}{\varepsilon }^{1/3} }$ in order to get decreasing perturbations in the “averaged” resonant variables. More precisely, we recover the size of the Hill’s sphere of the planet. We recall that $\varDelta$ denotes the minimal mutual distance, that is, the minimal distance between the particle and the planet, which is allowed in the considered domain ${{\mathfrak {D}}} _\kappa$. As a consequence, if we relate $\varDelta$ to ${\varepsilon }$ as follows:

$$\begin{aligned} \begin{aligned} \varDelta = {\mathrm N }_{\varepsilon }R_{\mathrm H }\quad \text{ with } \quad {\mathrm N }_{{\varepsilon }} ={\varepsilon }^{-\alpha },\quad 0< \alpha \le 1/3, \end{aligned} \end{aligned}$$

being $R_{\mathrm H }= \left( \frac{{\varepsilon }}{3}\right) ^{1/3}$ the Hill’s radius of the planet, then Theorem 1 ensures that the domain ${{\mathfrak {D}}} _{4/3}$ stands outside the exclusion zone of the averaged problem for ${\varepsilon }$ small enough and ${\mathrm N }_{{\varepsilon }}>1$, that is, for a minimal mutual distance larger than the Hill’s radius of the planet.

In spite of this feature, Theorem 1 does not establish that a given solution of the averaged problem that starts inside ${{\mathfrak {D}}} _{3/2}$, does not escape and does not cross the exclusion zone of the averaged phase space. To this end, a careful analyze of the behavior of the averaged solutions has to be led for each type of dynamics in mean-motion resonance. Nevertheless, assuming that the solution remains inside ${{\mathfrak {D}}} _{3/2}$ until a certain amount of time, a theorem of stability over finite times can be proven in the restricted three-body problem.

Before stating the theorem, let us denote a solution governed by the averaged Hamiltonian ${\varXi + \overline{H} }$, that starts in ${\mathbf{{X} }_0\in {{\mathfrak {D}}} _{1}}$ and remains inside this domain up to a given time ${{{\mathcal {T}} }_1>0}$, as

$$\begin{aligned} {{\mathop {\mathbf{{X} }}\limits _{\dot{}}}(t) = ({\mathop {\mathbf{{W} }}\limits _{\dot{}}}(t), \lambda '(t), {\mathop {\varXi }\limits _{\dot{}}}(t))} \end{aligned}$$

with

$$\begin{aligned}{\mathop {\mathbf{{W} }}\limits _{\dot{}}}(t)= & {} ( {\mathop {\theta }\limits _{\dot{}}}(t), {\mathop {u}\limits _{\dot{}}}(t), {\mathop {{\tilde{x} }}\limits _{\dot{}}}(t), {\mathop {x}\limits _{\dot{}}}(t), {\mathop { {\tilde{y}{}} }\limits _{\dot{}}}(t), {\mathop {y}\limits _{\dot{}}}(t)) \\&\text{ and }\,\,\,{\lambda '(t) = t}.\end{aligned}$$

For ${\left| t \right| \le {{\mathcal {T}} }_1}$ and ${{\mathrm N }_{{\varepsilon }} >1}$, ${\mathop {\mathbf{{X} }}\limits _{\dot{}}}(t)$ approximates the solution of the restricted three-body problem that starts in $\mathbf{{X} }_0$. In the resonant variables, the solution governed by ${\varXi + H}$ can be written as ${(\mathbf{{W} }(t), \lambda '(t), \varXi (t))}$ with

$$\begin{aligned} \begin{aligned} \theta (t)&= {\mathop {\theta }\limits _{\dot{}}}(t) + \delta _1(t),\\ {\tilde{x} }(t)&= {\mathop {{\tilde{x} }}\limits _{\dot{}}}(t) + \delta _3(t),\\ {\tilde{y}{}} (t)&= {\mathop { {\tilde{y}{}} }\limits _{\dot{}}}(t) + \delta _5(t),\\ \end{aligned}\quad \begin{aligned} u(t)&= {\mathop {u}\limits _{\dot{}}}(t) + \delta _2(t),\\ x(t)&= {\mathop {x}\limits _{\dot{}}}(t) + \delta _4(t),\\ y(t)&= {\mathop {y}\limits _{\dot{}}}(t) + \delta _6(t),\\ \end{aligned} \end{aligned}$$

being ${(\delta _i(t))_{i\le 6}}$ the functions that denote the error on each coordinate in the approximate solution given by the averaged problem.

Theorem 2

With the previous notations, the errors in the approximate solution satisfy the following upper bounds:

$$\begin{aligned} \begin{aligned} \left| \delta _1(t) \right| {\,\le \! \bullet \,}\frac{{\varepsilon }^{1/3}}{\sqrt{{\mathrm N }_{\varepsilon }} }, \quad \left| \delta _i(t) \right| {\,\le \! \bullet \,}\frac{{\varepsilon }^{1/3}}{{\mathrm N }_{\varepsilon }^{2} } \quad i = 2, \ldots 6,\\ \quad \text{ for } \quad \left| t \right| \le \min \left( {{\mathcal {T}} }, {{\mathcal {T}} }_1\right) \quad \text{ and } \quad {{\mathcal {T}} }= 2\pi \sqrt{{\mathrm N }_{\varepsilon }^{3}}. \end{aligned} \end{aligned}$$

In the following reasonings, it is assumed that ${{{\mathcal {T}} }\le {{\mathcal {T}} }_1}$. First of all, in the limit case given by ${{\mathrm N }_{{\varepsilon }}= {\varepsilon }^{-1/3}}$, that is, ${\varDelta = 1}$ and ${\rho {\, =\!\bullet \,}\sqrt{{\varepsilon }}}$, Theorem 2 ensures that, up to a finite time in ${{\mathcal {O}}} (1/\sqrt{{\varepsilon }})$, the approximate solution given by the averaged problem remains inside a neighborhood of order ${{\mathcal {O}}} (\sqrt{{\varepsilon }})$ of the solution obtained in the synodic reference frame. Hence, we obtain the results for which the particle is considered distant enough from the planet.

The other limit case, that is, for ${{\mathrm N }_{{\varepsilon }} \simeq 1}$, the particle can approach the edge of the Hill’s sphere while the distance to the resonance can reach the order ${{\mathcal {O}}} ({\varepsilon }^{1/3})$. Even though the gravitational influence of the planet is not dominant, it can be strong enough with respect to the one of the Sun. Hence, we can only ensure that the accuracy of the approximate solution will not exceed a quantity of order ${{\mathcal {O}}} ({\varepsilon }^{1/3})$ for one or few periods of revolution of the planet. In such a case, the solution of the averaged problem might not be reliable in order to approach the one obtained in the synodic reference frame.

By increasing ${{\mathrm N }_{\varepsilon }>1}$, the minimal mutual distance moves away from the Hill’s sphere, the gravitational effect of the planet becomes weaker with respect to the one of the Sun, and the upper bound on the distance to the mean-motion resonance decreases as ${\rho {\, =\!\bullet \,}\frac{{\varepsilon }^{1/3}}{\sqrt{{\mathrm N }_{{\varepsilon }}}}}$. Thus, the approximate solution becomes more accurate with an upper bound on the error that decreases as $1/\sqrt{{\mathrm N }_{{\varepsilon }}}$ for the resonant angle $\theta$ and ${1/{\mathrm N }_{{\varepsilon }}^{2}}$ for the other variables, and a time of stability that increases as ${\sqrt{{\mathrm N }_{{\varepsilon }}^3}}$. Consequently, multiplying by a factor 5 the minimal mutual distance divides the errors by a factor $\sqrt{5}\simeq 2$ and 25, respectively, on $\theta$ and the other variables, and multiplies the time of stability by a factor $5^{3/2}\simeq 10$.

In a more practical way, for a given number ${n>0}$ of revolutions of the planet, with ${n \le {{\mathcal {O}}} (1/\sqrt{{\varepsilon }})}$, this result provides a domain of initial conditions such that the approximate solution given by the averaged problem is reliable in order to approximate the one obtained in the synodic reference frame. The errors in the approximate solution being, respectively, ${{\varepsilon }^{1/3}n^{-1/3}}$ in $\theta$ and ${{\varepsilon }^{1/3}n^{-4/3}}$ in the other variables, the smaller the planet mass ratio is, the greater the accuracy would be.

3.4 Discussion

The proofs of Lemma 1, Theorems 1 and 2 are given in the Appendix A.

The key ingredient of the proof of Lemma 1 is our definition of the collisionless domains ${{\mathfrak {D}}} _\kappa$ given in terms of heliocentric coordinates instead of resonant variables in order to exclude a neighborhood of the collision manifolds. Since the Poincaré complex variables prevent singularities associated with the eccentricity or inclination equals to zero, the transformation $\varUpsilon$ is analytic and can be bounded independently to ${\varepsilon }$, $\rho$ and $\varDelta$. Hence, the estimates on $H_{\mathrm K }$, $H_{\mathrm P }$ and $\overline{H} _{\mathrm P }$ are deduced directly from ${{\mathcal {H}} }_{\mathrm K }$ and ${{\mathcal {H}} }_{\mathrm P }$.

The proof of Theorem 1 has two parts. We first characterize the conditions that allow to ensure that the transformation of averaging $\varUpsilon$ is close to identity and maps the domain ${{\mathfrak {D}}} _{3/2}$ in the domain ${{\mathfrak {D}}} _{2}$ inside which the estimates are computed in Lemma 1. In the second part, we estimate the remainder $H_*$, Eq. (8), and its associated vector field by using the Taylor expansions at zero and first order combined with the estimates of Lemma 1.

Finally, Theorem 2 is a direct application of the classical strategy to prove stability over finite times (see [2]). For that purpose, we compare the vector field of the approximation given by the averaged problem with the one of a solution of the original problem. Assuming that the two solutions remain in a given neighborhood up to a time ${{\mathcal {T}} }$, we can choose ${{\mathcal {T}} }$ such that the order on the errors in the approximation is of the same order as the one of the transformation in “averaged” resonant variables.

The validity of the averaged problem was discussed by Robutel and Pousse [30], Robutel et al. [29] and Pousse et al. [28] in the framework of the 1:1 mean-motion resonance. Moreover, it is a key ingredient of the proof given by Niederman et al. [25] on the existence⁴ of the horseshoe-shaped trajectories followed by the two Saturn’s moons, Janus and Epimetheus. Since the semimajor axes of the two small bodies are almost the same, the issue generated by periodical close encounters is manifest. For instance, in [30] and [28], the authors highlight, through a frequency analysis, that, when an initial condition tends to the singularity of mutual collision, the approximation given by the averaged problem has fundamental frequencies that increase and tend to infinity. This phenomenon is inconsistent with the hypothesis of timescales separation required by the averaged problem. For that reason, an arbitrary criterion⁵ on the frequencies was introduced in [28] in order to localize the exclusion zone in the averaged phase space.

The work of Robutel et al. [29] provides a rigorous treatment of the averaging process for resonant dynamics in the planar planetary three-body problem. In the framework of quasi-circular co-orbital trajectories, it gives quantitative estimates on the remainder generated by the averaging process as well as its vector fields in order to state a theorem of stability over finite times. The proof uses a complex domain of holomorphy inside which estimates are computed through the Cauchy inequality. The results of the present paper are based on the same idea but applied in the general case (eccentric and spatial trajectories) of a generic p:q mean-motion resonance of the restricted three-body problem. Even though the technique of complexifying used in [29] is very efficient in the case of quasi-circular and quasi-planar orbits, the definition of the minimal mutual distance $\varDelta$ in terms of resonant variables is really difficult in the general case. That is why, we have chosen the direct computation of estimates by taking advantage of the form of $H_{\mathrm K }$, as well as the one of the ${{\mathcal {H}} }_{\mathrm P }$, that only depends on $\mathbf{r}$ and $\lambda '$.

4 The co-orbital motion in the circular-planar case

In this section, we focus on the co-orbital motion (1:1 mean-motion resonance) in the circular-planar case. More precisely, in the framework of the averaged problem, we intend to approach the six families of periodic orbits described in Sect. 2.2.2 (the short-periodic ${{\mathscr {L}}}_j^s$ and long-periodic ${{\mathscr {L}}}_j^l$ for $j=4,5$, the Lyapunov family ${{\mathscr {L}}}_3$, and the family f) as well as the dynamics observed in their neighborhood (the tadpole motion, the horseshoe motion, the quasi-satellite motion, and the “satellized” retrograde satellite motion), and identify the limit of validity of the corresponding solutions by applying Theorems 1 and 2 developed in Sect. 3.

First of all, we introduce the resonant variables and apply the properties stated in Sect. 2.3 to the case of the 1:1 mean-motion resonance. The resonant degree of freedom is described by the angle ${\theta = \lambda -\lambda '}$ and the action ${u=\sqrt{a} - 1}$ that measures the distance to the exact mean-motion resonance given by the semimajor axis $\tilde{a}=1$. In the circular-planar case, the secular variations of the orbits are provided by $({\tilde{x} }, x)$ for which ${K= \left| x \right| ^2}$ is a first integral of the averaged problem. For a fixed K, seen as a parameter, the reduced averaged Hamiltonian, denoted as follows

$$\begin{aligned} \overline{H} ^K(\theta ,u) = \overline{H} (\theta , u, {\tilde{x} }(K), x(K)), \end{aligned}$$

is integrable with one degree of freedom, and thus allows to understand the co-orbital dynamics through a phase portrait.

Instead of using K, we introduce the parameter $e_0$ such as

$$\begin{aligned} K = 1 - \sqrt{1- e_0^2}. \end{aligned}$$

Hence, $e_0$ defines the eccentricity of a trajectory that crosses the orbit of the planet, that is, at the exact mean-motion resonance $u=0$. Furthermore, since

$$\begin{aligned} e = \sqrt{1 - \left( 1 - \frac{K}{(1+u)}\right) ^2} = e_0\left( 1 + {{\mathcal {O}}} (u)\right) , \end{aligned}$$

$e_0$ approximates the eccentricity of the trajectories that belong to a given phase portrait. Notice that $e_0$ is also connected to the Jacobi constant through Eq. (7). More precisely, Theorem 1 and Eq. (11) imply that inside the domain of validity of the averaged problem, denoted ${{\mathfrak {D}}} _1(\varDelta )$ in the previous section, the Jacobi constant ${{\mathscr {C}}}(\mathbf{R} , \dot{\mathbf{R} }) = c$ reads:

$$\begin{aligned} \begin{aligned} c&= - 2\overline{H} + 2\sqrt{1- e_0^2} + {{\mathcal {O}}} \left( \sqrt{\frac{{\varepsilon }^3}{\varDelta ^5}}\right) . \end{aligned} \end{aligned}$$

Consequently, Eq. (10) and the estimates of Lemma 1 ensure the following relation between the two quantities:

$$\begin{aligned} \begin{aligned} c&= 1 + 2\sqrt{1- e_0^2} + {{\mathcal {O}}} \left( \frac{{\varepsilon }}{\varDelta }\right) \end{aligned} \end{aligned}$$

Before going further, we will see in the next section how a trajectory of a given phase portrait is related to the solutions of the averaged problem. Besides, in order to bridge a gap between the classical and the perturbative approaches, we will detail how a solution of the averaged problem describes the motion of a particle in the synodic reference frame. These correspondences were described in [28], but the relationship with the synodic reference frame needed to understand the dynamics were lacking.

4.1 Reading a phase portrait

For a given value of ${e_0\ge 0}$ and a given initial condition ${(\theta _i,u_i)}$, a trajectory that belongs to the corresponding phase portrait is generally⁶ a periodic solution but can also be an equilibrium of $\overline{H} ^{K(e_0)}$. If we denote its frequency $\nu$, a periodic trajectory can be written as

$$\begin{aligned} \begin{aligned} \theta (t)&= \theta _i + F_1(\nu t),\\ u(t)&= u_i + F_2(\nu t), \end{aligned} \end{aligned}$$

where the functions $F_j$ are $2\pi$-periodic such that ${F_j(0) = 0}$.

The dynamics of the angle ${\varpi =\arg (x)}$ is required in order to relate this trajectory to the solutions of the averaged problem. Since

$$\begin{aligned} \dot{\varpi }(t) = -\frac{\partial }{\partial K}\overline{H} ^{K(e_0)}(\theta (t),u(t)) \end{aligned}$$

is $2\pi /\nu$-periodic, there exists $F_3$, a $2\pi$-periodic function with mean zero and ${F_3(0)=0}$, such that for all ${\varpi _i\in {{\mathbb {T}}}}$,

$$\begin{aligned} \varpi (t) = \varpi _i + gt + F_3(\nu t), \end{aligned}$$

where

$$\begin{aligned} g = -\frac{\nu }{2\pi }\int _0^{2\pi /\nu } \frac{\partial }{\partial K}\overline{H} ^{K(e_0)}(\theta (t), u(t)){\mathrm d }t \end{aligned}$$

is the secular precession frequency of $\varpi$. In other words, a solution of the averaged problem that starts in ${(\theta _i, u_i, {\tilde{x} }_i, x_i)}$ with

$$\begin{aligned} e_0 = \sqrt{1 - \left( 1 - \left| x_i \right| ^2\right) ^2}, \quad \varpi _i = \arg (x_i) \end{aligned}$$

can generally be written as

$$\begin{aligned} \begin{aligned} \theta (t)&= \theta _i + F_1(\nu t),\\ u(t)&= u_i + F_2(\nu t), \\ \end{aligned}\,\,\,\,\, \begin{aligned} x(t)&= x_i\exp i(gt + F_3(\nu t)),\\ {\tilde{x} }(t)&= {\tilde{x} }_i/ \exp i(gt + F_3(\nu t)), \end{aligned} \end{aligned}$$

(12)

and a periodic trajectory of a given phase portrait generally corresponds to a set of quasi-periodic solutions parametrized by $\varpi _i\in {{\mathbb {T}}}$, whose fundamental frequencies are given by $\nu$ and g. The same reasoning applies for an equilibrium of $\overline{H} ^{K(e_0)}$: it corresponds to a set of periodic solutions of the averaged problem, parametrized by $\varpi _i\in {{\mathbb {T}}}$, and that can be written as

$$\begin{aligned} \begin{aligned} \theta (t)&= \theta _i,\\ u(t)&= u_i, \\ \end{aligned}\qquad \begin{aligned} x(t)&= x_i\exp i(gt),\\ {\tilde{x} }(t)&= {\tilde{x} }_i/ \exp i(gt). \end{aligned} \end{aligned}$$

(13)

Nevertheless, $\varpi$ being ignorable when the osculating ellipses are circles ($e_0= 0$), the solutions have the same features in the averaged problem as in the phase portrait of $\overline{H} ^{K=0}$.

Theorem 2 ensures that a given solution of the averaged problem that lies outside the Hill’s sphere of the planet, approximates for a finite time the motion of a particle that starts at the same initial condition. Hence, in the Poincaré complex variables, the motion of a particle that crosses $(\lambda _i, \varLambda _i, {\tilde{x} }_i, x_i)$ with $\lambda _i = \theta _i$ and $\varLambda _i = 1+ u_i$ at $t=0$, can be approximated for a finite time by Eq. (12) or Eq. (13) such that

$$\begin{aligned} (\lambda (t), \varLambda (t), {\tilde{x} }(t), x(t)) \end{aligned}$$

with

$$\begin{aligned} \lambda (t) = t + \theta (t), \quad \varLambda (t) = 1 + u(t). \end{aligned}$$

In terms of orbital elements, the approximation of the variations reads

$$\begin{aligned} \begin{array}{llllllllll} a(t) &{}=&{}1 + 2u_i &{} &{} &{}+&{} 2F_1(\nu t) + {{\mathcal {O}}} _2(u(t)),\\ e(t) &{}=&{} e_0 &{} &{} &{}+&{}e_0{{\mathcal {O}}} (u(t)), \\ \varpi (t) &{}=&{} \varpi _i &{}+ &{}gt &{}+ &{}F_3(\nu t)\\ M(t) &{}=&{} \theta _i - \varpi _i &{}+ &{}(1-g)t &{}+&{}[F_1-F_3](\nu t) \end{array} \end{aligned}$$

Hence, the semimajor axis and the eccentricity experience a slow oscillation of frequency $\nu$ and of amplitude of the order ${{\mathcal {O}}} (u)$, respectively, about 1 and $e_0$. The variations of the longitude of the periaster correspond to the composition of a secular drift of frequency g with an oscillation of frequency $\nu$. Finally, the motion of the mean longitude is given by a fast drift of frequency $1-g$ composed with a slow oscillation of frequency $\nu$.

We recall that the orbital elements are related to the polar coordinates $(\phi ,R) = (\arg (\mathbf{R} ), \left\| \mathbf{R} \right\| )$ of the synodic reference frame as follows:

$$\begin{aligned} \phi= & {} \theta + v-M,\nonumber \\ \quad R= & {} a(1 -e\cos E)\nonumber \\ v= & {} M + G_1(e, M), \quad E =M + G_2(e,M). \end{aligned}$$

(14)

The functions $G_j$, that satisfy $G_j(e, M) ={{\mathcal {O}}} (e)$, derive from the Kepler equation ${M = E-e\sin E}$ and the difference between the true and eccentric anomaly ${\tan (v/2) = \sqrt{\frac{1+e}{1-e}}\tan (E/2)}$.

In the synodic reference frame, the approximate motion of the particle can be written as

$$\begin{aligned} \phi (t)= & {} \theta _i + G_1(e_0, M(t)) + F_1(\nu t) \\&+ {{\mathcal {O}}} _2(u(t), e_0) \\ R(t)= & {} 1 + 2u_i - e_0\cos (M(t)) + 2F_2(\nu t)\\&+{{\mathcal {O}}} _2(u(t), e_0) \end{aligned}$$

with ${M(t) = \theta _i - \varpi _i + (1-g)t + [F_1-F_3](\nu t)}$. As a consequence, a periodic trajectory of a given phase portrait generally provides a quasi-periodic approximation of the motion whose fundamental frequencies are $1-g$ and $\nu$. More precisely, the motion is characterized by R that oscillates about 1 with an amplitude of the order ${{{\mathcal {O}}} (e_0)+ {{\mathcal {O}}} (u(t))}$, while $\phi$ is the sum of the periodic oscillation generated by $\theta (t)$ with the quasi-periodic oscillations generated by $G_1$ whose amplitude is of the order ${{\mathcal {O}}} (e_0)$. The same reasoning applies for an equilibrium of $\overline{H} ^{K(e_0)}$: it provides a set of periodic trajectories of frequency $1-g$ whose motion follows:

$$\begin{aligned} \begin{array}{lllllll} \phi (t) &{}=&{} \theta _i&{} + &{} G_1\left( e_0, M(t)\right) &{}+&{} {{\mathcal {O}}} _2(u_i, e_0), \\ R(t) &{} =&{} 1 + 2u_i&{} - &{} e_0\cos (M(t)) &{}+&{}{{\mathcal {O}}} _2(u_i, e_0), \end{array} \end{aligned}$$

with ${M(t) = \theta _i - \varpi _i + (1 - g)t}$. Hence, the motion is characterized by an oscillation of frequency $1-g$ around a guiding center located in $(\phi , R) = (\theta _i, 1 + {{\mathcal {O}}} (u_i))$ and whose amplitude is of the order ${{\mathcal {O}}} (e_0)$. Finally, for ${e_0=0}$, the motion of the particle is approximated by

$$\begin{aligned} \begin{array}{lllllll} \phi (t) &{}=&{} \theta _i &{}+ &{}F_1(\nu t),\\ R(t) &{}=&{} 1 + 2 u_i&{} + &{}2F_2(\nu t) &{}+&{} {{\mathcal {O}}} _2(u(t)), \end{array} \end{aligned}$$

(15)

and a trajectory of the phase portrait provides an equilibrium in the synodic reference frame or a periodic trajectory of frequency $\nu$ characterized by R that oscillates around 1 with an amplitude of the order ${{\mathcal {O}}} (u)$, that is, much smaller than 1.

4.2 Phase portraits for a Sun–Jupiter-like system (${\varepsilon }= 1/1000$)

Fig. 3

Phase portrait of a particle in quasi-circular motion ($e_0=0$) for a Sun–Jupiter-like system (${\varepsilon }= 1/1000$). The black dot denotes the singularity associated with the collision with Jupiter, while the brown circle, orange circle, red circle and the two blue diamonds correspond, respectively, to $L_1$, $L_2$, $L_3$ and $L_j$ for $j=4,5$. The separatrices that originate from $L_1$, $L_2$ and $L_3$, represented, respectively, by brown, orange and red thick curves, divide the phase portrait in six regions. Although they are very close to each other, the separatrices of $L_1$ do not coincide with those that originate from $L_2$. The beige domain, centered on the singularity, embodies the Hill’s sphere of the planet, inside which the averaged Hamiltonian does not reflect properly the dynamics of the restricted three-body problem. The upper and lower grey domains lay outside the co-orbital resonance ($\theta$ circulates). The blue and red trajectories are level curves associated with tadpole-shaped and horseshoe-shaped periodic orbits, respectively. More precisely, the blue level curves belong to the families ${{\mathscr {L}}}_4^l$ and ${{\mathscr {L}}}_5^l$. Finally, the green curves exhibit the elements associated with a minimal mutual distance $\varDelta = NR_{\mathrm H }$, while the grey lines depict $\{\left| u \right| = {\varepsilon }^{1/3}/\sqrt{N}\}$. For a given N, they bound the domain ${{\mathfrak {D}}} _1(\varDelta )$ inside which Theorem 2 is applied . (Color figure online)

Figures 3 and 4 display the phase portraits of the reduced averaged Hamiltonian $\overline{H} ^{K(e_0)}$ associated with five values of $e_0$. They are obtained for a Sun–Jupiter-like system (${{\varepsilon }=1/1000}$) by implementing the algorithm of Nesvorný et al. [24]. They are equivalent to the one showed in [22, 24] and extensively described in [28]. We will limit ourselves to present what will be useful to understand the trajectories described in Sect. 2.2.2 as well as to apply the Theorems stated in Sect. 3. Notice that the phase portraits are invariant by the symmetry with respect to the u-axis $(\theta ,u) \mapsto (2\pi -\theta , u)$.

In Fig. 3, $e_0$ is equal to zero and particle’s motion is quasi-circular. Let us mention that in this case the reduced averaged Hamiltonian reads

$$\begin{aligned}&\overline{H} ^{0}(\theta , u) = -\frac{1-{\varepsilon }}{2a} - u \\&\quad + {\varepsilon }\left( \cos \theta - \frac{1}{\sqrt{a^2 + 1 -2a\cos \theta }} \right) \end{aligned}$$

with ${a= (1+u)^2}$, which allows to recover some classical analytical properties (see, e.g., [12, 23]) that will be recalled in the following. Being the computations similar to the ones given in [30], the details are not given.

First of all, the black dot at ${\theta =u=0}$ embodies the collision with the planet, where $\overline{H} ^0$ is not defined. The phase portrait possesses five equilibria that correspond to the Lagrange fixed points $L_j$. The two elliptic equilibria located in $(\theta _j,u_j) = \left( (-1)^j\times 60\,^{\circ },0\right)$, stand for $L_4$ and $L_5$ while the hyperbolic ones in

$$\begin{aligned} \begin{aligned} (\theta _3,u_3)&= \left( 180\,^{\circ }, 1 - \frac{7}{6}{\varepsilon }+ {{\mathcal {O}}} ({\varepsilon }^2)\right) ,\\ (\theta _j, u_j)&=\left( 0\,^{\circ }, (-1)^j\times \left( \frac{{\varepsilon }}{6}\right) ^{1/3} + {{\mathcal {O}}} ({\varepsilon }^{2/3})\right) \end{aligned} \end{aligned}$$

approximate, respectively, $L_3$ and $L_j$ for ${j=1,2}$. With respect to the synodic reference frame (see Sect. 2.2.2), $L_4$ are $L_5$ are recovered at their exact location while $L_3$ is approximated within an accuracy ${{\mathcal {O}}} ({\varepsilon })$. For ${j=1,2}$, $L_j$ are found within an accuracy ${{\mathcal {O}}} ({\varepsilon }^{1/3})$ which highlights the weakness of the averaged problem at the edge of the Hill’s sphere.

Fig. 4

Phase portraits of the reduced Hamiltonian $\overline{H} ^{K(e_0)}$ for a Sun–Jupiter-like system (${\varepsilon }=1/1000$). They enlarge the area bounded by $\{\left| u \right| = \sqrt{{\varepsilon }}\}$ in Fig. 4. For a, b, c and d, $e_0$ is equal to 0.15, 0.5, 0.75 and 0.925, respectively. The black curves represent collision with the planet. The blue, sky blue and red trajectories are level curves associated with tadpole, quasi-satellite and horseshoe motion, respectively. The red circles, sky blue and blue diamonds are equilibria. More precisely, they correspond, respectively, to orbits of the families of periodic orbits ${{\mathscr {L}}}_3$, f and ${{\mathscr {L}}}^s_j$ for $j=4,5$. From each hyperbolic equilibrium emerges a separatrix (red thick curve) that divides tadpole motion and horseshoe motion. For d, the red diamond denotes an orbit that belong to the stable part of ${{\mathscr {L}}}_3$. Finally, the green curves exhibit the elements associated with a minimal mutual distance $\varDelta = NR_{\mathrm H }$, and bound the domain ${{\mathfrak {D}}} _1(\varDelta )$ inside which Theorem 2 is applied. (Color figure online)

The phase portrait is characterized by six regions. The beige domain centered at the singularity and bounded by the separatrices originating from $L_1$ and $L_2$ seems to be the prograde satellite-like motion. However, since the domain belongs to the Hill’s sphere of the planet, it lies inside the exclusion zone and its trajectories fall outside the scope of the averaged problem. Hence, the corresponding dynamics will not be analyzed in this work. The upper and lower grey domains, that lay above the separatrices of $L_1$ and $L_2$, illustrate the non-resonant motion for which $\theta$ circulates (clockwise in the upper region and anti-clockwise in the lower one). Considering that the width along the u-axis of the region located inside the separatrices is of the order ${{\mathcal {O}}} ({\varepsilon }^{1/3})$, Theorem 1 implies that the non-resonant regions escape from the domain of validity of the averaged problem.

The three remaining regions are the ones of the co-orbital dynamics, for which $\theta$ oscillates about a given value. These regions are divided by the separatrix that originates from $L_3$. The solutions that librate around $L_4$ and $L_5$ are tadpole-shaped characterized by $\left| \theta \right|$ that oscillates about $60\,^{\circ }$ such that ${\varTheta _{0}<\left| \theta \right| <180\,^{\circ }}$ with

$$\begin{aligned} {\varTheta _{0} = 2\arcsin ((\sqrt{2}-1)/2) + {{\mathcal {O}}} ({\varepsilon })\simeq 23.9\,^{\circ }}, \end{aligned}$$

and u that oscillates around zero with an amplitude that can reach ${{\mathcal {O}}} (\sqrt{{\varepsilon }})$. According to Sect. 4.1, these trajectories are periodic and possess the same features as the ones of the long-periodic families ${{\mathscr {L}}}_4^l$ and ${{\mathscr {L}}}_5^l$. Outside the separatrix, the trajectories encompass $L_3$, $L_4$ and $L_5$, i.e., they are characterized by $\theta$ and u that oscillate, respectively, about $180\,^{\circ }$ and 0, with large amplitudes. More precisely, $\theta$ and u undergo large variations such that ${\theta \in [\varTheta _{1}, 2\pi - \varTheta _{1}]}$ with

$$\begin{aligned}{0<{{\mathcal {O}}} ({\varepsilon }^{1/3})<\varTheta _{1}< \varTheta _{0}}\end{aligned}$$

and ${\left| u \right| \le U_1}$ with ${{{\mathcal {O}}} (\sqrt{{\varepsilon }})<U_{1}< {{\mathcal {O}}} ({\varepsilon }^{1/3})}$. These solutions approximate periodic horseshoe-shaped trajectories (see, e.g., the study of Barrabés and Ollé [3] that focuses on these solutions).

With respect to Fig. 3, the phase portraits of Fig. 4a–d, respectively, associated with $e_0=0.15$, 0.5, 0.75, 0.925, enlarge the area bounded by $\left| u \right| = \sqrt{{\varepsilon }}\simeq 0.31$.

For $e_0>0$, the location of the singularities evolves: the origin becomes a regular point surrounded by a set of singular points that describes a curve. For small $e_0$ (e.g., Fig. 4a), a new domain of co-orbital motion appears inside the collision curve. It is centered on an elliptic equilibrium point located close to the origin. According to Sect. 2.2.2 and Sect. 4.1, the elliptic equilibrium point approximates a periodic orbit of the family f. Hence, the periodic trajectories that librate around, provide quasi-periodic approximations of quasi-satellite orbits. Outside the collision curve, the topology does not change with respect to the one depicted in Fig. 3 outside the Hill’s sphere: two elliptic equilibria close to $L_4$’s and $L_5$’s locations and a separatrix emerging from a hyperbolic equilibrium close to $L_3$ that divides the regions of tadpole and horseshoe motions. According to Sect. 4.1, the equilibria of the phase portraits approximate periodic trajectories whose guiding center are located, respectively, close to $L_3$, $L_4$ and $L_5$. Hence, the elliptic equilibria belong to ${{\mathscr {L}}}_4^s$ and ${{\mathscr {L}}}_5^s$ while the hyperbolic one corresponds to a trajectory of ${{\mathscr {L}}}_3$.

For higher values of $e_0$ (e.g., Fig. 4b–c), the size of the quasi-satellite domain increases while one of the tadpole domains shrinks when the two elliptic equilibria are getting closer to the hyperbolic one.

The evolution of the two elliptic equilibria illustrates the shift of the guiding center of ${{\mathscr {L}}}_4^s$ and ${{\mathscr {L}}}_5^s$ toward $L_3$ described in Sect. 2.2.2.

Finally, for very high $e_0$ (e.g. Fig. 4d), the tadpole domains vanished and remains a domain characterized by trajectories that librate around an elliptic equilibrium that belongs to ${{\mathscr {L}}}_3$. This bifurcation of ${{\mathscr {L}}}_3$ occurs for $e_0\simeq 0.917$, when the short-periodic families ${{\mathscr {L}}}_j^s$ merge with ${{\mathscr {L}}}_3$.

For a given minimal mutual distance $\varDelta = NR_{\mathrm H }$ with $1\le N \le {\varepsilon }^{-1/3}$ and $R_{\mathrm H }= \left( \frac{{\varepsilon }}{3}\right) ^{1/3}$ that denotes the Hill’s radius of the planet, we recall that the domain ${{\mathfrak {D}}} _1(\varDelta )$ introduces in Sect. 3.3 is defined by the resonant variables for which the distance between the planet and the particle is larger than $NR_{\mathrm H }$, and $\left| u \right|$ which is bounded by a quantity $\rho {\, =\!\bullet \,}\frac{{\varepsilon }^{1/3}}{\sqrt{N}}$. The grey lines and green curves that lay over the phase portraits approximate the boundaries of ${{\mathfrak {D}}} _1(\varDelta )$ for several value of $N=1,3,5,10$. The grey lines correspond to $\{\left| u \right| = \frac{{\varepsilon }^{1/3}}{\sqrt{N}}\}$ while the green curves exhibit the elements $(\theta , u, e(e_0,u))$ for which the minimal mutual distance is equal to $\varDelta = N R_{\mathrm H }$. They are computed by resolving the following equation:

$$\begin{aligned} \min _{M\in {{\mathbb {T}}}}(R^2 + 1 -2R\cos \phi )_{(\theta , u, e(e_0,u), M)}= N^2 R_{\mathrm H }^2. \end{aligned}$$

with the help of Eq. (14).

In Figs. 3 and 4, the exclusion zone of the averaged problem is depicted by the small areas centered on the collision curves and bounded by the continuous green curves associated with the minimal mutual distance $\varDelta =R_{\mathrm H }$. They show that, contrarily to the tadpole motion, some solutions in quasi-satellite and horsehoe motion intersects the Hill’s sphere and fall outside the scope of the averaged Hamiltonian. More generally, the phase portraits also show that, for a given minimal mutual distance ${\varDelta = N R_{\mathrm H }}$, a co-orbital solution which starts inside the area ${\{\left| u \right| \le \frac{{\varepsilon }^{1/3}}{\sqrt{N}}\}}$ can cross the sphere defined by ${\varDelta = N R_{\mathrm H }}$ and thus escape from the domain ${{\mathfrak {D}}} _1(\varDelta )$ inside which Theorems 1 and 2 are applied. However, a co-orbital solution which starts in the neighborhood of the section ${\{u = 0\}}$ at a given minimal mutual distance $\varDelta$, does not experience closest encounters with the Jupiter and remains inside ${{\mathfrak {D}}} _1(\varDelta )$. As a consequence, the section $\{u=0\}$ provides a convenient way to discuss about the validity and the time of stability of the solutions of the averaged problem without caring about times of escape from ${{\mathfrak {D}}} _1(\varDelta )$. This study is realized in the following section.

4.3 A “map” of the co-orbital motion in the circular-planar case

Fig. 5

“Map” of the co-orbital motion defined by the section $\{u=0\}$. The black and red thick curves stand, respectively, for the singularity of collision and the crossing of the separatrices that originate from ${{\mathscr {L}}}_3$ (red curve). They divide the map in three regions. The sky blue and blue regions correspond to the quasi-satellite and the tadpole motion. They are centered, respectively, on the family f (sky blue curve) and the short periodic families ${{\mathscr {L}}}_j^s$ (blue curves). The horseshoe region is represented in red. The dashed line is associated with the quasi-circular motion $(e_i=0)$ for which the tadpole and horseshoe solution correspond to periodic trajectories in the synodic reference frame. (Color figure online)

Fig. 6

(Left panel) Same figure as Fig. 5. The dashed green curves correspond to the element $(\theta _i,e_i)$ for which the minimal mutual distance $\varDelta$ is equal to ${\mathrm N }_{\varepsilon }R_{\mathrm H }$ where $R_{\mathrm H }$ denotes the Hill’s radius. The grey lines correspond to the initial condition for which the trajectory crosses the orbit of Mars and Saturn. (Right panel) Enlargement in the neighborhood of the collision curve

First of all, we summarize the situation. Six families of periodic orbits (f, ${{\mathscr {L}}}_3$, ${{\mathscr {L}}}_j^s$ and ${{\mathscr {L}}}_j^l$) and three types of trajectories (tadpole, horseshoe and quasi-satellite motion) described in Sect. 2.2.2 have been recovered in the averaged problem close to the exact mean-motion resonance $u=0$. Notice that the domain of “satellized” retrograde satellite mentioned in Sect. 2.2.2 is missing since it is located in the neighborhood of the family f that belongs to the Hill’s sphere (see [28] for more details).

Each domain of co-orbital motion extends quasi-symmetrically with respect to the exact mean-motion resonance $u=0$ and is neatly defined by the collision curves or the separatrices that originate from the hyperbolic equilibria associated with ${{\mathscr {L}}}_3$. In this section, we construct a “map” of the co-orbital motion in the circular-case, that is, a representation of the section $\{u=0\}$ which can be used in order to discuss about the stability of the solutions as well as to compute co-orbital trajectories in the synodic reference frame. Two parameters are required to identify a solution of the averaged problem that belongs to the section $\{u=0\}$: the resonant angle $\theta _i$ and the eccentricity of the orbit $e_i$, (we recall that $e_i = e_0$ when $u=0$). Hence, we compute the evolution of the cross sections of the boundaries of each domain (separatrix and collision curves) by varying the eccentricity $e_i$. To that end, we consider the following reduction of the reduced averaged Hamiltonian:

$$\begin{aligned} \overline{H} _0^{K(e_0)}(\theta , u) = -\frac{3}{2}u^2 + \overline{H} _P(\theta , 0, {\tilde{x} }(K), x(K)) \end{aligned}$$

which is derived from the Taylor expansions of $\overline{H} _{\mathrm P }$ and $H_{\mathrm K }$, respectively, at zero and second order in ${u=0}$. This reduction is reliable in the vicinity of the section ${\{u=0\}}$ and has the advantage to be independent of ${\varepsilon }$, under the following rescaling: ${{\varepsilon }^{-1}\overline{H} _0(\sqrt{{\varepsilon }}u, \theta , {\tilde{x} }, x)}$. Hence, a “map” of the section ${\{u=0\}}$ computed through $\overline{H} _0^{K(e_0)}$, is invariant under the variation of ${\varepsilon }$.

Figure 5 displays the map of the co-orbital motion in the circular-planar case. The black thick curves illustrate the collision with the planet. They can be approximated by $\left| \theta _i \right| = 2 e_i \times 180\,^{\circ }/\pi$ up to high eccentricities. They bound the sky blue region associated with the quasi-satellite motion. The red thick curves depict the crossings of the separatrices that originate from ${{\mathscr {L}}}_3$. It divides the blue and red regions of tadpole and horseshoe motion. Let us mention that for $e_i=0$, only two domains of co-orbital motion exist: $L_4$, $L_5$ and the long-periodic families ${{\mathscr {L}}}_4^l$ and ${{\mathscr {L}}}_5^l$ form the tadpole region while the other one corresponds to the periodic horseshoe-shaped trajectories. The left panel of Fig. 6 displays the map of the co-orbital motion with the elements $(\theta _i, e_i)$ for which the minimal mutual distance $\varDelta$ is equal to ${NR_{\mathrm H }}$, for a Sun–Jupiter-like system (${{\varepsilon }=1/1000}$). The two additional grey lines represent the elements $(\theta _i, e_i)$ for which the particle crosses the orbit of Mars and Saturn. Hence, they suggest the maximal value of eccentricity for which the solutions of the restricted three-body problem are reliable in order to describe the real motion in the Solar System. The right panel of Fig. 6 is an enlargement of the map on the region that surround the collision curve.

According to Theorems 1 and 2, for a given number ${1<N\le {\varepsilon }^{-1/3}}$, and a given type of co-orbital dynamics, we can define a set of elements $(\theta _i, e_i)$ which satisfy a mutual distance greater than $\varDelta = NR_{\mathrm H }$, and for which the time of stability of the solutions of the averaged problem is at least $\sqrt{N}^{3}$ revolutions of Jupiter. In the synodic reference frame, the couple $(\theta _i, e_i)$ provides a set of initial conditions, parametrized by $\varpi _i\in {{\mathbb {T}}}$ and that can be written as

$$\begin{aligned} \begin{aligned} \phi _i&= \theta _i + G_1(e_i, \theta _i - \varpi _i)\\ R_i&= 1 - e_i \cos \Big (\theta _i - \varpi _i + G_2(e_i, \theta _i - \varpi _i)\Big )\\ \dot{\mathbf{R} }_i&= \left( R_i - \frac{1}{\sqrt{1-e_i^2}}\right) \begin{pmatrix}\sin \phi _i\\ -\cos \phi _i \end{pmatrix}\\&\quad + \frac{e_i}{\sqrt{1-e_i^2}} \begin{pmatrix} \sin \varpi _i\\ -\cos \varpi _i \end{pmatrix} \end{aligned} \end{aligned}$$

(16)

Hence, Theorem 2 ensures that an initial condition, given by Eq. (16), provides a co-orbital trajectory of the same type, at least for a finite time. In other words, transitions to another co-orbital motion or escapes from the 1:1 mean-motion resonance cannot occur at least during a time ${{\mathcal {T}} }=2\pi \sqrt{N^3}$. For instance, for N equal to 3, 5 and 10, it ensures a time of stability corresponding approximately to 5, 10 and 30 revolutions of Jupiter, that is, more than 50, 125 and 350 years.

As mentioned at the end of the previous section, the quasi-satellite and the horseshoe domains intersect the exclusion zone of the averaged problem. More precisely, for high values of $e_i$, the quasi-satellite motion dominates the map and the size of the intersection between the quasi-satellite domain and the exclusion zone is small relatively to the whole domain. By decreasing $e_i$, since the quasi-satellite domain shrinks with the collision curve, the relative size of the intersection increases until a critical value for which the exclusion zone contains all the quasi-satellite orbits. In the case of a Sun–Jupiter-like system, this critical value occurs for $e_i \simeq 0.07$.

Notice that Pousse et al. [28] suggested, through a frequency analysis of the family f, a critical value of $e_i\simeq 0.18$ for the quasi-satellite orbits. This value was given by an arbitrary criterion for which a solution of the averaged problem is considered outside the exclusion zone, if the modulus of their fundamental frequencies $\nu$ and g are lower than $\dot{\lambda }'/4$, where $\dot{\lambda }'=1$ denotes the frequency of averaging. Theorem 1 provides a lower value of eccentricity and thus a larger domain of validity of the averaged Hamiltonian for the quasi-satellite motion. However, based on the results in [28], the quasi-satellite region that surround the Hill’s sphere is probably overlaped by secondary resonances, that is, the resonant structures generated by commensurabilities between frequencies $\nu$, g and $\dot{\lambda }'=1$, and especially between $\nu$ and $1-g$ due to the D’Alembert rules (see Sect. 2.3.2). In particular, it has been shown in this area (see, e.g., [28]) that the neighborhood of the family f is divided in three disjoint regions by two critical orbits of the family f associated with the commensurabilty $3\nu = 1-g$. As a consequence, a global study of the frequencies in the averaged problem will probably reveal the resonant structures that destabilizes the quasi-satellite region that surround the Hill’s sphere, and may also highlight some islands of quasi-satellite solutions for which the time of stability is larger than the one given by Theorem 2.

The horseshoe motion exists outside the exclusion zone for low and very high eccentricities. More precisely, by increasing $e_i$, the size of the intersection between the horseshoe domain and the exclusion zone increases until a critical value $e_i\simeq 0.4$ for which all the horseshoe-shaped trajectories cross the section $\{u=0\}$ inside the Hill’s sphere. Furthermore, there exists another critical value $e_i \simeq 0.6$ for which a part of the horseshoe domain goes outside the exclusion zone. Then, for increasing $e_i$, the relative size of the intersection between the horseshoe domain and the exclusion zone decreases.

Most of the solutions in horseshoe motion experiences closed encounters with Jupiter (less than 5 Hill’s radii), and thus have a relatively small time of stability according to Theorem 2. Similarly to the quasi-satellite region located at the edge of the Hill’s sphere, the horseshoe region is probably overlaped by secondary resonances which destabilize the domain. A global frequency analysis of the region may reveal these resonant structures.

4.4 Conclusions

In this paper, we showed that the averaged problem provides another approach in order to study some families of periodic orbits of the restricted three-body problem. More precisely, we proved that it is a valid approximation in a particular area of the phase space that focuses on mean-motion resonances. Through a rigorous treatment, we characterized the domain of validity of the averaged problem (Theorem 1) and proved that it is a reliable approximation as long as the considered trajectories lay outside the Hill’s sphere of the planet. A new result of stability over finite times has also been proved (Theorem 2). As a consequence, we provided a rigorous justification of the relevance of the averaged problem to study some specific solutions of the restricted three-body problem.

Our theoretical results allowed us to understand the co-orbital motion (1:1 mean-motion resonance), that is, the quasi-satellite, the tadpole and the horseshoe orbits, that comprise the family f, the short-periodic and long-periodic families that originate from $L_4$ and $L_5$, and the Lyapunov family associated with $L_3$. In particular, in the framework of the circular-planar case, we propose a method, illustrated by a “map” of the co-orbital motion, that takes advantage of the averaged problem in order to compute co-orbital trajectories in the synodic reference frame. The results are presented in the case of a Sun–Jupiter-like system, but the “map” of the co-orbital motion, plotted in the Fig. 5, is independent of the small parameter ${\varepsilon }$, that is, the mass ratio of the planet over the total masses of the system. Hence, only the elements for which the minimal mutual distance $\varDelta$ is equal to ${ NR_{\mathrm H }}$, must be computed in order to apply the method to a different Sun–planet system (or planet-moon system). For example, Fig. 7 displays the map of the co-orbital motion for a Sun-Earth like system (${\varepsilon }= 1/333333$). However, we recall that, since the accuracy of the averaged problem depends on ${\varepsilon }$, the larger ${\varepsilon }$ is, the less the map of Fig. 5 is reliable.

A practical application of our theoretical results interests the design of space missions. Let us consider a spacecraft affected by the gravitational forces of a Sun-Earth like system. The selected orbits are usually remarkable solutions in the synodic reference frame that is, the Lagrange fixed points and periodic or quasi-periodic trajectories, as well as their associated hyperbolic manifolds (when existing). However, except for the dynamics associated with $L_1$ and $L_2$, most of these solutions are located at a remote distance from the Earth, and thus the cost in terms of energy or time to reach them is usually not affordable. For instance, Fig. 7 shows that $L_3$, $L_4$, $L_5$, the short-periodic and long-periodic families and the Lyapunov family ${{\mathscr {L}}}_3$ lay at a distance larger than 40 Hill’s radii. Only the family f provides periodic orbits available at a lower distance, that is why it becomes an important topic for mission design, mainly in the aim to orbit small moons (e.g., the two Mars’s moons, Phobos and Deimos).

Our idea is the following: since the duration of a mission is limited, it is not necessary to target an equilibrium or a periodic solution in the synodic reference frame. With the help of our method, which characterizes the elliptic and hyperbolic dynamics of the co-orbital motion through the averaged problem as well as defines a time of stability of these solutions, it is easy to select an initial condition on the map of Fig. 7, that is located close enough to the Earth, and that satisfies a given co-orbital dynamics for the whole duration of the mission. For instance, for a 30-years mission, Theorem 2 ensures that a co-orbital solution, that is located outside 10 Hill’s radii of the Earth, will be stable at least during the time of the mission. As a consequence, the horseshoe, tadpole and quasi-satellite solutions become possible target trajectories.

Notice that co-orbital solutions that experience closest approaches with the Earth may also be stable for the considered time of the mission. For instance, in the case of planar and quasi-circular horseshoe orbits, Cors and Hall [7] provided a practical stability estimate (the order of magnitude of the time for which the trajectory remains qualitatively the same) which is much greater than the one given by Theorem 2. Hence, a complementary analyze could be a global numerical investigation of the time of stability of the co-orbital orbits that experience close approaches. A detailed study will be addressed in a forthcoming work.

Finally, we point out that the application of the averaged problem as presented here is not restricted to the co-orbital motion in the circular-planar case: it can also be applied to inclined co-orbital trajectories, or, more generally, to solutions associated with other mean-motion resonances. To this aim, a careful study of the averaged phase space must be realized.

Fig. 7

Map of the co-orbital motion for a Sun-Earth like system

Proofs

1.1 Remainders

We recall that the Hamiltonian flow at a time t, generated by an auxiliary function $h(\mathbf{{X} })$, satisfies the following property:

$$\begin{aligned} \frac{{\mathrm d }}{{\mathrm d }t}\left( g\circ \varPhi _t^h\right) = {{\mathcal {L}} }_hg \circ \varPhi _t^h \end{aligned}$$

(17)

where g is an auxiliary function. Thus, we have the following Taylor expansions:

$$\begin{aligned} g\circ \varPhi ^h_t&= g + \int _0^t {{\mathcal {L}} }_h g\circ \varPhi _s^h{\mathrm d }s, \end{aligned}$$

(18)

$$\begin{aligned} g\circ \varPhi ^h_t&= g + {{\mathcal {L}} }_hg + \int _0^t (1-s){{\mathcal {L}} }_h{{\mathcal {L}} }_h g\circ \varPhi _s^h{\mathrm d }s. \end{aligned}$$

(19)

1.2 Proof of Lemma 1

For given ${\rho {\,\bullet \! \le \,}1}$, ${\varDelta {\,\bullet \! \le \,}1}$, ${{\varepsilon }{\,\bullet \! \le \,}1}$ and ${\kappa >0}$, the domain ${{\mathfrak {D}}} _\kappa$ has been designed in order to exclude the collision manifold and make the perturbation $H_{\mathrm P }$ analytic. Hence, $H_{\mathrm P }$ is bounded on ${{\mathfrak {D}}} _\kappa$ as well as its partial derivatives with respect to $\theta$, u, ${\tilde{x} }$, x, ${\tilde{y}{}}$ or y for each order k lower or equal to an arbitrarily fixed ${n\ge 1}$. Their estimates are deduced from the following reasonings.

First of all, we recall the thresholds provided by the definition of ${{\mathfrak {D}}} _\kappa$:

$$\begin{aligned} \tilde{\varDelta }/\kappa {<}\left\| \mathbf{r} \circ \varUpsilon \right\| _{\kappa } {{\,\le \! \bullet \,}} 1, \, \varDelta /\kappa {\le } \left\| \mathbf{r} \circ \varUpsilon -\mathbf{r} ' \right\| _\kappa {{\,\le \! \bullet \,}} 1,\, \left\| \mathbf{r} ' \right\| _\kappa {\, =\!\bullet \,}1, \end{aligned}$$

where ${\tilde{\varDelta }={{\mathcal {O}}} (1)}$ since it is an arbitrarily fixed quantity that does not depend on ${\varepsilon }$, $\varDelta$ and $\rho$. For all order $k\le n$, the perturbation ${{\mathcal {H}} }_{\mathrm P }$ in heliocentric cartesian coordinates, Eq. (4), yields the following estimates on ${{\mathfrak {D}}} _\kappa$:

$$\begin{aligned} \left\| H_{\mathrm P } \right\| _\kappa {=} \left\| {{\mathcal {H}} }_{\mathrm P }\circ \varUpsilon \right\| _\kappa {{\,\le \! \bullet \,}} \frac{{\varepsilon }}{\varDelta }, \left\| \frac{\partial ^k{{\mathcal {H}} }_{\mathrm P }}{\partial \mathbf{r} ^k}\circ \varUpsilon \right\| _\kappa {{\,\le \! \bullet \,}} \frac{{\varepsilon }}{\varDelta ^{k+1}}.\nonumber \\ \end{aligned}$$

(20)

Since the transformation $\hat{\varUpsilon }$, that introduces the Poincaré complex variables, Eq. (5), is regular when eccentricity and inclination tend to zero, it does not have singularities. More precisely, it is an analytic transformation on ${{\mathfrak {D}}} _\kappa$ and, for all order $k\le n$, its derivatives can be bounded by a constant that does not depend on ${\varepsilon }$, $\rho$ and $\varDelta$. $\check{\varUpsilon }$, which introduces the resonant variables, Eq. (5), is an affine transformation that fulfills the same properties. As a consequence, $\varUpsilon$ is analytic and, for each order ${k\le n}$ and ${(W_i)_{i\le k} \in \{\theta ,u,{\tilde{x} },x, {\tilde{y}{}} ,y\}}$, the following threshold is satisfied:

$$\begin{aligned} \left\| \frac{\partial ^k(\mathbf{r} \circ \varUpsilon )}{\partial {W_1}\ldots \partial {W_k}} \right\| _{\kappa } {\,\le \! \bullet \,}1. \end{aligned}$$

(21)

Finally, for a given analytic function ${{\mathcal {F}} }(\mathbf{r} , \lambda ')$ and ${W\in \{\theta ,u,{\tilde{x} },x, {\tilde{y}{}} ,y\}}$, we recall the chain rule:

$$\begin{aligned} \frac{\partial {{\mathcal {F}} }\circ \varUpsilon }{\partial W} = \left( \frac{\partial {{\mathcal {F}} } }{\partial \mathbf{r} }\circ \varUpsilon \right) \bullet \frac{\partial (\mathbf{r} \circ \varUpsilon ) }{\partial W}. \end{aligned}$$

(22)

The bounds on the partial derivatives of $H_{\mathrm P }$ with respect to $\theta$, u, ${\tilde{x} }$, x, ${\tilde{y}{}}$ and y, and for all order $k\le n$ are deduced from the combination of the chain rule, Eq. (22), with the thresholds given by Eqs. (20) and  (21).

Since ${\left\| \overline{H} _{\mathrm P } \right\| _\kappa \le \left\| H_{\mathrm P } \right\| _\kappa }$, the results on the averaged perturbation is a direct consequence of the previous development.

On the domain ${{\mathfrak {D}}} _2$, $H_{\mathrm K }$ is analytic, is different from zero, and thus satisfies $\left\| H_{\mathrm K } \right\| _2 {\, =\!\bullet \,}1$ while, for each order k lower or equal to an arbitrarily fixed $n\ge 1$, its derivatives are bounded. More precisely,

$$\begin{aligned}&\left| H'_{\mathrm K } \right| = \frac{3pq^{-1}\sqrt{\tilde{a}}}{\left| \sqrt{\tilde{a}}+u \right| ^3}\left| u \right| \left| 1 + \sqrt{\tilde{a}}u + \frac{u^2}{3\sqrt{\tilde{a}}} \right| , \quad \\&\left| H''_K \right| = \frac{-3}{\left| \sqrt{\tilde{a}}+u \right| ^4} \end{aligned}$$

imply that $\left\| H'_{\mathrm K } \right\| _{2}{\,\le \! \bullet \,}\rho$ and $\left\| H''_{\mathrm K } \right\| _{2}{\,\le \! \bullet \,}1$.

1.3 Proof of Theorem 1

First of all, we recall some results about the construction of the transformation of averaging: ${\overline{\varUpsilon }=\varPhi _1^S}$ with S that reads:

$$\begin{aligned} \begin{aligned}&S(\theta , u, {\tilde{x} },x, {\tilde{y}{}} ,y,\lambda ') \\&\quad = \frac{1}{2\pi } \int _0^{2\pi } s (H_{\mathrm P }- \overline{H} _{\mathrm P })_{(\theta , u, {\tilde{x} },x, {\tilde{y}{}} ,y,\lambda ' + s)} {\mathrm d }s, \end{aligned} \end{aligned}$$

(23)

in order to satisfy the following property:

$$\begin{aligned} {{\mathcal {L}} }_S\varXi = -\frac{\partial S }{\partial \lambda '} = \overline{H} _{\mathrm P }- H_{\mathrm P }. \end{aligned}$$

(24)

Under these conditions, the remainder of the averaging process reads:

$$\begin{aligned} H_*= & {} (\exp {{\mathcal {L}} }_S - {{\mathrm I }{\mathrm d }})(H_{\mathrm K }+ H_{\mathrm P }) \nonumber \\&+ (\exp {{\mathcal {L}} }_S - {{\mathcal {L}} }_S - {\mathrm I }{\mathrm d })\varXi . \end{aligned}$$

(25)

Most of the estimates required for the proof are computed with the Taylor expansion at zero order, Eq. (18). More precisely, if we assume that there exists ${\kappa <2}$ such that ${\overline{\varUpsilon }({{\mathfrak {D}}} _\kappa )\subset {{\mathfrak {D}}} _{2}}$, then for a given function g that depends on the variables ${(\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y, \lambda ')}$, the following thresholds are ensured:

$$\begin{aligned}&\left\| g\circ \overline{\varUpsilon }- g \right\| _\kappa {\,\le \! \bullet \,}\left\| \frac{\partial S }{\partial W} \right\| _{2} \left\| \frac{\partial g }{\partial W} \right\| _{2} \\&\quad \text{ for } W\in \{\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y\}. \end{aligned}$$

For each order k lower or equal to an arbitrarily fixed ${n\ge 1}$ and ${(W_i)_{i\le k}\in \{\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y\}}$, we point out that Eq. (23) and Lemma 1 provide the following thresholds on the partial derivatives of S:

$$\begin{aligned} \left\| \frac{\partial ^k S}{\partial W_1\ldots \partial W_k} \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^{k+1}}. \end{aligned}$$

(26)

Hence, in ${{\mathfrak {D}}} _\kappa$ and for ${W\in \{\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y\}}$, we have the following:

$$\begin{aligned} \begin{aligned} \left\| \mathbf{r} \circ \overline{\varUpsilon }- \mathbf{r} ' \right\| _\kappa&\ge \left\| \mathbf{r} - \mathbf{r} ' \right\| _\kappa - \left\| {{\mathcal {L}} }_S(\mathbf{r} \circ \varUpsilon ) \right\| _{2}\\ \left\| \mathbf{r} \circ \overline{\varUpsilon } \right\| _\kappa&\ge \left\| \mathbf{r} \right\| _\kappa - \left\| {{\mathcal {L}} }_S(\mathbf{r} \circ \varUpsilon ) \right\| _{2}\\ \left\| W\circ \overline{\varUpsilon } \right\| _{\kappa }&\le \left\| W \right\| _\kappa + \left\| {{\mathcal {L}} }_S W \right\| _{2} \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \left\| {{\mathcal {L}} }_S(\mathbf{r} \circ \varUpsilon ) \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^2}, \quad \left\| {{\mathcal {L}} }_S W \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^2}. \end{aligned}$$

As a consequence, for ${{\varepsilon }{\,\bullet \! \le \,}\rho \varDelta ^2}$ and ${{\varepsilon }{\,\bullet \! \le \,}\varDelta ^3}$ with ${\varepsilon }$, $\rho$ and $\varDelta$ small enough, we can choose $\kappa = 3/2$ such that the symplectic transformation of averaging satisfies ${\overline{\varUpsilon }({{\mathfrak {D}}} _{\kappa })\subset {{\mathfrak {D}}} _{2}}$ and is close to identity such that

$$\begin{aligned} \left\| W\circ \overline{\varUpsilon }- W \right\| _{{3/2}} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^2}, \quad \left\| \frac{\partial \overline{\varUpsilon } }{\partial W} \right\| _{3/2} {\,\le \! \bullet \,}1 \end{aligned}$$

(27)

for ${W \in \{\theta , u, {\tilde{x} }, x, {\tilde{y}{}} , y\}}$.

It remains to prove the estimates on the remainder of the averaging process. The Taylor expansions at zero and first order, Eqs. (18–19), combined with the condition satisfied by S, Eq. (24), ensure that the remainder $H_*$, Eq. (25), can be written as

$$\begin{aligned} \begin{aligned} H_*&= \int _0^1 {{\mathcal {L}} }_SH_{\mathrm K }\circ \varPhi _s^S{\mathrm d }s + \int _0^1 s{{\mathcal {L}} }_SH_{\mathrm P }\circ \varPhi _s^S{\mathrm d }s \\&\quad + \int _0^1(1-s){{\mathcal {L}} }_S\overline{H} _{\mathrm P }\circ \varPhi _s^S{\mathrm d }s . \end{aligned} \end{aligned}$$

As a consequence, the thresholds given by Eq. (26) and Lemma 1 provide the following upper bound on the remainder:

$$\begin{aligned} \left\| H_* \right\| _{3/2} {\,\le \! \bullet \,}\left( \left\| {{\mathcal {L}} }_S H_{\mathrm K } \right\| _{2} + \left\| {{\mathcal {L}} }_S H_{\mathrm P } \right\| _{2} \right) \end{aligned}$$

with

$$\begin{aligned} \left\| {{\mathcal {L}} }_S H_{\mathrm K } \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }\rho }{\varDelta ^2}, \quad \left\| {{\mathcal {L}} }_S H_{\mathrm P } \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }^2}{\varDelta ^4}. \end{aligned}$$

The upper bound on the derivative of $H_*$ with respect to $\theta$, u, ${\tilde{x} }$, x, ${\tilde{y}{}}$ and y is deduced in the same way. For ${W\in \{\theta , u ,{\tilde{x} }, x, {\tilde{y}{}} , y\}}$, Lemma 1 and Eqs. (26–27) provide the following estimates:

$$\begin{aligned} \left\| \frac{\partial H_* }{\partial W} \right\| _{3/2} {\,\le \! \bullet \,}\left( \left\| \frac{\partial {{\mathcal {L}} }_S H_{\mathrm K } }{\partial W} \right\| _{2} + \left\| \frac{\partial {{\mathcal {L}} }_S H_{\mathrm P } }{\partial W} \right\| _{2} \right) \end{aligned}$$

with

$$\begin{aligned} \begin{aligned}&\left\| \frac{\partial {{\mathcal {L}} }_SH_{\mathrm P } }{\partial W} \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }^2}{\varDelta ^5}, \quad \left\| \frac{\partial {{\mathcal {L}} }_SH_{\mathrm K } }{\partial u} \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^2}, \quad \text{ and } \quad \\&\left\| \frac{\partial {{\mathcal {L}} }_SH_{\mathrm K } }{\partial W} \right\| _{2} {\,\le \! \bullet \,}\frac{{\varepsilon }\rho }{\varDelta ^3} \quad \text{ for } \quad W\in \{\theta , {\tilde{x} }, x, {\tilde{y}{}} , y \}. \end{aligned} \end{aligned}$$

1.4 Proof of Theorem 2

The proof follows the classical strategy described in [2]. The aim of the first part of the proof is to bound the Hamiltonian vector field linked to $H_*$ over the domain ${{\mathfrak {D}}} _{3/2}$. The second part comes from the size of the transformation of averaging $\overline{\varUpsilon }$ and the choice of a time ${{{\mathcal {T}} }>0}$ which gives terms of the same order in the upper bound on the error of approximation.

For a given initial condition ${\mathbf{{X} }_0{=}(\mathbf{{W} }_0, \lambda '_0, \varXi _0){\in }{{\mathfrak {D}}} _1}$ and a time of escape ${{{\mathcal {T}} }_1>0}$, we assume that the solution ${\mathop {\mathbf{{X} }}\limits _{\dot{}}}(t) = \left( {\mathop {{\mathrm X}}\limits _{\dot{}}}_i(t)\right) _{i\in {\{1,\ldots ,8\}}} = ({\mathop {\mathbf{{W} }}\limits _{\dot{}}}(t), \lambda '(t), {\mathop {\varXi }\limits _{\dot{}}}(t)$) governed by ${\varXi + \overline{H} }$, does not escape of ${{\mathfrak {D}}} _1$ for all ${\left| t \right| \le {{\mathcal {T}} }_{1}}$.

Hence, for given ${\varvec{\mu }= (\mu _i)_{i\in \{1,\ldots ,8\}}}$ that satisfies

$$\begin{aligned} 0< & {} \mu _i{\,\bullet \! \le \,}\varDelta \,\, \text{ for } i=1,\ldots , 8, \quad \text{ and } \quad \nonumber \\ 0< & {} \mu _2{\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^2}, \end{aligned}$$

(28)

we can ensure that the neighborhood

$$\begin{aligned} {{{\mathfrak {E}}}_{\varvec{\mu }}(t) = \left\{ \left\| {\mathop {{\mathrm X}_i}\limits _{\dot{}}}(t) - {\mathrm X}_i \right\| _{3/2} \le \mu _i \,\, \text{ for } i=1,\ldots , 8\right\} } \end{aligned}$$

belongs to ${{\mathfrak {D}}} _{3/2}$ for $\left| t \right| \le {{\mathcal {T}} }_{1}$.

For a given initial condition in ${\tilde{\mathbf{{X} }} }_0 = (\tilde{\mathbf{{W} }}_0, \lambda '_0, \tilde{\varXi }_0)\in {{\mathfrak {E}}}_{\varvec{\mu }}(0)$, ${{\tilde{\mathbf{{X} }} }(t) = (\tilde{\mathbf{{W} }}(t), \lambda '(t), \tilde{\varXi }(t))}$ denotes the solution at a time t generated by the flow of the original Hamiltonian ${\varXi + \overline{H} + H_*}$. We assume that there exists a time ${{\mathcal {T}} }>0$ such that ${\tilde{\mathbf{{X} }} }(t)$ belongs to the neighborhood ${{\mathfrak {E}}}_{\varvec{\mu }}(t)$ for ${\left| t \right| \le \min ({{\mathcal {T}} }, {{\mathcal {T}} }_1)}$.

We denote

$$\begin{aligned} {\mathbf{{W} }_*(t) = \left( {\mathrm W}_{*,i}(t)\right) _{i\in \{1,\ldots ,6\}} = {\tilde{\mathbf{{W} }} }(t) - {\mathop {\mathbf{{W} }}\limits _{\dot{}}}(t) } \end{aligned}$$

the “error” at a time t on the approximation given by the averaged problem with respect to the solution of the original one. The vector field of $\mathbf{{W} }_*(t)$, deduced from Eq. (17), can be written as $\dot{\mathbf{{W} }}_*(t) = \mathbf{{F} }_1(t) + \mathbf{{F} }_2(t) + \mathbf{{F} }_3(t)$ with ${\mathbf{{F} }_j(t) = ({\mathrm F }_{j,i}(t))_{i\in \{1,\ldots ,6\}}}$ and

$$\begin{aligned} \begin{aligned} \mathbf{{F} }_1(t)&= ({{\mathcal {L}} }_{H_*}\mathbf{{W} })({\tilde{\mathbf{{W} }} }(t), \lambda '(t)),\\ \mathbf{{F} }_2(t)&= ({{\mathcal {L}} }_{\overline{H} _{\mathrm P }}\mathbf{{W} })({\tilde{\mathbf{{W} }} }(t)) - ({{\mathcal {L}} }_{\overline{H} _{\mathrm P }}\mathbf{{W} })({\mathop {\mathbf{{W} }}\limits _{\dot{}}}(t)),\\ \mathbf{{F} }_3(t)&= ({{\mathcal {L}} }_{H_{\mathrm K }}\mathbf{{W} })({\tilde{\mathbf{{W} }} }(t)) - ({{\mathcal {L}} }_{H_{\mathrm K }}\mathbf{{W} })({\mathop {\mathbf{{W} }}\limits _{\dot{}}}(t)).\\ \end{aligned} \end{aligned}$$

$\mathbf{{F} }_1$ corresponds to the vector field of the remainder $H_*$ whose upper bounds of each coordinates have been computed in Theorem 1. $\mathbf{{F} }_2$ and $\mathbf{{F} }_3$ are derived from the difference between the two considered Hamiltonian flow. They have to be estimated. For that purpose, we apply the Taylor expansion at first order, Eq. (19), to

$$\begin{aligned} {\mathbf{{F} }_2(t) = \mathbf{{G} }\circ {{\mathcal {S}} }_1(t) - \mathbf{{G} }\circ {{\mathcal {S}} }_0(t)} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \mathbf{{G} }(\mathbf{{W} }) = ({{\mathcal {L}} }_{\overline{H} _{\mathrm P }}\mathbf{{W} })(\mathbf{{W} }),\quad {{\mathcal {S}} }_s(t) = {\tilde{\mathbf{{W} }} }(t) - s\mathbf{{W} }_*(t). \end{aligned} \end{aligned}$$

For $i\in \{1,\ldots ,6\}$, this provides the following threshold:

$$\begin{aligned} \left\| {\mathrm F }_{2,i}(t) \right\| _{3/2} \le \left( \left\| {\mathrm d }\mathbf{{G} } \right\| _{3/2} + \mu _i\left\| {\mathrm d }^2 \mathbf{{G} } \right\| _{3/2}\right) \left\| {\mathrm W}_{*,i}(t) \right\| _{3/2}. \end{aligned}$$

We deduce the following upper bounds from Lemma 1 and the conditions on $\varvec{\mu }$, Eq. (28),

$$\begin{aligned} \begin{aligned} \left\| {\mathrm F }_{2,i}(t) \right\| _{3/2}&{\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^3} \left\| {\mathrm W}_{*,i}(t) \right\| _{3/2}. \end{aligned} \end{aligned}$$

Finally, since $H_{\mathrm K }$ only depends on u, the condition on $\mu _2$, Eq. (28), provides the following upper bound:

$$\begin{aligned} \begin{aligned} \left\| {\mathrm F }_{3,1}(t) \right\| _{3/2} {\,\le \! \bullet \,}\frac{{\varepsilon }}{\varDelta ^2},\quad {\mathrm F }_{3,i}(t) = 0 \quad \text{ for } i=2,\ldots ,6\text{. } \quad \end{aligned} \end{aligned}$$

Hence, the upper bound on each coordinate of the vector field of $\mathbf{{W} }_*(t)$ can be written:

$$\begin{aligned} \left\| \dot{{\mathrm W}}_{*,i}(t) \right\| _{3/2} \le a\left\| {\mathrm W}_{*,i}(t) \right\| _{3/2} + b_i\\ \end{aligned}$$

with

$$\begin{aligned} a {\, =\!\bullet \,}\frac{{\varepsilon }}{\varDelta ^3}, \quad b_1 {\, =\!\bullet \,}\frac{{\varepsilon }}{\varDelta ^2}, \quad b_i {\, =\!\bullet \,}\frac{{\varepsilon }}{\varDelta ^2} \sqrt{\frac{{\varepsilon }}{\varDelta ^3}} \,\,\text{ for } i = 2,\ldots ,6\text{. } \end{aligned}$$

As a consequence, for a given ${d>0}$ such that

$$\begin{aligned} \left\| \dot{{\mathrm W}}_{*,i}(0) \right\| _1\le d<\mu _i, \quad \text{ and } \quad 0<t<{{\mathcal {T}} }, \end{aligned}$$

the error on the approximation are bounded by $\mu _i$ as

$$\begin{aligned} (d + b_it)\exp (at) \le \mu _i. \end{aligned}$$

(29)

From now on, we consider the initial condition ${\mathbf{{X} }_0\in {{\mathfrak {D}}} _1}$ in the (non-averaged) resonant variables. The properties on the transformation of averaging impose that there exists a ${{\tilde{\mathbf{{X} }} }_0\in {{\mathfrak {D}}} _{3/2}}$ such that $\left\| \mathbf{{W} }_0 - {\tilde{\mathbf{{W} }} }_0 \right\| {\,\le \! \bullet \,} \frac{{\varepsilon }}{\varDelta ^2}$. Hence, it imposes ${d{\, =\!\bullet \,}\frac{{\varepsilon }}{\varDelta ^2}}$ in order to get ${\tilde{\mathbf{{X} }} }_0$ in the neighborhood of the initial condition $\mathbf{{X} }_0$ in the “averaged” resonant variables. This choice on d fulfills the condition of Eq. (28) We can choose ${{{\mathcal {T}} }= 2\pi \sqrt{\frac{{\varepsilon }}{\varDelta ^3}}}$ in order to deal with terms of the same order in Eq. (29) which gives $\mu _i {\, =\!\bullet \,}\frac{{\varepsilon }}{\varDelta ^2}$ for i =2,...,6. Finally, this choice implies $\mu _1 {\, =\!\bullet \,}\sqrt{\frac{{\varepsilon }}{\varDelta }}$ which also fulfills Eq. (28).