Abstract
With increasing demand for rotor blades in engineering applications, improving the performance of such structures using morphing blades has received considerable attention. Resonant passive energy balancing (RPEB) is a relatively new concept introduced to minimize the required actuation energy. This study investigates RPEB in morphing helicopter blades with lag–twist coupling. The structure of a rotating blade with a moving mass at the tip is considered under aerodynamic loading. To this end, a three-degree-of-freedom (3DOF) reduced-order model is used to analyse and understand the complicated nonlinear aeroelastic behaviour of the structure. This model includes the pitch angle and lagging of the blade, along with the motion of the moving mass. First, the 3DOF model is simplified to a single-degree-of-freedom model for the pitch angle dynamics of the blade to examine the effect of important parameters on the pitch response. The results demonstrate that the coefficient of lag–twist coupling and the direction of aerodynamic moment on the blade are two parameters that play important roles in controlling the pitch angle, particularly the phase. Then, neglecting the aerodynamic forces, the 3DOF system is studied to investigate the sensitivity of its dynamics to changes in the parameters of the system. The results of the structural analysis can be used to tune the parameters of the blade in order to use the resonant energy of the structure and to reduce the required actuation force. A sensitivity analysis is then performed on the dynamics of the 3DOF model in the presence of aerodynamic forces to investigate the controllability of the amplitude and phase of the pitch angle. The results show that the bend–twist coupling and the distance between the aerodynamic centre and the rotation centre (representing the direction and magnitude of aerodynamic moments) play significant roles in determining the pitch dynamics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In many aerospace applications, it is required that the vehicle has a good performance in a broad range of conditions. For example, the minimum required power in helicopter rotors at various flight conditions is achieved from different twist distributions [1]. Inducing control on flexible aerostructures helps to optimize the aerodynamic loads and reduce the energy consumption in different flight conditions [2, 3]. In addition, energy exchange between different motions of rotor aerostructures such as flapping, lagging, and pitching is a property that has received attention for controlling such structures [4,5,6]. The shape-adapting capability of morphing aircraft gives the ability to control the performance of aerostructures. Indeed, morphing aircraft can be used not only to improve the performance of an aircraft in one specific flight condition and reduce the energy consumption, but also to broaden the range of good performance over different conditions. Ajaj et al. [4] presented a novel classification framework based on the functionality, operation, and the structural layout of morphing technology. A review of the morphing concept in wind turbine blades can be found in [5]. Vos et al. [7] introduced a new flight control mechanism employing piezoelectric bimorph bender actuators to apply control to an unmanned aerial vehicle with a deformable wing structure. The introduced piezoelectric flight control mechanism was applied to a morphing wing and the details of the design, modelling, and experiments were given in [8]. Fincham and Friswell [9] introduced an inner optimization strategy within the main aerodynamic optimization process to take the limitations of the possible morphing structure into account at the early stages of the design. Eguea et al. [10] exploited the genetic algorithm to find the optimum camber morphing winglet in order to minimize the fuel consumption of a business jet. The potential critical speed for a morphing wing with an active camber design was investigated by Zhang et al. [11] using a low-fidelity model. For this purpose, they also utilized both steady and unsteady aerodynamic models to develop an aeroelastic model for the structure under study.
The concept of bend–twist coupling in morphing structures to increase the controllability of flexible aerostructures has received considerable attention [12]. Bend–twist and extension-twist coupling were studied experimentally on a thin-walled composite beam [13]. It was shown by an analytical model [14] that, by using dynamic blade twist, the performance of a helicopter is enhanced and the power required for the rotor blade is reduced. Theoretical and experimental investigations on the bend–twist coupling concept in wind turbine blades were carried out in [15]. Gu et al. [16] utilized the twist morphing concept and designed a novel meta-material to increase the aerodynamic efficiency of a rotor blade by the passive twist generated by the bend–twist coupling. The designed meta-material was used to propose a concept design of a blade spar with a rectangular cross section to investigate the relation between the cell geometries of the core material and the bend–twist property of the spar.
The application of a lumped mass moving in the spanwise direction to absorb the vibrational energy and mitigate the oscillation of the helicopter rotor was investigated in [17,18,19]. They demonstrated that the stability of the helicopter rotor is influenced by the coupling of the flapwise oscillation and lagwise motion induced by the Coriolis forces. Kang et al. [20] carried out numerical and experimental analysis and demonstrated the improved stability of rotors resulting from the embedded chordwise absorbers. Combining the bend–twist concept with a movable mass at the tip of a morphing blade is a new concept that exploits the bending moment to generate the twist and control the aerodynamic performance of the structure. A morphing blade composed of a composite hingeless rotor blade and a moving lumped mass at the tip was studied by Amoozgar et al. [21]. The lumped mass is subjected to an actuation force and is allowed to move in the chordwise direction. The bending moment induced by the centrifugal force of the moving mass will generate a twist in the blade due to the bend–twist coupling.
In addition to tuning the structures and optimizing the parameters to increase the performance of aerial vehicles, passive energy balancing (PEB) is utilized to passively balance the energy between the aerostructure and the actuator and reduce the required actuation energy. Wang et al. [22] applied a new passive energy balancing mechanism using a spiral pulley to reduce the required actuation force in a morphing structure. Zhang et al. [23] introduced a negative stiffness mechanism for a passive energy balancing concept applied to a morphing wingtip with a linear actuator. Their target was to optimize the passive energy balancing design and minimize the energy consumption and the required actuation force.
A new extension of PEB is resonant passive energy balancing (RPEB). The mechanism of RPEB utilizes the resonant energy of the structure to provide a portion of the energy required to deflect the morphing structure. In this case, the energy can be gained in the vicinity of various resonances of the structure, depending on the properties and operating condition of the structure. These resonances can either be based on the natural frequencies of the blade and their sub- or super-harmonics, or an additional mechanism. However, in spite of the knowledge gained for PEB in morphing aircraft, this concept is still in its infancy. This study is a step forward in applying RPEB to an MDOF structure.
As described above, a recently introduced morphing concept uses a movable mass at the tip of the blade. In contrast to previous works on the dynamic of spanwise morphing beams [24, 25], this concept utilizes the bend–twist coupling in the blade to induce a twist angle from the centrifugal force applied to the moving mass. The moving mass is forced by an actuation mechanism to adjust the required amount of induced twist angle. The parameters of the structure and the moving mass are tuned so that the resonant oscillations are used to supply energy to actuate the moving mass. Hence, the RPEB concept can be used to reduce the actuation energy consumption [26].
This study investigates the application of the mechanism of RPEB in morphing blades with a moving mass at the tip. Indeed, the results shown in this study demonstrate how different parameters of a rotating blade affect the dynamic behaviour of the structure. Then, the controllability of the dynamics of rotor blades using bend–twist coupling and the aerodynamic moment is determined in the current study.
This study is focused on the investigation of RPEB for twist morphing helicopter blades, and a better understanding of the system results in a more efficient design. For instance, the nonlinear behaviour due to the structural nonlinearity of the blade and the nonlinear aerodynamic loading makes the prediction of the dynamics of the system complicated [27]. In addition, unwanted dynamical behaviour, such as quasi-periodic and chaotic responses, should be avoided in the design [28]. Therefore, analysing the nonlinear dynamics of the system is required. Thus, a morphing helicopter blade with an actuated moving mass at the tip is modelled using a three-degree-of-freedom (3DOF) discrete system. The pitch response and the lagging motion of the blade, in addition to the displacement of the moving mass, are the 3DOF in the model. The aerodynamic coefficients are estimated using experimental data [29,30,31,32]. A simplified single-degree-of-freedom (SDOF) model is used to demonstrate the effect of important parameters on the dynamics of the pitch response. The structural analysis is carried out on the parameters of the 3DOF model neglecting the effect of aerodynamic loading. The results of the structural analysis can be used to tune the parameters for desired purposes (e.g. locating resonant frequencies in the range of working rotating speed). The stability analysis of the 3DOF model is carried out and the controllability of the pitch response is discussed. Finally, a brief conclusion is provided.
2 Mathematical modelling
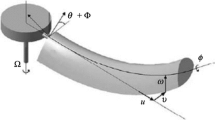
In this section, a reduced-order mathematical model of the structure is described. The schematic of the cross section of the main rotor blade of a helicopter is shown in Fig. 1. The movable mass \(m_2\) is assumed to be moving along the chord of the blade. That is, the flapwise bending moment induced by the centrifugal force of the movable mass is insignificant. Accordingly, there will not be any significant coupling between the flapwise bending moment induced by the movable mass and the blade twist angle. Hence, the structure of Fig. 1 is modelled by a 3DOF discrete system. The lag displacement \(x_1\) and the pitch angle \(\alpha \) of the blade are considered as two degrees of freedom of the reduced-order model of the blade, and the motion \(x_2\) of the moving mass \(m_2\) is considered as the third degree of freedom. In the figure, AC and RC denote, respectively, the aerodynamic centre and rotational centre of the aerofoil, and GC is the centre of gravity of the blade with mass of \(m_1\). l is the chord length of the aerofoil, and \(d_1\), \(d_2\), and \(d_\mathrm{ac}\) are, respectively, the distances of GC, the initial position of the moving mass, and AC with respect to RC. \(c_1\) and \(k_1\) are the damping coefficient and the stiffness of the blade in the lag direction. In fact, \(k_1\) is not really physical, but represents the lagwise bending stiffness of the beam. \(\kappa \) is the rotational (torsional) stiffness of the blade in the pitch angle direction. Aerodynamic force \(F_\mathrm{ac}\) is applied to the blade at the aerodynamic centre AC and the moving mass is excited by a harmonic force with amplitude \(f_\mathrm{m}\) and excitation frequency \(\omega _\mathrm{m}\). The aerodynamic moment at AC is neglected in this study. Note that this is a reasonable assumption because many helicopter blade sections are designed with zero coefficient of moment [33, 34]. \(c_2\), \(k_2\), and \(k_n\) are, respectively, the linear damping, linear stiffness, and nonlinear cubic stiffness through which the moving mass is connected to the blade. \(v_\mathrm{b}\) represents the velocity of the blade which is determined using the rotating velocity of the blade and the forward speed of helicopter as
where \(\omega _0\) denotes the rotating velocity of the main rotor, \(v_0\) is the translational velocity of the blade due to rotation and \(V_\mathrm{f}\) is the forward speed of helicopter.
2.1 Potential energy of bend–twist coupling deformation
Due to the bend–twist coupling introduced through the composite layup, the lagwise bending moment in the composite spar induces a twist angle in the spar. For the helicopter blade, a twist is induced in the spar due to the bending moment generated by the centrifugal force of the moving mass, as shown in Fig. 2. The distance of the moving mass from RC is a function of the rotating frequency \(\omega _0\), which in turn induces a periodic torsional moment.
where \(\beta \) is the angle between the direction of the centrifugal force of the moving mass and the longitudinal axis of the spar. The coordinate axes xyz are shown in Fig. 2. For the 3DOF discrete system, the second term on the right side of Eq. (2) is eliminated as there is no spatial variable z. The function \(\cos (\beta )=\frac{L}{\root \of {L^2+(d_2+x_2)^2}} \) is approximately 1 considering the dimensions of the blade. Therefore,
Then, the twist induced by bend–twist coupling is determined in the form
where \(T_\mathrm{b}\) is the torsional torque due to bend–twist coupling, D denotes the coefficient of bend–twist coupling, and \(\kappa \) and \(\alpha _\mathrm{bt}\) are the torsional stiffness and twist angle due to the bend–twist coupling, respectively. The potential energy \(U_\mathrm{bt}\) due to the bend–twist coupling is obtained as
2.2 Equations of motion: 3DOF model
To derive the equations of motion of the 3DOF system of Fig. 1, Lagrange’s equations are applied to the kinetic energy, potential energy, and non-conservative terms of the system. Displacements of \(m_1\) and \(m_2\) are determined with respect to RC as
where \(\hat{{\mathbf {i}}}\) and \(\hat{{\mathbf {j}}}\) are unit vectors in the x and y directions. Considering the velocity \(v_0\) of the tip of the rotating blade, the absolute velocities of \(m_1\) and \(m_2\) with respect to RC are obtained, respectively, as
Using the velocities \(\dot{{\mathbf {x}}}_{1_a}\) and \(\dot{{\mathbf {x}}}_{2_a}\), the kinetic energy of the system is written in the form
Using the potential \(U_\mathrm{bt}\) of Eq. (5) due to the bend–twist coupling of the blade, the potential energy and non-conservative terms of the 3DOF system are given, respectively, as
where \(\hat{{\mathbf {e}}}_{x_1}\), \(\hat{{\mathbf {e}}}_{x_2}\), and \(\hat{{\mathbf {e}}}_\alpha \) are, respectively, unit vectors in the directions of lagging motion \(x_1\), moving mass displacement \(x_2\), and the pitch angle \(\alpha \), and
\(F_\mathrm{L}\) and \(F_\mathrm{D}\) denote the aerodynamic lift and drag forces, respectively, given by
where \(c_\mathrm{L}\) and \(c_\mathrm{D}\) denote the lift and drag coefficients and \(\rho \) is the density of air. Applying Lagrange’s equations to the kinetic and potential energy, and non-conservative terms of the system, the equations of motion of the system can be derived as
Defining the dimensionless parameters as
the non-dimensional equations of motion of the 3DOF system are obtained as
where
and
The superscript * is removed for the sake of brevity in the subsequent discussions. The lift \(c_\mathrm{L} (\alpha )\) and drag \(c_\mathrm{D} (\alpha )\) coefficients are functions of the pitch angle of the blade. These functions are estimated according to the experimental data [29,30,31,32] of the Bo-105 blade for the lift and drag coefficients as
The coefficients \(A_1\), \(A_2\) and \(B_1\), \(B_2\), \(B_3\) are obtained by fitting a straight line and a quadratic curve to the experimental data for the lift and drag coefficients, respectively. Figure 3 shows the fitted curves to different experimental data for lift and drag coefficients. Table 2 gives the baseline coefficients for \(c_\mathrm{L}\) and \(c_\mathrm{D}\) in Eq. (17).
For reliable analysis of the dynamics of the system under study, the values of the non-dimensional parameters should be in a feasible range. Hence, a set of baseline values for the dimensional parameters of the Bo-105 blade is derived from real dimensions and experimental data and given in Table 1. \(\omega _\mathrm{ref}\) in Table 1 is the reference rotating speed of the helicopter in forward flight. These data are then used to estimate physically meaningful variations for the non-dimensional parameters of the system of Eq. (14). For example, from Table 1, \(\varOmega _{0_\mathrm{ref}} =\frac{\omega _\mathrm{ref}}{\omega _1}=1.5\) is obtained for the Bo-105 blade. Based on this, an approximate rotating frequency range of \(\varOmega _0 \approx 0 \sim 7\) is considered for the dynamic analysis of the structure to account for the variabilities of both the lagwise natural frequency and the blade rotating frequency of the aircraft. The baseline values of the non-dimensional parameters of the system are given in Table 2.
2.3 SDOF model
In the first step of this study, the dynamic response of a single-degree-of-freedom (SDOF) model of the morphing blade is investigated to examine the effect of important parameters on the dynamic behaviour of the pitch angle. To find the SDOF model, the lagwise motion of the blade is neglected from the equations of motion given by Eq. (14) and the motion of the moving mass is assumed to be harmonic. A linear dashpot with damping ratio \(\zeta _\alpha \) is added to the equation of motion to include the damping effect of blade lagging on the dynamics of the pitch angle. Hence, the equation of motion of the SDOF model is given as
where
Harmonic behaviour is assumed for the pitch angle. Thus
where \(\alpha _0\) and \(\alpha _i\) denote, respectively, the static deflection and the complex amplitude of the ith harmonic of the pitch angle. A frequency domain analysis method such as the incremental harmonic balance method (IHBM) or the complex averaging (CXA) technique can be used, along with numerical continuation to find the steady-state response of the pitch angle. In this section, CXA along with arc-length continuation is used to investigate the steady-state dynamics of the system of Eq. (18). The first five harmonics (\(\varOmega _0,\ldots ,5 \varOmega _0\)) are taken into account and the values given in Table 3 are used as the initial values of the parameters of Eq. (18).
The frequency-domain steady-state response of the SDOF model of the pitch angle for the initial values of Table 3
3 Results and discussion
In this section, the equations of motion of the structure under study are solved using different methods and the obtained results are discussed. To obtain the dynamic response of the system in this study, two different methods are used: direct integration (DI) using the ODE functions in MATLAB, and the complex averaging technique (CXA) [35] along with arc-length continuation. The former is used to find the response of the system in the time domain. However, the obtained response can be transformed into the frequency domain using methods such as the fast Fourier transformation (FFT). The CXA method, on the other hand, is used to find the steady-state dynamics in the frequency domain. Each method has its advantages and disadvantages. To find the time-domain dynamics of the system, either transient or steady state, direct integration (DI) is used. However, using DI is computationally expensive to obtain the steady-state response in the frequency domain, particularly for a wide range of frequencies. On the other hand, using the CXA technique reduces the computational cost significantly. The drawback of CXA is that it is very difficult to use for dynamical systems with high frequency content or non-periodic responses, such as those with chaotic responses.
3.1 SDOF analysis of RPEB
The steady-state frequency domain response of the system is given in Fig. 4 for the initial parameters given in Table 3. The values of other parameters of the SDOF model of Eq. (18) are given in Table 2. In the figure, \(\alpha _0\) is the static deflection, \(\alpha _i\) denotes the ith harmonic of the pitch angle, and \(|\alpha _i|\) and \(\phi _{\alpha _i}\) are, respectively, the amplitude and phase of \(\alpha _i\). The static deflection, amplitude–frequency diagram, and phase of the first three harmonics of the steady-state response of the pitch angle are given. The stability analysis on the analytical results obtained from the CXA method has been undertaken using Lyapunov’s First Theory of Stability. The red and blue colours in the figure denote the stable and unstable responses, respectively. A bifurcation analysis is carried out on the steady-state dynamic response of the system, and SN represents the saddle-node bifurcation. All of the phase values of the pitch angle in this study are calculated with respect to the aerodynamic force. The results show that the system responds with a hardening nonlinearity.
The effects of the variations of key parameters on the dynamics of the SDOF model of Eq. (18) are now investigated. The effect of variation in the parameter \(d_\mathrm{ac}\) on the dynamics of the pitch angle is shown in Fig. 5. The results illustrate that the blade behaves with a softening nonlinearity for \(d_\mathrm{ac}<0\), while altering \(d_\mathrm{ac}\) to positive values causes the nonlinearity of the system to change to hardening. This behaviour is due to the nonlinearity in the aerodynamic moment in Eq. (18). The sign of this nonlinear term is directly associated with the sign of \(d_\mathrm{ac}\), that is the direction of the aerodynamic moment. It is observed in Fig. 5b that changing the sign of \(d_\mathrm{ac}\) leads to a change in the sign of the static deflection. Indeed, the blade will pitch nose up and down, respectively, for positive and negative values of \(d_\mathrm{ac}\). According to the results, there exists an asymmetry in the static deflection of the pitch angle with respect to the value of \(d_\mathrm{ac}\). The reason is that, in the presence of \(x_2\), the aerodynamic force is not the only load applied to the system. Therefore, although the sign of the pitch angle changes with the sign of \(d_\mathrm{ac}\), the static pitch is not symmetric even for the case of zero bend–twist coupling. As expected, the vibration amplitude of the pitch response reduces when the magnitude of \(d_\mathrm{ac}\), and consequently aerodynamic moment, decreases. Figure 5d shows a shift in the phase of the steady-state response of the pitch angle due to changes in the value and sign of \(d_\mathrm{ac}\). The smaller phase shift takes place for changes in the magnitude of \(d_\mathrm{ac}\) and the larger shifts happen when the sign of \(d_\mathrm{ac}\) varies. Therefore, \(d_\mathrm{ac}\), or in other words, the value and sign of aerodynamic force/moment is a key parameter in determining the amplitude and phase of the pitch angle.
Figure 6 gives the results of the steady-state pitch oscillation in response to variations in the bend–twist coupling D, neglecting the effect of aerodynamic forces by setting \(d_\mathrm{ac}\) to zero. Figure 6a shows that the resonant amplitude of the pitch oscillations has a direct relation to the magnitude of D. The static deflection results in Fig. 6b show a similar behaviour as the deflection increases when the coupling D increases. Furthermore, Fig. 6b and c shows that both the static deflection and the amplitude of steady-state pitch dynamics are symmetric with respect to zero bend–twist coupling, \(D=0\). In other words, the magnitude of static deflection and the amplitudes of the pitch response for the same magnitude of coupling D but different signs (e.g. \(D=1\) and \(-1\)) are exactly the same. However, the direction of the static deflection varies when the sign of the coupling changes. Indeed, the blade will pitch nose up and down, respectively, for negative and positive values of D. The phase of the pitch response depends only on the sign of D and any change in the magnitude of coupling without altering its sign does not change the phase of the response, as shown in Fig. 6d. Hence, both the magnitude and sign of the bend–twist coupling D are important in determining the static deflection, and the amplitude and phase of the pitch response.
Figure 6 shows the pitch dynamics in the absence of aerodynamic loading. However, the aerodynamic forces and moments are vital for the dynamics of the blade and cannot be ignored. Figure 7 shows the effects of the aerodynamics with \(d_\mathrm{ac}=0.25\) on the dynamic behaviour of the pitch angle. It can be observed that the amplitude of vibration still varies by changing the coupling D. However, the sensitivity of the pitch oscillation amplitude to the variation of D has been significantly reduced. Also, including the aerodynamic forces removes the symmetry in the static pitch response, as shown in Fig. 7b. In this case, changing the bend–twist coupling from \(D=-1.5\) to \(D=1.5\) causes the static deflection to reduce, although the change in static deflection is not significant. The symmetry in the phase of the pitch response shown in Fig. 7c is not observed in this case. In fact, both the sign and magnitude of D will affect the phase of the pitch angle.
3.2 Structural analysis
In this section, the effects of important parameters of the 3DOF model of the structure of Fig. 1 on the dynamic behaviour are investigated. The main reason for this investigation is to show which structural parameters can be used for tuning the system according to desired purposes. To this end, the effect of aerodynamic loads is neglected, and the steady-state dynamics of the system is obtained in the frequency domain by applying the CXA technique with arc-length continuation to Eq. (14).
The effect of the natural frequency \(\varOmega _{t1}\) of the pitch angle on the dynamic pitch response is shown in Fig. 8. The results show that increasing \(\varOmega _{t1}\) reduces the resonant amplitudes of the dynamic pitch response at different resonant frequencies. Indeed, increasing the natural frequency of the pitch angle is equivalent to higher torsional rigidity, and this leads to lower resonant amplitudes. Furthermore, changing the natural frequency \(\varOmega _{t1}\) moves the locations of the resonant amplitudes associated with the pitch angle natural frequency and its higher harmonics. Figure 8c shows how increasing the pitch natural frequency reduces the pitch resonant amplitudes. In addition, higher values of \(\varOmega _{t1}\) increase the natural frequency of the moving mass due to the coupling between the pitch motion and the moving mass. Changes in the phase of the pitch angle in response to changes in \(\varOmega _{t1}\) are illustrated in Fig. 8d.
Response-frequency diagram of the steady-state dynamics of pitch angle for different values of the natural frequency \(\varOmega _{t1}\) of the pitch angle. a 3D waterfall diagram of the amplitude–frequency response; b static deflection of the pitch angle; c 2D amplitude–frequency diagram; d phase–frequency diagram
Response-frequency diagram of the steady-state dynamics of pitch angle for different values of the natural frequency \(\varOmega _{21}\) of the moving mass. a 3D waterfall diagram of the amplitude–frequency response; b static deflection of the pitch angle; c 2D amplitude–frequency diagram; d phase–frequency diagram
The steady-state response-frequency diagram of the pitch angle is shown in Fig. 9. The variation of \(\varOmega _{21}\) affects not only the resonant amplitudes of the pitch angle, but also the location of the resonant frequencies. It is observed that the pitch response of the blade experiences one resonance for each natural frequency of the pitch angle and the moving mass. There also exist other resonances related to higher harmonics of the pitch angle. The results show that the nonlinear behaviour of the pitch response is stronger for lower values of the natural frequency \(\varOmega _{21}\), as the linear stiffness of the moving mass decreases. By increasing \(\varOmega _{21}\), the resonant amplitudes of the pitch response increases up to \(\varOmega _{21}=2.5\) and then reduces for further increases in \(\varOmega _{21}\). The coupling between the motion of the moving mass and the pitch angle dynamics, means that for natural frequencies of the moving mass less than the torsional natural frequency (\(\varOmega _{21}<\varOmega _{t1}\)) the pitch resonance moves to the right (i.e. \(\varOmega _{{t1}_\mathrm{actual}}>\varOmega _{t1}\)). On the other hand, for \(\varOmega _{21}>\varOmega _{t1}\), the actual pitch resonant frequency \(\varOmega _{{t1}_\mathrm{actual}}\) is less than the uncoupled natural frequency \(\varOmega _{t1}\). Figure 9b illustrates that increasing the natural frequency \(\varOmega _{21}\) results in stiffening of the moving mass, and this consequently leads to less deflection of the moving mass and less static pitch deflection due to bend–twist coupling. From the results shown in Fig. 9, the parameter \(\varOmega _{21}\) provides the ability to tune the structure so that the rotating (excitation) frequency can be located at, or in the vicinity of, either the moving mass natural frequency or the pitch resonant frequency. Therefore, the structure can use the energy arising from the resonant oscillations. However, the resonant amplitude may be dangerous for the structure, particularly if it is a linear resonant amplitude. To deal with this problem, the parameters of the system are tuned so that the operating frequency is located in the vicinity of the nonlinear resonant amplitude. Having nonlinear resonant amplitude, instead of a linear resonance, restrains the amplitude of oscillations at a fixed rotating frequency. In the next section, it is shown how the nonlinear behaviour of the structure can be used for RPEB while avoiding the dangerous linear resonant amplitude that may lead to fracture in the blade. On the other hand, it is shown how the stability analysis of the morphing blade helps to better understand the nonlinear dynamics of the structure. The results of stability analysis are then used to determine the safe region of operation.
Figure 10 shows the amplitude/phase–frequency diagram of the steady-state pitch response of the blade within the rotating frequency bandwidth \(\varOmega _0=0 \sim 6.5\) for different values of lag–twist coupling D. In this case, by neglecting the aerodynamic loading, the only excitation on the structure is the actuation force applied to the moving mass. Therefore, the dynamic pitch response depends on the dynamics of the moving mass and the value of the coupling D. The waterfall diagram of the pitch response in Fig. 10a shows that changing the value of D leads to changes in the resonant vibration amplitudes of the pitch angle. For \(D=0\), as there is no coupling between the pitch angle and the moving mass, the pitch angle shows zero amplitude response. Increasing the magnitude of D leads to increases in the resonant amplitude, as the coupling between the moving mass and the pitch angle becomes stronger. In addition, new resonances appear in the response by increasing the value of D to greater than \(D=0.5\). The locations of these new resonances also depend on the value of the bend–twist coupling. The static deflection of the pitch angle depends on the sign of D, and the blade will pitch nose up or down, respectively, for negative and positive coupling D, as shown in Fig. 10b. Also, the blade will have greater static pitch deflection for higher magnitudes of D. In contrast to the magnitude of D, Fig. 10c shows that the sign of the bend–twist coupling does not have any effect on the amplitude of the pitch vibration, in the absence of aerodynamic forces. In other words, the amplitude–frequency diagram of the pitch angle is symmetric with respect to the value of D. However, altering the sign of the coupling D results in a change in the phase of the pitch angle by \(\pi \) rad, as shown in Fig. 10d. Therefore, the results of Fig. 10 demonstrate that both the magnitude and sign of the bend–twist coupling D can be useful in determining the dynamic properties of the pitch response.
Figure 11 shows the amplitude–frequency response of the steady-state pitch dynamics for different levels of actuation force \(F_\mathrm{m}\). Figure 11a, c illustrates the 3D waterfall diagram and 2D amplitude–frequency diagram of the first harmonic of the pitch oscillation, respectively. Figure 11b gives the static deflection of the pitch response, and the phase of the first harmonic of pitch oscillation is shown in Fig. 11d. \(\alpha _0\), \(|\alpha _1|\), and \(\phi _{\alpha _1}\) denote the static deflection, and the amplitude and phase of the first harmonic of pitch oscillation, respectively, The results show that increasing the actuation level increases the resonant amplitude of the pitch angle. Furthermore, increasing \(F_\mathrm{m}\) excites the nonlinearity in the structure and multiple solutions appear for higher values of \(F_\mathrm{m}\). In contrast to the vibration amplitude, the static deflection of the pitch angle is not affected by changes in the actuation force. Thus, the actuation force can be used to change the amplitude of the pitch oscillation without affecting the static pitch deflection. Figure 11d shows that there is a phase difference between the case without actuation force and with actuation force. However, in the presence of actuation, the phase of the response is not affected by the actuation level.
4 Sensitivity analysis
Based on the discussion in the previous sections, a parametric study is performed on the dynamics of the 3DOF model of the blade considering the variation of two important parameters: bend–twist coupling D and the aerodynamic distance \(d_\mathrm{ac}\). The lower and upper bounds of the variation range of the parameters are determined according to physically meaningful variations of the dimensional parameters of the blade. The selected lower and upper bounds are given in Table 4. First, the effect of the parameters’ variability is investigated on the dynamics of the 3DOF model of the blade. Then, the controllability of the pitch response is discussed.
The baseline values of the parameters of Table 2 are used to determine the dynamics of the 3DOF model of the blade using numerical direct integration in MATLAB. The simulation was performed for the frequency range \(\varOmega _0=0.5 \sim 6\) with frequency step \(\mathrm{d}\varOmega _0=0.025\). The simulation was performed for 800 cycles at each frequency and the last 150 cycles are used to ensure the steady-state response is considered. Figure 12 shows the static deflection and the amplitude of the first five harmonics of the pitch angle of the blade. \(\alpha _0\) and \(|\alpha _i|\) denote, respectively, the static deflection and the amplitude of the ith harmonic of the pitch response. The results show that there are some resonant amplitudes of different harmonics related to the natural frequencies of each degree of freedom. It is observed that by increasing the rotating speed (excitation frequency) \(\varOmega _0\), the magnitude of the static deflection of the pitch angle increases as expected. However, it is explained later that the magnitude and sign of the static deflection (pitch nose up or down) depend on the values of the parameters \(d_\mathrm{ac}\) and D and also the rotating frequency. In addition, the amplitudes of the pitch angle oscillations experience several resonances and jumps in the neighbourhood of the natural frequencies. The jumps in the dynamic response of the pitch angle are due to the nonlinearity of the system and are critical in tuning the parameters of the structure.
To better understand the nonlinear response of the pitch angle, the response obtained from numerical direct integration is compared with the response obtained using CXA. Figure 13 compares the amplitude of the first harmonic of the steady-state dynamic pitch response of the 3DOF model obtained using the CXA method and direct numerical integration in MATLAB. This comparison clarifies the exact nonlinear dynamic response of the pitch angle. The stability analysis on the analytical results obtained from the CXA method has been undertaken using Lyapunov’s First Theory of Stability. Unless the jump between two different stable branches is targeted for a special purpose, the region of multiple stable solutions is avoided in practical engineering systems. Besides, the existence of unstable branches in addition to various bifurcations generates different types of dynamic responses that is mostly avoided in engineering structures. For example, the results of Fig. 12 in the frequency range \(\varOmega _0=3.12\) to 3.5 shows that the amplitude of vibration changes non-smoothly in this region. This is because the system behaves with a variety of multi-frequency, quasi-periodic, and chaotic responses in this frequency range. The time histories and phase diagrams of the pitch response are given in Fig. 14 for three values of \(d_\mathrm{ac}=-0.25,0,0.25\) at two different rotating frequencies, \(\varOmega _0=3,3.25\). The results show that for \(d_\mathrm{ac}=-0.25\) and \(d_\mathrm{ac}=0\) the pitch angle shows periodic responses at both frequencies. However, for \(d_\mathrm{ac}=0.25\), pitch angle has a periodic response at \(\varOmega _0=3\), while it behaves with a chaotic response at \(\varOmega _0=3.25\). Various dynamic responses including periodic, quasi-periodic, and chaotic responses at different rotating frequencies are shown in Fig. 15. The results of Fig. 13 can also be used to determine the desirable operating range of the structure according to different dynamic responses at various frequencies. Of course, this decision depends on the application and design criteria. For example, the frequency ranges \(\varOmega _0<2.2\), \(2.7<\varOmega _0<3.1\), and \(\varOmega _0>3.8\) are safe with respect to undesired behaviours such as multiple stable solutions, jumps, quasi-periodic responses, or chaotic dynamics. However, despite a relatively high amplitude of vibration, an aircraft with variable rotating frequency might avoid the range of \(2.7<\varOmega _0<3.1\) which has various undesired dynamic responses. On the other hand, aerospace applications with a constant rotating frequency can benefit from high amplitude vibration for \(2.7<\varOmega _0<3.1\).
4.1 Controllability of the pitch response
Amplitude and phase of the pitch angle are important features of the dynamics of the blade which are required to be controlled. Sects. 3.1 and 3.2 show that the aerodynamic forcing/moment and the bend–twist coupling are two important parameters in determining the phase of pitch angle. Therefore, this section discusses the effect of aerodynamic forcing and bend–twist coupling on the phase of the pitch angle. The variations of two parameters, \(d_\mathrm{ac}\) and D, which determine, respectively, the signs of aerodynamic force and bend–twist coupling, are considered. For the other parameters, the baseline values of Table 2 are used. The results in this section are obtained using the 3DOF model of the helicopter morphing blade including the aerodynamic loading.
To investigate the effect of these two parameters on the phase of the pitch angle, three different cases are considered: (a) \(D=0\), (b) \(d_\mathrm{ac}=0\), and (c) \(D \ne 0\) & \(d_\mathrm{ac} \ne 0\).
(a) \(D=0\). In this case, the bend–twist coupling is neglected and the effect of \(d_\mathrm{ac}\) on the phase of the pitch angle is studied in the absence of bend–twist coupling. The aerodynamic force may have different signs depending on the location of aerodynamic centre AC. Accordingly, the aerodynamic forcing may have beneficial or adverse effects on the pitch angle. Therefore, \(d_\mathrm{ac}\), which indicates the distance between AC and RC, plays significant role in defining the desired phase. The appropriate \(d_\mathrm{ac}\) (i.e. the location of AC with respect to RC) is selected to obtain a response that is in phase, out of phase, or no oscillating response. The pitch angle of the blade is obtained for the range of \(d_\mathrm{ac}=-0.5 \sim 0.5\). Figure 16 shows the static deflection and the amplitude and phase of the first three harmonics of the pitch angle. The results show that without any bend–twist coupling in the blade dynamics, the phase of the pitch angle varies in response to changes in the sign and value of \(d_\mathrm{ac}\). At \(d_\mathrm{ac}=0\), no aerodynamic moment is applied to the blade and therefore no pitching response is observed. For \(d_\mathrm{ac}>0\), on the other hand, the pitch angle oscillates with approximately \(\pi \) rad phase difference with respect to the pitch angle for \(d_\mathrm{ac}<0\).
(b) \(d_\mathrm{ac}=0\). In this case, AC is located at RC and the aerodynamic force will not be able to generate any moment to affect the pitch angle. Hence, the only moment applied to the blade is due to bend–twist coupling. Changing the sign of the coupling will affect the amplitude and phase of the pitching response. For \(d_\mathrm{ac}=0\), the effect of variation of bend–twist coupling D on the dynamics of the pitch angle is shown in Fig. 17. In the figure, \(\alpha _0\), \(|\alpha _i|\), and \(\phi _{\alpha _i}\) denote, respectively, the static deflection, and the amplitude and phase of the ith harmonic of the pitch response. The results of the static pitch deflection illustrate that the blade would pitch nose up and down, respectively, for negative and positive values of D. It is also observed that the amplitude of the first three harmonics of the pitch angle is symmetric with respect to the coupling value \(D=0\). In other words, changing the sign of the bend–twist coupling in this case does not have any effect on the vibration amplitude of the pitch angle. On the other hand, there is almost a difference of \(\pi \) rad between the phase of the first harmonic of the pitch responses obtained for negative and positive bend–twist coupling. The results of Fig. 17 show that changing the sign of bend–twist coupling D determines the phase of the pitch angle if the aerodynamic force is neglected. The sign of D can be easily changed by flipping the orientation of fibres in the composite spars at the design stage.
(c) \(D \ne 0\) & \(d_\mathrm{ac} \ne 0\). This case is more practical than the previous two cases, where both aerodynamic moments and the moments generated due to bend–twist coupling affect the pitching response of the blade. The dynamic behaviour of the system is not as straightforward as the previous two cases. Figs. 18, 19 and 20 show the pitch response of the system for different values of \(d_\mathrm{ac}\) and D at three different rotating frequencies, \(\varOmega _0=1.5,2,3\). The figures include the static deflection, vibration amplitude, and the phase of the pitch angle. Figure 18 shows that the second harmonic of the pitch angle is excited at rotating frequency \(\varOmega _0=1.5\). Indeed, as \(\varOmega _0=1.5\) is equal to half of the natural frequency of the pitch angle, the second harmonic of the pitch angle is excited and for some values of \(d_\mathrm{ac}\) and D its amplitude even exceeds the amplitude of the primary harmonic. Figure 18 also demonstrates that the variation of D for a fixed value of \(d_\mathrm{ac}\) has a small effect on the static deflection and the amplitude of the first harmonic of \(\alpha \). However, this effect is pronounced on the amplitude of the 2nd and the 3rd harmonics of the pitch angle at higher positive values of \(d_\mathrm{ac}\). The results of the phase of \(\alpha \) show that D affects the phase of pitch response for small magnitudes of \(d_\mathrm{ac}\). This is because the effect of the aerodynamic moments is reduced for low magnitudes of \(d_\mathrm{ac}\) and the effect of D is strengthened. However, the aerodynamic moments are stronger for higher levels of \(d_\mathrm{ac}\) and the effect of D on the phase of the pitch response is weakened. On the other hand, the variation of \(d_\mathrm{ac}\) significantly affects the pitch response. Figure 18a shows that the blade will pitch nose up and down, respectively, for positive and negative values of \(d_\mathrm{ac}\). The results of vibration amplitude of \(\alpha \) in Fig. 18 illustrate that the aerodynamic moment is strengthened by increasing the magnitude of \(d_\mathrm{ac}\) and the amplitude of vibration increases. However, the amplitude of the 2nd harmonic is not significantly changed by the variation of negative values of \(d_\mathrm{ac}\). That is, \(d_\mathrm{ac}\) can also be used to control the amplitude of the higher harmonics of the pitch angle. It is also observed that the phase of the pitch angle varies by changing the sign of \(d_\mathrm{ac}\).
Figure 19 shows the pitch response of the system for the variation of \(d_\mathrm{ac}\) and D at \(\varOmega _0=2\). Although the significance of D at this frequency is greater than at \(\varOmega _0=1.5\), the variation of D for a fixed value of \(d_\mathrm{ac}\) does not significantly change the static deflection. It is also shown that at this frequency, the variation of D has a stronger effect on the amplitude and phase of the pitch oscillations, particularly for positive values of \(d_\mathrm{ac}\). Indeed, as the rotating frequency of the blade approaches the natural frequency of the moving mass, the effect of the oscillation of the moving mass on the pitch response becomes stronger. Accordingly, the bend–twist coupling D plays a more significant role at this frequency. In contrast to the response at \(\varOmega _0=1.5\), where the amplitude of the second harmonic is relatively large with respect to the primary harmonic, since \(\varOmega _0=2\) is not in the vicinity of any sub- or super-harmonic of the natural frequency of the pitch angle, the amplitude of the higher harmonics of the pitch response is significantly smaller than its primary harmonic. On the other hand, \(\varOmega _0=2\) is in the neighbourhood of the natural frequency of the moving mass. Therefore, the higher aerodynamic forces at higher values of \(d_\mathrm{ac}\) result in a resonant response of the moving mass. Accordingly, the resonant energy transfer of the moving mass to the pitch angle is increased for higher values of bend–twist coupling D. Hence, the highest vibration amplitudes of the pitch response are observed at the corners of Fig. 19b–d. Similar to the results in Fig. 18, the variation of the vibration amplitude of the pitch angle due to changes in positive values of \(d_\mathrm{ac}\) is more significant than its negative values. The results of the pitch response at \(\varOmega _0=3\) is shown in Fig. 20 for variations in bend–twist coupling D and parameter \(d_\mathrm{ac}\). The static deflection is function of both the magnitude and sign of D and \(d_\mathrm{ac}\). The results show that the bend–twist coupling has its greatest effects on the dynamics of the pitch angle at positive values of \(d_\mathrm{ac}\). The results in Figs. 18, 19, and 20 demonstrate that D and \(d_\mathrm{ac}\) are two significant determining factors in the dynamics of the pitch angle. However, the effect of these two parameters on the pitch response may vary at different rotating frequencies. Although most of aerospace applications operate at constant rotating frequencies, there are various applications such as unmanned aircraft that work over a range of rotating frequency. Therefore, the results of the analysis in this study can also be used to find the safe and desirable operating range. Also, \(\varOmega _0\) denotes the rotating frequency that is nondimensionalized with respect to the lagging natural frequency \(\omega _1\). Hence, \(\varOmega _0\) considers both the variability of \(\omega _1\) and the operating range of rotating frequency.
5 Conclusions
This study investigates the resonant passive energy balancing of a morphing blade with moving mass at the tip. To this end, the dynamics of the blade was modelled by a 3DOF discrete system in which the pitch angle, the lagwise motion, and the displacement of the moving mass are considered as the three degrees of freedom. A parametric analysis was carried out on the dynamic response of the 3DOF model of a morphing helicopter blade. The dimensions and mechanical properties of the Bo-105 blade with NACA23012 aerofoil section were used to find the baseline for the study. The aerodynamic coefficients are obtained using the experimental results in the literature. The reduced-order model of the rotor blade was used to study the controllability of the dynamic behaviour of the structure. The analyses and the results obtained in this study are given as follows:
-
1.
First, a simplified single-degree-of-freedom model of the 3DOF system is studied to examine the dynamics of the pitch angle in response to changes in important parameters of the structure. The results showed that the two parameters D, the bend–twist coupling, and \(d_\mathrm{ac}\), the distance of AC to RC, play significant roles in the dynamic response of the pitch angle.
-
2.
Then, neglecting the aerodynamic forces, the dynamic response of the structure of the 3DOF model was studied in response to variations in different structural parameters.
-
The aim of this study was to examine the dynamic sensitivity of the structure to different parameters. This can be used to appropriately tune the structure of the rotor blade. For example, the parameters of the structure can be selected so that the natural frequencies of the system are located within the desired rotating speed.
-
This helps the engineer use the resonant energy of the system to reduce the required actuation power.
-
The results of this analysis showed that the torsional natural frequency (i.e. the torsional rigidity and the moment of inertia of the blade) can change the location of torsional resonant frequencies.
-
Also, the natural frequency of the movable mass has a significant effect on the resonances of the pitch angle.
-
The bend–twist coupling D is the other effective parameter that determines the resonant pitch angle of the blade.
-
-
3.
Finally, a physically meaningful range of variation was considered for D and \(d_\mathrm{ac}\) and the effects of the variations of each parameter were investigated on the response of the 3DOF system including the aerodynamic forces.
-
Various dynamic responses of the structure under study including periodic, multi-frequency, quasi-periodic, and chaotic responses were illustrated. These dynamic responses are important in tuning the parameters of the structure, as quasi-periodic or chaotic responses are avoided in the system.
-
The controllability of the pitching response was discussed based on the results of the simulation.
-
The results showed that the bend–twist coupling D and the distance \(d_\mathrm{ac}\) between the aerodynamic centre AC and the rotating centre are the two important parameters in determining the static deflection, vibration amplitude, and phase of the pitch response. However, other structural parameters are used to tune the system desirably.
-
Although the present study is mainly focused on the dynamic analysis and parametric study of the morphing helicopter blade, the results of this study can be used in practical cases to improve the performance of the aircraft and reduce the required actuation energy. Having a linear resonant amplitude in the structure may be dangerous. However, the nonlinear behaviour of the structure restrains the amplitude of oscillations at the desired fixed rotating frequency. In addition, the stability analysis of the dynamic behaviour helps to better understand the structure and avoid undesired dynamic behaviours such as jumps, quasi-periodic response, or chaotic behaviour.
Data availability
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
Mistry, M., Gandhi, F., Nagelsmit, M., Gurdal, Z.: Actuation requirements of a warp-induced variable twist rotor blade. J. Intell. Mater. Syst. Struct. 22(9), 919–33 (2011)
Zhou, B., Li, Z., Zheng, Z., Tang, S.: Nonlinear adaptive tracking control for a small-scale unmanned helicopter using a learning algorithm with the least parameters. Nonlinear Dyn. 89, 1289–1308 (2017)
Kandil, A., El-Gohary, H.: Investigating the performance of a time delayed proportional-derivative controller for rotating blade vibrations. Nonlinear Dyn. 91, 2631–2649 (2018)
Ajaj, R.M., Beaverstock, C.S., Friswell, M.I.: Morphing aircraft: the need for a new design philosophy. Aerosp. Sci. Technol. 49, 154–166 (2016)
Lachenal, X., Daynes, S., Weaver, P.M.: Review of morphing concepts and materials for wind turbine blade applications. Wind Energy 16(2), 283–307 (2013)
Castillo-Rivera, S., Tomas-Rodriguez, M.: Helicopter flap/lag energy exchange study. Nonlinear Dyn. 88, 2933–2946 (2017)
Vos, R., Barrett, R., De Breuker, R., Tiso, P.: Post-buckled precompressed elements: a new class of control actuators for morphing wing UAVs. Smart Mater. Struct. 16, 919–926 (2007)
Vos, R., De Breuker, R., Barrett, R.M., Tiso, P.: Morphing wing flight control via postbuckled precompressed piezoelectric actuators. J. Aircraft 44, 1060–1068 (2007)
Fincham, J.H.S., Friswell, M.I.: Aerodynamic optimisation of a camber morphing aerofoil. Aerosp. Sci. Technol. 43, 245–255 (2015)
Eguea, J.P., da Silva, G.P.G., Catalano, F.M.: Fuel efficiency improvement on a business jet using a camber morphing winglet concept. Aerosp. Sci. Technol. 96, 105542 (2020)
Zhang, J., Shaw, A.D., Wang, C., Gu, H., Amoozgar, M., Friswell, M.I., Woods, B.K.S.: Aeroelastic model and analysis of an active camber morphing wing. Aerosp. Sci. Technol. 111, 106534 (2021)
Hong, C.H., Chopra, I.: Aeroelastic stability analysis of a composite rotor blade. J. Am. Helicopter Soc. 30(2), 57–67 (1985)
Chandra, R., Stemple, A.D., Chopra, I.: Thin-walled composite beams under bending, torsional, and extensional loads. J. Aircraft 27(7), 619–626 (1990)
Han, D., Vasileios, P., George, N.B.: Helicopter flight performance improvement by dynamic blade twist. Aerosp. Sci. Technol. 58, 445–452 (2016)
Fedorov, V.: Bend-Twist Coupling Effect in Wind Turbine Blades. PhD Thesis, Technical University of Denmark (2012)
Gu, H., Shaw, A.D., Amoozgar, M., Zhang, J., Wang, C., Friswell, M.I.: Twist morphing of a composite rotor blade using a novel metamaterial. Compos. Struct. 254, 112855 (2020)
Byers, L., Gandhi, F.: Helicopter rotor lag damping augmentation based on a radial absorber and coriolis coupling. In: Presented at the American Helicopter Society 61st Annual Forum. Grapevine, TX (2005)
Byers, L., Gandhi, F.: Rotor blade with radial absorber (Coriolis damper)-loads evaluation. In: Presented at the American Helicopter Society 62nd Annual Forum. Phoenix, AZ (2006)
Byers, L., Gandhi, F.: Embedded absorbers for helicopter rotor lag damping. J. Sound Vib. 325(4), 705–721 (2009)
Kang, H., Smith, E.C., Lesieutre, G.A.: Experimental and analytical study of blade lag damping augmentation using chordwise absorbers. J. Aircraft 43(1), 194–200 (2006)
Amoozgar, M.R., Shaw, A.D., Zhang, J., Friswell, M.I.: The effect of a movable mass on the aeroelastic stability of composite hingeless rotor blades in hover. J. Fluids Struct. 87, 124–136 (2019)
Wang, C., Zhang, J., Shaw, A.D., Amoozgar, M., Friswell, M.I., Woods, B.K.S.: Applying the Passive Energy Balancing Concept into the Actuation System of A Morphing Rotorcraft: Integration and Optimisation. AIAA SciTech Forum, 6–10. Orlando, FL (2020)
Zhang, J., Wang, C., Shaw, A.D., Amoozgar, M., Friswell, M.I.: Passive energy balancing design for a linear actuated morphing wingtip structure. Aerosp. Sci. Technol. 107, 106279 (2020)
Zhang, W., Sun, L., Yang, X.D., Jia, P.: Nonlinear dynamic behaviors of a deploying-and-retreating wing with varying velocity. J. Sound Vib. 332(25), 6785–6797 (2013)
Zhang, W., Lu, S.F., Yang, X.D.: Analysis on nonlinear dynamics of a deploying composite laminated cantilever plate. Nonlinear Dyn. 76(1), 69–93 (2014)
Zhang, J., Shaw, A.D., Wang, C., Gu, H., Amoozgar, M., Friswell1, M.I.: Resonant Passive Energy Balancing for a Morphing Helicopter Blade, Aerospace Science and Technology, Under review
Rezaei, M.M., Behzad, M., Haddadpour, H., Moradi, H.: Aeroelastic analysis of a rotating wind turbine blade using a geometrically exact formulation. Nonlinear Dyn. 89, 2367–2392 (2017)
Qi, G., Huang, D.: Modeling and dynamical analysis of a small-scale unmanned helicopter. Nonlinear Dyn. 98, 2131–2145 (2019)
Drela, M.: XFOIL: an analysis and design system for low Reynolds number airfoils. In: Mueller T.J. (eds) Low Reynolds Number Aerodynamics. Lecture Notes in Engineering, vol 54. Springer, Berlin (1989)
Jacobs, E.J., Clay, W.C.: Characteristics of the NACA23012 airfoil from tests in the full-scale and variable-density tunnels. National Advisory Committee for Aeronautics. NACA Report, vol. 530 (1935)
Platt, R.C., Abbott, I.H.: Aerodynamic characteristics of NACA 23012 and 23021 airfoils with 20-percent-chord external-airfoil flaps of NACA 23012 section. National Advisory Committee for Aeronautics. NACA Report, vol. 573 (1936)
Pouryoussefi, S.G., Mirzaei, M., Nazemi, M.M., Fouladi, M., Doostmahmoudi, A.: Experimental study of ice accretion effects on aerodynamic performance of an NACA 23012 airfoil. Chin. J. Aeron. 29(3), 585–595 (2016)
Kostic, I.: Some practical issues in the computational design of airfoils for the helicopter main rotor blades, Theoret. Appl. Mech., Vol. 31, No.3–4, pp. 281–315, Belgrade (2004)
Burger, R.L.: Procedures for the design 14 of low-pitching-moment airfoils, Langley Research Center, Hampton, Va. 23665, NASA Technical Note, NASA TN D-7982 (1975)
Taghipour, J., Dardel, M., Pashaei, M.H.: Vibration mitigation of a nonlinear rotor system with linear and nonlinear vibration absorbers. Mech. Mach. Theory 128, 586–615 (2018)
Acknowledgements
This research leading to these results has received funding from the European Commission under the European Union’s Horizon 2020 Framework Programme ‘Shape Adaptive Blades for Rotorcraft Efficiency’ Grant Agreement 723491.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Taghipour, J., Zhang, J., Shaw, A.D. et al. Resonant passive energy balancing of morphing helicopter blades with bend–twist coupling. Nonlinear Dyn 107, 617–639 (2022). https://doi.org/10.1007/s11071-021-07067-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-07067-x