Load prediction of hingeless helicopter rotors including drivetrain dynamics

Abstract

In contrast to analyses with constrained hub speed, the present study includes the dynamic response of coupled rotor-drivetrain modes in the aeromechanic simulation of rotor blade loads. The structural model of the flexible Bo105 rotor-drivetrain system is coupled to aerodynamics modeled by an analytical formulation of unsteady blade element loads combined with a generalized dynamic wake or a free wake, respectively. For two flight states, i. e. cruise flight and large blade loading, a time-marching autopilot trim of the rotor-drivetrain system in wind tunnel configuration is performed. The simulation results are compared to those of a baseline case with constant rotor hub speed. The comparison reveals a major change in the blade passage frequency harmonics of the lead-lag loads. Beside the full drivetrain model, reduced models are shown to accurately represent the drivetrain influence on blade loads, if the eigenfrequency of the coupled second collective lead-lag/drivetrain mode is properly predicted. In a sensitivity analysis, this eigenfrequency is varied by stiffness modification of a reduced drivetrain model. The resulting changes in blade loads are correlated to this eigenfrequency, which serves as a simple though accurate classification of the drivetrain regarding its influence on vibratory blade loads. Finally, the potential to improve lead-lag load predictions by application of a drivetrain model is demonstrated through the comparison of simulated loads with measurements from a wind tunnel test.

1 Introduction

To assure strength and predict fatigue, the precise determination of rotor blade loads is of crucial importance in helicopter development. Wind tunnel tests and numerical simulations enable blade load predictions prior to the completed design and production of the helicopter, and thus, contribute to a time- and cost-efficient development process.

Commonly, the fidelity of blade load predictions in the lead-lag direction is significantly poorer than that in flap direction, which holds for both wind tunnel tests [1] and simulations [2]. So far, the search for reasons, such as the aerodynamic model [3, 4], the structural blade model [5], actuation system modeling [6] or lead-lag damper modeling [2, 4], has not unveiled a certain source of errors.

Still widely unexplored is the impact of the drivetrain, which consists of mast, main gearbox, engines, tail rotor shaft and tail rotor. Since torsional drivetrain dynamics interact with the main rotor via the hub’s rotational degree of freedom, it potentially affects blade motion, and consequently, blade loads. Recently, this issue was taken up in several simulation studies with respect to the fully articulated rotor system of the UH-60A helicopter.

A freely rotating, modally reduced drivetrain model was coupled to the rotor [7], causing notable changes in lead-lag loads compared to a simulation with constant hub speed. However, in other studies [8, 9], the application of a drivetrain model alone was not sufficient to eliminate the poor lead-lag loads correlation between flight tests and simulations.

Despite this finding, an important common conclusion of [7,8,9] is the change in blade load $4/{\text {rev}}$ (blade passage frequency) harmonic magnitudes caused by the drivetrain. Based on this conclusion, the present study treats in detail the correlation between the structural properties (i.e. inertia and stiffness) of the drivetrain and its impact on blade loads with a focus on the blade passage frequency content. Moreover, in contrast to the previous studies, it addresses hingeless rotor systems. Due to direct moment transmission at the blade attachment, hingeless rotors are expected to be more influenced by the drivetrain than articulated rotors are.

The first step towards the profound understanding of drivetrain influence on rotor dynamics was the structural analysis (no aerodynamics included) of the coupled rotor-drivetrain system of the Bo105 helicopter [10]. The investigation showed that drivetrain inertia and stiffness have a considerable influence on the collective lead-lag modes. A remarkable observation was the reduction of the second collective lead-lag eigenfrequency from $\omega _\mathrm {L2}=4.33\,\varOmega _\mathrm {ref}$ to $\omega _{\mathrm {RD}_\mathrm {L2}}=3.52\,\varOmega _\mathrm {ref}$ (RD = rotor-drivetrain) due to finite drivetrain stiffness.¹ This coupling effect occurs around the blade passage frequency $4\,\varOmega _\mathrm {ref}$, which at the same time is the dominant excitation of any rotor-drivetrain mode. Consequently, drivetrain parameters (especially stiffness) are suspected to massively influence the dynamic response of the coupled $\mathrm {RD}_\mathrm {L2}$ mode.

The present paper expands the research by the assessment of blade loads in an aeromechanic simulation of the Bo105 rotor-drivetrain system. The goal of the study is not to accurately predict blade loads as measured in flight tests, which would require higher-level aerodynamic models, but to thoroughly understand the coupling between the drivetrain and the main rotor.

2 Methodology and simulation

The simulation framework consists of three programs, as depicted in Fig. 1. The rotor-drivetrain structure is modeled with the multibody simulation tool SIMPACK (block in the middle). The aerodynamic models, i. e. airloads and inflow model, are implemented in VAST, DLR’s new Versatile Aeromechanics Simulation Tool [11] (block above). The VAST libraries are called by a SIMPACK-internal user routine. The corresponding force element reads the motion of blade element markers, and in turn applies lift and drag forces as well as pitch moments at the markers. Control logic is implemented in Matlab-Simulink (block below). The connection to SIMPACK utilizes the TCP/IP protocol. Two control loops work in parallel: First, blade pitch motion is controlled by an autopilot trim in conjunction with a functional swashplate model. Second, rotor speed is governed by a model of the controlled engines or a simplified governor model, respectively.

Fig. 1

Simulation framework and schematic interfaces between VAST, SIMPACK and Matlab-Simulink

2.1 Structure

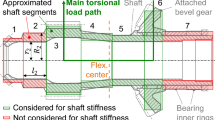
In general, both the drivetrain and the airframe of a helicopter consist of flexible structures that give rise to dynamic couplings between both systems [12]. However, the realistic modeling of a coupled drivetrain-airframe system would require an extremely detailed level of 3D-modeling that is far beyond the scope of the present study, which focuses on torsional drivetrain dynamics only. The drivetrain model consists of 16 discrete inertia elements and connecting flexible elements representing torsional flexibility of shafts and the flexibility of gear meshes. The flexible rotor blades are modeled as 1D-Euler-Bernoulli beams in the SIMPACK-internal FE-module SIMBEAM. The beam model features coupled bending and torsion and accounts for offsets between the elastic axis, the mass axis and the tension axis. Since any deformation in SIMBEAM is linear, the blades need to be segmented to accurately capture Coriolis-coupling between flap and lead-lag motion [13]. Each blade is divided into 8 segments, while the number of blade elements per segment varies between 3 and 16. Consequently, although each segment deforms linearly, a nonlinear behavior of the whole blade is accounted for. Exemplary, Fig. 2 shows the effect of radial contraction $\varDelta r$ due to bending of a segmented beam (green).

Fig. 2

Radial contraction due to bending deformation of segmented linear beam

The propeller moment, which leads to centrifugal stiffening of torsion modes, is not inherently captured by the 1D-beam formulation of SIMBEAM and thus, is modeled via force elements [14]. Control system flexibility is modeled by a torsional hinge with discrete stiffness and damping. Furthermore, a lead-lag hinge with very high stiffness and linear damping is placed near the location of the Bo105 rotor blade attachment. This approximately accounts for slip effects in the attachment, which were analyzed in [15], and improves lead-lag eigenfrequency correlation with measurements.

As an advantage of the segmented beam approach, the flexible blade kinematics is not limited to a pre-defined set of blade modes. In a conventional approach, these blade modes are the first lead-lag mode (L1), first flap mode (F1), second flap mode (F2), first torsion mode (T1) etc., called baseline modes in the following. The baseline modes are fully covered by the segmented beam approach, in which they are assembled from the segment modes². On top of that further modes may be assembled accurately, such as coupled rotor-drivetrain modes (RD), which differ significantly from the baseline modes in shape and eigenfrequency [10].

Drawbacks of the segmented beam approach are the increased computational cost and the difficulty to model structural damping. Typically, modal damping is applied in conventional blade models. However, the baseline blade modes are not pre-defined in the present approach to cover rotor-drivetrain modes as well. Consequently, modal damping is not applicable. Alternatively, stiffness-proportional damping is utilized, where the stiffness matrices of the segments are scaled by a constant damping factor $d_\mathrm {s}$ to obtain the corresponding damping matrices. By this approach, the modal damping ratio D of a segment mode linearly depends on its eigenfrequency [16]. Beside $d_\mathrm {s}$, the lead-lag hinge damping $d_\mathrm {L}$ and the torsion hinge damping $d_\mathrm {T}$ are tuned to obtain damping ratios in the typical range $D = 0.5 \ldots 2\,\%$ for the baseline modes.

Figure 3 depicts the resulting damping ratio D for varying $d_\mathrm {s}$, while the hinge damping values are set to $d_\mathrm {L} = 1100\,\mathrm {Nms}/\mathrm {rad}$ and $d_\mathrm {T} = 6.1\,\mathrm {Nms}/\mathrm {rad}$. Since the baseline modes are assembled from different segment modes, their damping ratios differ from each other. D tends to increase with rising mode order. For each mode, D depends linearly on $d_\mathrm {s}$.

Reasonable damping factors are between $d_\mathrm {s} = 0.5 \cdot 10^{-4}\,\mathrm {s}$ and $d_\mathrm {s} = 2 \cdot 10^{-4}\,\mathrm {s}$, which is the range investigated in the present study. The upper limit $d_\mathrm {s} = 2 \cdot 10^{-4}\,\mathrm {s}$ yields still very low damping ratios $D < 0.15\,\%$ for F1 and F2, which are acceptable in view of the large aerodynamic flap damping. $D(\mathrm {L1}) = 0.51\,\%$ and $D(\mathrm {L2}) = 1.97\,\%$ are placed within the target range mentioned above. The same holds for the first torsional mode damping $D(\mathrm {T1}) = 2.0\,\%$. At the lower limit $d_\mathrm {s} = 0.5 \cdot 10^{-4}\,\mathrm {s}$, all modes are damped less than $D = 1.2\,\%$, while the first lead-lag mode damping, which is important for stability, still features a damping of $D = 0.39\,\%$. Due to $d_\mathrm {L}$ and $d_\mathrm {T}$, a non-zero damping ratio remains for the lead-lag and torsion modes at $d_\mathrm {s} = 0\,\mathrm {s}$.

Fig. 3

Resulting damping ratios D of the first seven baseline modes depending on damping factor $d_\mathrm {s}$

In comparison to the baseline rotor model with the hub constraint $\varOmega = {\text {const}}.$, the rotor-drivetrain model features additional structural modes, the rotor-drivetrain modes. Linearization at nominal rotor speed $\varOmega = \varOmega _\mathrm {ref}$ (but with perturbations of $\varOmega$ allowed) yields the eigenfrequencies shown on the right side of Table 1, whereas the baseline frequencies $\left( \varOmega = {\text {const}}. \right)$ are listed to the left.

Table 1 Comparison of eigenfrequencies at nominal rotor speed. Baseline vs. coupled rotor-drivetrain (modes from [10], values adapted to improved rotor model)

It has been demonstrated by experiment [17] and analytically [18], that only collective rotor modes are affected by the drivetrain. At the remaining modes (four-bladed rotor: longitudinal, lateral, differential), blade root bending moments at the hub cancel each other out. Hence, in the example of L1, the eigenfrequency of these three remaining modes stays $\omega / \varOmega _\mathrm {ref} = 0.67$, whereas the collective mode transforms to a rotor-drivetrain mode ($\mathrm {RD}_\mathrm {L1}$) at a higher eigenfrequency of $\omega / \varOmega _\mathrm {ref} = 1.02$. This correlation is indicated by the arrows in Table 1. The collective L2 mode ($\omega / \varOmega _\mathrm {ref} = 4.33$) transforms into $\mathrm {RD}_\mathrm {L2}$ ($\omega / \varOmega _\mathrm {ref} = 3.52$) with a decrease in eigenfrequency. Due to structural couplings between L2 and T1, the collective T1 mode is also slightly affected by the drivetrain and turns into $\mathrm {RD}_\mathrm {T1}$. The minor contributions of T1 in $\mathrm {RD}_\mathrm {L2}$ and L2 in $\mathrm {RD}_\mathrm {T1}$ are indicated by dotted arrows. The collective flap modes are not noticeably affected.

One of the rotor-drivetrain modes, namely $\mathrm {RD}_\mathrm {L2}$, is of particular importance for the present study, as mentioned in the introduction and demonstrated later. Figure 4 shows the $\mathrm {RD}_\mathrm {L2}$ mode shape. The blade deformation resembles an L1 mode with free root distortion rather than the uncoupled, baseline L2 mode.³ A point of inflection, featured by the baseline L2 mode, is not visible in the rotor plane. Nodes of lead-lag displacement are located at a radial station of $r/R \approx 0.75$. The rotor hub contributes with a large torsional oscillation amplitude. Considerable deformation is observed in the rotor mast. Its flexibility almost “decouples” the rest of the drivetrain, that shows very weak contribution. Nodes of torsional drivetrain oscillation are present in the main gearbox (middle of the figure) and in the tail rotor (bottom right).

Fig. 4

$\mathrm {RD}_\mathrm {L2}$ mode shape, featuring lead-lag bending and torsional drivetrain oscillation. The shape slightly differs from that in [10] due to the improved rotor model

Further details on the drivetrain model and the blade model, the sensitivity of rotor-drivetrain eigenfrequencies on properties of the rotor and the drivetrain, as well as the variation of the $\mathrm {RD}_\mathrm {L2}$ mode shape due to drivetrain properties are presented in [10].

Beside the full drivetrain model (full DT), reduced drivetrain models are investigated regarding their usability in coupled rotor-drivetrain simulations (Fig. 5).

Fig. 5

Full drivetrain model (full DT), condensed drivetrain model $\left[ J_\mathrm {DT}, k_\mathrm {DT}\right]$ and minimal drivetrain model $\left[ k_\mathrm {DT}^*\right]$

The condensed drivetrain model consists of one inertia element $J_\mathrm {DT}$ and one stiffness element $k_\mathrm {DT}$, whereas the minimal drivetrain model features one stiffness element $k_\mathrm {DT}^*$ only, the lower end of it being constrained to $\varOmega = {\text {const}}.$ The parameters of both simplified drivetrain models are adapted such that the eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ of the rotor-drivetrain system equals that of the full drivetrain model. Note that this adaption leads to different stiffness values $k_\mathrm {DT} \ne k_\mathrm {DT}^*$ of the condensed and the minimal drivetrain model.

2.2 Aerodynamics

Aerodynamic loads are described by a semi-empirical analytical formulation of unsteady blade element loads [19]. The formulation accounts for the different physical mechanisms that are prevalent in unsteady aerodynamics. These are fully separated flow, detached circulatory flow and attached circulatory flow. The latter includes the important effect of dynamic stall.

Noncirculatory loads are not taken into account.⁴ This degrades the prediction accuracy of unsteady aerodynamic loads at inner radial stations on the retreating side of the rotor disk, where the reduced frequency of the flow variation is large. However, the mechanisms stated above (including dynamic stall) are fully covered by the applied airloads model throughout the whole rotor disc. The aerodynamic discretization features 20 elements per blade. The radial widths of the particular blade elements are chosen such that all related rotor disk fractions have the same ring area, i. e. blade element width decreases with increasing rotor radius. With 7 states per blade element, a total number of 560 states is obtained for the airloads model of the 4-bladed rotor. Blade tip loss is considered by application of a Prandtl function to the calculated lift as described in [20].

The inflow is computed by a generalized dynamic wake (GDW) model [21]. Since blade dynamics up to a frequency of $8\,\varOmega _\mathrm {ref}$ is considered in the present study, the number of harmonics in azimuthal direction is set to a slightly higher value of 10. With the corresponding 10 polynomials in radial direction, the inflow model features 66 states in total.

For verification purpose, some simulations are conducted with a more appropriate free wake model (FW) which originates from the work in [22]. Further developments included the calculation of induced velocities by surface integration of vorticity distributions on the wake panels instead of line integration of circulations on the vortex lattice. The model accounts for systems of multiple vortices behind each blade, tip vortex roll-up and Scully-type vortex cores. The FW is strongly coupled to the structural model, i. e. inputs and outputs are exchanged in every time step. This makes the FW simulations costly, which is the reason why most simulations in this study apply the GDW.

2.3 Control

The rotor controls $[\theta _\mathrm {0}~\theta _\mathrm {1c}~\theta _\mathrm {1s}]$ are trimmed by a time-marching autopilot method [23]. The freely-rotating drivetrain models (full DT and condensed model $\left[ J_\mathrm {DT}, k_\mathrm {DT}\right]$) require automatic control of rotor speed $\varOmega$, for which two different approaches are investigated. First, the “native $\varOmega$-control” is utilized, which includes dedicated dynamic models of the Allison 250-C20B engines with governors controlling the fuel flow. Second, a simplified governor is used, featuring proportional and integral feedback (PI) of rotor speed deviation on engine torque. At the current stage of development, the trim controllers are implemented in Matlab/Simulink.

2.4 Fidelity of baseline simulation

The chosen simulation approach is customized for the investigation of rotor-drivetrain coupling. The structural model implies simplifications (e.g. linear beam segments, propeller moment via force elements, stiffness-proportional damping) that degrade the simulation accuracy compared to state-of-the-art comprehensive codes. Moreover, the applied aerodynamic models are less accurate than CFD or the imposition of measured airloads. Consequently, the simulation fidelity is expected to be moderate.

The following figures provide the correlation of trim control angles as well as simulated blade loads with those measured in a full-scale wind tunnel test of the Bo105 main rotor[24]. All results refer to a cruise flight at advance ratio $\mu =0.30$ and blade loading $C_T/\sigma =0.075$, for which two recorded test runs are available. The rotor hub is constrained to $\varOmega = {\text {const}}.$ in the simulation (baseline case, no drivetrain). The simulation trim goals (thrust T, roll moment L, pitch moment M) as well as the rotor shaft angle are set to the values applied in the wind tunnel test. A structural damping factor of $d_\mathrm {s} = 0.5 \cdot 10^{-4}\,\mathrm {s}$ (lower limit of investigated range) is applied. The required trim control angles are in good accordance with the test data, as shown in Fig. 6. The inflow model upgrade from GDW to FW improves the correlation of $\theta _0$ and $\theta _\mathrm {1c}$.

Fig. 6

Trim control angles: wind tunnel test vs. simulations with Generalized Dynamic Wake (GDW) or Free Wake (FW) ($\mu =0.30$, $C_T/\sigma =0.075$)

The azimuthal waveforms of wind tunnel test loads have been reassembled from $0-12/{\text {rev}}$ harmonic data given in [25]. All mean values of the loads have been removed to account for divergent tare settings in wind tunnel test and simulation.

The flap bending moment at $r/R=0.57$ is presented in Fig. 7. While the overall waveforms of test runs and simulations are in good correlation, the peak-to-peak load is slightly underpredicted by the simulations. Furthermore, the test loads lag about $30 - 40$° in phase behind the loads with GDW. The application of FW provides a marginal improvement in both peak-to-peak load and phase correlation.

Fig. 7

Flap bending moment: wind tunnel test vs. simulations ($\mu =0.30$, $C_T/\sigma =0.075$)

As lead-lag bending moments are most important in the current study, these are presented at an inboard station $r/R=0.15$ as well as at midspan $r/R=0.57$. At the inboard station (Fig. 8), the simulated loads correlate well with one of the two measurements. As for the flap moment, a small phase shift is apparent. The other measurement shows an additional peak at $180$° azimuth, which could be due to a signal error. The loads with GDW and FW are similar. FW yields a slightly higher peak-to-peak load.

Fig. 8

Lead-lag bending moment (inboard): wind tunnel test vs. simulations ($\mu =0.30$, $C_T/\sigma =0.075$)

At midspan (Fig. 9), the predicted loads with both GDW and FW show a too small peak-to-peak amplitude and are phase-shifted even more than in the previous figures. The frequency content seems to be better captured with FW instead of GDW.

Fig. 9

Lead-lag bending moment (midspan): wind tunnel test vs. simulations ($\mu =0.30$, $C_T/\sigma =0.075$)

Torsion moment correlation is shown in Fig. 10 for $r/R=0.57$. While waveform and phase correlation between simulations and test results are acceptable, the peak-to-peak load correlation is remarkably poor. A potential reason for this discrepancy is the moderate accuracy of the applied airloads model regarding the aerodynamic pitching moment.

Fig. 10

Torsion moment: wind tunnel test vs. simulations ($\mu =0.30$, $C_T/\sigma =0.075$)

As expected, the simulation fidelity does not reach the level of state-of-the-art rotor simulations such as coupled CFD and comprehensive analysis. Nevertheless, waveforms are properly covered and load magnitudes are of reasonable size. The exception is the magnitude of the torsion moment, for which simulation results require a critical review. Concerning the phase discrepancies, errors could result not only from the simulation but also from the wind tunnel test measurements. The comparison of the two test runs reveals a phase difference of approximately 10–15°, which suggests problems with the rotor azimuth measurement.

The goal of the current study is not a perfectly accurate prediction of loads, but the understanding of the coupling mechanism between the main rotor and the drivetrain. First, this requires the capability to simulate coupled rotor-drivetrain modes. Second, aeromechanic phenomena and the resulting blade loads have to be covered plausibly, as shown above. Hence, this medium-fidelity simulation is well suited for the investigation of the drivetrain influence on the blade loads.

3 Influence of the Bo105 drivetrain

To obtain strong excitations of rotor-drivetrain modes, two flight states with large aerodynamic load variations at the rotor blades are investigated, as summarized in Table 2.

Table 2 Investigated flight states

These are the cruise flight, to which the previously presented comparison with wind tunnel test data refers to, as well as a state with high blade loading $C_\mathrm {T}/\sigma =0.120$. The resulting changes in blade loads caused by the drivetrain are qualitatively similar for the two states, although the drivetrain effect is larger for the high blade loading state. However, for consistency with the wind tunnel test comparison, only the cruise flight state is discussed in the text, whereas the corresponding results for the high blade loading state are given in “Appendix”. All loads are measured in the blade section-fixed reference frame, i.e. blade pitch motion and deformation are taken into account for the direction of load measurements. As before, the structural damping is set to $d_\mathrm {s} = 0.5 \cdot 10^{-4}\,\mathrm {s}$. Blade loads are presented for an inboard ($r/R=0.22$) and a midspan ($r/R=0.57$) radial station, the latter being identical to that of the wind tunnel test comparison above.

If a drivetrain model is applied ($\varOmega \ne {\text {const}}.$), the presentation of loads vs. rotor azimuth needs to be questioned because the latter is defined by the rotor hub rotation which is subject to oscillations. Strictly speaking, the waveforms of loads vs. rotor azimuth consequently do not equal those of loads vs. time, as it is the case for the baseline case $\varOmega = {\text {const}}.$ However, the oscillation magnitudes of the hub rotation are smaller than $0.12$° for all results presented in this paper. Hence, the rotor hub rotation is an appropriate reference to present loads not only for the baseline case but also for simulations with drivetrain.

Figure 11 depicts the flap, lead-lag and torsion moments at the inboard station as a function of the rotor azimuth. The graphs present results of both the baseline case ($\varOmega = {\text {const}}.$) and a simulation with the full Bo105 drivetrain model, wherein the hub speed $\varOmega$ is governed by models of the Allison 250-C20B engines and corresponding fuel controllers (“Full DT, native $\varOmega$-control”). The flap moment (above) is barely affected. For the lead-lag moment (middle), the waveforms of both cases are also similar, while the drivetrain leads to stronger higher harmonic content. The torsion moment (below) with and without drivetrain is almost identical.

Fig. 11

Rotor blade moments: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.30$, $C_T/\sigma =0.075$)

At midspan (Fig. 12), the situation is similar: Flap and torsion moments (above and below) hardly change due to the influence of the drivetrain, while the lead-lag moment (middle) is noticeably affected. Compared to the inboard station, the deviation between the lead-lag moments with and without drivetrain is clearly larger.

Fig. 12

Rotor blade moments: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.30$, $C_T/\sigma =0.075$)

As expected, the strongest effect of the drivetrain is observed for the loads in lead-lag direction at both the inboard and the midspan radial station. The following discussion will consequently focus on lead-lag loads.

The relatively low deviation of baseline and drivetrain case in the inboard lead-lag moment (Fig. 11 middle) is explained by the dominance of the $1/{\text {rev}}$ magnitude in the inboard lead-lag moment spectrum (cf. Fig. 13). Rotor-drivetrain modes are primarily excited in blade passage frequency $4\,\varOmega _\mathrm {ref}$ (all 4 blades contribute equally, but shifted in phase). Consequently, the $1/{\text {rev}}$ magnitude in Fig. 13 does not change due to the drivetrain. In accordance with the observations in [7,8,9], the $4/{\text {rev}}$ magnitude changes noticeably. With drivetrain, it is more than twice as large as in the baseline case, although the load level remains low compared to the previous harmonics. As the next integer multiple of the blade number harmonic, the $8/{\text {rev}}$ magnitude is affected. In the baseline case, it almost vanishes. With drivetrain, in contrast, it is even larger than the $4/{\text {rev}}$ magnitude.

Fig. 13

Lead-lag moment magnitudes: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.30$, $C_T/\sigma =0.075$)

The drivetrain may also reduce $4/{\text {rev}}$ lead-lag loads, as observed at the midspan station (Fig. 14) with a decrease of $55\%$. In relation to the $1/{\text {rev}}$ magnitude, the $4/{\text {rev}}$ magnitude at midspan is stronger than inboard, which explains the larger visibility of the drivetrain influence in the midspan lead-lag load waveforms (Fig. 12) compared to the inboard station (Fig. 11). The load-increasing effect on the $8/{\text {rev}}$ harmonic is again very strong. The effects of the drivetrain on the $4/{\text {rev}}$ and $8/{\text {rev}}$ lead-lag moments will be further examined in Sect. 5.

Fig. 14

Lead-lag moment magnitudes: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.30$, $C_T/\sigma =0.075$)

Figure 15 shows the radial courses of the $4/{\text {rev}}$ lead-lag moment magnitudes with and without drivetrain. The differences are attributed to the modified shape of the $\mathrm {RD}_\mathrm {L2}$ mode (Fig. 4) with respect to the baseline L2 mode. The above presented radial stations $r/R=0.22$ and $r/R=0.57$ show large $4/{\text {rev}}$ lead-lag moment differences between baseline and drivetrain. Contrarily, at $r/R=0.15$ and $r/R=0.29$, the $4/{\text {rev}}$ lead-lag moments are identical, and thus the drivetrain influence is small at these radial stations.

Fig. 15

$4/{\text {rev}}$ Lead-lag moment magnitudes vs. rotor radius: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.30$, $C_T/\sigma =0.075$)

4 Suitability of reduced models

Apart from the full drivetrain with native $\varOmega$-control, three further drivetrain models are assessed regarding their capability to accurately capture the dynamic influence of the drivetrain on the main rotor in steady flight. These are the full drivetrain model with simplified $\varOmega$-control, the condensed drivetrain model $\left[ J_\mathrm {DT}, k_\mathrm {DT}\right]$ with simplified $\varOmega$-control and the minimal drivetrain model $\left[ k_\mathrm {DT}^*\right]$, as presented in Fig. 5. “Simplified $\varOmega$-control” denotes the PI-feedback of rotor speed deviation on engine torque, while no actual engine model is used.

Remarkably, all these models yield identical blade loads, as shown exemplary in Fig. 16 for the lead-lag moment at $r/R=0.57$ in cruise flight. The graphs are hardly distinguishable. This observation shows that the simplified drivetrain models of Fig. 5 (middle and right) are capable of predicting the drivetrain influence on blade loads in steady flight, if (and this is a necessary requirement) the drivetrain parameters are adapted such that the rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ equals that of the full drivetrain model. In turn, a proper classification of any drivetrain model regarding its effect on blade loads in steady flight is the resulting eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ of the coupled rotor-drivetrain system, or, to keep it general, the eigenfrequencies of coupled rotor-drivetrain modes near the blade passage frequency. The dynamics of a governor-controlled gas turbine engine (no FADEC investigated here) does not influence the blade loads in steady flight.

Fig. 16

Lead-lag moment in baseline case ($\varOmega _\mathrm {hub} = {\text {const}}.$) and with various drivetrain models, each of them adapted to accurately represent the dynamic properties of the drivetrain ($\mu =0.30$, $C_T/\sigma =0.075$)

Since the reduced models feature much less parameters than the full drivetrain model, they are especially useful for sensitivity analysis. By variation of only one or two parameters, $\omega _{\mathrm {RD}_\mathrm {L2}}$ can be modified in a wide range. Furthermore, if a drivetrain model would need to be identified from a vibration test of a real helicopter, the system identification of the reduced models is simpler than that of the full drivetrain model.

5 Loads sensitivity to drivetrain properties

The results presented previously are based on the Bo105 drivetrain properties as determined in [10]. Due to modeling inaccuracies, the inertia and stiffness distribution could diverge in reality. Furthermore, the understanding of the blade loads sensitivity to drivetrain properties would be beneficial for the evaluation of other rotor-drivetrain systems or the design of new ones.

To keep a clear overview of parameter variations, the condensed model $\left[ J_\mathrm {DT}, k_\mathrm {DT}\right]$ is utilized for the sensitivity analysis instead of the full drivetrain model. Figure 17 shows the eigenfrequency of the $\mathrm {RD}_\mathrm {L2}$ mode as a function of $J_\mathrm {DT}$ and $k_\mathrm {DT}$, varying in a wide range of five orders of magnitude each. To generate Fig. 17, flap and torsion modes have been suppressed to prevent $\mathrm {RD}_\mathrm {L2}$ from coupling with them.⁵ However, all other results in this analysis are based on coupled blade modes. The baseline mode $\mathrm {L2}$ with quasi-infinite drivetrain inertia and stiffness⁶ is marked in grey to the left of Fig. 17, while the Bo105 configuration $[J_\mathrm {DT,Bo105}, k_\mathrm {DT,Bo105}]$ is marked in red. Note that prior to this chapter, the additional subscript “Bo105” has been omitted for simplicity, while $J_\mathrm {DT} = J_\mathrm {DT,Bo105}$ and $k_\mathrm {DT} = k_\mathrm {DT,Bo105}$ have been implied. Since the drivetrain influence on loads is completely determined through the value of $\omega _{\mathrm {RD}_\mathrm {L2}}$, the origin of changes in $\omega _{\mathrm {RD}_\mathrm {L2}}$ (whether $J_\mathrm {DT}$ or $k_\mathrm {DT}$) is not relevant for the drivetrain influence on blade loads. Around the Bo105 configuration, $\omega _{\mathrm {RD}_\mathrm {L2}}$ is more sensitive to $k_\mathrm {DT}$ than to $J_\mathrm {DT}$. Consequently, $k_\mathrm {DT}$ is chosen for the analysis of blade loads sensitivity to drivetrain properties.

Fig. 17

Eigenfrequency variation of $\mathrm {RD}_\mathrm {L2}$ mode due to simultaneous changes in $J_\mathrm {DT}$ and $k_\mathrm {DT}$

By use of the coupled (flap/lag/torsion) blade model with $J_\mathrm {DT} = J_\mathrm {DT,Bo105}$ and varying $k_\mathrm {DT}$, $\omega _{\mathrm {RD}_\mathrm {L2}}$ reaches values between $3.17\,\varOmega _\mathrm {ref}$ and $4.51\,\varOmega _\mathrm {ref}$ (cf. Fig. 18). With this range, all constructionally feasible drivetrain configurations are covered. The configuration $[J_\mathrm {DT,Bo105}, k_\mathrm {DT,Bo105}]$ is highlighted. At $\omega _{\mathrm {RD}_\mathrm {L2}} / \varOmega _\mathrm {ref} = 3.68$, the graph is interrupted due to the crossing of $\omega _{\mathrm {RD}_\mathrm {L2}}$ and $\omega _{\mathrm {RD}_\mathrm {T1}}$ with the necessary reassignment of modes. This discontinuity will also be visible in the following figures presenting the $4/{\text {rev}}$ magnitudes.

Fig. 18

Drivetrain stiffness $k_\mathrm {DT}$ corresponding to $\omega _{\mathrm {RD}_\mathrm {L2}}$. Left of $\omega _{\mathrm {RD}_\mathrm {L2}} / \varOmega _\mathrm {ref} = 3.68$: $\omega _{\mathrm {RD}_\mathrm {L2}} < \omega _{\mathrm {RD}_\mathrm {T1}}$. Right of $\omega _{\mathrm {RD}_\mathrm {L2}} / \varOmega _\mathrm {ref} = 3.68$: $\omega _{\mathrm {RD}_\mathrm {L2}} > \omega _{\mathrm {RD}_\mathrm {T1}}$

The sensitivity analysis is conducted for both the cruise flight state (discussed in the text) and the high blade loading flight state (results given in “Appendix”). Beside $k_\mathrm {DT}$, the structural damping is varied to capture its influence on loads. The applied values are $d_\mathrm {s} = 0.5 \cdot 10^{-4}\,\mathrm {s}$ (low), $d_\mathrm {s} = 1 \cdot 10^{-4}\,\mathrm {s}$ (medium) and $d_\mathrm {s} = 2 \cdot 10^{-4}\,\mathrm {s}$ (high). Since the drivetrain predominantly affects the $4/{\text {rev}}$ harmonic (cf. Fig. 13 and Fig. 14), the sensitivity analysis focuses on $4/{\text {rev}}$ lead-lag loads. A brief consideration of $8/{\text {rev}}$ content will follow later.

5.1 4/rev magnitudes

Any coupling between the rotor and the drivetrain is observable at the rotor hub. A coupled rotor-drivetrain mode (e. g. $\mathrm {RD}_\mathrm {L2}$, Fig. 4) always features a hub oscillation, unless a node of the torsional drivetrain deformation is located in the rotor hub. However, in the latter case, a baseline simulation with a constrained rotor hub $\varOmega = {\text {const}}.$ would yield identical results for rotor blade motion and loads, i. e. rotor and drivetrain would be dynamically decoupled. Consequently, the hub speed magnitude serves as a measure of rotor-drivetrain interaction.

Figure 19 depicts the $4/{\text {rev}}$ hub speed magnitude. Note that the diagram looks similar to the amplitude response of an underdamped harmonic oscillator (second order system), but the abscissa contains eigenfrequencies instead of excitation frequencies. The maximum interaction occurs at $\omega _{\mathrm {RD}_\mathrm {L2}} \approx 3.97\,\varOmega _\mathrm {ref}$, which is almost the blade passage frequency (resonance condition). There, a hub speed magnitude of $0.055\,\mathrm {rad}/\mathrm {s}$ is reached with low $d_\mathrm {s}$, which is equivalent to a magnitude of approximately $0.02$° in azimuth. Around the resonant condition, the magnitude noticeably depends on the structural damping. With $d_\mathrm {s} = 2 \cdot 10^{-4}\,\mathrm {s}$, the maximum magnitude is $33\,\%$ lower than with $d_\mathrm {s} = 0.5 \cdot 10^{-4}\,\mathrm {s}$.

Fig. 19

Sensitivity of $4/{\text {rev}}$ hub speed magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ ($\mu =0.30$, $C_T/\sigma =0.075$)

The Bo105 drivetrain causes an eigenfrequency of $\omega _{\mathrm {RD}_\mathrm {L2}}=3.52\,\varOmega _\mathrm {ref}$ clearly below the resonant condition (diamond mark). This results in $31\,\%$ [$46\,\%$] of the $4/{\text {rev}}$ hub speed magnitude of the resonant condition with low [high] $d_\mathrm {s}$. The diamond mark is far from resonance, and consequently the $4/{\text {rev}}$ hub speed magnitude is insensitive to the variation of $d_\mathrm {s}$ in the investigated range. A very high drivetrain stiffness $k_\mathrm {DT} \approx 14\cdot k_\mathrm {DT,Bo105}$ may shift the $\mathrm {RD}_\mathrm {L2}$ mode to the baseline eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}} = \omega _\mathrm {L2} = 4.33\,\varOmega _\mathrm {ref}$ (depicted as a triangle), decoupling the rotor from the drivetrain.⁷

The sensitivity of the $4/{\text {rev}}$ inboard lead-lag load magnitude to $\omega _{\mathrm {RD}_\mathrm {L2}}$ is presented in Fig. 20. The graphs look very similar to those of Fig. 19. Compared to the baseline case (green triangle), the $4/{\text {rev}}$ lead-lag moment magnitude of the Bo105 (green diamond) is raised by a factor of 2.2 due to the drivetrain.

Fig. 20

Sensitivity of $4/{\text {rev}}$ inboard lead-lag moment magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ ($\mu =0.30$, $C_T/\sigma =0.075$)

If the drivetrain would be poorly designed and feature a stiffness 3.5 times as large as that of the actual Bo105 drivetrain (leading to $\omega _{\mathrm {RD}_\mathrm {L2}}\approx 3.97\,\varOmega _\mathrm {ref}$), the $4/{\text {rev}}$ lead-lag moment magnitude would be 4.4 times larger than for the actual Bo105 case (diamond) and even 9.6 times larger than for the baseline case (triangle) with low $d_\mathrm {s}$. This shows that the $4/{\text {rev}}$ harmonic content (or in general: the blade passage frequency content) of the lead-lag loads strongly depends on the design of the drivetrain. For $\omega _{\mathrm {RD}_\mathrm {L2}}>\omega _\mathrm {L2}=4.33\,\varOmega _\mathrm {ref}$, the $4/{\text {rev}}$ inboard lead-lag load magnitude decreases further with growing $\omega _{\mathrm {RD}_\mathrm {L2}}$, although the $4/{\text {rev}}$ hub speed magnitude increases. This shows that a hub oscillation does not necessarily have a load-increasing influence on the blades.

The above described trends for the inboard station are similar at midspan, as depicted in Fig. 21. A difference is the load-decreasing influence of the drivetrain with respect to the baseline case. The $4/{\text {rev}}$ load magnitudes reached in resonant condition are about three times as large as those observed inboard. Compared to the Bo105 configuration, the $4/{\text {rev}}$ magnitudes in resonant condition are one order of magnitude larger with low $d_\mathrm {s}$.

Fig. 21

Sensitivity of $4/{\text {rev}}$ midspan lead-lag moment magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ ($\mu =0.30$, $C_T/\sigma =0.075$)

Of course, the simulated magnitudes of hub speed and loads in resonant condition exhibit large uncertainties due to the strong sensitivity to structural damping. The resulting $\mathrm {RD}_\mathrm {L2}$ damping ratios for the investigated ranges of $k_\mathrm {DT}$ and $d_\mathrm {s}$ are listed in Table 3. In resonant condition, D lies between $0.41\,\%$ and $1.10\,\%$ for the applied values of $d_\mathrm {s}$, which is a reasonable range. An even smaller damping could cause not only stronger loads, but also instability. In the design of a helicopter, a resonant rotor-drivetrain system with $\omega _{\mathrm {RD}_\mathrm {L2}}\approx 4\,\varOmega _\mathrm {ref}$ should therefore be avoided in any case.

Table 3 Resulting damping ratios D of the $\mathrm {RD}_\mathrm {L2}$ mode of the condensed model $\left[ J_\mathrm {DT}, k_\mathrm {DT}\right]$ for different values of $k_\mathrm {DT}$ with low, medium and high $d_\mathrm {s}$

5.2 8/rev magnitudes

As already mentioned, the rotor-drivetrain system is predominantly excited in blade passage frequency $4\,\varOmega _\mathrm {ref}$. For non-sinusoidal excitations such as airloads, higher harmonic content is concurrently included. Hence, beside $4/{\text {rev}}$, $8/{\text {rev}}$ harmonics of hub speed and blade loads are significantly influenced by the drivetrain. Figures 13 and 14 have shown this for the loads. This section treats the $8/{\text {rev}}$ sensitivity analysis for the cruise flight state ($\mu =0.30$, $C_T/\sigma =0.075$).

For the assessment of $4/{\text {rev}}$ magnitudes, a coupled rotor-drivetrain mode with an eigenfrequency near $4\,\varOmega _\mathrm {ref}$ (namely $\mathrm {RD}_\mathrm {L2}$) had been used to characterize the drivetrain concerning its influence on blade loads. Analogously, for assessment of $8/{\text {rev}}$ magnitudes, coupled rotor-drivetrain modes near $8\,\varOmega _\mathrm {ref}$ are relevant. In the case of the Bo105, this is obviously the $\mathrm {RD}_\mathrm {L3}$ mode with an eigenfrequency of $\omega _{\mathrm {RD}_\mathrm {L3}}=7.87\,\varOmega _\mathrm {ref}$ (cf. Table 1). Due to the modification of $k_\mathrm {DT}$ in the condensed drivetrain model $\left[ J_\mathrm {DT}, k_\mathrm {DT}\right]$ (same range as in $4/{\text {rev}}$ assessment), $\omega _{\mathrm {RD}_\mathrm {L3}}$ reaches values between $7.22\,\varOmega _\mathrm {ref}$ and $11.48\,\varOmega _\mathrm {ref}$.

Figure 22 presents the sensivity of the $8/{\text {rev}}$ hub speed magnitude to $\omega _{\mathrm {RD}_\mathrm {L3}}$. The discontinuities at $\omega _{\mathrm {RD}_\mathrm {L3}} / \varOmega _\mathrm {ref} \approx 7.4$, 9.7 and 10.7 (the latter two appear as a pair of dots each) originate from the crossing of $\omega _{\mathrm {RD}_\mathrm {L3}}$ with $\omega _\mathrm {F4}$, $\omega _{\mathrm {RD}_\mathrm {T2}}$ and $\omega _\mathrm {F5}$, respectively, with the necessary reassignment of modes. The Bo105 configuration (diamond) constitutes the “worst case”, as it lies in the resonant condition.

Fig. 22

Sensitivity of $8/{\text {rev}}$ hub speed magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L3}}$ ($\mu =0.30$, $C_T/\sigma =0.075$)

Due to resonance, the $8/{\text {rev}}$ midspan lead-lag load magnitude of the Bo105 configuration is very large compared to the baseline case, as shown in Fig. 23 and already observed in Fig. 14.

Fig. 23

Sensitivity of $8/{\text {rev}}$ midspan lead-lag moment magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L3}}$ ($\mu =0.30$, $C_T/\sigma =0.075$)

To conclude the sensitivity analysis, hub speed and lead-lag load magnitudes at blade passage frequency and related higher harmonics strongly depend on the proximity of coupled rotor-drivetrain mode eigenfrequencies to these harmonics. This has been demonstrated for the $4/{\text {rev}}$ and $8/{\text {rev}}$ harmonics. The eigenfrequencies of coupled rotor-drivetrain modes depend on the baseline rotor modes as well as the drivetrain properties. Beside the drivetrain stiffness that has been varied in the present analysis, also the drivetrain inertia affects the rotor-drivetrain modes, as documented in [10]. However, the eigenfrequencies alone sufficiently characterize the drivetrain regarding its influence on the blade loads.

The presented cruise flight state causes relatively low $4/{\text {rev}}$ lead-lag load magnitudes. In the high blade loading state, the results of which are presented in “Appendix”, the $4/{\text {rev}}$ lead-lag load magnitudes are more dominant in the load spectrum, especially at the midspan station (cf. Fig. 30). The drivetrain effect is therefore stronger in the high blade loading state. The $4/{\text {rev}}$ magnitudes reached in resonant condition (Figs. 32, 33 and 34) are more than 6 times higher than those of the cruise flight state (Figs. 19, 20 and 21).

6 Potential to improve lead-lag load prediction

As presented above, the drivetrain has a considerable influence on the lead-lag moment at blade passage frequency and higher harmonics. The correlation between simulation and wind tunnel test measurement in Fig. 9 can therefore be improved by application of a drivetrain model. Figure 24 shows the azimuthal waveforms of the midspan lead-lag moment of the test and the simulations with GDW. Apart from the baseline case with $\varOmega = {\text {const}}.$ (red), the whole series of condensed drivetrain models $\left[ J_\mathrm {DT}, \text {varying } k_\mathrm {DT}\right]$ from the sensitivity analysis has been applied (grey). Unfortunately, the structural data of the rotor test apparatus (RTA) used in the wind tunnel was unavailable upon request. The RTA is suspected to be stiffer than the drivetrain of the Bo105 flight vehicle. The case with the stiffness $k_\mathrm {DT,mod} = 1.8 \cdot k_\mathrm {DT,Bo105}$ represents the potential RTA property and is highlighted in blue. It appears somewhat nearer to the test measurements than the baseline case.

Fig. 24

Improvement of midspan lead-lag moment prediction by application of condensed drivetrain model $\left[ J_\mathrm {DT}, k_\mathrm {DT}\right]$ with GDW ($\mu =0.30$, $C_T/\sigma =0.075$)

However, a significant prediction improvement can only be achieved in conjunction with a more accurate aerodynamic model. Figure 25 presents the baseline case as well as the simulation with $\left[ J_\mathrm {DT}, k_\mathrm {DT,mod}\right]$, both of them featuring the FW as inflow model. The simulation with drivetrain yields a clearly better fit of the waveform. A phase shift similar to those in Figs. 7, 8 and 10 remains. As mentioned in the beginning, it could be attributed to deficiencies in both the measurements and the modeling.

Fig. 25

Improvement of midspan lead-lag moment prediction by application of condensed drivetrain model $\left[ J_\mathrm {DT}, k_\mathrm {DT,mod}\right]$ with FW ($\mu =0.30$, $C_T/\sigma =0.075$)

To quantify the correlation, Fig. 26 shows the harmonic magnitudes of baseline and drivetrain models with GDW and FW, compared to the test. In the baseline case, the replacement of GDW by FW improves the $4/{\text {rev}}$ magnitude already substantially. However, by application of the drivetrain model with FW, the correlation of the $4/{\text {rev}}$ magnitude is further improved. Moreover, the $8/{\text {rev}}$ magnitude is better captured with drivetrain since it practically vanishes in the baseline simulations.

Fig. 26

Harmonic magnitudes of midspan lead-lag moment: Wind tunnel test, baseline simulations and simulations with condensed drivetrain model $\left[ J_\mathrm {DT}, k_\mathrm {DT,mod}\right]$. ($\mu =0.30$, $C_T/\sigma =0.075$)

The precise quantification of the drivetrain impact on the $4/{\text {rev}}$ and $8/{\text {rev}}$ lead-lag loads measured in the wind tunnel test is not possible for the following reasons:

• The simulation approach has medium-fidelity.

• Phase shifts could be attributed to both the simulation results and the wind tunnel test measurements.

• The structural properties of the RTA are unknown.

However, it has been demonstrated that the drivetrain clearly affects the $4/{\text {rev}}$ and $8/{\text {rev}}$ lead-lag loads and contributes to a better correlation. Beside the improvement of the aerodynamic model, the application of a drivetrain model is, therefore, a valuable measure to improve the simulation.

7 Conclusions and outlook

Rotor and drivetrain dynamics are coupled via the rotor hub’s rotational degree of freedom. This coupling causes the collective lead-lag modes of the main rotor to transform to rotor-drivetrain modes with a related shift in eigenfrequency. The dynamic response of the Bo105 rotor-drivetrain system has been assessed by numerical simulations of a wind tunnel case for cruise flight and high blade loading.

In comparison to a baseline case with constant rotor hub speed, the inclusion of a drivetrain model changes the lead-lag loads of the rotor blades, while the effect on flap and torsion loads is small. The drivetrain primarily changes the harmonic magnitudes at blade passage frequency and its multiple harmonics, since these are the predominant excitation frequencies of rotor-drivetrain modes. Hence, the drivetrain influence is most significant where the blade passage frequency harmonics are a major part of the load spectrum. Contrarily, the influence is relatively small where other harmonics dominate the load spectrum (inboard: large $1/{\text {rev}}$ loads). At some radial stations, blade passage frequency harmonics of the lead-lag loads with and without drivetrain are identical, regardless of the magnitude.

To capture the drivetrain influence on the blade loads in steady flight, reduced drivetrain models are applicable with good accuracy. These may consist of one inertia and one stiffness element with simple rotor speed control or even of one stiffness element only. The dynamics of governor-controlled gas turbine engines do not affect blade loads in steady flight.

The necessary and sufficient requirement of a reduced model is that it yields the correct eigenfrequency of any coupled rotor-drivetrain mode near the blade passage frequency. In the case of the Bo105 helicopter, this is the $\mathrm {RD}_\mathrm {L2}$ mode. The corresponding eigenfrequency classifies the drivetrain concerning its influence on hub vibration and blade loads. To avoid high rotor hub speed oscillations and lead-lag load magnitudes at blade passage frequency, a drivetrain system should be designed such that a sufficient distance between the coupled rotor-drivetrain mode and the blade passage frequency is kept.

By inclusion of a drivetrain model in rotor simulation, the prediction of lead-lag load magnitudes at blade passage frequency could be improved. This has been demonstrated by the comparison of simulation results and wind tunnel test measurements for a midspan radial station. However, a significant improvement requires, beside the drivetrain model, an accurate aerodynamic model (in this case: FW instead of GDW).

The future work in the context of rotor-drivetrain interaction will include the examinations of further flight states such as the transition (low $\mu$), where blade-wake interactions are known to cause strong vibratory loads. In these examinations, simulations with CFD could help to quantify the drivetrain influence in test measurements more precisely. Furthermore, it is planned to assess an articulated rotor system to demonstrate the applicability of the current findings on a hinged blade attachment.

On top of that, the inclusion of the airframe and the investigation of coupled rotor-drivetrain-airframe modes are of great interest. With such an extended model, interactions in the hub’s remaining degrees of freedom (not limited to hub rotation) and their impact on loads in the subsystems can be examined. Finally, a free flight trim as well as maneuvers inducing transient rotor-drivetrain (-airframe) dynamics may be investigated.

Appendix

In the paper, the drivetrain influence on blade loads has been presented and discussed for the cruise flight state ($\mu =0.30$, $C_T/\sigma =0.075$). Figures 27, 28, 29, 30, 31, 32, 33, 34, 35 and 36 show the corresponding graphs for the high blade loading state ($\mu =0.24$, $C_T/\sigma =0.120$). Figure 37 is a schematic to illustrate the mode reassignment in coupling regions in a frequency diagram. 

Fig. 27

Rotor blade moments: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 28

Rotor blade moments: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 29

Lead-lag moment magnitudes: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 30

Lead-lag moment magnitudes: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 31

$4/{\text {rev}}$ Lead-lag moment magnitudes vs. rotor radius: baseline ($\varOmega _\mathrm {hub} = {\text {const}}.$) and full drivetrain model ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 32

Sensitivity of $4/{\text {rev}}$ hub speed magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 33

Sensitivity of $4/{\text {rev}}$ inboard lead-lag moment magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 34

Sensitivity of $4/{\text {rev}}$ midspan lead-lag moment magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L2}}$ ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 35

Sensitivity of $8/{\text {rev}}$ hub speed magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L3}}$ ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 36

Sensitivity of $8/{\text {rev}}$ midspan lead-lag moment magnitude to the coupled rotor-drivetrain eigenfrequency $\omega _{\mathrm {RD}_\mathrm {L3}}$ ($\mu =0.24$, $C_T/\sigma =0.120$)

Fig. 37

Schematic of coupling between $\mathrm {RD}_\mathrm {L2}$ and some other mode in a frequency diagram