Unlocking a nose landing gear in different flight conditions: folds, cusps and a swallowtail

Abstract

This paper investigates the unlocking of a non-conventional nose landing gear mechanism that uses a single lock to fix the landing gear in both its downlocked and uplocked states (as opposed to having two separate locks as in most present nose landing gears in operation today). More specifically, we present a bifurcation analysis of a parameterized mathematical model for this mechanical system that features elastic constraints and takes into account internal and external forces. This formulation makes it possible to employ numerical continuation techniques to determine the robustness of the proposed unlocking strategy with respect to changing aircraft attitude. In this way, we identify as a function of several parameters the steady-state solutions of the system, as well as their bifurcations: fold bifurcations where two steady states coalesce, cusp points on curves of fold bifurcations, and a swallowtail bifurcation that generates two cusp points. Our results are presented as surfaces of steady states, joined by curves of fold bifurcations, over the plane of retraction actuator force and unlock actuator force, where we consider four scenarios of the aircraft: level flight; steep climb; steep descent; intermediate descent. A crucial cusp point is found to exist irrespective of aircraft attitude: it corresponds to the mechanism being at overcentre, which is a position that creates a mechanical singularity with respect to the effect of forces applied by the actuators. Furthermore, two cusps on a key fold locus are unfolded in a (codimension-three) swallowtail bifurcation as the aircraft attitude is changed: physical factors that create these bifurcations are presented. A practical outcome of this research is the realization that the design of this and other types of landing gear mechanism should be undertaken by considering the effects of forces over considerable ranges, with a special focus on the overcentre position, to ensure a smooth retraction occurs. More generally, continuation methods are shown to be a valuable tool for determining the overall geometric structure of steady states of mechanisms subject to (external) forces.

1 Introduction

Landing gears on aircraft are designed to absorb ground loads during landing and taxiing. They have evolved over time from fixed external structures into mechanisms that are retracted when an aircraft becomes airborne. In order to transform from a mechanism to a structure, a modern retractable landing gear requires locking mechanisms to fix (or lock) its position in one of two states: when the aircraft is in contact with the ground, the landing gear needs to be fixed in its fully deployed position, or be downlocked; when the aircraft is flying, the landing gear needs to be fixed in its fully retracted position, or be uplocked. The design of a modern landing gear therefore requires consideration of its motion as a mechanism.

Traditional literature on landing gear mechanism analysis [1,2,3,4] considers the kinematics of a landing gear, with the aim of ensuring that retraction is achievable from a geometric perspective. Once initial analytical work has been conducted, landing gear designers in industry perform time history simulations with dynamic models of landing gear mechanisms. These models are created by using multibody dynamic simulation software, such as ADAMS [5] or SimMechanics [6], and incorporate further details of a landing gear’s design. Such an approach is also widely adopted in academic literature on landing gear analysis [7,8,9]. For engineers in industry, the advantage of using multibody simulation for landing gear mechanism design/analysis is that the dynamic models are straightforward to construct, and the respective software package can be used for multiple applications beyond mechanism analysis.

Although time history simulations are useful for investigating transient dynamic behaviour, it can be time-consuming to investigate the variation of long-term dynamics throughout a parameter space, due to the need for long simulations to be repeated for many different parameter values. Furthermore, crucial points that govern dynamic behaviour (such as bifurcations or unstable equilibria) are difficult to identify in this way. Moreover, while kinematic and simulation approaches are still used in current landing gear mechanism research [10, 11], increasing complexities associated with modern landing gear mechanisms have pushed researchers to explore different approaches for performing landing gear mechanism analysis—with a view to identifying methods that could be adopted within industrial design and analysis practices.

One approach to overcome these difficulties, from the field of dynamical systems theory, is numerical continuation. This techniques allows one to compute branches of different types of dynamic features, including equilibria, periodic orbits and their bifurcations under the simultaneous variation of one or more parameters. This is achieved, for suitably formulated models such as systems of differential equations, by setting up root finding problems whose solution branches are then solved, as a function of a continuation parameter, by combining prediction of nearby solutions with Newton-Raphson iterations. In particular, this allows one to find steady-state solutions as zeros of the governing system. Approaches with the latter capability, such as polynomial continuation, have been used as mechanism kinematic analysis methods for many years [12,13,14]. However, numerical continuation methods are able to additionally determine dynamic stability information and detect bifurcations. Bifurcation detection is achieved by checking bifurcation conditions, which for steady states either encode changes of stability (eigenvalues of the Jacobian matrix with zero real parts) or changes of certain higher-order terms. Appending such additional conditions to the original system of equations gives an extended root finding problem, whose solution branches trace the locus of the respective bifurcation points when an additional parameter is allowed to vary. The interested reader may refer to a variety of different texts [15,16,17,18] for further background information on bifurcation theory and numerical continuation methods.

These techniques have been implemented and are available as software packages, such as the numerical continuation code AUTO [19], and have been employed successfully in a variety of engineering disciplines, including a range of aerospace applications [20,21,22,23,24]. The more recent integration of numerical continuation software with SimMechanics [25] has made these tools more accessible to industrial engineers. This culminated in their adoption by Airbus as an analysis tool [26], with the specific suggestion that they be adopted for landing gear mechanism design and analysis.

Numerical continuation methods have to date been used to analyse conventional landing gear mechanisms [27,28,29,30] as well as some non-conventional ones with multiple sidestays [31, 32] or single lock mechanisms [33, 34]. In all cases, ensuring that the landing gear can be locked is critical to demonstrate its functionality—yet difficulties have been identified with both multiple side stay and single lock mechanisms. Current research has identified that fold bifurcations of steady states play an important role in separating these locked and unlocked positions [32, 33]. Some of these key bifurcations persist under parameter changes or variations in external loading conditions, whilst others do not [34]. Given the influence that these bifurcations can have on a landing gear mechanism’s operation, it is important for engineers to understand the physical interpretation of these types of bifurcations of steady states, and the conditions under which they persist. Without such knowledge, engineers risk designing landing gear mechanisms that may not function as expected under certain conditions, potentially leading to operational failures.

This paper presents an in-depth study of the unlocking process for a non-conventional landing gear mechanism: conventional landing gear designs use two different mechanisms to downlock and uplock the landing gear; the landing gear mechanism considered in this work uses a single mechanism to both downlock and uplock the nose landing gear. Such a mechanism offers weight savings over conventional designs, because there is no need for a separate uplock mechanism and actuator. The trade-off is that the process of unlocking the landing gear from uplock becomes more complicated, as the unlock and retraction actuator forces can work against each other. This negative coupling can be avoided by using a force measure, rather than the conventional proximity sensor, to define when the landing gear is unlocked from uplock [33]. Recent work [34] has shown that the use of a force measure prevents the unlock and retraction forces from working against each other, even under varying external (steady) load conditions; however, this does not explain the physical reasoning behind this observation. The bifurcation study presented here aims to investigate the unlocking from uplock of a single lock landing gear, to explain when and why this process is robust to changes in aircraft attitudes. Such changes in aircraft attitude may arise intentionally (due to the aircraft climbing or descending) or as a transient response to gusts or turbulence.

The paper is organised as follows. Section 2 presents some background on nose landing gear mechanisms, introduces the model equations for the specific landing gear mechanism under consideration, and provides a discussion of the motion of the landing gear. Section 3 then presents the in-depth analysis of the effects of aircraft attitude on the unlocking process. The final Sect. 4 provides some concluding remarks.

2 Background and model equations

A retractable nose landing gear of an aircraft conventionally uses planar mechanisms to operate, often as a 4-bar linkage mechanism with some constraints on the motion. While there are a range of differences in configurations, all nose landing gears will feature: a main strut to transfer vertical loads into the fuselage; some supporting elements to resist forces that may cause bending on the main structure; a means to lock the landing gear; sources of actuation to move the landing gear and disengage locks. A landing gear mechanism’s operation can be classified into three distinct phases: unlocking; extension/retraction; locking. The process of locking and unlocking the landing gear turns it from a structure into a mechanism, so that it may be extended or retracted.

Fig. 1

Example nose landing gear mechanisms, shown a downlocked, b retracting/extending and c in the uplocked position

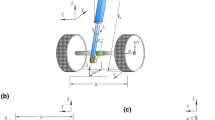
Figure 1 shows a schematic example of a landing gear mechanism in three positions: (a)—deployed and downlocked; (b)—moving between locked states; (c)—retracted and uplocked. The main strut, which is near vertical in the deployed position, is held in place by an overcentre mechanism, consisting of two sidestay links, which are in turn kept in the overcentre position by two lock links; the latter rest against physical stops (not shown) that limit their motion in one direction. When deployed, the vertical load on the landing gear transfers through the sidestays and pushes these stops together, keeping the lock engaged. To retract the landing gear, an unlock actuator is used to move the locklinks directly, unlocking the mechanism by overcoming an energy barrier. A larger retraction actuator is then able to retract the landing gear into the fuselage by rotating it around the rotational joint of the main strut. Once the landing gear has been retracted such that it is entirely stowed in the fuselage, it is clamped in position with a dedicated uplock mechanism. These mechanisms are typically latches that catch part of the landing gear structure, engaging automatically once the landing gear strut reaches its uplocked position. To deploy the landing gear, the uplock mechanism needs to be disengaged: this requires a specific uplock actuator to release the uplock. Conventional landing gears, such as the one shown in Fig. 1, therefore require three actuators, which each add weight and complexity to the landing gear system.

Fig. 2

Downlocked landing gear: a joint naming convention; b exploded view showing gravitational and internal mechanism forces

With appropriate design, it is possible to create a landing gear mechanism that can use the same locking mechanism to both uplock and downlock the landing gear. The landing gear of this type that is the subject of this paper is shown in Fig. 2a in the deployed position, while Fig. 3 shows it in its uplocked position. In contrast to the design in Fig. 1, the locklinks now connect to the main strut, rather than to their own support on the fuselage.

2.1 Mathematical model

The mathematical model of the landing gear in this study is formulated by considering the forces that act on each element of the mechanism shown in Figs. 2 and 3. The links are assumed to be rigid bodies, described in terms of their location and orientation with respect to a global co-ordinate system, and connected to one another by planar rotational joints. Previous work on landing gear mechanisms formulated the model as a set of algebraic equations to describe the mechanism’s equilibrium position in response to externally applied forces [27, 29, 30, 32]. Coetzee developed an approach that enables numerical continuation to be applied directly to mechanism models created in multibody dynamics software packages—a key enabler for their uptake within engineering industrial practice. Here, a mechanism’s rotational joints are replaced with equivalent elastic joints (bushes), which transforms an inelastically constrained system (described mathematically by index-3 differential algebraic equations (DAEs) that standard numerical continuation methods cannot handle) into a system with constraints that can ‘flex’ (described mathematically by ordinary differential equations (ODEs) that are amenable to numerical continuation methods). The key is that the mechanism is not rigid but can ‘flex’ a bit, so that it is described by systems of differential equations with energy barriers. For a landing gear model developed by Coetzee, the error introduced by ‘freeing up’ inelastic constraints in this manner was shown to have a minimal quantitative effect [34]. More generally, models with some flexibility may even provide results that are closer to a real-life system, as the landing gear mechanism also has finite-stiffness joints.

Fig. 3

Uplocked landing gear showing spring placement, unlock force and retraction moment; here ${\mathcal {L}}_{1}$ is the shock strut, ${\mathcal {L}}_{2}$ and ${\mathcal {L}}_{3}$ are the sidestay links, and ${\mathcal {L}}_{4}$ and ${\mathcal {L}}_{5}$ are the locklinks

In this spirit, all of the landing gear’s links are joined to each other in the mathematical model by flexible rotational joints, or bushes [34]. The equations of motion are derived by following a similar approach to that used to formulate the algebraic steady-state equations in earlier works on landing gear mechanism analysis [27, 28, 31, 33]: each individual link within the mechanism is considered in isolation from the rest of the mechanism, and three resulting equations are formed by balancing forces and moments for the link. Internal joint forces are applied at the points on the link where it joins to the rest of the mechanism—typically the end points.

To formulate the model, links are defined in the co-ordinate system indicated in Fig. 2a; all internal forces are indicated in Fig. 2b, where the directions and relative magnitudes of the forces are for illustrative purposes only. In addition to the gravitational and internal forces shown in Fig. 2, there are three ‘external’ forces: an unlock actuator force ($F_{ul}$); a downlock spring force ($F_{sp}$); a retraction actuator force ($F_{ret}$). For generality, the retraction actuator force in this model is applied to act with a constant moment arm ($\frac{L_{1}}{2}$) to create a retraction moment, $M_{ret}=F_{ret}\frac{L_{1}}{2}$. The positions of the external forces and moment are shown for the uplocked landing gear in Fig. 3, with the spring element highlighting the spring force’s line of action. For this model, the unlock actuator acts in the same direction as the downlock spring. Note that Fig. 3 also introduces the naming convention for the five links of the model.

Including these forces, the equations of motion are derived using a sign convention with positive directions as indicated in Fig. 2a. Moments are taken about each link’s centre of gravity. This process provides 15 equations to describe the motion of the mechanism (as in [34]), which are given per link by equations (1)–(5):

$$\begin{aligned} m_{1}\ddot{x}_{1} =&R^D_x-R^{C}_{x}-R^H_x+m_{6}g_{x} \nonumber \\&-F_{ret}\frac{L_{1}}{2}\sin {\theta _{1}}-F_{sp_x}+F_{ul_x}+m_{1}g_{x}; \nonumber \\ m_{1}\ddot{y}_{1} =&R^D_y-R^C_y-R^H_y-m_{6}g_{y} \nonumber \\&+F_{ret}\frac{L_{1}}{2}\cos \theta _{1}-F_{sp_y}+F_{ul_y}-m_{1}g_{y}; \nonumber \\ I_{1}\ddot{\theta }_{1} =&\frac{L_{1}}{2}\cos \theta _{1}(R^D_{y}-m_{6}g_{y}) -\frac{L_{1}}{2}\sin \theta _{1}(R^D_{x}-m_{6}g_{x})\nonumber \\&-(H_x-x_1)R^H_{y} +(H_y-y_1)R^H_{x} -(C_x-x_1)R^C_{y} \nonumber \\&+(C_y-y_1)R^C_{x}. \end{aligned}$$

(1)

$$\begin{aligned} m_{2}\ddot{x}_{2}=&R^B_x-R^A_x+m_{2}g_{x}; \nonumber \\ m_{2}\ddot{y}_{2} =&R^B_y-R^A_y-m_{2}g_{y}; \nonumber \\ I_{2}\ddot{\theta }_{2} =&\frac{L_{2}}{2}\cos \theta _{2}(R^B_y+R^A_y)-\frac{L_{2}}{2}\sin \theta _{2}(R^B_x+R^A_x). \end{aligned}$$

(2)

$$\begin{aligned} m_{3}\ddot{x}_{3}=&R^C_x-R^B_x+R^{Bb}_x+m_{3}g_x ; \nonumber \\ m_{3}\ddot{y}_{3} =&R^C_y-R^B_y+R^{Bb}_y-m_{3}g_y ; \nonumber \\ I_{3}\ddot{\theta }_{3} =&\frac{L_3}{2}\cos \theta _{3}(R^C_{y}+R^B_{y}-R^{Bb}_{y})\nonumber \\&-\frac{L_3}{2}\sin \theta _{3}(R^C_{x}+R^B_{x}-R^{Bb}_{x}) . \end{aligned}$$

(3)

$$\begin{aligned} m_{4}\ddot{x}_{4}=&R^E_{x}-R^{Bb}_{x}+m_{4}g_{x} ; \nonumber \\ m_{4}\ddot{y}_{4} =&R^E_{y}-R^{Bb}_{y}-m_{4}g_{y} ; \nonumber \\ I_{4}\ddot{\theta }_{4} =&\frac{L_{4}}{2}\cos \theta _{4}(R^E_{y}+R^{Bb}_{y})-\frac{L_{4}}{2}\sin \theta _{4}(R^E_{x}+R^{Bb}_{x}).\nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned} m_{5}\ddot{x}_{5}=&R^H_{x}-R^E_{x}+F_{sp_x}-F_{ul_x}+m_{5}g_{x}; \nonumber \\ m_{5}\ddot{y}_{5} =&R^H_{y}-R^E_{y}+F_{sp_y}-F_{ul_y}-m_{5}g_{y}; \nonumber \\ I_{5}\ddot{\theta }_{5} =&\frac{L_5}{2}\cos \theta _{5}(R^H_{y}+R^E_{y})-\frac{L_{5}}{2}\sin \theta _{5}(R^H_{x}+R^E_{x}) . \end{aligned}$$

(5)

Quantities in Eqs. (1)–(5) can be identified with reference to Figs. 2 and 3, noting the convention that (e.g.) $R^A_{x}$ is the component of vector $\mathbf {R_{A}}$ that acts in the global co-ordinate x direction, and $x_{1}$ and $y_{1}$ are the CG co-ordinates for link ${\mathcal {L}}_{1}$. The exception is the force between links ${\mathcal {L}}_{3}$ and ${\mathcal {L}}_{4}$, denoted as $R^{Bb}$. The terms $H_x$, $H_y$, $C_x$ and $C_y$ are the x and y co-ordinates of joints ${\mathbf {C}}$ and ${\mathbf {H}}$.

The equation for the spring force terms $F_{sp_x}$ and $F_{sp_y}$ is given in [34]:

$$\begin{aligned} \begin{aligned} F_{sp_x}=&k_{sp}(x_{1}-x_{5})\left( 1-\frac{l_{us}}{l_{tot}}\right) \\&+c_{sp}\left( (\dot{x}_{1}-\dot{x}_{5})\left( 1-\frac{l_{us}}{l_{tot}}\right) \right. \\&+\frac{(x_{1}-x_{5})}{l_{tot}^{2}}((x_{1}-x_{5})(\dot{x}_{1} -\dot{x}_{5})\\&\left. +(y_{1}-y_{5})(\dot{y}_{1}-\dot{y}_{5})) \right) ; \\ F_{sp_y}=&k_{sp}(y_{1}-y_{5})\left( 1-\frac{l_{us}}{l_{tot}}\right) \\&+c_{sp}\left( (\dot{y}_{1}-\dot{y}_{5}))\left( 1-\frac{l_{us}}{l_{tot}}\right) \right. \\&+\frac{(y_{1}-y_{5})}{l_{tot}^{2}}((x_{1}-x_{5})(\dot{x}_{1} -\dot{x}_{5})\\&\left. +(y_{1}-y_{5})(\dot{y}_{1}-\dot{y}_{5})) \right) , \end{aligned} \end{aligned}$$

(6)

where $l_{us}$ is the unsprung spring length and the total spring length, $l_{tot}=\sqrt{(x_{1}-x_{5})^2+(y_{1}-y_{5})^2}$.

The internal joint forces, for simplicity, are given as [34]:

$$\begin{aligned} \mathbf {R^A} \ =&\ k^A\left[ \begin{array}{l}x_2-\frac{L_2}{2}\cos \theta _2-A_x\\ y_2-\frac{L_2}{2}\sin \theta _2-A_y \end{array} \right] \nonumber \\&+ c^A \left[ \begin{array}{l}{\dot{x}}_2+\frac{L_2}{2}{\dot{\theta }}_2\sin \theta _2 \\ {\dot{y}}_2-\frac{L_2}{2}{\dot{\theta }}_2\cos \theta _2 \end{array} \right] ; \nonumber \\ \mathbf {R^B} \ =&\ k^B \left[ \begin{array}{l}(x_3-\frac{L_3}{2}\cos \theta _3)-(x_2+\frac{L_2}{2}\cos \theta _2) \\ (y_3-\frac{L_3}{2}\sin \theta _3)-(y_2+\frac{L_2}{2}\sin \theta _2) \end{array} \right] \nonumber \\&+ c^B \left[ \begin{array}{l} ({\dot{x}}_3+\frac{L_3}{2}{\dot{\theta }}_3\sin \theta _3)-({\dot{x}}_2 -\frac{L_2}{2}{\dot{\theta }}_2\sin \theta _2) \\ ({\dot{y}}_3-\frac{L_3}{2}{\dot{\theta }}_3\cos \theta _3)-({\dot{y}}_2 +\frac{L_2}{2}{\dot{\theta }}_2\cos \theta _2) \end{array} \right] \ ; \nonumber \\ \mathbf {R^{Bb}}=&\ k^{Bb} \left[ \begin{array}{l}(x_4-\frac{L_4}{2}\cos \theta _4) -(x_3-\frac{L_3}{2}\cos \theta _3) \\ (y_4-\frac{L_4}{2}\sin \theta _4)-(y_3-\frac{L_3}{\sin }\theta _3) \end{array} \right] \nonumber \\&+ c^{Bb} \left[ \begin{array}{l}({\dot{x}}_4+\frac{L_4}{2}{\dot{\theta }}_4\sin \theta _4)-({\dot{x}}_3+\frac{L_3}{2}{\dot{\theta }}_3\sin \theta _3) \\ ({\dot{y}}_4-\frac{L_4}{2}{\dot{\theta }}_4\cos \theta _4)-({\dot{y}}_3-\frac{L_3}{2}{\dot{\theta }}_3\cos \theta _3) \end{array} \right] ; \nonumber \\ \mathbf {R^C} \ =&\ k^C\left[ \begin{array}{l}C_x-(x_3+\frac{L_3}{2}\cos \theta _3) \\ C_y-(y_3+\frac{L_3}{2}\sin \theta _3) \end{array} \right] ; \nonumber \\ \mathbf {R^D} \ =&\ k^D\left[ \begin{array}{l}D_x-(x_1+\frac{L_1}{2}\cos \theta _1) \\ D_y-(y_2+\frac{L_1}{2}\sin \theta _1) \end{array} \right] \nonumber \\&- c^D \left[ \begin{array}{l} {\dot{x}}_1-\frac{L_1}{2}{\dot{\theta }}_1\sin \theta _1 \\ {\dot{y}}_1+\frac{L_1}{2}{\dot{\theta }}_1\cos \theta _1 \end{array} \right] ; \nonumber \\ \mathbf {R^E} \ =&\ k^E \left[ \begin{array}{l}(x_5-\frac{L_5}{2}\cos \theta _5)-(x_4+\frac{L_4}{2}\cos \theta _4) \\ (y_5-\frac{L_5}{2}\sin \theta _5)-(y_4+\frac{L_4}{2}\sin \theta _4) \end{array} \right] \nonumber \\&+ c^E \left[ \begin{array}{l}({\dot{x}}_5+\frac{L_5}{2}{\dot{\theta }}_5\sin \theta _5)-({\dot{x}}_4-\frac{L_4}{2}{\dot{\theta }}_4\sin \theta _4) \\ ({\dot{y}}_5-\frac{L_5}{2}{\dot{\theta }}_5\cos \theta _5)-({\dot{y}}_4+\frac{L_4}{2}{\dot{\theta }}_4\cos \theta _4) \end{array} \right] ; \nonumber \\ \mathbf {R^H} \ =&\ k^H \left[ \begin{array}{l}H_x-(x_5+\frac{L_5}{2}\cos \theta _5); \\ H_y-(y_5+\frac{L_5}{2}\sin \theta _5) \end{array} \right] . \end{aligned}$$

(7)

Table 1 Landing gear parameters/initial state variables

The k terms are the joint stiffness values; the c terms are the joint damping values. Previous work identified that the steady-state behaviour of the landing gear mechanism is insensitive to joint damping forces, provided the system has some damping [34]. Damping forces were therefore not included for $\mathbf {R_{C}}$ and $\mathbf {R_{H}}$ to keep the implementation of the equations of motion as simple as possible.

Table 1 presents the numerical values for the model parameters used in this study, as well as the initial conditions (state values) used to initiate the numerical continuation runs.

2.2 Landing gear mechanism motion

Although this paper focuses on the process by which the landing gear is unlocked from its uplocked state, this section introduces the motion of the landing gear throughout its operation to contextualise the subsequent analysis. Figure 4 provides some example landing gear positions that are achievable for the landing gear mechanism that is the subject of this current study. Panels (a1)–(a3) show the landing gear in ‘above-overcentre’ positions; panels (b1)–(b3) show the landing gear in ‘below-overcentre’ positions. Panel (c) shows the landing gear’s motion in terms of two states: $\theta _4$ is the angle that link ${\mathcal {L}}_{4}$ makes with the horizontal axis; $\theta _{ov}$ is the overcentre angle, defined as the difference in orientation between the two locklinks. The landing gear is said to be at overcentre when the overcentre angle is zero; this occurs at the two extreme points of the retraction cycle, when the landing gear is fully deployed (dot-dash line $Ov_{D}$, panel (c)) or fully retraced (dot-dash line $Ov_{U}$, panel (c)). The labels (a1)–(b3) in panel (c) correspond to landing gear positions depicted in panels (a1)–(b3).

In an actual landing gear, locking is achieved with physical stops that limit the below-overcentre motion of the landing gear’s locklinks, such that the landing gear cannot move beyond the positions shown in Fig. 4b1 (downlocked) or Fig. 4b3 (uplocked). While the analysis of the overall mechanism is able to cover the full motion of a landing gear mechanism, locklink stops would therefore constrain the landing gear’s motion, specifically, preventing it from reaching the dark grey lower section of the curve in Fig. 4c. The case shown in panel (b2) would therefore be unachievable for a real landing gear mechanism.

Fig. 4

Example landing gear positions. The mechanism’s motion is observed by moving clockwise or anti-clockwise around panel (c)

Fig. 5

An example landing gear actuator schedule. The solid line indicates the retraction actuator force; the dashed line indicates the unlock actuator force; vertical dash-dot lines indicate landing gear positions in Fig. 4

To achieve the motion described in Fig. 4, only two actuators are required for the landing gear to move: the retraction actuator, and a single unlock actuator. Figure 5 provides a graphical representation of how the retraction and unlock actuator forces may be scheduled to achieve a successful retraction. The first stage of retraction uses the unlock actuator force (dashed line, Fig. 5) to move the locklinks from below-overcentre ($\theta _{ov}<0$) to above-overcentre ($\theta _{ov}>0$): a motion of (b1) to (a1) in Fig. 4 will occur. Once the locklinks are raised, the retraction actuator force is increased to retract the landing gear: a motion of (a1) to (a3) will occur. When in position (a3), the landing gear is fully retracted but the lock links are unlocked, so to uplock the gear the unlock actuator force is reduced to zero: a motion of (a3) to (b3) will occur, driven by the force provided by the lock spring. At the end of this process, the landing gear will be in position (b3)—the retraction actuator force is then reduced, and the mechanism is fixed in position (b3) by the lock link stops.

Deploying the landing gear requires the reverse motion to be actuated; however, a challenge arises regarding the scheduling of actuator forces when attempting to unlock from uplock. Unlike unlocking from downlock, when unlocking from position (b3) the retraction actuator has to support the weight of the landing gear before the unlock actuator can disengage the locklinks. If not enough retraction actuator force is applied, or if too much retraction actuator force is applied, the unlock actuator will need to provide more force than necessary in order to move the landing gear from position (b3) to (a3). It is this portion of the extension process that will be the focus for the following analysis, which builds on previous work [33, 34] by considering four distinct flight load cases analogous to: straight and level flight; steep climb; steep descent; moderate descent.

3 Variations in retraction surface to changes in aircraft attitude

In this section, the process of unlocking the landing gear from uplock (to begin deployment) is studied to determine how changes in the landing gear’s load angle affect the underlying equilibrium structure. Although pilots typically attempt to maintain a reasonably constant attitude when deploying the landing gear, the aircraft will be susceptible to changes in loading caused by gusts of wind. Such gusts may create instantaneous changes in aircraft attitude and loading. While these disturbances are intrinsically transient, their influence on landing gear unlocking behaviour can be considered by changing the direction in which the external accelerations act on the gear mechanism. In a steady state, such changes in direction of external accelerations are analogous to considering the aircraft in a steady climb or descent.

The following subsections therefore consider four distinct flight cases: straight and level flight; a climb; a steep descent; a moderate descent. The case of straight and level flight has been considered in previous work [34]. It is included here because it provides the necessary context and starting point for the study presented here; moreover, we present an additional discussion of the physical reasoning behind the existence of key bifurcations, including those for level flight.

For each case of aircraft attitude, we compute the branches of steady states of Eqs. (1)–(5) with the actuator force $F_{ret}$ as the continuation parameter, while all other parameters remain fixed; see Table 1. This is achieved, after expressing Eqs. (1)–(5) as a system of first-order ODEs, with the numerical continuation code AUTO [19] as integrated into the MATLAB Dynamical Systems Toolbox [25]. We use the standard AUTO accuracy settings [19], which ensure that equilibria are computed with an accuracy of $10^{-6}$, while bifurcation points are detected with a maximal error of less than $10^{-3}$. Throughout, the computed steady states are represented by the angle $\theta _4$ between the two locklinks; see Fig. 4. Repeating such continuations for sufficiently closely spaced fixed values of the unlocking actuator force $F_{ul}$ allows us to render the steady states as surfaces in the three-dimensional $(F_{ret},F_{ul},\theta _4)$-space, which is done with MATLAB. During the continuation of branches of steady states AUTO detects fold bifurcations (with respect to $F_{ret}$) as saddle-node bifurcations, where the steady state has a real eigenvalue 0, that is, there is a change of stability. AUTO is able to then continue the fold in two paramters as curves in $(F_{ret},F_{ul},\theta _4)$-space; moreover, this package computes the scalar normal form on the (one-dimensional) centre manifold of the fold/saddle-node bifurcation, which allows one to detect cusp bifurcation points as points where the second-derivative of the normal form vanishes. When the third derivative of this normal form is also zero, which is a point of codimension three that may be encountered when an additional parameter—the attitude of the aircraft in our case—is changed, then there is a swallowtail bifurcation; see, for example, [16, 17, 35] for details on the cusp and swallow-tail bifurcations. As will be shown, in the $(F_{ret},F_{ul},\theta _4)$-space for fixed aircraft attitude, the swallowtail bifurcation manifests itself as the emergence or disappearance of a pair of cusp points on a curve of fold bifurcations.

Fig. 6

Bifurcation diagram of landing gear unlocking for an aircraft in straight and level flight; shown are: equilibria in the plane of angle $\theta _4$ versus the actuator force $F_{ret}$ for unlock actuator force a $F_{ul}=0$ N and b $F_{ul}=50$ N; c two-parameter continuation of fold points in the $(F_{ret},F_{ul})$-plane; d surface of equilibria and their bifurcations in $(F_{ret},F_{ul},\theta _4)$-space

3.1 Landing gear unlocking: straight and level flight

As our starting point, Fig. 6 shows a surface of equilibria for the NLG mechanism under purely vertical loading conditions, representative of an aircraft in undisturbed straight and level flight. Panel (a) shows the equilibrium structure for $F_{ul}=0$ N; panel (b) shows the equilibrium structure for $F_{ul}=50$ N. Note that the landing gear mass values have been scaled down from typical values, and that retraction actuator forces below 500N are not considered in order to separate bifurcation structures associated with downlock from this analysis (as much as possible). In both panels (a) and (b), light grey curves correspond to what will be referred to herein as ‘above-overcentre’ solutions, and dark grey curves show ‘below-overcentre’ solutions. Here and in all subsequent figures, dashed curves indicate unstable equilibria, with solid curves used to denote stable equilibria. Points of fold bifurcation are represented by black circles. Black dots labelled (a2), (a3), (b2) and (b3) refer to their respective landing gear positions in Fig. 4. Panel (c) shows the fold curves in isolation, in the actuator forces’ plane: the star representing $C*$ is coloured blue; all other cusp points are highlighted in red. The surface in panel (d) contains three loci of fold bifurcations, indicated by the solid black curves, which separate regions of stable (blue) and unstable (red) equilibria. Circles on the fold curves correspond to cusp bifurcations, with a star representing the crucial cusp point, $C*$.

The process of unlocking a nose landing gear from uplock in straight and level flight is known to require a fold point to transition between the below-overcentre and above-overcentre curves [33]. For the current study, fold point $F\!P_2$ provides this transition. With reference to Fig. 6a, the uplocked landing gear (i.e. one where the locklinks are below-overcentre) rests on the below-overcentre curve (at point (b3)). Unlocking the landing gear therefore requires forces to move the mechanism from point (b3) on the the below-overcentre curve (Fig. 6a) to point (a3) on the above-overcentre curve (Fig. 6b). When the unlock actuator force ${\mathcal {F}}_{ul}=0$ N, point (a3) cannot be reached with the retraction actuator alone. A qualitative change in the equilibria occurs as the unlock actuator force is increased, which enables the landing gear mechanism to be unlocked: the resulting equilibrium structure, once the unlock actuator force is increased to 50 N, is shown in Fig. 6b. It can be seen that unlike the case in panel (a), increasing the retraction actuator force can cause the NLG to transition from the below-overcentre curve [e.g. landing gear at point (b2)] to the above-overcentre curve (point (a3)). This transition through overcentre corresponds to the gear being unlocked from the stowed position. Once this transition has occurred, the landing gear can be extended by reducing the retraction actuator force. This extension process is represented by a movement along the above-overcentre curve, from point (a3) to point (a2) and beyond.

The surface in Fig. 6d provides a graphical representation of how the transition in equilibrium structure occurs as a function of the unlock force ${\mathcal {F}}_{ul}$. At the critical cusp point, $C*$, the system shows a transcritical bifurcation in the ($\theta _{4},F_{ret}$)-plane. It is at this point that the above- and below-overcentre equilibrium curves become jointed momentarily. When the unlock force is increased beyond the critical cusp point’s value, the connections between the stable and unstable equilibrium curves changes: this corresponds to the transition through a saddle point of the equilibrium surface in ($F_{ret},\theta _{4}, {\mathcal {F}}_{ul}$)-space [33, 36].

The other two fold bifurcations, $F\!P_{1}$ and $F\!P_{3}$, are reasoned to arise due to a change in moment balance between the retraction actuator force and the landing gear’s weight. Consider the shock strut ${\mathcal {L}}_{1}$ in isolation: as the mechanism retracts, the X position of the shock strut’s centre of gravity moves further from the X position of the shock strut’s attachment point D, which increases the moment created by the landing gear’s weight (which acts in the Y direction). When the shock strut is retracted to be $90^{\circ }$ to the gravitational force vector, the moment arm for the landing gear’s weight reaches its maximum value. Subsequent motion of the shock strut past $90^{\circ }$ reduces the moment arm for the landing gear’s weight. The fold points $F\!P_{1}$ and $F\!P_{3}$ represent the points in the above- and below-overcentre curves (respectively) when the moment arm for the landing gear’s weight reaches its maximum value, which in this case (due to the geometry and relative masses of the landing gear) is when $\theta _{1}\approx 88^{\circ }$. There is a very slight difference in retraction force value (observeable by careful consideration of Fig. 6c), due to the different locklink orientation between the two cases—$F\!P_{1}$ corresponds to the locklinks being above-overcentre, while $F\!P_{3}$ occurs when they are below-overcentre.

Given the intrinsic dependence of these two folds on a moment balance, the qualitative and quantitative nature of their existence depends on both the mass and geometry of the landing gear. Different mass distributions or landing gear geometries will change the point during retraction at which this moment balance occurs, so for some geometries or mass distributions this balance may not be exceeded during normal operation. Hence, the existence of fold points $F\!P_{1}$ and $F\!P_{3}$ is specific to the current mechanism.

While previous work identified that a transcritical bifurcation occurs at the crucial cusp point $C*$, and that it must be passed in order to unlock the landing gear [33], no reasoning was offered as to the physical significance of $C*$. To identify the physical significance of the transcritical bifurcation, the meaning of the fold bifurcation $F\!P_{2}$ must first be inferred through careful consideration of the landing gear’s behaviour close to this bifurcation. Moving through $F\!P_{2}$ by decreasing the retraction actuator force will cause the locklinks to ‘jump’ away from the retracted overcentre position of the landing gear. If $F\!P_{2}$ occurs in the below-overcentre curve (as in Fig. 6a), this jump will be from a position just below overcentre to a position further below overcentre. If $F\!P_{2}$ occurs in the above-overcentre curve (as in Fig. 6b), this jump will be from a position just above overcentre to a position further above overcentre. At the point where $F\!P_{2}$ transitions between the above-overcentre and below-overcentre curves, fold point $F\!P_{2}$ must be at a position that could jump to both below-overcentre and above-overcentre curves, i.e. $F\!P_{2}$ must correspond to the landing gear being at overcentre. As cusp $C*$ defines the transition of $F\!P_{2}$ between the two curves, the cusp point $C*$ corresponds to the landing gear being at overcentre. The overcentre position is significant because the retraction actuator is unable to move the mechanism from this position (without breaking the mechanism)—it is therefore a singularity with respect to one of the force parameters within the model.

3.2 Landing gear unlocking: steep climb

As the aircraft attitude changes from straight and level to climb, the equilibrium structure changes significantly from the case shown in Fig. 6. Figure 7 shows results for the NLG mechanism under an extreme non-vertical loading condition, where gravity is acting at $40^{\circ }$ to the vertical, pointing towards the rear of the aircraft. This corresponds to the case of an aircraft climbing at an extreme angle—an angle that would not be encountered in typical civilian aircraft flight. The case for the NLG mechanism with no unlock actuator force is shown in Fig. 7a. In comparison with the straight and level case, fold points $F\!P_{1}$, $F\!P_{2}$ and $F\!P_{3}$ still exist, although they have undergone quantitative changes. In addition to these quantitative changes from the straight and level case, the above overcentre equilibrium curve has changed qualitatively with the addition of fold point $F\!P_{4}$. When the unlock actuator force is increased to 50 N (panel (b)), fold point $F\!P_{4}$ disappears, leaving only quantitative differences between the climb and level flight cases for high unlock force values. The surface in Fig. 7d shows that the disappearance of $F\!P_{4}$ between the cases in panels (a) and (b) is due to a cusp bifurcation in the branch of fold points $F\!P_{4}$: when the unlock actuator force is increased past this cusp (point $C_{4}$, Fig. 7c), fold point $F\!P_{4}$ is destroyed.

Fig. 7

Bifurcation diagram of landing gear unlocking for an aircraft climbing at $40^{\circ }$; shown are: equilibria in the plane of angle $\theta _4$ versus the actuator force $F_{ret}$ for unlock actuator force a $F_{ul}=0$ N and b $F_{ul}=50$ N; c two-parameter continuation of fold points in the $(F_{ret},F_{ul})$-plane; d surface of equilibria and their bifurcations in $(F_{ret},F_{ul},\theta _4)$-space

Fig. 8

Bifurcation diagram of landing gear unlocking for an aircraft descending at $40^{\circ }$; shown are: equilibria in the plane of angle $\theta _4$ versus the actuator force $F_{ret}$ for unlock actuator force a $F_{ul}=0$ N and b $F_{ul}=50$ N; c two-parameter continuation of fold points in the $(F_{ret},F_{ul})$-plane; d surface of equilibria and their bifurcations in $(F_{ret},F_{ul},\theta _4)$-space

The value of $\theta _{4}$ at which fold points $F\!P_{1}$ and $F\!P_{3}$ occur has changed between the level and climbing aircraft cases, yet the retraction force value at which they occur has remained unchanged. As discussed in the previous section, these folds occur because of a moment balance between the retraction force and the landing gear’s weight. As the landing gear’s weight has not changed, the force value at which this balance occurs is unaffected; however, the point in the retraction cycle (and hence position of the landing gear) when this balance is reached is highly dependent on aircraft attitude. Gravity now acts perpendicular to the shock strut when $\theta _{1}=50^{\circ }$, so the moment balance between weight and retraction force occurs at $\theta _{1}\approx 48^{\circ }$.

When considering unlocking from uplock, two significant quantitative changes are observed in Fig. 7c compared to the straight and level case. First, the retraction actuator force at $F\!P_{2}$ has reduced significantly from the straight and level case due to two effects. In the retracted position, a smaller component of gravity acts to extend the landing gear, reducing the force required to maintain equilibrium—this is the main effect that contributes to a low retraction actuator force requirement. In addition, elements of the mechanism are now working to keep the landing gear retracted under their (local) gravitational loading. Consider a pretend line running through the shock strut’s pivot point, in the direction of gravity (i.e. $40^{\circ }$ to the vertical for this case). As the NLG mechanism is retracted, parts of the mechanism pass through this line. This means that their weight is now acting to aid retraction, rather than hinder it, thus further reducing the retraction actuator force requirement.

The second significant quantitative change from the straight and level case is that the unlock actuator force at the crucial cusp point $C*$, when the landing gear is at overcentre, has decreased. When climbing (compared to straight and level flight), there is an increase in the weight component that acts to rotate the locklinks to be above overcentre, which reduces the unlock actuator force needed to maintain equilibrium at the overcentre position. Although this reduction in unlock actuator force requirement is beneficial when considering unlocking from uplock, it is worth noting that the climb case would drive sizing of the lock springs to ensure that $C*$ will still occur at a positive unlock force value even if one lock spring were to fail (to provide appropriate system redundancy).

By considering the equilibrium surface of Fig. 7d, the only qualitative change that has resulted from increasing the gravity angle is the addition of the locus of fold points $F\!P_{4}$. This point is related to unlocking the landing gear from downlock (rather than uplock), and is present in the straight and level curve but outside of the retraction actuator force range considered in this work [33]. Figure 7c shows that $F\!P_{4}$ persists until the unlock force value reaches the cusp point $C_{4}$. This cusp point is the crucial cusp point for unlocking the landing gear from its downlocked position. Although not the specific focus of this paper (which is more concerned with unlocking from uplock), the significance of $C_{4}$ and the locus of point $F\!P_{4}$ will be discussed briefly.

Before the landing gear is retracted, the locklinks need to be raised to be above overcentre. This is achieved by using the unlock actuator. Point $C_{4}$ in Fig. 7c gives the minimum actuator forces required to unlock the landing gear from downlock. As the aircraft climbs, the fold locus $F\!P_{4}$ in Fig. 7c shifts to higher retraction forces but lower unlock actuator forces: the lower unlock actuator force arises because the component of the gravitational force acting to oppose the locklinks has reduced; the higher retraction force occurs because gravity has a greater moment arm to oppose the retraction of the shock strut. It is this shift that has brought point $F\!P_{4}$ into the force range considered in this study, while for the straight and level case $F\!P_{4}$ occurs for an ${\mathcal {F}}_{ret}$ value below 500 N.

Overall, no significant qualitative changes to unlocking from uplock have been observed for a climbing aircraft, compared to the baseline straight and level flight case. The one qualitative change that is observed relates to unlocking from downlock, although the features present in this change are known to occur for the straight and level case (albeit outside the force range considered). This change has been considered only briefly, as it is associated with unlocking from downlock rather than uplock. The quantitative changes observed suggest that the climbing case is likely to be a limiting case for the uplocking process rather than the process of unlocking from uplock.

3.3 Landing gear unlocking: steep descent

Figure 8 presents another extreme flight case, this time for an aircraft descending at $40^{\circ }$. Comparing the case in panel (a) (for $F_{ul}=0$ N) with the equivalent straight and level flight case (Fig. 6a), there are now no fold bifurcations in the below-overcentre curve. The single fold present in the above-overcentre is the same number of fold bifurcations as occur in the above-overcentre curve in Fig. 6a, but its physical interpretation has changed—hence, it is labelled $F\!P_2$. Increasing the unlock actuator force to $F_{ul}=50$ N results in the retraction curves of Fig. 8b: here, the one fold that occurred in panel (a) has transitioned from the above-overcentre curve to the below-overcentre curve. This behaviour is the opposite to the transition that occurred for $F\!P_{2}$ in straight and level flight (Fig. 6a, b), suggesting some high-level bifurcation occurs as the aircraft pitches nose down.

The retraction surface in Fig. 8d now has a single fold locus. Although this fold point still transitions between the above-overcentre and below-overcentre curves as the unlock force is varied, the projection in Fig. 8c shows a qualitative change has occurred between this case and the baseline straight and level case (Fig. 6c)—the cusp points now occur at a higher $F_{ret}$ value than the majority of the fold locus over the range considered, rather than at a lower force.

Despite the significant qualitative changes, the process of unlocking from uplock remains unchanged: increasing the retraction actuator force initially causes the uplocked landing gear to move along the below-overcentre curve; applying an unlock actuator force moves fold point $F\!P_{2}$ between the two curves, enabling the landing gear to be unlocked; the minimum required unlock force is indicated by the cusp point, $C*$, corresponding to the overcentre position of the landing gear.

The absence of folds $F\!P_{1}$ and $F\!P_{3}$, however, means that the landing gear response during extension and retraction has changed. The physical meaning of fold $F\!P_{2}$ has also changed subtly from the default straight and level case. These two points are discussed in the following two paragraphs.

A landing gear retraction and extension process will be designed, either via appropriate actuator placement or actuator control, so that the landing gear does not experience major ‘jumps’ during retraction or extension. The cases in Figs. 6 and 7 require equivalent streategies to ensure that the gear can be retracted smoothly past $F\!P_{1}$. The disappearance of fold $F\!P_{1}$ from the retraction surface in Fig. 8d, however, means a different retraction approach is required for an extreme nose-down case. Knowing how and where the qualitative change in retraction surface occurs as the aircraft pitches nose-down is therefore essential to ensure an appropriately robust retraction strategy is used.

The change in gravitational direction caused by an aircraft pitching nose down means that there is no longer a point in the retraction cycle when the landing gear reaches the moment balance point between the landing gear weight and retraction actuator moments. As a result of this, $F\!P_{2}$ now represents the point where the landing gear locklinks ‘jump’ directly between the above-overcentre and the below-overcentre curves. This contrasts with the straight and level case, where $F\!P_{2}$ corresponded to a jump either from just above-overcentre to further above-overcentre, or from just below-overcentre to further below-overcentre.

Two questions now need to be addressed: the first is how has the retraction surface changed as the aircraft pitches nose-down; the second is when does this change occur.

3.4 Landing gear unlocking: intermediate descent

The process through which the retraction surface has changed can be explained, in part, by considering an intermediate surface, as shown in Fig. 9: the case of an aircraft descending at $12^{\circ }$. Panels (a) and (b) are similar to their respective panels for the steep descent case in Fig. 8 (i.e. each contain one fold bifurcation). The retraction surface in Fig. 9d, however, shows that between the low and high unlock force values of panels (a) and (b) there is a region of the surface where multiple fold points exist for a single unlock force value. Within this region, the equilibria in the $(\theta _{4},F_{ret})$-plane are equivalent to the cases seen in Figs. 6 and 7. These regions are defined by features in the $F\!P_{2}$ fold curve, detailed in Fig. 9c.

Fig. 9

Bifurcation diagram of landing gear unlocking for an aircraft descending at $12^{\circ }$; shown are: equilibria in the plane of angle $\theta _4$ versus the actuator force $F_{ret}$ for unlock actuator force a $F_{ul}=0$ N and b $F_{ul}=50$ N; c two-parameter continuation of fold points in the $(F_{ret},F_{ul})$-plane; d surface of equilibria and their bifurcations in $(F_{ret},F_{ul},\theta _4)$-space

Unlike all of the other cases considered up to this point, the fold locus associated with unlocking (nominally the locus of fold point $F\!P_{2}$) now contains four cusp points within the force range considered—$C_{1}$,$C_{2}$,$C_{3}$ and $C*$. For unlock force values below $C_{3}$, the retraction curves are similar to those in Fig. 9a. When $F_{ul}$ is increased past $C_{3}$, two fold points appear in the below-overcentre curve, making it similar to the cases shown in Figs. 6a and 7a. The landing gear is unlocked from uplock when the unlock force passes the crucial cusp $C*$, and once unlocked the retraction curves are qualitatively as the cases shown in Figs. 6b and 7b. Increasing $F_{ul}$ beyond $C_{1}$ sees the two fold points in the above-overcentre curve merge and disappear, resulting in retraction curves that are similar to those in Fig. 9b.

The presence of cusp points $C_{1}$ and $C_{3}$ in Fig. 9c suggests that fold points $F\!P_{1}$, $F\!P_{2}$ and $F\!P_{3}$ in Figs. 6 and 7 are in fact part of the same fold locus. In Sects. 3.1 and 3.2, $F\!P_{1}$ and $F\!P_{3}$ were identified to correspond to the point in the retraction cycle where the moment arm for the landing gear’s weight is at a maximum value; $F\!P_{2}$ defines the point where the locklinks would ‘jump’ away from being close to overcentre to become more unlocked. Cusp points $C_{1}$ and $C_{3}$ must therefore occur when these two definitions coincide, i.e. when the unlock actuator force $F_{ul}$ (which aids retraction when applied in a positive direction) causes the locklink ‘jump’ to occur when the landing gear’s weight is at its maximum moment arm. Their existence is therefore dependent on the mass distribution and the kinematics of the landing gear. The transition from Figs. 9 to 8 as the aircraft pitches (nose down) from $-12^{\circ }$ to $-40^{\circ }$ is charachterised by a bifurcation occuring in the fold locus. The following subsection presents a two-parameter continuation of the fold locus to identify the bifurcation behind the qualitative change in retraction surface.

3.5 Two-parameter continuation of crucial fold $F\!P_{2}$

Figure 10 shows the loci of fold points $F\!P_{2}$ for aircraft flight angles of: (a) $0.0^{\circ }$; (b) $-5.0^{\circ }$; (c) $-6.0^{\circ }$; (d) $-7.5^{\circ }$; (e) $-12^{\circ }$; (f) $-18^{\circ }$. Cusp points are indicated by circles, with the crucial cusp $C*$ indicated with a star. Panel (a) presents the fold curve for the case shown in Fig. 6. The fold curve contains two cusp points, $C_2$ and $C*$, and is similar to the equivalent fold curve for the case of an aircraft climbing. As the aircraft descends to $-5^{\circ }$ (panel (b) of Fig. 10), an additional cusp point ($C_1$) appears in the unlock force range under consideration. A further decrease in aircraft attitude to $-6^{\circ }$ (panel (c)) shows that the unlock force value to reach cusp $C_1$ decreases as the aircraft pitches nose down. In panel (d), a fourth cusp point ($C_3$) enters the picture, and the subsequent decrease in aircraft attitude from $-7.5^{\circ }$ to $-12^{\circ }$ (moving from panel (d) to panel (e)) shows that the unlock force value to reach cusp $C_3$ increases as the aircraft pitches nose down. In addition to the movement in $C_3$, cusp $C_1$ has mover closer to $C_2$. Between panels (e) and (f), $C_{1}$ and $C_{2}$ coalesce, leaving $C*$ and $C_3$ as the only remaining cusp points once the aircraft has pitched nose down to $-18^{\circ }$ (panel (f) of Fig. 10). This coalescence of two cusp points is characteristic of the transition through a swallowtail bifurcation [35]; hence, the presence of a swallowtail bifurcation between the descent angles $-12^{\circ }$ and $-18^{\circ }$ is shown in Fig. 10e, f.

Fig. 10

Variation in crucial fold locus with changing aircraft flight angles: a $0.0^{\circ }$; b $-5.0^{\circ }$; c $-6.0^{\circ }$; d $-7.5^{\circ }$; e $-12^{\circ }$; f $-18^{\circ }$

Fig. 11

Variation in fold locus for gravity angles of: a $-13.2^{\circ }$; b $-14.9^{\circ }$; c $-16.0^{\circ }$; panels a2–c2 are enlarged views of panels a1–c1 near the point $C*$

Further evidence for the presence of the swallowtail bifurcation is presented in Fig. 11. Figure 11a1 shows the case for an aircraft pitching nose down at $-13.2^{\circ }$, with four cusp points visible. A zoomed view of the crucial cusp point $C*$, Fig. 11a2, highlights the shape of the fold locus in the neighbourhood of $C*$, showing that $C_2$ is closest (along the fold curve) to $C_1$. The overcentre cusp $C*$ does not look like the other cusps in the $(F_{ret},{\mathcal {F}}_{ul})$-plane, because the overcentre position is singular with respect to the retraction actuator force $F_{ret}$. Due to its unique physical meaning, $C*$ cannot be unfolded by a combination of ${\mathcal {F}}_{ul}$ and $F_{ret}$—it is structurally stable.

A further decrease in pitch angle to $-14.9^{\circ }$ sees cusp point $C_{1}$ move closer to $C_{2}$ and $C*$, such that they are virtually indistinguishable from one another in Fig. 11b1. The enlarged view in Fig. 11b2 shows that point $C_1$ is approaching $C_2$ as the aircraft pitches down. The qualitative change occurs by the time the aircraft pitches nose down to $-16.0^{\circ }$ (panel (c1)), as cusp points $C_{1}$ and $C_{2}$ disappear.

From the application perspective, the swallowtail bifurcation emerges as the geometric object via which the retraction surfaces change from the straight and level case in Fig. 6c to the steep descent case seen in Fig. 8c. The physical reasoning used previously to explain the presence of cusp point $C_1$ in Fig. 9 can be used here again: it implies that a more negative aircraft pitch angle that moves $C_1$ closer to the crucial cusp point $C*$ indicates that the moment balances that define $C_1$ happen closer to overcentre. Hence, the following can be concluded: for aircraft pitch attitudes above those of the swallowtail point the landing gear weight’s moment arm reaches a maximum value when the locklinks are above-overcentre (since $C_1$ exists); for the aircraft pitch attitude exactly at the swallowtail point the landing gear weight’s moment arm reaches the maximum when the landing gear is at overcentre; and for aircraft pitch attitudes below that of the swallowtail point, therefore, the landing gear weight’s maximum moment arm cannot be reached (since $C_1$ does not exist). In the latter case, the retraction moment is, hence, no longer able to exceed the required maximum value during the mechanism’s operation. In other words, the qualitative change in retraction actuator surface that arises due to the landing gear moving through the swallowtail bifurcation is significant from a design perspective: to achieve a smooth extension of the landing gear once it is unlocked, one must ensure that the location of the swallowtail bifurcation is outside the flight envelope; this requires the implementation of an appropriate retraction strategy, either with actuation control or appropriate actuator positioning.

The results in this section have also shown that, irrespective of the qualitative changes that occur in the fold curve, the crucial cusp $C*$ always separates the landing gear’s uplocked states from its unlocked states. This is because $C*$ occurs when the landing gear’s locklinks are parallel with one another, which means that they behave as a pinned structure. This means that the retraction force is unable to move the landing gear such that the ends of the locklinks (joints B and H in Fig. 2a) move. Only a force with a component perpendicular to the locklinks will achieve this, and such a force cannot be generated elsewhere in the mechanism (other than at the locklinks themselves). Hence, the crucial cusp point $C*$ cannot be removed in this way, meaning that it is inherent to this particular nose landing gear design—demonstrating that the strategy of using $C*$ to identify a force measure is robust to variations in external loading.

4 Concluding remarks

Our study demonstrated that knowledge of the geometric structure of the steady-state surface (over appropriate ranges of two key input forces) may be used as a tool to inform the design of a retraction mechanism that works smoothly (that is, without abrupt jumps) throughout the anticipated flight envelope (defined here as the range of aircraft attitudes). More specifically, we showed that the minimum forces required to unlock the landing gear from uplock can be identified by considering the mechanism in equilibrium at the overcentre position, that is, by determining the position of the cusp point $C*$. We remark that this does not require a simulation of the whole landing gear retraction or extension cycle, meaning that force requirements can be derived right at the start of the landing gear design process.

This work highlights several potential avenues for future investigations. The point at which the swallowtail bifurcation occurs is likely to depend heavily on a given gear’s geometry and mass distribution. Numerical continuation may provide an effective way of investigating how the unlocking or uplocking process changes when geometric quantities (lengths of links) are used as continuation parameters. This would provide a parameter map for landing gear designers, allowing them to identify, for example, whether their design needs an actuator that provides an ever-increasing retraction moment, or whether the retraction moment should peak before uplock to ensure a smooth retraction.

The use of a single locking actuator for both uplocking and downlocking has not been investigated for the case of a main landing gear. The process of maintaining uplock of a main landing gear mechanism during disturbances (such as an aircraft pitching under the action of a gust) would depend heavily on the geometry of the side stay in relation to the shock strut. The three-dimensional (rather than planar) nature of a main landing gear mechanism adds a considerable level of complexity. We suggest that the approach presented here may also prove beneficial for the analysis required to ensure correct operation of unlocking and deployment throughout the anticipated flight envelope also for such more complicated landing gear mechanisms.

While the subject of this study is a nose landing gear mechanism, the relation between detectable bifurcation points and the mechanism’s kinematic position demonstrates the general value of bifurcation analysis and numerical continuation for mechanism analysis. Mechanisms are used in a variety of applications, from robotics to suspension systems, and the approach presented here may lead to interesting discoveries in these other fields that relate key mechanism behaviour to detectable bifurcation points.