Nonlinear dynamic response of an isolation system with superelastic hysteresis and negative stiffness

Abstract

The negative stiffness exhibited by bi-stable mechanisms together with the tunable superelasticity offered by shape memory alloy (SMA) wires can enhance the dynamic resilience of a structure in the context of vibration isolation. The effects of negative stiffness and superelastic damping in base-isolated structures are here explored by carrying out an extensive study of the nonlinear dynamic response via pathfollowing, bifurcation analysis, and time integration. The frequency-response curves of the isolated structure, with and without the negative stiffness contribution, are numerically obtained for different excitation amplitudes to construct the acceleration and displacement transmissibility curves. The advantages of negative stiffness, such as damping augmentation and reduced acceleration/displacement transmissibility, as well as the existence of rich bifurcation scenarios toward quasi-periodicity and chaos, are discussed.

1 Introduction

Passive vibration isolation is one of the most popular and effective vibration control techniques. A SDOF oscillator subject to harmonic forcing exhibits a deamplification of the incoming accelerations for frequencies higher than $\sqrt{2}f_0$, where $f_0$ is the natural frequency of the oscillator. Therefore, lower is the natural frequency (i.e., the stiffness), larger is the isolated frequency bandwidth. On the other hand, an excessively low stiffness induces large static displacements. Hence, a suitable requirement for the isolation systems is an high-static and low-dynamic stiffness. A very promising technique to achieve this goal is the exploitation of negative stiffness mechanisms arranged in parallel with classical vibration isolation devices. Pasala et al. [1, 2] proposed an adaptive damper based on a negative stiffness component capable to reduce the seismic demands by simulating a global plastic behavior. In particular, a bilinear spring is used in parallel with negative stiffness element to achieve an initial gap in the restoring force of the device. Other methods to achieve negative stiffness responses consist in the use of reverse bending sliding surfaces or magneto-rheological dampers with linear voltage decay [3,4,5,6,7,8,9]. There are several developments of this concept applied to seismic isolation that show promising results in terms of reduction in both accelerations and displacements transmissibilities. In [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32], a linear vertical isolation system was enhanced by introducing a negative stiffness correction to obtain a high preload stiffness and a quasi-zero-stiffness (QZS) in the equilibrium position.

The nonlinear isolator response is usually described by a Duffing oscillator with a vanishing linear stiffness. Donmez et al. [33] studied the dynamic response of a dry-friction QZS isolator, showing that the hysteretic damping ensures a better performance than viscous damping in the out-of-resonance frequency range. In all of these works, negative stiffness correction is used to achieve zero stiffness in the equilibrium position, but as known, in typical civil applications dealing with seismic horizontal isolation, this is undesirable because of the need of a wind restraint. By delaying the negative stiffness contribution through an initial gap, the wind restraint is preserved, and transmissibility reduction can be achieved.

Liu et al. [34] proposed a novel isolation system composed by shape memory alloy (SMA) wires providing the superelastic effect and a prestressed spring. The stiffness of the SMA wires overcomes the negative stiffness exhibited by the prestressed spring until phase transformations occur. For larger displacements, the stiffness of SMA wires vanishes and the overall stiffness becomes quasi-zero. The transmissibility of a SDOF with the proposed response was analytically evaluated using a piece-wise linear constitutive law for the SMA response and a linear elastic law for the negative stiffness contribution.

In the present work, the dynamic response of a classical seismic isolation system made up of elastomeric bearings working in parallel with a negative stiffness mechanism and a SMA element (exhibiting the superelastic behavior) is explored. The SMA element is employed to realize the initial gap and, at the same time, to introduce hysteretic damping in the system. The negative stiffness contribution is used to achieve a zero dynamic stiffness away from the equilibrium position. The benefits associated with a negative stiffness mechanism together with a hysteretic damping for an improved seismic isolation system are multifaceted. One of the main is the possibility of reaching large levels of flexibility thus obtaining quasi-zero-stiffness and ultra-low-frequency isolation together with a substantial reduction in the acceleration transmissibility. Moreover, it is possible to introduce high levels of hysteretic damping without loss of performances due to the increase of the initial stiffness. In fact, this increase is neutralized by an appropriately tailored negative stiffness. The dynamic response provided by a SDOF system, representing the isolated structure controlled by a negative stiffness-SMA (NS-SMA) damping mechanism, is investigated by employing suitable hysteretic constitutive laws modeling the nonlinear response of the bearing devices and the superelastic response of the SMA element.

2 Negative stiffness-SMA damper for seismic isolation

In previous works, a bilinear spring is used in parallel with the negative stiffness in order to achieve an initial gap in the ensuing restoring force of the device. This gap allows to maintain the virgin isolation stiffness for low amplitudes and to realize a wind restraint. In this work, a superelastic spring is used instead of the bilinear spring in order to realize the initial gap and, at the same time, to deliver hysteretic damping to the system. The total restoring force f of the proposed isolation system is the summation of the force $f_i$ provided by traditional seismic elastomeric isolators, the superelastic force $f_s$ and the force $f_n$ provided by the negative stiffness mechanism. It reads

$$\begin{aligned} f=f_i+(f_n+f_s )=f_i+f_{ns}, \end{aligned}$$

(1)

where $f_{ns}=f_n+f_s$ is the overall force of the proposed rheological device. For displacements below the gap amplitude, the stiffness of the superelastic element is equal to the negative stiffness, hence the response is governed by the elastomeric element. For displacements larger than the gap, corresponding to the superelastic transition (i.e., where the stiffness drops), the negative stiffness strongly reduces the total force and stiffness. For larger displacements, the cubic term tends to overcome the negative stiffness contribution and the overall response returns to follow the baseline backbone response of the elastomeric bearings (see Fig. 1).

Fig. 1

Force-displacement cycles associated with (left) damper force $f_{ns}$ (black line) ensuing from $f_s$ (red line indicating the superelastic element) plus $f_n$ (blue line indicating the negative stiffness element) and with (right) the overall system response with and without damper (black and gray lines, respectively)

In the subsequent sections, three types of isolated SDOF systems are studied and compared. The baseline elastomeric isolation system (EIS) is referred to as $S_1$ and the associated restoring force is $f=f_i$. $S_2$ denotes the baseline isolation system together with the superelastic spring alone whose associated restoring force is $f=f_i+f_s$. Finally, $S_3$ indicates the compound isolation system constituted by the NS-SMA damper arranged in parallel with the elastomeric bearings and the associated total restoring force is $f=f_i+f_s+f_n$ (see Fig. 2).

Fig. 2

Schematic representation of the three different isolated systems referred to as $S_1$, $S_2$ and $S_3$, respectively

2.1 Rheological models

2.1.1 Elastomeric isolators

Elastomeric isolation systems are usually described by the Bouc-Wen model of hysteresis [35, 36] together with a linear viscous damping term. Therefore, the adopted model is the direct summation of a viscous damping force, an elastic force and a hysteretic force,

$$\begin{aligned} f_i=c{\dot{x}}+\alpha K_ix+(1-\alpha )K_i z, \end{aligned}$$

(2)

where the hysteretic force z is governed by

$$\begin{aligned} {\dot{z}}={\dot{x}}[1-(\gamma +\beta \text {sign}(z {\dot{x}})]|z|^n. \end{aligned}$$

(3)

The term c is the viscous damping coefficient, $\alpha$ is the ratio between the post-elastic and the stiffness $K_i$ at the origin, $\gamma$ and $\beta$ control the shape of the hysteresis loops, n regulates the smoothness of transition between the initial elastic and post-elastic stiffness. The upper and lower bounds of z are given by $z_m=\pm \root n \of {(1-\alpha )K_i/(\gamma +\beta )}$. In the present study, $\gamma +\beta$ is restricted to be positive in order to have a softening behavior and n is set to 1 (Fig. 3).

Fig. 3

Force-displacement cycles of isolation devices where $K_i$ indicates the stiffness at the origin and $\alpha K_i$ denotes the post-elastic stiffness

2.1.2 Negative stiffness mechanism

In most passive bi-stable mechanisms, the negative stiffness is produced by geometric nonlinearities within a given displacement range while out of this, the stiffness returns to be positive. In this work, the force exhibited over the displacement amplitude $x_f$, for which the force vanishes, is cancelled by means of a step function. Its expression reads

$$\begin{aligned} f_n=(-K_n x+K_3 x^3)\frac{(1+\text {sign}(x_f-|x|))}{2} \end{aligned}$$

(4)

where $K_n$ is the negative linear stiffness, $K_3$ is the positive cubic stiffness, and $x_f$ is the displacement corresponding to a vanishing force and is equal to $x_f= \sqrt{K_n/K_3}$. Another characteristic displacement is that leading to the maximum negative force and is given by $x_n= \sqrt{K_n/3K_3}$ (see Fig. 4).

Fig. 4

Force-displacement cycles provided by the negative stiffness force where $K_n$ indicates the negative stiffness while $x_f$ and $x_n$ denote the displacements for which the force vanishes or achieves the maximum negative value, respectively

2.1.3 Superelastic spring

The superelastic response is modeled according to the phenomenological superelastic model proposed by Charalampakis [37] given in rate form as:

$$\begin{aligned}&{\dot{f}}_s=(1-s) K_s [{\dot{x}}-|{\dot{x}}|\text {sign}(f_s-\beta _s )\nonumber \\&\quad \left( \frac{|f_s-\beta _s |}{Y}\right) ^{n_s}]+sK_m {\dot{x}}, \end{aligned}$$

(5)

$$\begin{aligned}&\beta _s=K_s \alpha _s \left[ x-\frac{f_s}{K_s} + f_t\text {tanh}(a_s x)\nonumber \right. \\&\left. \quad \left[ \frac{1+\text {sign}(-x{\dot{x}})}{2}\right] \right] , \end{aligned}$$

(6)

$$\begin{aligned}&s=\frac{\text {tanh}[c_s (|x|-x_m )]+1}{2}, \end{aligned}$$

(7)

where $K_s$ is the initial stiffness during the austenitic phase, Y is the yielding force and $\alpha _s$ controls the post-elastic stiffness. The parameter $n_s$ regulates the smoothness of transition from the initial elastic to the post-elastic phase while $f_t$ and $a_s$ controls the twinning hysteresis and super-elasticity and the pinching around the origin along the cycle, respectively. Finally, $K_m$ indicates the stiffness during the fully martensitic phase, $x_m$ is the displacement at which the transition from the post-elastic to the fully martensitic phase occurs and $c_s$ controls the smoothness of this transition (see Fig. 5).

Fig. 5

Force-displacement cycles of the superelastic element

Because of the large variability and dependence of $f_t$ and $a_s$ on the remaining parameters, two new parameters with a more straightforward physical interpretation, $y_s$ and ${\tilde{a}}_s$, are introduced. In terms of these parameters, $f_t$ and $a_s$ are expressed as:

$$\begin{aligned} f_t= & {} (2Y-y_s Y)/(\alpha _s K_s ), \end{aligned}$$

(8)

$$\begin{aligned} a_s= & {} \text {tanh}^{-1}({\tilde{a}}_s K_s)/(Y-y_s Y). \end{aligned}$$

(9)

The first parameter indicates the difference between the loading and unloading forces and it is expressed as percentage of Y. The second allows to set the residual displacement to a fixed value varying the other parameters (see Fig. 6). In particular, ${\tilde{a}}_s$ indicates the value assumed by tanh(${a}_sx$) where x is the displacement at which the unloading branch with stiffness $\alpha _s K_s$ intersects the elastic loading branch.

Fig. 6

Variation of the superelastic force-displacement cycles with the nondimensional parameters $y_s$ (left) and ${\tilde{a}}_s$ (right)

Fig. 7

Overall force-displacement cycles provided by $S_3$ where the gap displacement $x_g$ and the martensitic displacement $x_m$ are indicated

2.1.4 Design parameters

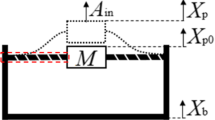
The main goal is to investigate the effects of the NS-SMA device in parallel with traditional elastomeric devices. Thus, the stiffness $K_i$ of the isolation system, the gap displacement $x_g=F_w/K_i$, (with $F_w$ indicating the maximum expected wind load) and the maximum allowed displacement $x_u$ are assumed as input parameters (see Fig. 7). In this study, $x_g$ is set to $0.05 x_u$. On the other hand, $K_n$, Y and $y_s$ are the design parameters. All the remaining parameters are set to fixed values ($c=0.1$, $\alpha =0.2$, $\beta =0.09$, $\gamma =0.01$, $n=1$, $\alpha _s=0.01$, $n_s=3$, ${\tilde{a}}_s=0.6$, $c_s=0.02$) or determined according to the following expressions: $x_f=x_m=0.7 x_u$, $K_3=K_n/x_f^2$, $K_s=Y/x_g$, $f_t=(2Y-y_s Y)/(\alpha _s K_s)$, $a_s=\text {tanh}^{-1}({\tilde{a}}_s K_s)/(Y-y_s Y)$, and $K_m=0.5K_s$.

Fig. 8

Equivalent nondimensional stiffness vs. nondimensional displacement amplitude (left) and equivalent damping vs. nondimensional amplitude (right) for $S_1$ (black line), $S_2$ with $Y=Z_m, y_s=(0.2, 0.5, 0.8)$ (dotted, dashed and solid red lines, respectively) and with $Y=1.6Z_m, y_s=0.8$ (dashed-dotted red line). The sub-figures show the hysteresis loops of device a and system b for the parameters described above

2.1.5 Nondimensional equation of motion

The equation of motion of a SDOF mass m subject to the hysteretic restoring force given by Eq. (1) reads:

$$\begin{aligned}&m\ddot{x}+c{\dot{x}}+\alpha K_i x+(1-\alpha )K_i z\nonumber \\&\quad +(-K_n x+K_3 x^3)\frac{(1+\text {sign}(x_f-|x|))}{2}\nonumber \\&\quad +f_s=P\text {sin}(\varOmega _gt). \end{aligned}$$

(10)

By choosing the characteristic displacement $x_0=x_u$ and the characteristic stiffness $K_i$ (i.e., the initial stiffness of the isolation system, equal to the initial stiffness of the Bouc–Wen model), the following nondimensional variables are introduced: ${\tilde{x}}=x/x_0$, ${\tilde{t}}=\omega t$, where $\omega =\sqrt{K_i/m}$. The nondimensional equation of motion is obtained dividing Eq. (10) by $N_0=K_i x_0$:

$$\begin{aligned}&\ddot{{\tilde{x}}}+\zeta \dot{{\tilde{x}}}+\alpha {\tilde{x}}+(1-\alpha ){\tilde{z}}+(-{\tilde{K}}_n {\tilde{x}}\nonumber \\&\quad +\,{\tilde{K}}_3 {\tilde{x}}^3)\frac{(1+\text {sign}({\tilde{x}}_f-|{\tilde{x}}|))}{2}+{\tilde{f}}_s={\tilde{P}}\text {sin}({\tilde{\varOmega }}_g{\tilde{t}}),\nonumber \\ \end{aligned}$$

(11)

where ${\tilde{P}}=P/N_0$, ${\tilde{\varOmega }}_g=\varOmega _g/\omega , \zeta =c\omega /K_i$. The nondimensional parameters for the Bouc–Wen model, the negative stiffness law and the SMA model are: ${\tilde{z}}=\frac{z}{x_0}, {\tilde{\gamma }}=\gamma x_0^n, {\tilde{\beta }}=\beta x_0^n, {\tilde{K}}_n=\frac{K_n}{K_i}, {\tilde{K}}_3= \frac{K_3 x_0^2}{K_i}, {\tilde{x}}_f=\frac{x_f}{x_0}, {\tilde{K}}_s=\frac{K_s}{K_i}, {\tilde{K}}_m= \frac{K_m}{K_i}, {\tilde{Y}}=\frac{Y}{N_0}, {\tilde{f}}_t=\frac{f_t}{x_0}, \tilde{a}=a_s x_0, \tilde{c}_s=c_s x_0, {\tilde{x}}_m=\frac{x_m}{x_0}$.

3 Equivalent stiffness and damping

A useful way to characterize the dynamic behavior of the nonlinear hysteretic oscillator is to make use of the equivalent linearization. The equivalent linear stiffness [38] and damping ratio [39] can be defined as function of the displacement amplitude (U) can be defined

$$\begin{aligned} K_{eq}=\frac{\int _{-U}^{U}K_t(x) dx}{2U} , \xi =\frac{E_d}{4\pi E_k }, \end{aligned}$$

(12)

where $K_t$ denotes the tangent stiffness function of x, $E_d$ denotes the total dissipated energy and $E_k$ is the stored energy for a given displacement of amplitude equal to U. Firstly, the equivalent stiffness and damping for the system composed by superelastic element alone arranged in parallel with the elastomeric device (system $S_2$) are investigated. In order to clarify the effects of the design parameters, four different cases are reported in Fig. 8: ($Y=Z_m, {\tilde{K}}_s=\alpha , y_s=0.2$) (red dotted line), ($Y=Z_m, {\tilde{K}}_s=\alpha , y_s=0.5$) (red dashed line), ($Y=Z_m,{\tilde{K}}_s=\alpha ,y_s=0.8$) (red solid line), ($Y=1.6 Z_m, {\tilde{K}}_s=1.6\alpha ,y_s=0.8$) (red dashed dotted line).

The trends of equivalent stiffness and damping in Fig. 8 show that for low ratios of super-elastic hysteresis ($y_s$) (see dotted red curve), the only effect is an increase in stiffness that causes a reduction of equivalent damping in the low amplitude range. For greater ratios of superelastic hysteresis, a small increase in damping is achieved for moderate and large displacements, whereas for low amplitudes, a decrease in damping persists. Increasing the yielding force (Y) entails an increase in initial stiffness; hence, the damping reduction at low amplitudes is more significant. Moreover, a damping increment is exhibited for large displacements. The introduction of the superelastic element within the isolation system, regardless from its hysteresis contribution, causes a decrease in seismic isolation performance for low-intensity earthquakes characterized by high frequency of occurrence (because of an increase in stiffness and a subsequent decrease in the damping). On the other hand, a slight improvement of performance is obtained for medium- and high-intensity earthquakes. By considering next the case ($Y=Z_m, y_s=0.8$), Fig. 9 shows that the introduction of negative stiffness drastically amplifies the equivalent damping. In fact, while the maximum increase in damping achieved with the superelastic element alone was of $\simeq 2\%$, with ${\tilde{K}}_n=(0.5, 1, 1.2) \alpha$, the achieved increments are $\simeq (5, 25, 40) \%$, respectively. As already seen for the system $S_2$, the increase in the hysteresis ratio $y_s$ entails an increase of the equivalent damping, while the increase in the yielding force Y gives rise to an increase in the initial stiffness and thus a drop of the equivalent damping over a broad range of displacements

Fig. 9

Equivalent nondimensional stiffness vs. nondimensional displacement amplitude (left) and equivalent damping vs. nondimensional amplitude (right) for $S_1$ (black line), $S_2$ with $Y=Z_m, y_s=0.8$ (red line), $S_3$ with ${\tilde{K}}_n=(0.5, 1, 1.2) \alpha$ (magenta, violet, blue lines, respectively); the blue dashed-dotted lines represent the case ${\tilde{K}}_n=1.2\alpha ,Y=1.6 Z_m,y_s=0.8$, while the sub-figures show the hysteresis loops for the assigned parameters

Fig. 10

Damping amplification $\Delta \xi$ vs. negative stiffness coefficient for a nondimensional displacement of 0.05 (left) and of 0.2 (right) for the $S_3$ system with $Y=Z_m, y_s=(0.2, 0.5, 0.8)$ (black dotted, dashed and solid lines, respectively) and with $Y=1.6 Z_m, y_s=0.8$ represented by dashed-dotted gray lines

In Fig. 10, the damping amplification due to negative stiffness is shown for two different displacement levels equal to (0.05, 0.2) $x_0$. The system $S_2$ exhibits a decrease in damping for low amplitudes, while a slight increase is observed for the second amplitude. With the introduction of the negative stiffness ($S_3$), a strong damping amplification is achieved for both amplitudes.

By numerically integrating the median line of the hysteresis cycles, the potential energy profile is obtained for the NS-SMA device alone and for the combined system $S_3$ (see Fig. 11). The potential energy profiles of the device reveal its bi-stable/tri-stable nature. In fact, for ${\tilde{K}}_n=(0.2, 0.5)\alpha$, the profile has three minima giving rise to three stable and two unstable equilibria. On the other hand, when the negative stiffness is equal or greater than the SMA elastic stiffness, ${\tilde{K}}_n=(1, 1.2)\alpha$, the two unstable equilibria coalesce at the origin into one unstable equilibrium point in place of the original stable point, and the device becomes bi-stable. The addition of the damper to the isolation system gives rise to an erosion of the global potential energy profile bringing it closer to the damped energy profile, increasing the ratio $E_d/E_k$ and thus the equivalent damping. Figure 12 shows that for ${\tilde{K}}_n=1.2\alpha$, the response exhibits a negative stiffness range and the damped energy profile along the associated branch is greater than the potential profile and the system becomes overdamped. For values of ${\tilde{K}}_n> 1.2\alpha$, the median line of the hysteresis loops intersects the abscissa line (i.e., the force vanishes). Consequently, two lateral minima in the energy profile appear and the system becomes globally tri-stable. In order to obtain a self-recentering system, the existence of two additional equilibrium positions is undesirable. This is the reason because the negative stiffness ${\tilde{K}}_n$ must be limited to value provided by eq. (13). In light of the above, the optimum negative stiffness can be identified within the range $\alpha<{\tilde{K}}_n<1.2\alpha$, where a consistent reduction in the stiffness and damping amplification without loss of self-recentering capacity is obtained. The limit value of negative stiffness past which the median line of the hysteresis loops intersects the abscissa axis and the system becomes tri-stable can be analytically obtained as

$$\begin{aligned}&{\tilde{K}}_{n\ MS \rightarrow TS}=-\alpha -\alpha _s{\tilde{K}}_s\nonumber \\&-3\root 3 \of {\frac{(-1+\alpha _s)^2 {\tilde{K}}_{3}{\tilde{K}}_{s}^2{\tilde{x}}_{g}^2}{4}}. \end{aligned}$$

(13)

Fig. 11

Potential energy profiles of the NS-SMA damper (left) and of the combined system $S_3$ (right) for ${\tilde{K}}_n=(0, 0.2, 0.5, 1, 1.2)\alpha$, denoted by red, fuchsia, magenta, violet and blue lines, respectively

Fig. 12

(left) Potential energy profiles of system $S_3$ with ${\tilde{K}}_n=(1,1.2,1.3)\alpha$ represented by magenta, blue, and violet lines, respectively, and damped energy profile denoted by gray dashed lines. The sub-figure shows the total force displacement cycles together with the average force in dashed-dotted lines. (right) Analytical curves separating mono-stability (MS) from tri-stability (TS) in the parameters space of the negative stiffness mechanism (${\tilde{K}}_n,{\tilde{K}}_3$) for the $S_3$ system with $y_s=0.8$ and $Y=(1, 1.6)Z_m$ represented by black solid and black dashed-dotted lines, respectively

4 Nonlinear dynamic response scenario

The frequency-response curves (FRCs) of the described hysteretic oscillators endowed with the rheological devices $S_1$, $S_2$, $S_3$ are numerically obtained for several excitation levels employing a continuation procedure based on the Poincarè map. The Poincarè map and the associated monodromy matrix are computed via the fourth-order Runge–Kutta integration scheme and the finite difference method, respectively. The stability and the bifurcations along the path of periodic solutions are ascertained according to the eigenvalues of the monodromy matrix [40]. In the next subsections, a full parametric analysis is carried out to investigate the sensitivity of the FRCs with respect to the design parameters.

Linear and nonlinear negative stiffness. Figure 13 shows the displacement and acceleration FRCs for the baseline isolation system ($S_1$) (denoted by black lines), for the isolation system with the SMA damper ($S_2$) assuming ${\tilde{K}}_s=\alpha , {\tilde{x}}_g=0.05, y_s=0.2$, (denoted by red lines) and for the isolation system with the same SMA damper plus the negative stiffness ($S_3$) with ${\tilde{K}}_n=(0.5, 1, 1.2)\alpha$ under two excitation amplitudes, ${\tilde{A}}_g=(0.01,0.015)$. As expected, the addition of the superelastic element induces an increase of stiffness that is larger for low amplitudes, and results in a shift of the curves to the right with an increase in the acceleration and a decrease in the displacement (see the red lines in Fig. 13). The addition of negative stiffness implies a reverse shift of the curves to the left, a decrease in the acceleration and an increase in the displacement. It is interesting to note that despite the stiffness of $S_3$ being much lower than that of the baseline system $S_1$, the maximum displacement is always smaller, at most equal, thanks to the beneficial effect of the augmented damping.

Fig. 13

Frequency-response curves (FRCs) in terms of nondimensional displacement (left) and acceleration (right) for a ground acceleration of 0.01 (a and b) and 0.015 (c and d). The response of $S_1$ is denoted by black lines, the response of $S_2$ (when $Y=Z_m, y_s=0.2$) by red lines while the response of $S_3$ by magenta (${\tilde{K}}_n=0.5\alpha$), violet (${\tilde{K}}_n=\alpha$) and blue lines (${\tilde{K}}_n=1.2\alpha$), respectively. The dashed lines indicate unstable periodic responses

Fig. 14

Frequency-response curves (FRCs) in terms of nondimensional displacement (left) and acceleration (right) for a ground acceleration set to 0.015. The response of $S_1$ is represented by black lines and that of $S_3$ (when $Y=Z_m, y_s=0.2, {\tilde{K}}_n=\alpha$ and ${\tilde{K}}_3=(1, 2, 4, 8, 10)10^{-6}{\tilde{K}}_n$) is denoted by solid violet lines with increasing thickness for increasing ${\tilde{K}}_3$

Besides the negative stiffness coefficient, also the nonlinear stiffness coefficient ${\tilde{K}}_3$ plays an important role on the nonlinear dynamic response. Figure 14 shows families of displacement and acceleration FRCs of the systems $S_1$ and $S_3$ upon variation of the nonlinear stiffness coefficient ${\tilde{K}}_3$. Note that an increase in ${\tilde{K}}_3$, associated with a smaller working displacement ${\tilde{x}}_f$, entails a stronger hardening nonlinearity that leads to a reduction in the peak displacement and an increase in the peak acceleration.

SMA mechanical characteristics. In Fig. 15, the FRCs of the system $S_1$ (black lines) are compared with those of $S_2$ (red lines) and $S_3$ (violet lines) for different levels of hysteresis ratio $y_s$ and for two excitation amplitudes, ${\tilde{A}}_g=(0.01, 0.015)$. The acceleration of the system $S_2$ shows, for low excitations and regardless of the hysteresis ratio, an increase in the acceleration compared to the baseline system $S_1$. On the contrary, $S_3$ exhibits a strong reduction in accelerations for both excitation amplitudes, while it also undergoes a strong reduction in displacements for medium and high hysteresis ratios of the superelastic element.

Fig. 15

Frequency-response curves in terms of nondimensional displacement (left) and acceleration (right) for a ground acceleration set to 0.01 (a and b) and 0.015 (c and d). The response of the $S_1$-isolated system is described by black lines, those of $S_2$ (when $Y=Z_m, y_s=(0.2, 0.5, 0.8)$) by red lines with increasing thickness for increasing $y_s$, and those of $S_3$ (when ${\tilde{K}}_n=\alpha , Y=Z_m, y_s=(0.2, 0.5, 0.8)$) by violet lines with increasing thickness for increasing $y_s$ and blue lines (when ${\tilde{K}}_n=\alpha , Y=1.6Z_m, y_s=0.8$), respectively

By increasing the yielding force of the superelastic element (with $Y=1.6 Z_m$), an additional reduction of displacement amplitude can be achieved but paying the cost of a stiffness increase and, accordingly, of the accelerations transmissibility.

5 Displacement and acceleration transmissibilities

The parametric study unfolds a meaningful sensitivity of the frequency-response with respect to the system parameters. Henceforth, the evolution of the response for increasing base accelerations is discussed. The FRCs of the system $S_3$ are computed for different excitation amplitudes (see Fig. 16). The strong softening-hardening nonlinearity of the system is reflected by the trend of the backbone curves. Other interesting phenomena are observed such as the emergence of detached resonance curves. For the case with large negative stiffness (${\tilde{K}}_n=1.2\alpha$) a disappearance of the peak occurs in the response within the displacement range in which the system turns out to be overdamped ($0.2<{\tilde{x}}<0.4$). Moreover, for the strongest base acceleration in the low-frequency range, there exists a bandwidth in which no stationary solutions could be obtained, a circumstance that suggests the existence of quasi-periodic/nonperiodic responses.

Fig. 16

FRCs in terms of nondimensional displacement (left) and acceleration (right) for the $S_3$ system with ${\tilde{K}}_n=\alpha , Y=Z_m, y_s=0.2$ (top) and with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.2$ (bottom) when the base accelerations are set to $(0.8, 1, 1.08, 1.2, 1.28, 1.3, 1.32, 1.36, 1.4, 1.48, 1.6, 1.8, 2)10^{-2}$

For the same excitation amplitudes, the FRCs are computed for the system $S_1$ and $S_2$ assuming various hysteresis ratios and yielding force levels, and for $S_3$ varying the negative stiffness and the amount of hysteresis. The ratios between the peak responses of $S_2$ or $S_3$ and those of the baseline system $S_1$ are reported in Fig. 17 as function of the base acceleration.

Fig. 17

Ratio between the peak response of the controlled systems ($S_2$ and $S_3$) and that of the baseline system ($S_1$) in terms of nondimensional displacements (left) and accelerations (right) as function of the nondimensional base acceleration. The responses of $S_2$ for $Y=Z_m$ and $y_s=(0.2, 0.5, 0.8)$ are represented by red dotted, red dashed and red solid lines, respectively, while the response of $S_2$ with $Y=1.6Z_m$ and $y_s=0.8$ is described by bordeaux solid lines. The responses of $S_3$ for ${\tilde{K}}_n=\alpha$ (top), $1.2\alpha$ (bottom), $Y=Z_m, y_s=(0.2, 0.5, 0.8)$ are described by blue dotted, blue dashed and blue solid lines, respectively, while the response of $S_3$ with ${\tilde{K}}_n=\alpha$ (top), $1.2\alpha$ (bottom), $Y=1.6 Z_m, y_s=0.8$ is indicated by violet solid lines

As expected, the insertion of the superelastic element alone causes an increase of accelerations response for weak excitations. The increase is about 30% when $Y=Z_m$ and 60% for $Y=1.6 Z_m$, respectively, and it is mainly due to the initial stiffness of the hysteretic damping and slightly to the damping ratio.

On the other hand, the damping ratio strongly affects the response for moderate and strong base accelerations. It turns out that reductions of 20%, 40% and 60% are obtained when $y_s=(0.2, 0.5, 0.8)$, respectively. By introducing the negative stiffness in parallel with the SMA damper (system $S_3$), the amplification of accelerations for weak excitations is totally cancelled and a mild reduction can be observed. In addition, a further 20% reduction of accelerations compared with the system $S_2$ is obtained for moderate and strong base excitations, achieving an overall acceleration reduction of 40%, 60%, and 80% for $y_s=(0.2, 0.5, 0.8)$, respectively. The trend in acceleration reduction coincides with the trend depicting the stiffness reduction. Therefore, it shows a bell shape with a peak corresponding to the displacement where the stiffness reduction is maximum. According to the presence of the cubic stiffness in the NS mechanism, the equivalent stiffness and consequently the maximum acceleration reach again the values of the baseline system $S_1$ for large displacements. The increase in the damping ratio results in the expansion of the bell, both in terms of width and height. If the initial stiffness of the SMA damper overcomes the negative stiffness, as is the case with ${\tilde{K}}_n=\alpha$ and $Y=1.6 Z_m$ (see violet line in Fig. 17b), a slight increase in the peak accelerations occurs for low excitations together with an expansion of the bell width and of the effective displacement range. By balancing the increase in SMA damper initial stiffness with an equivalent increase in negative stiffness as is the case with ${\tilde{K}}_n=1.2\alpha$ and $Y=1.6 Z_m$, (see violet line in Fig. 17d), the increase of the peak accelerations for low excitation amplitudes is cancelled again. For moderate and strong excitations, the increase in negative stiffness from $\alpha$ to $1.2\alpha$ causes an additional acceleration reduction of about 10%.

Regarding the displacements, it is worth highlighting a substantial coincidence between the reduction offered by the systems $S_2$ and $S_3$ with ${\tilde{K}}_n=\alpha$ for weak base excitations. The trend in reduction is for both systems quasilinear up to a maximum value corresponding to the displacement that yields the maximum damping. The maximum displacement reduction is quite similar for both systems except for low damping ratios ($y_s=0.2$) where it is about 20% for $S_3$ and 40% for $S_2$. This is because for $y_s=0.2$ the stiffness reduction is not balanced by a robust damping augmentation. For the remaining damping ratios, the peak displacements reduction for both systems is about 55% and 65% with $y_s=(0.2, 0.5)$, respectively. Past the maximum, the trend of the peak displacements reduction for $S_3$ deviates from the trend of $S_2$, showing a smaller reduction. The maximum deviation between the two responses occurs where the stiffness reduction is maximum.

Fig. 18

FRCs in terms of nondimensional displacements for the base accelerations set to $(0.8, 1, 1.08, 1.2, 1.28, 1.3, 1.32, 1.36, 1.4, 1.48, 1.6, 1.8, 2)10^{-2}$ for the $S_3$ system with ${\tilde{K}}_n=\alpha ,Y=Z_m, y_s=(0.5, 0.8)$ (parts a and b) and ${\tilde{K}}_n=\alpha , Y=1.6 Z_m, y_s=0.8$ (part c), and with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=(0.5, 0.8)$ (parts d and e) and ${\tilde{K}}_n=\alpha , Y=1.6 Z_m, y_s=0.8$ (part f)

The increase in yielding force (Y) from $Y=Z_m$ to $Y=1.6 Z_m$, hence, the increase in the initial superelastic stiffness, moves the curves to the right showing a smaller reduction for weak excitations and a larger reduction for moderate and strong base excitations. For the case with ${\tilde{K}}_n= 1.2\alpha$, the response reduction is smaller than that achieved with ${\tilde{K}}_n=\alpha$ and, for a certain range of base excitations, there exists an increase in the response. This range of base excitations corresponds to the FRCs where the displacement peak is due to the superharmonic resonance, as shown in Fig. 18.

Next, we address the force transmissibility in terms of frequency bandwidth where effective isolation is attained. We consider the force transmissibility as the ratio between absolute acceleration and base acceleration. As known, the response is considered effectively controlled when the transmissibility is lower than 1. For the nondimensional base acceleration of 0.02, the acceleration peak reduction for $S_3$ is minimum (i.e., 40%) and it is equal to that of $S_2$ (see Fig. 17b, d). By analysing the force transmissibility under the same base accelerations, useful considerations can be drawn about the isolation performance of the proposed system. While Fig. 17 shows only the reduction in peak accelerations, Fig. 19 portrays the bandwidth of the isolated frequencies.

Fig. 19

FRCs in terms of force transmissibility for a nondimensional base acceleration equal to 0.02. The response of $S_1$ is described by the black solid line, while the responses of $S_2$ when $y_s=0.8, Y=(1, 1.6)Z_m$ are denoted by the red solid and red dashed lines, respectively. The responses of $S_3$ when ${\tilde{K}}_n=\alpha , Y=(1, 1.6)Z_m$ are described by the violet solid and dashed lines and those of $S_3$ when ${\tilde{K}}_n=1.2\alpha , Y=(1, 1.6) Z_m$ are denoted by the blue solid and blue dashed lines, respectively. For all cases $y_s=0.8$

The introduction of the SMA damper alone increases the value of the first isolated frequency, thus reducing the bandwidth of the isolated frequencies of 69% and 87% for $Y=Z_m$ and $Y=1.6 Z_m$, respectively. On the other hand, the negative stiffness mechanism in parallel with the SMA damper, determines a reduction of the peak response together with an increase of the isolated frequency bandwidth reducing the value of the first isolated frequency of 25% and 44% with ${\tilde{K}}_n=\alpha$ and ${\tilde{K}}_n=1.2\alpha$, respectively. It can be observed that an increase in the SMA yielding force (Y) determines an increase in the initial superelastic stiffness not accompanied by an increase in negative stiffness. This yields a further reduction in peak response but the isolated frequency bandwidth is reduced (Table 1).

Table 1 Force transmissibility performance for the three kinds of isolated systems, $S_1$, $S_2$ and $S_3$

6 Primary, superharmonic and detached resonances

The severe softening nonlinearity associated with the softening hysteresis induces an interaction between the primary and the superharmonic resonances causing the emergence of detached resonance curves, a phenomenon that is well documented in the literature [41,42,43]. However, a new phenomenology is here documented. In Fig. 21, the evolution of the isolas for the system with two levels of negative stiffness is shown.

Fig. 20

Evolution of isolas topology for $S_3$ with ${\tilde{K}}_n=\alpha , Y=Z_m, y_s=0.2$ (top) for a nondimensional ground acceleration equal to 0.0128 a, 0.01288 b, 0.0130 c, 0.0132 d and for $S_3$ with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.2$ (bottom) for a nondimensional ground acceleration equal to 0.01072 e, 0.01088 f, 0.01112 g and 0.0112 h

The qualitative pattern in both cases consists in the birth of an outer isola in the neighborhood of the superharmonic resonance frequency which, for increasing base acceleration levels, coalesces first with the superharmonic resonance branch and, thereafter, upon further increase in the excitation amplitude, coalesces with the main resonance branch, giving rise to an inner isola.

It is possible to observe that for the system $S_3$ with ${\tilde{K}}_n=\alpha$, there exists only a small outer isola, while for the case with ${\tilde{K}}_n=1.2\alpha$, different outer isolas coexist. Indeed, for a ground acceleration of 0.01, two outer detached resonance isolas are visible in the proximity of the superharmonic resonances of order 1:3 and 1:5 (see Fig. 20e). For a higher amplitude, the two distinct isolas merge and a new isola is formed near the superharmonic resonance of order 1:7 (see Fig. 20f). Upon further increase in the excitation amplitude, all previous isolas merge with each other and with the 1:3 superharmonic resonance branch (see Fig. 20g). At a higher excitation amplitude, the primary resonance branch and the outer superisola merge and give rise to an inner isola for slightly higher excitation amplitudes (see Fig. 20h). Despite the very low- frequency range where the isolas appear, the outer isolas are detrimental for isolation purposes since they can give rise to an unwanted dynamic amplification. On the contrary, the inner isola can be used to reduce the response near the main resonance.

Fig. 21

Basins of attraction for the system $S_3$ with ${\tilde{K}}_n=\alpha , Y=Z_m, y_s=0.2$ (top) for a base acceleration ${\tilde{A}}_g=0.0128$ and frequency ${\tilde{\varOmega }}^2=0.022$, corresponding to the outer isola (left), and for a base acceleration ${\tilde{A}}_g=0.0132$ and frequency ${\tilde{\varOmega }}^2=0.05$, corresponding to the inner isola (right). (bottom) Basins of attraction for the system $S_3$ with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.2$ for a base acceleration of ${\tilde{A}}_g=0.01072$ and ${\tilde{\varOmega }}^2=0.022$, corresponding to the outer isola (left), and for a base acceleration of ${\tilde{A}}_g=0.0112$ and ${\tilde{\varOmega }}^2=0.05$, corresponding to the inner isola (right). In red, the initial conditions that lead to the low-amplitude solution, while in blue those that lead to the high-amplitude solution

The factors that determine whether the mass will move along the detached solution curve or along the main branch are the initial conditions or the perturbations causing jumps between the coexisting attractors. In order to obtain the basins of attraction of the system for the isolas (see Fig. 21), the equations of motion are numerically integrated for a fixed harmonic excitation over 1000 periods for a grid of initial conditions. The initial conditions, in terms of displacement and velocity, that lead to different attractors are denoted by different colors. In particular, the initial conditions that lead to the low-amplitude solution are represented in red, while in blue those associated with the high-amplitude solution. It is possible to note that the system with ${\tilde{K}}_n=\alpha$ shows much thinner basins of attraction for both the outer and inner isola than the system with ${\tilde{K}}_n=1.2\alpha$, denoted by larger blue and red regions for the outer and inner isolas, respectively.

For a more thorough characterization of the two coexisting attractors exhibited by the system with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.2$, the force-displacement cycles, the phase portraits, the time histories and the FFTs of the response for a harmonic base excitation with ${\tilde{A}}_g=0.01072$ and ${\tilde{\varOmega }}^2=0.022$ are shown in Fig. 22.

Fig. 22

Force-displacement cycles a, phase portraits b, time histories c and FFTs d of the system S3 (with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.2$) for ${\tilde{A}}_g=0.01072$ and ${\tilde{\varOmega }}^2=0.022$. In red the response to a zero initial condition along to the main solutions branch, while in blue the solution for the initial conditions ${\tilde{x}}=0.2, {\tilde{v}}=0$, giving rising to the isola solution curve

The response belonging to the main solution branch is richer due to the presence of more superharmonic components. In fact, while in the first case, third, fifth and seventh harmonics are relevant in terms of amplitude, in the case of the isola, only the third harmonic is considerable. From the FFT, it is also possible to see that, for solutions belonging to the isola, the amplitude of the main harmonic is larger than that of the overall response (sum of all harmonics) while for the solution along the main curve, the fundamental harmonic exhibits the same amplitude of the overall response. This suggests a different relative phase between the main harmonic and higher harmonics for the two solutions.

Fig. 23

Harmonic decomposition of the superharmonic response along the main resonance branch (left) and detached resonance (right). The first, third, fifth and seventh harmonics and the total response are represented by red, blue, violet, magenta and black lines, respectively

The harmonic decomposition of the two different responses shows that for the solution belonging to the main branch, the peak of main harmonic component corresponds to the zero of all other harmonics having thus a relative phase of $\pi /2n$ with n representing the order of the harmonic component (see Fig. 23).

Fig. 24

Nondimensional displacement (left) and phase angle (right) vs. nondimensional frequency for $S_3$ with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.2$ and ${\tilde{A}}_g=0.01072$. Black lines show the amplitude and phase angle of the overall response, red lines and blue lines represent the amplitude and phase angle of the main harmonic and of the first superharmonic of order 1:3, respectively. The phase angle between the main harmonic and the first superharmonic is reported in red dashed lines

Fig. 25

FRCs of the system $S_3$ with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.5$ for a nondimensional ground acceleration equal to ${\tilde{A}}_g=0.0148$ (left) and imaginary parts vs. real parts of Floquet multipliers (right)

By focusing on the third harmonic, a relative phase of $\pi /6$ means that the peak of the main harmonic coincides with the zero value along the descending branch of the superharmonic and this is equivalent to the out-of-phase condition or deamplification condition. On the other hand, the solution along the detached curve shows that the peak of the main harmonic coincides with the minimum of the third harmonic, thus giving rise to a $\pi /2$ relative phase. Thus, for the solutions belonging to the detached curve, the higher harmonics are phased with the main harmonic, producing a less distorted and larger motion. Figure 24 shows the amplitudes and the phases of the overall response, of the main harmonic and of the first superharmonic and the relative phase between the main harmonic and the first superharmonic in the frequency domain. Note that the main harmonic of the solution belonging to the detached resonance curve shows a phase equal to $\pi /2$ at the peak. This condition is shared only with the solution of the primary resonance.

Fig. 26

Bifurcation diagram for the system with ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.5$ for a nondimensional ground acceleration equal to ${\tilde{A}}_g=0.0148$

Fig. 27

FFTs of the response a, force-displacement cycles b, phase portraits c and Poincarè map d of the system $S_3$ when ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.5$, the nondimensional ground acceleration is set to ${\tilde{A}}_g=0.0148$ for the frequencies corresponding to sections 1, 2

Fig. 28

FFTs of the response a, force-displacement cycles b, phase portraits c and Poincarè map d of the system $S_3$ when ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.5$ for a nondimensional ground acceleration equal to ${\tilde{A}}_g=0.0148$ for the frequencies referred to as 3, 4, 5, 6, 7, 8 in Fig. 26

Fig. 29

FFTs of the response a, force-displacement cycles b, phase portraits c and Poincarè map d of the system $S_3$ when ${\tilde{K}}_n=1.2\alpha , Y=Z_m, y_s=0.5$ for a nondimensional ground acceleration equal to ${\tilde{A}}_g=0.0148$ for the frequencies referred to as 9 and 10 in Fig. 26

6.1 Bifurcation scenarios and quasi-periodicity

As mentioned above, for low frequencies and high base accelerations, the periodic response of the system $S_3$ with ${\tilde{K}}_n=1.2\alpha$ undergoes a loss of stability. By restricting our analysis to the frequency range reported in Fig. 25, a rich sequence of bifurcations is found. Moving from low to high frequencies, the first encountered bifurcation is a Neimark-Sacker or secondary Hopf bifurcation (A), signaled by a pair of Floquet multipliers crossing the unit circle away from the real axis (red circles). The solution emerging out of the Neimark-Sacker bifurcation is a quasi-periodic solution. However, past the bifurcation, the continuation of the unstable periodic solution cannot be successfully achieved. On the other hand, between C and D, a stable branch of periodic solutions is found, which loses its stability at C due to a symmetry-breaking bifurcation. The two branches of mirror nonsymmetric periodic attractors lose their stability at B due to a period-doubling bifurcation, circumstance indicated by the fact that one of the Floquet multipliers crosses the unit circle through -1.

In D the solution experiences a fold bifurcation, whereby one of the Floquet multipliers crosses the unit circle along the positive real axis. Finally, in E a new Neimark-Sacker bifurcation is manifested and afterwards path following of the stationary solutions breaks down. To investigate more in depth the scenario between the Neimark-Sacker bifurcation at A and the period-doubling at B, bifurcation diagrams were constructed by direct numerical integration of the equations of motion (see Fig. 26). The time step was fixed by dividing the excitation period into 4,096 equally spaced points. The integration was carried out over 2,000 cycles of the excitation by considering as initial conditions those obtained at the previous excitation frequency and the last 64 points of the Poincaré map were recorded.

It is possible to note that at A the solution becomes quasi-periodic, through the mentioned secondary Hopf bifurcation, while from B to the left the solution becomes quasi-periodic by means of a more complex sequence of bifurcations. Figures 27, 28, 29 shows a symmetry-breaking bifurcation at the frequency denoted by sect. 2 (see Fig. 26), singled out by the birth of an even superharmonic component, after the limit cycle exhibited at sect. 1. This symmetry-breaking paves the way to two distinct branches of nonsymmetric mirror solutions, whose orbits include the limit cycle and toward the latter they extend. In this frequency range, the solution turns out to jump from one nonsymmetric branch to the other for any small frequency variation. Each of these branches undergoes a cascade of successive period-doubling bifurcations induced by the birth of a subharmonic component of order 2:1 at sect. 3 and of subharmonics of order 4:1 and 2:1 at sect. 4. This cascade of period-doubling bifurcations, giving rise to a rich nidification of subharmonics and superharmonics, may lead to a chaotic attractor. When the orbits of the nonsymmetric solutions touch the orbit of the limit cycle, there is a reverse symmetry-breaking and the solution regains symmetry. This is signaled by the disappearance of the even superharmonic component (sect. 6). In the frequency range between 2.04 and 2.09, the ratio between the modulation frequency and the carrier frequency locks into a rational number, due to the so-called frequency-locking phenomenon with three-period motions, supported by the 3:1 subharmonic component (sect. 7). Past this window, a new symmetry-breaking is experienced by the 3-T solution, yielding two distinct branches of 3-T solutions in which, in addition to the 3:1 subharmonic, there appears an even superharmonic of order 1:2 (sect. 8). The symmetry-breaking forces the solution to transition towards a quasi-periodic, symmetric solution regime (sect. 9). Finally, the amplitude of the phase plane portion covered by the trajectory progressively gets reduced until reaching the frequency indicated by 10, where a reverse secondary Hopf bifurcation makes the solution stable.

6.1.1 Bifurcation scenarios for the tri-stable configuration

For ${\tilde{K}}_n=1.2\alpha$, the bifurcation scenario engages only ultra-low frequencies and a small displacements range. On the other hand, when ${\tilde{K}}_n>1.2\alpha$, the bifurcation scenario involves much larger ranges of frequencies and displacements. As shown, for ${\tilde{K}}_n>1.2\alpha$ the system is tri-stable and the presence of the two lateral attractors breaks the symmetry of the response. Because of the existence of symmetry-breaking and period-doubling bifurcations, the response is quasi-periodic for most of the frequencies within the considered range. In order to obtain the FRCs of the tri-stable configuration (i.e., ${\tilde{K}}_n=1.4\alpha$), the equations of motion are numerically integrated for a harmonic base excitation over 1,000 periods and the maximum amplitudes exhibited in the last 50 cycles, together with the Poincaré sections, are recorded for each frequency within the range (see Fig. 30).

Fig. 30

FRCs in terms of nondimensional displacements a and accelerations b and bifurcation diagram c for the system $S_3$ with ${\tilde{K}}_n=1.4\alpha , Y=Z_m, y_s=0.2$ for a ground acceleration equal to ${\tilde{A}}_g=0.0142$. Blue lines represent the responses obtained for the forward frequency sweep, while red lines denote those obtained in reverse sweep. Magenta and cyan lines indicate the responses of the system with initial conditions ${\tilde{x}}_0=0.5$ and of ${\tilde{x}}_0=-0.5$, respectively. Finally, for comparative purposes, the responses of the mono-stable system with ${\tilde{K}}_n=1.2\alpha$ are represented by gray lines

Fig. 31

FFTs of the response a, force-displacement cycles b, phase portraits c and Poincarè map d of the system $S_3$ when ${\tilde{K}}_n=1.4\alpha , Y=Z_m, y_s=0.2$ and the nondimensional ground acceleration is set to ${\tilde{A}}_g=0.0142$ for the frequencies referred to as 0, 1, 2, 3, 4, 5, 6 in Fig. 30

Depending on the initial conditions, the mass can vibrate around the origin, the left or the right equilibrium positions. Regardless of the equilibrium around which the mass vibrates, the adjacent attractor breaks the symmetry of the response and leads to quasi-periodicity. Further, when the mass vibrates around one of the lateral equilibria, due to the stronger effects of the cubic stiffness, the acceleration transmissibility is higher compared with that exhibited by the mass vibrating around the origin. For limited frequency intervals, the phase-locking phenomenon is observable together with a reduction of transmissibility with respect to the adjacent quasi-periodic response. By analysing more in depth the response in Fig. 30, we can note that for low frequencies ($0<{\tilde{\varOmega }}^2<0.022$), the system has sufficient energy to complete symmetric periodic cycles. For higher frequencies ($0.022<{\tilde{\varOmega }}^2<0.042$), because of a folding bifurcation, two different responses are exhibited by the system depending on the initial conditions.

Fig. 32

a Basins of attraction for the system with ${\tilde{K}}_n=1.4\alpha , Y=Z_m, y_s=0.2$ for a base acceleration ${\tilde{A}}_g=0.0142$ and frequency ${\tilde{\varOmega }}^2=0.125$. Parts b, c and d are zoomed-in regions bounded by the dashed rectangles. Magenta and red dots denote the initial conditions that lead to the left stable (LS) and unstable (LU) attractors, respectively, while cyan and blue dots represent the initial conditions that lead to the right stable (RS) and unstable (RU) attractors, respectively

The high amplitude response, such as the response of the previous frequency range, exhibits stable cycles. On the other hand, the low amplitude solution, with a lower associated energy, suffers the attraction of the lateral equilibria and shows a quasi-periodic behavior. By increasing the frequency up to ${\tilde{\varOmega }}^2=0.042$, a downward jump occurs together with the birth of two mirrored nonsymmetric solutions, each of which experiences cascades of period-doubling bifurcations. In the frequency range $0.118<{\tilde{\varOmega }}^2<0.18$, the existing solutions regain periodicity and two new mirrored nonsymmetric and quasi-periodic solutions appear along the lateral right and left equilibria. Finally, when ${\tilde{\varOmega }}^2=0.165$, the first two mirrored solutions coalesce into one symmetric periodic solution while the two lateral nonsymmetric solutions regain stability. In the latter frequency range, an amplification of both accelerations and displacements is observable. In Fig. 31 the FFTs, the hysteresis loops, phase portraits and Poincarè maps associated with the frequencies highlighted in Fig. 30 are reported. By focusing on sect. 6, the coexistence of four different types of response for the same excitation frequency is noted. The basins of attraction obtained for this frequency are reported in Fig. 32. The coexistence of four different attractors, namely, the left stable (LS) and unstable (LU) and the right stable (RS) and unstable (RU) equilibria, gives rise to in a high sensitivity of the dynamic response to the initial conditions, as manifested by the richness of the basins. From the progressive zooming of the basins of attraction (see Fig. 32c, d), it is remarkable that the strict adherence to the attractors succession order (LS, LU, RU, RS) leads to a fractal-like pattern.

7 Conclusions

A novel vibration isolation system featuring a negative stiffness mechanism and superelastic damping arranged in parallel with classical elastomeric isolation devices is parametrically investigated for different levels of negative stiffness, superelastic damping ratio, and yielding force.

The introduction of superelasticity alone, without negative stiffness, leads to a detrimental increase in the initial stiffness and, hence, to an increase in accelerations for low base excitations. On the other hand, by accurately tuning the negative stiffness with the superelastic damping, a remarkable reduction of displacement and acceleration amplitudes can be achieved, while preserving a self-recentering capability and without incurring an increase in acceleration transmissibility for low excitations. To ensure an effective acceleration transmissibility reduction and, at the same time, the mono-stability and self-recentering capability of the isolated system, the optimum negative stiffness coefficient ${\tilde{K}}_n$ must be bounded in the range $\alpha<{\tilde{K}}_n<1.2\alpha$, where $\alpha$ is the ratio between the post-elastic and the initial isolators stiffness. Regarding the superelastic rheological element, the initial stiffness must be equal to the negative stiffness in order to keep the stiffness of the isolation system unaltered at the origin while exhibiting sufficiently high damping. By considering the lower bound for the negative stiffness, ${\tilde{K}}_n=\alpha$, the optimum superelastic yielding force was found to be ${\tilde{Y}}=\alpha {\tilde{x}}_g$, where ${\tilde{x}}_g$ is the ratio between the gap displacement and the maximum allowable displacement. Moreover, a high hysteresis ratio $y_s$ was shown to entail a better isolation performance.

The study of the nonlinear dynamic response and its bifurcations revealed extremely rich bifurcation scenarios with detached resonances and unusual interactions between the primary resonance and superharmonic resonances, or between superharmonic resonances of various orders, featuring multiplicity of coexisiting attractors, secondary Hopf bifurcations responsible for quasi-periodicity, synchronization, symmetry-breaking and period-doubling cascades towards chaos. The detached resonance curves and bifurcations were numerically explored for high levels of negative stiffness and their nonlinear impact on isolation performance was discussed. In particular, when ${\tilde{K}}_n=\alpha$, the peak of the detached resonance curve was found to be lower than the peak of the main resonance curve, thus not affecting the isolation performance. On the contrary, for a higher negative stiffness value (i.e., ${\tilde{K}}_n=1.2\alpha$), the peak of the detached resonance curve was found to be larger than the primary resonance peak, hence, largely affecting the isolation performance. Moreover, the quasi-periodicity of the response of the tri-stable configuration (i.e., ${\tilde{K}}_n=1.4\alpha$) together with the subsequent dynamic amplification were illustrated. The obtained results pave the way towards a streamlined design process which aims to optimize the isolation performance of the proposed negative stiffness superelastic device in terms of transmissibility and dynamic stability.