Critical thresholds for mode-coupling instability in viscoelastic sliding contacts

Abstract

Mode-coupling instabilities are known to trigger self-excited vibrations in sliding contacts. Here, the conditions for mode-coupling (or “flutter”) instability in the contact between a spherical oscillator and a moving viscoelastic substrate are studied. The work extends the classical 2-Degrees-Of-Freedom conveyor belt model and accounts for viscoelastic dissipation in the substrate, adhesive friction at the interface and nonlinear normal contact stiffness as derived from numerical simulations based on a boundary element method capable of accounting for linear viscoelastic effects. The linear stability boundaries are analytically estimated in the limits of very low and very high substrate velocity, while in the intermediate range of velocity the eigenvalue problem is solved numerically. It is shown how the system stability depends on externally imposed parameters, such as the substrate velocity and the normal load applied, and on contact parameters such as the interfacial shear strength $\tau _{0}$ and the viscoelastic friction coefficient. In particular, for a given substrate velocity, there exist a critical shear strength $\tau _{0,crit}$ and normal load $F_{n,crit}$, which trigger mode-coupling instability: for shear stresses larger than $\tau _{0,crit}$ or normal load smaller than $F_{n,crit}$, self-excited vibrations have to be expected.

1 Introduction

Friction-induced vibrations (FIVs) are an incredibly widespread phenomenon, where friction plays an unexpected role: in fact, instead of acting as a damping source, attenuating the system dynamics, dissipative forces are the original cause that triggers this class of vibrations. The large interest in the analysis of FIVs is not only theoretical and aimed to assess the intricate correlation with friction [1,2,3], but it is also largely motivated by the variety and the importance of fields and applications, where FIVs occur: these range from automotive and railway systems [4,5,6,7,8,9,10,11] to the aerospace field [12,13,14] and include also areas far from industrial engineering, like bio-mechanics [15,16,17,18]. In all these different systems, FIVs may be related to unwanted acoustic emissions and to occurrence of additional stresses in the components affected by this phenomenon.

Fig. 1

Friction-induced vibrations are commonly experienced in several applications including inter alia, finger-tip contact, viscoealstic dampers, tip rubbing in turboengines, face seals, wipe-blade contact

Several mechanisms can originate FIVs. Among these: (i) the “sprag-slip effect”, pioneeringly investigated by Spurr in Ref. [19], was related to “jamming” phenomena at the interface level, (ii) the “Stribeck’s effect”, which is due to a falling characteristic of the friction law [20,21,22,23,24,25] and (iii) the “mode-coupling” instability (also referred as flutter), which is the result of the coupling of two stable vibrational modes that originates one stable and one unstable mode [26]. The latter is due to friction-related non-symmetric entries in the stiffness matrix, which makes the system not conservative and allows energy to flow from the interface to the vibrational motion [4]. In the last two decades, a large research effort has been dedicated to characterize the origin of FIVs, developing a minimal, yet representative, model consisting in a 2-DOF (Degrees Of Freedom) oscillator, in contact with a moving frictional substrate [4] [11]. The basic model has been originally conceived by Hamabe et al. in 1999 [20] to investigate the insurgence of FIVs in drum brakes; later on, the scheme has been extensively employed for a number of different applications and, more generally, for improving our understanding of FIVs main features [22, 23, 26,27,28,29,30,31,32,33]. It is important to notice that, although real structures may be affected by a much higher level of complexity, this 2-DOF dynamic system is a paradigmatic and illustrative scheme that allows us to explore the main features of FIVs at a fundamental level. By means of such a model, in Ref. [29] an intuitive explanation is provided for the insurgence of FIVs, by showing that out-of-phase variation of the frictional force and tangential displacement may lead to energy transfer from interface to the mechanical system. Furthermore, in Ref. [30], Hoffmann and Gaul investigated the effect of added linear damping to the insurgence of flutter instability, while in Ref. [31], an approximate estimation of the limit cycle oscillations has been proposed. These studies have provided fundamental contributions to the FIVs assessment, but, at the same time, most of them have been affected by a significant issue: the interface interactions between the oscillator and the moving substrate are treated by means of phenomenological laws, the simplest one being the classical Coulomb model, aimed at describing the contact interactions between the oscillator and the substrate [33]. However, this phenomenological approach leads to a strong simplification of the contact mechanics occurring at the interface: for example, contact stiffness is often assumed linear [34] and/or the frictional resistance is taken proportional to the contact normal force [22, 35,36,37,38].

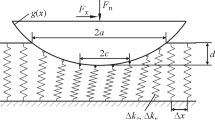
Only very recently, some attempts have been made to account for a more realistic description of the interfacial phenomena, as in Ref. [11], where the problem of a spherical punch in contact with a viscoelastic substrate has been investigated. Nevertheless, Ref. [11] was specifically focused on enlightening the role that viscoelastic dissipation plays in triggering the instability, but the analysis did not consider any elastic cross-coupling in the mechanical system between the horizontal and vertical motion and neglected the Coulomb “adhesive” part of the friction coefficient. As a consequence, the possible mechanisms for instability were restricted just to the Stribeck’s effect. However, as previously pointed out, and as schematically depicted in Fig. 1, in practical applications, cross-coupling may play a fundamental role. Among these applications, we recall the case of tip rubbing in turbomachinery, where self-excited vibrations are triggered by the contact between a rotating blade and the external (fixed) case, which is coated by a polymer viscoelastic layer. Self-sustained vibrations and internal resonances may originate unexpected large stresses, wear and damage [12,13,14]. Similar issues may arise when a rubber-made face seal is inserted between rotor and stator in a mechanical system [39]: because of the roughness at the microscales, there may occur friction-induced vibrations [40]. There exist similar conditions, again at a microscale level, in the windscreen wiper blades, where FIVs are correlated with tedious acoustic emissions [41], and, even in the bio-mechanical field, when fingers touch and slide over rough surfaces [15,16,17,18]. Finally, when dealing with dampers [42, 43], where rigid punches are put into contact with viscoelastic layers, FIVs can occur and change the operational parameters according to which the system has been designed. All these systems are characterized by an elastic structure in contact with a moving soft substrate, marked by a time-dependent viscoelastic rheology. Consequently, we focus on the simple yet representative 2-DOF conveyor belt model (see Fig. 1). Such a scheme is a classical lumped model to study FIVs, but here we introduce two fundamentally new aspects, enabling us to obtain a better description of the interface interactions and, thus, of the conditions for instability. First of all, contact stiffness and viscoelastic dissipation are obtained from adhesiveless (steady-state) contact mechanics boundary element method numerical simulations [39, 44,45,46,47,48,49]. Secondly, in accordance with up-to-date contact mechanics experiments involving soft contacts (polymers and elastomers, [50,51,52,53]), the Coulomb-like fraction of the friction forces is assumed to be proportional, through a characteristic interfacial shear-strength $\tau _{0},$ to the apparent contact area A, being in viscoelastic contacts a time-varying quantity.

The paper is organized as follows. In Sect. 2, the problem is defined mathematically, by introducing the equations of motion and the form of the contact forces that will be used along the paper. In Sect. 3, a linear stability analysis is performed, and the stability boundaries are derived analytically in the limit of low and high sliding velocity. In Sect. 4, the results of the stability analysis are discussed and, finally, in the conclusions, final remarks are drawn.

2 Mathematical definition of the problem

2.1 Dynamic model

Fig. 2

Sketch of the 2-DOF mechanical oscillator considered in the analysis

The mechanical system under investigation is constituted by a rigid spherical oscillator with radius R, mass m, horizontal and vertical stiffness $k_{x}$ and $k_{y}$, off-diagonal spring $k_{xy}$ (inclined by an angle $\alpha ,$ see Fig. 2), horizontal and vertical linear damping coefficients $c_{x}$ and $c_{y}$. The oscillator is pressed by a normal force $F_{n}$ against a viscoelastic substrate moving at velocity $v_{d}$ in the horizontal direction; x is the parameter corresponding to the horizontal displacement of the center of mass of the spherical oscillator, whereas y is the vertical displacement. The latter is equal to 0 when the sphere first touch the substrate: thus, y corresponds to the sphere indentation into the moving viscoelastic substrate.

$$\begin{aligned} \left\{ \begin{array} [c]{c} m\overset{\cdot \cdot }{x}+c_{x}\overset{\cdot }{x}+\left( k_{x}+k_{xy}\cos ^{2}\alpha \right) x+\left( k_{xy}\sin \alpha \cos \alpha \right) y=F_{\mu }\\ m\overset{\cdot \cdot }{y}{+}c_{y}\overset{\cdot }{y}{+}\left( k_{y}{+}k_{xy}\sin ^{2}\alpha \right) y{+}\left( k_{xy}\sin \alpha \cos \alpha \right) x{=}F_{n}{-}F_{k} \end{array} \right. \nonumber \\ \end{aligned}$$

(1)

where a dot superposed means differentiation with respect to time. Regarding the external forces, $F_{\mu }$ is the frictional force acting along the x-axis and is related to the hysteresis occurring due to deformation of the viscoelastic substrate (see Ref. [44] for more details); $F_{k}$ is the normal contact force in the vertical direction and is, thus, equal to the integral of the contact pressure over the contact area. $F_{k}$ is larger than 0 when the sphere indents the substrate, i.e., for $y>0$. Consequently, both $F_{\mu }$ and $F_{k}$ depend on the viscoelastic properties of the substrate and have been numerically obtained by means of boundary element method simulations.

The interaction between the spherical punch and the viscoelastic substrate determines the normal restoring force $F_{k}$ and the friction force $F_{\mu }$ acting on the sphere. In general, as shown in detail in Ref. [11], these components depend on the kinematic parameters that determine the relative motion between the sphere and the substrate, hence for a viscoelastic material with a single relaxation time $\tau$ we have:

$$\begin{aligned} F_{\mu }= & {} F_{\mu }\left( \frac{x-v_{d}t}{R},\frac{\left( \dot{x}-v_{d}\right) \tau }{R},\frac{y}{R}\right) ,\qquad \nonumber \\ F_{k}= & {} F_{k}\left( \frac{x-v_{d}t}{R},\frac{\left( \dot{x}-v_{d}\right) \tau }{R},\frac{y}{R}\right) \end{aligned}$$

(2)

Ultimately, this occurs as, in the mechanics between viscoelastic elements, the contact solution depends, at each time step, on the current deformation of the substrate and on the velocity at which the material is being deformed. Furthermore, in the contact mechanics analysis we have conducted via boundary element method, we have accounted for the material hysteretic dissipative behavior in the in-plane motion, i.e., along the $x-$direction, which plays a major role as determines the viscoelastic part of the friction coefficient, while the dissipation occurring in the vertical motion will be accounted through the linear damping coefficient $c_{y}$.

Now, when looking at Eq. (2), it is clear that viscoelastic materials respond differently when excited at different frequencies. Then, if the punch is oscillating in the horizontal direction with frequency $\omega$ and amplitude $A_{x},$ then the dimensionless frequency of the punch oscillation, with respect to the moving substrate, is:

$$\begin{aligned} \varXi =\left( \omega -v_{d}/A_{x}\right) \tau \end{aligned}$$

(3)

If $\varXi<<1$, the rigid punch will get in contact with a material that had enough time to relax or that was never deformed; hence, we can drop the dependence on the punch relative position $\frac{x-v_{d}t}{R}$. Therefore, $F_{ \mu }$ and $F_{k}$ are written as a function of the following dimensionless groups:

$$\begin{aligned} F_{\mu }=F_{\mu }\left( \widehat{v}_{rel},\widehat{y}\right) ,\qquad F_{k}=F_{k}\left( \widehat{v}_{rel},\widehat{y}\right) \end{aligned}$$

(4)

where we have introduced the groups $\widehat{v}_{rel}=v_{rel}\tau /R$ and $\widehat{y}=y/R$, being $v_{rel}=\overset{\cdot }{x}-v_{d}$ the relative velocity between the punch and the substrate. When writing the friction force $F_{\mu }$, two contributions are considered: (i) the viscoelastic part of the friction coefficient $\mu _{visc}\left( \widehat{v}_{rel},\widehat{y}\right)$ originated by the internal dissipation in the viscoelastic material and (ii) the adhesive part of the frictional force that, as suggested by robust experimental outcomes [50,51,52,53], is assumed proportional to the apparent contact area $A\left( \widehat{v}_{rel} ,\widehat{y}\right)$ through a characteristic interfacial shear-strength $\tau _{0}$. Hence, the tangential force $F_{\mu }\left( \widehat{v} _{rel},\widehat{y}\right)$ is equal to:

$$\begin{aligned} F_{\mu }\left( \widehat{v}_{rel},\widehat{y}\right)= & {} -\text {sgn}\left( \widehat{v}_{rel}\right) \left[ F_{n}\mu _{visc}\left( \widehat{v} _{rel},\widehat{y}\right) \right. \nonumber \\&\left. +A\left( \widehat{v}_{rel},\widehat{y}\right) \tau _{0}\right] \end{aligned}$$

(5)

Notice that both $\mu _{visc}\left( \widehat{v}_{rel},\widehat{y}\right)$ and $A\left( \widehat{v}_{rel},\widehat{y}\right)$ are time varying quantities that depends at every time instant on the indentation of the spherical punch and on the relative horizontal velocity between the punch and the moving substrate [44, 45, 47,48,49]. This is briefly recalled in Appendix A, where the main peculiarities of viscoelastic materials and the Boundary Element Method implemented to study the viscoelastic contact mechanics are summarized.

Let us define, now, the dimensionless viscoelastic contact force $\widetilde{F}_{k}=F_{k}/E_{0}^{*}R^{2}$ and the dimensionless contact area $\widetilde{A}=A/R^{2}$, where $E_{0}^{*}=E_{0}/\left( 1-\nu ^{2}\right)$ is the composite modulus, with $E_{0}$ the viscoelastic modulus of the substrate at zero frequency, i.e., $E_{0}=E\left( \omega =0\right)$, and $\nu$ the Poisson’s ratio. As shown with more details in Appendix A, in fact, a generic linear viscoelastic material is characterized by the so-called rubbery modulus, that is $E_{0}$, by the glassy modulus $E_{\infty }$, being the viscoelastic modulus for $\omega$ tending to infinite, and by a series of relaxation times $\tau$. The simulations have been performed using a single relaxation time linear viscoelastic material with $E_{0}=10^{6}$ Pa , $E_{\infty }=10^{7}$ Pa, $\tau =0.01$ s, $R=0.01$ m and $\nu =0.5$. Such a choice is consistent with the approach adopted in the entire paper: the simple one-relaxation time material allows us to clearly see which are the possible mechanisms of instability in a viscoelastic material and how these depend on the relative velocity between the oscillator and the moving substrate, including the correct elastic limits at low and high relative speed. Although real materials have several relaxation times, we expect our results to be paradigmatic of the general behavior expected in these conditions. Furthermore, let us notice that, once the relaxation spectrum is known for a real viscoelastic material, the method presented here could be repeated to determine the stability boundaries for any given application.

Fig. 3

Fitting of the numerical data obtained with boundary element method simulations (black dots) with the analytical functions (shaded surfaces): a friction coefficient (Eq. (38)), b dimensionless contact area (Eq. (36)), c dimensionless reaction force (Eq. (8)). In all the panel the fitted analytical equations are shown as shaded surfaces as a function of $\log \left( y/R\right)$ and $\log \left( v_{rel}\tau /R\right)$

Turning back to our simplified model, Fig. 3 shows: (a) the reaction force $\widetilde{F}_{k},$ (b) the contact area $\widetilde{A}$ and (c) the viscoelastic friction coefficient $\mu _{visc}$ as a function of $\log _{10}\widehat{y}$ and $\log _{10}\widehat{v}_{rel}$. The black dots represent the numerical results obtained from the boundary element method analysis, while the shaded surfaces refer to the analytical functions used to fit the numerical results. Notice that the fitting laws for all the three quantities have been selected based on physical considerations and on the knowledge of the contact mechanics problem. Indeed, the advantage of using analytical fitting functions is twofold: (i) it guarantees a fast calling and evaluation of the numerical functions during the dynamical simulations and (ii) it allows any researcher to easily replicate or extend this study in the future.

Let us further comment on the physical ratio for the fitting equations employed for $\widetilde{F}_{k}$ , $\widetilde{A}$ and $\mu _{visc}$ (for more numerical detail on the fitting procedure the reader is referred to Appendix B). As for the viscoelastic friction coefficient, $\mu _{visc}\left( \widehat{v} _{rel},\widehat{y}\right)$ is proportional to the imaginary part of the viscoelastic modulus ${\text {Im}}(E(\omega ))$ and, thus, for a one relaxation time material, the dependence of $\mu _{visc}$ on the speed $\widehat{v}_{rel}$ has a bell shape and is well described by a Gaussian function. The dependence on the indentation $\widehat{y}$ can be easily recalled by using the Hertzian theory. The viscoelastic friction force $F_{visc}$ is proportional to the volume being deformed and, thus $F_{visc}\propto a^{2}y$ with a being the contact radius; in an Hertzian contact $a=\left( Ry\right) ^{1/2}$ with R the radius of the spherical indenter, hence $F_{visc}\propto y^{2}$. By recalling that the normal force is proportional to $y^{3/2}$ one obtains $\mu _{visc}\propto y^{1/2}$. Consequently, we have implemented the following fitting equation:

$$\begin{aligned} \mu _{visc}=c_{1}\widehat{y}^{1/2}\exp \left( -\frac{\left( \log _{10} \widehat{v}-\left( c_{2}\log _{10}\widehat{y}+c_{3}\right) \right) ^{2} }{2c_{4}^{2}}\right) \nonumber \\ \end{aligned}$$

(6)

which has provided a coefficient of determination $r^{2}=0.9957$ (see Fig. 3a). Notice that the viscoelastic friction monotonically increases with the indentation y/R as a larger penetration implies a larger volume that deforms and dissipates. Furthermore, with respect to the velocity dependence, the bell-shaped trend in the semi-logarithmic scale, where friction vanishes at very low and very high speed values, occurs as in the limit of very high and very low speeds, the material behaves elastically, whereas it reaches a maximum in the range of intermediate velocity.

With regard to the contact area $A\left( \widehat{v}_{rel},\widehat{y}\right)$, according to Hertz theory, the apparent contact area should depend linearly on the indentation $\widehat{y}$, whereas the dependence on velocity resemble a flipped Gaussian function. The fitting equation results:

$$\begin{aligned} \widetilde{A}=b_{1}\widehat{y}\left[ b_{2}-\exp \left( -\frac{\left( \log _{10}\widehat{v}-\left( b_{3}\log _{10}\widehat{y}+b_{4}\right) \right) ^{2}}{2b_{5}^{2}}\right) \right] \nonumber \\ \end{aligned}$$

(7)

which gave a coefficient of determination $r^{2}=0.9995$ (see Fig. 3b). Indeed, the contact area $\widetilde{A}$ is constant at low and high velocity, where the material behaves elastically and the contact radius is only defined by the imposed indentation $\widehat{y}$ as predicted by Hertzian theory, while, as shown in Ref. [44], due to viscoelasticity, it reaches a minimum in the range of intermediate velocities.

Finally, the substrate reaction force should be proportional to $\propto \widehat{y}^{3/2},$ while the dependence on the velocity can be well captured by an ${\text {erf}}\left( x\right)$ function. An excellent fit was obtained using the fit equation

$$\begin{aligned} \widetilde{F}_{k}=a_{1}\widehat{y}^{3/2}\frac{1}{2}\left[ a_{2} +{\text {erf}}\left( a_{3}\log _{10}\widehat{v}+\left( a_{4}\log _{10}\widehat{y}+a_{5}\right) \right) \right] \nonumber \\ \end{aligned}$$

(8)

which provided a coefficient of determination $r^{2}=0.9999$ (see Fig. 3c). For a given penetration, the elastic reaction force increases moving from the rubbery to the glassy region, i.e., from low to high velocity.

2.2 Dimensionless formulation

After introducing the equilibrium equations in the horizontal and vertical directions and the equations that determine the contact forces, we develop here a dimensionless formulation, that will be used along the rest of the paper. Let us introduce the damping ratio $\xi _{x}$ and $\xi _{y}$, referred to the motion components, respectively, along the $-x$ axis and the $-y$ axis, and, similarly, the natural frequencies $\omega _{nx}$, $\omega _{ny}$ and $\omega _{nxy}$:

$$\begin{aligned}&\xi _{x}=\frac{c_{x}}{2\sqrt{k_{x}m}};\qquad \xi _{y}=\frac{c_{y}}{2\sqrt{k_{x} m}};\nonumber \\&\omega _{nx}=\sqrt{\frac{k_{x}}{m}};\qquad \omega _{ny}=\sqrt{\frac{k_{y}}{m} };\qquad \omega _{nxy}=\sqrt{\frac{k_{xy}}{m}}. \nonumber \\ \end{aligned}$$

(9)

By defining the dimensionless time $\theta$ and a reference displacement $x_{0}$ as

$$\begin{aligned} \theta =t\omega _{nx};\qquad x_{0}=\frac{F_{n}}{k_{x}}; \end{aligned}$$

(10)

we introduce the following dimensionless parameters:

$$\begin{aligned} \widetilde{y}= & {} \frac{y}{x_{0}};\qquad \widetilde{x}=\frac{x}{x_{0}} ;\qquad \widetilde{v}_{rel}=\frac{v_{rel}}{x_{0}\omega _{nx}};\qquad \nonumber \\ \widetilde{\tau }= & {} \omega _{nx}\tau ;\qquad \widetilde{A}=\frac{A}{R^{2}};\qquad \widetilde{\tau }_{0}=\frac{\tau _{0}}{E_{0}^{*}};\nonumber \\ \varOmega= & {} \frac{\omega _{ny}}{\omega _{nx}};\qquad \eta =\frac{\omega _{nxy}}{\omega _{nx}};\qquad \widetilde{R}=\frac{R}{x_{0}};\qquad \nonumber \\ \widetilde{F}_{k}= & {} \frac{F_{k}}{E_{0}^{*}R^{2}};\qquad \widetilde{F}_{n}=\frac{F_{n} }{E_{0}^{*}R^{2}}. \end{aligned}$$

(11)

Using (9,11) and $\frac{d}{dt}=\omega _{nx}\frac{d}{d\theta }$, the equilibrium equations can be written in dimensionless form as

$$\begin{aligned} \left\{ \begin{array} [l]{l} \overset{\cdot \cdot }{\widetilde{x}}+2\xi _{x}\overset{\cdot }{\widetilde{x} }+(1+\eta ^{2}\cos ^{2}\alpha )\widetilde{x}+\left( \eta ^{2}\sin \alpha \cos \alpha \right) \widetilde{y}=-\text {sign}(\widetilde{v}_{rel})\left[ \mu _{visc}\left( \widehat{v}_{rel},\widehat{y}\right) +\frac{\widetilde{\tau }_{0} }{\widetilde{F}_{n}}\widetilde{A}\left( \widehat{v}_{rel},\widehat{y}\right) \right] \\ \overset{\cdot \cdot }{\widetilde{y}}+2\xi _{y}\overset{\cdot }{\widetilde{y} }+\left( \varOmega ^{2}+\eta ^{2}\sin ^{2}\alpha \right) \widetilde{y}+\left( \eta ^{2}\sin \alpha \cos \alpha \right) \widetilde{x}=1-\frac{\widetilde{F} _{k}\left( \widehat{v}_{rel},\widehat{y}\right) }{\widetilde{F}_{n}} \end{array} \right. \end{aligned}$$

(12)

Notice that, in case of lift-off of the spherical punch, no contact between the punch and the substrate occurs, hence, in such conditions, $\widetilde{F}_{k}\left( \widehat{v},\widehat{y}\right) {=}0$ and $\mu _{visc}\left( \widehat{v},\widehat{y}\right) =0$; Eqs. (12) will be modified accordingly:

$$\begin{aligned} \left\{ \begin{array} [l]{l} \overset{\cdot \cdot }{\widetilde{x}}+2\xi _{x}\overset{\cdot }{\widetilde{x} }+(1+\eta ^{2}\cos ^{2}\alpha )\widetilde{x}+\left( \eta ^{2}\sin \alpha \cos \alpha \right) \widetilde{y}=0\\ \overset{\cdot \cdot }{\widetilde{y}}+2\xi _{y}\overset{\cdot }{\widetilde{y} }+\left( \varOmega ^{2}+\eta ^{2}\sin ^{2}\alpha \right) \widetilde{y}+\left( \eta ^{2}\sin \alpha \cos \alpha \right) \widetilde{x}=1 \end{array} \right. \nonumber \\ \end{aligned}$$

(13)

If not differently stated, in the next sections, we will assume the following model parameters:

$$\begin{aligned}&\xi _{x}=0.01;\qquad \xi _{y}=0.01;\qquad \varOmega =1;\qquad \eta =1;\qquad \alpha =\pi /4; \nonumber \\&\omega _{nx}=40\text {rad/s};\qquad k_{x}=50\text {N/m}. \end{aligned}$$

(14)

where the parameters in the second row may be useful if one wants to go back from dimensionless to dimensional quantities. Here, we are focusing our attention on the particular case $\varOmega =\eta =1$: such a choice is carried out as we aim at investigating how Stribeck and mode-coupling instabilities co-exist and interact. Clearly, setting a vanishing (or infinite) value for $\varOmega$ or $\eta$ would give the system two far apart modes, thus preventing the mode-coupling instability to take place.

3 Linear stability analysis

Let us assume that the substrate is sliding at a given velocity $\widehat{v}_{d}$ and a steady state solution exists so that $\overset{\cdot }{\widetilde{x}}=\overset{\cdot }{\widetilde{y}}=0$ and $\widehat{v} _{rel}=-\widehat{v}_{d}$. From Eq. (12), the static equilibrium position $\left( \widetilde{x}_{e},\widetilde{y}_{e}\right)$ can be obtained by solving the following algebraic system of equations:

$$\begin{aligned} \left\{ \begin{array} [l]{l} (1+\eta ^{2}\cos ^{2}\alpha )\widetilde{x}_{e}+\left( \eta ^{2}\sin \alpha \cos \alpha \right) \widetilde{y}_{e}=\left[ \mu _{visc}\left( \widehat{v} _{rel},\widehat{y}_{e}\right) +\frac{\widetilde{\tau }_{0}}{\widetilde{F}_{n} }\widetilde{A}\left( \widehat{v}_{rel},\widehat{y}_{e}\right) \right] \\ \left( \varOmega ^{2}+\eta ^{2}\sin ^{2}\alpha \right) \widetilde{y}_{e}+\left( \eta ^{2}\sin \alpha \cos \alpha \right) \widetilde{x}_{e}=1-\frac{\widetilde{F}_{k}\left( \widehat{v}_{rel},\widehat{y}_{e}\right) }{\widetilde{F}_{n}} \end{array} \right. \end{aligned}$$

(15)

where $\widehat{y}_{e}=\widetilde{y}_{e}/\widetilde{R}$. By defining $\widetilde{u}\left( t\right) =\widetilde{x}\left( t\right) -\widetilde{x}_{e}$ and $\widetilde{q}\left( t\right) =\widetilde{y}\left( t\right) -\widetilde{y}_{e}$, the system of equations (12) is linearized and written in matrix form as:

$$\begin{aligned}&\begin{bmatrix} 1 &{} 0\\ 0 &{} 1 \end{bmatrix} \begin{Bmatrix} \overset{\cdot \cdot }{\widetilde{u}}\\ \overset{\cdot \cdot }{\widetilde{q}} \end{Bmatrix} + \begin{bmatrix} 2\xi _{x} &{} 0\\ 0 &{} 2\xi _{y} \end{bmatrix} \begin{Bmatrix} \overset{\cdot }{\widetilde{u}}\\ \overset{\cdot }{\widetilde{q}} \end{Bmatrix}\nonumber \\&\qquad + \begin{bmatrix} 1+\eta ^{2}\cos ^{2}\alpha &{} \eta ^{2}\sin \alpha \cos \alpha \\ \eta ^{2}\sin \alpha \cos \alpha &{} \varOmega ^{2}+\eta ^{2}\sin ^{2}\alpha \end{bmatrix} \begin{Bmatrix} \widetilde{u}\\ \widetilde{q} \end{Bmatrix}\nonumber \\&\quad = \begin{Bmatrix} \frac{\widetilde{\tau }}{\widetilde{R}}\left( \frac{\partial \mu }{\partial \widehat{v}_{rel}}+\frac{\widetilde{\tau }_{0}}{\widetilde{F}_{n} }\frac{\partial \widetilde{A}}{\partial \widehat{v}_{rel}}\right) _{\left( \widehat{v}_{rel},\widehat{y}_{e}\right) }\overset{\cdot }{\widetilde{u} }+\frac{1}{\widetilde{R}}\left( \frac{\partial \mu }{\partial \widehat{y}} +\frac{\widetilde{\tau }_{0}}{\widetilde{F}_{n}}\frac{\partial \widetilde{A} }{\partial \widehat{y}}\right) _{\left( \widehat{v}_{rel},\widehat{y} _{e}\right) }\widetilde{q}\\ -\frac{\widetilde{\tau }}{\widetilde{R}\widetilde{F}_{n}}\left. \frac{\partial \widetilde{F}_{k}}{\partial \widehat{v}_{rel}}\right| _{\left( \widehat{v}_{rel},\widehat{y}_{e}\right) }\overset{\cdot }{\widetilde{u} }-\frac{1}{\widetilde{R}\widetilde{F}_{n}}\left. \frac{\partial \widetilde{F}_{k}}{\partial \widehat{y}}\right| _{\left( \widehat{v}_{rel} ,\widehat{y}_{e}\right) }\widetilde{q} \end{Bmatrix}\nonumber \\ \end{aligned}$$

(16)

where we have used

$$\begin{aligned} \frac{\partial }{\partial \overset{\cdot }{\widetilde{u}}}=\frac{\partial }{\partial \overset{\cdot }{\widetilde{x}}}=\frac{\partial }{\partial \widetilde{v}_{rel}};\qquad \frac{\partial }{\partial \widetilde{q}} =\frac{\partial }{\partial \widetilde{y}}. \end{aligned}$$

(17)

Equation (16) can be rewritten in the classical form:

$$\begin{aligned}&\mathbf {M}\overset{\cdot \cdot }{\widetilde{U}}+\mathbf {C}\overset{\cdot }{\widetilde{U}}+\mathbf {K}\widetilde{U}=0\rightarrow \end{aligned}$$

(18)

$$\begin{aligned}&\begin{bmatrix} 1 &{} 0\\ 0 &{} 1 \end{bmatrix} \begin{Bmatrix} \overset{\cdot \cdot }{\widetilde{u}}\\ \overset{\cdot \cdot }{\widetilde{q}} \end{Bmatrix} + \begin{bmatrix} c_{11} &{} c_{12}\\ c_{21} &{} c_{22} \end{bmatrix} \begin{Bmatrix} \overset{\cdot }{\widetilde{u}}\\ \overset{\cdot }{\widetilde{q}} \end{Bmatrix} \nonumber \\&\qquad + \begin{bmatrix} k_{11} &{} k_{12}+k_{12c}\\ k_{21} &{} k_{22} \end{bmatrix} \begin{Bmatrix} \widetilde{u}\\ \widetilde{q} \end{Bmatrix} = \begin{Bmatrix} 0\\ 0 \end{Bmatrix} \end{aligned}$$

(19)

where $\mathbf {M,}$ $\mathbf {C,}$ $\mathbf {K}$ are, respectively, the mass, damping and stiffness matrix, $\widetilde{U}^{T}=\left\{ \widetilde{u},\widetilde{q}\right\}$ and

$$\begin{aligned}&c_{11}=2\xi _{x}-\frac{\widetilde{\tau }}{\widetilde{R}}\left( \frac{\partial \mu }{\partial \widehat{v}_{rel}}+\frac{\widetilde{\tau }_{0} }{\widetilde{F}_{n}}\frac{\partial \widetilde{A}}{\partial \widehat{v}_{rel} }\right) _{\left( \widehat{v}_{rel},\widehat{y}_{e}\right) };\qquad \nonumber \\&c_{21}=\frac{\widetilde{\tau }}{\widetilde{R}\widetilde{F}_{n}}\left. \frac{\partial \widetilde{F}_{k}}{\partial \widehat{v}_{rel}}\right| _{\left( \widehat{v}_{rel},\widehat{y}_{e}\right) }; \nonumber \\&c_{22}=2\xi _{y};\qquad c_{12}=0;\nonumber \\&k_{11}=1+\eta ^{2}\cos ^{2}\alpha ;\qquad k_{12}=k_{21}=\eta ^{2}\sin \alpha \cos \alpha ; \nonumber \\&k_{12c}=-\frac{1}{\widetilde{R}}\left( \frac{\partial \mu }{\partial \widehat{y}}+\frac{\widetilde{\tau }_{0}}{\widetilde{F}_{n}}\frac{\partial \widetilde{A}}{\partial \widehat{y}}\right) _{\left( \widehat{v}_{rel},\widehat{y} _{e}\right) };\qquad \nonumber \\&k_{22}=(\varOmega ^{2}+\eta ^{2}\sin ^{2}\alpha )+\frac{1}{\widetilde{R}\widetilde{F}_{n}}\left. \frac{\partial \widetilde{F}_{k} }{\partial \widehat{y}}\right| _{\left( \widehat{v}_{rel},\widehat{y} _{e}\right) }. \end{aligned}$$

(20)

The stability of the equilibrium state $\left( \widetilde{x}_{e} ,\widetilde{y}_{e}\right)$ can be determined by solving the eigenvalue problem

$$\begin{aligned} \text {det}(\mathbf {A}-\lambda \mathbf {I})=\varvec{0} \end{aligned}$$

(21)

being $\mathbf {A}$ the state matrix

$$\begin{aligned} \mathbf {A}= \begin{bmatrix} \left[ \mathbf {0}\right] &{} \left[ \mathbf {I}\right] \\ \left[ -\mathbf {M}^{-1}\mathbf {K}\right] &{} \left[ -\mathbf {M} ^{-1}\mathbf {C}\right] \end{bmatrix} _{{4*4}} \end{aligned}$$

(22)

If all eigenvalues $\lambda _{i}$ have negative real parts $\left( {\text {Re}}\left( \lambda _{i}\right) <0,\text { }\forall \text { } \lambda _{i}\right)$ the equilibrium solution $\left( \widetilde{x} _{e},\widetilde{y}_{e}\right)$ is linearly stable against small perturbations.

4 Results

4.1 Equivalent damping in the horizontal direction

Let us preliminary focus on the damping matrix $\mathbf {C}$ and, in particular, on the search for possible sources of negative damping. As well known in literature, in fact, negative damping is one of the elements that trigger FIVs. When looking at matrix $\mathbf {C}$, we realize that the component $c_{12}$ is null, while the term $c_{22}$ is positive and depends on the external structural source of damping. As for $c_{21}$, this correlates the damping in the horizontal direction to the oscillations in the vertical motion: $c_{21}$ is always positive as $\widetilde{F}_{k}$ increases monotonically with the sliding velocity (see Fig. 3c). Finally, the remaining term $c_{11}\$contains two contributions, one originated by the external damping $\xi _{x}$, the other related to the dissipative processes occurring in the viscoelastic substrate. Specifically, we can define the system equivalent damping ratio $\xi _{eq}$ along the x-direction as $\xi _{eq}=c_{11}/2$, and, then, write $\xi _{eq}$ as:

$$\begin{aligned} \xi _{eq}=\xi _{x}+\frac{\widetilde{\tau }}{2\widetilde{R}}\left( \frac{\partial \mu }{\partial \widehat{v}_{rel}}+\frac{\widetilde{\tau }_{0} }{\widetilde{F}_{n}}\frac{\partial \widetilde{A}}{\partial \widehat{v}_{rel} }\right) _{\left( \widehat{v}_{d},\widehat{y}_{e}\right) } \end{aligned}$$

(23)

Fig. 4

Equivalent damping $\xi _{eq}$ as a function of the substrate dimensionless velocity $\widehat{v}_{d},$ for $\widetilde{F}_{n} =7.5*\left[ 10^{-5},10^{-4},10^{-3},10^{-2}\right]$ and $\widetilde{\tau }_{0}=[0,0.01,0.05,0.1].$ In the insets, a zoom in the range of $\widehat{v}_{d}=\left[ 10^{-2},10^{0}\right]$ is shown

Now, in Fig. 4, for the model parameters previously fixed, the equivalent damping ratio $\xi _{eq}$ is plotted as a function of the dimensionless substrate velocity $\widehat{v}_{d},$ for different values of the normal force $\widetilde{F}_{n}=7.5*\left[ 10^{-2},10^{-3} ,10^{-4},10^{-5}\right]$ and the tangential stress $\widetilde{\tau } _{0}=[0,0.01,0.05,0.1]$.

Let us recall that the friction $\mu _{visc}$ vanishes at low and high values of the sliding substrate velocity, i.e., when the substrate acts as elastic, respectively, in the rubbery and the glassy regimes; in these limits, the contact area $\widetilde{A}$ assumes the constant values given by the elastic Hertzian solution. Thus, in the limits of vanishing or infinite sliding velocity, the derivatives $\partial \mu /\partial \widehat{v}_{rel}$ and $\partial \widetilde{A}/\partial \widehat{v}_{rel}$ go to zero and, thus, the equivalent damping coefficient is very small and equal to the linear damping coefficient $\xi _{eq} = \xi _x$, which is pretty small when compared to the interfacial damping. On the other hand, as soon as the speed is slightly increased, the viscoelastic friction markedly increases. This is the region where the transition from “stick to slip” takes place, which implies a large value for the derivative term $\partial \mu /\partial \widehat{v}_{rel}$ and ultimately a large equivalent damping. The latter behavior is well-known in tribology, particularly for the rate and state friction models developed mostly by the geophysics community [54,55,56].

For very small values of $\widetilde{\tau }_{0}$ , the equivalent damping is uniquely defined by the viscoelastic friction (see, in all the panels in Fig. 4, the pale blue curves): starting from a value asymptotically tending to $\xi _{x}$, $\xi _{eq}$ increases with the speed, reaches a maximum and then decreases, eventually becoming negative for $\widehat{v}_{d}$ being approximately equal to approximately $\widehat{v} _{d}\approx 10^{-2}$ as visible in Fig. 4 insets. Finally, for very large values of $\widehat{v}_{d}$ , $\xi _{eq}$ tends to $\xi _{x}$.

Regarding the dependence on the interfacial shear stresses, by increasing $\widetilde{\tau }_{0}$, the effect of $\partial \widetilde{A}/\partial \widehat{v}_{rel}$ becomes dominant. We employ $\widetilde{\tau }_{0}\in \left[ 0.01,0.1\right]$ as this is a representative range for soft materials. Figure 4 shows that increasing $\widetilde{\tau }_{0}$ reduces $\xi _{eq}$ in the range of intermediate velocity. For low normal loads, this reduction may be strong enough to bring $\xi _{eq}$ in the negative half-plane. Although this may resemble counterintuitive, in Fig. 3b, it can be seen that the contact area $\widetilde{A}$ decreases with velocity, reaches a minimum and, only after that, increases again. This means that there is a speed range, where $\partial \widetilde{A}/\partial \widehat{v}_{rel}$ is negative and there occurs a negative damping effect. Ultimately, the faster the sphere goes, the smaller the contact area gets, the smaller the “adhesive” shear resistance is. Conversely, in the range of high velocity (see Fig. 4), where the contact area provides a positive damping ($\partial \widetilde{A}/\partial \widehat{v}_{rel}$ $>0$, see Fig. 3b), the higher $\widetilde{\tau }_{0}$ the higher $\xi _{eq}$.

4.2 Linear stability for high/low velocity

Before proceeding with the stability map, it is interesting to consider the system under investigation in the limit of very low or very high driving velocity. In this limit, all the dissipative interfacial contributions vanishes as the material behaves elastically, and $\partial \mu /\partial \widehat{v}_{rel}$ and $\partial \widetilde{A}/\partial \widehat{v}_{rel}$ goes to zero; there exist the externally imposed damping ratios $\xi _{x}$ and $\xi _{y}$, but, as typical in most of the mechanical structures, these can be assumed very small (in the order of 0.01). It is hence licit to neglect the contribution of the damping matrix in the stability analysis $\left( \mathbf {C=0}\right)$ to determine the system eigenvalues. With this approximation, it is possible to obtain, from the state matrix $\mathbf {A}$, two pairs of complex-conjugate eigenvalues:

$$\begin{aligned} \lambda _{1,2}&{=}\pm \frac{1}{\sqrt{2}}\sqrt{{-}\left( k_{11}{+}k_{22}\right) -\sqrt{4k_{12}\left( k_{12}{+}k_{12c}\right) {+}\left( k_{11}{-}k_{22}\right) ^{2}}} \end{aligned}$$

(24)

$$\begin{aligned} \lambda _{3,4}&=\pm \frac{1}{\sqrt{2}}\sqrt{-\left( k_{11}{+}k_{22}\right) {+}\sqrt{4k_{12}\left( k_{12}+k_{12c}\right) {+}\left( k_{11}{-}k_{22}\right) ^{2}}} \end{aligned}$$

(25)

where $\lambda _{1,2}$ are purely imaginary, while $\lambda _{3,4}$ can be real or complex depending on the terms in the stiffness matrix. Incidentally, notice that we have neglected the contribution of the damping matrix, but the effect of the viscoelastic substrate still remains through the stiffness matrix $\mathbf {K}$. While the terms $k_{11}$ and $k_{12}$ depend only on the structural stiffness, the terms $k_{12c}$ and $k_{22}$ depend on the substrate properties and its deformation: although the layer, in this conservative limit of small and large speeds, behaves elastically, contact area and substrate restoring force still depend on the indentation.

Fig. 5

a Real and b imaginary part of the system eignevalues as a function of the interfacial shear strength $\widehat{\tau }_{0}$ for $\widehat{v}_{d}=10^{-4}$ and $\widetilde{F}_{n}=7.5*10^{-6}$

Fig. 6

a Real and b imaginary parts of the system eignevalues as a function of the dimensionless normal force $\widetilde{F}_{n}$ for $\widehat{\tau }_{0}=0.01$ and $\widehat{v}_{d}=1.58*10^{-4}$

Figure 5 shows the system eigenvalues as a function of the interfacial shear strength $\widetilde{\tau }_{0}$ for $\widehat{v}_{d} =10^{-4}$ and $\widetilde{F}_{n}=7.5*10^{-6}$. At low interfacial shear strength, two purely imaginary eigenvalues exist, and then, at about $\widetilde{\tau }_{0crit}\approx 3.5*10^{-2}$ the two modes merge and a pair of eigenvalues develop: one of these has a positive real part, showing the classical picture of a flutter type instability. In Fig. 6, the eigenvalues $\lambda _{i}$ are plotted as a function of the normal force $\widetilde{F}_{n}$ for a given $\widetilde{\tau }_{0}=0.01$ and $\widehat{v}_{d}=1.58*10^{-4}$. One recognizes that for $\widetilde{F}_{n} \gtrsim 7.5*10^{-7}$ there exist two purely imaginary eigenvalues (recall we set $\mathbf {C=0}$), while for a smaller normal force the two modes merge and a pair of eigenvalues, one with positive real part, appear. We conclude that both low normal forces and high interfacial shear stresses will promote flutter instability.

Fig. 7

Critical interfacial shear strength $\widetilde{\tau }_{0,crit}$ above which the system is linearly unstable as a function of the driving velocity $\widehat{v}_{d}$ and for different normal forces $\log _{10}\widetilde{F} _{n}=\left[ -8,-7,...,-4\right]$

Fig. 8

$\widetilde{F}_{n,crit}$ below which one has flutter instability as a function of the substrate velocity $\widehat{v}_{d}$ and for $\widetilde{\tau }_{0}=\left[ 0.01,0.05,0.1\right]$

Looking at Fig. 5 and 6, it could be interesting to determine the critical interfacial shear strength $\widetilde{\tau }_{0,crit}$ and the critical normal force $\widetilde{F}_{n,crit}$ at which the flutter instability originates: we will, be able to define the “critical point”, where the two modes merges. From Eq. (25), one obtains

$$\begin{aligned} k_{12c}=-\frac{\left( k_{11}-k_{22}\right) ^{2}}{4k_{12}}-k_{12}, \end{aligned}$$

(26)

which can be cast in terms of critical shear strength $\tau _{0,crit}$ and critical normal load ${F_{n,crit}}$: for shear stresses larger than $\tau _{0,crit}$ and normal load smaller than $F_n$, self-excited vibrations will be triggered. These critical values are, respectively:

$$\begin{aligned} \widetilde{\tau }_{0,crit}&=\left[ \widetilde{k}_{x}\left( \frac{\left( 1+\eta ^{2}\cos 2\alpha -\varOmega ^{2}-\frac{1}{\widetilde{k}_{x}}\left. \frac{\partial \widetilde{F}_{k}}{\partial \widehat{y}}\right| _{\left( \widehat{v}_{rel}^{\prime },\widehat{y}^{\prime }\right) }\right) ^{2}}{2\eta ^{2}\sin 2\alpha }+\frac{\eta ^{2}\sin 2\alpha }{2}\right) \right. \nonumber \\ {}&\left. -\widetilde{F}_{n}\left. \frac{\partial \mu }{\partial \widehat{y}}\right| _{\left( \widehat{v}_{rel}^{\prime },\widehat{y}^{\prime }\right) }\right] \left. \frac{\partial \widetilde{A}}{\partial \widehat{y}}\right| _{\left( \widehat{v}_{rel}^{\prime },\widehat{y}^{\prime }\right) }^{-1} \end{aligned}$$

(27)

$$\begin{aligned} \widetilde{F}_{n,crit}&=\left[ \widetilde{k}_{x}\left( \frac{\left( 1+\eta ^{2}\cos 2\alpha -\varOmega ^{2}-\frac{1}{\widetilde{k}_{x}}\left. \frac{\partial \widetilde{F}_{k}}{\partial \widehat{y}}\right| _{\left( \widehat{v}_{rel}^{\prime },\widehat{y}^{\prime }\right) }\right) ^{2}}{2\eta ^{2}\sin 2\alpha }+\frac{\eta ^{2}\sin 2\alpha }{2}\right) \right. \nonumber \\ {}&\left. -\widetilde{\tau }_{0}\left. \frac{\partial \widetilde{A}}{\partial \widehat{y}}\right| _{\left( \widehat{v}_{rel}^{\prime },\widehat{y}^{\prime }\right) }\right] \left. \frac{\partial \mu }{\partial \widehat{y}}\right| _{\left( \widehat{v}_{rel}^{\prime },\widehat{y}^{\prime }\right) }^{-1} \end{aligned}$$

(28)

where we introduce the dimensionless tangential stiffness $\widetilde{k} _{x}=k_{x}/\left( E_{0}^{*}R\right)$. Figure 7 shows the critical shear strength $\widetilde{\tau }_{0,crit}$, above which the system is linearly unstable, as a function of the speed $\widehat{v}_{d}$ for several values of the applied normal force $\widetilde{F}_{n,crit}$. This critical shear stress $\widetilde{\tau }_{0,crit}$ increases both with the substrate velocity and with the applied normal force. Notice that for a soft material a realistic value of $\widetilde{\tau }_{0,crit}$ is in the range $\left[ 0.01,0.1\right]$: hence, low normal forces can easily lead to flutter. Figure 8 shows the critical normal force $\widetilde{F}_{n,crit}$ below which there exists flutter instability as a function of the substrate velocity $\widehat{v}_{d}$ and for different values of $\widetilde{\tau } _{0}=\left[ 0.01,0.05,0.1\right]$. Ultimately, it is shown that $\widetilde{F}_{n,crit}$ decreases with $\widehat{v}_{d}$ and increases with $\widetilde{\tau }_{0}$: thus, for a given $\widetilde{\tau }_{0}$ a smaller velocity promotes instability.

4.3 Stability map for the full system

The dynamical system considered is linearly stable to small perturbations if $\max \left[ {\text {Re}}\left( \lambda _{i}\right) \right] <0$, being $\lambda _{i}$ the $i-$th eigenvalue obtained from Eq. (21). Here, the stability maps of the full system are shown for a given set of governing parameters: this has been carried out by accounting for the damping matrix $\varvec{C}$. Indeed, Fig. 9 shows the stability maps as a function of the driving velocity $\widehat{v}_{d}$ and of the interfacial shear stress $\widetilde{\tau }_{0}$ , for different values of the normal force $\widetilde{F}_{n}$.

Fig. 9

Linear stability map for the full (damped) system as a function of the driving velocity $\widehat{v}_{d}$ and of the interfacial shear strength $\widetilde{\tau }_{0}$. The stable (unstable) region corresponds to $\max \left[ {\text {Re}}\left( \lambda _{i}\right) \right] <0$ $\left( \max \left[ {\text {Re}}\left( \lambda _{i}\right) \right] >0\right) ,$ being $\lambda _{i}$ the eigenvalue computed from Eq. (21). Dashed black line indicates the stability boundary obtained from the conservative system (Eq. (27)), while the red solid line is the stability boundary obtained with the full system but setting $\eta =0$. Panel (a) for $\widetilde{F}_{n}=10^{-6}$ while panel (b) for $\widetilde{F}_{n}=10^{-3}$

Fig. 10

Linear stability map for the full (damped) system as a function of the driving velocity $\widehat{v}_{d}$ and of the normal force $\widetilde{F}_{n}$. The stable (unstable) region corresponds to $\max \left[ {\text {Re}}\left( \lambda _{i}\right) \right] <0$ $\left( \max \left[ {\text {Re}}\left( \lambda _{i}\right) \right] >0\right) ,$ being $\lambda _{i}$ the eigenvalues computed from Eq. (21). The dashed black line indicates the stability boundary obtained from the conservative system (Eq. (28)), while the red solid line is the stability boundary obtained with the full system but setting $\eta =0$. Panel (a) for $\widetilde{\tau }_{0}=10^{-2}$ while panel (b) for $\widetilde{\tau } _{0}=10^{-1}$

Now, for small values of the normal force and, specifically, for $\widetilde{F}_{n}=10^{-6}$, panel (a) shows that the stability boundary of the full system (obtained from Eq. (21), black dashed line in 9) is in good agreement with the estimate obtained neglecting the damping matrix $\varvec{C}$ over all the velocity range, except in the range between $\widehat{v}_{d}\simeq 10^{-6}\sim 10^{-4}$. The agreement seems to worsen for larger normal forces, as clear in panel (b), where the stability analysis is carried out for $\widetilde{F}_{n}=10^{-3}$. We easily understand this observing that dissipation in the viscoelastic substrate is proportional to the volume of material deformed during the normal sliding, thus, at low normal forces, the only damping remaining in the system is related to $\xi _{x}$ and $\xi _{y}$ whose values are indeed quite small. For a higher normal force, (panel (b)) Eq. (27) gives an accurate result both at high and low driving velocity while it overestimates the stability range at intermediate velocity. This is immediately explained when one remembers the rheology of viscoelastic materials: they behave elastically (no dissipation occurs) at low and high frequency of excitation (glassy and rubbery region) while they dissipate energy for intermediate frequency (transition regime). It may result unexpected that the full system shows an instability region that is larger than the conservative counter-part. Nevertheless, Fig. 4 shows that the system equivalent damping (x-direction) is strongly affected by the contact area evolution with the driving velocity. In particular, negative damping is achieved for relatively small normal forces (see Fig. 4 bottom panels), which clearly foster instability. Furthermore, at very low interfacial shear strength ($\widetilde{\tau }_{0}\simeq 10^{-3} \sim 10^{-4}$), the terms related to the contact area variation in the damping matrix $\mathbf {C}$ vanish and the only remaining contribution is related to the variation in the viscoelastic friction coefficient $\mu _{visc}$. Clearly, two different mechanisms of instability are supervening here: one related to the mode coupling instability, the other to the so-called Stribeck effect. To isolate the effect of the negative damping induced by the variation in the viscoelastic friction coefficient and of the contact area with the relative velocity, we show in Fig. 9 the stability boundary (red solid line) that one would obtain by setting $\eta =0$. Indeed, for $\eta =0$ the two modes are decoupled, which prevents the development of flutter instability. In the region of intermediate velocity, the prevailing mechanism for instability is due to a Stribeck effect. In this respect, the accuracy of Eq. (27) can be reconsidered: the analysis in the limit of low or high velocities, where viscoelastic dissipation vanishes, correctly predicts the stability boundary due to flutter in the region where the latter is the dominant mechanism for instability.

Figure 10 shows the stability maps as a function of the driving velocity $\widehat{v}_{d}$ and of the applied normal force $\widetilde{F} _{n}$ for two interfacial shear stresses $\widetilde{\tau }_{0}=\left[ 0.01,0.1\right]$, respectively, in panel (a) and panel (b). As shown in Fig. 9, the stability boundary obtained by employing Eq. (28) for the conservative system (dashed black line) matches the full system stability boundary only at low and high sliding velocity. On the other end in the transition region the viscoelastic properties of the substrate strongly affect the system stability introducing the positive/negative damping contributions originated by the contact area variation and the friction coefficient evolution with the relative velocity. By comparing panel (a) and panel (b), one notices that the unstable region enlarges for materials with a higher interfacial shear strength: this is clearly determined by the terms related to the contact area variation in the damping matrix. This is demonstrate by the stability boundary we have obtained by setting $\eta =0$: this again shows how, in the region of intermediate velocities, the prevailing mechanism for instability is due to a Stribeck’s effect.

5 Post-instability behavior

To better understand the importance of accounting for the effect of a time varying contact area in determining the dynamical response of a mechanical system in relative motion with a viscoelastic substrate, here we focus on the post-instability response of the dynamical system by means of time integration results. An illustrative case is considered for $\widetilde{F}_{n}=7.5*10^{-4}$, $\widetilde{v}_{d}=5*10^{-3}$ and a varying characteristic interfacial shear strength $10^{-4}<\widetilde{\tau }_{0}<5*10^{-2}$. Since the Coulomb part of the frictional resistance is proportional to the interfacial shear strength, a vanishing $\widetilde{\tau }_{0}$ “suppresses” the effect of the varying contact area, while this gets stronger for high values of $\widetilde{\tau }_{0}$. Figure 11 shows the root-mean-square vibration amplitude $\widetilde{X}_{rms}$ as a function of $\widetilde{\tau }_{0}$. Increasing $\widetilde{\tau }_{0}$ completely changes the stability of the system. Indeed, for $\widetilde{\tau }_{0}\lesssim 2*10^{-3}$, the system is stable against small perturbations and the vibration amplitude is about 0. For larger $\widetilde{\tau }_{0}$ the system becomes unstable and the vibration amplitude $\widetilde{X}_{rms}$ strongly increases with $\widetilde{\tau }_{0}$. Clearly, accounting for the time varying contact area strongly influences the system dynamics.

Fig. 11

Dimensionless vibration amplitude (root-mean-square) $\widetilde{X}_{rms}$ for $\widetilde{F}_{n}=7.5*10^{-4}$, $\widetilde{v}_{d}=5*10^{-3}$, and $10^{-4}<\widetilde{\tau }_{0}<5*10^{-2}$

Fig. 12

Dimensionless a horizontal displacement, b relative velocity and c contact area as a function of the dimensionless time $\theta$ for the simulations with $\widetilde{\tau }_{0}=10^{-4}$ and $\widetilde{\tau }_{0}=0.05$, respectively, dashed blue and solid black lines

Figure 12 shows the dimensionless (a) horizontal displacement, (b) relative velocity, and (c) contact area as a function of the dimensionless time $\theta$ for the simulations in Fig. 11 with $\widetilde{\tau }_{0}=10^{-4}$ and $\widetilde{\tau }_{0}=0.05$ (respectively, dashed blue and solid black lines). For $\widetilde{\tau }_{0}=10^{-4}$ the system is linearly stable and $\{\widetilde{x},\widetilde{A},\widetilde{\tau }_0\}$ are constant. For $\widetilde{\tau }_{0}=5*10^{-2}$ a high amplitude limit cycle develops, characterized by “stick-slip” like motion. Notice that, during the “slip” phase ($\widetilde{v}_{rel}<0$), a rapid reduction in the contact area takes place, and this comes along with a sudden reduction in the Coulomb part of the frictional resistance, further strengthening the instability effect.

6 Conclusions

In this work, the linear stability analysis of a spherical oscillator moving on a viscoelastic substrate has been studied, by determining the contact interactions between the substrate and the punch through simulations based on a boundary element formulation. The frictional dissipation has been modeled adding up the viscoelastic contribution due to bulk hysteresis in the viscoelastic material to a Coulomb “adhesive” contribution that, consistently with recent measurements, has been assumed to be proportional to the apparent contact area via a characteristic interfacial shear strength.

Such a simple yet representative model has allowed us to investigate how two different instability mechanisms, that is, the Stribeck’s one related to the falling characteristic of the friction law with the sliding velocity and the mode-coupling one, co-exist and compete in the context of viscoelastic contact. We have performed a linear stability analysis, which in the limit of low and high velocity, has provided analytical results in closed form, thus enabling us to estimate the critical point for flutter instability in terms of critical shear strength (normal force) above (below) which instability occurs. Comparisons with the full stability maps have shown that the critical points determined analytically are accurate in the limit of high/low velocity or when the applied normal force is small. Conversely, in the range of intermediate velocity, the analytical estimates are not accurate as we have shown that the dominant mechanism for instability is due to a Stribeck effect, i.e., it is dominated by the viscoelastic damping (positive or negative) introduced by the variation in friction coefficient and contact area with the relative velocity is.

Our results show how, the evolution of the apparent contact area at the interface may play a fundamental role in the developing of unstable vibrations and show once more how common simplifications of adopting a constant friction coefficient or a linear contact stiffness, can largely oversimplify the problem of detecting the parametric regions where mechanical systems experience self-sustained vibrations. This calls for further development of physics-based theoretical/numerical approaches capable of correctly accounting for the interactions that take place at the interface between contacting bodies.

Appendices

Appendix - A

1.1 Viscoelastic contact mechanics

A linear viscoelastic material responds to the following integral equation [57]:

$$\begin{aligned} \varepsilon \left( t\right) =\int _{-\infty }^{t}d\tau \mathcal {J}\left( t-\tau \right) \dot{\sigma }\left( \tau \right) \end{aligned}$$

(29)

which relates the time-dependent strain $\varepsilon \left( t\right)$ to the time derivative of the stress $\sigma \left( t\right)$ by means of the creep function $\mathcal {J}\left( t\right)$. The latter satisfies causality, i.e., $\mathcal {J}\left( t<0\right) =0$ and can be written as $\mathcal {J}\left( t\right) =\mathcal {H}\left( t\right) \left[ 1/E_{0}-\int _{0}^{+\infty }d\tau \mathcal {C}\left( \tau \right) \exp \left( -t/\tau \right) \right]$ with $\mathcal {H}\left( t\right)$ being the Heaviside step function, while $E_{0}$ is the rubber elastic modulus of the material at zero-frequency, $\mathcal {C}\left( \tau \right)$ is a strictly positive function defined as the creep spectrum [57, 58] and $\tau$ is the relaxation time, continuously distributed on the real axis. Obviously, in order to employ practically the creep function in a numerical formulation, we have to discretize the aforementioned relation and, so, rewrite $\mathcal {J}\left( t\right)$ as $\mathcal {J}\left( t\right) =\mathcal {H}\left( t\right) \left[ 1/E_{0}-\sum _{k=1}^{n}C_{k}\exp \left( -t/\tau _{k}\right) \right]$.

Now, it is possible to Fourier-transform the equations presented above by writing $\varepsilon \left( \omega \right) =\sigma \left( \omega \right) /E\left( \omega \right)$ with $E\left( \omega \right)$ being the viscoelastic modulus. The latter, defined as $E\left( \omega \right) =\left[ i\omega J\left( \omega \right) \right] ^{-1}$, can be written as:

$$\begin{aligned} {\frac{1}{E(\omega )}}= & {} \frac{1}{E_{0}}-\int _{0}^{\infty }d\tau {\frac{i\omega \tau \mathcal {C}\left( \tau \right) }{1+i\omega \tau }}\nonumber \\= & {} {\frac{1}{E_{\infty }}}+\int _{0}^{\infty }d\tau {\frac{\mathcal {C}\left( \tau \right) }{1+i\omega \tau }} \end{aligned}$$

(30)

which, in the discretized form, becomes $1/E\left( \omega \right) =1/E_{\infty }+\sum _{k=1}^{n}C_{k}/(1+i\omega \tau _{k})$ .

As shown in Fig. 13, at low frequencies, the viscoelastic material is in the elastic ‘rubbery’ region, where $E(\omega )$ becomes real and tends to $E_{0}$, whilst for very large frequencies, $E\left( \omega \right)$ is again real, but this time tends to $E_{\infty \text { }}$ and the material is in the so-called glassy region. Finally, in the intermediate frequency range, we have the proper viscoelastic region: the loss tangent $\mathrm {{\text {Im}}}E\left( \omega \right) /\mathrm {{\text {Re}}}E\left( \omega \right)$ is, then, very large [see Fig. 13b]. Energy dissipation in the sliding contact will be, indeed, originated in this region of the viscoelastic spectrum .

Fig. 13

Real $E_{1}={\text {Re}}\left[ E\left( \omega \right) \right]$ and the imaginary $E_{2}={\text {Im}}\left[ E\left( \omega \right) \right]$ parts of the viscoelastic modulus $E\left( \omega \right)$ of a typical rubber-like material, (a); loss tangent $E_{2}\left( \omega \right) /E_{1}\left( \omega \right)$, (b)

Now, let us briefly describe the Boundary Element formulation necessary to tackle the viscoelastic contact mechanics problem and determine the solution in terms of stresses, strains and, ultimately, friction. Basically, by recalling the translational invariance and the elastic–viscoelastic correspondence principle [57], we can formulate the general linear-viscoelastic contact problem between a three-dimensional rigid indenter and a viscoelastic slab in terms of an integral Equation relating the normal surface displacement u of the viscoelastic solid and the normal interfacial stress $\sigma$:

$$\begin{aligned} u\left( \mathbf {\eta },t\right)= & {} \int _{-\infty }^{t}d\tau \int d^{2} \eta ^{\prime }\mathcal {J}\left( t-\tau \right) \mathcal {G}\left( \mathbf {\eta -\eta }^{\prime }\right) \nonumber \\&\dot{\sigma }\left( \mathbf {\eta }^{\prime },\tau \right) , \end{aligned}$$

(31)

where $\mathbf {\eta }$ is the in-plane position vector referred to a frame moving with the rigid indenter and t is the time, while the integral kernel is given by $\mathcal {J}\left( t\right)$ and by the elastic Green’s function $\mathcal {G}\left( \mathbf {\eta }\right)$. Now, if we assume that the sliding occurs at constant velocity, thus implying that the rigid punch always slides over completely relaxed material regions, Eq. (31) can be re-written in the following form:

$$\begin{aligned} u\left( \mathbf {\eta }\right) =\int d^{2}\eta G\left( \mathbf {\eta -\eta }^{\prime },\mathbf {v}\right) \sigma \left( \mathbf {x}^{\prime }\right) \end{aligned}$$

(32)

where $\mathbf {v}$ is the speed by which the viscoelastic solid is deformed. In the contact configuration adopted in this paper (see Fig. 2), , the velocity $\mathbf {v}$ is then equal to $\mathbf {v}$ $\mathbf {=} v_{rel}\mathbf {i}$ with $\mathbf {i}$ being the unit vector along the $x-$ direction. By employing the expression for the viscoelastic Green’s function $G\left( \mathbf {\eta },\mathbf {v}\right)$ explicitly given in Ref. [44], the viscoelastic problem requires to solve Eq. [44] in the contact area. The latter can be be found by following the iterative numerical scheme aimed at determining the contact solution [49]: we discretize the contact domain in N square cells and assume that, in each square element, the normal stress $\sigma$ is constantly equal to $\sigma _{k}=\sigma \left( \mathbf {\eta }_{k}\right)$ where $\mathbf {\eta }_{k}$ is the position vector of the center of the square cell $D_{k}$ . Thus, the normal displacement $u_{i}=u\left( \mathbf {\eta } _{i}\right)$ at the center of the i-th square cell can be related to $\sigma _{k}$ with the following linear system:

$$\begin{aligned} u_{i}=L_{ik}\left( \mathbf {\mathbf {\mathbf {v}}}\right) \sigma _{k} \end{aligned}$$

(33)

where each element of the response matrix $L_{ik}\left( {{\mathbf {v}}}\right)$ is equal to $L_{ik}\left( {{\mathbf {v}}}\right) =G\left( \mathbf {\eta }_{i}\mathbf {-\eta }_{k}, \mathbf {v}\right)$ and parametrically depends on the velocity $\mathbf {v}$. Eq. (33) can be easily solved and, then, to determine the contact area, the iterative procedure described in details in Ref. [49] can be adopted. Once the contact stresses and displacements are known, by recalling that $\mathbf {v}=v\mathbf {i}$ , it is possible to compute the friction force as $F_{fric}=\int _{\varOmega }d^{2} \eta \sigma (\mathbf {\eta })\partial u/\partial \eta$.

Appendix - B

In this paper, as detailed in Sect. 2, we have fitted the contact solution in terms of friction force, normal force and contact area. Here, we report the fitting coefficients obtained from the fitting procedure (we used MATLAB). For the viscoelastic reaction force, the fitting function

$$\begin{aligned} \widetilde{F}_{k}= & {} a_{1}\widehat{y}^{3/2}\frac{1}{2}\left[ a_{2} +{\text {erf}}\left( a_{3}\log _{10}\widehat{v} \right. \right. \nonumber \\&\left. \left. +\left( a_{4}\log _{10}\widehat{y}+a_{5}\right) \right) \right] \end{aligned}$$

(34)

with coefficients

$$\begin{aligned} a_{1}= & {} 11.890;\qquad a_{2}=1.199;\qquad a_{3}=0.873;\qquad \nonumber \\ a_{4}= & {} -0.449;\qquad a_{5}=0.412; \end{aligned}$$

(35)

gave a coefficient of determination $r^{2}=0.9999$ (see Fig. 3a).

Fig. 14

Comparison between the a normal contact force, b contact area, c friction coefficient, as obtained from boundary element method simulations and from the fitting equations proposed above

For the contact area, the fitting function

$$\begin{aligned} \widetilde{A}{=}b_{1}\widehat{y}\left[ b_{2}{-}\exp \left( -\frac{\left( \log _{10}\widehat{v}-\left( b_{3}\log _{10}\widehat{y}+b_{4}\right) \right) ^{2}}{2b_{5}^{2}}\right) \right] \nonumber \\ \end{aligned}$$

(36)

with coefficients

$$\begin{aligned}&b_{1}=1.440;\qquad b_{2}=2.118;\qquad b_{3}=0.493;\nonumber \\&\qquad b_{4}=-1.328;\qquad b_{5}=0.826; \end{aligned}$$

(37)

gave a coefficient of determination $r^{2}=0.9995$ (see Fig. 3b).

For the viscoelastic friction coefficient, the fitting function

$$\begin{aligned} \mu _{visc}=c_{1}\widehat{y}^{1/2}\exp \left( -\frac{\left( \log _{10}\widehat{v}-\left( c_{2}\log _{10}\widehat{y}+c_{3}\right) \right) ^{2}}{2c_{4}^{2} }\right) \nonumber \\ \end{aligned}$$

(38)

with coefficients

$$\begin{aligned} c_{1}= & {} 0.450;\qquad c_{2}=0.489;\qquad \nonumber \\ c_{3}= & {} -1.682;\qquad c_{4}=0.766; \end{aligned}$$

(39)

gave a coefficient of determination $r^{2}=0.9957$ (see Fig. 3c).

Figure 14 compares the numerical results with the predictions obtained using the fitting equations proposed above. In each panel, the coefficient of determination $r^2$ is reported.