Vibration suppression of nonlinear rotating metamaterial beams

Abstract

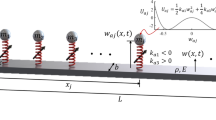
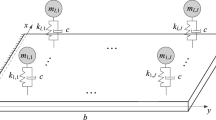
In this paper, we investigate the nonlinear vibration of a metamaterial structure that consists of a rotating cantilever beam attached to a periodic array of spring–mass–damper subsystems deployed for vibration suppression. The full nonlinear model of the system is developed. The nonlinear response due to a primary resonance excitation is investigated, and the capability of the metastructure to suppress vibration is examined. The mass of the resonators (absorbers) comes at the expense of the host structure’s mass itself, which makes the total mass of the system conservative. Free and forced vibration analyses are performed. We first use the method of multiple scales to analyze the nonlinear behavior of rotating beams. The perturbation solutions are validated against their numerical counterparts. Results show the presence of a critical rotational speed at which the beam undergoes bifurcation and starts to flutter. The addition of the absorbers is observed to slightly reduce this critical speed. Nevertheless, the amplitude of limit-cycle oscillations beyond bifurcation is found to decrease when equipping the rotating beam with local absorbers. The results demonstrate the capability of the metamaterial structure as an efficient damping treatment. Furthermore, we show that careful placement of the absorbers along the cantilever beam (close to the tip) enables further vibration mitigation.

Appendix

The coefficients used in Eqs. (19) and (20) are defined as

$$ A_{ij} = \mathop \int \limits_{0}^{1} \left[ {\left( {1 - u} \right) \psi_{j}^{''} - \psi_{j} '} \right] \psi_{i} {\text{d}}u $$

(A.1)

$$ B_{ij} = \mathop \int \limits_{0}^{1} \left[ {\frac{1}{2} \left( {1 - u^{2} } \right)\psi_{j}^{''} - u\psi_{j} '} \right] \psi_{i} {\text{d}}u $$

(A.2)

$$ C_{ijkl} = \mathop \int \limits_{0}^{1} \left( {\psi_{j}^{'} \mathop \int \limits_{0}^{u} \psi_{k}^{'} \psi_{l}^{'} {\text{d}}\sigma + \psi_{j}^{'} \psi_{k}^{''} \mathop \int \limits_{u}^{l} \psi_{l} {\text{d}}\sigma - \psi_{j}^{''} \mathop \int \limits_{u}^{1} \mathop \int \limits_{0}^{\sigma } \psi_{k}^{'} \psi_{l}^{'} {\text{d}}\eta {\text{d}}\sigma - \frac{1}{2}\psi_{j}^{'} \psi_{k}^{'} \psi_{l} } \right) \psi_{i} {\text{d}}u $$

(A.3)

$$ D_{ijkl} = \mathop \int \limits_{0}^{1} \left( {\psi_{j}^{'} \mathop \int \limits_{0}^{u} \psi_{k}^{'} \psi_{l}^{'} {\text{d}}\sigma - \psi_{j}^{''} \mathop \int \limits_{u}^{1} \mathop \int \limits_{0}^{\sigma } \psi_{k}^{'} \psi_{l}^{'} {\text{d}}\eta {\text{d}}\sigma } \right) \cdot \psi_{i} {\text{d}}u $$

(A.4)

$$ E_{ijkl} = \mathop \int \limits_{0}^{1} \left( {\frac{1}{2}\psi_{j}^{iv} \psi_{k}^{'} \psi_{l}^{'} + 3\psi_{j}^{'} \psi_{k}^{'} \psi_{l}^{'} + \psi_{j}^{''} \psi_{k}^{''} \psi_{l}^{''} } \right) \cdot \psi_{i} {\text{d}}u $$

(A.5)

$$ F_{ijkl} = \mathop \int \limits_{0}^{1} \left( {\frac{1}{2}\psi_{j}^{'} \mathop \int \limits_{0}^{u} \psi_{k}^{'} \psi_{l}^{'} {\text{d}}\sigma + \psi_{j}^{'} \psi_{k}^{''} \mathop \int \limits_{u}^{1} \psi_{l} {\text{d}}\sigma - \frac{1}{2}\psi_{j}^{''} \mathop \int \limits_{u}^{1} \mathop \int \limits_{0}^{\sigma } \psi_{k}^{'} \psi_{l}^{'} {\text{d}}\eta {\text{d}}\sigma - \frac{1}{2}\psi_{j} \psi_{k}^{'} \psi_{l}^{'} } \right) \psi_{i} {\text{d}}u $$

(A.6)

$$ G_{ijkl} = \mathop \int \limits_{0}^{1} \left( {\psi_{j}^{'} \psi_{k} - \mathop \int \limits_{0}^{u} \psi_{j}^{'} \psi_{k}^{'} {\text{d}}\sigma - \psi^{\prime\prime}\mathop \int \limits_{u}^{1} \psi_{k} {\text{d}}\sigma } \right) \psi_{i} {\text{d}}u $$

(A.7)

$$ H_{im} = \mathop \int \limits_{0}^{1} \psi_{i} \left\{ {\mu_{m} \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.8)

$$ I_{ijm} = \mathop \int \limits_{0}^{1} \psi_{i} \cdot \left\{ { \left[ {\mu_{m} \cdot \psi_{j} } \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.9)

$$ J_{ijm} = \mathop \int \limits_{0}^{1} \psi_{i} \left\{ {\left[ {\mu_{m} \cdot \psi_{j}^{'} } \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u \quad K_{ijm} = \mathop \int \limits_{0}^{1} \psi_{i} \left\{ {\left[ {\mu_{m} \cdot u \cdot \psi_{j}^{'} } \right] \delta \left( {u - u_{m} } \right)} \right\}{\text{d}}u $$

(A.10)

$$ L_{ijkm} = \mathop \int \limits_{0}^{1} \psi_{i} \cdot \left\{ {\mu_{m} \cdot \left[ {\psi_{j} \psi_{k}^{'} } \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.12)

$$ M_{ijkm} = \mathop \int \limits_{0}^{1} \psi_{i} \cdot \left\{ {\left[ {\mu_{m} \cdot \mathop \int \limits_{0}^{u} \psi_{j}^{'} \psi_{k} ' } \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.13)

$$ N_{ijklm} = \mathop \int \limits_{0}^{1} \psi_{i} \left\{ {\mu_{m} \left[ { - 0.5 \psi_{j}^{'} \psi_{k}^{'} \psi_{l} + \psi_{j}^{'} \mathop \int \limits_{0}^{u} \psi_{k}^{'} \psi_{l} {\text{d}}u } \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.14)

$$ O_{ijklm} = \mathop \int \limits_{0}^{1} \psi_{i} \left\{ {\left[ {\psi_{j} ' \cdot \mu_{m} \cdot \mathop \int \limits_{0}^{u} \psi_{k} ' \psi_{l} '} \right]\delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.15)

$$ P_{ijklm} = \mathop \int \limits_{0}^{1} \psi_{i} \cdot \left\{ {\left[ {\psi_{j} \cdot \mu_{m} \cdot \psi_{k}^{'} \psi_{l}^{'} } \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.16)

$$ R_{ijkm} = \mathop \int \limits_{0}^{1} \psi_{i} \cdot \left\{ {\left[ {\psi_{j} ' \cdot \mu_{m} \cdot \mathop \int \limits_{0}^{u} \psi_{k}^{'} \psi_{l} '} \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.17)

while the coefficients of absorbers are given below

$$ \bar{H}_{im} = \mathop \int \limits_{0}^{1} \left\{ {\mu_{m} \delta \left( {u - u_{m} } \right)} \right\}{\text{d}}u $$

(A.18)

$$ \bar{I}_{ijm} = \mathop \int \limits_{0}^{1} \left\{ { \left[ {\mu_{m} \cdot \psi_{j} } \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.19)

$$ \bar{J}_{ijm} = \mathop \int \limits_{0}^{1} \left\{ {\left[ {\mu_{m} \cdot \psi_{j}^{'} } \right] \delta \left( {u - u_{m} } \right)} \right\}{\text{d}}u $$

$$ \bar{K}_{ijm} = \mathop \int \limits_{0}^{1} \left\{ {\left[ {\mu_{m} \cdot u \cdot \psi_{j}^{'} } \right] \delta \left( {u - u_{m} } \right)} \right\}{\text{d}}u $$

(A.20)

$$ \bar{L}_{ijkm} = \mathop \int \limits_{0}^{1} \left\{ {\mu_{m} \cdot \left[ {\psi_{j} \psi_{k}^{'} } \right] \delta \left( {u - u_{m} } \right)} \right\}{\text{d}}u $$

(A.21)

$$ \bar{M}_{ijkm} = \mathop \int \limits_{0}^{1} \left\{ {\left[ {\mu_{m} \cdot \mathop \int \limits_{0}^{u} \psi_{j}^{'} \psi_{k} ' } \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.22)

$$ \bar{N}_{ijklm} = \mathop \int \limits_{0}^{1} \left\{ {\mu_{m} \left[ { - 0.5 \psi_{j}^{'} \psi_{k}^{'} \psi_{l} + \psi_{j}^{'} \mathop \int \limits_{0}^{u} \psi_{k}^{'} \psi_{l} du } \right] \delta \left( {u - u_{m} } \right)} \right\}{\text{d}}u $$

(A.23)

$$ \bar{O}_{ijklm} = \mathop \int \limits_{0}^{1} \left\{ {\left[ {\psi_{j} ' \cdot \mu_{m} \cdot \mathop \int \limits_{0}^{u} \psi_{k} ' \psi_{l} '} \right]\delta \left( {u - u_{m} } \right)} \right\}{\text{d}}u $$

(A.24)

$$ \bar{P}_{ijklm} = \mathop \int \limits_{0}^{1} \left\{ {\left[ {\psi_{j} \cdot \mu_{m} \cdot \psi_{k}^{'} \psi_{l}^{'} } \right] \delta \left( {u - u_{m} } \right)} \right\}{\text{d}}u $$

(A.25)

$$ \bar{R}_{ijkm} = \mathop \int \limits_{0}^{1} \left\{ {\left[ {\psi_{j} ' \cdot \mu_{m} \cdot \mathop \int \limits_{0}^{u} \psi_{k}^{'} \psi_{l} '} \right] \delta \left( {u - u_{m} } \right)} \right\} {\text{d}}u $$

(A.26)