Nonlinear dynamics of a vehicle with a displacement-sensitive mono-tube shock absorber

Abstract

The paper presents a new concept of absorbing car body vibrations, which consists in a modification of the construction of the classical mono-tube hydraulic shock absorber by the introduction of an additional inner cylinder with an auxiliary piston. By making an appropriate selection of the system parameters, one may obtain the damping force characteristics dependent on the excitation amplitude and frequency. In the case of driving on a good-quality road surface, the shock absorber displays the soft characteristics which are desired as far as the driving comfort is concerned. In the case of worse-quality roads or while overcoming large obstacles, the hard characteristics ensure a higher level of safety and protect the shock absorber from getting damaged. The developed nonlinear model makes it possible to effectively analyse the system responses to harmonic, impulse and random excitations. On the basis of the analysis of the impact of harmonic excitations on the driving comfort and safety indexes, one may estimate the optimal values of the shock absorber construction parameters. Impulse and random excitations are applied in order to finally verify the effectiveness of the operation of the proposed shock absorber.

1 Introduction

The constructions of modern car vehicles suspensions undergo changes together with the development of technology. The shock absorber is one of the suspension elements responsible for minimizing car body displacements, and in this way responsible for the driving safety and comfort. One may list numerous designs of car shock absorbers, starting with the simplest hydraulic ones with constant characteristics of the damping force, to the most complex active ones in which the damping force is dependent on a type of the road surface. Until recently, due to a high level of reliability and low exploitation costs, passive shock absorbers with a classical construction were most frequently used as the principle of their operation is relatively simple. Such shock absorbers contain springy and damping elements of nonlinear characteristics. Depending on the construction of flow channels, a shock absorber may possess the so-called soft or hard characteristics. The so-called hard suspensions ensure better vehicle driving but, at the same time, they lower the passenger ride comfort.

In order to find a compromise one more and more frequently applies active or semi-active shock absorbers, e.g. magnetorheological ones [1,2,3], whose characteristic adjusts to a type of the driven road surface. However, due to a considerably more complex construction they are more expensive to produce and exploit than passive shock absorbers. For these reasons, manufacturers develop more and more modern passive shock absorbers with modified constructions, whose characteristics possess similar properties as in the case of active shock absorbers.

One of such designs is the hydraulic damper with an additional flow channel (bypass), controlled by a relative displacement of the piston [4, 5]. For large amplitudes of excitations (worse roads), the modified construction of the shock absorber ensures a similar level of safety as in the case of hard shock absorbers. During the trip on a good-quality road surface, i.e. in the case of lower amplitudes of excitations, the characteristic of the damping force of the shock absorber with a bypass is similar to the one present in the soft shock absorber, thus resulting in better driving comfort. Therefore, the characteristic of the shock absorber with a bypass is dependent on the amplitude of excitation. A sample design for shock absorber with bypass is proposed by Lee and Moon [5]. The additional flow between the compression chamber and the rebound chamber is realized by an appropriate shape of the cylinder’s inner surface.

A series of other shock absorbers with innovative constructions [6,7,8] may also be classified within the group of hydraulic dampers with a variable characteristic of the damping force. One of them is a twin-tube hydraulic shock absorber with an additional inner cylinder presented in the paper [6]. The characteristic of the damping force depends on the amplitude of excitation since the flow of oil between the chambers of the main and the inner cylinder is controlled by the displacement of the auxiliary piston.

In order to analyse the effectiveness of the operation of shock absorbers, one most frequently applies two-mass, the so-called quarter-car models [2, 4, 6, 9]. One of the masses, the so-called sprung mass, represents the car body, whereas the other one (un-sprung mass) represents the wheel with appropriate suspension elements. The quarter-car model allows for carrying out a dynamic analysis of the system in two resonance ranges, which are important from the point of view of the driving comfort and safety. The driving comfort depends on the level of vibrations of the car’s body. Typically, the RMS (root mean square) of the displacement or acceleration of the sprung mass is the measure of the comfort [10, 11], which reaches a maximum value in the first resonance range. Vibrations of the un-sprung mass are dominant within the range of high frequencies. Within this range, the momentary forces of the wheel pressure on the road surface are decreased, which in turn impacts driving safety. The dynamic component of the reaction [11] or its minimal value and the associated EUSAMA indicator [9] are frequently applied as the safety index.

The level of vibration felt by the driver depends to a large extent on the road surface and the speed driving. Various realizations of stochastic processes are used to describe the road profile [12,13,14,15]. During the design process, harmonic excitations with constant or variable frequency are also useful for that purpose. Typically a constant amplitude of the excitation is used, but it is better to assume that the amplitude is a decreasing function of frequency. This approach is proposed by Funke [16], which assumes a constant value of the maximum speed of excitation, so that the amplitude is a function inversely proportional to the frequency.

In recent years, there have appeared more and more various kinds of speed breakers on roads in the areas where extra caution is required, e.g. in places with intense pedestrian traffic or near schools. The purpose of implementing such solutions is to force drivers to considerably reduce the driving speed. Impulse functions [17], e.g. of a unit step type, are used to describe this kind of excitations. The implementation of shock absorbers with adjustable characteristics of the damping force in the suspension system makes it possible to overcome unevenness of an impulse character while maintaining the highest possible driving comfort.

There are many works in the literature devoted to modelling and analysis of both twin-tube shock absorbers [4, 16, 18,19,20] and mono-tube shock absorbers [21,22,23,24]. However, most of them consider classic constructions, in which the oil flow between the compression and rebound chambers takes place under the influence of the oil pressure difference only through the channels in the main piston. Frequently the orifices of the channels are assumed to be covered by a stack of circular plates, and the details of their modelling can be found, e.g. in the works of Alonso [18], Farjoud [23] and Talbott [24]. The vibration of valves and the occurring acoustic discomfort is analysed by Benazis in the paper [25].

A new design of the mono-tube hydraulic shock absorber, definitely different from most of the classical constructions discussed in the available literature, has been proposed in this paper. Although this construction has some similarities to the shock absorber shown in the paper [6], its operating principle is quite different. Both solutions have an additional inner cylinder with an auxiliary piston, but the role of the piston in each of them is different. In the considered work [6], the variable shock absorber characteristic is the effect of the flows between the chambers of the inner cylinder and the compression or rebound chamber. In the shock absorber presented in this paper, an auxiliary piston directly controls the oil flow between the compression and the rebound chamber. In addition, the currently proposed solution is applied to a mono-tube shock absorber, whereas the model of a twin-tube shock absorber is previously tested. The results of numerical simulations of vibration damping of the vehicle body presented in the paper confirm the effectiveness of the proposed shock absorber.

Fig. 1

Model of the mono-tube shock absorber

2 Model of the system

2.1 Model of the hydraulic shock absorber

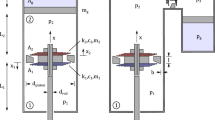
A model of the studied shock absorber is illustrated in Fig. 1. The main element of the classical shock absorber is the tube known as the working cylinder, connected to the vehicle suspension (so-called un-sprung mass).

The working cylinder consists of two chambers: the rebound chamber $K_{1}$ and the compression chamber $K_{2}$, which separates the main piston. The main piston is connected by the piston rod to the car body, i.e. the sprung mass. In the working cylinder, there is a floating piston which separates the chamber $K_{2}$ filled with oil from the chamber $K_{6}$, filled with high pressure nitrogen (approx. 2 MPa).

In the proposed concept of the shock absorber, there is an additional cylinder which is rigidly fixed with the piston rod. Inside this cylinder, there is an appropriately shaped auxiliary piston, which divides this cylinder into the chambers $K_{3}$ and $K_{4}$ of a variable volume, and the chamber $K_{5}$ of a constant volume.

The oil flow between the chambers $K_{1}$ and $K_{2}$ takes place through the channels which are always open (o$_1$ and o$_2$, Fig. 1) and covered with low-stiffness plates (o$_3$ and o$_4$), the flow between the chambers of the additional cylinder is via c$_1$–c$_9$ channels.

In order to determine oil pressures in the chambers $K_{n}$ ($n=1,2,\ldots ,5$), the following equation may be used [6]:

$$\begin{aligned} \dot{{p}}_{n} =\beta \left[ {\frac{Q_{n} }{m_{n} }-\frac{\dot{{V}}_{n} }{V_{n} }} \right] \end{aligned}$$

(1)

where $m_{n}$ are the oil mass in the chambers $K_{n}$ ($n=1,2,\ldots ,5$), while $\beta$ stands for the compressibility modulus. The volumes $V_{n}$ of the chambers $K_{n}$ are expressed by the formulae:

$$\begin{aligned} V_{1}= & {} V_{10} -A_{\mathrm{tp}} (x_{\mathrm{b}} -x_{\mathrm{w}}) \end{aligned}$$

(2)

$$\begin{aligned} V_{2}= & {} V_{20} +A_{\mathrm{p}} (x_{\mathrm{b}} -x_{\mathrm{fp}}) \end{aligned}$$

(3)

$$\begin{aligned} V_{3}= & {} V_{30} -A_{\mathrm{ap}} (x_{\mathrm{ap}} -x_{\mathrm{b}}) \end{aligned}$$

(4)

$$\begin{aligned} V_{4}= & {} V_{40} +A_{\mathrm{ap}} (x_{\mathrm{ap}} -x_{\mathrm{b}}) \end{aligned}$$

(5)

$$\begin{aligned} V_{5}= & {} V_{50} \end{aligned}$$

(6)

The parameters $V_{n0}$ constitute the initial volumes of the chambers $K_{n}$, and the parameters $A_{\mathrm{tp}}=A_{\mathrm{p}}-A_{\mathrm{pr}}$, $A_{\mathrm{p}}$ and $A_{\mathrm{ap}}$ determine the upper and lower surface of the main piston, respectively, as well as the surface of the auxiliary piston.

The change of the oil mass in the chambers $K_{n}$ is defined by the equation:

$$\begin{aligned} \dot{{m}}_{n} =Q_{n} \end{aligned}$$

(7)

where

$$\begin{aligned} Q_{1}= & {} Q_{21} -Q_{12} +Q_{31} -Q_{13} +Q_{51} -Q_{15} \end{aligned}$$

(8)

$$\begin{aligned} Q_{2}= & {} Q_{12} -Q_{21} +Q_{42} -Q_{24} +Q_{52} -Q_{25} \end{aligned}$$

(9)

$$\begin{aligned} Q_{3}= & {} Q_{13} -Q_{31} \end{aligned}$$

(10)

$$\begin{aligned} Q_{4}= & {} Q_{24} -Q_{42} \end{aligned}$$

(11)

$$\begin{aligned} Q_{5}= & {} Q_{25} -Q_{52} +Q_{15} -Q_{51} \end{aligned}$$

(12)

where $Q_{mn}$ is mass flow rate from the chamber $K_{m}$ ($m=1,2,\ldots ,5, m \ne \hbox {n}$) to the chamber $K_{n}$. In the case of a turbulent flow [26], the flow rate $Q_{mn}$ is determined from the formula:

$$\begin{aligned} Q_{mn} =C_{\mathrm{d}} A_{mn} H(p_{m} -p_{n}) \sqrt{2\rho _{m} \vert p_{m} -p_{n} \vert } \end{aligned}$$

(13)

where the parameter $C_{\mathrm{d}}$ is the discharge coefficient and $A_{mn}$ is an effective cross-sectional area of an appropriate channel. The function H() of the unit step type ensures that the condition: $Q_{mn}=0$ for $p_{m} < p_{n}$ is fulfilled.

The oil flow control usually depends on the difference in oil pressures in the adjacent chambers, and in some cases in addition to the relative displacement $z=x_{\mathrm{ap}}-x_{\mathrm{b}}$ of the auxiliary piston. We assume that in the general case the total effective cross-sectional area of the channels connecting the chambers $K_{m}$ and $K_{n}$ is the sum: $A_{mn} =A_{mn}^{0} +A_{mn}^{1} +A_{mn}^{2}$. The upper index k of the parameter $A_{mn}^{k}$ depends on the valve type. In the case of the resilient valve, which is pushed by downforce (eg for channels o$_3$ and o$_4$ in the main piston) the function $A_{mn}^{1}$ can be written as follows [6]:

$$\begin{aligned} A_{mn}^{1} =A_{mn}^{10} \phi (p_{m} -p_{n} ,\sigma _{nm} ,k_{nm}) \end{aligned}$$

(14)

where

$$\begin{aligned}&\phi (p_{m} -p_{n} ,\sigma _{mn} ,k_{mn})\nonumber \\&\quad =H(p_{m} -p_{n} -\sigma _{mn} )\tanh {(p_{m} -p_{n} -\sigma _{mn} )} /{k_{mn}}\nonumber \\ \end{aligned}$$

(15)

The parameter $A_{mn}^{10}$ is the maximum cross-sectional area of the appropriate channel, $k_{mn}$ is associated with spring stiffness and $\sigma _{mn}$ is the difference in oil pressures $p_{m}$ and $p_{n}$ above, in which the valve is opened. In the absence of the downforce ($\sigma _{mn}=0$) for very flexible springs ($k_{mn}\approx 0$), the functions (14) are approximately constant. In this case, the corresponding cross-sectional areas are marked with symbols $A_{mn}^{0}$ (e.g. for channels o$_1$ and o$_2$).

The channels c$_1$–c$_5$ in the additional cylinder may be covered with the auxiliary piston, which means that the oil flow to the chambers $K_{3}$, $K_{4}$ and $K_{5}$ takes place within a limited range of relative displacement $z=x_{\mathrm{ap}}-x_{\mathrm{b}}$ of this piston. The effective cross-sectional areas $A_{mn}^{2}$ of these channels are described as follows:

$$\begin{aligned} A_{mn}^{2} =A_{mn}^{20} \vartheta _{nm} (z) \end{aligned}$$

(16)

where $A_{mn}^{20}$ is the maximum value of the area $A_{mn}^{2}$. The function $\vartheta$ is defined as follows:

$$\begin{aligned} \vartheta (z,h,r)=\left\{ {{\begin{array}{ll} 1 &{}\quad {z\leqslant h-r}\\ {(h+r-z)/2r} &{}\quad {h-r<z<h+r}\\ 0 &{}\quad {z\geqslant h+r}\\ \end{array} } } \right. \end{aligned}$$

(17)

where the parameters h and r determine the position of orifices and their radii. For the proposed system (Fig. 1), the functions $\vartheta _{51} (z)=\vartheta (-z,h_{1} ,r_{1})$ and $\vartheta _{31} (z)=\vartheta (z,h_{2} ,r_{2})$ describe the process of covering the channels connecting the chamber $K_{1}$ with the chamber $K_{5}$ ($\hbox {c}_{1}, \hbox {c}_{2}$) and $K_{3}$ ($\hbox {c}_{4}$), respectively. By analogy, the functions $\vartheta _{52} (z)=\vartheta (z,h_{1} ,r_{1}$) and $\vartheta _{42} (z)=\vartheta (-z,h_{2} ,r_{2}$) describe the flow between the chambers $K_{2}$ and $K_{5}$ ($\hbox {c}_{3}$) as well as $K_{2}$ and $K_{4}$ ($\hbox {c}_{5}$).

Apart from the valves controlled by relative displacement, in the chambers $K_{3}$ and $K_{4}$ there are also channels which are always open ($\hbox {c}_{8}, \hbox {c}_{9}$) and covered with low-stiffness plates ($\hbox {c}_{6}, \hbox {c}_{7}$). In order to describe the oil flow through the channels $\hbox {c}_{6}$ and $\hbox {c}_{7}$, the formula (14) may be used. Ultimately, for $m=3$ and $n=1$, $m=5$ and $n=1$, $m=4$ and $n=2$, $m=5$ and $n=2$ (analogically for the flows in reverse direction) the total effective cross-sectional areas are described by the formula $A_{mn} =A_{mn}^{0} +A_{mn}^{1} +A_{mn}^{2}$. The effective cross-sectional areas of the channels in the main piston (for $m=1$, $n=2$ or $m=2$, $n=1$) are the sum: $A_{mn} =A_{mn}^{0} +A_{mn}^{1}$.

Equations (1–17) determine pressure changes in the chambers $K_{n}$ ($n=1,2,\ldots ,5$). Gas pressure in the chamber $K_{6}$ may be determined after accepting the adiabatic process from the equation:

$$\begin{aligned} p_{6} =p_{0} \frac{V_{\mathrm{g}0}^{\kappa } }{[V_{\mathrm{g}0} +A_{\mathrm{p}} (x_{\mathrm{fp}} -x_{\mathrm{w}} )]^{\kappa }} \end{aligned}$$

(18)

where $\kappa$ is the adiabatic index, and $V_{\mathrm{g0}}$ is the initial gas volume (in the state of equilibrium).

Fig. 2

Quarter-car model

2.2 Quarter-car suspension model

In order to test the effectiveness of vibration, damping the quarter-car model of the vehicle should be examined (Fig. 2). Assuming that the coordinates: $x_{\mathrm{w}}, x_{\mathrm{b}}, x_{\mathrm{fp}}, x_{\mathrm{ap}}$ determine the movement of the un-sprung mass $m_{\mathrm{w}}$ and the sprung mass $m_{\mathrm{b}}$ as well as floating piston $m_{\mathrm{fp}}$ and the auxiliary piston $m_{\mathrm{ap}}$, the vibrations around the equilibrium can be described by the system of four second-order differential equations in the following form:

$$\begin{aligned}&m_{\mathrm{w}} \ddot{{x}}_{\mathrm{w}} =k_{\mathrm{b}} (x_{\mathrm{b}} -x_{\mathrm{w}} )+k_{\mathrm{w}} (x_{\mathrm{r}} -x_{\mathrm{w}} )+F_{\mathrm{w}} \end{aligned}$$

(19)

$$\begin{aligned}&m_{\mathrm{b}} \ddot{{x}}_{\mathrm{b}} =-k_{\mathrm{b}} (x_{\mathrm{b}} -x_{\mathrm{w}} )-F_{\mathrm{b}} +F_{\mathrm{bump}} \end{aligned}$$

(20)

$$\begin{aligned}&m_{\mathrm{fp}} \ddot{{x}}_{\mathrm{fp}} =(p_{\mathrm{g}} -p_{2} )A_{\mathrm{p}} -F_{\mathrm{fp}} \mathrm{sgn}(\dot{{x}}_{\mathrm{fp}} -\dot{{x}}_{\mathrm{w}}) \end{aligned}$$

(21)

$$\begin{aligned}&m_{\mathrm{ap}} \ddot{{x}}_{\mathrm{ap}} =(p_{4} -p_{3} )A_{\mathrm{ap}} +k_{\mathrm{ap}} (x_{\mathrm{b}} -x_{\mathrm{ap}} )-F_{\mathrm{bump}}\nonumber \\ \end{aligned}$$

(22)

The parameters $k_{\mathrm{w}}$ and $k_{\mathrm{b}}$ and $k_{\mathrm{ap}}$ are the stiffness of the tyre and the spring, respectively, while $k_{\mathrm{ap}}$ is the stiffness of the mounting of additional mass. Nonlinear forces $F_{\mathrm{b}}$ and $F_{\mathrm{w}}$ are expressed with the following formulae:

$$\begin{aligned} F_{\mathrm{w}}= & {} (p_{\mathrm{1}} {-}p_{0} )A_{\mathrm{tp}} -(p_{\mathrm{g}} {-}p_{0} )A_{\mathrm{p}} {+}F_{\mathrm{p}} \hbox { sgn}(\dot{{x}}_{\mathrm{b}} -\dot{{x}}_{\mathrm{w}} )\nonumber \\&+\,F_{\mathrm{fp}} \hbox { sgn}(\dot{{x}}_{\mathrm{fp}} -\dot{{x}}_{\mathrm{w}}) \end{aligned}$$

(23)

$$\begin{aligned} F_{\mathrm{b}}= & {} (p_{\mathrm{1}} -p_{0} )A_{\mathrm{tp}} -(p_{\mathrm{2}} -p_{0} )A_{\mathrm{p}} +(p_{4} -p_{3} )A_{\mathrm{ap}} \nonumber \\&+\,F_{\mathrm{p}} \hbox { sgn}(\dot{{x}}_{\mathrm{b}} -\dot{{x}}_{\mathrm{w}} )+k_{\mathrm{ap}} (x_{\mathrm{b}} -x_{\mathrm{ap}}) \end{aligned}$$

(24)

where $F_{\mathrm{p}}$ and $F_{\mathrm{fp}}$ are friction forces between the piston rod and the guideway [4] as well as between the floating piston and the cylinder, respectively. The force $F_{\mathrm{bump}}$, which describes the impact of the bumpers, is defined as follows:

$$\begin{aligned} F_{\mathrm{bump}} {=}\left\{ {{\begin{array}{ll} {k_{\mathrm{bump}} (x_{\mathrm{ap}} {-}x_{\mathrm{b}} -h_{3} )} &{}\quad {x_{\mathrm{ap}} {-}x_{\mathrm{b}} \geqslant h_{3} }\\ 0 &{}\quad {-h_{3}<x_{\mathrm{ap}} {-}x_{\mathrm{b}} <h_{3} }\\ {k_{\mathrm{bump}} (x_{\mathrm{ap}} {-}x_{\mathrm{b}} +h_{3} )} &{}\quad {\;x_{\mathrm{ap}} {-}x_{\mathrm{b}} \leqslant -h_{3} }\\ \end{array} }} \right. \end{aligned}$$

(25)

Owing to the fact that the displacements are measured with respect to the static equilibrium, the force $k_{\mathrm{w}}(x_{\mathrm{r}}-x_{\mathrm{w}})$ describes only the dynamic component of the reaction affecting the car wheel. In the case of permanent contact of car wheels with a road surface the sum of the static $(m_{\mathrm{w}}+m_{\mathrm{b}})g$ and dynamic reactions should be higher than zero, and hence the condition $k_{\mathrm{w}}(x_{\mathrm{r}}-x_{\mathrm{w}})+(m_{\mathrm{w}}+m_{\mathrm{b}})g> 0$ should be fulfilled. Therefore, the lowest possible values $\vert k_{\mathrm{w}}(x_{\mathrm{r}}-x_{\mathrm{w}})\vert$ are recommended for reasons of the driving safety.

2.3 Modelling of a road profile

Depending on the purpose of the research, the road profile can be described by harmonic, impulse or random functions. Harmonic excitations are particularly useful in studying the impact of construction parameters on the efficiency of the shock absorber. In such analyses, it is advisable to assume that the amplitude depends on the frequency of excitation [6].

For a constant amplitude and higher frequencies, wheels can detach from the road surface (contact loss condition: $k_{\mathrm{w}}(x_{\mathrm{r}}-x_{\mathrm{w}})+(m_{\mathrm{w}}+m_{\mathrm{b}})g< 0$, which usually does not happen in reality. In the case of a road with a worse surface (for larger amplitudes), the driving speed should be lower, which is also associated with a lower frequency of excitation. We will assume further excitation in the form of:

$$\begin{aligned} x_{\mathrm{r}} (t)=({a_{0} f_{0} } / f)\sin 2\pi ft \end{aligned}$$

(26)

where $a_{0}$ is the amplitude of the excitation for the frequency $f=f_{0}$. From the formula (26) follows the condition: $\dot{{x}}_{\mathrm{r}}^{\max } (t)=2\pi f_{0} a_{0} =\hbox {const}$.

Impulse excitations of various types are applied in order to describe excitations arising while a vehicle is overcoming obstacles. It is convenient to use for this purpose the ‘rounded pulse’ function [6] which is defined as follows (Fig. 3):

$$\begin{aligned} x_{\mathrm{r}} (s)=He^{2}\xi ^{2}\exp (-2\xi ) \end{aligned}$$

(27)

where $\xi =s/L$ and H is the height of the obstacle ($x_{\mathrm{r}}=H$ for $\xi =1$). After the substitution $s=v_{0} t$, one obtains the formula describing the dependence of the surface irregularity on time:

$$\begin{aligned} x_{\mathrm{r}} (t)=\frac{1}{4}He^{2}(\nu t)^{2}\exp (-\nu t) \end{aligned}$$

(28)

where $\nu =2v_{0}/L$. A function similar to (28) is utilized in paper [17] to study the reaction of dampers to different types of impulse excitations.

Fig. 3

The rounded pulse function

Random excitations [12,13,14,15, 27,28,29] are useful in the final step of designs for an overall evaluation of the vehicle behaviour while being driven over various kinds of road surfaces. The surface irregularity is being approximated using either a sine or cosine series, although the difference between the equations that specify the amplitudes, phases and natural frequencies is minor. The profile of the road presented below has been compiled from the proposals presented in works [13, 14, 27]. The realization of the stochastic excitation may be described by the polyharmonic function in the following form:

$$\begin{aligned} x_{\mathrm{r}} (s)=\sum \limits _{k=1}^N {A_{k} \sin (2\pi n_{k} s-\varphi _{k} )} \end{aligned}$$

(29)

where N is a number of the given frequencies. The amplitudes $A_{k}$ of the successive harmonics depend on the spectral power density $S_{\mathrm{r}}$ as follows [27]:

$$\begin{aligned} A_{k} =\sqrt{4S_{\mathrm{r}} (n_{k} )\Delta n} \end{aligned}$$

(30)

The values of frequencies are determined from the formula [13]:

$$\begin{aligned} n_{k} =n_{\mathrm{l}} +(k-0.5+\varepsilon \chi _{k})\Delta n \end{aligned}$$

(31)

where

$$\begin{aligned} \Delta n=(n_{\mathrm{u}} -n_{\mathrm{l}} )/N \end{aligned}$$

(32)

The parameters $n_{\mathrm{l}}$ and $n_{\mathrm{u}}$ represent the lower and upper cutoff spatial frequencies, respectively. The phases $\varphi _{k}$ and $\chi _{k}$ are random variables with uniform probability distribution within the ranges (–$\pi$, $\pi$) and (–1, 1). Including a random change of frequency in the formula (31) (it was assumed that $\varepsilon =0.05$) ensures the lack of excitation periodicity [13]. The power spectral density function $S_{\mathrm{r}}$ is determined by the formula [14]:

$$\begin{aligned} S_{\mathrm{r}} (n_{k} )=S_{\mathrm{r0}} (2\pi n_{k} )^{-\eta } \end{aligned}$$

(33)

where the exponent $\eta =2$ for $n\leqslant n_{0}$ and $\eta =1.5$ for $n> n_{0}$ (where $n_{0}=1/2\pi$ cycles/m). The parameter $S_{\mathrm{r0}}$ depends on a class of the driven road and may be determined from the dependence:

$$\begin{aligned} S_{\mathrm{r0}} =4^{K}10^{-6} \end{aligned}$$

(34)

where the successive road classes (starting with class A) correspond with the values $K=1,2,3\ldots$ [14].

Fig. 4

Stochastic excitation characteristics: a$x_{\mathrm{r}}$ PSD for A–H class roads, b$x_{\mathrm{r}}$ displacement for A–D class roads

Figure 4a presents the comparison of power spectral density graph for signal ${x}_{\mathrm{r}}$ (for ${N}=152$, $n_{\mathrm{l}}=0.005$, $n_{\mathrm{u}}=10$) with the PSD graphs calculated using equations (33) and (34) according to ISO 8608. In order to increase the clarity of the figure, the PSD $x_{\mathrm{r}}$ graph comparison has been limited to the roads of class A, C, E and G. Figure 4b shows the representation of the stochastic excitation $x_{\mathrm{r}}$ for roads of class A, B, C and D.

3 Results of the simulations

After the transformation of Eqs. (1, 7, 19–22), the vibrations of the system are described by the system of 18 strongly nonlinear first-order differential equations. The analysis of these equations may be carried out practically only with the use of numerical methods. In numerical simulations carried out on the basis of the programmes written in the Fortran 77 programming language, the Runge–Kutta–Verner methods of 5th and 6th order are applied for this purpose.

It is an important issue to analyse the impact of essential model parameters on certain indexes which are responsible for the driving safety and comfort. For the reason of a large number of the system parameters in simulations, we will assume constant values for many of these parameters (illustrated in Table 1), thus limiting the analysis to the examination of the impact of the parameters responsible for controlling the oil flow.

Table 1 Parameters of the quarter-car model

The majority of the values of the physical parameters of the hydraulic damper listed in Table 1 result from the analysis of the existing designs of mono-tube shock absorbers. For instance, the value $A_{\mathrm{p}}=16~\hbox {cm}^{2}$ refers to the damper approximately 4.5cm in diameter, the surface ratio $A_{\mathrm{pr}}/A_{\mathrm{p}}$ in the majority of dampers is equal to approx. 0.2, hence $A_{\mathrm{tp}}=A_{\mathrm{p}}-A_{\mathrm{pr}}=12.8~\hbox {cm}^{2}$. The volumes of chambers depend on the assumed value of the damper stroke, the values of parameters: $\beta =1.5~\hbox {GPa}$, $\rho _{0}=890~\hbox {kg/m}^{3}$ are practically independent of a type of the damper.

Certain dimensionless parameters are better suited for a more complex evaluation of the damper. In numerical simulations one uses, among others, the following parameters: $\alpha _{nm}=A_{nm}^{0}/A_\mathrm{p}$, $\beta _{nm}=A_{nm}^{1}/A_\mathrm{p}$ and $\gamma _{nm}=A_{nm}^{2}/A_\mathrm{p}$, which determine the surface areas of appropriate flow channels. The majority of numerical calculations are carried out for the following parameter values: $\sigma _{{21}}=\sigma _{{12}}=0.2p_{0}$, $k_{{12}}=k_{{21}}=0.4p_{0}$ and $\sigma _{mn}=0$ as well as $k_{mn}\approx 0$ (hence $\beta _{nm}=0$) for $n\ne 1$ and $m\ne 2$ or $n\ne 2$ and $m\ne 1$, characterizing the pressure-controlled valves.

3.1 Damper characteristics

Because of the large number of parameters that define the damper model presented in this paper, the parametric optimization of the system is complex and in the worst case might not even be possible. Its operation quality criterion should on the one hand include the comfort of travel on the road of different surfaces, while on the other hand should consider an appropriate level of safety. Depending on the chosen priorities, the optimal solutions can widely differ. These priorities and solutions will be different between the racing or cross-country vehicles and passenger cars, which for most of the time drive on roads of good quality. One possible way to accommodate for those contradictory requirements might be the utilization of active damping systems, which permit the adjustment of the damping force characteristic based on the conditions on the road.

The main purpose of the simulations presented in this paper is to prove that a passive damping system which is generally cheaper to produce and more reliable in operation, can behave similar like an active damping system.

In these analyses, the focus was on determining the influence of the proposed dimensionless parameters on the oil flow control process and the damping force characteristic.

In the classical damper, the damping force increases together with a decreasing surface of the channels in the main piston, i.e. together with a decrease in the values of the dimensionless parameters $\alpha _{nm}$ and $\beta _{nm}$ ($n, m=1, 2$). The ratio of the maximum damping force in the rebound and compression phase depends on the coefficients: $\alpha _{{21}}/\alpha _{{12}}$ and $\beta _{{21}}/\beta _{{12}}$. Typically the oil flow in the rebound phase is accomplished through the channels of smaller cross-sectional area: $\alpha _{{12}}< \alpha _{{21}} \hbox { i } \beta _{{12}} < \beta _{{21}}$. Very often an approximate relation $\alpha _{{12}}/\alpha _{{21}}=\beta _{{12}}/\beta _{{21}}=0.5$ proves true, which denotes that the damping force in the rebound phase is twice as high as during the compression phase.

Parameters $\alpha _{{12}}$ and $\alpha _{{21}}$, that characterize the oil flow through the permanently open channels between the $K_{1}$ and $K_{2}$ chambers, exhibit the highest influence on the damping force. With their increase, the damper becomes “soft”, which is desirable when the vehicle is moving on the good-quality roads. For the roads of low quality, a “hard” damper is more advisable, mostly due to the fact of better vibration damping when traversing roads of high roughness. However, as must be pointed out, the damper should not be either too “soft” or too “hard”.

For the purpose of comparison, a very “soft” damper (SD) of parameters $\alpha _{{21}}=2\alpha _{{12}}=0.024$ and a very “hard” damper (HD) of parameters $\alpha _{{21}}=2\alpha _{{12}}=0.004$ are introduced, in which the coefficients $\beta _{{21}}=2\beta _{{12}}=0.02$. The limiting values of the parameter $\alpha _{{21}}$ have been assumed, based on the analysis of existing constructions and the study of the simulation results. Depending on the weighting factor, which determines the share of comfort and safety indices in the considered quality criterion, the optimal value of parameter $\alpha _{{21}}$ is within the range $0.004< \alpha _{{21}} < 0.024$.

The modified damper (MD) is supposed to accommodate for the partially contradictory criteria of comfort and safety. It is expected to behave as a HD damper in the case of bad-quality roads and as a SD damper in the opposite case (e.g. on highways).

The model for the proposed MD damper is defined using a larger number of parameters ($\alpha _{nm}, \beta _{nm}$ and an additional coefficient $\gamma _{nm}$ for $n> 2$ or $m > 2$). These parameters characterize the flows between the chambers of the inner cylinder ($K_{3}, K_{4}, K_{5}$) and the chambers in the main cylinder ($K_{1}, K_{2}$).

The parameters: $\gamma _{{51}}, \gamma _{{25}}$ (and the flow rates $Q_{{51}}, Q_{{25}}$ in the compression phase, which depend on them) as well as $\gamma _{{15}}, \gamma _{{52}}$ ($Q_{{15}}, Q_{{52}}$ in the rebound phase) to a high degree influence the characteristic of the damping force. For small relative displacements $x_{\mathrm{ap}}-x_{\mathrm{b}}$ of the additional mass, the flow from the chamber $K_{1}$ to $K_{2}$ in the rebound phase takes place both through the channels in the main piston and through the channels $\hbox {c}_{2}$ and $\hbox {c}_{3}$ in the inner cylinder (Fig. 1), and in the compression phase additionally through the channel $\hbox {c}_{1}$. Therefore, the damping force is decisively smaller than in the case of larger displacements during which the orifices of these channels are covered by the auxiliary piston. In order to maintain the assumed proportion between the maximum forces in both phases of the damper operation, we will assume the same cross-sectional areas of the channels $\hbox {c}_{1}$ and $\hbox {c}_{2}$. Then the relation occurs: $\gamma _{{15}}/\gamma _{{51}}=0.5$. In the case when the channels $\hbox {c}_{1}$, $\hbox {c}_{2}$ or $\hbox {c}_{3}$ are blocked, the characteristic of the damper practically depends only on the parameters $\alpha _{{21}}, \beta _{{21}}, \alpha _{{12}}, \beta _{{12}}$ (the hard characteristics), and in the opposite case it additionally depends on $\gamma _{{51}}, \gamma _{{25}}, \gamma _{{15}}, \gamma _{{52}}$ (the soft characteristics).

The parameters: $\alpha _{{31}}, \beta _{{31}}, \gamma _{{31}} \alpha _{{24}}, \beta _{{24}}, \gamma _{{24}}$, (flow rates $Q_{{31}}, Q_{{24}}$ in the compression phase) and $\alpha _{{13}}, \beta _{{13}}, \gamma _{{13}}, \alpha _{{42}}, \beta _{{42}}, \gamma _{{42}}$ ($Q_{{13}}, Q_{{42}}$ in the rebound phase) influence the movement of the additional mass, hence they play a crucial role in the process of controlling the flow between particular chambers. The correct operation of the damper depends on the appropriate selection of values of these parameters. An effectively working shock absorber should possess the hard characteristics for high amplitudes of excitations and the soft characteristics for lower amplitudes. In the former case, the orifices of the channels $\hbox {c}_{1}$, $\hbox {c}_{2}$ or $\hbox {c}_{3}$ should be covered, and in the latter one they should be open at all times. Therefore, the parameters $\alpha _{{13}}, \alpha _{{31}}, \alpha _{{24}}, \alpha _{{42}}, \beta _{{13}}, \beta _{{31}}, \beta _{{24}}, \beta _{{42}}, \gamma _{{13}}, \gamma _{{31}}, \gamma _{{24}}, \gamma _{{42}}$ characterizing the oil flow through the channels $\hbox {c}_{1}{-}\hbox {c}_{9}$ are of crucial importance.

We will further determine the values of the parameters in the following way: $\alpha _{{21}}=0.004, \alpha _{{12}}=0.002, \beta _{{21}}=0.02, \beta _{{12}}=0.01, \gamma _{{25}}=\gamma _{{52}}=0.02, \gamma _{{51}}=0.02, \gamma _{{15}}=0.01$, by analysing the impact of the remaining ones on the damper characteristics. In the case when the orifices $\hbox {c}_{1}$, $\hbox {c}_{2}$ or $\hbox {c}_{3}$ are covered the damper MD works in a similar way to a hard damper HD with the parameters: $\tilde{{\alpha }}_{21} =2\tilde{{\alpha }}_{12} =\alpha _{21} =0.004$. For the channels $\hbox {c}_{1}$, $\hbox {c}_{2}$, $\hbox {c}_{3}$ which are always open the damper MD behaves similarly to the soft damper SD with the parameters: $\bar{{\alpha }}_{21} =2\bar{{\alpha }}_{12} =\alpha _{21} +\gamma _{51} =0.024$.

Fig. 5

Damper characteristics ($f=1.2~\hbox {Hz}$, $a=2.5~\hbox {cm}$; $f=2~\hbox {Hz}$, $a=1.5~\hbox {cm}$; $f=12~\hbox {Hz}$, $a=0.25~\hbox {cm}$; $f=15~\hbox {Hz}$, $a=0.2\hbox {cm}$): a force–relative displacement diagram, b force–relative velocity diagram

Figure 5 illustrates the characteristics of the damping force of a properly designed shock absorber with the parameters: $\gamma _{{31}}=\gamma _{{13}}=0.0004, \gamma _{{42}}=\gamma _{{24}}=0.004, \alpha _{{31}}=\alpha _{{13}}=\alpha _{{24}}=\alpha _{{42}}=0.00004, \beta _{{13}}=\beta _{{24}}=0, \beta _{{31}}=\beta _{{42}}=0.004, h_{1}=0.5~\hbox {cm}, h_{2}=0.6~\hbox {cm}, h_{3}=0.9~\hbox {cm}$.

The characteristics are determined for four frequencies of harmonic excitation (26), where the excitation amplitudes become lower with an increase in frequency. The values of frequencies were selected from two resonance ranges near 1.2 Hz and 12 Hz.

In the absence of damping in the system (no shock absorber), the quarter-car model of the vehicle is a linear system with two degrees of freedom. Therefore, it is easy to determine resonance frequencies ($f_{r1}\approx 1.18~\hbox {Hz}$ and $f_{r2}\approx 11.26~\hbox {Hz}$) and eigenvectors. The analysis of the form of vibrations indicates that in the first resonance range the vibrations of the sprung mass (car body) are dominant. In the other range, the vibrations of the un-sprung mass (vehicle wheels) are dominant.

In the first resonance, within the range of lower frequencies and at the same time larger amplitudes (for $f=1.2~\hbox {Hz}$ and $f=2~\hbox {Hz}$), the shock absorber MD possesses the stiff characteristics in steady-state vibrations (Fig. 5b), and in the other range for $f=12~\hbox {Hz}$ and $f=15~\hbox {Hz}$ the soft characteristics (considerably smaller gradient of the curves in Fig. 5b) may be observed. It may be demonstrated that practically identical results are obtained by using the shock absorber HD in the first range, and SD in the other one. The characteristics illustrated in Fig. 5 are asymmetrical. The value of the resistance force of the damper during the rebound is bigger than that of the force during the compression. Such a characteristic is desirable [30] while driving on surfaces with large irregularities (e.g. while going over a high obstacle). The ratio of the maximum value of the force to the minimum value depends on the ratio of the effective surfaces of oil flow during the compression and the rebound ($\alpha _{{21}}/\alpha _{{12}}, \beta _{{21}}/\beta _{{12}}$). In the graphs, one can also observe points of inflection whose position depends actually on the value of the parameters $\sigma _{{21}}$ and $\sigma _{{12}}$.

Fig. 6

Pressure time histories ($f=1.2~\hbox {Hz}, a=2.5~\hbox {cm}$)

The pressure time histories $p_{n}$ in the chambers $K_{n}$ ($n=1,\ldots ,5$), which are illustrated in Fig. 6, provide essential information regarding the operation of the damper. The graphs correspond with the hard characteristics (Fig. 5 for $f=1.2~\hbox {Hz}$, $a=2.5~\hbox {cm}$). A slightly bigger impact on the damping force is exerted by the pressure $p_{1}$ in the rebound chamber, which is more clearly different with respect to the pressure $p_{2}$ in the compression chamber (mild changes of $p_{2}$ are a result of the impact of the compensation chamber $K_{6}$). In the analysed case, the orifices of the channels $\hbox {c}_{1}$ and $\hbox {c}_{2}$ are covered, so the chamber $K_{5}$ is connected only with the chamber $K_{2}$ ($p_{5}\approx p_{2}$). Also the pressure histories in the chambers $K_{1}$ and $K_{3}$ are similar to each other. The pressure in the chamber $K_{4}$ in the compression phase is slightly lower than the pressure $p_{1}$, however in the rebound phase it is similar to the pressure $p_{2}$.

Fig. 7

Pressures and mass flow rates ($f=15~\hbox {Hz}, a=0.2~\hbox {cm}$)

In the case of smaller amplitudes of excitation (Fig. 7), the pressures in the damper chambers are definitely different. Now the chamber $K_{5}$ is all the time connected with both the chamber $K_{1}$ and $K_{2}$, so the pressure $p_{5}$ has intermediate values between the pressures $p_{1}$ and $p_{2}$ (but closer to $p_{2}$). The values of the pressures $p_{3}$ and $p_{4}$ are similar to each other. In the compression phase, they are slightly higher than the pressure $p_{2}$, whereas in the rebound phase they are lower. The oil flow to the rebound chamber is the sum of three flows ($Q_{{21}}, Q_{{31}}, Q_{{51}}$), where the impact of the flow between the chambers $K_{3}$ and $K_{1}$ on the force characteristic is practically negligible (because $Q_{{31}}\ll Q_{{21}}$ and $Q_{{31}}\ll Q_{{51}}$). Due to larger effective cross-sectional areas of the channels in the inner cylinder with respect to the channels in the piston ($\gamma _{{51}}> \alpha _{{21}}, \gamma _{{52}}> \alpha _{{12}}$), the flow rate $Q_{{51}}$ is larger than $Q_{{21}}$. Similar graphs to the ones illustrated in Fig. 7 may be prepared for flow rates to the compression chamber.

In order to analyse the impact of the parameters: $\beta _{{13}}, \beta _{{31}}, \beta _{{24}}, \beta _{{42}}, \gamma _{{13}}, \gamma _{{31}}, \gamma _{{24}}, \gamma _{{42}}$ on the operation of the shock absorber, in Fig. 8 there are presented graphs of relative displacements of additional mass $m_\mathrm{ap}$ in the transitional (unspecified) state of vibrations. Simulations are carried out for four selected combinations of parameter values, which characterize the flow through the channels $\hbox {c}_{4}{-}\hbox {c}_{8}$. The following indicators were adopted: $k_{1}$ for $\beta _{{31}}=\beta _{{13}}=\beta _{{24}}=\beta _{{42}}=0.0004$, $\gamma _{{31}}=\gamma _{{13}}=\gamma _{{24}}=\gamma _{{42}}=0.004$, $k_{2}$ for $\beta _{{31}}=\beta _{{42}}=0.0004$, $\beta _{{13}}=\beta _{{24}}=0$, $\gamma _{{31}}=\gamma _{{13}}=\gamma _{{24}}=\gamma _{{42}}=0.004$, $k_{3}$ for $\beta _{{31}}=\beta _{{13}}=\beta _{{24}}=\beta _{{42}}=0.0004$, $\gamma _{{31}}=\gamma _{{13}}=0.0004$, $\gamma _{{24}}=\gamma _{{42}}=0.004$, $k_{4}$ for $\beta _{{31}}=\beta _{{42}}=0.0004$, $\beta _{{13}}=\beta _{{24}}=0$, $\gamma _{{31}}=\gamma _{{13}}=0.0004$, $\gamma _{{24}}=\gamma _{{42}}=0.004$. In the calculations the constant values of the parameters: $\alpha _{{31}}=\alpha _{{13}}=\alpha _{{24}}=\alpha _{{42}}=0.00004$ were assumed, which characterize the flow through the narrow channels $\hbox {c}_{8}$ and $\hbox {c}_{9}$.

Fig. 8

Relative displacements of auxiliary piston: a$f=1.2~\hbox {Hz}$, $a=0.25~\hbox {cm}$, b$f=6~\hbox {Hz}$, $a=0.05~\hbox {cm}$

For the correctly selected parameters, the shock absorber characteristics should adjust from the soft to the hard one within the range of the first resonance (e.g. for $f=1.2~\hbox {Hz}$—Fig. 8a). The damper works effectively if during the movement of the auxiliary piston the orifice of the channel $\hbox {c}_{3}$ (or $\hbox {c}_{1}$ and $\hbox {c}_{2}$) is all the time closed in steady-state vibrations. Additionally, the transient state should be as short as possible in order for the damper to quickly adjust in the case when the vehicle is going over a large obstacle.

Apart from the resonance (e.g. for $f=6~\hbox {Hz}$—Fig. 8b), the soft characteristics are indicated, and therefore the movement of the additional mass $m_{\mathrm{ap}}$ should take place within a limited range so that the mass $m_{\mathrm{ap}}$ does not close the channels $\hbox {c}_{1}$ and $\hbox {c}_{3}$ (i.e. $\vert x_{\mathrm{ap}}-x_{\mathrm{b}}\vert < h_{2}+r_{2}$).

Only in the case of the curve $k_{4}$, the conditions given above are fulfilled at the same time. In the remaining cases, one most frequently observes cyclic closing and opening of orifices, which results in more complex characteristics of the damping force (as in Fig. 11).

3.2 Response of the system to harmonic excitation

The effectiveness of the damper operation may be concluded by analysing the frequency characteristics of the quarter-car model of the vehicle. Figure 9 illustrates the graphs for three indexes: $\Theta _{\mathrm{w}}$, $\Theta _{\mathrm{b}}$ and $\Theta _{\mathrm{r}}$, in the excitation frequency function. The indexes $\Theta _{\mathrm{w}}$ and $\Theta _{\mathrm{b}}$ are defined as the ratios of the RMS displacement values $x_{\mathrm{w}}$ and $x_{\mathrm{b}}$ of the un-sprung and sprung mass to the RMS value of the signal $x_{\mathrm{r}}$. The index $\Theta _{\mathrm{r}}$ is the ratio of the reaction dynamic component to the static component (the total weight of the vehicle). In comparison, Fig. 9 also illustrates appropriate characteristics of classical dampers HD and SD. It was assumed that the excitation parameters fulfil the condition (26) of constant maximum velocity.

Fig. 9

Frequency characteristics ($a=2~\hbox {cm}$): a index $\Theta _{\mathrm{w}}$, b index $\Theta _{\mathrm{b}}$, c index $\Theta _{\mathrm{r}}$

Observing the results of the analysis two basic resonance ranges may be noticed. The first one in the vicinity of $f\approx 1.2~\hbox {Hz}$ and the other one for $f\approx 12~\hbox {Hz}$. In the first resonance range, particularly in the case of the damper SD, the index $\Theta _{\mathrm{b}}$ assumes high values (Fig. 9b), which is important from the point of view of the driving comfort. The indexes $\Theta _{\mathrm{w}}$ (Fig. 9a) and $\Theta _{\mathrm{r}}$ (Fig. 9c) for the dampers SD and MD achieve their maximum levels in the second resonance range. In the case of large amplitudes of wheels vibrations, the value of the reaction dynamic component increases, which means that the momentary downforce of the wheel on the road surface decreases. In a drastic case, the contact with the road surface may be lost. Therefore, the second resonance range is important from the point of view of the driving safety. Within this range, the damper MD behaves similarly to the damper SD, and it is better than the damper HD as far as the driving comfort is concerned (Fig. 9b). In a narrow range of frequencies (in the vicinity of $f=12~\hbox {Hz}$) in terms of the driving safety the damper MD is worse than the damper HD (Fig. 9c). The damper HD, however, is characterized by a relatively very high level of damping, which results in a qualitative change of the frequency characteristics visible in Fig. 9 (it is similar to the characteristics of the system with one degree of freedom). Only within selected frequency ranges (mainly in the first resonance) the damper MD should behave like the damper HD.

The values of the index $\Theta _{\mathrm{b}}$ that decides about the driving comfort are for the damper MD in almost all the frequency range smaller than for the dampers SD and HD. Only in the first resonance the damper HD is slightly more effective than the damper MD.

Fig. 10

Frequency characteristics: a displacement of sprung mass, b acceleration of sprung mass

Figure 10 illustrates the graphs of the RMS values of displacements $x_{\mathrm{b}}$ and accelerations $a_{\mathrm{b}}$ for two values of the parameter $a_{0}$ that characterizes excitation (26). Since the excitation amplitude decreases together with frequency, the displacement $x_{\mathrm{b}}$ decreases as well (Fig. 10a). The comparison of the values of amplitudes in the first resonance indicates that the damper MD, with reference to the damper SD, is more effective in the case of larger excitations. For example, for $f=1.2~\hbox {Hz}$ and $a=1~\hbox {cm} \Theta _{\mathrm{b}}^{\mathrm{MD}} = 2.167$, $\Theta _{\mathrm{b}}^{\mathrm{SD}} =3.294$ (a reduction of approx. 1.5 times), and for $f=1.2~\hbox {Hz}$ and $a=3~\hbox {cm}$$\Theta _{\mathrm{b}}^{\mathrm{MD}} =1.289$, $\Theta _{\mathrm{b}}^{\mathrm{SD}} =2.777$ (over 2 times).

In the graphs of the modified damper MD illustrated in Figs. 9 and 10, jumps between the characteristics of the damper SD and HD may be observed. Within the ranges in which the characteristics of MD overlap with these of SD or HD, the graphs of the damping force are similar to the ones illustrated in Fig. 5. In the remaining ones, the characteristic of the force is more complex, which is a result of closing and opening orifices of the channels $\hbox {c}_{1}{-}\hbox {c}_{5}$ by the auxiliary piston. Figure 11 illustrates selected courses of the relative displacement $x_{\mathrm{ap}}-x_{\mathrm{b}}$ of the mass $m_{\mathrm{ap}}$ and the corresponding damping forces. The channel $\hbox {c}_{3}$ is closed or opened for $x_{\mathrm{ap}}-x_{\mathrm{b}}\approx -h_{1}$, the channel $\hbox {c}_{5}$ for $x_{\mathrm{ap}}-x_{\mathrm{b}}\approx -h_{2}$, and in the case of $x_{\mathrm{ap}}-x_{\mathrm{b}}=-h_{3}$ the mass hits a quite rigid bumper.

Fig. 11

Relative displacements of auxiliary piston and force-velocity diagram: a$f=1.2~\hbox {Hz}$, $a_{0}=1~\hbox {cm}$; b$f=1.1~\hbox {Hz}$, $a_{0}=3~\hbox {cm}$

Fig. 12

Impact of parameter H on displacement of sprung mass ($L=1~\hbox {m}$, $v_{0}=5~\hbox {m/s}$): a damper MD, b damper SD

3.3 Response of the system to impulse excitation

The advantage of the damper MD over the damper SD may be seen even more clearly while analysing the responses of the system to impulse excitation (28), which describes in a simplified way the initial phase of the process of overcoming an obstacle by a vehicle. Figure 12 illustrates the displacements of the sprung mass of the quarter-car model with the damper MD (Fig. 12a) and SD (Fig. 12b) while overcoming an obstacle of the same shape but of a different height H. Only for $H=1~\hbox {cm}$, the responses of the systems MD and SD are identical. In this case, the additional mass in the damper MD moves between the orifices of the channels $\hbox {c}_{1}$ and $\hbox {c}_{3}$, not closing them. In the remaining cases, the characteristic of the damper MD adjusts within a short period of time from soft to hard, as a result of which the vibrations of the car body are very quickly damped.

Fig. 13

Impact of driving velocity $v_{0}$ on displacement $x_{\mathrm{b}}$ and index $\Theta _{\mathrm{r0}}$ ($H=5~\hbox {cm}, L=1~\hbox {m}$): a damper MD, b damper SD

Figure 13 illustrates the time histories of displacement $x_{\mathrm{b}}$ and index $\Theta _{\mathrm{r0}}$ while a vehicle is overcoming the same obstacle with different driving speeds. The index $\Theta _{\mathrm{r0}}$ is defined as the ratio of the total reaction (the sum of weight and dynamic reaction) exerted on the vehicle wheel to the static reaction. When the index $\Theta _{\mathrm{r0}}$ reaches the zero value, it means that wheels have lost contact with the road surface.

Fig. 14

Displacements and accelerations of sprung mass and characteristic of the damping force ($K=4$, $v_{0}=7.5~\hbox {m/s}$, $n_{\mathrm{l}}=0.04~\hbox {cycle/m}$, $n_{\mathrm{u}}=4~\hbox {cycle/m}$, $N=512$)

Fig. 15

Relative displacements of the main and floating piston: ($K=4$, $v_{0}=7.5~\hbox {m/s}$ and $v_{0}=15~\hbox {m/s}$, $n_{\mathrm{l}}=0.04~\hbox {cycle/m}$, $n_{\mathrm{u}}=4~\hbox {cycle/m}$, $N=512$): a damper MD, b damper SD

Also this comparison of the operation of the dampers MD and SD shows better properties of vibrations damping in the car body by the damper MD. While driving at high speeds the maximum value of the displacement admittedly decreases, but this takes place at the expense of increased accelerations and reaction from the road surface. In the case of the damper HD appropriate time histories (not included in the work) are very similar to the ones illustrated in Fig. 13a. The damper HD damps down vibrations slightly faster, however for $v_{0}=20~\hbox {m/s}$ the reaction minimum value reaches the zero value, which means that wheels lost contact with the road surface. In this case, the better behaviour of the damper MD is due to the fact that in the initial phase of overcoming the obstacle its characteristic is close to the soft one.

3.4 Response of the system to random excitation

In order to verify the designed shock absorber, one should also examine the behaviour of the quarter-car model while driving over surfaces described by the random function (29). Random excitation depends on a number of parameters, including above all the class of the road surface (parameter K) and the driving speed $v_{0}$. When the quality of the road surface becomes worse (i.e. the value of the parameter K increases), the driving velocity $v_{0}$ should be adequately lower – and then one should expect the values of all indexes, responsible for both driving comfort and driving safety, to be more similar to one another.

Figures 14, 15 and 16 illustrate selected results of the analysis for the case of driving over a poor-quality surface (class $K=4$) at a relatively low speed $v_{0}=7.5~\hbox {m/s}$ (27 km/h) and driving over a road of class $K=1$ at a four times higher speed $v_{0}=30~\hbox {m/s}$ (108 km/h).

Fig. 16

Displacements and accelerations of sprung mass and characteristic of the damping force ($K=1$, $v_{0}=30~\hbox {m/s}$, $n_{\mathrm{l}}=0.04~\hbox {cycle/m}$, $n_{\mathrm{u}}=4~\hbox {cycle/m}$, $N=512$)

Figure 14 illustrates the courses of displacements $x_{\mathrm{b}}$ and accelerations $a_{\mathrm{b}}$ of the sprung mass as well as the characteristic of the damping force$F_{\mathrm{b}}$ for $K=4$ and $v_{0}=7.5\hbox {m/s}$. Numerical simulations are carried out for: $N=512$, $n_{\mathrm{l}}=0.04~\hbox {cycle/m}$, $n_{\mathrm{u}}=4~\hbox {cycle/m}$. For the driving speed $v_{0}=7.5~\hbox {m/s}$, the low and high frequencies of excitation are equal: $f_\mathrm{l}=0.3~\hbox {Hz}$, $f_\mathrm{u}=30~\hbox {Hz}$, which means that the range which they determined encompasses both resonance frequencies of the system.

In accordance with expectations, in the case of a poor road surface the damper MD possesses the characteristics of the hard damper HD (Fig. 14b). Since the graphs for responses of the systems with the dampers MD and HD overlap almost throughout the whole time duration, for a better clarity Fig. 14 illustrates only the results of the analysis of the dampers MD and SD.

The application of the damper MD reduces mainly the extreme values of displacements in relation to the system SD. The scope of the change of displacements of both systems is similar, although they are slightly larger for the system MD. During a short transitional period ($t< 0.4~\hbox {s}$), the damper MD behaves like the soft damper SD (Fig. 14a). The calculated RMS values of displacements and accelerations are equal to: $x_{\mathrm{b}}^{\mathrm{RMS}}=2.07~\hbox {cm}$ and $a_{\mathrm{b}}^{\mathrm{RMS}}=3.51~\hbox {m/s}^{2}$ for MD and $x_{\mathrm{b}}^{\mathrm{RMS}}=2.39~\hbox {cm}$ and $a_{\mathrm{b}}^{\mathrm{RMS}}=2.78~\hbox {m/s}^{2}$ for SD, respectively.

The damper MD has one more positive feature in comparison with the damper SD. The change of its characteristics from soft to hard in the case of a very poor road surface and additionally high driving speeds limits the movement of the main piston, thus protecting the system from undesired collisions with the floating piston or with the cylinder walls. Figure 15 illustrates the graphs of relative displacements $z_{\mathrm{b}} =x_{\mathrm{b}}-x_{\mathrm{w}}$ and $z_{\mathrm{fp}}=x_{\mathrm{fp}}-x_{\mathrm{w}}$ for the systems with the dampers MD and SD. For the damper SD already for the speed $v_{0}=7.5~\hbox {m/s}$ the distance between the main piston and the floating piston is dangerously small, and in the case of a twice higher speed we are practically confronted with collisions of both pistons in numerous points in time, which may lead to the damper damage. In the case of the system MD the situation is completely different.

Figure 16 illustrates the courses of displacements and accelerations of the sprung mass while driving on a road surface of the class $K=1$ at a speed of $v_{0}=30~\hbox {m/s}$ (108 km/h). In this case, the damper MD behaves like the soft damper SD, and appropriate graphs overlap. For the evaluation of the effectiveness of the operation of the damper MD, Fig. 16 illustrates also the responses of the system with the damper HD.

In the case of a good road surface, the displacements in both cases are relatively small and from the point of view of the driving comfort accelerations are this time more important. The damper MD damps down high harmonics decisively better, which results in an approximately twofold decrease in the RMS values of accelerations in comparison with the system HD. The RMS values of displacements and accelerations are equal to: $x_{\mathrm{b}}^{\mathrm{RMS}}=0.20~\hbox {cm}$ and $a_{\mathrm{b}}^{\mathrm{RMS}}=0.47~\hbox {m/s}^{2}$ for the damper MD and $x_{\mathrm{b}}^{\mathrm{RMS}}=0.22~\hbox {cm}$ and $a_{\mathrm{b}}^{\mathrm{RMS}}=0.91~\hbox {m/s}^{2}$ for the damper HD, respectively.

To summarize, the damper MD ensures high driving comfort on good surface roads (then it is better than the damper HD), but in the case of worse surface roads limits it maximally deflections and better damps down vibrations in comparison with the damper SD.

4 Conclusion

The paper proposes a modification of the classical mono-tube shock absorber which consists in an introduction of an additional cylinder with an auxiliary piston controlling the oil flow between the compression and rebound chambers. As a result of such a modification of the damper, the shock absorber characteristic depends on the amplitude and frequency of excitation.

In order to analyse the effectiveness of the operation of the shock absorber, a nonlinear model of a vehicle with the tested damper has been developed. The flow between the main chambers of the shock absorber depends on the difference between oil pressures in these chambers, and in the case of the chambers of the inner cylinder also on the relative displacements of the auxiliary piston. The proposed simplified model of flows on the one hand well describes basic features of the damper, and on the other hand allows for an effective analysis of the vehicle model for harmonic, impulse and random excitations. In the case of large amplitudes of excitation (e.g. during an initial stage of overcoming a large obstacle by a vehicle), the oil flow through additional channels in the inner cylinder is blocked, as a result of which the damping force increases and vibrations disappear faster.

The conducted numerical simulations make it possible to analyse in detail the impact of the construction parameters of the damper on the characteristics of the damping force as well as indexes responsible for the driving comfort and safety. On the basis of various analyses, one may estimate the values of the damper parameters (characterizing mainly valves), which ensure its proper operation in various conditions. In comparison with the classical damper with hard characteristics the proposed damper reduces the amplitudes of vibrations of the sprung mass (mainly accelerations) within the ranges of higher frequencies, thus improving the driving comfort. Within the range of the first resonance, the shock absorber acts as the ‘hard’ damper, clearly limiting the amplitudes of vibrations. The change of the characteristics from soft to hard also protects the damper from getting damaged in the case of large amplitudes of excitations.