Skip to main content
SpringerLink
Log in

Dynamics comparison between non-spatial and spatial systems of the plankton–fish interaction model

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

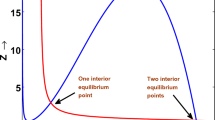
Abstract

This paper considers a plankton–fish interaction model by comparing the dynamics between non-spatial and spatial systems. In the model, both the fish and phytoplankton populations are assumed to be growing logistically, the fish population is nonlinearly harvested, and the interaction between phytoplankton and zooplankton is described by the Crowley–Martin functional response. Stability analyses for the plankton–fish interaction model have been carried out for both non-spatial and spatial systems. The theoretical results are then supported by numerical simulations. In the case of non-spatial system, single-parameter bifurcation diagrams are used, while in the spatial system numerical simulations for one- and two-dimensional cases are performed. In the case of a non-spatial system, the conditions for the existence of a positive equilibrium point, as well as their local and global stability analyses, have been obtained. In the spatial system, the stability and existence of Hopf bifurcation have been discussed, and different conditions for Turing pattern information have been established through diffusion-driven instability analysis. Taken together, these results show that spatial heterogeneity, the mortality rate of phytoplankton, and the constant harvesting of the fish population play important roles in the dynamical behavior of the marine system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Baek, H., Jung, D.I., Wang, Z.W.: Pattern formation in a semi-ratio-dependent predator–prey system with diffusion. Discret. Dyn. Nat. Soc. 2013, 1–14 (2013)

    Article  MathSciNet  Google Scholar 

  2. Belkhodja, K., Moussaoui, A., Alaoui, M.A.: Optimal harvesting and stability for a prey–predator model. Nonlinear Anal. Real World Appl. 39, 321–336 (2018)

    Article  MathSciNet  Google Scholar 

  3. Berryman, A.A.: The origin and evolution of predator–prey theory. Ecology 73(5), 1530–1535 (1992)

    Article  Google Scholar 

  4. Crowley, P.H., Martin, E.K.: Functional responses and interference within and between year classes of a dragonfly population. J. North Am. Benthol. Soc. 8(3), 211–221 (1989)

    Article  Google Scholar 

  5. Chow, S.N., Hale, J.K.: Methods of Bifurcation Theory, vol. 251. Springer, Berlin (2012)

    MATH  Google Scholar 

  6. Clark, C.W.: Mathematical Boieconomics: The Optimal Management of Renewable Resources. Wiley, New York (1976)

    Google Scholar 

  7. Das, A., Pal, M.: Theoretical analysis of an imprecise prey-predator model with harvesting and optimal control. J. Optim. 2019, 1–12 (2019)

    MathSciNet  MATH  Google Scholar 

  8. Dubey, B., Agarwal, S., Kumar, A.: Optimal harvesting policy of a prey–predator model with Crowley–Martin-type functional response and stage structure in the predator. Nonlinear Anal. Modell. Control 23(4), 493–514 (2018)

    Article  MathSciNet  Google Scholar 

  9. Han, X., Bi, Q., Zhang, C., Yu, Y.: Study of mixed-mode oscillations in a parametrically excited van der Pol system. Nonlinear Dyn. 77(4), 1285–1296 (2014)

    Article  MathSciNet  Google Scholar 

  10. Han, X., Xia, F., Zhang, C., Yu, Y.: Origin of mixed-mode oscillations through speed escape of attractors in a Rayleigh equation with multiple-frequency excitations. Nonlinear Dyn. 88(4), 2693–2703 (2017)

    Article  Google Scholar 

  11. Han, X., Bi, Q., Ji, P., Kurths, J.: Fast-slow analysis for parametrically and externally excited systems with two slow rationally related excitation frequencies. Phys. Rev. E 92(1), 012911 (2015)

    Article  MathSciNet  Google Scholar 

  12. Kar, T.K., Chaudhuri, K.S.: Harvesting in a two-prey one-predator fishery: a bioeconomic model. ANZIAM J. 45(3), 443–456 (2004)

    Article  MathSciNet  Google Scholar 

  13. Meng, X.Y., Wu, Y.Q.: Bifurcation and control in a singular phytoplankton–zooplankton–fish model with nonlinear fish harvesting and taxation. Int. J. Bifurc. Chaos 28(03), 1850042 (2018)

    Article  MathSciNet  Google Scholar 

  14. Medvinsky, A.B., Petrovskii, S.V., Tikhonova, I.A., Malchow, H., Li, B.L.: Spatiotemporal complexity of plankton and fish dynamics. SIAM Rev. 44, 311–370 (2002)

    Article  MathSciNet  Google Scholar 

  15. Maiti, A.P., Dubey, B.: Stability and bifurcation of a fishery model with Crowley–Martin functional response. Int. J. Bifurc. Chaos 27(11), 1750174 (2017)

    Article  MathSciNet  Google Scholar 

  16. Pontryagin, L.S., Boltyanskii, V., Gamkrelidze, R., Mischchenko, E.F.: The Mathematical Theory of Optimal Process. Inter-Science, New York (1962)

    Google Scholar 

  17. Pascual, M., Caswell, H.: Environmental heterogeneity and biological pattern in a chaotic predator–prey system. J. Theoret. Biol. 185(1), 1–13 (1997)

    Article  Google Scholar 

  18. Pascual, M.: Diffusion-induced chaos in a spatial predator–prey system. Proc. R. Soc. Lond. Ser. B Biol. Sci. 251(1330), 1–7 (1993)

    Article  Google Scholar 

  19. Panja, P., Mondal, S.K., Jana, D.K.: Effects of toxicants on phytoplankton–zooplankton–fish dynamics and harvesting. Chaos Solitons Fract. 104, 389–399 (2017)

    Article  MathSciNet  Google Scholar 

  20. Raw, S.N., Mishra, P.: Modeling and analysis of inhibitory effect in plankton–fish model: application to the hypertrophic Swarzedzkie Lake in Western Poland. Nonlinear Anal. Real World Appl. 46, 465–492 (2019)

    Article  MathSciNet  Google Scholar 

  21. Ren, J., Yu, L., Siegmund, S.: Bifurcations and chaos in a discrete predator–prey model with Crowley–Martin functional response. Nonlinear Dyn. 90(1), 19–41 (2017)

    Article  MathSciNet  Google Scholar 

  22. Ryu, K., Ko, W., Haque, M.: Bifurcation analysis in a predator-prey system with a functional response increasing in both predator and prey densities. Nonlinear Dyn. 94(3), 1639–1656 (2018)

    Article  Google Scholar 

  23. Sandri, M.: Numerical calculation of Lyapunov exponents. Math. J. 6(3), 78–84 (1996)

    Google Scholar 

  24. Shi, X., Zhou, X., Song, X.: Analysis of a stage-structured predator–prey model with Crowley–Martin function. J. Appl. Math. Comput. 36(1–2), 459–472 (2011)

    Article  MathSciNet  Google Scholar 

  25. Sun, G.Q.: Mathematical modeling of population dynamics with Allee effect. Nonlinear Dyn. 85(1), 1–12 (2016)

    Article  MathSciNet  Google Scholar 

  26. Smith, J.: Models in Ecology. Cambridge University Press, Cambridge (1974)

    MATH  Google Scholar 

  27. Upadhyay, R.K., Tiwari, S.K., Roy, P.: Complex dynamics of wetland ecosystem with nonlinear harvesting: application to Chilika Lake in Odisha, India. Int. J. Bifurc. Chaos 25(07), 1540016 (2015)

    Article  MathSciNet  Google Scholar 

  28. Upadhyay, R.K., Roy, P.: Disease spread and its effect on population dynamics in heterogeneous environment. Int. J. Bifurc. Chaos 26(01), 1650004 (2016)

    Article  MathSciNet  Google Scholar 

  29. Upadhyay, R.K., Tiwari, S.K.: Ecological chaos and the choice of optimal harvesting policy. J. Math. Anal. Appl. 448(2), 1533–1559 (2017)

    Article  MathSciNet  Google Scholar 

  30. Upadhyay, R.K., Kumari, S., Kumari, S., Rai, V.: Salton Sea: an ecosystem in crisis. Int. J. Biomath. 11(08), 1850114 (2018)

    Article  MathSciNet  Google Scholar 

  31. Upadhyay, R.K., Naji, R.K.: Dynamics of a three species food chain model with Crowley–Martin type functional response. Chaos Solitons Fract. 42(3), 1337–1346 (2009)

    Article  MathSciNet  Google Scholar 

  32. Upadhyay, R.K., Kumari, S., Kumar, P., Rai, V.: Spatial distribution of microalgae in marine system: a reaction–diffusion. Ecol. Complex. 39(2019), 100771 (2019)

    Article  Google Scholar 

  33. Volpert, V.A.: Elliptic Partial Differential Equations. Birkhäuser, Boston (2011)

    Book  Google Scholar 

  34. Wang, J., Liu, X., Liang, J.: Bogdanov–Takens bifurcation in an oscillator with positive damping and multiple delays. Nonlinear Dyn. 87(1), 255–269 (2017)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors express their gratitude to the associate editor and the reviewers whose comments and suggestions have helped to improve the manuscript. The authors thank Dr. Vikas Rai for helpful discussion during revision. This work has been supported by the Science & Engineering Research Board (SERB), DST, Govt. of India, under grant No. MTR/2017/000301 to the corresponding author.

Author information

Authors and Affiliations

  1. Department of Mathematics and Computing, Indian Institute of Technology (Indian School of Mines), Dhanbad, Dhanbad, Jharkhand, 826004, India

    Sarita Kumari & Ranjit Kumar Upadhyay

Authors
  1. Sarita Kumari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ranjit Kumar Upadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ranjit Kumar Upadhyay.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this article.

Ethical standard

The authors state that this research complies with ethical standards. This research does not involve either human participants or animals.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumari, S., Upadhyay, R.K. Dynamics comparison between non-spatial and spatial systems of the plankton–fish interaction model. Nonlinear Dyn 99, 2479–2503 (2020). https://doi.org/10.1007/s11071-019-05415-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05415-6

Keywords

Search

Navigation