Fractal analysis and control of the fractional Lotka–Volterra model

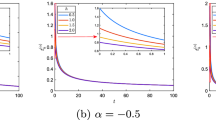
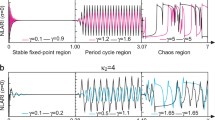
Abstract

This paper reports the investigation of a fractional Lotka–Volterra model from the fractal viewpoint. A Julia set of a discrete version of this model is introduced and its state feedback control is realized. Coupled terms are designed to realize the synchronization of two Julia sets with different parameters. Numerical simulations are presented to further verify the correctness and effectiveness of the main theoretical results.

Appendix

From the discussion of discretization of fractional derivatives in Sect. 2, system (8) can be seen as a truncation of the following system:

$$\begin{aligned} u_{n+1}= & {} r_1u_n - a_1u_n^2 - b_1u_nv_n - \sum \limits _{k=1}^n\omega _k^{(\alpha )}u_{n-k+1}, \nonumber \\ v_{n+1}= & {} -r_2v_n + a_2u_nv_n - b_2v_n^2 - \sum \limits _{k=1}^n\omega _k^{(\beta )}v_{n-k+1},\nonumber \\ \end{aligned}$$

(A.1)

where $n\in {\mathbb {N}}_+$. System (A.1) is a nonlinear Volterra system in which the future state $(u_{n+1},v_{n+1})$ depends on not only the present state $(u_n,v_n)$ but also all past states from $(u_{n-1},v_{n-1})$ to $(u_0,v_0)$ (cf. [28]). This kind of system that has been widely used as mathematical models in population dynamics has memory effect like a fractional system. Once given the initial condition $(u(0),v(0)) = (u_0,v_0)$, one can generate the solution to systems (8) and (A.1). As a matter of fact, system (8) can be treated as a nonlinear system containing two 200th-order nonlinear difference equations, and the initial conditions $(u_0,v_0)$, $(u_1,v_1), \ldots , (u_{199},v_{199})$ of this system can be totally generated by $(u_0,v_0)$.

Let

$$\begin{aligned}&z_1(n) = u_{n-199}, z_2(n) = u_{n-198}, \ldots , z_{200}(n) = u_n, \\&z_{201}(n) = v_{n-199}, z_{202}(n) = v_{n-198}, \ldots , z_{400}(n) = v_n. \end{aligned}$$

Then, system (8) can be converted to the system

$$\begin{aligned} {\mathbf {z}}(n+1) = {\mathbf {H}}({\mathbf {z}}(n)), \quad n\in {\mathbb {N}}, \end{aligned}$$

(A.2)

where

$$\begin{aligned} {\mathbf {z}}(n)= & {} (z_1(n),z_2(n), \ldots , z_{400}(n))^{\mathrm {T}},\\ {\mathbf {H}}= & {} (h_1,h_2, \ldots , h_{400})^{\mathrm {T}} \end{aligned}$$

and

$$\begin{aligned}&h_i(z_1,z_2,\ldots ,z_{400}) \nonumber \\&\quad = z_{i+1}, \quad i = 1,2,\ldots ,199,201,202,\ldots ,399,\\&h_{200}(z_1,z_2,\ldots ,z_{400}) = r_1z_{200} - a_1z_{200}^2 \\&\qquad - b_1z_{200}z_{400}- \sum \limits _{k=1}^{N}\omega _k^{(\alpha )}z_{201-k},\\&h_{400}(z_1,z_2,\ldots ,z_{400}) = -r_2z_{400} + a_2z_{200}z_{400} \\&\qquad - b_2z_{400}^2 - \sum \limits _{k=1}^{N}\omega _k^{(\beta )}z_{401-k}. \end{aligned}$$

Point $(u^*,v^*)\in {\mathbb {R}}^2$ is a fixed point of system (8) if ${\mathbf {F}}(u^*,v^*) = (u^*,v^*)$. This corresponds to the fixed point

$$\begin{aligned} {\mathbf {z}}^* := (\underbrace{u^*,\ldots ,u^*}_{200},\underbrace{v^*,\ldots ,v^*}_{200})^{\mathrm {T}}\in {\mathbb {R}}^{400} \end{aligned}$$

for system (A.2). Therefore, a fixed point of system (8) is stable if and only if the corresponding fixed point of system (A.2) is stable.

Denote

$$\begin{aligned} \xi _1:= & {} \frac{\partial h_{200}}{z_{200}}\Big |_{{\mathbf {z}}^*} = r_1-\omega _1^{(\alpha )}-2a_1u^*-b_1v^*,\\ \xi _2:= & {} \frac{\partial h_{400}}{z_{400}}\Big |_{{\mathbf {z}}^*} = -r_2-\omega _1^{(\beta )}+a_2u^*-2b_2v^*. \end{aligned}$$

Then, the Jacobian matrix of system (A.2) at the fixed point ${\mathbf {z}}^*$ is

(A.3)

Noticing the equivalence between systems (8) and (A.2), the matrix ${\mathbf {J}}$ represented by (A.3) can also be called the Jacobian matrix of system (8) at the fixed point $(u^*,v^*)$.

Let $\alpha$, $\beta$, $r_i$, $a_i$ and $b_i$ ($i = 1,2$) satisfy (9). Then, the spectral radius of the Jacobian matrix ${\mathbf {J}}$ at $P_c = (1.6905,0.7294)$ is 0.9725, denoting $\rho ({\mathbf {J}}) = 0.9725$. From [28, Corollary 4.34], the fixed point $P_c$ is stable. Further, let $a_1 = b_2 = 0$. Then, $P_c = (1.3987,1.0675)$ and $\rho ({\mathbf {J}}) = 0.9728$.

Next, controlled system (11) is handled with the same method. In this case,

$$\begin{aligned} {\overline{\xi }}_1= & {} \theta _1+r_1-\omega _1^{(\alpha )}-2a_1u^*-b_1v^*,\\ {\overline{\xi }}_2= & {} \theta _2-r_2-\omega _1^{(\beta )}+a_2u^*-2b_2v^*. \end{aligned}$$

Substitute $\xi _1$ and $\xi _2$ in (A.3) with ${\overline{\xi }}_1$ and ${\overline{\xi }}_2$, respectively. Then, one gets the Jacobian matrix of controlled system (11) at the fixed point $(u^*,v^*)$, and we denote it as $\overline{{\mathbf {J}}}(\theta _1,\theta _2)$. Obviously, $\overline{{\mathbf {J}}}(\theta _1,\theta _2)$ is continuous about $\theta _1$ and $\theta _2$. According to [28, Corollary 4.34] and the above discussion, the fixed point $(u^*,v^*)$ is stable if $\rho \big (\overline{{\mathbf {J}}}(\theta _1,\theta _2)\big ) < 1$. Setting $\theta _1 = \theta _2 = \theta$, we have $\theta \in [-1.5749,0.6139]$ that satisfies $\rho \big (\overline{{\mathbf {J}}}(\theta ,\theta )\big ) < 1$ with the help of computer-aided calculation.