About the optimal harvesting of a fuzzy predator–prey system: a bioeconomic model incorporating prey refuge and predator mutual interference

Abstract

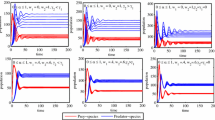
To understand roles of fuzzy biological parameters, in this paper, we propose a fuzzy predator–prey harvesting model that incorporates both the effects of prey refuge and predator mutual interference. Using the triangular fuzzy numbers for the imprecise parameters, we first study the existence of the feasible equilibria and their global stability and then discuss the bionomic equilibrium and the possible optimal harvesting policy. Numerical simulations are carried out to illustrate our analytical results, based on which discussions and conclusions are made. They show that the fuzziness of biological parameters can greatly affect the dynamics of the ecological system.

Appendices

Appendix A: Mathematical preliminaries

We introduce some results concerning fuzzy sets, triangular fuzzy number and utility function. For more details see [24, 30].

Definition 1

(Fuzzy subset) A fuzzy subset $\widetilde{A}$ of a universal set X is defined by the set of pairs $\widetilde{A}=\{(x, \mu _{\widetilde{A}}(x)): x\in X\}$, where the mapping $\mu _{\widetilde{A}}: X\rightarrow [0, 1]$ is called the membership function and $\mu _{\widetilde{A}}(x)$ gives to x its membership grade to the subset $\widetilde{A}$.

We would like to point out that a classic subset A of X is a special fuzzy set, where the membership function is replaced by characteristic function of A, $\chi _A: X\rightarrow \{0, 1\}$.

Definition 2

($\alpha$-cut of fuzzy subset) Let $\mathscr {F}(X)$ indicates the family of fuzzy sets in X. For any $\widetilde{A}\in \mathscr {F}(X)$ and $\alpha \in (0, 1]$, a crisp set

$$\begin{aligned} A_{\alpha }=\{x\in X: \mu _{\widetilde{A}}(x)\ge \alpha \} \end{aligned}$$

is called $\alpha$-cut of fuzzy set $\widetilde{A}$. Here, $\alpha$ is called the confidence level. For $\alpha =0$, $A_0$ is defined as $A_0=\overline{\{x\in X: \mu _{\widetilde{A}}(x)>0\}}$.

Clearly, $\alpha$-cut of fuzzy subset is a classical set, which determines the clear attribution of an element to a fuzzy subset. Therefore, Definition 2 provides a method to convert a fuzzy subset into a classical set.

Definition 3

(Fuzzy number) Let $\widetilde{A}$ be the fuzzy set on the real number set $\mathbb {R}$, i.e., $\widetilde{A}\in \mathscr {F}(\mathbb {R})$. Then the fuzzy set $\widetilde{A}$ is called a fuzzy number if it has the following properties:

• (i) $\widetilde{A}$ is a normal fuzzy set, i.e., there exists a $x\in \mathbb {R}$ such that $\mu _{\widetilde{A}}(x)\equiv 1$;

• (ii) $\widetilde{A}$ is a convex fuzzy set, i.e., for all $\alpha \in [0, 1]$, the $\alpha$-cut set $A_{\alpha }$ is a closed bounded interval.

Remarkably, let $\widetilde{A}\in \mathscr {F}(\mathbb {R})$, the $\alpha$-cut set $A_{\alpha }$ can be described by $A_{\alpha }=[A_L^{\alpha }, A_R^{\alpha }]$, where $A_L^{\alpha }=\inf \{x\in \mathbb {R}: \mu _{\widetilde{A}}(x)\ge \alpha \}$ and $A_R^{\alpha }=\sup \{x\in \mathbb {R}: \mu _{\widetilde{A}}(x)\ge \alpha \}$.

Definition 4

(Triangular fuzzy number (TFN)) Let $a_1$, $a_3$ and $a_2$ denote, respectively, the lower bound, the upper bound and the maximum possible value of a fuzzy number, then the fuzzy number $\widetilde{A}=(a_1, a_2, a_3)$ is called a TFN, where the membership function $\mu _{\widetilde{A}}: \mathbb {R}\rightarrow [0, 1]$ is defined as follows:

$$\begin{aligned} \mu _{\widetilde{A}}(x)=\left\{ \begin{array}{lll} \frac{x-a_1}{a_2-a_1}, &{}\quad \hbox {if}\,\, a_1 \le x \le a_2; \\ \frac{a_3-x}{a_3-a_2}, &{}\quad \hbox {if}\,\, a_2 \le x \le a_3; \\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

It is clear from definition 4 that $\alpha$-cut of TFN $\widetilde{A}=(a_1, a_2, a_3)$ is a closed and bounded interval $[A_L^{\alpha }, A_R^{\alpha }]$, where

$$\begin{aligned}&A_L^{\alpha }=\inf \{x\in \mathbb {R}: \mu _{\widetilde{A}}(x)\ge \alpha \}=a_1+\alpha (a_2-a_1),\\&A_R^{\alpha }=\sup \{x\in \mathbb {R}: \mu _{\widetilde{A}}(x)\ge \alpha \}=a_3-\alpha (a_3-a_2). \end{aligned}$$

We now list some arithmetic operations on fuzzy numbers.

Lemma 1

If $\widetilde{A}, \widetilde{B}\in \mathscr {F}(\mathbb {R})$, then for all $\alpha \in (0,1]$, the following conclusions are valid.

• (i) $[\widetilde{A}+\widetilde{B}]_{\alpha }=[A_L^{\alpha }+B_L^{\alpha }, A_R^{\alpha }+B_R^{\alpha }]$;

• (ii) $[\widetilde{A}\cdot \widetilde{B}]_{\alpha }=\Big [\min \{A_L^{\alpha }B_L^{\alpha }, A_L^{\alpha }B_R^{\alpha }, A_R^{\alpha }B_L^{\alpha }, A_R^{\alpha }B_R^{\alpha }\}, \max \{A_L^{\alpha }B_L^{\alpha }, A_L^{\alpha }B_R^{\alpha }, A_R^{\alpha }B_L^{\alpha }, A_R^{\alpha }B_R^{\alpha }\}\Big ]$;

• (iii) $[\widetilde{A}-\widetilde{B}]_{\alpha }=[A_L^{\alpha }-B_R^{\alpha }, A_R^{\alpha }-B_L^{\alpha }]$.

Finally, we give a method called the utility function, which plays a critical role in building our model. A utility function is usually defined according to the relative importance of the objective $h_i$. Let $\varpi _i$ denote the weight assigned to the ith objective, then a simple utility function of the ith objective can be defined as $\varpi _ih_i$. Thus, the total utility may be expressed by

$$\begin{aligned} U=\sum \limits _{i=1}^l\varpi _ih_i,\quad \varpi _i\ge 0, \end{aligned}$$

where $\sum \nolimits _{i=1}^l\varpi _i=1$. Obviously, the total utility is the weighted sum of all objectives.

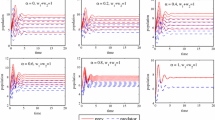
Appendix B: Analysis the effects of $\theta$ and m on predator–prey species

Suppose model (6) exists a unique interior equilibrium $M^*(x^*,y^*)$, then we have

$$\begin{aligned} {\left\{ \begin{array}{ll} M\equiv a-bx^*-c(1-m)(y^*)^{\theta }-q_1E_1=0,\\ N\equiv e(1-m)x^*(y^*)^{\theta -1}-d-q_2E_2=0. \end{array}\right. } \end{aligned}$$

(40)

Furthermore,

$$\begin{aligned} H&=\frac{\partial (M,N)}{\partial (x^*,y^*)}=\left| \begin{array}{cc} M_{x^*} &{} \quad M_{y^*} \\ N_{x^*} &{}\quad N_{y^*} \end{array} \right| \\&=e(1-m)(y^*)^{\theta -1}\left[ \frac{b(1-\theta )x^*}{y^*}+\theta c(1-m)(y^*)^{\theta -1}\right] , \end{aligned}$$

which implies that $H>0$, for any $0<\theta \le 1$ and $0\le m<1$. Thanks to the existence theorem of implicit function, equation (40) determines two implicit functions as follows: $x^*=x^*(\theta ,m), y^*=y^*(\theta ,m).$ After some simple calculations, we have

$$\begin{aligned} \frac{\partial x^*}{\partial \theta }&=-\frac{1}{H}\frac{\partial (M,N)}{\partial (\theta , y^*)}\\&=-\frac{ce(1-m)^2x^*(y^*)^{2\theta -2}}{H}\ln y^*,\\ \frac{\partial y^*}{\partial \theta }&=-\frac{1}{H}\frac{\partial (M,N)}{\partial ( x^*,\theta )}\\&= -\frac{e(1-m)(y^*)^{\theta -1}}{H}(a-q_1E_1-2bx^*)\ln y^*,\\ \frac{\partial x^*}{\partial m}&= -\frac{1}{H}\frac{\partial (M,N)}{\partial (m, y^*)}\\&=\frac{ce(1-m)x^*(y^*)^{2\theta -2}}{H},\\ \frac{\partial y^*}{\partial m}&= -\frac{1}{H}\frac{\partial (M,N)}{\partial ( x^*,m)}\\&=\frac{e(y^*)^{\theta -1}}{H}(a-q_1E_1-2bx^*). \end{aligned}$$

We then have the following conclusions:

• (a) $x^*(\theta )$ is strictly increasing if $0<y^*<1$; $x^*(\theta )$ is strictly decreasing if $y^*>1$;

• (b) $y^*(\theta )$ is strictly increasing if $x^*>\frac{a-q_1E_1}{2b}$ and $y^*>1$ (or $0<x^*<\frac{a-q_1E_1}{2b}$ and $0<y^*<1$); $y^*(\theta )$ is strictly decreasing if $x^*>\frac{a-q_1E_1}{2b}$ and $0<y^*<1$ (or $0<x^*<\frac{a-q_1E_1}{2b}$ and $y^*>1$);

• (c) $x^*(m)$ is strictly increasing for all $0\le m<1$;

• (d) $y^*(m)$ is strictly increasing if $0<x^*<\frac{a-q_1E_1}{2b}$; $y^*(m)$ is strictly decreasing if $x^*>\frac{a-q_1E_1}{2b}$.