Predator interference and stability of predator–prey dynamics

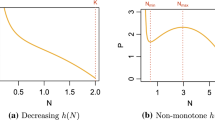
Abstract

Predator interference, that is, a decline in the per predator consumption rate as predator density increases, is generally thought to promote predator–prey stability. Indeed, this has been demonstrated in many theoretical studies on predator–prey dynamics. In virtually all of these studies, the stabilization role is demonstrated as a weakening of the paradox of enrichment. With predator interference, stable limit cycles that appear as a result of environmental enrichment occur for higher values of the environmental carrying capacity of prey, and even a complete absence of the limit cycles can happen. Here we study predator–prey dynamics using the Rosenzweig–MacArthur-like model in which the Holling type II functional response has been replaced by a predator-dependent family which generalizes many of the commonly used descriptions of predator interference. By means of a bifurcation analysis we show that sufficiently strong predator interference may bring about another stabilizing mechanism. In particular, hysteresis combined with (dis)appearance of stable limit cycles imply abrupt increases in both the prey and predator densities and enhanced persistence and resilience of the predator–prey system. We encourage refitting the previously collected data on predator consumption rates as well as for conducting further predation experiments to see what functional response from the explored family is the most appropriate.

Appendix A

1.1 A.1 Fold bifurcation

Here we show that if a coexistence equilibrium of the model (1) exists then the condition (10) is equivalent to the existence of one zero eigenvalue of the Jacobian of this model evaluated at this equilibrium. Let us define a function $g(N,P)$ such that $f(N,P) = N g(N,P)$ where $f(N,P)$ is the predator functional response (2). In addition, let $A$ denote the Jacobian of the model (1) and $[N^*,P^*]$ any coexistence equilibrium of this model. By direct computation we have

$$\begin{aligned} A=\left( \begin{array}{ll} r-r\tfrac{2N^*}{K} - P^*g-P^*N^*g_N &{} -N^*g-P^*N^*g_P \\ eP^*g+eP^*N^*g_N &{} eN^*g+eP^*N^*g_P-m \end{array}\right) \!, \end{aligned}$$

(24)

where $g=g(N^*,P^*)$, $g_N=\partial g(N^*,P^*)/\partial N$ and $g_P=\partial g(N^*,P^*)/\partial P$. Since for the coexistence equilibrium $eN^*g=m$, we get

$$\begin{aligned} {{\mathrm{tr}}}A = r-r\tfrac{2N^*}{K} - P^*g-P^*N^*g_N +eP^*N^*g_P \end{aligned}$$

(25)

and

$$\begin{aligned} \det A = r\left( 1-\tfrac{2N^*}{K}\right) eP^*N^*g_P+mP^*g+\tfrac{m^2}{eg}P^*g_N. \end{aligned}$$

(26)

Since the functional response (2) implies $g(N,P) = \lambda (P)/[1+h\lambda (P)N]$, we have

$$\begin{aligned} g_N=-g^2h \quad \text{ and } \quad g_P=\lambda ' \tfrac{g^2}{\lambda ^2}\,. \end{aligned}$$

(27)

Substituting (27) and (6) into (26), we get

$$\begin{aligned} \det A = P^*gm \left( r \left( 1-\tfrac{2C_2}{\varLambda } \right) \tfrac{\varLambda '}{\varLambda ^2} +\tfrac{e-hm}{e} \right) \!. \end{aligned}$$

(28)

Consequently, the condition (10) is equivalent to the condition $\det A = 0$ at a coexistence equilibrium $[N^*,P^*]$ and is a necessary condition for this equilibrium to be a limit point. Generic change in a single model parameter will change sign of the determinant $\det A$. Consequently, the local phase space changes qualitatively.

1.2 A.2 Hopf bifurcation

For a Hopf bifurcation to occur at a parameter value in a two-dimensional system, real parts of the complex eigenvalues of the Jacobian evaluated at the respective system equilibrium have to transversally cross zero (i.e. change sign) when the parameter crosses that value. Denoting by $a$ the bifurcation parameter and by $\mu (a) \pm i \omega (a)$ the respective pair of complex eigenvalues, we require $\mu (a_c)=0$, $\omega (a_c)>0$, and $\mu '(a_c) \ne 0$ at a bifurcation point $a=a_c$ as a necessary conditions for a Hopf bifurcation to occur. we note that

$$\begin{aligned} \mu (a)=\frac{{{\mathrm{tr}}}A(a)}{2} \quad \text {and}\quad \omega (a)=\det A(a)\,. \end{aligned}$$

(29)

where $A(a)$ denotes the Jacobian evaluated at the system equilibrium corresponding to the parameter $a$.

Now we will prove that if a coexistence equilibrium of the model (1) exists then the condition (15) is necessary and sufficient for vanishing of the trace of the Jacobian of the model (1) at that equilibrium. Denoting $g(N,P)=f(N,P)/N$ then at the coexistence equilibrium

$$\begin{aligned} P^*g=r\left( 1-\tfrac{N^*}{K}\right) \!. \end{aligned}$$

(30)

Consequently, at this equilibrium the trace (25) of the Jacobian of the model (1) simplifies to

$$\begin{aligned} {{\mathrm{tr}}}A = -r\tfrac{N^*}{K} +r\left( 1-\tfrac{N^*}{K}\right) N^*g\left( h+e\tfrac{\varLambda '}{\varLambda ^2}\right) \!. \end{aligned}$$

(31)

Since $r>0$ and according to (6) $\tfrac{N^*}{K} = \tfrac{C_2}{\varLambda } > 0$ at the coexistence equilibrium, we have

$$\begin{aligned} {{\mathrm{tr}}}A = -r\tfrac{N^*}{K}\left( 1 +K\left( \tfrac{C_2}{\varLambda }-1\right) g\left( h+e\tfrac{\varLambda '}{\varLambda ^2}\right) \right) , \end{aligned}$$

(32)

where $C_2=\tfrac{m}{K(e-hm)}$. Since the model (1) implies $g=r\lambda /C_1$, a necessary and sufficient condition for vanishing of the trace of the Jacobian of the model (1) at the coexistence equilibrium is

$$\begin{aligned} 1=K\left( 1-\tfrac{m}{K(e-hm)\varLambda }\right) \frac{\varLambda (e-hm)}{e}\left( h+e\tfrac{\varLambda '}{\varLambda ^2}\right) \end{aligned}$$

(33)

or

$$\begin{aligned} 1=\frac{(K(e-hm)\varLambda -m)(h\varLambda ^2+e\varLambda ')}{e\varLambda ^2} \end{aligned}$$

(34)

which is equivalent to the condition (15).

Similar manipulation with the expression (28) and replacement of $\varLambda '$ with the right-hand side of (15) gives the second necessary condition

$$\begin{aligned} \frac{r(K\varLambda (e-hm)-2m)(\varLambda Kh(e-hm)-(e+hm))^2}{K(e-hm)\varLambda ^2 e(\varLambda K(e-hm)-m)}+\frac{e-hm}{e}>0. \end{aligned}$$

(35)

This second condition $\det A > 0$ excludes the neutral saddle case (with two real opposite eigenvalues).

1.3 A.3 Hopf bifurcation in the special case of $\lambda (P)$ satisfying (4)

For the special case of $\lambda (P)$ satisfying (4), the condition (15) simplifies to (17). We give here some properties of the polynomial $\varphi (\varLambda )=A\varLambda ^3+B\varLambda ^2+C\varLambda +D$ on the left-hand side of (17).

For a coexistence equilibrium to exist, we must have $e-hm>0$. Consequently, $A=K^2hb(e-hm)^3>0$ and $D=erm(e+hm)>0$. The cubic polynomial $\varphi (\varLambda )$ then satisfies $\varphi (0)>0$ and $\lim _{\varLambda \rightarrow \infty } \varphi (\varLambda )=\infty$. Let $w_B=\frac{hKer-b(e+hm)}{Ke(e-hm)}$ be the value of $w$ at which $B=0$. Analogously, let $w_C=\frac{r(2hm+e)}{m(e-hm)}$ be the value of $w$ at which $C=0$. Since

$$\begin{aligned} w_C-w_B=\frac{(e+hm)(bm+Ker)}{emK(e-hm)}>0 \end{aligned}$$

(36)

at the coexistence equilibrium, $B$ decreases linearly with $w$ and $C$ increases linearly with $w$, $B$ or $C$ need to be negative for any $w$ at the coexistence equilibrium. (The proof is evident: let us suppose that $B \ge 0$ and $C \ge 0$ concurrently, consequently $w \le w_B$ and $w \ge w_C$ which is the contrary to $w_B<w_C$.)

Let $\varLambda _{min} = -\frac{B}{3A} + \frac{\sqrt{B^2-3AC}}{3A}$ denote the local minimum of the cubic polynomial $\varphi (\varLambda )$. Now we will show that this local minimum indeed exists, i.e.} that the discriminant $d(w)=B^2-3AC$ is positive for any $w$ at the coexistence equilibrium. The function $d(w)$ is a quadratic convex function of $w$ with minimum in $w_{min}=\frac{bhm+2hKer-2be}{2Ke(e-hm)}$. From this,

$$\begin{aligned} d(w_{min})=\frac{3}{4}(bhm^2+4mhKer+4bem+4e^2Kr)hb(e-hm)^4K^2>0. \end{aligned}$$

(37)

Consequently $\varLambda _{min}$ exists and for $B<0$ it has to be positive. If $B\ge 0$, then $C<0$ and consequently $\sqrt{B^2-3AC}>B$ also gives positivity of $\varLambda _{min}$. Simulations show that $\varphi (\varLambda _{min})\le 0$ and hence that the polynomial (17) has a positive root for any $w$, but we don’t have any analytical proof for $\varphi (\varLambda _{min})\le 0$ yet.

1.4 A.4 Bogdanov–Takens bifurcation can occur for small handling times $h$

Let us have the handling time $h$ small enough so that $r < \tfrac{e-hm}{h}$. This implies $A<0$ in (20) and since $C>0$, there exists one positive real root $\varLambda _c$ of the quadratic equation (19). We will show that this $\varLambda _c$ satisfies the condition (8) necessary for the corresponding $P^*$ to be a coexistence equilibrium. Let $0 < \varLambda _c \le C_2=\tfrac{m}{K(e-hm)}$. Consequently,

$$\begin{aligned} 0=A \varLambda _c + B +\tfrac{C}{\varLambda _c} \ge A C_2 + B +\tfrac{C}{C_2} = Ker(e-hm)>0, \end{aligned}$$

(38)

which cannot happen and thus the contrary $\varLambda _c>C_2$ is true. Consequently, the critical Bogdanov–Takens bifurcation point occurs at the coexistence equilibrium $[N^*, P^*]$ that satisfies $P^*=\lambda ^{-1}(\varLambda _c)$ and $N^*=\tfrac{m}{(e-hm)\varLambda _c}$. Generic change of any two of the parameters $\lambda _0, \, K, \, e, \, h, \, m$, and $r$ will change sign of the trace and determinant of the Jacobian at the corresponding coexistence equilibrium and violate the existence of two zero eigenvalues. This change then necessarily causes a saddle separatrix loop split near the critical parameters.