Abstract
The dynamical behavior of a single-degree-of-freedom system that experiences friction-induced vibrations is studied with particular interest on the possibility of the so-called hard effect of a subcritical Hopf bifurcation, using a velocity weakening–strengthening friction law. The bifurcation diagram of the system is numerically evaluated using as bifurcation parameter the velocity of the belt. Analytical results are provided using standard linear stability analysis and nonlinear stability analysis to large perturbations. The former permits to identify the lowest belt velocity \(({v_\mathrm{lw}})\) at which the full sliding solution is stable, the latter allows to estimate a priori the highest belt velocity at which large amplitude stick–slip vibrations exist. Together the two boundaries \([v_\mathrm{lw}, v_\mathrm{up}] \) define the range where two equilibrium solutions coexist, i.e., a stable full sliding solution and a stable stick–slip limit cycle. The model is used to fit recent experimental observations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Subcritical as well as supercritical Hopf bifurcations are often encountered in different engineering applications, e.g., aeroelastic response of airfoils with structural nonlinearities [1, 2], dynamics of ball joints [3], brake squeal [4]. Engineers are generally more concerned about subcritical (hard) bifurcations as a small perturbation around the equilibrium position can lead the system to large amplitude vibration states, which the structure may not tolerate [5]. A number of authors have studied the “Mass-on-moving-Belt” model (“MB model” in the following), Tondl [6], Hetzler et al. [7], Hetzler [8], Won and Chung [9], Nayfeh and Mook [10], Mitropolskii and Van Dao [11], Popp [12], Popp et al. [13], Hinrichs et al. [14], Andreaus and Casini [15], Awrejcewicz and Holicke [16], Awrejcewicz et al. [17], which present various types of analysis of a mass-on-belt system with various kinds of friction laws, and provide in some cases, analytical expressions for the change between stick–slip and pure-slip oscillations. Many authors have attempted to use fast vibrations which in some respects seems to transform classical Coulomb friction into viscous-like damping ([5, 18]). Most often, supercritical bifurcations are found, namely where the system undergoes a smooth transition to a limit cycle (generally involving stick–slip) when the control parameter is varied.
In [19] Hoffmann studied the effect of LuGre type friction law [20] on the stability of the classical MB model. It was shown that rate-dependent effects act against the destabilizing effect of the velocity decaying friction characteristic. The reader is referred to the review by Awrejcewicz and Olejnik [21] where the dynamical behavior of different lumped mechanical systems (see also [22]) with various friction laws has been investigated.
Hetzler et al. [7] (see also [23]) studied the dynamic behavior of the MB model using different friction characteristics, (exponential and polynomial decaying). They assumed a weakly nonlinear behavior and used a first-order averaging method to find approximate solutions. It was shown that the exponential decaying leads to subcritical Hopf bifurcation while, using a cubic polynomial friction law, the dynamical behavior (subcritical/supercritical) depends on the friction law parameters [7].
Also in [8] Hetzler showed that adding a Coulomb frictional damping to the self-excited MB model leads to an “imperfect” Hopf bifurcation scenario where it does not make sense to ask for stability of the steady state but rather one should seek for stability to a certain level of perturbation.
Recently, Papangelo et al. [24] have found localized vibration states in a self-excited chain of mechanical oscillators weakly elastically coupled, which lead to the so-called snaking bifurcations in the bifurcation diagram. A key feature of the system was that, if isolated from the structure, each nonlinear oscillator experiences a subcritical Hopf bifurcation in a certain range of the control parameter (yielding bistabilityFootnote 1). However, Papangelo et al. [24], adopted a polynomial nonlinearity quite remote from a real friction law. Here, perhaps with an eye to the classical Stribeck curve, for the MB model we propose an exponentially weakening and linearly strengthening friction law. We show that this friction model yields to bistability thus vibration localization phenomena are expected as in Papangelo et al. [24] if those oscillators were coupled together.
Hoffmann [25] showed that even with a 2-DOF model, but using the Coulomb friction model with a static \(\left( \mu _\mathrm{st}\right) \) and dynamic \(\left( \mu _\mathrm{d}\right) \) friction coefficient \(\left( \mu _\mathrm{st} >\mu _\mathrm{d}\right) \), bistability can be obtained. For the given set of parameters Hoffmann [25] showed that at \(\mu _\mathrm{d}=0.4\) the usually called “mode coupling instability” takes place and the system becomes (linearly) unstable under small oscillations. What is particularly interesting for us is that if \(\mu _\mathrm{st}/\mu _\mathrm{d}>1\) a stick–slip limit cycle exists even in the range where the steady sliding state is linearly stable.
Saha et al. [26] studied the MB model (see Fig. 1) with the aim to control friction-induced oscillations using a time-delay feedback force. They also introduce two different friction models for the dependence of the frictional force on the sliding speed: one exponentially decaying, the other with polynomial decay. They carry out the analysis using the method of multiple scales in a quite elaborate manner limited to the full sliding case. Interestingly, they show that the bifurcation is supercritical for polynomially decaying and subcritical for exponentially decaying friction law. This confirms that the choice of the shape of the friction law is in a sense a delicate point.
Recently Saha et al. [27] published experimental results of a mass-on-moving-belt model test rig (see Fig. 1). These results are very instructive in general, since they clearly show a bifurcation diagram with a subcritical Hopf bifurcation in a single-degree-of-freedom model. Saha et al. [27] plot the friction law obtained from measurements which surprisingly shows very large hysteretic effects, both during the slip and the “stick” state (even if talking about a proper “stick state” becomes difficult, cfr. their Fig. 6). On the other hand, we notice that they use a sample of mild steel on a belt of silicon rubber, thus viscoelastic effects (maybe thermal effects) are at play.
Velocity weakening–strengthening behavior of the friction force with the relative velocity has been observed for different materials in dry (see [28]) and lubricated condition (see [29,30,31,32,33,34]). It has been shown that the dynamical behavior can be highly influenced by the strengthening branch of the friction curve ([35,36,37]) thus we will consider a friction law with an exponential decay plus a linear strengthening which will also give a good fit of the experimental data from Saha et al. [27]. In Tables 1 and 2 typical values of \(\mu _\mathrm{st},\mu _\mathrm{d}\) and \(\mu _\mathrm{st}/\mu _\mathrm{d}\) are reported for a given couple of materials. The data are taken from reliable sources and show that \(\mu _\mathrm{st}/\mu _\mathrm{d}\) can be easily greater than 2. In the next paragraphs we will show how the dynamical behavior of our model (particularly the bistability region) can be highly affected by \(\mu _\mathrm{st}/\mu _\mathrm{d}\).
Finally, in the last paragraph, we will use our model to qualitatively fit Saha et al. [27] experimental results.
2 The mass-on-moving-belt model
2.1 The model
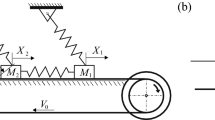
The model is constituted by a linear oscillator of mass m, stiffness k, linear damping coefficient c, (see Fig. 1) which is placed on a frictional belt driven at a constant velocity \(v_\mathrm{d}\). The dynamical equilibrium equation of the mass is
with
where \(x\left( t\right) \), \(\overset{.}{x}\left( t\right) \), \(\overset{..}{x}\left( t\right) \) are, respectively, the displacement, velocity and acceleration of the mass, F is the friction force, N is the normal contact force, \(\mu \left( v_\mathrm{rel}\right) \) is the friction coefficient which is a function of the relative velocity \(v_\mathrm{rel}=\overset{.}{x}-v_\mathrm{d}\) and sign\(\left( \bullet \right) \) is the sign function.
Friction between the mass and the belt is described using a velocity weakening–strengthening friction law of the relative velocity \(v_\mathrm{rel}\)
where \(v_{0}\) is a reference velocity, \(\mu _\mathrm{v}\) is a constant, \(\mu \left( 0\right) =\mu _\mathrm{st}\) and \(\mu \left( v_\mathrm{rel}\rightarrow +\infty \right) =\mu _\mathrm{d}\). Notice that a steeper weakening (strengthening) of the friction law behavior is obtained for small \(v_0\) (large \(\mu _\mathrm{v}\)).
We define the following quantities
and make all displacements dimensionless using \(x_{0}\). Substituting \(\frac{\mathrm{d}}{\mathrm{d}t}=\omega _\mathrm{n}\frac{\mathrm{d}}{\mathrm{d}\tau }\) the dynamical equilibrium Eq. (1) is rewritten as
where a tilde superposed indicates a dimensionless quantity, and derivatives are made with respect to the dimensionless time \(\tau \).
2.2 Linear stability analysis
Assume to linearize the system about the static equilibrium position \(\widetilde{x}_\mathrm{e}=\) \(\mu \left( \widetilde{v}_\mathrm{rel}\right) =\) \(\mu \left( -\widetilde{v}_\mathrm{d}\right) \) and write \(\widetilde{x}\left( \tau \right) =\widetilde{x}_\mathrm{e}+\widetilde{y}\left( \tau \right) \) where \(\widetilde{y}\left( \tau \right) \) is a small perturbation \(\left( \overset{.}{\widetilde{y}}\left( \tau \right) <\widetilde{v}_\mathrm{d}\right) \). Substituting, \(\widetilde{x}\left( \tau \right) \) in (5) one obtains
where \(\mu ^{\prime }\left( \widetilde{v}_\mathrm{d}\right) =\left. \frac{d\mu \left( \widetilde{v}_\mathrm{rel}\right) }{d\widetilde{v}_\mathrm{rel}}\right| _{\widetilde{v}_\mathrm{rel}=\widetilde{v}_\mathrm{d}}\) and \(T=\left( \xi +\frac{\mu ^{\prime }\left( \widetilde{v}_\mathrm{d}\right) }{2}\right) \). Equation (7) is a linear second-order ODE, thus its solution can be written in exponential form \(y\left( t\right) =Ye^{\lambda t}\), with in general \(\lambda \in \mathbb {C}\). Solving the eigenvalues problem we obtain
The equilibrium is
\(T\le -1\) | \(-1<T<0\) | \(T=0\) | \(0<T<1\) | \(T\ge 1\) |
|---|---|---|---|---|
Unstable node | Unstable focus | Center | Stable focus | Stable node |
The condition for linear stability is \(T>0\) which translates into the condition
Putting \(\beta =1\) and using (3) one obtain an equation for \(\widetilde{v}_\mathrm{lw}\) which is the threshold above which steady sliding is stable (\(v_\mathrm{rel}>0\))
The linear strengthening coefficient has to be \(\mu _\mathrm{v}>-2\xi \widetilde{v} _{0},\) otherwise the overall damping would be negative. On the other hand if \(\mu _\mathrm{v}\) exceed \(\left( \mu _\mathrm{st}-\mu _\mathrm{d}\right) -2\xi \widetilde{v}_{0}\) then \(\widetilde{v}_\mathrm{lw}=0\) and steady sliding will be stable for any driving velocity.
3 Stability to large amplitude perturbations
In this section we investigate the stability of the SS solution against non-infinitesimal perturbations. Let us approximate the system response to be harmonic sliding \(x=A\cos \left( \omega t+\phi \right) +x_\mathrm{e}\), \(\overset{\cdot }{x}=-A\omega \sin \left( \omega t+\phi \right) \) about an equilibrium full sliding position, without reaching stick. The energy dissipated by the viscous damper \(E_\mathrm{v}\) is
and depends on the amplitude squared. The total amount of energy dissipated by dry friction is \(E_\mathrm{f}^{T}\)
which is clearly constituted by two contributions: one “mean” contribution due to the sliding at \(v=v_\mathrm{d}\) and the other from the oscillation \(x\left( t\right) \). Notice that the mean sliding term is purely dissipative. For defining a stability criterion to high amplitude perturbations only the contribution \(E_\mathrm{f}\) due to the oscillation around the equilibrium position is considered which is
where we use the condition \(\overset{\cdot }{x}<v_\mathrm{d}\). The frictional dissipated energy is
where \(I_\mathrm{B}\left( 1,\frac{A\omega }{v_{0}}\right) \) is the modified Bessel function of the first kind, in Mathematica BesselI[n,z]. Notice that the weakening part of the friction law feeds energy into the system, while the strengthening part acts like a further viscous damping which dissipate energy. The stability condition to large perturbations is obtained imposing that the overall frictional energy provided by the velocity weakening friction law is less than the energy dissipated by the damper in a cycle, thus
which permits a simple determination of the amplitude threshold. The stability condition (14) in dimensionless form reads
where we estimate \(\frac{\omega }{\omega _{n}}\simeq \sqrt{1-\xi ^{2}}\). Notice that in deriving the energy “provided” by the friction law we made the hypothesis \(\overset{\cdot }{x}-v_\mathrm{d}<0\), thus the criterion (14) holds up to the critical point where \(A\omega =v_\mathrm{d}\), then the stick phase will come into play. This allows to estimate an upper bound of validity for the criterion (14) “\(v_\mathrm{up}\)” that is obtained imposing in (14) \(\frac{-E_\mathrm{f}}{E_\mathrm{v}}=1\) and \(A\omega =v_\mathrm{d}\).
3.1 A numerical example
In this paragraph a numerical example is presented where the equation of motion of the mass (5) is solved using the built-in MATLAB time integration solver ode23t, which integrate the system equations using the trapezoidal rule with a “free” interpolant, has no numerical damping and is recommended for moderately stiff problem. The friction force is implemented using the switch model which defines a narrow band of vanishing relative velocity where the stick equations are solved and makes the problem not stiff (the reader is referred to [39] for more details). We assumed that the mass sticks to the belt if \(\left| \widetilde{v}_\mathrm{rel}\right| <10^{-4}\).
For a numerical example assume \(\xi =0.05\) and the following parameter for the exponential decaying friction law (3).
Weakening–strengthening friction law with \(\mu _\mathrm{d}=0.5\), \(\frac{\mu _\mathrm{st}}{\mu _\mathrm{d}}=2\), \(\widetilde{v}_{0}=0.5, \xi =0.05\) and \(\mu _\mathrm{v}=\left[ -0.03, 0, 0.02, 0.05\right] \). The red square (circle) indicate \(\widetilde{v}_\mathrm{lw}\) \(\left( \widetilde{v}_\mathrm{up}\right) \). (Color figure online)
Imposing \(\beta =1\) in (9) and using (14), with \(\frac{-E_\mathrm{f}}{E_\mathrm{v}}=1\) and \(\widetilde{A}=\widetilde{v}_\mathrm{d}\), the lower (upper) boundary is computed \(\widetilde{v}_\mathrm{lw}\) \(\left( \widetilde{v} _\mathrm{up}\right) \). In Fig. 2 the friction law is reported: the bistable region is expected for values of the driving velocity \(\widetilde{v}_\mathrm{d}\) in between the two boundaries \(\widetilde{v}_\mathrm{lw}\) and \(\widetilde{v}_\mathrm{up}\) which are labeled, respectively, with a square and a circle. Notice that exponentially decaying friction laws with \(\mu _\mathrm{v}=0\) are commonly used in the literature for example for break squeal analysis [40]. On the other hand Bar-Sinai et al. [28] showed experimental observations of velocity weakening–strengthening friction in various materials, thus we will focus on the case \(\mu _\mathrm{v}\ge 0\).
Bifurcation diagram for the MB model, limit cycle amplitude versus the driving velocity (dimensionless form). The equilibrium solutions are obtained increasing (blue circles) and decreasing (red triangles) the driving velocity \(\widetilde{v}_\mathrm{d}\). The gray squares represent unstable limit cycle obtained solving the ODE backwards in time. The results are coincident with the full criterion line (solid blue line) as it exactly represents the situation \(-E_\mathrm{f}/E_\mathrm{v}=1\) (see 14). (Color figure online)
(a–b–c) displacement \(\widetilde{x}(\tau )\) as a function of time \(\tau \) in dimensionless form for driving velocity \(\widetilde{v}_\mathrm{d}=1.5\), and friction law parameters as in Fig. 3 but with \(\mu _\mathrm{v}=0\). Respectively, a stick–slip LC, b ULC (backward time integration), c SS state. On the right panel the phase plot is shown. (Color figure online)
In Fig. 3 the bifurcation diagram for the MB model is shown where the dimensionless amplitude of the vibration is plotted against the driving velocity in dimensionless form with \(\mu _\mathrm{v}=0\). Notice that Steady Sliding solutions (“SS”) have \(\widetilde{A}=0\). The equilibrium solutions are obtained increasing (blue circles) and decreasing (red triangles) the driving velocity \(\widetilde{v}_\mathrm{d}\). A bistable zone is found for \(\widetilde{v} _\mathrm{lw}<\widetilde{v}_\mathrm{d}<\widetilde{v}_\mathrm{up}\) as expected, where Limit Cycles (“LC”) and SS solutions coexists. In between the two stable solutions the gray squares represent Unstable Limit Cycles (“ULC”) that have been obtained solving the ODE backwards in time. Notice that those solutions match almost perfectly the equation \(\frac{-E_\mathrm{f}}{E_\mathrm{v}}=1\), that is the stability criterion (14, blue solid line) when one imposes a perfect balance between the energy supplied and dissipated in the system. The solution is unstable as a small perturbation leads either on the stick–slip LC or on the SS solution.
Figure 4 reports on the left side (a–b–c) time integration results for \(\widetilde{v}_\mathrm{d}=1.5\), while on the right the solutions are reported together in the phase plane. Respectively, Fig. 4a represents the case of stick–slip LC, Fig. 4b refers to the ULC (full sliding solution) and Fig. 4c shows a case where vibrations are damped down up to the steady sliding state. The unstable limit cycle divides the phase plane into two basins of attraction: every solution initialized outside the ULC ends up in the stick–slip LC, otherwise SS is obtained. Below we summarize the possible dynamical behavior of the mass as a function of the driving velocity:
Figure 5 shows the curves of \(\widetilde{v}_\mathrm{lw}\) (Fig. 5a) and \(\left( \widetilde{v}_\mathrm{up}-\widetilde{v}_\mathrm{lw}\right) \) (Fig. 5b) plotted against \(\widetilde{v}_{0}\) for different \(\mu _\mathrm{s}/\mu _\mathrm{d}=\left[ 1.4-5\right] \) and for \(\xi =0.05\), \(\mu _\mathrm{d}=0.5\) and \(\mu _\mathrm{v}=0\). The lower boundary \(\widetilde{v}_\mathrm{lw}\) vanishes for both very small and high \(\widetilde{v}_{0}\) [panel (a)]. In the limit, the first case would be the classical Coulomb friction model with two friction coefficients \(\mu _\mathrm{s}>\mu _\mathrm{d}\), while, due to very slow decreasing of \(\mu _\mathrm{s}(v_\mathrm{rel})\), the second case would be in the limit of infinite \(\widetilde{v}_{0}\) the Coulomb friction model with just one friction coefficient. In both cases \(\widetilde{v}_\mathrm{lw}=0\) and even a small viscous damping will make steady sliding always stable, at any driving velocity provided \(\xi >0\). In between those two limit cases \(\widetilde{v}_\mathrm{lw}\) as well as \(\left( \widetilde{v}_\mathrm{up}-\widetilde{v}_\mathrm{lw}\right) \) reaches a maximum value. Figure 5b shows that the width of the bistability region vanishes only for high \(\widetilde{v}_{0}\) (thus in the limit of Coulomb friction with one friction coefficient), while even at very small \(\widetilde{v}_{0}\) \(\left( \text {e.g., }\widetilde{v}_{0}\simeq 10^{-3}\right) \), a well-defined bistable zone exists, even if of small size (Fig. 6). This agrees with [41] which found a subcritical bifurcation in a MB model even with the classical Coulomb friction model with a sharp jump from \(\mu _\mathrm{s}\) to \(\mu _\mathrm{d}\). It is shown that higher the ratio \(\mu _\mathrm{s}/\mu _\mathrm{d}\) the stronger is the dependence of \(\left( \widetilde{v}_\mathrm{up}-\widetilde{v}_\mathrm{lw}\right) \) on \(\widetilde{v}_{0}\).
Friction force \(F\left( v_\mathrm{rel}\right) /N\) versus the relative velocity as reported in Saha et al. [27] (red circles). Black stars indicate the points considered in the fitting with the exponential decaying friction law with (blue dashed line) and without (black solid line) the strengthening term. (Color figure online)
Bifurcation diagram, amplitude versus driving velocity. Experimental results from Saha et al. [27] red squares, numerical results obtained by sequential continuation from the right to the left and viceversa (blue circles). The panels (a, b) report, respectively, the results obtained with the VW and VWS friction law. (Color figure online)
4 Comparison with experimental results
Recently Saha et al. [27] performed an experimental investigation on a MB model and found experimentally that in their set up the bifurcation is a subcritical Hopf bifurcation where a bistable region exists. The test rig is constituted of a spring–mass system where a rectangular block made of mild steel slides on a silicone rubber belt. In [27] all the necessary parameters that characterize the experimental test rig are provided
which leads to \(\xi =0.0113\). The experimentally measured friction force obtained by Saha et al. [27] is reported in Fig. 7 with red circles. Notice that there is not any “stick phase” while a hysteresis loop appears to dominate the zone of small relative velocity. The hysteresis phenomena also exist in the slip phase but are less important. Clearly, a weakening–strengthening friction law as the one considered in this work can not be able to reproduce such a behavior, particularly because Saha et al. [27] reported the overall friction force, without any information about the normal load, which makes it impossible to retrieve the actual friction coefficient at the interface. In fact Saha et al. [27] admit that the measured oscillations were modulated by external unwanted factors, such as: joint in the belt, nonuniform surface properties of the belt, flexibility of the belt and vibration of the supporting structure. Being aware of those limitations, we try to use our model and compare with those experiments, which are quite rare in the literature, with the aim to reproduce at least a the same dynamical behavior experimentally observed.
For estimating the parameters of the friction model (3) we neglect the hysteretic loop of the friction law close to \(v_\mathrm{rel}\sim 0\), instead we consider only the points indicated in Fig. 7 with black stars. Here the results of two friction curves are considered, respectively, with (Fig. 7, blue dashed curve, “VWS” friction law in the following) and without (Fig. 7, black solid curve, “VW” friction law in the following) linear strengthening. As there were no information about the normal load magnitude, we arbitrarily assume \(N=30\) N which led to a reasonable set of parameters \(\left( \text {eg. }\mu _\mathrm{st},\mu _\mathrm{d}\right) \) for both VW and VWS friction laws:
In Fig. 8a–b the bifurcation diagram reported in Saha et al. [27] is shown in dimensionless notation (red squares), where the vibration amplitude is reported against the driving velocity. Notice that there is no SS state measured in the experiment, but more precisely a limit cycle of small amplitude. The authors explain in [27] this is due to modulation of the normal load (which in the MB model is assumed constant). Figure 8a reports the numerical results obtained by sequential continuation from the right to the left and viceversa using the exponential decaying friction law without strengthening. Although the upper and lower limit do not match exactly the vibration amplitude of the stick–slip LC is quantitatively predict by the MB model. Notice that any other choice of the normal load N would just rescale the bifurcation diagram without affecting its shape. Figure 8b reports the numerical results obtained when the effect of linear strengthening is taken into account in the friction law. Even though the friction law seems to fit better the experimental measured friction law (Fig. 7, dashed line) the results in term of bifurcation diagram are poorer. Those discrepancies could arise from the modulation of the normal load, but unfortunately we do not have quantitative information about it, thus we can not make further improvements in this direction. The results surely show that the in such a system the dynamical behavior is very sensitive to the exact shape of the friction law.
5 Conclusions
The dynamical behavior of a single-degree-of-freedom system (the classical mass-on-moving-belt model) has been studied, focusing on the possibility of the so-called hard effect of a subcritical Hopf bifurcation, using a velocity weakening–strengthening friction law \(\mu \left( v_\mathrm{rel}\right) \). It has been shown that in the range of driving velocity \(\widetilde{v} _\mathrm{lw}<\widetilde{v}_\mathrm{d}<\widetilde{v}_\mathrm{up}\) two stable solutions coexist, one in steady sliding, the other as a stick–slip limit cycle. Linear stability analysis provides \(\widetilde{v}_\mathrm{lw}\) while a stability analysis to large perturbations provides the upper boundary \(\widetilde{v}_\mathrm{up}\). For a given \(\mu _\mathrm{s}/\mu _\mathrm{d}\) very sharp decaying of the friction coefficient to the dynamic value does not eliminate the bistable region, while if the decaying is slow enough the bistability region shrinks and only the steady sliding state survives. Introducing the strengthening branch has little effect on \(\widetilde{v}_\mathrm{lw}\), but strongly decreases \(\widetilde{v}_\mathrm{up}\), reducing the bistability region. In the last paragraph we used our model to fit the experimental results provided by Saha et al. [27]. It was shown that the vibration amplitude at a given velocity of the belt seems to correlate well with experiments, nevertheless the width of the bistability region is very sensitive to the shape of the friction law.
Notes
“In a dynamical system, bistability means the system has two stable equilibrium states.” From: Wikipedia (https://en.wikipedia.org/wiki/Bistability).
References
Pereira, D.A., Vasconcellos, R.M., Hajj, M.R., Marques, F.D.: Insights on aeroelastic bifurcation phenomena in airfoils with structural nonlinearities. Math. Eng. Sci. Aerosp. (MESA), 6(3), 399–424 (2015)
Liu, J.K., Zhao, L.C.: Bifurcation analysis of airfoils in incompressible flow. J. Sound Vib. 154(1), 117–124 (1992)
Weiss, C., Morlock, M.M., Hoffmann, N.: Friction induced dynamics of ball joints: instability and post bifurcation behavior. Eur. J. Mech. A/Solids 45, 161–173 (2014)
Gräbner, N., Tiedemann, M., Von Wagner, U., Hoffmann, N.: Nonlinearities in friction brake NVH-experimental and numerical studies (No. 2014-01-2511). SAE Technical Paper
Thomsen, J.J.: Vibrations and Stability: Advanced Theory, Analysis, and Tools (2nd edn., revised). Springer, Berlin (2003). ISBN 3-540-40140-7
Tondl, A.: Quenching of Self-excited Vibrations. Elsevier Science Pub Co., New York (1991)
Hetzler, H., Schwarzer, D., Seemann, W.: Steady-state stability and bifurcations of friction oscillators due to velocity-dependent friction characteristics. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 221(3), 401–412 (2007)
Hetzler, H.: On the effect of nonsmooth Coulomb friction on Hopf bifurcations in a 1-DoF oscillator with self-excitation due to negative damping. Nonlinear Dyn. 69(1), 601–614 (2012)
Won, H.I., Chung, J.: Stick–slip vibration of an oscillator with damping. Nonlinear Dyn. 86, 257 (2016). doi:10.1007/s11071-016-2887-x
Nayfeh, H., Mook, D.T.: Nonlinear Oscillations. Wiley, New York (1979)
Mitropolskii, Y.A., Van Dao, N.: Applied Asymptotic Methods in Nonlinear Oscillations. Kluwer, Dorderecht (1997)
Popp, K.: Some model problems showing stick–slip motion and chaos. Frict. Induc. Vib. Chatter Squeal Chaos ASME DE 49, 1–12 (1992)
Popp, K., Hinrichs, N., Oestreich, M.: Analysis of a self-excited friction oscillator with external excitation. In: Guran, A., Pfeiffer, F., Popp, K. (eds.) Dynamics with Friction. Modeling, Analysis and Experiment 2 Part I. World Scientific, Singapore (1996)
Hinrichs, N., Oestreich, M., Popp, K.: On the modelling of friction oscillators. J. Sound Vib. 216, 435–459 (1998)
Andreaus, U., Casini, P.: Dynamics of friction oscillators excited by a moving base and/or driving force. J. Sound Vib. 245(4), 685–699 (2001)
Awrejcewicz, J., Holicke, M.M.: Smooth and Nonsmooth High Dimensional Chaos and the Melnikov-type Methods, vol. 60. World Scientific, Singapore (2007)
Awrejcewicz, J., Andrianov, I.V., Manevitch, L.I.: Asymptotic Approaches in Nonlinear Dynamics: New Trends and Applications, vol. 69. Springer, Berlin (2012)
Thomsen, J.J.: Using fast vibrations to quench friction-induced oscillations. J. Sound Vib. 228(5), 1079–1102 (1999)
Hoffmann, N.P.: Linear stability of steady sliding in point contacts with velocity dependent and LuGre type friction. J. Sound Vib. 301, 1023 (2007)
De Wit, C.C., Olsson, H., Astrom, K.J., Lischinsky, P.: A new model for control of systems with friction. IEEE Trans. Autom. Control 40(3), 419–425 (1995)
Awrejcewicz, J., Olejnik, P.: Analysis of dynamic systems with various friction laws. Appl. Mech. Rev. 58(6), 389–411 (2005)
Brommundt, E., Krmer, E.: Instability and self-excitation caused by a gear coupling in a simple rotor system. Forschung im Ingenieurwesen 70(1), 25–37 (2005)
Hetzler, H., Schwarzer, D., Seemann, W.: Analytical investigation of steady-state stability and Hopf-bifurcations occurring in sliding friction oscillators with application to low-frequency disc brake noise. Commun. Nonlinear Sci. Numer. Simul. 12(1), 83–99 (2007)
Papangelo, A., Grolet, A., Salles, L., Hoffmann, N., Ciavarella, M.: Snaking bifurcations in a self-excited oscillator chain with cyclic symmetry. Commun. Nonlinear Sci. Numer. Simul. 44, 108–119 (2017)
Hoffmann, N.: Transient growth and stick–slip in sliding friction. J. Appl. Mech. 73(4), 642–647 (2006)
Saha, A., Bhattacharya, B., Wahi, P.: A comparative study on the control of friction-driven oscillations by time-delayed feedback. Nonlinear Dyn. 60(1–2), 15–37 (2010)
Saha, A., Wahi, P., Bhattacharya, B.: Characterization of friction force and nature of bifurcation from experiments on a single-degree-of-freedom system with friction-induced vibrations. Tribol. Int. 98, 220–228 (2016)
Bar-Sinai, Y., Spatschek, R., Brener, E.A., Bouchbinder, E.: On the velocity-strengthening behavior of dry friction. J. Geophys. Res. Solid Earth 119(3), 1738–1748 (2014)
Jacobson, B.: The Stribeck memorial lecture. Tribol. Int. 36(11), 781–789 (2003)
Stribeck, R.: Kugellager für beliebige Belastungen. Zeitschrift des Vereines deutscher Ingenieure (part I) 45(3), 73–79 (1901)
Stribeck, R.: Kugellager für beliebige Belastungen. Zeitschrift des Vereines deutscher Ingenieure (part II) 45(4), 118–125 (1901)
Stribeck, R.: Die wesentlischen Eigenschaften der Gleit- und Rollenlager. Zeitschrift des Vereines deutscher Ingenieure (part I) 46(37), 1341–1348 (1902)
Stribeck, R.: Die wesentlischen Eigenschaften der Gleit- und Rollenlager. Zeitschrift des Vereines deutscher Ingenieure (part II) 46(38), 1432–1438 (1902)
Stribeck, R.: Die wesentlischen Eigenschaften der Gleit- und Rollenlager. Zeitschrift des Vereines deutscher Ingenieure (part III) 46(39), 1463–1470 (1902)
Papangelo, A., Ciavarella, M.: Some observations on Bar Sinai, Brener and Bouchbinder (BSBB) model for friction. Meccanica 52, 1–8 (2016)
Bouchbinder, E., Brener, E.A., Barel, I., Urbakh, M.: Slow cracklike dynamics at the onset of frictional sliding. Phys. Rev. Lett. 107(23), 235501 (2011)
Bar Sinai, Y., Brener, E.A., Bouchbinder, E.: Slow rupture of frictional interfaces. Geophys. Res. Lett. 39(3), L03308 (2012). doi:10.1029/2011GL050554
Rabinowicz, E.: The nature of the static and kinetic coefficients of friction. J. Appl. Phys. 22(11), 1373–1379 (1951)
Leine, R.I., Van Campen, D.H., De Kraker, A., Van den Steen, L.: Stick–slip vibrations induced by alternate friction models. Nonlinear Dyn. 16(1), 41–54 (1998)
Oberst, S., Zhang, Z., Lai, J.: Model updating of brake components and subassemblies for improved numerical modelling in brake squeal. In: Presented at the International Congress on Sound and Vibration (ICSV22). Florence, Italy (2015)
Leine, R.I., Van Campen, D.H.: Discontinuous bifurcations of periodic solutions. Math. Comput. Model. 36(3), 259–273 (2002)
Acknowledgements
A. P. and N. H. are thankful to the DFG (German Research Foundation) for funding the project HO 3852/11-1.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Papangelo, A., Ciavarella, M. & Hoffmann, N. Subcritical bifurcation in a self-excited single-degree-of-freedom system with velocity weakening–strengthening friction law: analytical results and comparison with experiments. Nonlinear Dyn 90, 2037–2046 (2017). https://doi.org/10.1007/s11071-017-3779-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-017-3779-4