1 Introduction

Mechanical systems usually consist of several substructures assembled by joints in which nonlinear contact interactions inevitably occur [1]. The dissipative dry frictional interactions often provide the dominant contribution to the overall energy dissipation in mechanical systems [2]. Besides vibration mitigation, friction damping has acquired high technical relevance because of its stabilizing effect on otherwise unstable self-excited vibrations. These are the consequence of destabilizing negative damping contributions which can be encountered in various applications: flutter vibrations of airfoils [3], chatter in machining processes [4, 5] like in rolling mills [6], in control tasks [7,8,9], in robotics [10], and in brake squeal [11]. The driving example for the current work is cascade flutter vibrations of turbomachinery blades [12, 13]. Additional frictional interfaces are here often deliberately introduced to mitigate vibrations of the blades [2]. In this application, the self-excitation mechanism is caused by the unstable aerodynamical interference of blades within a blade row. In a recent study, we numerically analyzed the stability of self-excited friction-damped vibration states in the presence of internal resonance conditions based on a minimal model [14]. The main contribution of the present work is the analytical derivation of existence conditions of quasi-periodic oscillations for closely spaced modes. In the following paragraphs, we will briefly recap the most important results related to this work, before discussing the purpose and outline of this article.

1.1 Preliminaries

Sinha and Griffin [15] were the first to show that friction damping can be used to bound otherwise diverging self-excited vibrations caused by negative (viscous) damping. In case of negative damping of a single mode and well-separated eigenfrequencies, the amplitude-dependent friction damping leads to periodic limit cycle oscillations (LCO). If the negative damping exceeds the point of maximum friction damping, a fold bifurcation occurs such that the LCO becomes unstable giving rise to divergent behavior. The dynamics may become even more complicated when several modes are subjected to negative damping. Based on a simplified model of an aerodynamically unstable rotor stage, the stability limit of LCOs was determined by generalized energy relations based on an averaging technique [16]. However, the bifurcation type associated with the stability limit was not addressed in these works. It is well known that friction nonlinearity can trigger modal interactions in the presence of internal resonance conditions (e.g., 1:1 or 1:3 resonances). In [14], we studied numerically a friction-damped two-degree-of-freedom (2DOF) system subjected to negative viscous damping. The configuration of the investigated 2DOF system is motivated by the analysis of rotationally symmetric structures, e.g., bladed disks, where so-called traveling wave modes occur. The 2DOF system’s modes are representatives of a forward and backward traveling mode. Neglecting frictional effects, the system remains symmetric, with both modes closely spaced based on the assumption of light aeroelastic coupling. Under the influence of friction damping on one of the oscillators, symmetric behavior will only occur in the case of sticking contact. In the case of sliding friction, energy dissipation affects both modes, but also leads to asymmetrical behavior. This asymmetry causes strong modal coupling, so that a strong energy exchange between both modes is expected close to internal resonance conditions.

Fig. 1
figure 1

Self-excited friction-damped system with closely spaced modes: Bifurcation diagram of vibration amplitude versus viscous damping. LCO curve (‘black,’ ‘dashed’), steady-state solutions (‘black,’ ‘solid’), and areas of bounded behavior (‘blue’ and ‘gray’). Arrows indicate increasing and decreasing vibration levels. (Color figure online)

Full size image

In Fig. 1, the characteristic behavior for the case of closely spaced modes (near 1:1 internal resonance) is illustrated in a schematic bifurcation diagram with the viscous damping being considered as control parameter. The trivial case of positive damping leads to exponentially decaying oscillations that approach the static equilibrium position (A). Going from positive to negative damping induces a Hopf bifurcation, causing dynamic instability of the static equilibrium. The vibrations grow until dissipative sliding friction compensates the self-excitation and an LCO is formed from the dynamical balance (B). A secondary Hopf bifurcation causes the loss of periodicity of the LCO beyond a critical level of negative damping, as indicated by the splitting of maximum and minimum steady-state vibration amplitudes (C). Then, the oscillations take the form of limit torus oscillations (LTOs) at first, much in line with the well-known case of coupled van-der-Pol oscillators. More severe negative damping may introduce chaos. Finally, the non-periodic attractor collapses yielding divergent behavior well before the fold bifurcation of the LCO (D) is reached. These findings imply that the common practice to compute only the LCOs (using, e.g., Harmonic Balance and numerical continuation), without properly analyzing their stability, may lead to incomplete modeling of the nonlinear dynamics, and, hence, to potentially dangerous design decisions in practical applications.

1.2 Purpose of the present work

In this work, we seek to better understand the emergence of the non-periodic oscillations encountered for the 2DOF system discussed in [14] for the case of closely spaced modes. In particular, we would like to establish conditions for the secondary Hopf bifurcation and analyze how the quasi-periodic oscillations further bifurcate into chaos. In the analytical development, the key challenge is the treatment of the Jenkins elementFootnote 1. To the authors’ knowledge, this is the first work that shows how a consistent perturbation approach can be formally applied to analyze this nonlinearity in order to derive closed-form analytical expressions for the emergence of LCOs and their bifurcations.

1.3 Outline of the article

The article is structured as follows: In Sect. 2 we describe the investigated 2DOF system. In Sect. 3, we use averaging to derive an approximation for the slow flow dynamics in the neighborhood of the LCO. In Sect. 3.3, we analyze the transition from limit torus oscillations to chaotic oscillations. In Sect. 4, we focus on the secondary Hopf bifurcation and use perturbation calculus to establish the conditions leading to limit torus oscillations. We end this work with some concluding remarks, summarizing the main contributions and providing some related open problems that can be further investigated.

Fig. 2
figure 2

a 2DOF model considering in-phase \(\xi _1\) and out-of-phase damping \(\xi _2\), b Jenkins element and c corresponding hysteresis cycle for prescribed periodic motion of the coordinate \(x_1\)

Full size image

2 Model description

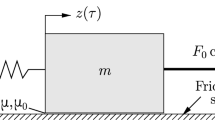
We investigate a 2DOF oscillator (see Fig. 2a), consisting of two unity masses coupled via linear springs in parallel to viscous damper elements. The nonlinear dry friction force acting on the first oscillator is modeled by a Jenkins element, see Fig. 2b. The equations of motion are then given through

$$\begin{aligned}&\ddot{x}_1+ \frac{1}{2}(\xi _1+\xi _2) {\dot{x}}_1 + \frac{1}{2}(\xi _1-\xi _2) {\dot{x}}_2 +(1-\gamma ) {x}_1 \nonumber \\&\quad + \kappa ({x}_1-{x}_2) + \gamma f_\mathrm {t}[ {x}_1] = 0,\, \end{aligned}$$
(1)
$$\begin{aligned}&\ddot{x}_2+ \frac{1}{2}(\xi _1+\xi _2) {\dot{x}}_2 + \frac{1}{2}(\xi _1-\xi _2){\dot{x}}_1 \nonumber \\&\quad + {x}_2 + \kappa ({x}_2-{x}_1) = 0 , \end{aligned}$$
(2)

where \(x_1\) and \(x_2\) indicate the generalized coordinates and \({\dot{\square }}\) indicates derivative with respect to time t. The nonlinear friction force \(f_{\mathrm {t}}[x_1]\) is defined by the hysteretic differential law

$$\begin{aligned} \mathrm {d}f_\mathrm {t} = {\left\{ \begin{array}{ll} \mathrm {d}x_1 &{} \Vert f_\mathrm {t} + \mathrm {d}x_1 \Vert < 1 \\ 0 &{} \text {otherwise} \end{array}\right. }, \end{aligned}$$
(3)

where the dependency on time history is indicated by the operator \([\,\cdot \,]\). An advantage of this formulation is the straightforward implementability within numerical time-step integration methods by substituting the differential by a finite time-step. Figure 2c illustrates the corresponding hysteresis cycle under prescribed periodic motion of the coordinate \(x_1\), including the initial loading curve. The hysteresis cycle divides into sticking and sliding phase of the friction element, transitioning as soon as the spring force exceeds the friction limit force of 1. In the sliding phase, the magnitude of the nonlinear force remains constant.

A similar dynamical system was obtained by non-dimensionalization in [14]. The non-dimensionalization takes into account time normalization with respect to the natural frequency of the in-phase mode in sticking condition, the normalization of the nonlinear force by the friction limit force, and the normalization of the generalized coordinates by the fraction of nonlinear spring stiffness and friction limit force. This reduces the set of parameters to the coupling spring stiffness \(\kappa \), the modal damping \(\xi _{1,2}\), and the friction intensity \(\gamma \) acting on the first oscillator. Note that the Jenkins element itself remains independent of \(\gamma \), but it appears as a factor in front of the nonlinear force, preserving the symmetry of the system in sticking condition. Thus, the linear modes of vibration correspond to symmetric in-phase and out-of-phase motions. The corresponding in-phase natural frequency results to \(\omega ^\mathrm {st} = 1\) (due to normalization). The natural frequency of the out-of-phase mode is given by \(\sqrt{1+2\kappa }\) [14]. Thus, for \(\kappa \ll 1\) (i.e., for weak coupling between oscillators) the linear natural frequencies are closely spaced. The (weak) damper coefficients are designed such that \(\xi _{1}\) is associated with the symmetric in-phase and \(\xi _{2}\) with the symmetric out-of-phase motion. Throughout this paper, we set \(\xi _1<0\) and \(\xi _2>0\). For sufficiently large vibrations, the force in the friction element saturates, which leads to nonlinear stick-slip behavior and generally asymmetrical behavior.

3 Analysis of the slow dynamics in the neighborhood of the limit cycle

In the following, we gain deeper understanding of the dynamics by analyzing the slow dynamics of the system near the LCO. To this end, we use the complexification-averaging (CX-A) method [17]. Of particular interest is the bifurcation point of the first LCO stability loss, i.e., the secondary Hopf bifurcation point, giving rise to LTOs. Furthermore, the transition process from the LTOs to chaos will be analyzed.

3.1 Extraction of the slow dynamics using CX-A

In the following, we briefly explain the main ideas behind the CX-A technique, following [17], while generally there exist several books discussing averaging techniques. CX-A is based on a coordinate transform from a fixed to a rotating coordinate system, which can be expressed by a new complex-valued variable \(\Psi \), yielding

$$\begin{aligned} x_j&= \dfrac{\Psi _j + {{\bar{\Psi }}}_j}{2}, \; \dot{x}_j= \mathrm{i}\omega \dfrac{\Psi _j - {{\bar{\Psi }}}_j}{2}, \; \nonumber \\ \ddot{x}_j&= \mathrm{i}\omega \left( {{\dot{\Psi }}}_j - \mathrm{i}\omega \dfrac{\Psi _j - {{\bar{\Psi }}}_j}{2} \right) , \end{aligned}$$
(4)

with the oscillation frequency \(\omega \), the complex conjugate \({\bar{\square }}\) and \(\mathrm{i}=\sqrt{-1}\). This transformation reduces the order of the differential equation system from 2nd to 1st, while retaining the number of equations. At this point, dynamics dominated by a single harmonic are assumed, allowing to introduce the complex-valued ansatz

$$\begin{aligned} \Psi _j(t)\approx {a_j(t) \mathrm {e}^{{\mathrm {i}}\theta _j(t)} \mathrm {e}^{{\mathrm {i}}\int \omega \mathrm {d}t}}.\, \end{aligned}$$
(5)

Note, that the integral over frequency \(\int \omega \mathrm {d}t\) degenerates to \(\omega t\) only in case of time invariance. Based on this, the dynamics with respect to \(x_j\) is assumed to be decomposable into a fast oscillation with the instantaneous (fast) oscillation frequency \(\omega \) and a slow modulation of amplitude \(a_j\) and phase \(\theta _j\). Under the premise of well-separable time scales, averaging over the fast dynamics and splitting into real and imaginary parts, leads to a set of explicit first-order differential equations with respect to the slow dynamics. Applied to Eqs. (1) and (2), the following set of equations is obtained

$$\begin{aligned} \dot{a}_1&= -\frac{1}{2\,\omega } \left( \kappa \,a_{2}\,\sin \left( \theta _1 - \theta _2\right) \right. \nonumber \\&\quad +\frac{1}{2}(\xi _1-\xi _2)\omega \,\,a_{2}\,\cos \left( \theta _1 - \theta _2\right) \nonumber \\&\quad \left. +\frac{1}{2}(\xi _1+\xi _2)\,\omega \,a_{1}+\gamma \,\omega \,d_\mathrm {eq}(a_1)\,a_{1}\right) , \end{aligned}$$
(6)
$$\begin{aligned} {{\dot{\theta }}}_1&= -\frac{1}{2\,a_{1}\,\omega } \left( \kappa \,a_{2}\,\cos \left( \theta _1 - \theta _2\right) \right. \nonumber \\&\quad -\frac{1}{2}(\xi _1-\xi _2)\,\omega \,a_{2}\,\sin \left( \theta _1 - \theta _2\right) \nonumber \\&\quad \left. -\left( -{\omega }^2+\kappa -\gamma +\gamma \,k_\mathrm {eq}(a_1) +1\right) \,a_{1} \right) , \end{aligned}$$
(7)
$$\begin{aligned} \dot{a}_2&= -\frac{1}{2\,\omega } \left( \frac{1}{2}(\xi _1+\xi _2)\,\omega \,a_{2}-\kappa \,a_{1}\,\sin \left( \theta _1 - \theta _2\right) \right. \nonumber \\&\quad \left. +\frac{1}{2}(\xi _1-\xi _2)\,\omega \,a_{1}\,\cos \left( \theta _1 - \theta _2\right) \right) , \end{aligned}$$
(8)
$$\begin{aligned} {{\dot{\theta }}}_2&= -\frac{1}{2\,a_{2}\,\omega } \left( {\omega }^2\,a_{2}\right. \nonumber \\&\quad +\frac{1}{2}(\xi _1-\xi _2)\,\omega \,a_{1}\,\sin \left( \theta _1 - \theta _2\right) \nonumber \\&\quad \left. -a_{2}-\kappa \,a_{2}+\kappa \,a_{1}\,\cos \left( \theta _1 - \theta _2\right) \right) , \end{aligned}$$
(9)

in terms of the unknowns \(a_1,a_2,\theta _1,\theta _2\) and their associated time derivatives. Without loss of generality, the amplitudes are defined as positive \(a_1>0\), \(a_2>0\). The terms \(k_{\mathrm {eq}}(a_1)\) and \(d_{\mathrm {eq}}(a_1)\) are the equivalent stiffness and damping of the Jenkins element as defined later.

Without loss of generality, one can reduce the problem to an autonomous set of 3 equations governing the slow amplitude modulations \(a_1\) and \(a_2\) and the slow phase difference (lag) which is defined as \(\Delta \theta = \theta _1 - \theta _2\). This leads to what we will refer to as slow flow equations,

$$\begin{aligned} \dot{a}_1&= -\frac{1}{2\,\omega } \left( \kappa \,a_{2}\,\sin \left( \Delta \theta \right) \right. \nonumber \\&\quad +\frac{1}{2}(\xi _1-\xi _2)\omega \,\,a_{2}\,\cos \left( \Delta \theta \right) \nonumber \\&\quad \left. +\frac{1}{2}(\xi _1+\xi _2)\,\omega \,a_{1}+\gamma \,\omega \,d_\mathrm {eq}(a_1)\,a_{1}\right) , \end{aligned}$$
(10)
$$\begin{aligned} \dot{a}_2&= -\frac{1}{2\,\omega } \left( \frac{1}{2}(\xi _1+\xi _2)\,\omega \,a_{2}-\kappa \,a_{1}\,\sin \left( \Delta \theta \right) \right. \nonumber \\&\quad \left. +\frac{1}{2}(\xi _1-\xi _2)\,\omega \,a_{1}\,\cos \left( \Delta \theta \right) \right) , \end{aligned}$$
(11)
$$\begin{aligned} \Delta {\dot{\theta }}&= \frac{1}{2\omega } \left( -\gamma +\gamma \,k_\mathrm {eq}(a_1) + \kappa \,\cos \left( \Delta {\theta }\right) \left( \,{\frac{a_{1}}{a_2}-\frac{a_{2}}{a_1}}\right) \right. \nonumber \\&\quad \left. +\frac{1}{2}(\xi _1-\xi _2)\,\omega \,\sin \left( \Delta {\theta }\right) \left( {\frac{a_{1}}{a_2}+\frac{a_{2}}{a_1}}\right) \right) . \end{aligned}$$
(12)

Averaging the nonlinear force of the Jenkins element, \(f_\mathrm {t}[x_1]\), yields the expressions for the amplitude-dependent equivalent stiffness \(k_{\mathrm {eq}}\) and damping \(d_{\mathrm {eq}}\) [18] as follows:

$$\begin{aligned} k_{\mathrm {eq}}(a_1)&= \frac{2\tau ^*(a_1)-\sin ( 2\tau ^*(a_1))}{2\pi } ,\nonumber \\ \omega d_{\mathrm {eq}}(a_1)&= \frac{1}{\pi }\sin ^2(\tau ^*(a_1)) \end{aligned}$$
(13)
$$\begin{aligned} \text {with}\quad \tau ^*(a_1)&= {\left\{ \begin{array}{ll} \text {acos}(1-\frac{2}{a_1}) &{} a_1>1\\ \pi &{} 0< a_1\le 1 \end{array}\right. } \,. \end{aligned}$$
(14)

The parameter \(\tau ^*\) can be interpreted as the stick-slip transition time. In the sticking case it holds that, \(a_1\le 1\). In this case, the stick-slip transition does obviously not occur, which corresponds to \(\tau ^*=\pi \) (due to symmetry of hysteresis cycle). Consequently, the Jenkins element correctly degenerates to a conservative spring with \(k_\mathrm {eq}=1\) and \(d_\mathrm {eq}=0\). For increasing vibration levels beyond the sticking limit, i.e., \(a_1>1\), the stick-slip transition occurs earlier along one period of vibration, i.e., \(\tau ^*\) decreases. The maximum equivalent damping is reached for \(\tau ^*=\pi /2\), where \(k_\mathrm {eq}=0.5\). As the amplitude goes to infinity, the friction effect becomes negligible such that both \(k_\mathrm {eq}\) and \(d_\mathrm {eq}\) asymptotically approach zero. The nonlinear dependence of the equivalent damping and stiffness with respect to the parameter \(\tau ^*\) is depicted in Fig. 3. The gray shaded area, limited by \(\tau ^*(a_1(\xi _\mathrm {1,div}))\), indicates divergent curve ranges, i.e., \(\tau ^*\) related to unbounded amplitude growth. The indicated limit is based on numerical results for the given parameter values.

Fig. 3
figure 3

Behavior of \(k_\mathrm {eq}\) and \(d_\mathrm {eq}\) with respect to \(\tau ^*\); point of divergence \(\xi _{1,\mathrm {div}}\) determined by numerical simulation of Eqs. (1) and (2) with \(\xi _1<0\), \(\xi _2=0.011\), \(\kappa =0.1\), \(\gamma =0.5\)

Full size image

3.2 Approximation of the energy-dependent oscillation frequency

Fig. 4
figure 4

Frequency–energy relation along the LCO obtained under variation of \(\xi _1<0\): The discrete points (‘black,’ ‘x’) are obtained by solving the slow flow equations (10)–(12) (\(\dot{a}_1=\dot{a}_2=\Delta {{\dot{\theta }}}=0\)), initialized with small/high mechanical energy for solutions along the lower/upper half of the LCO curve (cf. Fig. 1), or, continuous interpolation of the discrete solution points by piecewise cubic splines (‘blue,’ ‘solid’); indication of limit cases for sticking slider \(\omega _\mathrm {st}\) and frictionless sliding \(\omega _\mathrm {sl}\); point of divergence \(\xi _{1,\mathrm {div}}\) determined by numerical simulation of Eqs. (1) and (2); \(-\,0.216 \le \xi _1 \le 0\), \(\xi _2=0.011\), \(\kappa =0.1\), \(\gamma =0.5\). (Color figure online)

Full size image

To simulate the slow flow given by Eqs. (10)–(12), the oscillation frequency \(\omega \) needs to be specified. We are interested in the dynamics near the LCO. Indeed, to compute the LCO with frequency \(\omega \), we impose conditions for periodicity, namely, \(\dot{a}_1=\dot{a}_2={{\dot{\theta }}}_1={{\dot{\theta }}}_2=0\). With this, Eqs. (6)–(9) degenerate to an algebraic system of four equations for the four unknowns \(a_1\), \(a_2\), \(\Delta \theta \) and \(\omega \), which are solved numerically. The resulting frequency of the LCO is illustrated in Fig. 4, where it is depicted as function of the corresponding mechanical energy of the system averaged over one period of vibration when it oscillates on the LCO, obtained by varying the negative damping \(\xi _1<0\). The averaged mechanical energy, i.e., the averaged sum of potential and kinetic energy, is formally given by

$$\begin{aligned} E_\mathrm {mech}&= \dfrac{1}{4}(1-\gamma + \kappa )a_1^2 +\dfrac{1}{4}(1+\kappa )a_2^2 \nonumber \\&\quad - \dfrac{1}{2} \kappa a_1 a_2 \cos (\Delta \theta ) \nonumber \\&\quad + \dfrac{1}{2 \pi } \int _0^{2 \pi } \int f_\mathrm {t}[x_1] \dot{x}_1 \mathrm {d} t \mathrm {d}\tau \nonumber \\&\quad + \dfrac{1}{4}\omega ^2 ( a_1^2 + a_2^2 ) \, , \end{aligned}$$
(15)

where \(\tau = \omega t\). This frequency–energy relation holds strictly only at the LCO, i.e., for the time-periodic solution, which represents a special stationary solution of the mechanical system with negative damping. Perturbing the initial conditions corresponding to the LCO, but staying sufficiently close in the neighborhood of the LCO, we postulate that this frequency–energy relation still provides a reasonable approximation denoted symbolically in the form,

$$\begin{aligned} \omega = {\tilde{\omega }} \left( E_\mathrm {mech}(a_1,a_2,\Delta \theta ) \right) . \end{aligned}$$
(16)

Of course, the above described numerical solution method only generates a discrete sequence of points. To simulate the slow flow equations (10)–(12), however, a continuous expression (i.e., a function) of the oscillation frequency in terms of the states \(a_1,a_2,\Delta \theta \) is needed, which we obtained using interpolation. To this end, we applied a piecewise cubic Hermite interpolation between about 400 discrete solution points in the interval \(E_\mathrm {mech}\in (0,500)\). Note, that this interval contains also energy levels beyond the fold bifurcation (i.e., points along the upper half of the LCO curve), cf. Fig. 1.

Fig. 5
figure 5

Comparison of the slow flow approximation (Eqs. (10)–(12)) against the initial system (Eqs. (1) and (2)) with respect to the amplitude-damping diagram: The discrete points are obtained by direct numerical integration initialized on the LCO considering a small perturbation; \(\xi _1 < 0\), \(\xi _2=0.011\), \(\kappa =0.1\), \(\gamma =0.5\)

Full size image
Fig. 6
figure 6

Phase space projection (‘gray,’ ‘solid’) and Poincaré map (‘black,’ ‘.’) associated with section \({\mathcal {S}}\) (associated with the fast time scale), obtained by direct numerical simulations of the initial system [Eqs. (1) and (2)]

Full size image
Fig. 7
figure 7

Phase space projection (‘gray,’ ‘solid’) and Poincaré map (‘black,’ ‘.’) associated with section \({\mathcal {S}}\) (associated with the fast time scale), obtained from the analytical slow flow approximation

Full size image

3.3 Cascade of period doubling leads to chaos

Now, we are in the position to analyze to what extent the slow flow approximation, Eqs. (6)–(9) together with Eq. (16) reproduce the dynamics of the initial system [Eqs. (1) and (2)]. We note at this point that the ansatz used for the previous complexification-averaging analysis is based on the assumption that there exists a single fast frequency \(\omega \), and that there is a slow–fast separation of the non-stationary dynamics, i.e., that there is no mixing of scales. Whenever either of these conditions is not satisfied we expect that our analytical predictions will diverge compared to the exact solutions derived by direct numerical simulations of the initial system of governing equations. In Fig. 5, we compare the bifurcation diagrams, with respect to the negative damping parameter \(\xi _1\). The vibration level is depicted in terms of the maximum, \(a_\mathrm {1,max}\), and minimum, \(a_\mathrm {1,min}\), vibration amplitudes at steady state; we note that the derived steady state is not necessarily periodic, nor even stationary. In spite of the complexity of the dynamics of the system, both the secondary Hopf bifurcation point, \(\xi _\mathrm {1,Hopf}\), and the point of divergence, \(\xi _\mathrm {1,div}\), are captured by the analysis with remarkable accuracy. The minor deviations are attributed to the aforementioned analytical simplifications: Truncation to a single harmonic, separation of time scales, and presumed invariance of frequency–energy dependence.

Fig. 8
figure 8

Phase space projection (‘gray,’ ‘solid’) and Poincaré map (‘black,’ ‘.’) associated with \({\mathcal {D}}\) (associated with the slow time scale), obtained from the slow flow approximation; ‘\({{\underline{\square }}}\)’ represents mean-free variables

Full size image

Figure 6 depicts Poincaré maps associated with a Poincaré section \({\mathcal {S}}\) (associated with the fast time scale). To this end, given that the initial system [Eqs. (1) and (2)] is four-dimensional, we introduce the following Poincaré section,

$$\begin{aligned} {\mathcal {S}} = \{ {\varvec{x}} | x_2 = 0, \dot{x}_2>0 \} \end{aligned}$$
(17)

with respect to the initial, fast variables \({\varvec{x}}=[x_1,x_2, \dot{x}_1, \dot{x}_2]^\mathrm {T}\). Studying the intersections of the orbits of the dynamical system with the Poincaré section \({\mathcal {S}}\) we obtain a three-dimensional Poincaré map. For simplicity, we depicted just two-dimensional projections of this three-dimensional map, namely the \(\dot{x}_1\)-\(x_1\)-plane. It can be seen that the LTO transitions toward chaotic oscillations for increasing magnitude of the negative damping. Analytical predictions obtained from the slow flow approximation are depicted in Fig. 7. Here, the evolution of the variables \({\varvec{x}}\) on the fast time scale was recovered using Eqs. (4) and (5). Again, the slow flow approximation is in good agreement with the exact numerical simulation, however, a slight shift of the dynamics appears to be introduced below \(\xi _1<-0.1\). We conclude that the proposed slow flow approximation, including the assumptions on the frequency–energy dependence, is sufficiently accurate to further characterize the dynamics on the slow time scale.

Figure 8 depicts two-dimensional projections of the three-dimensional Poincaré maps associated with a different Poincaré section \({\mathcal {D}}\) for the slow flow dynamics [Eqs. (10)–(12)],

$$\begin{aligned} {\mathcal {D}} = \{ {\varvec{a}} | \underline{{a}}_2 = 0, \underline{{\dot{a}}}_2>0 \}, \end{aligned}$$
(18)

with respect to the slow variables \({\varvec{a}}=[\underline{{a}}_1,\underline{{a}}_2,\underline{\dot{a}}_1,\underline{{\dot{a}}}_2]^\mathrm {T}\). Here, \({{\underline{\square }}}\) denotes mean-free variables. Note that the amplitudes \(a_1\) and \(a_2\) typically do not have zero crossings. Hence, the steady-state mean value is subtracted so that one can use the common formulation of the Poincaré section in Eq. (18) (involving zero crossings).

The slow time scale provides a clearer picture of the dynamics: The (quasi-periodic) limit torus oscillations are seen as closed curves in the phase projections within Fig. 8. The Poincaré map consists of a single point for \(\xi _1=-0.055\). Apparently, a cascade of period-doubling bifurcations takes place until the chaotic regime is reached. This behavior is consistent with the results shown in Fig. 5 for the original system, but occurs slightly shifted for \(\xi _1<-0.1\)Footnote 2. In Table 1, we listed estimations for the first successive period-doubling bifurcation points and their ratios \(\delta _i\) for the slow flow system. Apparently, the period doublings do not approach the Feigenbaum ratio (\(\delta _\mathrm {F}\approx 4.6692\)) [19], at least for the slow flow system.

Table 1 Estimation of the first period-doubling bifurcations i with the associated self-excitation level \(\xi _{1,i}\) and their ratio \(\delta _i\) for the slow flow approximation
Full size table

In [14], the chaotic nature of the original system’s dynamics past the secondary Hopf bifurcation was confirmed by numerically estimated Lyapunov exponents following [19]. This method is particularly suitable for smooth systems, while the results for non-smooth systems (e.g., due to frictional forces) should generally be taken with caution. The estimation of Lyapunov exponents for this type of systems is still under research, a summary of different approaches can be found for example in [20].

4 Analytical investigation of the secondary Hopf bifurcation

We now focus on the transition from limit cycle oscillations to limit torus oscillations. We seek to establish analytically the conditions for the emergence of non-periodic oscillations in the mechanical system of Fig. 2, and to obtain a closed-form approximation for the point of the secondary Hopf bifurcation. To this end, we use perturbation calculus to approximate the family of LCOs and analyze its stability. The accuracy and efficacy of the analytical methodology are evaluated by comparison against the exact numerical simulation of the initial problem [Eqs. (1) and (2)].

4.1 Approximation of the fixed points of the slow flow by means of perturbation analysis

The LCO (time-periodic solution) on the fast time scale corresponds to a fixed point of the slow flow and is determined by setting the left hand sides of Eqs. (6)–(9) to zero. It turned out to be useful to transform the slow flow by introducing a new set of variables: Instead of \(a_1\), \(a_2\), we introduce the new variables \(\rho =a_2/a_1\) and \(\tau ^*\) (stick-slip transition time) which is uniquely related to \(a_1\) as defined in Eq. (14). With this variable transformation, the governing algebraic equations determining the fixed points of the slow flow can be cast into the form:

$$\begin{aligned} 0&= \kappa \, \hat{\rho }\, \sin \left( \Delta \hat{\theta }\right) + \frac{1}{2}(\xi _1-\xi _2)\, \hat{\omega }\, \hat{\rho }\cos \left( \Delta \hat{\theta }\right) \nonumber \\&\quad +\frac{1}{2}(\xi _1+\xi _2) \hat{\omega }+\gamma \, \hat{\omega }\,d_\mathrm {eq}(\hat{\tau }^*), \end{aligned}$$
(19)
$$\begin{aligned} 0&= \kappa \,\hat{\rho }\,\cos \left( \Delta \hat{\theta }\right) - \frac{1}{2}(\xi _1-\xi _2)\,\hat{\omega }\,\sin \left( \Delta \hat{\theta }\right) \hat{\rho }\nonumber \\&\quad +{\hat{\omega }}^2-\kappa +\gamma -\gamma \,k_\mathrm {eq}(\hat{\tau }^*)-1, \end{aligned}$$
(20)
$$\begin{aligned} 0&= \frac{1}{2}(\xi _1+\xi _2)\, \hat{\omega }\,\hat{\rho }- {\kappa }\, \sin \left( \Delta \hat{\theta }\right) \nonumber \\&\quad + {\frac{1}{2}(\xi _1-\xi _2)}\, \hat{\omega }\, \cos \left( \Delta \hat{\theta }\right) , \end{aligned}$$
(21)
$$\begin{aligned} 0&= {\hat{\omega }}^2 + \frac{1}{2}(\xi _1-\xi _2)\,\hat{\omega }\,\sin \left( \Delta \hat{\theta }\right) \hat{\rho }^{-1}\nonumber \\&\quad -1 -\kappa +\kappa \,\hat{\rho }^{-1}\,\cos \left( \Delta \hat{\theta }\right) . \end{aligned}$$
(22)

We use perturbation calculus to approximate the fixed points of this set of transformed algebraic equations. To this end, we introduce the small parameter \(\varepsilon \) which will act as the formal perturbation parameter of our analysis. To introduce the small parameter we assume that the coupling and damping terms are small, scaled according to the following relations:

$$\begin{aligned} \kappa = \varepsilon {{\bar{\kappa }}}, \quad \xi _1 = \varepsilon ^2 \bar{\xi }_1, \quad \xi _2 = \varepsilon ^2 {{\bar{\xi }}}_2. \end{aligned}$$
(23)

Recall that the condition of weak coupling is needed to have closely spaced natural frequencies in the mechanical system of Fig. 2: The ratio of the natural frequencies in the linear case when only sticking contact occurs equals \(\sqrt{1+2\kappa }\). A typical value for \(\kappa \) is 0.1 leading to about \(10\%\) difference in the natural frequencies. Moreover, the secondary Hopf bifurcation occurs already for very light damping, with typical values for \(\xi _\mathrm {1}\) of \(-\,0.035\) and for \(\xi _\mathrm {2}\) of 0.011. Thus, it holds that \(\Vert \xi _{1,2} \Vert \ll \kappa \ll 1\), as defined in Eq. (23). It should be emphasized that nonlinearity is not assumed as weak, i.e., \(\gamma \) is considered to be a system parameter of order \({\mathcal {O}}(\varepsilon ^0)\). Yet we impose the condition \(\gamma \le 1\) which is necessary to have positive stiffness values for all springs in the model (Fig. 2).

We seek an approximation to the fixed point in terms of \(\hat{\tau }^*, {{\hat{\rho }}}\), \(\Delta {{\hat{\theta }}}\) and \({{\hat{\omega }}}\), where \({\hat{\square }}\) denotes fixed point quantities. In accordance with regular perturbation theory (see, e.g., [17]), these quantities are expanded in regular power series in \(\varepsilon \), of the form

$$\begin{aligned} f&= f_0 + f_1 \varepsilon + f_2 \varepsilon ^2 + {\mathcal {O}}(\varepsilon ^3)\,. \end{aligned}$$
(24)

As will be shown later, reasonable results are achieved already for a second-order approximation (up to and including the \(\varepsilon ^2\) term). The power series and Eq. (23) are substituted into Eqs. (19)–(22). The equations contain several nonlinear terms, namely, \(\sin (\Delta {{\hat{\theta }}})\), \(\cos (\Delta {{\hat{\theta }}})\), \(\omega d_\mathrm {eq}(\tau ^*)\), \(k_\mathrm {eq}(\tau ^*)\), and \(1/\rho \). In accordance with perturbation calculus, each nonlinear term is expanded into a Taylor series of sufficient order, and the power series of the unknowns (Eq. (24)) is substituted. The unknown coefficients of the power series are then determined successively by matching (balancing) the coefficients at each order separately, starting with the leading-order \({\mathcal {O}}(\varepsilon ^0)\) terms. With this, the following second-order approximation of the fixed point of the slow flow equations is obtained:

$$\begin{aligned} {{\hat{\tau }}}^*&= \pi -\sqrt{\frac{-2\pi \, \,{{\bar{\xi }}}_1}{\gamma }} \varepsilon + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$
(25)
$$\begin{aligned} {{\hat{\rho }}}&= 1 + \left( \frac{{{{\bar{\xi }}} _{1}}^2}{{{\bar{\kappa }}} ^2}-\frac{{{\bar{\xi }}} _{1}\,{{\bar{\xi }}} _{2}}{2\,{{\bar{\kappa }}} ^2} -\frac{4}{3 {{\bar{\kappa }}}}\,\sqrt{ \frac{-2 {{{\bar{\xi }}} _{1}}^{3}\pi }{\gamma }} \right) \varepsilon ^2 \nonumber \\&\quad + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$
(26)
$$\begin{aligned} \Delta {{\hat{\theta }}}&= \frac{ {{\bar{\xi }}}_1}{{{\bar{\kappa }}}} \varepsilon + {\mathcal {O}}(\varepsilon ^3) , \end{aligned}$$
(27)
$$\begin{aligned} {{\hat{\omega }}}&= 1 + {\mathcal {O}}(\varepsilon ^3) . \end{aligned}$$
(28)

As expected, non-trivial fixed points only exist for \(\xi _1\le 0\).

Fig. 9
figure 9

Critical damping \(\xi _\mathrm {1,Hopf}\) at the secondary Hopf bifurcation: a dependence of analytical result on out-of-phase damping \(\xi _2\) and coupling-to-nonlinearity ratio \(\kappa ^2/\gamma \); b–d comparison of the analytical result (‘pink’) to exact result determined by direct numerical simulation of the original equations of motion [Eqs. (1) and (2)] (‘black’) under variation of \(\xi _2\), \(\kappa \) and \(\gamma \). Nominal parameters are set to \(\xi _2=0.011\), \(\kappa = 0.1\), \(\gamma = 0.5\). The point of divergence \(\xi _{1,\mathrm {div}}\) was determined by numerical simulation of Eqs. (1) and (2). (Color figure online)

Full size image
Fig. 10
figure 10

Examples for which the limit cycle regains stability via another secondary Hopf bifurcation: a \(\kappa = 0.074, \xi _2=0.011, \gamma = 0.5\), b \(\kappa = 0.21, \xi _2=0.011, \gamma = 0.5\), c \(\gamma = 0.7, \kappa = 0.1, \xi _2=0.011\). Analytical result in ‘pink,’ numerical reference in ‘black.’ The parameter sets are indicated in Fig. 9

Full size image

4.2 Calculation of the secondary Hopf bifurcation point

Clearly, the limit torus on the fast time scale corresponds to a periodic orbit on the slow time scale, and the bifurcation of the limit cycle to the limit torus corresponds to a secondary Hopf bifurcation. Consequently, on the slow time scale, this point is associated with (primary) Hopf bifurcation of the fixed point of the slow flow equations given by Eqs. (25)–(28). Hence, to locate this point and establish conditions for its existence, it suffices to analyze the asymptotic stability of the approximated fixed point of the slow flow and prove that the conditions for Hopf bifurcation hold at the point of instability of the fixed point. This is done in the conventional way, based on the eigenvalues of the Jacobian with respect to the slow flow equations (10)–(12). Accordingly, the characteristic equation governing the eigenvalues, \(\lambda \), can be explicitly computed by imposing the following condition,

$$\begin{aligned} \frac{1}{2} \begin{vmatrix} -j_1-{d_1} - \lambda&\quad -d_2 \,c-{\bar{\kappa }} \,s&\quad -{\bar{\kappa }\, \hat{\rho }}\, c+ \hat{\rho }\, d_2 \,s \\ -d_2 \, c+{\bar{\kappa }}\, s&\quad -d_1 - \lambda&\quad {\bar{\kappa }} \, c+d_2 \, s \\ \bar{\kappa }\left( \hat{\rho }+ \hat{\rho }^{-1} \right) c- d_2 \left( \hat{\rho }- \hat{\rho }^{-1} \right) s{+} j_2&\quad -\bar{\kappa }\left( 1 {+}\hat{\rho }^{-2} \right) c{+} d_2 \left( 1 {-} \hat{\rho }^{-2} \right) s&\quad d_2 \left( \hat{\rho }{+} \hat{\rho }^{-1} \right) c{+} \bar{\kappa }\left( \hat{\rho }{-} \hat{\rho }^{-1} \right) s {-} \lambda \end{vmatrix} {=} 0, \end{aligned}$$

where the following abbreviations have been introduced, \(d_1 = \frac{1}{2}\left( {{\bar{\xi }}}_1 + {{\bar{\xi }}}_2 \right) \), \(d_2 = \frac{1}{2}\left( {{\bar{\xi }}}_1 - {{\bar{\xi }}}_2 \right) \), \(s = \sin \left( \Delta {{\hat{\theta }}} \right) \) and \(c = \cos \left( \Delta \hat{\theta }\right) \), together with the additional notations,

$$\begin{aligned} j_1&= \gamma \,\frac{\partial a_1 d_\mathrm {eq}\left( a_{1}\right) }{\partial a_{1}}\bigg \vert _{a_1 = \hat{a} _1}\\&= \gamma \,\frac{(\cos (\hat{\tau }^*) - 1)^2}{\pi }= \frac{4 \gamma }{\pi }+{4 \bar{\xi }_1}\varepsilon ^2 +\mathcal {O}(\varepsilon ^3), \\ j_2&= \gamma \,a_{1}\,\frac{\partial k_\mathrm {eq}\left( a_{1}\right) }{\partial a_{1}} \bigg \vert _{a_1 = \hat{a} _1}\\&= -\gamma \,\frac{2 \left( \cos ( \hat{\tau }^*) - 1 \right) \left( \cos (\hat{\tau }^*)^2 - 1 \right) }{\pi \sin (\hat{\tau }^*)} \\&= 4 \sqrt{\frac{-2 \gamma \bar{\xi }_1}{\pi }}\varepsilon +\mathcal {O}(\varepsilon ^3). \end{aligned}$$

The solution of the characteristic equation yields the following second-order analytical approximation for the eigenvalues:

$$\begin{aligned} \lambda ^{(1)}&= -\frac{2\,\gamma }{\pi }\nonumber \\&\quad -\frac{\,\left( (9\,{{\bar{\xi }}} _{1}+{{\bar{\xi }}} _{2})\, \gamma -\pi \,{{\bar{\kappa }}} ^2-2\,{{\bar{\kappa }}} \,\sqrt{-2 \pi \gamma {{\bar{\xi }}}_1 }\right) }{4\,\gamma } \varepsilon ^2\nonumber \\&\quad + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$
(29)
$$\begin{aligned} \lambda ^{(2,3)}&= \pm \mathrm {i} \frac{\sqrt{2}}{2}\,{{\bar{\kappa }}} \,\varepsilon \nonumber \\&\quad -\frac{-({{\bar{\xi }}}_1 -3{{\bar{\xi }}}_2 ) \gamma +\pi \,{\bar{\kappa }}^2+2\,{{\bar{\kappa }}}\,\sqrt{-2\pi \gamma {{\bar{\xi }}}_1}}{8\, \gamma }\; \varepsilon ^2\nonumber \\&\quad + {\mathcal {O}}(\varepsilon ^3). \end{aligned}$$
(30)

Recalling that \(\xi _1< 0\), one can infer that \(\lambda ^{(1)}\) remains real-valued, whereas \(\lambda ^{(2,3)}\) appear as a complex-valued pair. Thus, the sought bifurcation occurs when \(\lambda ^{(2,3)}\) crosses the imaginary axis. This is the necessary condition for the realization of the Hopf bifurcation; it can also be shown (not reported here) that the additional sufficient conditions are also met [21]. So indeed a Hopf bifurcation occurs at the point of instability of the fixed point and a new limit cycle oscillation is generated in the slow flow dynamics which corresponds to the limit torus oscillation in the fast dynamics.

The condition \(\mathfrak {R}\lbrace \lambda ^{(2,3)} \rbrace =0\) leads to the following value for the critical damping,

$$\begin{aligned} \breve{\xi }_\mathrm {1,Hopf}^\mathrm {start/end}&= 3\xi _2\,\left( 1 - \nu \,\left( 1\mp \frac{2\sqrt{2}}{3}\,\sqrt{ 1 - \frac{3}{\nu } } \right) \right) \end{aligned}$$
(31)
$$\begin{aligned} \mathrm {with} \quad \nu&= \frac{\pi \kappa ^2}{\gamma \xi _2}. \end{aligned}$$
(32)

Apparently, besides the expected transition from limit cycle to limit torus, another transition back to a stable cycle is possible. This will be further discussed in the next subsection. It is interesting to note that the bifurcation value \(\breve{\xi }_\mathrm {1,Hopf}^\mathrm {start/end}\) is a function of the out-of-phase damping \(\xi _2\) and the coupling-to-nonlinearity-ratio \(\kappa ^2/\gamma \). This relation is illustrated in Fig. 9a. Solutions for \(\breve{\xi }_\mathrm {1,Hopf}^\mathrm {start/end}\) only exist for \(\nu \ge 3\), i.e., if \(\frac{\kappa ^2}{\gamma }\ge \frac{3\xi _2}{\pi }\). This means that the positive damping of the (out-of-phase) higher-frequency mode must be sufficiently small (for given \(\gamma \) and \(\kappa \)) for this bifurcation to occur.

4.3 Assessment of the analytical results against the exact numerical simulations

We now compare the previous analytical results to the results of exact numerical simulations. The location of the secondary Hopf bifurcation, in terms of the critical damping value \(\xi _\mathrm {1,Hopf}\), is illustrated in Fig. 9. The corresponding analytical result is given in Eq. (31). As throughout this work, the numerical reference was obtained by simulation of the initial system [Eqs. (1) and (2)].

Overall the analytical result is in good agreement with the numerical reference. Deviations occur at the ranges where the assumptions underlying the perturbation approach are violated. More specifically, the assumption concerning the hierarchy of the orders of magnitude, \(\Vert \xi _{1,2} \Vert \ll \kappa \ll \gamma \) (cf. Eq. (23)) must hold to ensure reasonable accuracy. For instance, the analytical results are accurate for \(\xi _2<0.02\) (Fig. 9b) and \(\xi _2<\kappa < 0.2\) (Fig. 9c). In contrast, if \(\Vert \xi _1 \Vert \) or \(\xi _2\) approach the order of \(\kappa \), the accuracy is poor (as expected). Similarly, if \(\kappa \) approaches the order of \(\gamma \) (order \(\varepsilon ^0\)), the analytical result is no longer valid.

As noted earlier, the analytical approximation yields two critical values of \(\xi _1\), as expressed in Eq. (31). The one with smaller magnitude, \(\breve{\xi }_\mathrm {1,Hopf}^\mathrm {start}\), corresponds to the point where the limit cycle becomes unstable giving rise to a stable limit torus. The one with larger magnitude, \(\breve{\xi }_\mathrm {1,Hopf}^\mathrm {end}\), refers to another secondary Hopf bifurcation where the limit cycle regains stability. As seen from these results, for a wide range of parameters, \(\breve{\xi }_\mathrm {1,Hopf}^\mathrm {end}\) lies beyond the point of divergence, \(\xi _\mathrm {1,div}\), and, therefore, it is never reached. The point of divergence and the corresponding gray shaded area indicate parameter ranges leading to unbounded amplitude growth based on numerical simulation of Eqs. (1) and (2). For other parameter combinations, however, the secondary Hopf bifurcation can be reached, e.g., for \(0.6<\gamma <0.8\) in Fig. 9d, or for \(\kappa \approx 0.074\) and \(\kappa \approx 0.21\) in Fig. 9c. The resulting bifurcation diagram is illustrated in Fig. 10 for three different parameter sets. Again, reasonable agreement between the analytical results and numerical solutions is achieved with respect to the bifurcation point.

5 Conclusions

We considered a system of two weakly coupled oscillators, with an elastic dry friction element attached to one of the oscillators, subjected to negative viscous damping of the symmetric in-phase and positive damping of the out-of-phase motion. When increasing the magnitude of the negative damping, the well-understood limit cycle oscillations lose stability and bifurcate into limit torus oscillations. For some parameter ranges, an additional secondary Hopf bifurcation may occur beyond which the limit cycle regains stability. In other cases, the quasi-periodic oscillations further bifurcate into chaotic dynamics. The analysis of the slow flow in the neighborhood of the limit cycle revealed that chaos is reached via a cascade of period-doubling bifurcations. Assuming weak coupling, of \({\mathcal {O}}(\varepsilon )\), (leading to closely spaced natural frequencies) and even weaker damping, of \({\mathcal {O}}(\varepsilon ^2)\), we derived an analytical approximation of the limit cycle using perturbation calculus. A stability analysis provided a closed-form expression for the point of the secondary Hopf bifurcation and conditions for its existence. In particular, it was established that non-periodic oscillations occur for sufficiently weak coupling and sufficiently strong nonlinearity. The quality of the analytical results was thoroughly validated by comparing them against exact numerical simulations of the original equations of motion of the initial dynamical system.

The key challenge for deriving the closed-form approximations was the treatment of the dry friction nonlinearity (Jenkins element). To tackle this, a change of variables was carried out, involving the normalized stick-slip transition time. As the Jenkins element is commonly used to model nonlinear hysteresis (including tribology and material behavior), we believe that the proposed approach will be instrumental to analyze systems far beyond the one considered in this work. Here, we anticipate that our results will trigger more efforts within our scientific community to derive analytical approximations in order to gain deep understanding of parameter dependencies, in addition to systematic numerical simulation. This will help in predictive design of oscillating systems with dry friction undergoing instabilities, LCOs, LTOs, and chaotic motions.