Stability, convergence, limit cycles and chaos in some models of population dynamics

Abstract

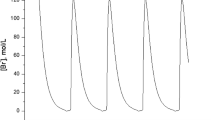
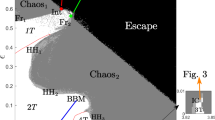
In this paper, we study three models of population dynamics: (i) the classical delay logistic equation, (ii) its variant which incorporates a harvesting rate and (iii) the Perez–Malta–Coutinho (PMC) equation. For all these models, we first conduct a local stability analysis around their respective equilibria. In particular, we outline the necessary and sufficient condition for local stability. In the case of the PMC equation, we also outline a sufficient condition for local stability, which may help guide design considerations. We also characterise the rate of convergence, about the locally stable equilibria, for all these models. We then conduct a detailed local bifurcation analysis. We first show, by using a suitably motivated bifurcation parameter, that the models undergo a Hopf bifurcation when the necessary and sufficient condition gets violated. Then, we use Poincaré normal forms and centre manifold theory to study the dynamics of the systems just beyond the region of local stability. We outline an analytical basis to establish the type of the Hopf and determine the stability of the limit cycles. In some cases, we are able to derive explicit analytic expressions for the amplitude and period of the bifurcating limit cycles. We also highlight that in the PMC model, variations in one of the model parameters can readily induce chaotic dynamics. Finally, we construct an equivalent electronic circuit for the PMC model and demonstrate the existence of multiple bifurcations in a hardware-based circuit implementation.

Appendices

Appendix 1: Local stability analysis

In this Appendix, we present the local stability analysis of a general nonlinear delay differential equation, as applicable to the models under study. Consider the following equation:

$$\begin{aligned} {\dot{x}}(t) = \eta f\big (x(t),x(t-\tau ),p\big ), \end{aligned}$$

(42)

where $\tau \ge 0$ denotes the feedback delay, $\eta > 0$ is the exogenous non-dimensional bifurcation parameter, and p represents the set of system parameters. Let $(x^*,y^*)$ be the non-trivial equilibrium of system (42). Recall that f is a nonlinear function. The first step towards analysing the stability of such a nonlinear system would be to study its linear approximation about the equilibrium. This would help us characterise the conditions for local stability of the system. To that end, we now linearise Eq. (42) and study the underlying linear system.

We define $u(t) = x(t) - x^*$, and linearise Eq. (42) to obtain

$$\begin{aligned} {\dot{u}}(t) = -\eta a u(t) - \eta b u(t-\tau ), \end{aligned}$$

(43)

where $a \ge 0,~b>0$ are given by $a = -f^{\prime }_x|_{(x^*,y^*)}$ and $b = -f^{\prime }_y|_{(x^*,y^*)}$ and $b > a$. Looking for exponential solutions of Eq. (43), we have the following characteristic equation:

$$\begin{aligned} \lambda + \eta a + \eta b \hbox {e}^{-\lambda \tau } = 0. \end{aligned}$$

(44)

Following the analysis outlined in [30], a sufficient condition for stability of Eq. (43) is

$$\begin{aligned} \eta b\tau < \frac{\pi }{2}, \end{aligned}$$

(45)

and the necessary and sufficient condition is

$$\begin{aligned} \eta \tau \sqrt{b^2-a^2} < \cos ^{-1}\Big (\frac{-a}{b}\Big ). \end{aligned}$$

(46)

It has been shown that the model transits into instability via a Hopf bifurcation when the necessary and sufficient condition (46) is violated, see [30]. Recall that, we wish to choose $\eta$ as the bifurcation parameter as it enables us to capture the effect of variation in any of the parameters. It has been shown that the system undergoes a Hopf bifurcation at a critical value of $\eta$ that satisfies the following condition

$$\begin{aligned} \eta _c \tau _c \sqrt{b^2 - a^2} = \cos ^{-1}\Big (\frac{-a}{b}\Big ). \end{aligned}$$

(47)

When condition (47), known as the Hopf condition, is met the system exhibits limit cycles with a period of $2\pi \tau /\cos ^{-1}(-a/b)$.

Having established that the system undergoes a Hopf bifurcation, we now present the analysis that enables us to explore the bifurcation properties of the system. In particular, the following analysis enables us to characterise the type of the Hopf bifurcation and determine the orbital stability of the emergent limit cycles.

Appendix 2: Hopf bifurcation analysis

Recall that $u(t)=x(t)-x^*$. A Taylor series expansion of Eq. (42) about equilibrium $x^*$ including the linear, quadratic and cubic terms is

$$\begin{aligned}&{\dot{u}}(t) =\,\, \eta \xi _x u(t) + \eta \xi _y u(t-\tau )+ \eta \xi _{xy}u(t)u(t-\tau ) \nonumber \\&\quad +\eta \xi _{yy}u^2(t-\tau )+\cdots , \end{aligned}$$

(48)

where

$$\begin{aligned}&\xi _{x} = \frac{\partial f}{\partial x}\bigg |_{(x^*,y^*)},\quad \xi _{y}=\frac{\partial f}{\partial y}\bigg |_{(x^*,y^*)},\\&\xi _{xy}= \frac{\partial ^2 f}{\partial x\partial y}\bigg |_{(x^*,y^*)},\quad \xi _{yy}=\frac{1}{2}\frac{\partial ^2 f}{\partial y^2}\bigg |_{(x^*,y^*)}. \end{aligned}$$

Note that we retain only those terms that appear in the Taylor series expansion of the DLE, MDLE and the PMC equation. We now perform the requisite analysis. We closely follow the style of analysis outlined in [22, 30]. Consider the following autonomous delay differential equation

(49)

where for $t>0,~\mu \in {\mathbb R}$ and ,

Let $\mathcal {L}_{\mu }$, be a family of linear operators in parameter $\mu$,

The nonlinear terms of the Taylor series expansion are contained in ${\mathcal {F}}(u_t,\mu ):\,\,C[-\tau ,0]\rightarrow {\mathbb {R}}$. Assume that ${\mathcal {F}}(u_{t},\mu )$ is analytic and that ${\mathcal {F}}$ and ${{\mathcal {L}}_{\mu }}$ depend on the bifurcation parameter $\eta =\eta _c+\mu$ for small $|\mu |$. With this representation, Eq. (48) can be written in the form of Eq. (49). Observe that Eq. (49) contains both u and $u_t$. Therefore, we transform it into the following form

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} u_{t} = {\mathcal {A}}(\mu )u_{t} + {\mathcal {R}}u_{t}, \end{aligned}$$

(50)

which contains only $u_{t}$ rather than both u and $u_{t}$. We first transform the linear terms $(\hbox {d}/\hbox {d}t)u(t)={\mathcal {L}}_{\mu }u_{t}$. For this, we use the Riesz representation theorem. This theorem enables us to define an $n \times n$ matrix-valued function $\rho (.,\mu ):\,\,[-\tau ,0]\rightarrow {\mathbb {R}}^{n^{2}}$, such that each component of $\rho$ has bounded variation and for all $\phi \in C[-\tau ,0]$

$$\begin{aligned} {\mathcal {L}}_{\mu }\phi = \int _{-\tau }^{0}\,\hbox {d}\rho (\theta ,\mu )\phi (\theta ). \end{aligned}$$

In particular

$$\begin{aligned} {\mathcal {L}}_{\mu }u_{t} = \int _{-\tau }^{0}\,\hbox {d}\rho (\theta ,\mu ) u(t+\theta ), \end{aligned}$$

(51)

where

$$\begin{aligned} \hbox {d}\rho (\theta ,\mu ) = \eta \big (\xi _{x}\delta (\theta )+ \xi _{y}\delta (\theta +\tau )\big )\hbox {d}\theta , \end{aligned}$$

and $\delta (\theta )$ is the Dirac-delta function that satisfies Eq. (51). We now define, for $\phi \in C^{1}[-\tau ,0]$, the following operators

$$\begin{aligned}&{\mathcal {A}}(\mu )\phi (\theta ) = \left\{ \begin{array}{ll} \frac{\hbox {d}\phi (\theta )}{\hbox {d}\theta },&{} \theta \in [-\tau ,0)\\ &{} \int _{-\tau }^{0}\,\hbox {d}\rho (s,\mu )\phi (s)\equiv {\mathcal {L}}_{\mu }\phi , \theta =0,\end{array}\right. \end{aligned}$$

(52)

$$\begin{aligned}&{\mathcal {R}}\phi (\theta )= \left\{ \begin{array}{ll} 0,&{} \theta \in [-\tau ,0)\\ {\mathcal {F}}(\phi ,\mu ),&{}\theta =0. \end{array}\right. \end{aligned}$$

(53)

Then, as $\hbox {d}u_t/\hbox {d}\theta \equiv \hbox {d}u_t/\hbox {d}t$, Eq. (49) becomes (50). We now proceed to derive the coefficients required for the Hopf bifurcation analysis. Note that $\eta$ is the bifurcation parameter and $\eta =\eta _c$ at the Hopf boundary. As instability begins to set in, we would have $\eta = \eta _c + \mu$. In order to study the bifurcation properties at the Hopf boundary, we set $\mu = 0$ and compute the required terms at the point of bifurcation.

Let $q(\theta )$ be the eigenfunction for ${\mathcal {A}}(0)$ corresponding to $\lambda (0)$, namely

$$\begin{aligned} {\mathcal {A}}(0)q(\theta ) = i\omega _{0}q(\theta ), \end{aligned}$$

and define the adjoint operator ${\mathcal {A}}^{*}(0)$ as

$$\begin{aligned} {\mathcal {A}}^{*}(0)\alpha (s) = \left\{ \begin{array}{ll} -\frac{\hbox {d}\alpha (s)}{\hbox {d}s},&{} s\in (0,\tau ]\\ \int _{-\tau }^{0}\hbox {d}\rho ^{\tau }(t,0)\alpha (-t), &{}s=0,\end{array}\right. \end{aligned}$$

where $\rho ^{T}$ denotes the transpose of $\rho$. The domain of ${\mathcal {A}}^*$ being $C^1[0,\tau ]$. If $q(\theta )$ is the eigenvector of ${\mathcal {A}}$ corresponding to the eigenvalue $\lambda (0)$, then ${\bar{\lambda }}(0)$ is an eigenvalue of ${\mathcal {A}}^*$, and

$$\begin{aligned} {\mathcal {A}}^{*}q^{*} = -i\omega _{0}q^{*}, \end{aligned}$$

where $q^{*}$ is some nonzero vector. We now define an inner product. For $\phi \in C[-\tau ,0]$ and $\psi \in C[0,\tau ]$, define

$$\begin{aligned}&\langle \psi ,\phi \rangle = {\bar{\psi }}(0)\cdot \phi (0)\nonumber \\&\quad - \int _{\theta =-\tau }^{0} \int _{\zeta =0}^{\theta }{\bar{\psi }}^{T}(\zeta -\theta )\,\hbox {d}\eta (\theta )\phi (\zeta )\hbox {d}\zeta . \end{aligned}$$

(54)

Let $q(\theta )=\hbox {e}^{i\omega _0\theta }$ and $q^{*}(s) = D\hbox {e}^{i\omega _0s}$ be the eigenvectors of ${\mathcal {A}}$ and ${\mathcal {A}}^*$ corresponding to the eigenvalues $i\omega _0$ and $-i\omega _0$. We may now use the inner product defined by (54), to find D such that the normalisation condition, $\langle q^*,q\rangle = 1$, is met. This yields

$$\begin{aligned} D = \frac{1}{1+\tau \eta \xi _y \hbox {e}^{i\omega _0\tau }}. \end{aligned}$$

(55)

For $u_{t}$, a solution of (50) at $\mu = 0$, define

$$\begin{aligned}&z(t) = \langle q^{*},u_{t}\rangle ,\quad \text {and} \\&{\mathsf {w}}(t,\theta ) = u_{t}(\theta )- 2 \text {Re}\big (z(t)q(\theta )\big ). \end{aligned}$$

Then, on the manifold, $C_{0},~{\mathsf {w}}(t,\theta ) = {\mathsf {w}}\big (z(t),{\bar{z}}(t),\theta \big )$ where

$$\begin{aligned}&{\mathsf {w}}(z,{\bar{z}},\theta ) = {\mathsf {w}}_{20}(\theta )\frac{z^{2}}{2}+ {\mathsf {w}}_{11}(\theta )z{\bar{z}}\nonumber \\&\quad + {\mathsf {w}}_{02}(\theta )\frac{{\bar{z}}^{2}}{2}+\cdots . \end{aligned}$$

(56)

In the directions of the eigenvectors $q^{*}$ and ${\bar{q}}^{*}$, z and ${\bar{z}}$ are local coordinates for $C_{0}$ in C, respectively. Using these coordinates, Eq. (49) can be reduced to an ordinary differential equation for a single complex variable on $C_{0}$. At $\mu = 0$, we have

$$\begin{aligned} z^{\prime }(t)&= \langle q^{*},{\mathcal {A}}u_{t} + {\mathcal {R}}u_{t}\rangle \nonumber \\&= i\omega _{0}z(t) + {\bar{q}}^{*}(0)\\&\quad \cdot {\mathcal {F}}\Big ({\mathsf {w}}(z,{\bar{z}},\theta )+ 2\text {Re}\big (z(t)q(\theta )\big )\Big )\nonumber \\&= i\omega _{0}z(t) + {\bar{q}}^{*}(0)\cdot {\mathcal {F}}_{0}(z,{\bar{z}})\nonumber \\&=i\omega _{0}z(t) + g(z,{\bar{z}}),\nonumber \end{aligned}$$

(57)

where $g(z,{\bar{z}})$ can be expanded in powers of z and ${\bar{z}}$ as

$$\begin{aligned} g(z,{\bar{z}})&= {\bar{q}}^{*}(0)\cdot {\mathcal {F}}_{0}(z,{\bar{z}})\nonumber \\&= g_{20}\frac{z^{2}}{2} + g_{11}z {\bar{z}} + g_{02}\frac{{\bar{z}}^{2}}{2}+ g_{21}\frac{z^{2}{\bar{z}}}{2}+ \cdots . \end{aligned}$$

(58)

We now need to determine the ${\mathsf {w}}_{ij}(\theta )$ in (56). Following [22] we write

$$\begin{aligned} {\mathsf {w}}^{\prime } = u^{\prime }_{t} - z^{\prime }q - {\bar{z}}^{\prime }{\bar{q}}, \end{aligned}$$

and using (50) and (57) we obtain

$$\begin{aligned} {\mathsf {w}}^{\prime } = \left\{ \begin{array}{ll} {\mathcal {A}}{\mathsf {w}} - 2\text {Re}\big ({\bar{q}}^*(0)\cdot {\mathcal {F}}_0q(\theta )\big ),&{} \theta \in [-\tau ,0)\\ {\mathcal {A}}{\mathsf {w}} - 2\text {Re}\big ({\bar{q}}^*(0)\cdot {\mathcal {F}}_0q(0)\big )+{\mathcal {F}}_0, &{} \theta = 0, \end{array}\right. \end{aligned}$$

which can be written as

$$\begin{aligned} {\mathsf {w}}^{\prime } = {\mathcal {A}}{\mathsf {w}} + H(z,{\bar{z}},\theta ), \end{aligned}$$

(59)

using (57), where

$$\begin{aligned} H(z,{\bar{z}},\theta ) = H_{20}(\theta )\frac{z^{2}}{2} + H_{11}(\theta )z{\bar{z}} + H_{02}(\theta )\frac{{\bar{z}}^{2}}{2} + \cdots . \end{aligned}$$

(60)

Now, on the manifold $C_{0}$, near the origin

$$\begin{aligned} {\mathsf {w}}^{\prime } = {\mathsf {w}}_{z}z^{\prime } + {\mathsf {w}}_{{\bar{z}}}{\bar{z}}^{\prime }. \end{aligned}$$

(61)

Use Eqs. (56) and (57) to replace ${\mathsf {w}},~z^{\prime }$ (and their conjugates) and equating this with (59), we obtain

$$\begin{aligned}&(2i\omega _{0}- {\mathcal {A}}){\mathsf {w}}_{20}(\theta ) = H_{20}(\theta ), \end{aligned}$$

(62)

$$\begin{aligned}&-{\mathcal {A}}{\mathsf {w}}_{11}(\theta ) = H_{11}(\theta ), \end{aligned}$$

(63)

$$\begin{aligned}&-(2i\omega _{0}+ {\mathcal {A}}){\mathsf {w}}_{02}(\theta ) = H_{02}(\theta ), \end{aligned}$$

(64)

as in [22]. We now expand the nonlinear terms in (48) using the following expansion in terms of the z coordinates,

$$\begin{aligned} u_{t}(\theta )&= {\mathsf {w}}(z,{\bar{z}},\theta )+ zq(\theta ) + {\bar{z}}{\bar{q}}(\theta )\nonumber \\&= {\mathsf {w}}_{20}(\theta )\frac{z^{2}}{2} + {\mathsf {w}}_{11}(\theta )z{\bar{z}} + {\mathsf {w}}_{02}(\theta )\frac{{\bar{z}}^{2}}{2} + z\hbox {e}^{i\omega _{0}\theta }\nonumber \\&\quad +\,{\bar{z}}\hbox {e}^{-i\omega _{0}\theta }+ \cdots , \end{aligned}$$

(65)

to obtain $u_{t}(0)$ and $u_{t}(-\tau )$. Retaining only the coefficients of $z^2,~z{\bar{z}},~{\bar{z}}^2,~z^2{\bar{z}}$, we have

$$\begin{aligned} u_{t}(0)u_{t}(-\tau )&= z^{2}\hbox {e}^{-i\omega _{0}\tau } {+} z{\bar{z}}(\hbox {e}^{i\omega _{0}\tau }+ \hbox {e}^{-i\omega _{0}\tau } ) {+} {\bar{z}}^{2}\hbox {e}^{i\omega _{0}\tau }\nonumber \\&\quad +\,z^{2}{\bar{z}}\big ({\mathsf {w}}_{11}(0)\hbox {e}^{-i\omega _{0}\tau } + \frac{{\mathsf {w}}_{20}(0)}{2}\hbox {e}^{i\omega _{0}\tau } \nonumber \\&\quad +\,{\mathsf {w}}_{11}(-\tau ) + \frac{{\mathsf {w}}_{20}(-\tau )}{2}\big )+ \cdots ,\nonumber \\ u_{t}^{2}(-\tau )&= z^{2}\hbox {e}^{-2i\omega _{0}\tau }+ {\bar{z}}^{2}\hbox {e}^{2i\omega _{0}\tau }+ 2z{\bar{z}}\nonumber \\&\quad +\,z^{2}{\bar{z}}\big (2\hbox {e}^{-i\omega _{0}\tau }{\mathsf {w}}_{11}(-\tau )\nonumber \\&\quad +\,\hbox {e}^{i\omega _{0}\tau }{\mathsf {w}}_{20}(-\tau )\big )+ \cdots . \end{aligned}$$

(66)

Using Eqs. (58) and (66), we obtain

$$\begin{aligned} g_{20}&= 2{\bar{q}}^{*}(0)\eta \big (\xi _{xy} \hbox {e}^{-i\omega _0\tau }+\xi _{yy} \hbox {e}^{-2i\omega _{0}\tau }\big ),\nonumber \\ g_{11}&={\bar{q}}^{*}(0)\eta \big (\xi _{xy}(\hbox {e}^{i\omega _0\tau }+\hbox {e}^{-i\omega _0\tau })+2\xi _{yy}\big ),\nonumber \\ g_{02}&=2{\bar{q}}^{*}(0)\eta \big (\xi _{xy}\hbox {e}^{i\omega _{0}\tau }+\xi _{yy}\hbox {e}^{2i\omega _{0}\tau }\big ),\nonumber \\ g_{21}&={\bar{q}}^{*}(0)\eta \bigg (\xi _{xy}\Big (2{\mathsf {w}}_{11}(0)\hbox {e}^{-i\omega _0\tau }+{\mathsf {w}}_{20}(0)\hbox {e}^{i\omega _0\tau }\nonumber \\&+\,2{\mathsf {w}}_{11}(-\tau )+{\mathsf {w}}_{20}(-\tau )\Big )\nonumber \\&+\,\xi _{yy}\Big (4{\mathsf {w}}_{11}(-\tau )\hbox {e}^{-i\omega _{0}\tau }\nonumber \\&+\,2{\mathsf {w}}_{20}(-\tau )\hbox {e}^{i\omega _{0}\tau }\Big )\bigg ). \end{aligned}$$

(67)

The expression for $g_{21}$ has ${\mathsf {w}}_{11}(0),~{\mathsf {w}}_{11}(-\tau ),~{\mathsf {w}}_{20}(0)$ and ${\mathsf {w}}_{20}(-\tau )$ which need to be evaluated. Now, for $\theta \in [-\tau ,0)$

$$\begin{aligned} H(z,{\bar{z}},\theta )&= -2\text {Re}\big ({\bar{q}}^{*}(0)\cdot {\mathcal {F}}_{0} q(\theta )\big )\\&= -2 \text {Re} \big (g(z,{\bar{z}})q(\theta )\big )\\&= -\left( g_{20}\frac{z^{2}}{2} + g_{11}z{\bar{z}} + g_{02}\frac{{\bar{z}}^{2}}{2}+\cdots \right) q(\theta )\\&\quad -\left( {\bar{g}}_{20}\frac{{\bar{z}}^{2}}{2} + {\bar{g}}_{11}z{\bar{z}} + {\bar{g}}_{02}\frac{z^{2}}{2}+\cdots \right) {\bar{q}}(\theta ). \end{aligned}$$

From (60), we have

$$\begin{aligned} H_{20}(\theta )&= -g_{20}q(\theta )-{\bar{g}}_{02}{\bar{q}}(\theta ),\\ H_{11}(\theta )&= -g_{11}q(\theta )-{\bar{g}}_{11}{\bar{q}}(\theta ). \end{aligned}$$

Using Eqs. (52), (62) and (63), we get

$$\begin{aligned} {\mathsf {w}}^{\prime }_{20}(\theta )&= 2i\omega _{0}{\mathsf {w}}_{20}(\theta ) + g_{20}q(\theta )+ {\bar{g}}_{02}{\bar{q}}(\theta ), \end{aligned}$$

(68)

$$\begin{aligned} {\mathsf {w}}^{\prime }_{11}(\theta )&= g_{11}q(\theta ) + {\bar{g}}_{11}{\bar{q}}(\theta ). \end{aligned}$$

(69)

Solving the differential Eqs. (68) and (69), we obtain

$$\begin{aligned} {\mathsf {w}}_{20}(\theta )&= -\frac{g_{20}}{i\omega _{0}}q(0)\hbox {e}^{i\omega _{0}\theta }\nonumber \\&\quad -\frac{{\bar{g}}_{02}}{3i\omega _{0}}{\bar{q}}(0)\hbox {e}^{-i\omega _{0}\theta } + E_{1}\hbox {e}^{2i\omega _{0}\theta }, \end{aligned}$$

(70)

$$\begin{aligned} {\mathsf {w}}_{11}(\theta )&= \frac{g_{11}}{i\omega _{0}}q(0)\hbox {e}^{i\omega _{0}\theta } - \frac{{\bar{g}}_{11}}{i\omega _{0}}{\bar{q}}(0)\hbox {e}^{-i\omega _{0}\theta } + E_{2}, \end{aligned}$$

(71)

where $E_{1},~E_{2}$ need to be determined. For $H(z,{\bar{z}},0) = -2\text {Re}\big ({\bar{q}}^{*}\cdot {\mathcal {F}}_{0} q(0)\big ) + {\mathcal {F}}_{0}$, we have

$$\begin{aligned} H_{20}(0)&= -g_{20}q(0)-{\bar{g}}_{02}{\bar{q}}(0) \nonumber \\&\quad +2\eta (\xi _{xy} \hbox {e}^{-i\omega _0\tau }+\xi _{yy}\hbox {e}^{-2i\omega _{0}\tau }), \end{aligned}$$

(72)

$$\begin{aligned} H_{11}(0)&= -g_{11}q(0)-{\bar{g}}_{11}{\bar{q}}(0) \nonumber \\&\quad +\eta (\xi _{xy}(\hbox {e}^{i\omega _0\tau }+\hbox {e}^{-i\omega _0\tau })+2\xi _{yy}). \end{aligned}$$

(73)

From Eqs. (52), (62) and (63), we get

$$\begin{aligned}&\eta \xi _{x}{\mathsf {w}}_{20}(0) + \eta \xi _{y}{\mathsf {w}}_{20}(-\tau )-2i\omega _{0}{\mathsf {w}}_{20}(0) = g_{20}q(0)\nonumber \\&\quad +{\bar{g}}_{02}{\bar{q}}(0)-2\eta (\xi _{xy} \hbox {e}^{-i\omega _0\tau }+\xi _{yy}\hbox {e}^{-2i\omega _{0}\tau }), \end{aligned}$$

(74)

$$\begin{aligned}&\eta \xi _{x}{\mathsf {w}}_{11}(0) + \eta \xi _{y}{\mathsf {w}}_{11}(-\tau ) = g_{11}q(0)\nonumber \\&\quad +{\bar{g}}_{11}{\bar{q}}(0) - \eta (\xi _{xy}(\hbox {e}^{i\omega _0\tau }+\hbox {e}^{-i\omega _0\tau })+2\xi _{yy}). \end{aligned}$$

(75)

We find ${\mathsf {w}}_{20}(0),~{\mathsf {w}}_{20}(-\tau ),~{\mathsf {w}}_{11}(0)$ and ${\mathsf {w}}_{11}(-\tau )$ using Eqs. (70) and (71) and substitute in Eqs. (74) and (75) to evaluate $E_{1},~E_{2}$. We finally obtain

$$\begin{aligned} E_{1}&= \frac{\Theta _{1}}{\eta \xi _{x}+\eta \xi _{y}\hbox {e}^{-2i\omega _{0}\tau }-2i\omega _{0}},\quad E_{2} = \frac{\Theta _{2}}{\eta (\xi _{x}+\xi _{y})}, \end{aligned}$$

where

$$\begin{aligned} \Theta _{1} =&(\eta \xi _{x}-2i\omega _{0})\bigg (\frac{g_{20}}{i\omega _{0}} + \frac{{\bar{g}}_{02}}{3i\omega _{0}}\bigg )\\&+\eta \xi _{y}\bigg (\frac{g_{20}}{i\omega _{0}}\hbox {e}^{-i\omega _{0}\tau } + \frac{{\bar{g}}_{02}}{3i\omega _{0}}\hbox {e}^{i\omega _{0}\tau }\bigg )\\&+g_{20}q(0)+{\bar{g}}_{02}{\bar{q}}(0)\\&-2\eta (\xi _{xy} \hbox {e}^{-i\omega _0\tau }+\xi _{yy}\hbox {e}^{-2i\omega _{0}\tau }),\\ \Theta _{2} =&-\eta \xi _{x}\bigg (\frac{g_{11}}{i\omega _{0}}-\frac{{\bar{g}}_{11}}{i\omega _{0}}\bigg )\\&-\eta \xi _{y}\bigg (\frac{g_{11}}{i\omega _{0}}\hbox {e}^{-i\omega _{0}\tau } -\frac{{\bar{g}}_{11}}{i\omega _{0}}\hbox {e}^{i\omega _{0}\tau }\bigg )\\&+g_{11}q(0)+{\bar{g}}_{11}{\bar{q}}(0)\\&-\eta (\xi _{xy}(\hbox {e}^{i\omega _0\tau }+\hbox {e}^{-i\omega _0\tau })+2\xi _{yy}). \end{aligned}$$

Using the above derived quantities, we may find the following expressions that will enable us to analyse the Hopf bifurcation [22]

$$\begin{aligned}&c_{1}(0) = \frac{i}{2\omega _{0}}\left( g_{20}g_{11} - 2|g_{11}|^{2} - \frac{1}{3}|g_{02}|^{2}\right) + \frac{g_{21}}{2}, \end{aligned}$$

(76)

$$\begin{aligned}&\mu _{2} = \frac{-\text {Re}\big (c_{1}(0)\big )}{\alpha ^{\prime }(0)}, \quad \beta _{2} = 2\text {Re}\big (c_{1}(0)\big ), \end{aligned}$$

(77)

$$\begin{aligned}&{\mathcal {P}} = \frac{2\pi }{\omega _0}(1+\epsilon ^2{\mathcal {T}}_2+\text {higher order terms}),\quad \text {where}\nonumber \\&{\mathcal {T}}_2 = -\bigg (\frac{\text {Im}\big (c_1(0)\big ) + \mu _2 \omega ^{\prime }(0)}{\omega _0}\bigg )\quad \text {and}\nonumber \\&\epsilon = \sqrt{\frac{\eta -\eta _c}{\mu _2}}, \end{aligned}$$

(78)

where $g_{20}, g_{11}, g_{02}, g_{21}$ are defined by Eq. (67), and $c_{1}(0)$ is the lyapunov coefficient. The terms

$$\begin{aligned} \alpha ^{\prime }(0)=\text {Re}(\hbox {d}\lambda /\hbox {d}\eta ) \end{aligned}$$

and $\omega ^{\prime }(0)=\text {Im}(\hbox {d}\lambda /\hbox {d}\eta )$ are evaluated at $\eta =\eta _c$. The period of the bifurcating solutions is given by (78), which reduces to $2\pi /\omega _0$ for small values of $|\mu |$. The bifurcating solutions are of the form

$$\begin{aligned} u(t) = \sqrt{\frac{4(\eta -\eta _c)}{\mu _2}} \cos \bigg (\frac{\pi t}{2\tau }\bigg ) + \text {higher order terms}, \end{aligned}$$

for $0\le t \le {\mathcal {P}}$. Therefore, the amplitude of the bifurcating solutions is

$$\begin{aligned} A = \bigg |\sqrt{\frac{4(\eta -\eta _c)}{\mu _2}}\bigg |. \end{aligned}$$

(79)

With the expressions for $\mu _2$ and the Floquet exponent $\beta _2$ at hand, we may characterise the type of Hopf bifurcation and determine the stability of the bifurcating periodic solutions using the following conditions:

• i. The sign of $\mu _2$ determines the type of Hopf bifurcation. The Hopf bifurcation is super-critical if $\mu _2>0$ and sub-critical if $\mu _2<0$.

• ii. The sign of the Floquet exponent, $\beta _2$, determines the asymptotic orbital stability of the bifurcating periodic solutions. The periodic solutions are stable if $\beta _2 < 0$ and unstable if $\beta _2 > 0$.